Resource Allocation Games with Multiple Resource Classes

Abstract

We define and study a resource-allocation game, arising in Media on Demand (MoD) systems where users correspond to self-interested players who choose a MoD server. A server provides both storage and broadcasting needs. Accordingly, the user’s cost function encompasses both positive and negative congestion effects.

A system in our model consists of m identical servers and n users. Each user is associated with a type (class) and should be serviced by a single server. Each user generates one unit of load on the server it is assigned to. The load on the server constitutes one component of the user’s cost. In addition, the service requires an access to an additional resource whose activation-cost is equally shared by all the users of the same class that are assigned to the same server. In MoD systems, the bandwidth required for transmitting a certain media-file corresponds to one unit of load. The storage cost of a media-file on a server is shared by the users requiring its transmission that are serviced by the server.

We provide results with respect to equilibrium existence, computation, convergence and quality. We show that a pure Nash Equilibrium (NE) always exists and best-response dynamics converge in polynomial time. The equilibrium inefficiency is analyzed with respect to the objective of minimizing the maximal cost. We prove that the Price of Anarchy is bounded by m and by the size of the smallest class and that these bounds are tight and almost tight, respectively. For the Price of Stability we show an upper bound of 2, and a lower bound of $2- \frac{1}{m}$. The upper bound is proved by introducing an efficient 2-approximation algorithm for calculating a NE. For two servers we show a tight bound of $\frac{3}{2}$.

A brief-announcement introducing this work was presented in the 8th International Symposium on Algorithmic Game Theory (SAGT), 2015.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Resource allocation problems consider scenarios in which tasks or clients have to be assigned to resources under a set of constraints. Resource allocation applications exist in a variety of fields ranging from production planning to operating systems. Game theoretic considerations have been studied in many resource allocation problems. The game theoretic view assumes that users have strategic considerations acting to maximize their own utility, rather than optimizing a global objective. In resource allocation problems, this means that users choose which resources to use rather than being assigned to resources by a centralized designer. Media streaming is among the most popular services provided over the Internet. The lack of a central authority that controls the users, motivates the analysis of Media on Demand (MoD) services using game theoretic concepts.

Two main approaches exist with respect to the cost function associated with the usage of a resource. One approach considers congestion games in which user’s cost increases with the load on the resource. The other approach considers cost sharing games in which users share the activation-cost of a resource, and thus, user’s cost decreases with the load on the resource. Feldman and Tamir introduced and studied a model in which both considerations apply [4]. In this work we generalize this model further and study games corresponding to systems in which resources have both positive and negative congestion effects, and different users may require different resources. Our work is motivated by Media-on-Demand systems, in which the above cost scheme applies.

A system in our model consists of a set of identical servers. Each user of the system is associated with a type (class) and should be serviced by a single server. Every user generates one unit of load on the server it is assigned to. In addition, the service requires an access to an additional resource whose activation-cost is equally shared by all the users of the same type that are assigned to the server.

A configuration of the system is characterized by an allocation of users to servers. The cost of a user in a given allocation is the sum of two components: the load-cost determined by the total load on his server, and his share in the class activation-cost.

A pure Nash equilibrium (NE) is a configuration in which no individual player can migrate and reduce his cost. We study the multi-class resource model with respect to NE existence, calculation and efficiency. When considering equilibrium inefficiency we use the standard measures of price of anarchy (PoA) [7] and price of stability (PoS) [2]. For the PoA and PoS measures we use an egalitarian objective function, i.e., we measure the maximal cost among users compared with the maximal cost in an optimal allocation. In addition to the theoretical analysis of this model, we present efficient algorithms for finding good stable solutions. The algorithms combine load-balancing ideas used in packing algorithms, such as element-grouping and handling the elements in decreasing-size order, together with ideas used in algorithmic game theory, such as performing a sequence of improving steps in a specific, supervised, order.

Applications: There are several real-world systems that fit the above multi-class resource allocation scenario. In particular, our study is motivated by media-on-demand (MoD) systems. A MoD system (see, e.g., [13, 17]) consists of a large database of media files and a set of servers. The servers provide both storage and broadcasting needs. Each client specifies a media stream request and receives the stream via one of the servers. The server’s bandwidth corresponds to the load resource – each client generates one unit of load on the server. The media-file specifies the client’s class. Each media-file (class) has an activation-cost reflecting the cost of copying the media file from the central database, and storing it in the server’s local memory. The server’s bandwidth (load) is distributed among all its clients, while the class activation-cost is shared among all clients requiring the same media file stream.

Another example is infrastructure-as-a-service (IAAS) in cloud computing. IAAS (see e.g. [10]) is a cloud computing service model which offers computers, either physical or virtual machines. Each client has a task that has to be performed on a machine. In IAAS system, each machine acts as a server. The machine’s network bandwidth corresponds to the load resource and the required software installation for the client’s task specifies the class. The load on the virtual machine affects all the machine’s clients, while the software installation cost is shared among all clients requiring it.

Production planning is another example of a multi-class resource allocation application, arising in computer systems and in many other areas. Consider a set of machines, each having a limited capacity of some physical resource (e.g. quantity of production materials). In addition, hardware specifications allow each machine to produce items of different types, each associated with some configuration set-up or training. The quality of service reduces with the total congestion on the resource. The configuration set-up cost is required for every class on every machine.

1.1 Model and Preliminaries

An instance of the multi-class resource allocation game is defined by a tuple $G = \langle I, M, A, U \rangle$, where I is a set of players, M is a set of servers and A is a set of classes. Let $n=|I|$ and $m=|M|$. Each player belongs to a single class from A, thus, $I= I_1 \cup I_2 \cdot \cdot \cdot \cup \; I_{|A|}$, where all players from $I_k$ belong to class k. For $i \in I$, let $a_i \in A$ denote the class to which player i belongs. The parameter $U \in \mathbb {R}^+$ is the class activation-cost, which is assumed to be uniform for all classes.

An allocation of players to servers is a function $f: I \rightarrow M$. Given an allocation, the load on server j, denoted by $L_j(f)$, is the number of players assigned to j. We denote by $L_{j,k}(f)$ the number of players from $I_k$ assigned to j. When clear in the context we omit f and use $L_j$ and $L_{j,k}$, respectively.

The cost of a player i in an allocation f consists of two components: the load on the server the player is assigned to, and the player’s share in the class activation-cost. The class activation-cost is shared evenly among the players from this class serviced by the server. Formally, $c_f(i) = L_{f(i)} + \frac{U}{L_{f(i),a_i}}$.

A step by a player i with respect to an allocation f is a unilateral deviation of i, i.e., a change of f to $f'$ such that $\forall _{\ell \ne i}f'(\ell )=f(\ell )$ and $f'(i)\ne f(i)$. An improving step of player i with respect to an allocation f is a step which reduces the player’s cost, that is, $c_{f'}(i)<c_f(i)$. An allocation f is said to be a Pure Nash Equilibrium (NE) if no player has an improving step, i.e., for each player i and for every allocation $f'$ such that $\forall _{\ell \ne i}f'(\ell )=f(\ell )$ it holds $c_f(i)\le c_{f'}(i)$.

Best-Response Dynamics (BRD) is a local search method where in each step some player is chosen and plays its best improving step, given the strategies of the other players.

It is well known that decentralized decision-making may lead to sub-optimal solutions from the point of view of society as a whole. We quantify the inefficiency incurred due to self-interested behavior according to the PoA and PoS measures. The PoA is the worst-case inefficiency of a NE, while the PoS measures the best-case inefficiency of a NE. Formally, let $\mathcal {G}$ be a family of games, and let $G \in \mathcal {G}$ be some game in this family. Let NE(G) be the set of Nash equilibria of the game G, let val(f) be the social cost of a NE f with respect to some objective function, and let OPT(G) be the value of an optimal solution. If $NE(G)\ne \emptyset$, then $PoA(G) = \max _{f\in NE(G)} \frac{val(f)}{OPT(G)},$ and $PoA(\mathcal {G}) = Sup_{G \in \mathcal {G}}PoA(G).$ Similarly, $PoS(G) = \min _{f\in NE(G)} \frac{val(f)}{OPT(G)},$ and $PoS(\mathcal {G}) = Sup_{G \in \mathcal {G}}PoS(G).$

In this paper, we evaluate the performance of a solution with respect to the objective of minimizing the maximal cost among the players; that is, given an allocation f, the social cost of f is given by $c_{max}(f)=\max _{i \in I}c_f(i).$

1.2 Related Work

The study of resource allocation games with multiple resource classes combines challenges arising in the two classical problems of multi-dimensional packing and resource-sharing games. Class-constrained multiple knapsack (CCMK) [13, 14] is the variant of a centralized packing problem closest to our model. In CCMK each item has a type, a size and a value. Each knapsack has in addition to its size, a number of compartments which define the number of different item types it can contain. The optimization goal in CCMK is to maximize the total value of items packed into the knapsacks. The problem is NP-hard even with unit size and unit profit items. In our game, as in [13], all items have unit size. The main difference between the models is that servers in our game have no limited capacity, thus a placement that packs all the items always exists. The load-component in our cost-function provides the incentive to avoid highly loaded servers and to balance the load among the servers.

In cost-sharing games, a possibly unlimited amount of resources is available. The activation of a resource is associated with a cost which is shared among the players using it. A well-studied cost sharing game is network design. Nash equilibrium always exists in network design games and the price of stability with respect to the total-cost objective function is H(k), where k is the number of players and H is the harmonic function [1]. In cost sharing games, congestion has a positive effect, and players have an incentive to use resources that are used by others. Other related work deal with congestion games, in which congestion has a negative effect, and players wish to avoid loaded resources. In congestion games, the cost of using a resource increases with the load on it. Congestion games were first introduced in [11], and arise naturally in network routing (see e.g. [12]), and job-scheduling [16].

In [4], Feldman and Tamir studied a model incorporating both positive and negative congestion effects. In their model, a job-scheduling setting with unlimited set of identical machines is studied. Each job j has a length $p_j$ and each machine has a fixed activation cost U. The set of players corresponds to the set of individual jobs and the action space of each player j is the set of machines. The cost function of job j in a given schedule is composed of the load on the job’s machine and the job’s share in the machine’s activation cost. For the uniform sharing rule in which the machine’s activation cost is uniformly shared between the jobs allocated to it, a NE may not exists. For the proportional sharing rule in which the share of a job in the machine’s activation cost is proportional to its length, the price of anarchy with respect to the makespan can be arbitrarily high. The price of stability is tightly bounded by 5 / 4. This model of conflicting congestion effects was studied further in [3], where equilibrium inefficiency was studied with respect to the total-cost objective, and in [5, 8], where closer analysis of the PoA and PoS is provided. In this work, we generalize the model of conflicting congestion effects, by allowing several resources on a single server. This generalization provides one additional step in modeling real-world systems using game theoretical tools.

1.3 Our Results

We provide answers to the basic questions regarding resource allocation games with multiple resource classes. Namely, equilibrium existence, convergence, calculation and efficiency. We present polynomial-time algorithms for calculating a stable solution whose cost almost matches the bound for the PoS.

We prove that a NE exists for any instance of the game by presenting an exact potential function for the game. By analyzing this function we conclude that any application of better-response dynamics converges to a NE within time $O(n^4)$. The equilibrium inefficiency is analyzed with respect to the objective of minimizing the maximal cost among the players. We first provide several lower-bounds on the optimal solution, and then combine them to present a tight bound of m for the PoA. An additional almost tight bound depends on the size of a least popular class. Let $\theta = \min _{1 \le k \le |A|} |I_k|$. We show that $PoA \le \theta + 1$, and a game for which $PoA \ge \theta -\epsilon$ exists.

We show that for any number of servers, there exists a game for which the PoS is $2-\frac{1}{m}$. This lower bound is almost matched - we present a polynomial time algorithm that constructs a NE with max-cost at most twice the optimum. For two servers, we present a matching upper bound: that is - a polynomial time algorithm that constructs a NE with max-cost at most 3/2 times the optimum.

Our algorithms for finding a good stable assignment are based on two new methods:

• 1. While all the players create the same unit-load on the servers, our algorithms group the players into sets, based on their classes. An initial assignment is found by considering these sets as an instance of a multiple-knapsack packing problem with arbitrary-size elements. This method enables analysis of the assignment using known packing techniques and their properties.

• 2. The stabilization phase that follows the initial assignment consists of iterations in which the algorithm may reassign complete sets of players, or perform a supervised sequence of improving steps. The sequence is initiated by one player i, and is then limited to players of i’s class who may benefit from following i by performing exactly the same migration. Analyzing the configuration after each improving step is complex; however, it is possible to analyze the effect of each supervised sequence of improving steps on the potential function and to bound the cost of an assignment derived by this method.

It is interesting to compare our results with the model studied in [4], in which all users belong to a single class, and the number of servers is unlimited. In our model, it is not relevant to study instances with unlimited number of servers, since players from different classes have only negative effect on the cost of each other, thus, different classes will never share a server, and the problem reduces to a single-class problem. The PoA is not bounded by a constant in both models, however, in our model it is bounded by m – the number of servers and $\theta +1$ - where $\theta$ is the size of the smallest class, while in [4] it is bounded by $\frac{1+U}{2\sqrt{U}}$ – which is a function of the class (machine) activation-cost.

A tight bound of $\frac{5}{4}$ for the PoS is shown in [4]. Our bound on the PoS implies that increasing the number of classes from 1 to arbitrary |A| only slightly increases the PoS - from $\frac{5}{4}$ to 2. Thus, in both models the PoS is a relatively small constant.

Due to space constraints, some proofs as well as the $\frac{3}{2}$-approximation algorithm for two servers are omitted from this extended abstract.

2 Equilibrium Existence and BRD Convergence

We show that the multi-class resource allocation game is a potential game [9]. This implies that a series of improving steps always converges to a NE. Given an allocation f, consider the following potential function,

$$\begin{aligned} \varPhi (f)= \sum _{1\le j\le m} U \cdot (H_{L_{j,1}(f)}+H_{L_{j,2}(f)}+\ldots +H_{L_{j,|A|}(f)}) + \frac{L_{j}(f)^2}{2}, \end{aligned}$$

(1)

where $H_k$ is the $k^{th}$ harmonic number, that is, $H_0=0$, and $H_k=1+\frac{1}{2}+\ldots +\frac{1}{k}$.

Theorem 1

$\varPhi (f)$ is an exact potential function.

Thus, BRD converges and a NE exists. Next, we show that BRD converges to a NE in polynomial time. Specifically,

Theorem 2

For every instance G, BRD converges to a NE within $O(n^4)$ steps.

Proof

Consider the potential function defined in (1), since $H_k \le k$, and for all $1\le j\le m$ and $1 \le i \le |A|$, $L_{j,i} \le L_j$, the left addend of the sum can be bounded as follows,

$$ \sum _{1\le j\le m}U \cdot (H_{L_{j,1}(f)}+H_{L_{j,2}(f)}+\ldots +H_{L_{j,|A|}(f)}) \le \sum _{1\le j\le m} U \cdot L_j = U \cdot n. $$

The right addend of the potential function is trivially bounded by $\frac{n^2}{2}$ and we conclude that for all f, $\varPhi (f)\le U\cdot n + \frac{n^2}{2}$. Consider an improving step by some player i. Since the potential function is an exact potential function, the difference in the potential is exactly the improvement in i’s cost. That is $\varDelta \varPhi = c_{f}(i)-c_{f'}(i) = \varDelta c^\ell (i) + \varDelta c^s(i)$. The difference in the load is an integer while the difference in the activation-cost is $\frac{U}{L_{f(i),a}(f)+1} - \frac{U}{L_{f(i),a}(f)}$ where a is the class of i. Since $L_{j,a}$ is an integer and $L_{j,a}\le n$ for all a, j, the denominator of the activation-cost diff is at most $n(n-1)$. Thus, an improving step reduces the potential by at least $\frac{1}{n(n-1)}$, that is, $\varDelta \varPhi \ge \frac{1}{n(n-1)}$. Since the potential is always positive, BRD converges in at most $\frac{max_f\varPhi (f)}{min\varDelta \varPhi } = \frac{O(n^2)}{\varOmega (\frac{1}{n^2})} = O(n^4)$ steps.    $\square$

3 Equilibrium Inefficiency - Price of Anarchy

In this section we study the inefficiency caused due to strategic behavior, as quantified by the Price of Anarchy (PoA). We evaluate the performance of a solution with respect to the objective of minimizing the highest cost among all the players; that is, given an allocation f, the social cost of f is given by $c_{max}(f)=\max _{i \in I}c_f(i).$ For a server j, define the cost of j as the maximal cost among players allocated to j. That is, $c_f(j)=\max _{f(i)=j}c_f(i)$. Let OPT denote the maximal cost of a player in an optimal assignment minimizing the maximal cost. Some of our bounds are a function of $\theta = \min _{1 \le k \le |A|} |I_k|$, the size of a least popular class. For simplicity, we use $\theta$ to denote both the class and its size. We prove a tight bound of m for the PoA, and an almost tight bound of $\theta +1$, implying that the existence of a single small class guarantees low PoA. We start with the lower bound based on the number of servers. Specifically, we show that the PoA may be $m-\epsilon$ for any $\epsilon >0$.

Theorem 3

For any $m\ge 2$ servers and any $\epsilon > 0$, there exists an instance G for which $PoA(G)> m-\epsilon$.

Proof

Let k be an integer such that $\frac{1}{m^k} \le \epsilon$. Consider an instance G with $n=m^{k+3}$ players, $U=n$ and a single class. Let f be the allocation in which all the players are allocated to a single server. The cost of each player in f is $c_1 = n+1 = m^{k+3}+1$. A player migrating to an empty server would have a cost of $1+U = n+1 = c_1$. Thus, f is stable. On the other hand, consider an allocation $f'$ in which the players are equally distributed between the servers. Each server is allocated with $m^{k+2}$ players, each having cost $c'_1 = m^{k+2} + m$. Therefore,

$$PoA(G) \ge \frac{c_1}{c'_1} = \frac{m^{k+3}+1}{m^{k+2}+m} > m - \frac{1}{m^k} \ge m - \epsilon .$$

   $\square$

In order to prove the upper bound, we first provide several lower bounds on OPT. Let $d = \max (\frac{n}{m}, \sqrt{U})$.

Claim 4

$OPT \ge \max (\frac{n+\frac{U}{\theta }}{m}, \left\lceil \frac{n}{m} \right\rceil , \frac{U}{\theta }, 2\sqrt{U}, d + \frac{U}{d})$.

When $\theta \le \frac{n}{m}$, we can bound OPT further as a function of $\theta$ and U.

Claim 5

If $\theta \le \frac{n}{m}$, then $OPT \ge \theta + \frac{U}{\theta }$.

Theorem 6

For any resource allocation game G with multiple resource classes, $PoA(G) \le m$.

Proof

Let f be a stable allocation, and let $j_1$ be a server such that $c_f(j_1)=c_{max}(f)$. Let i be a class with minimal group-size on $j_1$. Thus, $c_1 = L_1 + \frac{U}{L_{j_1,i}}$ is the maximal cost of a player in f. We show that $c_1 \le n + \frac{U}{\theta }$. By Claim 4, this implies that the PoA is at most m.

If $j_1$ is the only server that services players from class i then $L_{j_1,i} \ge \theta$. Thus, $c_1 \le n + \frac{U}{\theta }$.

If players from class i are assigned in f to more than a single server, let $j_2\ne j_1$ be a least loaded server that services class-i players in f. Denote $\ell _1=L_{j_1,i}$ and $\ell _2=L_{j_2,i}$. The cost of a class-i player on $j_2$ is $c_2 = L_2 + \frac{U}{\ell _2}$. Since f is stable, a migration of an i-player from $j_1$ to $j_2$ is not beneficial. Combining the fact that $c_2 \le c_1$, we get

$$\begin{aligned} L_2+ \frac{U}{\ell _2} \le L_1 + \frac{U}{\ell _1} \le L_2+1+\frac{U}{\ell _2+1}. \end{aligned}$$

(2)

Equation (2) implies that $U \le \ell _2(\ell _2 + 1)$.

On the other hand, a migration of an i-player from $j_2$ to $j_1$ is also not beneficial. Thus, $L_2 + \frac{U}{\ell _2} \le L_1 + 1 + \frac{U}{\ell _1+1}$ and we get

$$\begin{aligned} L_2 + 1 + \frac{U}{\ell _2 + 1} \le L_2 + 1 + \frac{U}{\ell _2} \le L_1 + 2 + \frac{U}{\ell _1+1}. \end{aligned}$$

(3)

Combining Eqs. (2) and (3), we conclude that

$$\begin{aligned} U \le \min (2\ell _1(\ell _1 + 1), \ell _2(\ell _2 + 1)). \end{aligned}$$

(4)

If class-i players are allocated to exactly two servers, the analysis is technically involved and is omitted due to space constraints.

If class-i players are allocated to more than two servers then since $j_2$ is the least loaded server with class-i players, except possibly $j_1$, we have $\ell _2 \le L_2 < \frac{n}{2}$ and $c_1 \le L_2+1+\frac{U}{\ell _2+1} \le L_2+1+\ell _2 < n$. Thus, for every possible allocation of class-i players, we showed that $c_1 \le n + \frac{U}{\theta } \le m\cdot OPT$.    $\square$

Our next bound depends on the size of the smallest class. We start with the upper bound.

Theorem 7

For any resource allocation game G with multiple resource classes, and any $\epsilon > 0$, $PoA(G) \le \theta + 1$.

Proof

Let f be a stable allocation, and let j be a server such that $c_f(j)=c_{max}(f)$. Let $L_1$ be the load on j and let $L_0$ be the load on the least loaded server in f. If $L_1 \le \left\lceil \frac{n}{m} \right\rceil$ then $c_{max}(f)\le \left\lceil \frac{n}{m} \right\rceil +U$. Otherwise, by the pigeonhole principle, $L_0 < \left\lceil \frac{n}{m} \right\rceil$. Since f is stable, $c_f(j)\le L_0 + U +1 \le \left\lceil \frac{n}{m} \right\rceil +U$. By Claim 4, $OPT\ge \max (\left\lceil \frac{n}{m} \right\rceil , \frac{U}{\theta }$). Thus, $PoA \le \frac{\left\lceil \frac{n}{m} \right\rceil +U}{OPT} \le \theta + 1$.    $\square$

This bound is almost matched.

Theorem 8

For any $\theta \ge 1$ and $\epsilon > 0$, there exists an instance G for which $PoA(G)> \theta -\epsilon$.

Proof

Given $\epsilon$ and $\theta$, let U be a constant such that $\epsilon \ge \frac{\theta ^3}{U+\theta ^2}$. Consider an instance with $n=U(1-\frac{1}{\theta })$ players from two classes, where $|I_1|=\theta$ and $|I_2|=n-\theta$. Let $m=n/\theta$. Note that U can be selected such that n and m are integers.

Let f be the allocation in which all the players are allocated to a single server. Players of $I_1$ have the max-cost in f, which is $c_1 = n+ \frac{U}{\theta }$. A player migrating to an empty server would have a cost of $U+1$. Since $U=n+\frac{U}{\theta }= c_1$, such a migration is not beneficial. Thus, f is stable. On the other hand, consider an allocation $f'$ in which the players are equally distributed between the servers, each server accommodating $\theta$ players from the same class. All the players have cost $c' = \theta + \frac{U}{\theta }$. Therefore,

$$PoA(G) \ge \frac{c_1}{c'} = \frac{n + \frac{U}{\theta }}{\theta + \frac{U}{\theta }}= \frac{U}{\theta + \frac{U}{\theta }}\ge \theta -\epsilon .$$

   $\square$

4 Equilibrium Inefficiency - Price of Stability

In this section we analyze the Price of Stability with respect to the max-cost objective. For systems with arbitrary number of servers, m, we show that $2-\frac{1}{m}\le PoS\le 2$. For two servers, the lower bound is tight. Specifically, we present an $O(|A| \log |A| + n)$-time algorithm for calculating a NE assignment that achieves max-cost at most $\frac{3}{2} OPT$. The algorithm is omitted from this extended abstract.

Our main result is an algorithm for arbitrary number of servers. The algorithm combines load-balancing ideas used in packing algorithms, such as element-grouping and handling of elements in decreasing-size order, together with ideas used in algorithmic game theory, such as performing BRD in a specific order.

We begin with a lower bound of $2-\frac{1}{m}$.

Theorem 9

For every $\epsilon > 0$ and a system with $m \ge 2$ servers, there exists an instance G such that $PoS(G) > 2-\frac{1}{m}-\epsilon$.

Proof

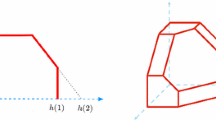
Given $\epsilon > 0$, let $n = \max (\left\lceil \frac{4(m-1)}{\epsilon } \right\rceil , 4m)$. Consider an instance G with $m\ge 2$ servers, and $A=\{a_1,a_2\}$, where a single player belongs to class $a_1$ and all other players belong to class $a_2$. Let $U=\frac{n-1}{m-1}-2$. A possible allocation for this instance is illustrated in Fig. 1(a). The players who belong to $a_2$ are split evenly among $m-1$ servers and the player of $a_1$ is solely allocated to the remaining server. The maximal cost for this allocation is for players who belong to $a_2$ and is $c_1=\frac{n-1}{m-1}+1-\frac{2(m-1)}{n-1}$. The only NE (up to server renaming) for this instance is illustrated in Fig. 1(b). The player of $a_1$ has the maximal cost for this allocation $c_2=\frac{n}{m}+\frac{n-1}{m-1}-2$. A player of $a_2$ has cost at most $c_3=\frac{n}{m}+\frac{U}{\frac{n}{m}-1}$, a player of $a_2$ migrating to a different server would have cost at least $c_4=\frac{n}{m}+1+\frac{U}{\frac{n}{m}+1}$. Since $n\ge 4m$ and $m\ge 2$, $\frac{n-1}{m-1}-1<\frac{n}{m}$ and $U<\frac{n}{m}-1$. Thus, $c_3<c_4$ and the allocation is stable. We conclude that the PoS is at least

$$\frac{c_2}{c_1}=\frac{\frac{n}{m}+\frac{n-1}{m-1}-2}{\frac{n-1}{m-1}+1-\frac{2(m-1)}{n-1}}\ge \frac{\frac{n}{m}+\frac{n-1}{m-1}-2}{\frac{n-1}{m-1}+1} \ge 2-\frac{1}{m}-\frac{4(m-1)}{n}\ge 2-\frac{1}{m}-\epsilon .$$

   $\square$

Fig. 1.

(a) An optimal non-stable allocation, (b) A best NE.

4.1 An Algorithm for Multiple Servers

For a system with an arbitrary number of servers, we present a polynomial time algorithm that constructs a NE with max-cost at most 2OPT. We use the term big classes when referring to classes with at least $\frac{n}{m}$ players. Similar to the case $m=2$, Algorithm 1, given below, assigns complete classes to servers while only splitting big classes. This initial assignment is similar to Longest Processing Time (LPT) algorithm for job scheduling [6], that is, it assigns the sets greedily, in non-increasing order, on a least loaded server. If the resulting assignment is not stable, a stabilization phase is performed. This phase consists of migrations of complete classes or sequences of supervised improving steps. The improvement steps are in ‘Follow-a-leader’ phases. That is, once one member of a class performs a beneficial migration, an identical migration is considered for other members of his class. While it is complex to analyze the change in the social cost of arbitrary sequence of improving steps, we are able to analyze it for this structured stabilization phase. Recall that $d = \max (\frac{n}{m}, \sqrt{U})$.

Let f denote the allocation produced in step 4. We start by characterizing f and show that $c_{max}(f)<2OPT$. We then consider the case that f is not stable and the stabilization phase is applied. We show that this phase is guaranteed to converge to a NE allocation $f'$ for which $c_{max}(f')< 2OPT$. We first characterize some cases in which any NE $f_0$ fulfills $c_{max}(f_0) < 2OPT$, and then analyze the stabilization phase for the remaining cases.

Claim 10

The maximal load on a server in the allocation f is at most $2d-1$.

Proof

Assume by contradiction that there is a server s with load at least 2d. Step 2 guarantees that the maximal set-size is at most $2d-1$. Thus, there are at least two different sets allocated to s. Let $\varGamma$ be the first set allocated to s that increases the load beyond $2d-1$. Let $\ell$ be the load on s before $\varGamma$ is added. Since the sets are ordered by decreasing order of their sizes, $\varGamma \le \ell$. If $\ell \ge \frac{n}{m}$ then by the pigeonhole principle there is a server $s_0$ such that $L_{s_0}<\frac{n}{m}$, contradicting the assignment of $\varGamma$ to s. If $\ell < \frac{n}{m}$ then $|\varGamma |+\ell \le 2\ell < \frac{2n}{m} \le 2d$, contradicting the assumption that s gets load at least 2d.    $\square$

Lemma 11

$c_{max}(f) < 2OPT$.

Proof

Consider a server s such that $c_{max}(f) = c_f(s)$. By Claim 10 the maximal load on s is at most $2d-1$. If all the players in s belong to the same class, $c_f(s)\le 2d-1 + \frac{U}{d}< 2d+\frac{U}{d}$. By Claim 4, $OPT\ge d+\frac{U}{d}$. Thus, $c_{max}(f) < 2OPT$. Let $\theta _0$ be the last set assigned to s, if s is assigned with players of different classes, then $\theta _0 < \frac{n}{m}$ since the sets are assigned by LPT order. By the pigeonhole principal, the load on s is at most $\frac{n}{m}+\theta _0$. Thus, $c_f(s) \le \frac{n}{m} + \theta _0 + \frac{U}{\theta _0}$. Since $\theta \le \theta _0 \le \frac{n}{m}$ and $x + \frac{U}{x}$ is a convex function, using Claims 4 and 5, we conclude $\theta _0 + \frac{U}{\theta _0} \le \max (\theta + \frac{U}{\theta }, \frac{n}{m} + \frac{Um}{n})\le OPT$ and $c_f(s) < 2OPT$.    $\square$

Next, we show the stabilization phase converges to a stable assignment. The proof of the following claim is based on analyzing the change in the potential function $\varPhi (f)$ defined in (1). We show that every iteration of Step 1 of Algorithm 2 reduces the potential. By Theorem 1, this is valid also for Step 2.

Claim 12

The stabilization phase converges to a NE.

We turn to analyze the cost of the stable assignment $f'$ produced by the stabilization phase. For some cases, a 2-ratio can be shown for any stable assignment.

Lemma 13

If $U\le \frac{n}{m}$ or $\frac{n}{m}<U<4$ or $\theta = 1$, then for any NE $f'$ it holds that $c_{max}(f')\le 2OPT$.

For the remaining cases, we analyze the outcome of the stabilization phase. We use below known properties of assignment produced by LPT algorithm.

Claim 14

If f is not stable then $U < 2d$.

Proof

By Claim 10, the maximal load on a server in f is at most $2d-1$. Let i be a player in server $s_1$ with a beneficial move to $s_2$. The load difference between $s_1$ and $s_2$ is at most $2d-1$. The big classes are equally distributed in Step 2 to sets of size at least d. Since $d\ge \frac{n}{m}$ and the sets are allocated in non-increasing order of size, servers with a set of a big class are only assigned players of that class. Thus, since $d \ge \sqrt{U}$, players of big classes can only have a beneficial move to servers not servicing the same class. Players of small classes are all in the same set generated in Step 1 and are all allocated to the same server. Obviously, such players can only have a beneficial move to a server not assigned with their class. Let $\varGamma$ be the last set assigned to $s_1$ in Step 4. Since the sets are assigned in non-increasing order of size, $L_1-L_2 < |\varGamma |$ and the cost of i prior to the improving step is at most $c_1=L_{1} + \frac{U}{|\varGamma |}$. The cost after the step is $c_2=L_{2}+1+U$. Since $c_2 < c_1$ we have $L_{2}+1+U < L_{1} + \frac{U}{|\varGamma |}$. Thus, $U(\frac{|\varGamma |-1}{|\varGamma |}) < L_1-L_2-1 \le |\varGamma |-1$ and $U\le |\varGamma |\le 2d-1$.    $\square$

Lemma 15

If $U\ge 4$ and $\theta > 1$, then Step 2 of the stabilization phase results in an allocation with at least two players in any class allocated to a server.

Lemma 16

The maximal load on a server in the allocation $f'$ is at most $2d-1$.

We summarize with the following Theorem.

Theorem 17

Algorithm 1 produces a NE assignment with max-cost at most 2OPT.

Proof

If the allocation f generated in Step 3 is stable then by Lemma 11 its max-cost is at most 2OPT. If f is not stable, and $\theta = 1$ or $U\le \frac{n}{m}$ or $\frac{n}{m}<U<4$, then by Lemma 13, any NE has max-cost at most 2OPT. If f is not stable, $\theta > 1$, $U>\frac{n}{m}$ and $U\ge 4$ then by Claim 12 and Lemma 15, the stabilization phase converges to a stable allocation $f'$ in which the smallest set on each server is of size at least 2. Assume by contradiction that $c_{max}(f') > 2OPT$. Let s be a server such that $c_{f'}(s) > 2OPT$. The cost of s is at most $L_{f'}(s) + \frac{U}{2}$. Using Claim 14 we have $U<2d$ thus $c_{f'}(s)<L_{f'}(s) + d$ and $L_{f'}(s) > d$. If there is a single class allocated to s then $c_{f'}(s) \le L_{f'}(s) + \frac{2d}{L_{f'}(s)}$. By Lemma 16, $L_{f'}(s)< 2d$ and $c_{f'}(s)<2d$. If there are multiple classes allocated to s then by Lemma 15 the smallest set of a players $\varGamma$ who belong to the same class on s is at least 2. Since $\varGamma$ was not moved by Step (1) of the stabilization phase, we conclude $c_{f'}(s) \le \frac{n}{m}-1 +|\varGamma | +\frac{U}{|\varGamma |}\le d-1+|\varGamma |+\frac{U}{|\varGamma |}$. Since $2\le |\varGamma | \le \frac{n}{m}$ we have $|\varGamma |+\frac{U}{\varGamma } \le \max (2+\frac{U}{2}, \frac{n}{m} + \frac{Um}{n}\le d+\frac{U}{d})$. Claim 4 implies that $2OPT \ge 2d+\frac{2U}{d}$ and also $2d+\frac{U}{2d}\ge d-1+|\varGamma |+\frac{U}{|\varGamma |}$. Finally, since $2d+\frac{2U}{d}\ge 2d+\frac{U}{2d}$, we get $c_{max}{f'}(s) \le 2OPT$.    $\square$

5 Conclusions and Open Problems

We studied a resource-allocation game with multiple resource classes in which user’s cost function encompasses both negative and positive, class-dependent, congestion effects. Our study of the game reveals that even for the basic model of unit-load players and identical servers, the equilibrium inefficiency may by very high. On the other hand, an assignment whose cost is at most twice the optimum exists and can be calculated in poly-time. We list below some open problems and possible directions for future work.

• 1. Heterogeneous systems: our work considers systems with identical servers and unit-load requirements. One possible generalization is to study systems with unrelated servers and/or non-identical load requirements. In the classic load balancing game, there is a significant difference between the results regarding related and unrelated systems. It would be interesting to study the corresponding differences in the multi-class model.

• 2. Players with class preferences or with multiple classes: In our work players belong to a single class. In a possible generalization of this game (studied in [15] for the centralized model), a player may belong to several classes and has preferences regarding his class. This scenario fits for example MoD systems in which a client is ready to see one of several movies, and provides his preferences for broadcast. In the corresponding game, the utility of a player depends also on the class to which it is assigned. Another direction is to study systems in which a player requires more than a single resource for his processing. Thus, a player may belong to multiple classes and needs to pay his share in the activation cost of all the resources he needs.

• 3. We calculated inefficiency with respect to the max-cost objective function. Future work could also consider other objective functions such as sum-cost.

• 4. BRD convergence time: We have shown that BRD converges within an upper bound of $O(n^4)$ steps. A lower bound of $\varOmega (n\log n)$ steps follows from the analysis in [4] for a single class. Closing the gap and providing a tight bound for BRD convergence time remains open.

• 5. Strong Equilibrium: In a work in progress we have shown that a SE may not exist for $U>2$, while for $U=0$ a SE always exist. The existence of SE for $0<U\le 2$ is an open question. Characterizing conditions in which an SE exists and analyzing SE inefficiency are additional open directions.

• 6. Capacitated Model: We assumed that servers have unlimited capacity. Studying the capacitated game, in which servers have limited storage and/or limited load capacities arise new challenges.