Self-organizing Neural Network for Adaptive Operator Selection in Evolutionary Search

Abstract

Evolutionary Algorithm is a well-known meta-heuristics para-digm capable of providing high-quality solutions to computationally hard problems. As with the other meta-heuristics, its performance is often attributed to appropriate design choices such as the choice of crossover operators and some other parameters. In this chapter, we propose a continuous state Markov Decision Process model to select crossover operators based on the states during evolutionary search. We propose to find the operator selection policy efficiently using a self-organizing neural network, which is trained offline using randomly selected training samples. The trained neural network is then verified on test instances not used for generating the training samples. We evaluate the efficacy and robustness of our proposed approach with benchmark instances of Quadratic Assignment Problem.

This work is funded by the National Research Foundation, Singapore under its Corp Lab @ University scheme.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Evolutionary algorithms (EAs) such as genetic algorithm (GA) and memetic algorithm (MA) have been widely used for solving NP-hard problems [8, 10, 21]. Using EA, a population of chromosomes representing the candidate solutions to an NP-hard problem are evolved over a number of generations. The aim of the search process is to optimize some objective value. These evolutionary operators constitute the algorithmic core of the evolutionary search (ES). Therefore, the quality of the evolutionary operators is critical for the performance of EAs [5].

Many genetic operators are known, and the applicability of these operators vary across problems. And this is also true even among different instances in the same problem [4]. The success of an evolutionary operator depends (among other things) on the characteristics of the fitness landscape of the problem. This information, however, is usually not readily available. Although the literature might provide comparisons between operators on certain problem instances, an evolutionary search algorithm designer is left with a difficult choice of operator selection when designing an evolutionary search algorithm for a new problem. These technical choices quite often lead to the design of ad-hoc methods to solve specific problem instances.

Automated tuning algorithms [3, 15] can be used to adjust parameters of evolutionary search prior to testing it on new problems. This does not, however, exploit the fact that the usefulness of the operators often changes during the evolutionary search. Besides, dependencies between operators can exist and the interaction of multiple operators might lead to better results than when used alone. During the search for a solution to the problem, the application rates of the variation operators can be controlled using recent performance of the operators. Such methods are categorically referred to as Adaptive Operator Selection (AOS) [7]. At each iteration, AOS provides an adaptive mechanism for selecting suitable variation operators during the evolutionary search. Recent works [12, 19] have proposed such adaptive mechanisms for general evolutionary search with possibly many variation operators whose behavior may be unknown, giving rise to uncertainty.

Against this backdrop, we propose a formulation of a Markov Decision Process (MDP) [23] for selecting crossover operators adaptively. Uncertainty over the outcomes of applying a certain crossover operator suggests that MDP can be an alternative approach for performing AOS. Furthermore, MDP uses concepts of states and transitions, which is in line with the fact that the best choice of the operator is very much dependent on, among others, the multi-modality of the fitness landscape and the diversity levels of the population.

We claim the following contributions for this chapter.

• 1. We formulate a MDP with continuous states and discrete actions for AOS with discrete action space. Decisions are made in discrete time. The state features are generic in that they are problem-independent, i.e., they represent common features found in most ES methods for solving optimization problems.

• 2. We proposed the use of a self-organizing neural network within such a MDP. In this work, our self-organizing neural network is trained offline using training samples of problem instances to discover action policies.

• 3. We compare and contrast the proposed neural network approach to several benchmark AOS methods on QAP instances. Results of our experiments show our approach have the best performance outcome for the optimization of QAP instances using evolutionary search.

This chapter continues with Sect. 2 where the related works are surveyed. Section 3 formulates AOS as MDP with continuous states and discrete actions. Components of the MDP and our proposed neural network approach are also described. The experiments and the results are presented in Sect. 5. Section 6 concludes and suggests some extensions to this work.

2 Related Works

Reactive Tabu Search (RTS) [2] is a state-based adaptive search method. The tabu list length is adjusted based on whether or not repeated solutions appear or a new best-so-far solution is found. Enhancement to the original RTS [1] features a Markov Decision Process (MDP) model with continuous states. The states include among others the current objective function value.

In evolutionary computing context, reinforcement learning (RL) has been used to adapt the step size in $(1+1)$ evolutionary strategy [22] while solving continuous optimization problem. Furthermore, reinforcement learning has also been used to adapt crossover probability, mutation probability, and population size based on some continuous states including best fitness, mean fitness, standard deviation, breeding success number, average distance from the best, number of evaluations, and fitness growth [9].

While these works deal with the adaptation of numerical parameters, more recently, a discrete-state RL has been proposed to deal with the adaptation of categorical parameters [14] in the context of memetic algorithm. Specifically, the crossover operator is the parameter being adapted.

This work differs from the above works in two ways. Firstly, we propose the use of continuous state features for learning action policies used for AOS. Secondly, we learn the action policies offline using a self-organizing neural network. This is in line with the spirit of [13] which found the advantage of offline-tuning the parameters of an algorithm for online adaption.

3 Adaptive Operator Selection as Markov Decision Process

Adaptive Operator Selection (AOS) is used in several context. In [18], AOS is employed in the context of multi-objective evolutionary algorithms. In [17] and [29], AOS is used to select local search operators and meta-heuristics algorithms, respectively. In this chapter, AOS seeks out crossover operators best suited to the current stage of evolutionary search.

At times, a crossover operator can degrade the overall quality of a population in the immediate steps but may lead to a global optimum eventually. Therefore, it is essential to choose the crossover operators strategically to optimize the cumulative reward over a sequence of heuristic search. To employ the exploratory operators at the right stage of the search, we propose to model AOS as a markov decision process (MDP) with continuous states and discrete actions.

We define such a MDP as a 5-tuple $<\mathbf{S},\mathbf{A},T,R,\gamma>$ [30] where

• $\mathbf S$ is the set of states, also known as the state space

• $\mathbf A$ is a finite set of action choices, also known as the action space

• $T:S \times A \times S$ is the transition function specifying the probability of going from state $s_1$ to state $s_2$.

• $R: S \times A \times S$ is the reward function giving a numerical reward value $r \in [0.0,1.0]$ received at time t after transiting from state $s_1$ to state $s_2$ as a result of applying action choice a at time $t-1$

• $\gamma$ is the discount factor of the feedback signals recieved over time

The state space, action space and reward function of this AOS and the function approximator are described below.

3.1 The State Space

A total of 15 features is defined as the state features. The state features are dichotomized into fitness landscape features and parent-oriented features. The eight continuous and a binary fitness landscape features are described below.

• 1. Restart $rs \in \{0,1\}$: At each generation, if $div(p) < div_t(p)$ where $div_t(p)$ is a threshold of population diversity or when the average fitness has remained unchanged for $g_{es}$ generations, the population will be restarted. All the chromosomes except the best chromosomes are mutated to give $dist(c_o, p_{c1}) > \delta _{dist}$ and $dist(c_o, p_{c2}) > \delta _{dist}$ where $\delta _{dist}$ is the percentage of differences among the parent chromosomes.

• 2. Population Diversity $div(P) \in [0.0,1.0]$: Different crossover operators may be preferred at different population diversity. The population diversity tracks the number of differences among the corresponding elements of a pair of chromosomes. It is normalized by the size of a problem instance n and the number of pairs of chromosomes $n_{pair}$.

• 3. Population Fitness Diversity $fdiv(P) \in [0.0,1.0]$: The population fitness diversity tracks the fitness differences between a pair of chromosomes. It is normalized by the number of pairs of chromosomes.

• 4. Proportion of new best offspring $N_{best} \in [0.0,1.0]$: Offsprings are created by crossover and mutation processes. An offspring is a new best offspring when its fitness level $f_o$ is better than the best fitness level from the previous generation $f_{best}$. In this work, an offspring is considered to be better than the best offspring from the previous generations when $f_o < f_{best}$. $N_{best}$ is normalized using the number of crossover operations $N_{co}$ and the number of mutation operation $N_{mu}$.

• 5. Proportion of improving offspring $N_{imp} \in [0.0,1.0]$: An offspring is improving when $f_o < f_{better}$ where $f_{better}$ is the fitness level of the better parent chromosome $c_{better}$. $N_{imp}$ tracks the number of improving offspring and is normalized using the number of crossover operations $N_{co}$.

• 6. Proportion of worsening chromosomes $N_{wrs} \in [0.0,1.0]$: An offspring is worsening when $f_o > f_{worse}$ where $f_{worse}$ is the fitness level of the worse parent chromosome $c_{worse}$. $N_{wrs}$ tracks the number of worsening offsprings and is normalized using the number of crossover operations $N_{co}$.

• 7. Proportion of equal quality offspring $N_{eql} \in [0.0,1.0]$: It may also be possible that $f_{better}< f_o < f_{worse}$. Such offspring is considered to be of equal quality to the parent chromosomes. $N_{eql}$ tracks the number of equal quality offsprings and is normalized using the number of crossover operations $N_{co}$.

• 8. Amount of improvements $\varDelta _{imp} \in [0.0,1.0]$: The amount of improvement $\varDelta _{imp}$ is recorded as $\frac{f_{better} - f_o}{f_{better}}$. It is aggregated over $N_{co}$ crossover operations in a generation. $\varDelta _{imp}$ is normalized using $N_{co}$.

• 9. Amount of worsening $\varDelta _{wrs} \in [0.0,1.0]$: The amount of worsening to the fitness level $\varDelta _{wrs}$ is recorded as $\frac{f_o - f_{worse}}{f_{worse}}$. It is aggregated over $N_{co}$ crossover operations in a generation and then normalized using $N_{co}$.

An offspring is a product of the parent chromosomes after crossover operation. Therefore, the following parent-oriented features are included as the observable features.

• 1. Normalized distance between parent chromosomes $dist(c_{p1},c_{p2}) \in [0.0,1.0]$: This is a measure of the number of differences between the corresponding elements of $c_{better}$ and $c_{worse}$. $dist(c_{worse},c_{better})$ is normalized using the size of the given QAP instance n.

• 2. Normalized fitness gap between parent chromosomes $fgap(c_{p1},c_{p2}) \in [0.0, 1.0]$: This is a measure of the amount of difference between the fitness levels of $c_{worse}$ and $c_{better}$, i.e., $\frac{f_{worse} - f_{better}}{f_{worse}}$.

• 3. Mean distance of $c_{better}$ with population $dist(c_{better},P) \in [0.0,1.0]$: The number of differences between the corresponding elements of $c_{better}$ and chromosome $c_i$ where $c_i \ne c_{better}$ and $c_i \ne c_{worse}$ is tracked as part of the observable feature. $dist(c_{better},P)$ is derived using $\frac{1}{p-2}\sum _{i=0}^p dist(c_{better},c_i)$.

• 4. Mean distance of $c_{worse}$ with population $dist(c_{worse},P) \in [0.0,1.0]$: The number of differences between the corresponding elements of $c_{worse}$ and $c_i$ where $c_i \ne c_{better}$ and $c_i \ne c_{worse}$ is tracked as part of the observable feature. $dist(c_{worse},P)$ is derived using $\frac{1}{p-2}\sum _{i=0}^p dist(c_{better},c_i)$.

• 5. Mean fitness gap of $c_{better}$ with population $fgap(c_{better},P) \in [0.0,1.0]$: The amount of differences between the fitness levels of $c_{better}$ with $c_i$ where $c_i \ne c_{better}$ and $c_i \ne c_{worse}$ is also tracked as part of the observable feature. $fgap(c_{better},P)$ is derived using $\frac{1}{p-2}\sum _{i=0}^p fgap(c_{better},c_i)$.

• 6. Mean fitness gap of $c_{worse}$ with population $fgap(c_{worse},P) \in [0.0,1.0]$: Similarly, the amount of differences between the fitness levels of $c_{worse}$ and $c_i$ where $c_i \ne c_{better}$ and $c_i \ne c_{worse}$ is also tracked as part of the observable feature. $fgap(c_{worse},P)$ is derived using $\frac{1}{p-2}\sum _{i=0}^p fgap(c_{worse},c_i)$.

3.2 The Action Space

The action choices are the crossover operators $c \in \varGamma$ where $\varGamma$ is the set of all crossover operators. This implies $\varGamma$ is equivalent to action space A. Four crossover operators from [13] are used here.

• 1. Cycle crossover (CX): This crossover operator first include the elements of the chromosome common to parent chromosomes $c_{p1}$ and $c_{p2}$ for creating offspring $c_o$. An unassigned element of $c_o$ indexed at j is then chosen. $c_o(j)$ is then given the value at $c_{p1}(j)$, i.e., $c_o(j) = c_{p1}(j)$. A second element of $c_o$ indexed at k is again picked. $c_o(k)$ is then given the value at $c_{p2}(j)$, i.e., $c_o(k) = c_{p2}(j)$.

• 2. Distance-preserving crossover (DPX): This crossover operator produces $c_o$ equi-distance apart from $c_{p1}$ and $c_{p2}$. Like CX, this crossover operator first include the elements of the chromosome common to $c_{p1}$ and $c_{p2}$ for creating $c_o$. The remaining unassigned elements of $c_o$ are given values that is the permutation of $c_{p1}$ and $c_{p2}$. In this way, $c_o$ will have the same distance to $c_{p1}$ and $c_{p2}$.

• 3. Partially-mapped crossover (PMX): This crossover operator chooses randomly indices j and $j'$ where $j < j'$. $c_o(k)$ is then assigned the value at $c_{p1}(k) \forall k \notin [j,j']$ and $c_o(k))$ is assigned the value at $c_{p2}(k) \forall k \in [j,j']$. If $c_o$ is an invalid permutation, then for each $c_o(k)$ and $c_o(z)$ where $j< z < j'$, $c_o(k) = c_{p1}(z)$.

• 4. Order crossover (OX): Like PMX, this crossover operator also chooses randomly indices j and $j'$ where $j < j'$. $c_o(k)$ is assigned the value at $c_{p1}(k) \forall k \in [j,j']$. The $k^{th}$ unassigned elements of $c_o$ is assigned the value of the $k^{th}$ element of $c_{p2}$ such that $c_{p2}(k) \ne c_o(z)$ for $j \le z \le j'$.

3.3 The Reward Function

The feedback signal $r_c$ is derived using a reward function R. Known reward functions differ mainly in the calculation of the credit and the measurement method [7, 12, 16, 28]. Our reward function makes reference to the current best, and the reward is assigned only when the offspring improves over both its parents. The feedback signal $r_c$ is derived using

$$\begin{aligned} r_c = \min \left\{ \frac{\mathcal {C}_\text {best}}{\mathcal {C}_\text {offspring}}\text {sign}(\mathcal {C}_\text {parent} - \mathcal {C}_\text {offspring}), \zeta \right\} \end{aligned}$$

where $\zeta \in [0.5, 1.0]$. The $\text {sign}(\cdot )$ function returns 1 if the offspring is better than the fitter parent. Otherwise, 0 is returned. The feedback signal $r_c$ is used in (1) to estimate the long-term value Q(s, a) of choosing the crossover operators.

3.4 Function Approximator

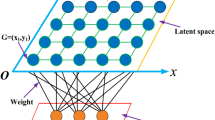
The state space described in Sect. 3.1 is continuous. Other than discretizing the continuous state space, a function approximator can be used to generalize the states. The function approximator used here is a self-organizing neural known as FL-FALCON [26]. Based on the adaptive resonance theory (ART) [6], it can learn incrementally in real time while generalizing on the states without compromising on its prediction accuracy.

Structure and Operating Modes. Seen in Fig. 1, FL-FALCON has a two-layer architecture, comprising an input/output (IO) layer and a knowledge layer. The IO layer has a sensory field $F_1^{c1}$ for accepting state vector $\mathbf{S}$, a motor field $F_1^{c2}$ for accepting action vector $\mathbf{A}$, and a feedback field $F_1^{c3}$ for accepting reward vector $\mathbf{R}$. The category field $F^c_2$ at the knowledge layer stores the committed and uncommitted cognitive nodes. Each cognitive node j has template weights $\mathbf{w}^\mathrm{ck}$ for $k=\{1,2,3\}$.

FL-FALCON operates in one of the following modes. In PERFORM mode, the Fusion-ART algorithm is used to select cognitive node J for deriving action choice a for state s. In LEARN mode, FL-FALCON learns the effect of action choice a on state s.

Fig. 1.

The FL-FALCON architecture.

The Fusion-ART Algorithm. The Fusion-ART algorithm [25] is used for selecting winning cognitive node J from a collection of committed cognitive nodes. In PERFORM mode, cognitive node J is used to derive action choice a. In LEARN mode, the weights $\mathbf{w}^{ck}_J$ for $k=\{1,2,3\}$ of cognitive node J will be updated using template learning. The performance of FL-FALCON is dependent on the use of suitable vigilance parameters $\rho ^{ck}$ for the operating modes.

Using activity vector $\mathbf{x}^{ck}$ for $k=\{1,2,3\}$ as the inputs, the process of selecting winning cognitive node J begins with the code activation procedure. This procedure derives the choice function $T^c_j$ using

$$\begin{aligned} T_j^c = \sum _{k=1}^3 \gamma ^{ck} \frac{|\mathbf{x}^{ck} \wedge \mathbf{w}_j^{ck}|}{\alpha ^{ck}+|\mathbf{w}_j^{ck}|}, \end{aligned}$$

where the fuzzy AND operation $(\mathbf{p} \wedge \mathbf{q})_i \equiv min (p_i,q_i)$, the norm $||.||$ is defined by $|\mathbf{p}|\equiv \sum _i p_i$ for vectors $\mathbf{p}$ and $\mathbf{q}$, $\alpha ^{ck} \in [0,1]$ is the choice parameters, $\gamma ^{ck} \in [0,1]$ is the contribution parameters and $k=\{1,2,3\}$.

The choice function $T^c_j$ is then used for selecting a winning cognitive node J during the code competition procedure. This procedure selects cognitive node J using

$$\begin{aligned} J = \arg \max _j\{T_j^c: \text {for all}\,F_2^c\,\text {node}\,\text {j}\}. \end{aligned}$$

The match function $m^{ck}_J$ of cognitive node J is then derived in the template matching procedure using

$$\begin{aligned} m_J^{ck} = \frac{||\mathbf{x}^\mathrm{ck} \wedge \mathbf{w}_J^{ck}||}{|\mathbf{x}^\mathrm{ck}|} \ge \rho ^{ck}, \end{aligned}$$

where $\rho ^{ck} \in [0,1] \text { for } k = \{1,2,3\}$ are the vigilance parameters.

A resonance state is attained when the vigilance criterion, $\mathbf{m}^{ck} \ge \mathbf{\rho }^{ck}$ for $k=\{1,2,3\}$, is satisfied. Otherwise, a reset is performed by $T^c_J = 0.0$ and the state vigilance $\rho ^{c1}$ is modified in a match tracking procedure using

$$\begin{aligned} \rho ^{c1} = \min \{m^\mathrm{c1}_J + \psi , 1.0\}, \end{aligned}$$

where $\psi$ is a very small step increment to match function $m^{c1}_J$.

After that, another winning cognitive node J is determined using the code competition procedure. The process repeats until the vigilance criterion is satisifed.

The attainment of the resonance state in LEARN mode leads to the template learning procedure. This procedure updates $\mathbf{w}^{ck}_J$ of cognitive node J using

$$\begin{aligned} \mathbf{w}_J^{ck \mathrm{(new)}} = (1-\beta ^{ck}) \mathbf{w}_J^{ck \mathrm{(old)}} + \beta ^{ck} (\mathbf{x}^{ck} \wedge \mathbf{w}_J^{ck \mathrm{(old)}}), \end{aligned}$$

where $\beta ^{ck} \in [0,1]$ is the learning rate.

The attainment of the resonance state in PERFORM mode leads to the activity readout procedure. The action choice a is obtained by decoding action vector $\mathbf{x}^{c2(new)}$ using

$$\begin{aligned} \mathbf{x}^{c2(new)} = \mathbf{x}^{c2(old)} \wedge \mathbf{w}^{c2}_J. \end{aligned}$$

In this work, FL-FALCON operates in LEARN mode when it is trained offline. After that, the trained FL-FALCON operates in PERFORM mode to select the crossover operators during evolutionary search.

Offline Training. The action policies $\pi$ for selecting crossover operators are discovered by presenting training samples to FL-FALCON operating in LEARN mode. The training samples are gathered from the experiments conducted based on the problem instances.

To train FL-FALCON, training samples comprising the state features, the selected crossover operator and the estimated value function Q(s, a) are presented to the sensory, motor and feedback fields respectively as $\mathbf{x}^{ck} = \{S,A,Q(s,a)\}$. Depending on the degree of match $\mathbf{x}^{ck}$ has with the existing cognitive nodes, the presented training sample is either learned as a new cognitive node or used to update a matching cognitive node J. One-shot training of FL-FALCON is performed by presenting randomly selected training samples to it.

The trained FL-FALCON is used in PERFORM mode for AOS. The choice of crossover operators is made by selecting a winning cognitive node J using the Fusion-ART algorithm. FL-FALCON is used in this way because the scope of this work is limited to testing its generalization capability for AOS.

4 The Operator Selection Policies

This section briefly reviews various strategies for AOS. Based on a recent study [13], there are two probabilistic and one deterministic allocation strategies, namely probability matching (PM), adaptive pursuit (AP) and Multi-Armed Bandit (MAB). In addition, for the sake of comparing with an MDP-based approach, we will review a reinforcement learning (RL) approach [14] for finding the action policy.

4.1 Probabilistic Matching

As the feedback signal $R_c$ is received only after applying crossover operator c, it is difficult to estimate the quality of c using a fixed strategy. A probabilistic strategy (PS) that biases towards the good-performing operators while still allowing unused operators to be chosen would be desirable. Such a PS tuner assigns a probability value proportional to the credits of crossover operators.

At each generation, c is then randomly chosen following this probability distribution. For this purpose, each crossover operator c is assigned a quality $Q_c \in [0.0,1.0]$ which is updated using $Q^{old}_c + \alpha (R_c - Q^{old}_c)$. Using a probability matching (PM) mechanism, the probability $P_c$ of choosing a crossover operator c is then derived using $P_{min}+ (1-|\varGamma |P_{min})\frac{Q_c}{\sum _{c^{\prime }}Q_{c^{\prime }}}$ where $\varGamma$ is the set of all crossover operators considered. The lower threshold $P_{min}$ is included to guarantee that every operator has a chance to be chosen. A drawback of PM is that convergence of $P_c$ can be slow in some cases.

4.2 Adaptive Pursuit

The adaptive pursuit mechanism [27] may be used to speed up convergence of $P_c$ using

$$\begin{aligned} P_c= {\left\{ \begin{array}{ll} P_c + \beta (P_{max}-P_c), &{}\text {if } Q_c = \max _{c^{\prime }}Q_{c^{\prime }}\\ P_c + \beta (P_{min}-P_c), &{}\text {otherwise,} \end{array}\right. } \end{aligned}$$

where $P_{max} = 1 - (|\varGamma | - 1)P_{min}$. Eventually, $P_c$ of a promising operator converge to $P_{max}$ while $P_c$ of the less promising crossover operators is reduced to $P_{min}$.

4.3 Multi-armed Bandit

The problem of Multi-armed Bandit (MAB) [24] chooses a slot machine to minimize the regret level over a fixed time horizon. The players are initially unaware of the amount of payoff from the slot machines. The players would begin discovering the payoff of the slot machines. As the players gain more knowledge of the payoff of the slot machines, decisions have to be made on whether to explore further or to exploit the existing knowledge. Well-studied methods to solve MAB problem are widely applied in real world domains such as network routing, financial investment, machine controller and clinical trials.

In the context of AOS [11], each crossover operator can be modelled as a slot machine. The corresponding problem is then to choose crossover operator c that maximize reward over time using $\mathop {\text {argmax}}\nolimits _{c\in \varGamma }\Big \{\overline{Q_c}+\gamma \sqrt{\frac{2 \ln \sum _{c^{\prime }}n_{c^{\prime }}}{n_c}}\Big \}$ where $\overline{Q_c}$ is the average reward computed since the beginning of the search and $n_c$ is the number of times the crossover operator c is chosen. The second term in the above equation is an exploratory term with similar significance to $P_{min}$ seen in the probabilistic strategies.

4.4 Reinforcement Learning

Following [14], the evolutionary search is modelled as a Markov Decision Process (MDP). This approach estimates the expected Q-value Q(s, a) of each state-action (s, a) pair using

$$\begin{aligned} Q(s,a) = R(s,a)+ \sum _{s^{\prime }}P(s^{\prime },a,s)\max _{{a}^{\prime }}Q(s^{\prime },a^{\prime }), \end{aligned}$$

(1)

where $P(s^{\prime },a,s)$ is the probability of entering into new state $s^{\prime }$ and R(s, a) is the expected reward from executing action a in state s.

Given that R(s, a) and $P(s^{\prime },a,s)$ are well estimated, Q(s, a) can be estimated using (1). However, in the evolutionary search domain, Q(s, a) is instance-specific value. Significant number of runs on several instances is needed to estimate the model. This is infeasible and has also gone out of the scope of this work. Therefore, a model-free RL approach such as the Q-learning is used to solve the MDP-based search progressively. Using Q-learning, the Q-value of using different action choices can be explored and learned as part of the action policies. Within the MDP framework, Q(s, a) is estimated using Q-learning [24].

$$\begin{aligned} Q_{t+1}(s_{t},a_{t}) = Q_t(s_t,a_t) + \alpha _t(s_t,a_t) TD_{err}, \end{aligned}$$

where $\alpha _t(s_t,a_t)$ is the learning rate and $TD_{err}$ is derived using

$$\begin{aligned} TD_{err} = R_{t+1}(s_t,a_t) + \delta \max _{a}Q_t(s_{t+1}, a)- Q_t(s_t,a_t), \end{aligned}$$

where $\delta$ is the discount rate. It is used in our search process to reflect the fact that the chance of improvement is reduced as the search continues.

5 Performance Evaluation

This section presents experiments that evaluate and compare the efficacy of our proposed approach on QAP instances [20].

5.1 Experiment Setup

The AOS methods used as the benchmark methods are the Reinforcement Learning approach (RL), Probability Matching (PM), Adaptive Pursuit (AP), Multi-Armed Bandit (MAB), and a naive (N) allocation strategies. Due to similar context to [13], the following parameter settings from [13] were used.

$$\begin{aligned} \begin{array}{ll} \text {PM: } \alpha _{pm} = 0.30, P_{min} = 0.05; &{} \text { AP: } \alpha _{ap} = \beta = 0.30, P_{min} = 0.05; \\ \text {MAB: } \gamma _{mab} = 1.00; &{} \text { RL: } \alpha = 0.03, \delta =0.90 \\ \end{array} \end{aligned}$$

For the memetic algorithm, a population size p of 40 chromosomes was adopted. At each generation, as many as 20 offsprings were produced using a selected crossover operator c. Each offspring was then refined using the random-order first-improvement 2-opt local search. When the average distance over all pairs of chromosomes is below 10 or the average fitness has remained unchanged for 30 generations, restart was initiated. This was achieved by mutating all but the best chromosomes in the population until each resulting chromosome differed from its parent by as much as $\delta _{dist} = 0.30$ of problem size n. Each run is terminated after 100 generations.

There are two rounds of experiments. The first round of experiments described in Sect. 5.2 is the offline training of the neural network-based function approximator. The second round of experiments described in Sect. 5.3 compares our proposed approach to the benchmark AOS methods.

5.2 Offline Training of Neural Network

The training samples were prepared by experimenting each crossover operator $c \in \varGamma$ on each QAP instance $p_i$ taken from the QAPLib (from bur26a to scr20). Experiments were performed using four crossover operators mentioned in Sect. 3.2. Each experiment based on the pairing of c and $p_i$ was performed for 100 generations. A training sample is produced for each generation of the evolutionary process.

Fig. 2.

The mean rank of different train-test configurations.

A training sample is assembled as state s comprising 15 state features, action choice a which a particular crossover operator $c \in \varGamma$ and feedback signal $r_c$. State s and action choice a are taken at time t while the feedback signal $r_c$ is taken at time $t+1$. This means a training sample $t_s =\{s,a,r_c\}$ is only fully assembled at time $t+1$. For $t=0$, state s comprise the initial value of the state features, action choice a comprise the crossover operator c used for that round of experiment based on problem instance $p_i$.

The raw form of the test results are the aggregated fitness levels of the offsprings. Comparisons are made among the neural networks by ranking the aggregated fitness levels in ascending order. Smaller rank value is given to train-test configuration with lower aggregated fitness level. The ranks of 100 train-test configurations are illustration in Fig. 2.

Fig. 3.

The mean rank of the trained neural networks for the QAP instances.

From Fig. 2, the neural network has the best test performance across the different problem instances when trained using Bur-based problem instances. The worst test performance across the different problem instances is observed when neural network is trained using the Rou-based problem instances. The mean rank of the train instances plotted using the dotted line illustrates the aggregated effect of using different problem instances to train the neural network.

Following the above observation, the performance of neural networks trained differently are ranked and compared directly. Seen in Fig. 3, the mean rank of NN-S is based on the mean fitness values of neural networks trained using the same train and test problem instances. The mean rank of NN-D is based on the mean fitness values of neural networks trained using training samples of problem instances not used for testing. Following this train-test criteria, for each test problem instance $p_i \in \mathcal {P}$, $|\mathcal {P} - p_i|$ other QAP instances can be used for training NN-D. The heterogeneity of training samples are ensured by picking it randomly from those QAP instances. Then, there is NN whose rank is based on the mean fitness values of the best performing neural network trained using a problem instance selected based on Table 1.

From Fig. 3, NN is observed having the best ranking of 1.0 when compared to NN-S and NN-D. NN-S has the next best ranking of the three trained neural network while NN-D is the trained neural network with the lowest rank. The rank of NN-S imply that the neural network may not necessarily have the best performance when trained using the problem instances used for testing it. The rank of NN-D implies that the neural network cannot be trained arbitrarily and expect it to generalize well. The rank of NN shows that the neural network can generalize well when trained selectively.

Table 1. Mean rank of train-test configurations

5.3 Adaptive Operator Selection

Further experiments were conducted to compare the performance of the neural network-based approach with the several benchmark AOS methods. The benchmark AOS methods include Reinforcement Learning (RL), Probability Matching (PM), Adaptive Pursuit (AP), Multi-Armed Bandit (MAB), naïve (N) allocation strategy and the proposed neural network (NN) approach. The RL approach regards AOS as a finite MDP while the neural network-based approach regards AOS as a MDP. The test results using fixed crossover operators such as Cycle crossover (CX), Distance-preserving crossover (DPX), Partially-mapped crossover (PMX) and Order crossover (OX) are also compared in Fig. 5.

Fig. 4.

Mean rank of the AOS methods for the QAP instances

Fig. 5.

Aggregation of the mean rank of the AOS methods

The test results are the mean ranks on the mean fitness values of the AOS methods. The mean value is based on 10 runs of each experiment. Test results for the QAP instances mentioned in Sect. 5.2 are presented here. The neural network can be trained using any problem instance that has the lowest mean rank as seen in Table 1.

The illustration of the mean rank of the AOS methods for the QAP instances in Fig. 4 shows a broad spectrum of performance characteristics. The dotted-line plot shows the mean value of the mean rank of the AOS methods and it implies the level of difficulty of the QAP instances. It can be observed that many AOS methods perform quite well for Bur, Els, Had and Scr type of QAP instances, The more challenging QAP instances are Chr, Kra, Lipa, Nug and Rou.

Aggregation of the mean rank of the AOS methods over all QAP instances used here confirms NN to be the best performing approach while DistPres to be the worst performing approach. It turns out that the AP, Cycle and DistPres methods are performing worse than the naïve allocation strategy N. The best performance of NN implies the robustness of the neural network for selecting crossover operators during the evolutionary search aimed at optimizing a broad spectrum of QAP instances.

6 Conclusions

Many methods for AOS such as Probability Matching, Adaptive Pursuit, Multi-Armed Bandit and Reinforcement Learning (RL) are known to date. In this chapter, we propose the use of a self-organizing neural network for AOS. In contrast to the RL approach where AOS is formulated as discrete state MDP, our neural network approach is better suited for AOS modelled as MDP with continuous states and discrete actions.

The neural network used is a self-organizing neural network based on the Adaptive Resonance Theory (ART) known for addressing the generalization-specialization dilemma [6]. This work evaluates the generalization capability of such a self-organizing neural network for AOS. To do that, the neural network was trained offline using training samples from the problem instances. Several train-test configurations were used to study the performance of the trained neural network rigorously. To generalize well on the test instances, the results imply that the neural network has to be trained properly using training samples from the suitable problem instances.

The performance of the neural network is compared with the benchmark AOS methods. The test results reveal several characteristics of the AOS methods and the problem instances. Firstly, there are problem instances that can be optimized using any AOS methods. There are also problem instances where several AOS methods are performing worse than the naïve allocation strategy. In such cases, MDP-based approaches such as RL and our proposed neural network approach are among the better performing AOS methods. Such observations imply the feasibility of using MDP-based approaches for AOS in evolutionary search. Last but not least, aggregation of the mean rank of the AOS methods shows the proposed neural network to be sufficiently robust to give the best performance for all the QAP instances.

There are several directions to extend this work. First, we should determine the performance of the neural network in more challenging QAP instances as well as other permutation-based instances such as the flow-shop scheduling problem (FSP). Second, the incremental learning capability of the neural network can be tested using RL during evolutionary search. Doing so, allow the neural network to improve on the learned action policies while performing AOS during evolutionary search. The hypothesis here is that the neural network may able to be converge faster for simpler problem instances and still converge on the more challenging problem instances using available resources.