1 Pattern Formation in Morphogenesis

Morphogenic proteins play a key role in Developmental Biology, acting as signaling molecules mediating intracellular communication. In particular they mediate cellular differentiation processes like those taking place during embryonic development. Understanding how morphogens induce distinct cell fates becomes then a paramount issue.

Morphogenic proteins are usually issuing from localized sources in the extracellular medium, originating a concentration gradient. Several mathematical models have been proposed to explain how morphogens are transported through the extracellular matrix; these have been usually based on reaction-diffusion equations after the pioneering works of Turing, Crick and Meinhardt [13, 19, 24]. Reaction terms account for the set of chemical reactions (known as the signaling pathway) taking place inside each cell after morphogens attach to their membrane receptors; the final result of these intracellular processes is a specific change in gene transcription.

An important scenario which has been the subject of intensive research is that of the neural tube (particularly in chick embryos), which is the precursor of the spinal cord in the adult individual. Owing to the natural propagation direction in this structure, one-dimensional reaction-diffusion models have been widely used to describe how gradients of morphogen concentration are dynamically created in the neural tube, see e.g. [22] and references therein. Such mathematical models assume that morphogens are transported through the medium by means of linear diffusion, whereas chemical reactions taking place within individual cells can be described in terms of a system of ordinary differential equations.

Several recent experimental findings have come to question the validity of the linear diffusion assumption in this context (see [23, 26] for an account of this). Here we focus on the results by Dessaud et al. [14], stating that the concentration of morphogen that cells receive and the exposure time have the same importance (e.g. very small morphogen concentration can exert noticeable effects if the exposure time is long enough). To see why this property cannot be replicated by a linear diffusion model, let us consider the one-dimensional FKPP equation [15, 17],

$$\displaystyle{ u_{t} =\nu u_{xx} + k\,u(1 - u) }$$

which displays classical, C ∞-smooth traveling waves u(t, x) = u(x −σt) for wavespeeds \(\sigma \geq 2\sqrt{k\nu }.\) These traveling profiles are supported in the whole real line, matching with zero by means of an exponentially decaying profile. This is rooted in the fact that the linear diffusion equation has the property of infinite speed of propagation. It entails the fact that traveling waves as such propagate some (chemical) information instantaneously, which spoils any attempt to track exposure times on the sole basis of this model. In fact, no a posteriori engineering procedures seem to quantify in a reasonable way experimental observations [23, 26].

It is mandatory to have mathematical descriptions allowing to track in a very precise way exposure times for the sake of having accurate models for morphogenesis (and specifically for the case of the neural tube). It is a natural idea to test if nonlinear diffusion can perform better in this setting, particularly when models having finite propagation speed are used. We try to get some clues dealing with simplified settings in the following section.

2 Nonlinear Reaction-Diffusion Models

Describing traveling wave solutions in nonlinear reaction-diffusion equations constitutes a full research area in itself. It is tempting to think that traveling waves for reaction diffusion equations having finite speed of propagation will be supported on half lines. The actual scenario is a bit more complicated. As a prototypical example, we may consider the porous medium equation (see e.g. [25]) coupled with a logistic reaction term,

$$\displaystyle{ u_{t} =\nu (u^{m-1}u_{ x})_{x} + k\,u(1 - u),\quad m > 1. }$$
(1)

For each value of m > 1 there is a one-parametric family of traveling wave solutions. All the members of this family are supported on the whole real line, except for the slowest wave of each family, which is a continuous profile which is supported on a half line. See [20] for details.

This subject has been treated in great generality to find that this behavior is not specific of porous media equations but rather of parabolic equations with finite propagation speed, see the book [16]. Here we want to draw attention on a family of degenerate parabolic equations having the property of finite speed of propagation which does not fall in the scope of [16]. These are know as flux saturated or flux limited diffusion equations, arguably introduced in the works by Rosenau [21] and Levermore and Pomraning [18]. A prototypical example is

$$\displaystyle{ \frac{\partial u} {\partial t} =\nu \ \mbox{ div}\,\left ( \frac{\vert u\vert \nabla _{x}u} {\sqrt{u^{2 } + \frac{\nu ^{2 } } {c^{2}} \vert \nabla _{x}u\vert ^{2}}}\right ). }$$
(2)

Note that when c → ∞ we get the heat equation. This model is known in the mathematical literature as the “relativistic heat equation” after [5], in which a connection with optimal transport theory was found. In fact, the form of the cost function hints that (2) should have a finite speed of propagation given by c above, a fact that was also pointed out in [21]. This is proved in [3]. In fact, this model is also able to propagate discontinuous interfaces, which is a desirable feature for the morphogen transport problem, as we explain below. These properties are somewhat natural in the light of the degenerate functional framework which is needed to tackle such models, see e.g. [1, 2] (where an entropy solution framework is introduced). For a recent account on the research done on flux-saturated equations we refer to [8].

In the light of the previous considerations, we want to probe what sort of traveling waves arise in connection with these degenerate diffusion mechanisms. As a test case, we can mix the mechanisms of flux saturation and porous-media-type diffusion and consider the following equation for m ≥ 1:

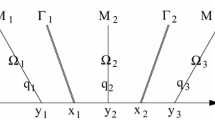
$$\displaystyle{ u_{t} =\nu \, \left ( \frac{u^{m}u_{x}} {\sqrt{\vert u\vert ^{2 } + \frac{\nu ^{2 } } {c^{2}} \vert u_{x}\vert ^{2}}}\right )_{x} + k\,u(1 - u). }$$
(3)

It was shown in [9, 11] that this family of equations admits traveling wave solutions which are supported on a half line and whose interfaces are discontinuous. When m = 1 such singular waves exist only for wavespeeds equal to c, any other (necessarily faster) traveling waves are classical. If m > 1 then there exist two bifurcation values σ smooth > σ ent . If the wavespeed coincides with σ ent then the corresponding traveling waves are again discontinuous and supported on a half line. If the wavespeed exceeds σ smooth then the associated waves are classical, while those with speeds between the two bifurcation values consist on two smooth branches joined by a jump discontinuity and their support is the whole line. These results are proved by reducing the problem of constructing wave solutions to describing the orbits of a planar dynamical system. Singular traveling waves arise as admissible concatenation of several orbits of the planar diagram, being the compatibility conditions at the matchin points given by Rankine–Hugoniot’s jump conditions plus some geometric information coming from the entropy solution framework, see [12].

These results in [9, 11] are no isolated phenomena but part of a robust framework. It has been tested that similar families of traveling profiles are obtained under a number of generalizations of (3), see [6, 8–10].

3 Nonlinear Models for Morphogen Propagation

The analytical findings in the previous section suggest that replacing the linear diffusion mechanism on mophogen propagation models with a nonlinear mechanism having finite speed of propagation may allow to get a better description of the overall dynamics. One of the concerns we need to address is to track exposure times carefully, a task for which saturation mechanisms like that in (2) seem quite suited -note that propagation speed is universal, in contrast with the porous medium case, for which it depends on the initial datum [25]. This specific feature was tested on a simplified model for morphogen propagation in the neural tube introduced in [7],

$$\displaystyle{ \left \{\begin{array}{ll} \frac{\partial u} {\partial t} = \left ( \frac{\vert u\vert u_{x}} {\sqrt{u^{2 } + \frac{\nu ^{2 } } {c^{2}} \vert u_{x}\vert ^{2}}}\right )_{x} &\hspace{5.69046pt} \mbox{ in }[0,T] \times [0,L]\:, \\ \\ -\mathbf{a}(u(t,0),u_{x}(t,0)) =\beta > 0\mbox{ and }u(t,L) = 0&\hspace{5.69046pt} \mbox{ on}\hspace{4.26773pt} t \in [0,T]\:,\end{array} \right. }$$
(4)

The non-homogeneous Neumann boundary condition encodes the fact that there is an incoming morphogenic signal. It was shown in [4] that the incoming flux of morphogens propagates with speed c in the form of a sharp traveling front, quite related with the results mentioned in the previous section. This supports the proposal of a complete model in [26]. Morphogen propagation along the neural tube would be described by an equation like (4), with the addition of suitable reaction terms accounting for attachment and detachment effects linked with the availability of membrane receptors at each individual cell. This partial differential equation is coupled with a system of ordinary differential equations representing the signaling pathway at each cell according to the amount of attached morphogens and the time of exposure to their action. In such a way, the chemical signal is propagated as a traveling front (as shown by numerical simulations), thus allowing different biological responses at different times. We refer to [26] for a detailed exposition. We think that the model proposed in [26] opens a new perspective on the subject, since its qualitative behavior is in close correspondence with biological observations, opposed to what is predicted by linear diffusion models. Therefore, morphogen propagation seems to be an inherently nonlinear process, of which some features could be well approximated by some nonlinear diffusion mechanisms. The proposal in [26] can be an interesting departing point from which we may develop more accurate theories and models.