Stability of Concatenated Traveling Waves

Abstract

We consider a reaction–diffusion equation in one space dimension whose initial condition is approximately a sequence of widely separated traveling waves with increasing velocity, each of which is individually asymptotically stable. We show that the sequence of traveling waves is itself asymptotically stable: as $t\rightarrow \infty$, the solution approaches the concatenated wave pattern, with different shifts of each wave allowed. Essentially the same result was previously proved by Wright (J Dyn Differ Equ 21:315–328, 2009) and Selle (Decomposition and stability of multifronts and multipulses, 2009), who regarded the concatenated wave pattern as a sum of traveling waves. In contrast to their work, we regard the pattern as a sequence of traveling waves restricted to subintervals of $\mathbb {R}$ and separated at any finite time by small jump discontinuities. Our proof uses spatial dynamics and Laplace transform.

1 Introduction

Consider the system of reaction–diffusion equations in one space dimension

$$\begin{aligned} u_t = u_{xx} + f(u), \end{aligned}$$

(1.1)

where $f\in C^2(\mathbb {R}^n)$. Throughout this paper we assume that the solutions of (1.1) are in $H^{2,1}_{loc}(\mathbb {R}\times \mathbb {R}^+)$ and both sides of (1.1) are in $L^2_{loc}(\mathbb {R}\times \mathbb {R}^+)$ . Notice that $H^{2,1}_{loc} (\mathbb {R}\times \mathbb {R}^+)$ is continuously imbedded in $C_{loc}(\mathbb {R}\times \mathbb {R}^+)$ therefore $f(u)\in L^2_{loc}(\mathbb {R}\times \mathbb {R}^+)$. We choose the diffusion terms $u_{xx}$ to simplify the illustration of our method. More general systems, such as $u_t = A u_{xx} + f(u)$ in [24, 26], where $A$ is positive definite, can be treated by our method.

We assume that (1.1) has $m$ traveling wave solutions, with widely separated centers, that connect $m+1$ spatially constant, time-independent solutions. These spatially constant solutions correspond to $m+1$ equilibria $e_0,\ldots ,e_{m}$ of the ordinary differential equation $u_t=f(u)$. The $j$th traveling wave, which has speed $c_j$, is $q_j(\xi _j)$, $\xi _j=x-y_j-c_jt$. It connects $q_j(-\infty )=e_{j-1}$ to $q_j(\infty )=e_{j}$.

We write $\xi$ instead of $\xi _j$ if it is clear which $y_j$ and $c_j$ are used. In the coordinates $(\xi ,t)$, $q_j(\xi )$ is a stationary solution of

$$\begin{aligned} u_t = u_{\xi \xi } + c_j u_\xi + f(u), \quad \xi =\xi _j = x-y_j -c_j t. \end{aligned}$$

(1.2)

The traveling wave $q_j(\xi )$ satisfies the ODE

$$\begin{aligned} q^{\prime \prime }_j + c_j q^\prime _j + f(q_j) =0, \quad 1\le j \le m. \end{aligned}$$

The function $(u(\xi ),v(\xi ))=(q_j(\xi ), q^\prime _j(\xi ))$ is a heteroclinic orbit of the associated first-order system

$$\begin{aligned} u_\xi =v, \quad v_\xi = -c_j v - f(q_j) \end{aligned}$$

(1.3)

that connects the equilibria $(e_{j-1},0)$ and $(e_j,0)$.

After a phase shift, we may assume for definiteness that $|q^\prime _j(0)| = \max \{|q^\prime _j(\xi )|: \xi \in \mathbb {R}\}$. Then $q_j(0)$, which we regard as the center of the wave $q_j$, travels on the characteristic line $\xi =0$, which corresponds to $x= y_j+ c_j t$. We assume the waves are widely separated, i.e., $y_1 << y_2 << \cdots << y_m$, and we assume $c_1 < c_2 < \cdots < c_m$.

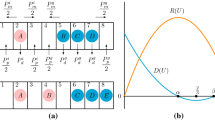
We define a concatenated wave pattern by dividing the domain $(x,t) \in \mathbb {R}\times \mathbb {R}^+$ into $m$ sectors and placing one traveling wave in each sector. More precisely, for $1\le j\le m-1$, let $\bar{c}_j=(c_j+ c_{j+1})/2$ be the average speed of the waves $q_j$ and $q_{j+1}$, and let $x_j = (y_j+y_{j+1})/2$, . For convenience let $x_0=-\infty$ and $x_m =\infty$. Define

$$\begin{aligned} M_j&=\{(x,t): x= y_j + c_j t,\; t\ge 0\},\\ \Gamma _j&= \{(x,t): x= x_j + \bar{c}_j t,\; t\ge 0\},\\ \Omega _j&=\{(x,t): x_{j-1} + \bar{c}_{j-1} t < x < x_j + \bar{c}_j t,\; t \ge 0\}, \end{aligned}$$

so that $M_j$ is inside $\Omega _j$, and $\Gamma _j$ separates $\Omega _j$ and $\Omega _{j+1}$. Define the concatenated wave pattern to be

$$\begin{aligned} u^{\mathrm{con}}(x,t) = q_j(x-y_j - c_j t) \text { for }(x,t)\in \Omega _j,\; 1\le j\le m. \end{aligned}$$

The center of the wave $q_j$ in $\Omega _j$ moves on the line $M_j$, and the lines $M_1,\dots ,M_m$ spread apart as $t \rightarrow \infty$. The concatenated pattern satisfies (1.1) in each $\Omega _j$ but is not continuous across the $\Gamma _j$ (Fig. 1).

Fig. 1

For the case $m=3$, the concatenated pattern consists three waves separated by two lines $\Gamma _1$ and $\Gamma _2$

For $\eta >0$ and $\pi /2 <\theta < \pi$, define the sector

$$\begin{aligned} \Sigma (-\eta , \theta )=\{s\in \mathbb {C}: |\arg (s +\eta )| \le \theta \}. \end{aligned}$$

$\Sigma (-\eta , \theta )$ has vertex at $s=-\eta$ and opens to the right with opening angle $2\theta$. It contains the half plane $\mathfrak {R}(\uplambda )\ge -\eta$.

For $1\le j\le m$, the linearization of (1.2) at the traveling wave $q_j(\xi )$ is

$$\begin{aligned} u_t= u_{\xi \xi } + c_j u_\xi + Df(q_j(\xi ))u, \quad \xi =\xi _j = x-y_j -c_j t. \end{aligned}$$

(1.4)

Define the linear operator $L_{j}$ on $L^2(\mathbb {R})$ with domain $H^2(\mathbb {R})$ by

$$\begin{aligned} {L}_{j} u =u_{\xi \xi } + c_j u_\xi + Df(q_j(\xi ))u. \end{aligned}$$

Throughout this paper we make the following standard assumptions.

H1 :

For $0\le j\le m$, $\mathfrak {R}\sigma ( Df(e_{j})) <0$.

H2 :

For $1\le j\le m$, the operator ${L}_{j}$ on $L^2(\mathbb {R})$, with domain $H^2(\mathbb {R})$, has the simple eigenvalue $\uplambda =0$, with one-dimensional eigenspace spanned by $q^\prime _j$.

From H1, for $0\le j\le m$, the linear first-order system $u_\xi =v,\;v_\xi = -c v -Df(e_j) u$ has, counting multiplicity, $n$ eigenvalues with negative real part and $n$ eigenvalues with positive real part. Together with H2, we can show that there are numbers $\eta >0$ and $\theta$, with $\pi /2 <\theta < \pi$, such that

(A1):

for $0\le j\le m$, the spectrum of the operator $u \rightarrow u_{\xi \xi } + c_j u_\xi + Df(e_j)u$ on $L^2$ is contained in the complement of $\Sigma (-\eta ,\theta )$;

(A2):

for $1\le j\le m$, the spectrum of the operator ${L}_{j}$ on $L^2$, is contained in the complement of $\Sigma (-\eta ,\theta )$ (essential spectrum), plus the simple eigenvalue $0$.

Let ${L}_{j}^*$ be the adjoint operator for ${L}_{j}$ on $L^2(\mathbb {R})$, with domain $H^2(\mathbb {R})$:

$$\begin{aligned} {L}_{j}^* z = z_{\xi \xi } - c_j z_\xi + Df(q_j(\xi ))^* z. \end{aligned}$$

(1.5)

Hypothesis (H2) implies that the adjoint equation $L_{j}^* z =0$ has a unique (up to constant multiples) bounded solution $z_j$. Moreover, since $q^\prime _j$ is not in the range of ${L}_{j}$, $\int _{-\infty }^\infty <z_j, q^\prime _j> \, d\xi \ne 0$. Assume that

$$\begin{aligned} \int _{-\infty }^\infty < z_j, q^\prime _j> \, d\xi =1, \quad 1\le j \le m. \end{aligned}$$

(1.6)

Let $H^{2,1}(\Omega _j,\gamma ),\;\gamma \le 0$, be the space of functions $u$ on $\Omega _j$ such that $e^{-\gamma t}u(x,t) \in H^{2,1}(\Omega _j)$. Let $I_j$ be the interval $(x_{j-1}, x_j)$.

For $u\in H^{2,1}_{loc}(\mathbb {R}\times \mathbb {R}^+)$, the function $t\rightarrow u(\cdot ,t)$ is continuous in $H^1_{loc}(\mathbb {R})$. So it is natural to consider the initial condition $u(x,0)=u_0(x) \in H^1_{loc}(\mathbb {R})$. We assume further that on the first and last intervals, $u_0(\cdot ) - q( \cdot -y_j) \in H^1(I_j), \; j=1,m$. If $v\in H^{2,1}(\Omega _j)$, and if $\Gamma$ is a line in the closure of $\Omega _j$, then by the trace theory, $(v,v_{x})$ has well-defined limit in $H^{0.75}(\Gamma ) \times H^{0.25}(\Gamma )\overset{def}{=}H^{0.75\times 0.25}(\Gamma )$, denoted by $(v(\Gamma ), v_x(\Gamma ))$. In particular, let

$$\begin{aligned} W_j=(q_j,q_j^\prime ), \; J_{j0}=W_j(\Gamma _j)-W_{j+1}(\Gamma _j), \text { then }J_{j0}\in H^{0.75\times 0.25}(\Gamma _j). \end{aligned}$$

Consider

$$\begin{aligned} q_j(\Gamma _j)=&q_j( x_j-y_j + (\bar{c}_j - c_j)t),\\ q_j(\Gamma _{j-1})=&q_j(x_{j-1}-y_j + (\bar{c}_{j-1} - c_j)t). \end{aligned}$$

From $x_j-y_j=y_j-x_{j-1} \ge \inf \{y_{j+1} - y_j \}/2$, there exist $\bar{C}>0, \mu <0, -\eta <0$ such that for all $1\le j \le m$,

$$\begin{aligned} \begin{aligned} |q_j(\Gamma _j)-e_j|+ |q_{j\xi }(\Gamma _{j})|&\le \bar{C} e^{-\eta \inf \{y_{j+1} - y_j \}/2},\quad t=0,\\ |q_{j+1}(\Gamma _{j})-e_{j}|+|q_{j+1,\xi }(\Gamma _{j})|&\le \bar{C} e^{-\eta \inf \{y_{j+1} - y_j \}/2},\quad t=0,\\ |q_j(\Gamma _j)-e_j|+ |\partial _t q_{j}(\Gamma _{j})|&\le \bar{C} e^{\mu t},\quad t \ge 0,\\ |q_{j+1}(\Gamma _{j})-e_{j}|+|\partial _t q_{j+1}(\Gamma _j)|&\le \bar{C} e^{\mu t},\quad t \ge 0,\\ \end{aligned} \end{aligned}$$

(1.7)

Definition 1.1

The concatenated wave pattern $u^{\mathrm{con}}(x,t)$ is exponentially stable with the rate $e^{\gamma t}$, provided there exist $\gamma <0$ and $\delta _0>0$ for which the following is true.

• (1) The set $S_{init}:=\{u_0 \in H^1_{loc}(\mathbb {R}): \max _j\{|u_0(x) - q_j(x-y_j)|_{H^1(I_j) }<\delta _0\}$ is nonempty.

• (2) For any $u_0\in S_{init}$, there exist a unique solution $u(x,t)\in H^{2,1}_{loc}(\mathbb {R}\times \mathbb {R}^+)$ to (1.1) and a sequence of numbers $r_1,\ldots ,r_m$ such that $u(x,0) = u_0(x)$. Moreover, if $\rho :=\max _j\{|u_0(x) - q_j(x-y_j)|_{H^1(I_j)}$, and if in each $\Omega _j$, $u(x,t) = q_j(x - y_j$ $-c_j t + r_j)+ u_j(x,t)$, then

  $$\begin{aligned}\partial _t u_j \in L^2(\Omega _j,\gamma ) \text { and } |u_j(\cdot ,t)|_{H^1(x)}<C \rho e^{\gamma t},\quad t\ge 0. \end{aligned}$$

Intuitively, on each $\Omega _j$, $u(x,t)$ exponentially approaches a shifted concatenated wave as $t\rightarrow \infty$. Different shifts are allowed in different $\Omega _j$. Note if $\max \{|u_0(x) - q_j(x-y_j|)_{H^1(I_j)}\}= \rho$, then $\max \{|J_{j0}|\}\le C\rho$. Given a concatenated patter $u^{con}$, if $\delta _0$ is too small, then $S_{init}$ is an empty set.

We now state the main result of this paper.

Theorem 1.1

Assume that the conditions (H1) and (H2) hold. Let $-\eta$ and $\mu$ be the constants in (A1), (A2) and (1.7) and let $\gamma$ satisfies $\max \{-\eta , \mu \} <\gamma <0$. Then there exists a sufficiently large $\ell >0$, a small $\delta _0>0$ and a constant $C_1>0$ such that if

$$\begin{aligned} \inf \{y_{j+1} - y_j \} \ge \ell , \text { and } \bar{C} e^{-\eta \inf \{y_{j+1} - y_j \}/2} < \delta _0, \end{aligned}$$

then the concatenated wave $u^{\mathrm{con}}(x,t)$ is stable with the rate $e^{\gamma t}$. Moreover, $u_0\in H^1_{loc}(\mathbb {R})$ is in $S_{init}$ if

$$\begin{aligned} \bar{C} e^{-\eta \inf \{y_{j+1} - y_j \}/2}<\max \{|u_0(x) - q_j(x-y_j)|_{H^1(I_j) } \}<\delta _0. \end{aligned}$$

Remark 1.1

First, $\ell$ must be sufficiently large so that the existence of exponential dichotomies and related contraction rates conditions, as will be introduced later, are satisfied. We may need to choose $\inf \{y_{j+1} - y_j \}$ even greater so the set $S_{init}$ is nonempty.

The “spatial dynamics” used in this paper were developed by Kirchgassner [7], Renardy [20], Mielke [18], Sandstede, Scheel, and collaborators [1, 19], and others. This approach treats the space variable as “time”, and evolve functions of $t$ which is natural to handle the concatenated waves that are placed side by side with jumps along common boundaries. In [11, 12], the interaction of stable, standing waves for a boundary value problem of parabolic systems in finite domain was considered by the method similar to that used in this paper. However, $\uplambda =0$ was not an eigenvalue and wave speed was not an issue in those papers. The new contribution of this paper is to treat the eigenvalue $\uplambda =0$ and the variation of wave speeds and shifts related to $\uplambda =0$. To simplify the notation, the equation considered in this paper is similar to that of [11]. Using the ideas of this paper, but changing the trace spaces to the more general ones used in [12], we should be able to handle interactions of traveling waves of general higher order parabolic systems as in [12]: $u_t+ (-1)^mD_x^{2m}u$ $=f(u,u_x,\dots ,(D_x)^{2m-1}u),\quad u\in \mathbb {R}^{n}.$

To illustrate our method, consider the simple case of two traveling waves $q_j(x-c_jt), j=1,2$ of (1.1) moving in opposite direction: $c_1 < 0 < c_2$. Define the concatenated wave $u^{con}(x,t)$ separated by $\Gamma =\{x=0, t\ge 0\}$ as follows

$$\begin{aligned} u^{con}(x,t)=q_1(x+N -c_1 t) \text { if }x<0,\quad u^{con}(x,t)=q_2(x-N -c_2 t) \text { if } x>0. \end{aligned}$$

(1.8)

Assume $N>0$ is a large constant so that the jumps along $\Gamma$, $[u^{con},u^{con}_x](\Gamma )$, are small and decay to zero as functions of time $t$.

Consider the perturbation of the initial data around $u^{con}(x,0)$. Notice that $u^{con}$ is not a solution of (1.1). Let the exact solution be

$$\begin{aligned} u(x,t)=u^{con} + u_1(x,t) \text { for }x<0, \quad u(x,t)=u^{con}+u_2(x,t) \text { for }x>0. \end{aligned}$$

(1.9)

The corrections $u_1(x,t)$ and $u_2(x,t)$ will be solved as initial-boundary value problems of PDEs in $x\le 0$ and $x\ge 0$ respectively, cf. (2.3). The boundary values are determined by two conditions: (1) The boundary values for $u_1,u_2$ at $\Gamma$ must compensate the jumps of $u^{con}$ at $\Gamma$ as follows

$$\begin{aligned} u_2(0,t) - u_1(0,t) = - (u^{con}(0+ ,t) - u^{con}(0-,t)),\\ u_{2x}(0,t) - u_{1x}(0,t) = - (u^{con}_x(0+ ,t) - u^{con}_x(0-,t)). \end{aligned}$$

(2) The boundary conditions for $u_1$ at $x=0-$ (or for $u_2$ at $x=0+$) must belong to the unstable subspace (or stable subspace) of the dichotomies of the “spatial dynamics” of the system (such dichotomies exist at least near each equilibirum point). So with the help of the variations of wave speeds as parameters, the solution $u_1(x,t)$ (or $u_2(x,t)$) can pass the center of $q_1$ (or $q_2$) where the left half and right half of exponential dichotomies do not match, and still decay to zero as $x\rightarrow -\infty$ (or $x\rightarrow \infty$). The condition (2) may sound complicated but it is based on how Lions and Magenes treated the boundary values of PDEs in the popular text book [15].

Now consider the concatenation of $m$ traveling waves. After linearization, the correction term $u_j$ defined in $\Omega _j, j=1,\dots ,m$, should satisfy the initial-boundary value problems with prescribed jump $J_j(\Gamma )$ along $\Gamma _j$, as in (2.6):

$$\begin{aligned}&u_{jt}= u_{j,xx} + Df(q_j)u_j + h_j(x,t),\quad u_j(x,0) = u_{j0}(x), \\&([\{u_j\}], [\{u_{jx}\}])(\Gamma _j) = J_j(\Gamma _j). \end{aligned}$$

If the linear system can be solved then the exact $\{u_j\}_1^m$ is obtained by the contraction mapping argument. Compared to the “inverse systems” used in other papers to treat wave interactions, this system is simpler, and highly localized such that the coefficient of the $j$th equation only depends on $q_j$. It can easily be adapted to many nonstandard cases where $q_j$ is not a saddle to saddle connection, or some $e_j$ is non-hyperbolic and $q_j$ connects to its center manifold, or weighted norm must be used to ensure the stability of each individual wave, etc. See discussions of the generalized Fisher/KPP equation in Sect. 6.

Essentially the same result was proved by Wright [26] and Selle [24], who regarded the concatenated wave pattern as a sum of traveling waves. Besides being easier to treat some less standard systems as mentioned above, the other advantage of our approach is that it directly links the wave speeds and phase shifts to the perturbations of initial conditions and the jumps between adjacent waves, cf. (4.6), (4.22) and (5.4) where $\beta _j(t) q_j'(\xi )$ is in the eigenspace associated to $\uplambda =0$. This information can be useful in some practical applications where we are not only interested in the existence of the the concatenated traveling wave, but also in how each wave component is changed by the interaction with other waves.

Here is a brief outline of the paper. In Sect. 2 we outline the proof. The structure of the proof is based on the approach of Sattinger [23], in which the linear variational system is obtained around the original traveling wave, not around an undetermined shift of the wave (here shifts of the waves). When linear variational systems are considered, the unknown shifts appear as multiples of $q^\prime _j$. The nonlinear system is considered in the last section where we solve for the entire solution and asymptotic shift (here shifts) simultaneously by a contraction mapping principle. We remark that Rottmann-Matthes has developed a method parallel to Sattinger’s approach [21, 22].

In Sect. 3 we give some background about exponential dichotomies and Laplace transform. In Sect. 3.1, we discuss exponential dichotomies in frequency domain where the equation can be treated pointwise in $s$. In Sect. 3.2, we discuss exponential dichotomies where the equation in frequency domain cannot be treated pointwise in $s$. In Sect. 3.3, we discuss the roughness of exponential dichotomies for general abstract equations in Banach spaces. In Sect. 3.4 we discuss exponential dichotomies for linear variational system near the equilibrium $e_j$. In Sect. 3.5 we discuss exponential dichotomies for linear variational system near the traveling wave solution $q_j$. In Sect. 4 we study the linear non-homogeneous system obtained by linearizing (1.1) at the discontinuous concatenated wave solution $u^{\text {con}}(x,t)$. A solution to the non-homogeneous system, ignoring jump discontinuities along the $\Gamma _j$, is obtained in Sect. 4.1, and a solution to the homogeneous system with prescribed jumps is obtained in Sect. 4.2. In Sect. 5 we complete the proof of Theorem 1.1 by solving the nonlinear initial value problem using our solution of the linearized problem and a contraction mapping argument. In Sect. 6, we discuss the wave interaction of the generalized Fisher/KPP equation where an important proposition used in [26] is not satisfied, but may still be treated by our method.

2 Outline of Proof

Let $\Omega =I\times \mathbb {R}^+$ or an open subset of $\mathbb {R}\times \mathbb {R}^+$, always thought of as xt-space. Define the following Banach spaces:

$$\begin{aligned} H^k(\mathbb {R}^+)&=W^{k,2}(\mathbb {R}^+,\mathbb {R}^n), \; k\ge 0, \text { the usual Sobolev space.}\\ H^{k_1\times k_2}(\mathbb {R}^+)&= H^{k_1}(\mathbb {R}^+) \times H^{k_2}(\mathbb {R}^+),\;k_1\ge 0,\, k_2 \ge 0. \\ H^{2,1}(\Omega )&=\{u:\Omega \rightarrow \mathbb {R}^n\; |\; u,u_{xx} \text { and } u_t \in L^2(\Omega ; \mathbb {R}^n\}.\\ |u|_{H^{2,1}(\Omega )}&= |u|_{L^2} + |u_{xx}|_{L^2}+ |u_t|_{L^2}. \end{aligned}$$

As usual, $H^0=L^2$ and $H^k_0(\mathbb {R}^+)\subseteq H^k(\mathbb {R}^+)$ consists of functions that are 0 at $t=0$. We say $u(x,t)\in H^{2,1}_{loc}(\Omega )$ if it is in $H^{2,1}$ when restricted to a bounded subset of $\Omega$.

For a constant $\gamma < 0$, define:

$$\begin{aligned} H^k(\mathbb {R}^+,\gamma )&= \{u:\mathbb {R}^+ \rightarrow \mathbb {R}^n\;|\;e^{-\gamma t} u\in H^k(\mathbb {R}^+ \}; \;|u|_{H^k(\mathbb {R}^+,\gamma )}=|e^{-\gamma t}u|_{H^k(\mathbb {R}^+)}.\\ H^{k_1\times k_2}(\mathbb {R}^+,\gamma )&= H^{k_1}(\mathbb {R}^+,\gamma ) \times H^{k_2}(\mathbb {R}^+,\gamma ). \\ L^2(\Omega ,\gamma )&=\{u:\Omega \rightarrow \mathbb {R}^n\;|\;e^{-\gamma t} u\in L^2(\Omega ) \};\; |u|_{L^2(\Omega ,\gamma )} =|e^{-\gamma t}u|_{L^2(\Omega )}.\\ H^{2,1}(\Omega , \gamma )&=\{ u:\Omega \rightarrow \mathbb {R}^n\;|\;e^{-\gamma t} u\in H^{2,1}(\Omega ) \};\; |u|_{H^{2,1}(\Omega ,\gamma )}=|e^{-\gamma t} u|_{H^{2,1}(\Omega )}. \end{aligned}$$

Let $X^1(\mathbb {R}^+,\gamma )$, or $X^1(\gamma )$ for short, be the space of functions $\beta (t)$ such that $\dot{\beta }\in L^2(\gamma ),\; \gamma <0$. Define the norm in $X^1(\gamma )$ as

$$\begin{aligned} |\beta |_{X^1(\gamma )}:= |\beta (0)| + |\dot{\beta }|_{L^2(\gamma )}. \end{aligned}$$

For $\beta \in X^1(\gamma )$, the limit $\beta (\infty )$ exists. By the Cauchy-Schwarz inequality, have

$$\begin{aligned} |\beta (t) - \beta (\infty )|=|\int _t^\infty e^{\gamma t} (e^{-\gamma t}\dot{\beta }(t)) dt| \le Ce^{\gamma t}|\dot{\beta }|_{L^2(\gamma )}. \end{aligned}$$

(2.1)

The change of coordinates $\xi =x-y-ct$ converts $\Omega$ to a subset $\tilde{\Omega }$ of $\mathbb {R}\times \mathbb {R}^+$, with coordinates $(\xi ,t)$, and converts a function $u(x,t)$ on $\Omega$ to a function $\tilde{u}(\xi ,t)=u(\xi +y+ct,t)$ on $\tilde{\Omega }$.

Lemma 2.1

The map $u\rightarrow \tilde{u}$ is a linear isomorphism of $H^{2,1}(\Omega , \gamma )$ to $H^{2,1}(\tilde{\Omega }, \gamma )$. The map $u\rightarrow \tilde{u}$ and its inverse $\tilde{u} \rightarrow u$ both have norm at most $1+|c|$.

Proof

Let $u \in H^{2,1}_0(\Omega ,\gamma )$. Then $\tilde{u}_\xi = u_x, \; \tilde{u}_{\xi \xi } = u_{xx}, \; \tilde{u}_t = u_t + c_j u_x$. Thus

$$\begin{aligned} |\tilde{u}| + |\tilde{u}_\xi | + |\tilde{u}_{\xi \xi }|+ |\tilde{u}_t| \le |u|+|u_x|+ |u_{xx}| + |u_t| + |c| |u_x|. \end{aligned}$$

Here all the norms are in $L^2(\Omega ,\gamma )$. The lemma follows easily.$\square$

Let $\Gamma (x_0,c)=\{(x,t):x=x_0-ct, \, t\ge 0\}$.

Lemma 2.2

If $\Gamma (x_0,c)\subset \Omega$, then the mapping $u \rightarrow u|_{\Gamma (x_0,c)}$ is bounded linear from $H^{2,1}(\Omega ,\gamma )$ to $H^{0.75\times 0.25}(\mathbb {R}^+,\gamma )$. Moreover, there is a number $K>0$, independent of $x_0$ and $c$, such the norm of the linear map is at most $K(1+|c|)$.

Proof

For $c=0$, see [15, 25]. For $c\ne 0$, use Lemma 2.1 followed by letting $c=0$.$\square$

Now assume that $v \in H^{2,1}_\mathrm{{loc}}(\mathbb {R}\times \mathbb {R}^+)$, and $\Gamma (x_0,c)$ is the line as in Lemma 2.2. It follows from a localization process and Lemmas 2.1 and 2.2, the restriction of $v$ to $\Gamma$, as a function of $t$, belongs to $H^{0.75\times 0.25}_\mathrm{{loc}}(\mathbb {R}^+)$.

Lemma 2.3

Let $x=0$ be the line that divides $\{x\in \mathbb {R}, t \ge 0\}$ into two regions: $\Omega ^- =\{(x,t):x<0,t\ge 0\}$ and $\Omega ^- =\{(x,t):x>0, t\ge 0\}$. Let $v^-\in H^{2,1}(\Omega ^-)$ and $v^+\in H^{2,1}(\Omega ^+)$. Assume the traces $v^-|_{x=0} =v^+|_{x=0}$ in the space $H^{0.75\times 0.25}(\mathbb {R}^+)$. Then the function $v$ that equals $v^-$ on $\Omega ^-$ and $v^+$ on $\Omega ^+$ is in the space $H^{2,1}(\mathbb {R}\times \mathbb {R}^+)$.

Proof

The proof is a simple excise of the trace theory, and is outlined below. Let $w$ be defined on $\{x\in \mathbb {R}, t\ge 0\}$, and equals to $D_x v^-$ (or $D_x v^+$) on $\Omega ^-$ (or $\Omega ^+$). Using integration by parts, it is easy to show that $D_x v = w$ in $\mathbb {R}\times \mathbb {R}^+$. Thus $v_x\in L^2(\mathbb {R}\times \mathbb {R}^+)$. Same proof shows that $v_{xx}, v_t\in L^2(\mathbb {R}\times \mathbb {R}^+)$. Therefore $v\in H^{2,1}(\mathbb {R}\times \mathbb {R}^+)$.$\square$

Remark 2.1

Suppose $v\in L^2_\mathrm{loc}(\mathbb {R}\times \mathbb {R}^+)$, and its restrictions to the left and right of $\Gamma$, $v^-$ and $v^+$, are locally $H^{2,1}$ functions. Using the cut-off functions and change of coordinates as in Lemma 2.1, it is easy to see that $v\in H^{2,1}_\mathrm{loc}(\mathbb {R}\times \mathbb {R}^+)$ if and only if the traces of $v^-$ and $v^+$ on $\Gamma$ are equal.

2.1 Deriving the Linear Variational System

Write the exact solution of (1.1), with the initial condition $u^{ex}(x,0)=u^{ex}_0(x)$, as $u^{ex}(x,t) = u^{ap}(x,t) + u^{cor}(x,t),\; (x,t)\in \mathbb {R}\times \mathbb {R}^+$, with $u^{ap}(x,t)= q_j(x-y_j- c_j t + r_j)$ in $\Omega _j$. For the rest of the paper, denote $u^{cor}(x,t)$ by $u(x,t)$, and its restriction to $\Omega _j$ by $u_j$.

Let $\{r_j\}_{j=1}^m=(r_1,\dots ,r_m)$, often with the range of $j$ omitted, same notation for a sequence of functions $\{u_j\}$. The $\{r_j\}$ are parameters to be determined so that $u_j(x,t)$ will lie in the appropriate space. The equation for $u_j$, the perturbation to $q_j(x-y_j- c_j t + r_j)$, is

$$\begin{aligned} u_t= u_{xx}+Df(q_j(x-y_j - c_j t + r_j))u + \mathcal {O}(u^2),\quad (x,t)\in \Omega _j \end{aligned}$$

The initial value for $u_j(x,t)$ in $\Omega _j$ is

$$\begin{aligned} u_{j0}(x)=u_j(x,0)=u^{ex}_0(x)- q_j(x-y_j+ r_j), \quad x\in I_j=(x_{j-1},x_j). \end{aligned}$$

Recall that $\Gamma _j=\{(x,t ): x=x_j+\bar{c}_j t, \, t\ge 0\}$ separates $\Omega _j, \Omega _{j+1}$. The traces $u_j(\Gamma _j)$ and $u_{j+1}(\Gamma _j)$ exist. Define the jump of $\{u_j\}$ across $\Gamma _j$, a function of $t$, by

$$\begin{aligned}{}[\{u_j\}](\Gamma _j)=u_{j+1}(\Gamma _j)-u_{j}(\Gamma _j). \end{aligned}$$

We will use this notation for any sequence of functions defined on $\{\Omega _j\}$, such as $\{q_j(\xi + y_j+ c_j t)\}$, and even after the change of variables to $\xi _j$ in $\Omega _j$. With this notation, the jump conditions along $\Gamma _j$ are

$$\begin{aligned}{}[\{u_j\},\{u_{jx}\}](\Gamma _j)=-[u^{ap},u^{ap}_x](\Gamma _j), \quad 1\le j \le m-1. \end{aligned}$$

(2.2)

The jump conditions depend on the parameters $\{r_j\}$ since $u^{ap}$ does.

Notice the compatibility between the jump conditions at $t=0$ and the jumps of the initial condition at $x=x_j$:

$$\begin{aligned}{}[\{u_j\},\{u_{jx}\}](\Gamma _j)|_{t=0} = [\{u_j0\},\{\dot{u}_{j0}\}](x_j), \quad 1\le j \le m-1. \end{aligned}$$

The unknown $\{r_j\}$ appears in the argument of $u^{ap}(x,t)$. To avoid having an undetermined $r_j$ in $Df(u^{ap})$, we shall follow the idea of Sattinger [23] to linearize around $q_j(x-y_j - c_j t)$. With the moving coordinate $\xi _j=x-y_j- c_j t$, denoted by $\xi$ when there should be no ambiguity, the exact solution in $\Omega _j$ becomes $\tilde{u}^{ex}(\xi ,t)=u^{ex}(\xi +y_j+c_jt,t)$. However, both the approximate solution and the perturbation depend on the parameter $r_j$. To show this dependence, in $\Omega _j$ we write

$$\begin{aligned} \tilde{u}^{ex}(\xi ,t)=q(\xi +r_j)+\tilde{u}(\xi ,t;r_j), \quad \tilde{u}(\xi ,t;r_j)=u^{ex}(\xi +y_j+c_jt,t)-q_j(\xi +r_j). \end{aligned}$$

We find that $\tilde{u}(\xi ,t;r_j)$ is a solution of the following differential equation:

$$\begin{aligned} u_t= u_{\xi \xi } + c_i u_\xi +Df(q_j(\xi ))u + B_j(r_j)u + R_j(u,r_j), \quad (\xi ,t) \in \Omega _j, \end{aligned}$$

(2.3)

where $B_j(r_j)u +R_j(u,r_j) = f(q_j(\xi + r_j) +u) -f(q_j(\xi +r_j))-Df(q_j(\xi )) u$, and

$$\begin{aligned} B_j(r_j)&= Df(q_j(\xi \!+\!r_j))\!-\!Df(q_j(\xi )) \!=\! r_j\int _0^1 D^2f(q_j(\xi \!+\!s r_j))q_j^\prime (\xi \!+\! s r_j) ds\!=\!\mathcal {O}(r_j),\\ R_j(u,r_j)&= f(q_j(\xi +r_j) +u) -f(q_j(\xi +r_j)) - Df(q_j(\xi +r_j))u=\mathcal {O}(|u|^2). \end{aligned}$$

Since $B(r_j)u=\mathcal {O}(r_j|u|)$, so the terms $B(r_j)u$, $R(u,r_j)$ are of second order in $(u,r_j)$.

When $r_j=0$, the initial condition for the perturbation $\tilde{u}$ is

$$\begin{aligned} \tilde{u}(\xi ,0;0)=u^{ex}(\xi +y_j,0)-q_j(\xi ) \overset{def}{=}\bar{u}_{j0}(\xi ). \end{aligned}$$

For general $r_j$, the initial condition for the perturbation is

$$\begin{aligned} \tilde{u}(\xi ,0;r_j)=u^{ex}(\xi +y_j,0)-q_j(\xi +r_j)=\bar{u}_{j0}(\xi )+q_j(\xi )-q_j(\xi +r_j). \end{aligned}$$

Let $g_j(\xi ,r_j)=q_j(\xi ) - q_j(\xi + r_j)+ r_j q_j^\prime (\xi )=\mathcal {O}(r_j^2)$. We have the initial conditions for the correction term

$$\begin{aligned} u_j(\xi ,0) = \bar{u}_{j0}(\xi ) -r_j q^\prime _j(\xi ) + g_j(\xi ,r_j),\quad x\in I_j. \end{aligned}$$

(2.4)

Let $W_j=(q_j,q_j^\prime ),\;\{r_j\}=(r_1,\dots , r_m)$. We rewrite the jump conditions (2.2) to emphasize the dependence on $\{r_j\}$

$$\begin{aligned} -[u^{ap},u_\xi ^{ap}](\Gamma _j)\overset{def}{=} J_j(\Gamma _j, \{r_j\})&=W_j(\Gamma _j + r_j)- W_{j+1}(\Gamma _j + r_{j+1})\\&= W_j(\Gamma _j)-W_{j+1}(\Gamma _j)+G_j(\{r_j\}), \end{aligned}$$

where

$$\begin{aligned}G_j(\{r\}):= W_{j+1}(\Gamma _j)-W_{j+1}(\Gamma _j+r_{j+1})\\ +\,W_j(\Gamma _j + r_j) - W_j( \Gamma _j). \end{aligned}$$

Recall that $J_{j0}= W_j(\Gamma _j)- W_{j+1}(\Gamma _j)$, which is the jump condition when $\{r_j\}=0$. Now (2.2) can be written as

$$\begin{aligned}{}[\{u_j\},\{u_{jx}\}](\Gamma _j)= J_j(\Gamma _j,\{r_j\})= J_{j0}(\Gamma _j) + G_j(\{r_j\}), \quad 1\le j \le m-1. \end{aligned}$$

(2.5)

As shown in Lemma 2.3 and the remark that follows, to have $u^{con} \in H^{2,1}_{loc}(\mathbb {R}\times \mathbb {R}^+)$, the jumps across each $\Gamma _j$ must satisfy

$$\begin{aligned} u_{j+1}(\Gamma _j) - u_{j}(\Gamma _j)&= q_j(\Gamma _j+r_j)- q_{j+1}(\Gamma _j+r_{j+1}) \in H^{0.75}(\Gamma _j),\\ u_{j+1,x}(\Gamma _j) - u_{j,x}(\Gamma _j)&= q_{j,x}(\Gamma _j+r_j)- q_{j+1,x}(\Gamma _j+r_{j+1}) \in H^{0.25}(\Gamma _j). \end{aligned}$$

In order to solve the nonlinear system (2.3), (2.4), (2.5), we shall first consider the following nonhomogeneous linear system:

$$\begin{aligned}&u_{jt}= u_{j,xx} + Df(q_j)u_j + h_j(x,t),\quad u_j(x,0) = u_{j0}(x), \end{aligned}$$

(2.6a)

$$\begin{aligned}&([\{u_j\}], [\{u_{jx}\}])(\Gamma _j) = J_j(\Gamma _j), \end{aligned}$$

(2.6b)

$$\begin{aligned}&[\{u_{j0}\}, \{\dot{u}_{j0}\}](x_j)=J_j(\Gamma _j)|_{t=0}. \end{aligned}$$

(2.6c)

In these equations, for $j=1,\ldots m$, $h_j\in L^2(\Omega _j,\gamma )$, $\gamma <0$, $u_j(x,0) \in H^1(I_j)$; and for $j=1,\ldots m-1$, $J_j(\Gamma _j) \in H^{0.75\times 0.25}(\gamma )$. Temporarily they do not depend on $(\{r_j\},\{u_j\})$. The last one is the compatibility between the initial conditions and the jump conditions. We look for $u_j\in H^{2,1}(\Omega _j,\gamma )+ span\{\beta (t) q_j^\prime (\xi ),\beta (t) \in X^1(\gamma )\}$, as will be specified in Sect. 4.

For the nonlinear systems (2.3–2.5), the forcing terms, initial and jump conditions depend on the parameters $\{r_j\}$, since $u^{ap}$ does. In Sect. 5, the correction term $u(x,t)$, together with shifts $\{r_j\}$ will be solved by letting

$$\begin{aligned} \begin{aligned} h_j&= B_j(r_j) u + R_j(r_j,u_j), \\ u_{j0}&= \bar{u}_{j0}(\xi ) - r_j q_j^\prime (x-y_j) + g_j(\xi ,r_j) \text { for }x\in I_j, \\ J_j(\Gamma _j)&=J_{j0}(\Gamma _j) + G_j(\{r_j\}). \end{aligned} \end{aligned}$$

(2.7)

We look for $(\{u_j\},\{r_j\})$ with $u_j \in H^{2,1}(\Omega _j,\gamma )$ by using a contraction mapping argument adapted from [23].

3 Function Spaces and Exponential Dichotomies

The following definitions come from [11]. A function $f(s)$ is in the Hardy-Lebesgue class $\mathcal {H}(\gamma ), \gamma \in \mathbb {R}$, if

• (1) $f(s)$ is analytic in $\mathfrak {R}(s) > \gamma$;

• (2) $\{\sup _{\sigma > \gamma } (\int _{-\infty }^\infty |f(\sigma +i\omega )|^2 d\omega )^{1/2}\}< \infty$.

$\mathcal {H}(\gamma )$ is a Banach space with norm defined by the left side of (2).

According to the Paley–Wiener Theorem [28], $u(t) \in L^2(\mathbb {R}^+,\gamma )$ if and only if its Laplace transform $\hat{u}(s) \in \mathcal {H}(\gamma )$, and the mapping $u \rightarrow \hat{u}$ is a Banach space isomorphism.

For $k, k_1, k_2 \ge 0$ and $\gamma \in \mathbb {R}$, let

$$\begin{aligned} \mathcal {H}^k(\gamma )&= \{u(s)\;|\; u(s)\text { and }(s-\gamma )^k u(s) \in \mathcal {H}(\gamma )\},\\ |u|_{\mathcal {H}^k(\gamma )}&= |u|_{\mathcal {H}^k(\gamma )}+|(s-\gamma )^k u|_{\mathcal {H}^k(\gamma )}, \\ \mathcal {H}^{k_1\times k_2}(\gamma )&= \mathcal {H}^{k_1}(\gamma )\times \mathcal {H}^{k_2}(\gamma ). \end{aligned}$$

An equivalent norm on $\mathcal {H}^k(\gamma )$ is

$$\begin{aligned} |u|_{\mathcal {H}^k(\gamma )}=\left( \sup _{\sigma > \gamma }\int _{-\infty }^\infty |u(\sigma + i\omega )|^2(1+|\sigma +i\omega |^{2k})d\omega \right) ^{1/2}\!\!. \end{aligned}$$

It can be shown that $u(t) \in H^k_0(\mathbb {R}^+,\gamma )$ if and only if $\hat{u}(s) \in \mathcal {H}^k(\gamma )$, and the mapping $u \rightarrow \hat{u}$ is a Banach space isomorphism. Clearly $(u,v) \in H^{k_1\times k_2}_0(\mathbb {R}^+,\gamma ), \; k_1,k_2 \ge 0$, if and only if $(\hat{u}, \hat{v})\in \mathcal {H}^{k_1 \times k_2}(\gamma )$, and the mapping $(u,v) \rightarrow (\hat{u},\hat{v})$ is a Banach space isomorphism.

To treat Laplace transformed linear systems that depend on the parameter $s$, following [11, 12], we introduce the following family of norms on $u\in \mathbb {C}^n$ and $\mathbb {C}^n\times \mathbb {C}^n$:

Definition 3.1

For $Re(s) > \gamma$ and $k_1\ge 0$, let $E^{k_1}(s)$ denote $\mathbb {C}^n$ with the weighted norm

$$\begin{aligned} \left| u \right| _{E^{k_1}(s)}=(1+|s|^{k_1})|u|, \end{aligned}$$

and let $E^{k_1\times k_2}(s)$ denote $\mathbb {C}^n\times \mathbb {C}^n$ with the weighted norm

$$\begin{aligned} \left| (u,v)^\tau \right| _{E^{k_1\times k_2}(s)}=(1+|s|^{k_1})|u| + (1+|s|^{k_2})|v|, \end{aligned}$$

where $|u|$ and $|v|$ are the usual norms on $\mathbb {C}^n$.

Using $E^{k_1}(s)$ and $E^{k_1\times k_2}(s)$, we define some equivalent norms for $u\in \mathcal {H}^{k_1}(\gamma )$ and $(u,v)^\tau \in \mathcal {H}^{k_1\times k_2}(\gamma )$:

$$\begin{aligned} \left( \sup _{\sigma > \gamma } \int _{-\infty }^\infty |u|^2_{E^{k_1}(\sigma + i\omega )} d\omega \right) ^{1/2}\!,\quad \left( \sup _{\sigma > \gamma } \int _{-\infty }^\infty |(u,v)^\tau |^2_{E^{k_1\times k_2}(\sigma + i\omega )} d\omega \right) ^{1/2}\!. \end{aligned}$$

Consider the second order linear equation and its Laplace transform

$$\begin{aligned}&u_t= u_{\xi \xi } + c u_\xi + A(\xi ,t) u,\quad u(\xi ,0)=0, \end{aligned}$$

(3.1)

$$\begin{aligned}&\hat{u}_{\xi \xi }= s\hat{u} - c\hat{u}_\xi -\hat{A}(\xi ,s)\overset{s}{*} \hat{u}. \end{aligned}$$

(3.2)

Here $A(\xi ,t)$ is $C^1$ in $t\in \mathbb {R}^+$ for each fixed $\xi$, and is piecewise continuous in $\xi$ in the $C^1(\mathbb {R}^+)$ norm. Examples are $A(\xi ,t)= Df(e_j)$, $A(\xi ,t) = Df(q_j(\xi ))$, and $A(\xi ,t)= Df(q_j(\xi + kt)), t \ge 0, \xi \in \mathbb {R}$. The convolution represents the operator $\mathcal {L}(A(\xi ,t)\mathcal {L}^{-1}\hat{u}(\xi ,s))$ and is performed along the vertical axis in $\mathbb {C}$ where both $\hat{b}$ and $\hat{u}$ are defined:

$$\begin{aligned} \hat{A}(\xi ,s)\overset{s}{*} \hat{u}(\xi ,s) := \frac{1}{2\pi i} \int _{\sigma -i\infty }^{\sigma +i\infty } \hat{A}(\xi ,p)\hat{u}(\xi ,s-p)dp. \end{aligned}$$

Convert (3.1), (3.2) to the equivalent first order system and its Laplace transform

$$\begin{aligned} u_\xi&= v,\quad v_\xi = u_t - c v - A(\xi ,t) u,\quad u(\xi ,0)=0, \end{aligned}$$

(3.3)

$$\begin{aligned} \hat{u}_\xi&= \hat{v},\quad \hat{v}_\xi = s \hat{u} - c\hat{v} -\hat{A}(\xi ,s)\overset{s}{*} \hat{u}. \end{aligned}$$

(3.4)

3.1 Exponential Dichotomies if $A(\xi )$ is Independent of $t$

If $A(\xi ,t)= A(\xi )$ is independent of time $t$, then (3.4) becomes

$$\begin{aligned} \hat{u}_\xi =\hat{v},\quad \hat{v}_\xi = s \hat{u} - c\hat{v} - A(\xi ) \hat{u}. \end{aligned}$$

(3.5)

This equation is defined point-wise in $s$ and can be solved one $s$ at a time.

Let $T(\xi ,\zeta ; s)$ be the principal matrix solution for (3.5), $s$ be a parameter in $\mathcal {S}\subset \mathbb {C}$, $I \subset \mathbb {R}$ be an interval, and $Id$ be an identity matrix.

Definition 3.2

We say that (3.5) has an $s$-dependent exponential dichotomy for $s\in \mathcal {S}$ and $\xi \in I$ if there exist projections $P_s(\xi ,s) + P_u(\xi ,s)=Id$ on $\mathbb {C}^{2n}$, analytic in $s$ and continuous in $\xi$, such that, with the $s$-dependent constants $K(s), \beta (s)>0$, the following properties hold:

$$\begin{aligned} \begin{aligned} T(\xi ,\zeta ;s)P_s(\zeta ,s)&= P_s(\xi ,s)T(\xi ,\zeta ;s), \quad \xi \ge \zeta ,\\ |T(\xi ,\zeta ;s)P_s(\zeta ,s)|_{R^{2n}}&\le K(s) e^{-\beta (s)|\xi -\zeta |}, \quad \xi \ge \zeta ,\\ |T(\xi ,\zeta ;s)P_u(\zeta ,s)|_{R^{2n}}&\le K(s) e^{-\beta (s)|\xi -\zeta |}, \quad \xi \le \zeta . \end{aligned} \end{aligned}$$

(3.6)

We say that (3.5) has a uniform exponential dichotomy on the spaces $E^{(k+0.5) \times k}(s), k\ge 0$ for $s\in \mathcal {S}$ and $\xi \in I$ if it has an $s$-dependent exponential dichotomy, and in addition there are constants $K, \alpha >0$, independent of $s$ and $\xi$, such that

• (1) $|P_s(\xi ,s)| \le K$ and $|P_u(\xi ,s)|\le K$ for all $s\in \mathcal {S}$ and $\xi \in I$,

• (2) each $K(s)\le K$, and

• (3) $\beta (s) = \alpha (1+ |s|^{0.5})$.

Here $|P_s(\xi ,s)|$ and $|P_s(\xi ,s)|$ are calculated using the norms on $E^{(k+0.5) \times k}(s)$. The $s$ dependent stable and unstable subspaces for the dichotomy shall be denoted by

$$\begin{aligned} E_s(\xi ,s)=RP_s(\xi ,s),\quad E_u(\xi ,s) = RP_u(\xi ,s). \end{aligned}$$

Given $\xi _0\in \mathbb {R}$, if $I=(-\infty ,\xi _0]$, then the unstable subspace $E_u(\xi ,s),\xi \in I$ is unique, although the exponential dichotomy in $I$ is not unique. Similarly, If $I=[\xi _0,\infty )$, then $E_s(\xi , s)$ is unique, although the exponential dichotomy in $I$ is not unique.

3.2 Exponential Dichotomies if $A(\xi ,t)$ Depends on $t$

In general (3.4) involves a global operator $\hat{u}(\xi ,s)\rightarrow \hat{A}(\xi ,s)\overset{s}{*} \hat{u}(\xi ,s)$ so the exponential dichotomy cannot be considered by fixing one $s$ at a time. We find the following lemma useful.

Lemma 3.1

Let $B(\xi ,t)$ be a $C^1$ bounded function in $t$ for each $\xi$ and is piecewise continuous in $\xi$ in the norm of $|B |_{C^1(t)}$. Then

$$\begin{aligned} B(\xi ,t)u(\xi ,t) |_{H_0^{0.75}(\mathbb {R}^+)} \le |B(\xi ,t)|_{C^1(t)} |u|_{H_0^{0.75}(\mathbb {R}^+)}. \end{aligned}$$

Moreover, after the Laplace transform, we have

$$\begin{aligned} |\hat{B}(\xi ,s)\overset{s}{*} \hat{u}(\xi ,s)|_{\mathcal {H}^{0.75}(0)} \le |B(\xi ,t)|_{C^1(t)} |\hat{u}(\xi ,s)|_{\mathcal {H}^{0.75}(0)}. \end{aligned}$$

Proof

It is straightforward to show that $u(\xi ,t)\rightarrow B(\xi ,t) u(\xi ,t)$ is bounded in the spaces $H_0^k(\mathbb {R}^+)$, for $k=0,1$:

$$\begin{aligned} |B(\xi ,t)u(\xi ,t) |_{H_0^k(\mathbb {R}^+)} \le |B|_{C^1} |u|_{H_0^k(\mathbb {R}^+)},\; k=0,1. \end{aligned}$$

Expressed as the interpolation of two spaces $H^{0.75}_0=[L^2, H_0^1]_{0.75}$, the first estimate of the lemma can be obtained by the theory of interpolations [15, 16]. The second estimate can be obtained by applying the Laplace transform to $Bu$.$\square$

Consider the abstract differential equation $U_\xi = L(\xi ) U, \; \xi \in I$ in the Banach space $E$. Here $I$ is a bounded or unbounded interval in $\mathbb {R}$, $L(\xi ): E \rightarrow E$ is a linear (possibly unbounded) operator for each $\xi \in I$.

Definition 3.3

We say $U_\xi = L(\xi )U$ has an exponential dichotomy on $E$ defined for $\xi \in I$, if there exist projections $P_s(\xi ) + P_u(\xi ) = Id$ in $E$, continuous in $\xi \in I$, and a solution operator $T(\xi ,\zeta )$ that is defined and invariant on subspaces of $E$ as in (3.7a), (3.7b). Moreover there exist constants $K,\alpha >0$ such that the last inequalities (3.7c), (3.7d) are satisfied.

$$\begin{aligned}&T(\xi ,\zeta ): R P_s(\zeta ) \rightarrow R P_s(\xi ) \text { is defined and continuous for } \xi \ge \zeta ; \end{aligned}$$

(3.7a)

$$\begin{aligned}&T(\xi ,\zeta ): R P_u(\zeta ) \rightarrow R P_u(\xi ) \text { is defined and continuous for } \xi \le \zeta ; \end{aligned}$$

(3.7b)

$$\begin{aligned}&|T(\xi ,\zeta )P_s(\zeta )|_E \le K e^{-\alpha |\xi -\zeta |}, \quad \xi \ge \zeta ; \end{aligned}$$

(3.7c)

$$\begin{aligned}&|T(\xi ,\zeta )P_u(\zeta )|_E \le K e^{-\alpha |\xi -\zeta |}, \quad \xi \le \zeta . \end{aligned}$$

(3.7d)

We assume that $T(\xi ,\zeta ) u$ is a solution of the differential equation $u_\xi = L(\xi ) u$ if

• (1) $u\in RP_s(\zeta )$ and $\xi \ge \zeta$, or

• (2) $u\in RP_u(\zeta )$ and $\xi \le \zeta$.

For each initial data $(\hat{u}, \hat{v}) \in \mathcal {H}^{0.75\times 0.25}(\gamma )$ at $\zeta \in I$, there may not exist a solution of (3.4) in $\mathcal {H}^{0.75\times 0.25}(\gamma )$ for $\xi \le \zeta$ or $\xi \ge \zeta$. Assume that $\hat{u}(\xi ,s) \rightarrow \hat{A}(\xi ,s)\overset{s}{*} \hat{u}(\xi ,s)$ is a bounded operator in $\mathcal {H}^{0.25}(\gamma )$, (3.4) can be written as $U_\xi = L(\xi ) U$ in the Banach space $E= \mathcal {H}^{0.75\times 0.25}(\gamma )$ where $U=(\hat{u},\hat{v})$.

Definition 3.4

We say that (3.4) has an exponential dichotomy in $E=\mathcal {H}^{0.75\times 0.25}(\gamma )$ for $\xi \in I$ if there exist projections $P_s(\xi ) + P_u(\xi )=Id$, partially defined solution operator $T(\xi ,\zeta )$ and constants $K,\alpha >0$ as in Definition 3.3.

Suppose that $u\in H^{2,1}_0(\mathbb {R}\times \mathbb {R}^+)$ is a solution of (3.1). Then for any $\xi _0 \in \mathbb {R}$ the trace $(u,u_\xi )(\xi _0)$ can be defined and is a continuous function $\mathbb {R} \rightarrow H^{0.75\times 0.25}_0(\mathbb {R}^+)$, cf. [15]. However, to each $(u_0,v_0)\in H^{0.75\times 0.25}_0(\mathbb {R}^+)$, there may not exist a solution for (3.1) in $H^{2,1}_0(I \times \mathbb {R}^+)$ such that the trace at $\xi _0$ is $(u_0,v_0)$.

To be more specific, consider (3.3) as a first order system with the independent variable $\xi$, we look for $(u,v)\in H_0^{0.75\times 0.25}(\gamma )$ in the space of functions in $t$. The function $A(\xi ,t)$ should be smooth enough such that the mapping $u \rightarrow A(\xi ,t) u$ is continuous from $H^{0.75}_0(\gamma ) \rightarrow H_0^{0.25}(\gamma )$.

Definition 3.5

We say that (3.3) has an exponential dichotomy in $E=H_0^{0.75\times 0.25}(\gamma )$ for $\xi \in I$ if if there exist projections $\check{P}_s(\xi ) + \check{P}_u(\xi )=Id$, partially defined solution operator $\check{T}(\xi ,\zeta )$ and constants $K,\alpha >0$ as in Definition 3.3.

Lemma 3.2

• (1) Assume that (3.4) or (3.5) has an exponential dichotomy in $\mathcal {H}^{0.75\times 0.25}(\gamma )$ for $\xi \in \mathbb {R}$. Then (3.3) has an exponential dichotomy in ${H}_0^{0.75\times 0.25}(\gamma )$ with the projections $\check{P}_j(\xi )=\mathcal {L}^{-1} P_j(\xi ) \mathcal {L}$ where $j=s,u$ and the partially defined solution operator $\check{T}(\xi ,\zeta ) = \mathcal {L}^{-1} T(\xi ,\zeta ) \mathcal {L}$ for $\xi ,\zeta \in I$.

• (2) Assume that (3.5) has an exponential dichotomy in $E^{(k+0.5)\times k}(s)$ for $k\ge 0, Re(s) \ge \gamma , \xi \in \mathbb {R}$. Then (3.5) has an exponential dichotomy in $\mathcal {H}^{(k+0.5)\times k}(\gamma )$ with the same projections derived from those in $E^{(k+0.5)\times k}(s)$, and the same constants $K,\alpha$.

Proof

• (1) Observe that $(u_0,v_0) \rightarrow \mathcal {L}(u_0,v_0), \; H_0^{0.75\times 0.25}(\gamma ) \rightarrow \mathcal {H}^{0.75\times 0.25}(\gamma )$ is a Banach spaces isomorphism.

• (2) The proof of part (2) follows from that of Lemma 3.1 in [11].

$\square$

3.3 Roughness of Exponential Dichotomies

Consider the abstract differential equation $u_\xi = A(\xi ) u, \; \xi \in I$ in the Banach space $E$. The following result gives the basic facts about persistence of exponential dichotomies under perturbation in a Banach space $E$.

Theorem 3.3

(Roughness of Exponential Dichotomies) Assume that $I$ is a bounded or unbounded interval in $\mathbb {R}$, $A(\xi ): E \rightarrow E$ is a bounded operator for each $\xi \in I$ and is in $L^\infty (I)$ in the norm of bounded operators in $E$, and the linear differential equation in $E$, $u_\xi =A(\xi ) u$, has an exponential dichotomy on $I$ with projections $P^0(\xi )+Q^0(\xi )=Id$ and constants $K_0,\,\alpha _0>0$. Assume that $B(\xi ): E\rightarrow E$ is another bounded linear operator in $L^\infty (I)$ with $\delta =\sup \{|B(\xi )|, \, \xi \in I\}<\infty$.

Consider the perturbed linear equation

$$\begin{aligned} u_\xi = (A(\xi ) + B(\xi ))u. \end{aligned}$$

(3.8)

Let $0<\tilde{\alpha }< \alpha _0$, and assume that $\delta$ is sufficiently small so that

$$\begin{aligned} C_1\delta <1 \text { and }C_2\delta <1, \text { where }C_1=\frac{2K_0}{\alpha _0-\tilde{\alpha }},\; C_2= \frac{2K_0^2}{(\alpha _0-\tilde{\alpha })(1-C_1\delta )}. \end{aligned}$$

(3.9)

Then (3.8) also has an exponential dichotomy on $I$ with projections $\tilde{P}(\xi )+\tilde{Q}(\xi )=Id$ and the exponent $\tilde{\alpha }$. The multiplicative constant is $\tilde{K} = K_0(1-C_1\delta )^{-1}(1-C_2\delta )^{-1}$ and the following inequalities hold for $\xi , \, \zeta \in I$: There exists a partially defined and invariant solution operator $T_B(\xi ,\zeta )$ for the linear system (3.8) that satisfies (3.7a), (3.7b) with $T$ replaced by $T_B$. And

$$\begin{aligned} |T_B(\xi ,\zeta )\tilde{P}(\zeta )|&\le \tilde{K} e^{-\tilde{\alpha }(\xi -\zeta )},\quad \zeta \le \xi ;\\ |T_B(\xi ,\zeta )\tilde{Q}(\zeta )|&\le \tilde{K} e^{-\tilde{\alpha }(\zeta -\xi )},\quad \xi \le \zeta ;\\ |\tilde{P}(\xi ) - P^0(\xi )|&\le \frac{C_2\delta }{1-C_2 \delta }. \end{aligned}$$

If $E$ is finite dimensional, then the proof of Theorem 3.3 is well known, [3]. If $E$ is an infinite dimensional Banach space, we cannot write the solution operator backwards in time, the proof is quite different, [5, 10]. For a shorter proof with almost identical notations, see [13] (simply replace the rate function $a(x)$ by $e^x$ and the decay rate $(a(x)/a(y))^{-\alpha }$ be $e^{-\alpha (x-y)}$).

3.4 Exponential Dichotomies for Linear Variational Systems Around $e_j$

We study the linear variational system around $e_j$ and a small perturbation that depends on time $t$. Consider the linear variational system around $e_j$ and its Laplace transform:

$$\begin{aligned} u_\xi&= v, \quad v_\xi = u_t -\bar{c}_j v - Df(e_j) u, \quad u(\xi ,0)=0, \end{aligned}$$

(3.10)

$$\begin{aligned} \hat{u}_\xi&= \hat{v}, \quad \hat{v}_\xi = (sI -Df(e_j))\hat{u} - \bar{c}_j \hat{v}. \end{aligned}$$

(3.11)

Let $b(\xi ,t)$ be piecewise continuous in $\xi$ and is $C^1$ in $t\in \mathbb {R}^+$. Consider the following perturbed system and its Laplace transform:

$$\begin{aligned} u_\xi&= v, \quad v_\xi = u_t -\bar{c}_j v - Df(e_j) u - b(\xi ,t)u , \quad u(\xi ,0)=0, \end{aligned}$$

(3.12)

$$\begin{aligned} \hat{u}_\xi&= \hat{v}, \quad \hat{v}_\xi = (sI -Df(e_j))\hat{u} -\hat{b}\overset{s}{*}\hat{u} - \bar{c}_j \hat{v}. \end{aligned}$$

(3.13)

Lemma 3.4

• (1) If (H1) is satisfied, then system (3.11) has an exponential dichotomy in the function space $E^{(k+0.5)\times k}(s)$ for $k\ge 0,\; Re(s) \ge \gamma ,\; \xi \in \mathbb {R}$.

• (2) Assume that the linear operator $\hat{u}(\xi ,s) \rightarrow \hat{b} \overset{s}{*} \hat{u}$ is piecewise continuous in $\xi \in \mathbb {R}$, uniformly bounded from $\mathcal {H}^{0.75}(\gamma ) \rightarrow \mathcal {H}^{0.25}(\gamma )$, and satisfies

  $$\begin{aligned} |\hat{b} \overset{s}{*} \hat{u}|_{\mathcal {H}^{0.25}(\gamma )} \le \delta |\hat{u} (\xi ,s) |_{\mathcal {H}^{0.75}(\gamma )}, \quad \xi \in \mathbb {R}. \end{aligned}$$

Then if $\delta >0$ is sufficiently small, the first order system (3.13) also has an exponential dichotomy in $\mathcal {H}^{0.75\times 0.25}(\gamma )$ for $\xi \in \mathbb {R}$.

Proof

• (1) Simply use the spectral projections of (3.11) as the projections of the dichotomy.

• (2) Result from part (1) implies that (3.11) has an exponential dichotomy in $\mathcal {H}^{0.75\times 0.25}(\gamma )$. If $\delta$ is small, we can treat (3.13) as a small perturbation of (3.11), then apply Theorem 3.3.

$\square$

Lemma 3.5

Assume the conditions of Lemma 3.4 are satisfied. Let $E_s(\xi ), E_u(\xi )$ be the stable and unstable subspaces of the dichotomy for (3.13) in $\mathcal {H}^{0.75\times 0.25}(\gamma )$.

• (1) Let $\phi \in E_s(a)$. For $\xi \ge a$, define $(u,v)^\tau (\xi ,t)= \mathcal {L}^{-1}(T(\xi ,a)P_s(a)\phi )$. Then $u\in H^{2,1}_0([a,\infty ) \times \mathbb {R}^+,\gamma )$ and is a solution to (3.1). Moreover

  $$\begin{aligned} |u|_{H^{2,1}(\gamma )} \le C |\phi |_{\mathcal {H}^{0.75 \times 0.25}(\gamma )}. \end{aligned}$$

  (3.14)

• (2) Let $\phi \in E_u(a)$. For $\xi \le a$, define $(u,v)^\tau (\xi ,t)= \mathcal {L}^{-1}(T(\xi ,a)P_u(a)\phi )$. Then $u\in H^{2,1}_0((-\infty , a] \times \mathbb {R}^+,\gamma )$ and is a solution to (3.1). Estimate (3.14) is also satisfied.

Proof

We shall prove (1) only. By the definition of $(u,v)$, we have $\hat{u} \in \mathcal {H}^{0.75}(\gamma )$.

From Lemma 3.1, $\hat{b} \overset{s}{*} \hat{u} \in \mathcal {H}^{0.75}(\gamma ) \subset \mathcal {H}^0(\gamma )$. Thus $g= (0,\hat{b}\overset{s}{*} \hat{u})^\tau \in \mathcal {H}^{0.5\times 0}(\gamma )$. Rewrite (3.13) as a first order system

$$\begin{aligned} \begin{pmatrix}\hat{u}\\ \hat{v} \end{pmatrix}_\xi =\begin{pmatrix} 0 &{} I\\ sI-Df(e_j) &{} -\bar{c}_j \end{pmatrix}\begin{pmatrix}\hat{u}\\ \hat{v} \end{pmatrix}+ g. \end{aligned}$$

(3.15)

Let the projections of the dichotomy for (3.10), in $E^{0.75\times 0.25}(s)$ be $P_s(\xi ,s)$ and $P_u(\xi ,s)$. Using the solution mapping $T(\xi ,\zeta ;s)$, the solution of (3.15) in $\xi \ge a$ can be expressed as

$$\begin{aligned} (\hat{u},\hat{v})^\tau&= T(\xi ,a;s)P_s(a,s)\phi (s) + \int _a^\xi T(\xi ,\zeta ;s)P_s(\zeta ,s)g(\zeta )d\zeta \\&\quad + \int _\infty ^\xi T(\xi ,\zeta ;s)P_u(\zeta ,s) g(\zeta ) d\zeta . \end{aligned}$$

Therefore, $(u,v)^\tau )=\mathcal {L}^{-1}(\hat{u},\hat{v})^\tau$ can be expressed as $(u^{(1)}, v^{(1)})^\tau + (u^{(2)}, v^{(2)})^\tau$, where $(u^{(1)}, v^{(1)})^\tau$ and $(u^{(2)}, v^{(2)})^\tau$ are the inverse L-transform of the first term and the two integral terms respectively. From Lemma 3.1 in [11], $u^{(1)} \in H^{2,1}_0(\xi \ge a,\gamma )$ and is bounded by $|\phi |_{\mathcal {H}^{0.75 \times 0.25}(\gamma )}$. From Lemma 3.8 in [11], $u^{(2)} \in H^{2,1}_0(\xi \ge a,\gamma )$ and is bounded by $|g|_{\mathcal {H}^{0.5\times 0}(\gamma )}\le C|\phi |_{\mathcal {H}^{0.75 \times 0.25}(\gamma )}$. The proof of part (1) has been completed.$\square$

3.5 Exponential Dichotomies for Linear Variational Systems Around $q_j$

We remark that if $b(\xi ,t)=b(\xi )$ is independent of $t$, then

$$\begin{aligned} \hat{b}(\xi ) \overset{s}{*}\hat{u}(\xi ,s)) = b(\xi ) \hat{u}(\xi ,s). \end{aligned}$$

This is the case considered in this subsection where $b(\xi ) = Df(q_j(\xi )) - Df(e_k)$, $k=j-1$ or $j$. The principle matrix solution $T(\xi ,\eta ,s)$ with a parameter $s$ of the linear system

$$\begin{aligned} U_\xi =V,\quad V_\xi = (s I - Df(q_j(\xi )))U - c_j V, \quad \xi \in \mathbb {R}. \end{aligned}$$

(3.16)

can be viewed as a linear flow in the Banach space $E^{0.75\times 0.25}(s)$. We now consider the existence of exponential dichotomies for the linear system (3.16).

Lemma 3.6

Let $(q_j(\xi ), q^\prime _j(\xi ))$ be the heteroclinic solution connecting $(u,v)=(e_{j-1},0)$ to $(e_j,0)$. Assume that (H1) and (H2) are satisfied. Then in the space $E^{0.75\times 0.25}(s)$, system (3.16), with $s\in \Sigma (-\eta ,\theta )\backslash \{0\}$, has an exponential dichotomy on $\mathbb {R}$. The projections of the dichotomy are analytic in $s$. For any $\epsilon >0$, if $|s| \ge \epsilon$ then the Projections $P_s(\xi ,s)$ and $P_u(\xi ,s)$ are uniformly bounded by $K(\epsilon )>0$. The exponent is ${\alpha }(1+|s|^{0.5})$ for some $\alpha >0$.

Moreover, let $P_s(e_{j-1},s)$ and $P_u(e_j,s)$ be the spectral projections at the two limiting points $(e_{j-1},0)$ or $(e_j,0)$. There is a large constant $M>0$ such that depending on $|s| \ge M$ or $|s|<M$, we have

$$\begin{aligned} \begin{aligned} | P_s(\xi ,s) - P_s(e_{j-1},s)|&\le \frac{16 K^2(\epsilon ) \delta _k}{\alpha (1+|s|^{0.5})}, \quad \xi \le -N,\\ | P_u(\xi ,s) - P_u(e_j,s)|&\le \frac{16 K^2(\epsilon ) \delta _k}{\alpha (1+|s|^{0.5})}, \quad \xi \ge N, \end{aligned} \end{aligned}$$

(3.17)

where the constant $\delta _k$ are as follows. If $|s| \ge M$ then $k=1$ and if $\epsilon \le |s| \le M$ then $k= 2$, with $\delta _1= \sup _\xi |Df(q_j(\xi ))|$ and $\delta _2$ as in (3.20).

Proof

The proof is adapted from that of [11], see also [14].

Step 1: Exponential dichotomy for $|s| \ge M$. Let $M>0$ be a sufficiently large constant. In the region $\{|s| \ge M\}\cap \Sigma (-\eta ,\theta )$, we treat (3.16) as perturbations to the system

$$\begin{aligned} U_\xi =V,\quad V_\xi = s U + c_j V. \end{aligned}$$

(3.18)

From [11], the system above has an exponential dichotomy in $E^{0.75\times 0.25}(s)$ with the constant $K_0$ and the exponent $\alpha _0 =\alpha (1+|s|^{0.5})$.

Although $\delta _1= \sup _\xi |Df(q_j(\xi ))|$ is not small, but the conditions $C_1\delta _1< 1$ and $C_2 \delta _1 <1$ in Theorem 3.3 can be satisfied if we choose $\tilde{\alpha }= \alpha (1+|s|^{0.5}) /2$. Then from $\alpha _0= \alpha (1+|s|^{0.5})$, $\alpha _0 - \tilde{\alpha }$ = $\alpha (1+|s|^{0.5})/2$ can be large from the condition $|s| \ge M$ for a large constant $M$. If $M$ is sufficiently large then (3.9) in Theorem 3.3 is satisfied and system (3.16) has exponential dichotomies in $E^{0.75\times 0.25}(s)$ with the constant $\tilde{K}$ independent of $s$. The exponent of the dichotomy is $\tilde{\alpha }=\frac{\alpha }{2}(1+|s|^{0.5})$. The projections satisfy (3.17) with $k=1$.

Observe that the stable and unstable subspaces of (3.18) are analytic in $s$. Since the perturbed equaion is analytic in $s$, and the contraction mapping principle is used to find the stable and unstalbe subspace of (3.16), Thus the projections $P_s(\xi ,s)$ and $P_u(\xi ,s)$ are analitic in $s$ for $\{|s| >M\}\cap \Sigma (-\eta ,\theta )$.

Step 2: Exponential dichotomies on $\mathbb {R}$ for $0<|s| \le M$. After $M>0$ has been determined, for any $0<\epsilon <M$, we consider the spectral equation in the compact set $\{\epsilon \le |s| \le M\}\cap \Sigma (-\eta ,\theta )$.

Assume that $N>0$ is a sufficiently large constant so that on $I_-=(-\infty ,-N]$ or $I_+=[N,\infty )$, $q_j(\xi )$ is close to $e_{j-1}$ or $e_j$ respectively. Consider the following system with constant coefficient, where $s$ as a parameter:

$$\begin{aligned} U_\xi =V,\quad V_\xi = (s I - Df(e_k))U - c_j V,\quad k=j-1, j. \end{aligned}$$

(3.19)

From (H1), the eigenvalues for the constant system has $n$ eigenvalues with positive real parts and $n$ eigenvalues with negative real parts. Thus, (3.19) has exponential dichotomies with the common exponent $\alpha _0(s) >0$, and the projections depend analytically on $s$. Also in $\Sigma (-\eta ,\theta )$, the constant $K$ is uniformly valid with respect to $s$.

For such $N>0$, let

$$\begin{aligned} \delta _2 \!=\!\max \{\sup \{|Df(q_j(\xi ))\!-\!Df(e_{j-1})|:\xi \!\le \! -N\}, \sup \{|Df( q_j(\xi ))-Df(e_j)|:\xi \ge N\}\}. \end{aligned}$$

(3.20)

If $\delta _2$ as in (3.20) is sufficiently small, then system (3.16) has nonunique exponential dichotomies in $I_-$ and $I_+$. The unstable subspace $E_u(\xi ,s), \xi \le -N$ and the stable subspace $E_s(\xi ,s), \xi \ge N$ are unique. Since they are constructed by contraction mapping principle, both spaces depend analytically on $s\in \Sigma (-\eta ,\theta )$. We shall use them to construct the unified dichotomy on $\mathbb {R}$. The stable subspace $E_s(\xi ,s), \xi \le -N$ and unstable subspace $E_u(\xi ,s), \xi \ge N$ are not unique, and shall be modified as follows.

Using the unique subspaces $E_u(-N,s),\; E_s(N,s)$, we extend them by

$$\begin{aligned} E_u(\xi ,s)&= T(\xi ,-N,s)E_u(-N,s),\quad \text {for } -N \le \xi \le \infty ,\\ E_s(\xi ,s)&= T(\xi ,N, s)E_s(N,s) \quad \text {for } -\infty \le \xi \le N. \end{aligned}$$

From (H1) and (H2), if $s\ne 0$, $T(N,-N,s)E_u(-N,s)$ intersects with $E_s(N,s)$ transversely, or equivalently $T(-N,N,s) E_s(N,s)$ intersects with $E_u(-N,s)$ transversely. The dichotomy has been extended to $\xi \in \mathbb {R}$, and is analytic for $s \in \Sigma (-\eta ,\theta ) \backslash \{0\}$ and $|s|\le M$. The exponent of the dichotomy is $\alpha _1(1+|s|^{0.5})$ where $\alpha _1$ is independent of $s$.

In the compact set $\{\epsilon \le |s| \le M\}\cap \Sigma (-\eta ,\theta )$, the angle between $E_u(\pm N,s)$ and $E_s(\pm N,s)$ are bounded below by a constant that depends on $\epsilon$. Thus, the constant $K(\epsilon )$ depends on $\epsilon$.

Final Step: If we combine the two cases and select any $0<\alpha < \min \{ \tilde{\alpha }/2, \alpha _1\}$, then (3.16) has an exponential dichotomy in $E^{0.75\times 0.25}(s)$ for $\xi \in \mathbb {R}$ and $s \in \Sigma (-\eta ,\theta ) \backslash \{0\}$. The exponent is ${\alpha }(1+|s|^{0.5})$. This completes the proof of the lemma $\square$

In the next lemma we discuss exponential dichotomies of (3.16) for $s\approx 0$ which is treated as a perturbation of $s=0$.

Lemma 3.7

Let $a=-N$ or $N$ where $N>0$ is the constant as in (3.20).

• (1) For a small $\epsilon >0$ and $|s| \le \epsilon$, let $E_u(\xi ,s),\;\xi \le a$ be the unstable subspace and $E_s(\xi ,s),\; \xi \ge a$ be the stable subspace for (3.16). Then the angle between $E_u(a_-,s)$ and $E_s(a_+,s)$ are bounded below by $C|s|,\;C>0$.

• (2) For a small $\epsilon >0$, if $|s|\le \epsilon$, then (3.16) has two separate dichotomies on $\xi \in (-\infty , a]$ and $[a,\infty )$ respectively. The two separate dichotomies are not unique. However they can be constructed such that the projections, denoted by

  $$\begin{aligned} P^-_s(\xi ,s) + P_u^-(\xi ,s)=Id,\; \xi \le a; \quad P_s^+(\xi ,s) + P_u^+(\xi ,s)=Id, \;\xi \ge a, \end{aligned}$$

are analytic in $s$ and satisfy the property

$$\begin{aligned} |P^\pm _s(\xi ,s)| + |P^\pm _u(\xi ,s)| \le K, \text { for all }|s| \le \epsilon . \end{aligned}$$

Proof

We prove part (1) first. For each vector $\phi \in E_s(\xi ,s=0)$ there exists a unique $\tilde{\phi }\in E_s(\xi , s)$ such that $\tilde{\phi }-\phi \in E_u(\xi , s=0)$ and $|\tilde{\phi }-\phi | =\mathcal {O}(|s|)$. Similarly for each vector $\phi \in E_s(\xi , s=0)$ there exists a unique $\tilde{\phi }\in E_u(\xi ,s)$ such that $\tilde{\phi }- \phi \in E_s(\xi ,s=0)$ and $|\tilde{\phi }- \phi |= \mathcal {O}(|s|)$. The perturbation argument used in the proof also shows that the spaces $E_s(\xi ,s)$ and $E_u(\xi ,s)$ are analytic in $s$. When $s=0$, the intersection of $E_u(a_-,s=0)$ and $E_s(a_+,s=0)$ is one dimensional, spanned by $(q^\prime _j(a), q^{\prime \prime }_j(a))$. Melnikov’s method can be used to show that the 1D intersection breaks if $s\ne 0$ and small. And the angle is of $\mathcal {O}(|s|)$. See Lemma 3.9 of [9].

To prove part (2), let us consider $a=-N$ only for the case $a=N$ is similar. In $(-\infty , -N]$, define $E_s(-N,s)$ to be a subspace that is orthogonal to $E_u(-N,s=0)$. Then use the flow $T(\xi , -N,s)$ to define $E_s(\xi ,s)$ for $\xi \le -N$. In $[-N,\infty )$, let the stable subspace be the extension of $E_s(N,s)$ by the flow. Define $E_u(-N,s)$ to be the subspace that is orthogonal to $E_s(-N,s=0)$, then extend it to $\xi \ge -N$ by the flow. Once the subspaces $E_s(\xi ,s)$ and $E_u(\xi ,s)$ are defined for $\xi \le -N$ and $\xi \ge -N$ respectively , the exponential dichotomies on the two separate intervals are determined.

The validity of extension of dichotomies used above has been proved in Lemmas 2.3 and 2.4 in [8].$\square$

The definition of angles between two subspaces and its relation to the norms of $P_u, P_s$ can be found in Lemma 3.9 of [9]. In Lemma 3.10 of that paper, perturbation of a linear system from $\epsilon =0$ to $\epsilon \ne 0$ but small is discussed, see also [4]. The result can apply to our case by changing $\epsilon$ to $s$. The perturbation argument used in the proof also shows that the dichotomies near $s=0$ are analytic in $s$. In particular, based on part (1) of Lemma 3.7, we have the following corollary.

Corollary 3.8

For the unified dichotomy as in Lemma 3.6, the projections satisfy the property $|P_s(0,s)| + |P_u(0, s)| \le C/|s|$.

4 Solution of the Nonhomogeneous Linear System (2.6)

In Sect. 4.1, we solve the initial value problem (2.6a), ignoring the jump condition (2.6b). Then in Sect. 4.2, we solve the full linear system (2.6) with $h_j=0$ and $u_{j0}=0$. These results can be combined to solve (2.6).

4.1 Solve the Nonhomogeneous System with Initial Conditions

In this subsection we look for a solution $u_j$ of the nonhomogenous system with the initial condition in each $\Omega _j, 1\le j\le m$.

$$\begin{aligned} u_{jt} = u_{jxx} + Df(q_j)u_j + h_j, \quad u_j(x,0) = u_{j0}(x), \end{aligned}$$

(4.1)

where $u_{j0}(x)$ is the restriction of $u_{0}(x)$ to $(x_{j-1}, x_j)$. We will ignore the jump conditions and leave them for the next subsection.

Assume that $u_{j0}\in H^1(x_{j-1}, x_j)$ and $h_j \in L^2(\Omega _j,\gamma ), \gamma <0$. We extend the initial data and the forcing term to the whole space $u_{j0}(x) \rightarrow \tilde{u}_{j0}(x), \; h_j(x,t) \rightarrow \tilde{h}_j(x,t)$ so the fundamental solution can be used to solve (4.1). In particular, we make the zero extension of $h_{j}$ to $\tilde{h}_{j}$ outside $\Omega _j$. We extend $u_{j0}\in H^1(x_{j-1},x_j)$ to $\tilde{u}_{j0} \in H^1(\mathbb {R})$ by a bounded extension operator $H^1(x_{j-1},x_j)\rightarrow H^1(\mathbb {R})$. Then consider the initial value problem in $\mathbb {R}\times \mathbb {R}^+$,

$$\begin{aligned} \tilde{u}_{jt} = \tilde{u}_{jxx} + Df(q_j)\tilde{u}_j + \tilde{h}_j(x,t),\quad \tilde{u}_j(x,0) = \tilde{u}_{j0}(x). \end{aligned}$$

In the moving coordinates $\xi =x- y_j-c_j t$, we have

$$\begin{aligned} \tilde{u}_{jt} = \tilde{u}_{j\xi \xi } + c_j \tilde{u}_{j\xi } + Df(q_j)\tilde{u}_j + \tilde{h}_j(\xi ,t),\quad \tilde{u}_j(\xi ,0) = \tilde{u}_{j0}(\xi ). \end{aligned}$$

(4.2)

Recall that $\uplambda =0$ is always an eigenvalue for the associated homogeneous equation to (4.2). We want to show that the solution $u_j$ will have a term $\beta _j(t) q^\prime _j$ in the eigenspace associated to $\uplambda =0$, and the remaining part approaches zero exponentially.

Consider the general linear equation

$$\begin{aligned} U_t = U_{\xi \xi } + c_j U_\xi + Df(q_j)U,\quad 1 \le j \le m. \end{aligned}$$

Recall that $q^\prime _j(\xi )\in \ker ({L}_{cj})$, $z_j \in \ker ({L}_{cj}^*)$ and $\int _{-\infty }^\infty <z_j, q_j> dx =1,\; 1\le j \le m$. The spectral projection to the eigenspace corresponding to $\uplambda =0$ is

$$\begin{aligned} P_j U(x) = \left( \int _{-\infty }^\infty <z_j(x),U(x)> dx \right) q^\prime _j(x). \end{aligned}$$

The complementary projection is $Q_j:=Id-P_j$. Define

$$\begin{aligned} \mathcal {X}_j:= \{Y : \int _{-\infty }^\infty <z_j, Y> dx =0\}. \end{aligned}$$

(4.3)

Then $R Q_j = \mathcal {X}_j$, which is an invariant subspace with all the spectrum points in the complement of $\Sigma (-\eta , \theta )$. See the condition (A2) following H1 and H2.

By the spectral decomposition, $u_j(\xi ,t)= Y_j(\xi ,t) + \beta _j(t) q^\prime _j$ where $Y_j \in \mathcal {X}_j$. The operator ${L}_j Y = Y_{xx} + c_j Y_x + Df(q_j) Y$ defined on $\mathcal {X}_j$ is sectorial and generates an analytic semigroup $e^{{L}_{cj} t}$. For $\tilde{u}_{j0}\in H^1(\mathbb {R})$ and $\tilde{h}_j\in L^2(\gamma )$, we have

$$\begin{aligned} Y_j = e^{{L}_{j} t}Q_j \tilde{u}_{j0} + \int _0^t e^{{L}_{j} (t-\tau )}Q_j \tilde{h}_j(\tau )d\tau . \end{aligned}$$

(4.4)

From Lemma 3.11 of [11], it is easy to show if $-\eta <\gamma <0$, then $Y_j \in H^{2,1}(\mathbb {R}\times \mathbb {R}^+,\gamma )$ and satisfies

$$\begin{aligned} |Y_j|_{H^{2,1}(\gamma )} \le C(|\tilde{u}_{j0}| + |\tilde{h}_j| )\le C(|u_{j0}|_{H^1(\mathbb {R})} + | h_j|_{L^2(\gamma )} ) . \end{aligned}$$

(4.5)

We then consider the equation in $R P_j$:

$$\begin{aligned} \dot{\beta }_j(t) = \int _{-\infty }^\infty <z_j(\xi ), \tilde{h}_j(\xi ,t)>d\xi , \quad \beta _j(0) = \int _{-\infty }^\infty <z_j(\xi ),\tilde{u}_{j0}(\xi )> d\xi . \end{aligned}$$

(4.6)

Since $\tilde{h}_j \in L^2(\gamma )$, we have $\dot{\beta }_j \in L^2(\gamma ), \gamma <0$. By solving this ODE we obtain the solution $\beta _j(t)q^\prime _j(x)$ in the space $R P_j$. Using also (2.1), we have

$$\begin{aligned} \begin{aligned}&|\beta _j(0)| \le C |\tilde{u}_{j0}|\le C | u_{j0}|_{H^1(\mathbb {R})},\quad |\dot{\beta }_j|_{L^2(\gamma )} \le C |h_j|_{L^2(\gamma )}, \\&|\beta _j(\infty ) - \beta _j(t)| \le Ce^{\gamma t}|h_j|_{L^2(\gamma )}, \quad |\beta _j|_{X^1(\gamma )}\le C (| u_{j0}|_{H^1(\mathbb {R})} + |h_j|_{L^2(\gamma )}). \end{aligned} \end{aligned}$$

(4.7)

By restricting $Y_j$ to $\Omega _j$, we have the following theorem.

Theorem 4.1

In each $\Omega _j, 1\le j\le m$, the initial value problem (4.1) has a solution $u_j(\xi ,t)= Y_j(\xi ,t) + \beta _j(t) q^\prime _j$ where $Y_j \in H^{2,1}(\Omega _j, \gamma )$ satisfies (4.5) and $\beta _j\in X^1(\gamma )$ satisfies (4.7). The solution is the restriction of the solution of (4.2) in $\mathbb {R}\times \mathbb {R}^+$ to $\Omega _j$, and is unique once the extension operators are fixed.

4.2 System of Equations with Jumps Along $\Gamma _j$

Let $\{u_j^{(1)}(x,t)\}$ be the solution of (4.1) obtained in Sect. 4.1 and

$$\begin{aligned} \tilde{J}_j(\Gamma _j) := -([\{u_j^{ap}+u_j^{(1)}\}, \{u_{jx}^{ap}+u_{jx}^{(1)}\}])(\Gamma _j) =J_j(\Gamma _j)- ([\{u_j^{(1)}\},\{u^{(1)}_{jx}\}])(\Gamma _j). \end{aligned}$$

In this subsection, we consider the linear system for $u_j$ defined on $\Omega _j$ with nonzero jump conditions along $\Gamma _j$:

$$\begin{aligned} u_{jt} = u_{j,xx} + Df(q_j)u_j,\; (x,t) \in \Omega _j, \quad u_j(x,0) = 0, \quad ([\{u_j\}\{u_{jx}\}])(\Gamma _j)=\tilde{J}_j(\Gamma _i), \end{aligned}$$

(4.8)

The main results of this subsection are summarized in the following theorem:

Theorem 4.2

Given $\{\tilde{J}_j(\Gamma _j)\} \in \prod _1^{m-1} H_0^{0.75\times 0.25}(\gamma )$, under (H1)–(H2), if $y_{j+1}- y_j$ is sufficiently large, then the linear system (4.8) has a unique solution $\{u_j(x,t)\}$ that can be expressed as $u_j = \beta _j(t) q^\prime _j + Y_j$, where $Y_j \in H^{2,1}_0(\Omega _j,\gamma )$, $\beta _j(0)=0, \dot{\beta }_j(t) \in L^2(\gamma )$. The solution mapping, expressed as $\{\tilde{J}_j(\Gamma _j)\}_{j=1}^{m-1} \rightarrow (\{(Y_j, \beta _j)\}_{j=1}^m$ is a bounded operator

$$\begin{aligned} \prod _1^{m-1} H_0^{0.75\times 0.25}(\gamma ) \rightarrow \prod _1^m (H_0^{2,1}(\Omega _j,\gamma )\times X^1(\gamma )). \end{aligned}$$

Proof

Let $N$ be the fixed large constant defined in Lemma 3.6 and let

$$\begin{aligned} \begin{aligned} y_j^-= y_j-N,\quad&M_j^- =\{(x,t):x= y_j^- + c_j t,\;t\ge 0\}, \\ y_j^+ = y_j+N, \quad&M_j^+= \{(x,t): x=y_j^+ + c_j t,\; t\ge 0\}. \end{aligned} \end{aligned}$$

(4.9)

See Fig. 2. The proof of the theorem is based on an iteration process by repeating Part A and Part B described below. First, we use Pat A to achieve the prescribed jumps along $\Gamma _j, 1\le j \le m-1$. In doing so we introduced some jump error along the line $M_j^\pm , 1\le j\le m$. Then we use Pat B to eliminate the jumps along $M_j^\pm$ which in turn introduces some jump errors back to $\Gamma _j$. However the jump errors along $\Gamma _j$ are exponentially smaller than the prescribed jumps along $\Gamma _j$. We can repeat procedures in Part A and Part B to treat the jump errors along $\Gamma _j$, each time reduce the errors by an exponentially small factor. The iteration process converges to the exact solution with the prescribed jump conditions along $\Gamma _j$.

Due to the lack of a unified exponential dichotomy when looking for a solution with the prescribed jump along $M_j^\pm$, we introduce a term $\beta _j(t)q^\prime _j$ in the solution of the linear system. This is done each time the iteration is performed so the term $\beta _j(t) q^\prime _j$ is the sum of an infinite series that converges at the rate of a geometric series. Details will be given at the end of this section.$\square$

Part A: We look for a piecewise smooth $u(x,t)$ that is defined between $M_j^+$ and $M_{j+1}^-$, with the jump $\delta _j$ along $\Gamma _j$, and satisfies the equations:

$$\begin{aligned}&u_t= u_{xx} + Df(q_j)u, \quad \text { if }(x,t) \text { is between } M_j^+ \text { and }\Gamma _j, \end{aligned}$$

(4.10)

$$\begin{aligned}&u_t =u_{xx} + Df(q_{j+1})u,\quad \text { if }(x,t) \text { is between }\Gamma _j \text { and }M_{j+1}^-. \end{aligned}$$

(4.11)

$$\begin{aligned}&u(x,0) = 0 \quad [(u,u_x)](\Gamma _j)=\delta _j. \end{aligned}$$

(4.12)

We are interested in solutions that decay exponentially as $(x,t)$ moves away from $\Gamma _j$. The solution between $M_j^+$ and $M_{j+1}^-$ is non-unique, depends on the modification of the vector fields to the left of $M_j^+$ and the right of $M_{j+1}^-$, as will be specified in the proof.

Fig. 2

Illustration of the lines $M_j^{\pm ^{}}$ defined in (4.9)

Lemma 4.3

For each $\delta _j \in H^{0.75\times 0.25}_0(\gamma )$ defined on $\Gamma _j$, there exists a piecewise smooth solution $u$ defined on $\mathbb {R}\times \mathbb {R}^+$ that satisfies equations (4.10), (4.11) and jump condition (4.12). The support of $u$ is between $M_j^+$ and $M_{j+1}^-$. Moreover the solutions satisfy the following estimates

$$\begin{aligned} |u(x,t)|_{M_j^+} | + | u(x,t)|_{M_{j+1}^-}| \le C (e^{-\alpha (x_j - y_j-N)} + e^{-\alpha (y_{j+1}-x_j -N)})|\delta _j|. \end{aligned}$$

(4.13)

where all the norms are in $H^{0.75\times 0.25}_0(\gamma )$.

Proof

Using the moving coordinate $\xi = x -x_j - \bar{c}_j t$, the line $\Gamma _j$ becomes $\xi =0$. Equations (4.10), (4.11) become

$$\begin{aligned} u_t =u_{\xi \xi } + \bar{c}_j u_\xi + Df(q_k) u,\;k=j,j+1 \end{aligned}$$

respectively.

From the definitions of $y_j^\pm$ and $M_j^\pm$ in (4.9) and $\xi = x -x_j - \bar{c}_j t$, we have

$$\begin{aligned} M_j^+&= \{(\xi ,t): \xi =y_j-x_j+N + (c_j-\bar{c}_j)t,\;t\ge 0\},\\ M_{j+1}^-&= \{(\xi ,t):\xi =y_{j+1}-x_j-N + (c_{j+1}-\bar{c}_j)t,\;t\ge 0\}. \end{aligned}$$

To the left and right of $\Gamma _j$, let $u^{ap}(x,t)= q_k(x-y_k- c_k t ),k=j,j+1$. If $(\xi ,t)$ is between $M_j^+$ and $M_{j+1}^-$, let $A(\xi ,t)= Df(u^{ap}(\xi + x_j + \bar{c}_j t, t))$. Ussing a smooth cut-off function, we can extend $A(\xi ,t)$ to all $\mathbb {R}\times \mathbb {R}^+$, so that to the left of $M_j^+$,

$$\begin{aligned}&A(\xi ,t)=Df(q_j(N), \quad \xi = y_j-x_j+N + (c_j-\bar{c}_j)t,\\&A(\xi ,t)=Df(e_j),\quad \xi < y_j-x_j+N -1+ (c_j-\bar{c}_j)t. \end{aligned}$$

Similarly to the right of $M_{j+1}^-$,

$$\begin{aligned}&A(\xi ,t)=Df(q_{j+1}(-N)),\quad \xi = y_{j+1}-x_j-N + (c_{j+1}-\bar{c}_j)t,\\&A(\xi ,t)=Df(e_j),\quad \xi \ge y_{j+1}-x_j-N +1 + (c_{j+1}-\bar{c}_j)t. \end{aligned}$$

Also $B(\xi ,t):=A(\xi ,t)- Df(e_j)=\mathcal {O}(e^{\gamma t})$ is piecewise continuous in $\xi$ and $C^1$ in $t$. It is uniformly small for all $\xi \in \mathbb {R}$ if $N$ is sufficiently large. Since the system $u_\xi =v,\;v_\xi = u_t - \bar{c}_j v - Df(e_j)u$ has an exponential dichotomy for $\xi \in \mathbb {R}$, by the roughness of exponential dichotomies, the linear system

$$\begin{aligned} u_\xi =v,\;v_\xi = u_t - \bar{c}_j v - A(\xi ,t)u \end{aligned}$$

has an exponential dichotomy for all $\xi \in \mathbb {R}$ in $H^{0.75\times 0.25}_0(\gamma )$. Applying the exponential weight function to $Bu$ and $u$, from Lemma 3.1, we have $|Bu|_{H_0^{0.75}(\gamma )} \le |B|_{C^1}|u|_{H_0^{0.75}(\gamma )}$. Since $\delta = |\hat{B}(\xi ,s)|_{{C}^1}$ can be arbitrarily small if $N$ is sufficiently large, the existence of the exponential dichotomy follows from Theorem 3.3.

Let the projections of this dichotomy be denoted $\check{P}_u(0-) +\check{P}_s(0+)=Id$ at $\xi =0$. For the given $\delta _j \in H^{0.75\times 0.25}_0(\gamma )$, let

$$\begin{aligned} u_-^1(\xi ) = -T(\xi ,0)\check{P}_u(0-) \delta _j, \quad u_+^1(\xi ) = T(\xi ,0)\check{P}_s(0+) \delta _j. \end{aligned}$$

Then

$$\begin{aligned} |u_-^1(y_j^+)| \le C e^{-\alpha (x_j - y_j-N)} |\delta _j|,\quad |u_+^1(y_{j+1}^-)| \le C e^{-\alpha (y_{j+1} - x_j-N)} |\delta _j|. \end{aligned}$$

To the left of $\xi =y_j^+$, or to the right of $\xi =y_{j+1}^-$, we have

$$\begin{aligned} |u_-^1|_{H^{2,1}(\gamma )} \le C e^{-\alpha (x_j - y_j-N)} |\delta _j|,\quad |u_+^1|_{H^{2,1}(\gamma )} \le C e^{-\alpha (y_{j+1} - x_j-N)} |\delta _j|, \end{aligned}$$

Therefore, the traces of $u_-^1$ and $u_+^1$ on $M_j^+$ and $M_{j+1}^-$ are exponentially small. This proves (4.13). Finally we truncate $u_\pm ^1$ so that to the left of $M_j^+$ and to the right of $M_{j+1}^-$, $u_\pm ^1=0$.$\square$

For the truncated $u_\pm ^1$, the jump condition (4.12) along $\Gamma _j$ is satisfied, but the function $u_\pm ^1$ has jump discontinuities along $M_j^+$ and $M_{j+1}^-$. Notice that

$$\begin{aligned} x_j-y_j-N=y_{j+1} - x_j-N=(y_{j+1}-y_{j})/2 -N,\quad 1\le j \le m-1. \end{aligned}$$

From (4.13), the jumps are exponentially small in $H_0^{0.75\times 0.25}(\gamma )$ if $y_{j+1}-y_{j},\; 1\le j \le m-1$ are sufficiently large.

Part B: We consider a linear variational PDE around $q_j(\xi _j)$ in the domain $\mathbb {R} \times \mathbb {R}^+$ with the zero initial condition and two prescribed jumps along $M_j^\pm$:

$$\begin{aligned} u_t= u_{xx} + Df(q_j) u,\quad u(x,0)=0, \;[(u,u_x)](M_j^\pm ) = \phi _j^\pm . \end{aligned}$$

We can treat one jump at a time. To combine the two cases, let $a= -N$ or $N$, where $N>0$ is the fixed large constant in Lemma 3.6 and let $M_a:=\{\xi =a\}=\{x=a+y_j +c_j t\}$. In the moving coordinates, the equations before and after the Laplace transform are:

$$\begin{aligned}&u_t = u_{\xi \xi } +c_j u_{\xi } + Df(q_j(\xi ))u,\quad u(\xi ,0)=0, \quad [(u,u_{\xi })](M_a) = \phi _a, \end{aligned}$$

(4.14)

$$\begin{aligned}&0=\hat{u}_{\xi \xi } +c_j \hat{u}_{\xi } -s \hat{u}+ Df(q_j(\xi ))\hat{u},\quad [(\hat{u},\hat{u}_{\xi })](M_a) = \hat{\phi }_a. \end{aligned}$$

(4.15)

Converting to the first order system

$$\begin{aligned} \hat{u}_\xi =\hat{v},\; \hat{v}_\xi = (sI-Df(q_j(\xi )))\hat{u} -c_j \hat{v},\quad [(\hat{u},\hat{v})](M_a) = \hat{\phi }_a. \end{aligned}$$

(4.16)

The specified jump $\phi _a(t)$ is a function in $H^{0.75\times 0.25}_0(\gamma )$, and $\hat{\phi }_a(s)$ is in $\mathcal {H}^{0.75\times 0.25}(\gamma )$. We look for solutions that decay to zero as $\xi$ moves away from $M_a$.

Lemma 4.4

For $s\in \Sigma (-\eta ,\theta )\backslash \{0\}$, system (4.15) has a unique solution that decays exponentially as $\xi \rightarrow \pm \infty$. If $0<\epsilon \le |s|$, then the solution satisfies

$$\begin{aligned}&|\hat{u}(\cdot ,s)|_{L^2(\xi \le a)}+|\hat{u}(\cdot , s)|_{L^2(\xi \ge a)} \le \frac{C(\epsilon )}{1+|s|} |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}, \end{aligned}$$

(4.17)

$$\begin{aligned}&|(\hat{u},\hat{v})(\xi ,s)|_{E^{0.72\times 0.25}(s)} \le C(\epsilon ) e^{-\alpha |\xi -a|} |\hat{\phi }_a|_{E^{0.72\times 0.25}(s)}. \end{aligned}$$

(4.18)

The constant $C(\epsilon )=\mathcal {O}(1/\epsilon )$ as $\epsilon \rightarrow 0$.

Proof

Using the unified exponential dichotomy which is analytic in $s\in \Sigma (-\eta ,\theta )\backslash \{0\}$, we can express the solution of (4.15) as follows:

$$\begin{aligned} \begin{aligned}&(\hat{u}(\xi ,s),\hat{v}(\xi ,s))^\tau =-T(\xi , a,s)P_u(a,s) \hat{\phi }_a(s) ,\quad \xi \le a, \\&(\hat{u}(\xi ,s),\hat{v}(\xi ,s))^\tau =T(\xi , a,s)P_s(a,s) \hat{\phi }_a(s) , \quad \xi \ge a. \end{aligned} \end{aligned}$$

(4.19)

The analytic functions $(\hat{u},\hat{v})$ may have a simple pole at $s=0$.

The proof of (4.17), (4.18) follows from the existence of an exponential dichotomy for (4.15) and part (2) of Lemma 3.1 in [11].$\square$

Our next step is to treat (4.15) at $s \approx 0$. To this end, we write $u(\xi ,t) = Y(\xi ,t) + \beta (t) q^\prime (\xi )$ where $Y(\cdot ,t)\in \mathcal {X}_j$ is defined in (4.3). The initial conditions are $Y(\xi ,0)=0$ and $\beta (0)=0$. Then before and after the Laplace transform, we have

$$\begin{aligned}&Y_t=Y_{\xi \xi }+ c_j Y_\xi + Df(q_j)Y - \dot{\beta }(t) q^\prime (\xi ),\quad [(Y,Y_{\xi })](M_a)=\hat{\phi }_a, \nonumber \\&\quad \hat{Y}_{\xi \xi } + c_j \hat{Y}_\xi + Df(q_j)\hat{Y} - s\hat{Y} = s\beta (s) q^\prime (\xi ), \quad [(\hat{Y},\hat{Y}_\xi )](a) = \hat{\phi }_a . \end{aligned}$$

(4.20)

Multiplying by $z_j$ and integrating by parts, we obtain a necessary condition for (4.20) to be solvable in the domain $\hat{Y}\in \mathcal {X}_j$, $s\in \Sigma (-\eta ,\theta )$:

$$\begin{aligned} \int _{-\infty }^\infty <z_j(\xi ), s\beta (s) q^\prime (\xi )> d\xi + <(c_j z_j - z_j', z_j)(a), \hat{\phi }_a> =0. \end{aligned}$$

(4.21)

From (4.21) and $\int <z_j(\xi ), q^\prime _j(\xi )> d\xi =1$, we have:

$$\begin{aligned} s\hat{\beta }(s) = - <(c_j z_j - z_j', z_j)(a), \hat{\phi }_a>. \end{aligned}$$

(4.22)

From $\hat{\phi }_a \in \mathcal {H}^{0.75\times 0.25}(\gamma ),\; s\beta (s) \in \mathcal {H}^{0.25}(\gamma )$. Thus, for $t\ge 0$, $\dot{\beta }(t)= \mathcal {L}^{-1}(s\beta (s))$ is determined and $|\dot{\beta }(t)|_{L^2(\gamma )} \le C |\phi (a)|_{L^2(\gamma )}, \gamma <0$. This together with $\beta (0)=0$ determines $\beta (t)$ for all $t\ge 0$. We also find that $|\beta (t)-\beta (\infty )| \le C e^{\gamma t} |\phi (a)|_{L^2(\gamma ) }$. From (4.22), the function $s\beta (s)$ is analytic for $s \in \Sigma (-\eta ,\theta )$, $\beta (s)$ has an isolated pole at $s=0$. Denote $\hat{h}=(0, s\beta (s) q^\prime )^\tau$. Clearly for each $\xi$, $\hat{h}(\xi ,\cdot )\in \mathcal {H}^{0.75\times 0.25}(\gamma )$ and hence as a function of $s$, $|\hat{h}|_{L^2(\mathbb {R})} \in \mathcal {H}^{0.75\times 0.25}(\gamma )$.

Express (4.20) as a first order system:

$$\begin{aligned} (\hat{Y}, \hat{Z})^\tau _\xi =(\hat{Z}, (sI-Df(q_j))\hat{Y} -c_j\hat{Z})^\tau + \hat{h}(\xi ,s), \quad [(\hat{Y},\hat{Y}_\xi )](a) = \hat{\phi }_a . \end{aligned}$$

(4.23)

In Lemma 4.4, we have obtained $(u,u_\xi )$ for $s\in \Sigma (-\eta ,\theta )\backslash \{0\}$. Converting the results to $(\hat{Y},\hat{Z})$, we find that $(\hat{Y},\hat{Z})$ are analytic for $s\in \Sigma (-\eta ,\theta )\backslash \{0\}$ and satisfy

$$\begin{aligned} \begin{aligned}&|\hat{Y}(\cdot ,s)|_{L^2(\xi \le a)} + |\hat{Y}(\cdot ,s)|_{L^2(\xi \ge a)} \le \frac{C(\epsilon )}{1+|s|} |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}, \\&|(\hat{Y},\hat{Z})(\xi ,s)|_{E^{0.72\times 0.25}(s)} \le C(\epsilon ) e^{-\alpha |\xi -a|} |\hat{\phi }_a|_{E^{0.72\times 0.25}(s)}. \end{aligned} \end{aligned}$$

(4.24)

Lemma 4.5

If for the dichotomies to the left and right of $\xi =a$,

$$\begin{aligned} E_s(a_+,s=0) \cap E_u(a_-,s=0)= span\{(q^\prime _j(a), q^{\prime \prime }_j(a)) \}, \end{aligned}$$

and if $\hat{\beta }(s)$ satisfies (4.22), then in a neighborhood of $s=0$, the functions $(\hat{Y}, \hat{Z})$ are holomorphically extendable over $s=0$. Moreover, if $|s| \le \epsilon$,

$$\begin{aligned}&{|\hat{Y}(\cdot ,s)|_{L^2(\xi \le a)} + |\hat{Y}(\cdot ,s)|_{L^2(\xi \ge a)} \le C |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}, } \end{aligned}$$

(4.25)

$$\begin{aligned}&|(\hat{Y},\hat{Z})(\xi ,s)|_{E^{0.72\times 0.25}(s)} \le C e^{-\alpha |\xi -a|} |\hat{\phi }_a|_{E^{0.72\times 0.25}(s)}. \end{aligned}$$

(4.26)

Proof

For each $|s|\le \epsilon$, there exist two separate dichotomies for (4.23), one for $\xi \in (-\infty , a]$ the other for $\xi \in [a,\infty )$. The projections are denoted by $P^-_s + P_u^-=Id$ for $\xi \le a$ and $P_s^+ + P_u^+=Id$ for $\xi \ge a$. Observe that unlike the unified dichotomy defined for all $\xi \in \mathbb {R}$, The two separate dichotomies satisfy the property

$$\begin{aligned} |P^\pm _s(\xi ,s)| + |P^\pm _u(\xi ,s)| \le K, \text { for all }|s| \le \epsilon . \end{aligned}$$

We can express the solution of (4.23) as follows:

$$\begin{aligned} \begin{aligned}&(\hat{Y}(\xi ,s),\hat{Z}(\xi ,s))^\tau = T(\xi , a,s )P^-_u(a,s)(\hat{Y}(a,s),\hat{Z}(a,s)) \\&\quad + \int _{-\infty }^\xi T(\xi ,\zeta ,s) P^-_s(\zeta ,s) (\hat{h}(\zeta ,s))d\zeta + \int _a^\xi T(\xi ,\zeta ,s )P^-_u(\zeta ,s) (\hat{h}(\zeta ,s)) d\zeta ,\text { for } \xi \le a, \\&(\hat{Y}(\xi ,s),\hat{Z}(\xi ,s))^\tau = T(\xi ,a,s)P^+_s(a,s)(\hat{Y}(a,s),\hat{Z}(a,s))\\ {}&+ \int _a^\xi T(\xi ,\zeta ,s)P^+_s(\zeta ,s) (\hat{h}(\zeta ,s))d\zeta +\quad \int _{\infty }^\xi T(\xi ,\zeta ,s)P^+_u(\zeta ,s) (\hat{h}(\zeta ,s)) d\zeta , \text { for } a\le \xi . \end{aligned} \end{aligned}$$

(4.27)

The solution is determined by a pair of vectors:

$$\begin{aligned} \mu _u(a_-,s):= P^-_u(a,s)(\hat{Y}(a,s),\hat{Z}(a,s)), \quad \mu _s(a_+,s):=P^+_s(a,s)(\hat{Y}(a,s),\hat{Z}(a,s)). \end{aligned}$$

To satisfy the jump condition at $\xi =a$, we need

$$\begin{aligned}&\mu _s(a_+,s)-\mu _u(a_-,s) = \nonumber \\&\quad \hat{\phi }_a \!+\!\int _{-\infty }^a T(a,\zeta ,s)P_s^-(\zeta ,s) (\hat{h}(\zeta ,s))d\zeta \!+\! \int _a^{\infty } T(a,\zeta ,s)P^+_u(\zeta ,s)(\hat{h}(\zeta ,s)) d\zeta .\nonumber \\ \end{aligned}$$

(4.28)

Let the right hand side of (4.28) be $d(a, s)$ which is analytic for $|s| \le \epsilon$ and satisfies

$$\begin{aligned} |d(a,s)|_{E^{0.75\times 0.25}(s)} \le C |\phi _a|_{E^{0.75\times 0.25}(s)}. \end{aligned}$$

We wish to solve the equation $\mu _s(a_+,s)-\mu _u(a_-,s) = d(a,s)$ in $E^{0.75\times 0.25}(s)$ such that $\mu _s(a_+,s)\in R P_s^+(a_+,s)$ and $\mu _u(a_-,s)\in R P_u^-(a_-,s)$. Notice that

$$\begin{aligned} R P_s^+(a_+,s) =E_s(a_+,s),\quad R P_u^-(a_-,s)=E_u(a_-,s), \\ E_s^+(a_+,s) \oplus E_u^-(a_-,s)=\mathbb {R}^{2n}, \quad \text { if } s\in \Sigma (-\eta ,\theta )\backslash \{0\}. \end{aligned}$$

For such $s$, the unique pair of solutions $(\mu _s(a_+,s), \mu _u(a_-,s))$ can be expressed by the unified dichotomy that is defined on all $\mathbb {R}$:

$$\begin{aligned} \mu _s(a_+,s)= P_s(a,s) d(a,s),\quad \mu _u(a_-,s) = - P_u(a,s) d(a,s). \end{aligned}$$

(4.29)

The analytic functions $(\mu _s(a_+,s), \mu _u(a_-,s))$ may have a simple pole at $s=0$. We now show that the pole is removable, that is, in $E^{0.75\times 0.25}(s)$,

$$\begin{aligned} |\mu _s(a_+,s)| + |\mu _u(a_-,s)| \le C |\hat{\phi }_a|, \text { if }0<|s|\le \epsilon . \end{aligned}$$

(4.30)

In the above, as well as in the rest of this section, any unmarked norms are $E^{0.75\times 0.25}(s)$ norms.

The idea of the proof follows from that of Lemma 3.10 of [11], which also shows that the dichotomy has a pole at $s=0$. Recall that $z_j$ satisfies the adjoint equation

$$\begin{aligned} z_j'' -c_j z_j + Df(q_j)^* z_j =0. \end{aligned}$$

Converting this second order equation into a first order system, we can show that the adjoint equation of (4.16) has a bounded solution $\Psi = (\psi _1,\psi _2):=(c_j z_j -z_{j\xi }, z_j)$, which satisfies

$$\begin{aligned} \Psi (a)\perp E_u(a,s=0)+ E_s(a,s=0). \end{aligned}$$

From (4.21), we have $<\Psi (a),d(a, s=0)> =0$. Therefore $|<\Psi (a),d(a, s)>| \le C|s|$. Apply the orthogonal projections to $d(a,s)$ so that $d(a,s)=d^T(a,s) + d^\perp (a,s)$ where $d^T(a,s) \in E_s(a_+,s=0)+ E_u(a_-,s=0)$ and $d^\perp (a,s)\in \text {span}\{\Psi (a)\}$. From $<\Psi (a),d(a,s=0)> =0$, we have $d^\perp (a,0)=0$, thus $|d^\perp (a,s)|\le C |s|$. From Lemma 3.7, the unified projections satisfy $|P_s(a,s)|+ |P_u(a,s)| \le C/|s|$. Therefore

$$\begin{aligned} |P_s(a,s)d^\perp (a,s)| +|P_u(a,s)d^\perp (a,s)| \le C|\phi _a|,\quad \text {if }0<|s| \le \epsilon . \end{aligned}$$

(4.31)

We now prove that if $0<|s| \le \epsilon$ for a small $\epsilon >0$, then

$$\begin{aligned} |P_s(a,s)d^T(a,s)|+|P_u(a,s)d^T(a,s)| \le C|\phi _a|. \end{aligned}$$

(4.32)

We can write $d^T(a,s) = d_1(a,s) + d_2(a,s)$ where $d_1(a,s) \in E_s(a_+,s=0)$ and $d_2(a,s) \in E_u(a_-,s=0)$. We further require that $d_2(a,s) \perp \text {span}\{(q^\prime _j(a),q^{\prime \prime }_j(a)) \}$ so the decomposition is unique and satisfies:

$$\begin{aligned} |d_1(a,s)| + |d_2(a,s)| \le C |d^T(a,s)|. \end{aligned}$$

We now consider the perturbations of $d_1(a,s)$ and $d_2(a,s)$. First, a perturbation theorem to the stable subspace, see Lemma 3.5 of [10], shows that for $0<|s|\le \epsilon$, there exists a unique $\tilde{d}_1(a,s)$ such that $\tilde{d}_1(a,s) \in E_s(a_+, s)$ and $\tilde{d}_1(a,s) -d_1(a,s)\in E_u(a_+,s=0)$. Moreover $d_1(a,s)- \tilde{d}_1(a,s) =\mathcal {O}(s)$. A simpler proof for finite dimensional spaces can be find in Lemma 2.3 of [13] (simply change the algebraic decay rate to exponential decay rate). Similarly, there exists a unique $\tilde{d}_2(a,s)$ such that $\tilde{d}_2(a,s) \in E_u(a_-,s)$ and $d_2(a,s) - \tilde{d}_2(a,s)\in E_a(a_-,s=0)$. Moreover $d_2(a,s) - \tilde{d}_2(a,s) = \mathcal {O}(s)$.

We can easily check the following:

$$\begin{aligned} P_s(a,s)d^T(a,s)&= P_s(a,s)(d_1+d_2)=\tilde{d}_1+ P_s\left( (d_1 - \tilde{d}_1) +(d_2- \tilde{d}_2)\right) ,\\ |P_s(a,s) d^T(a,s)|&\le |\tilde{d}_1(a,s)| + |P_s| (|\tilde{d}_1 -d_1| +| \tilde{d}_2 - d_2|). \end{aligned}$$

Using $|\tilde{d}_1(a,s)|\le C |d_1(a,s)|\le C |d^T(a,s)|$, $|P_s|=\mathcal {O}(1/s)$ and $|d_j(a,s) - \tilde{d}_j(a,s)| =\mathcal {O}(s), j=1.2$, we have $|P_s(a,s) d^T(a,s)|\le C |d^T(a,s)|$ for $0<|s|\le \epsilon$.

Similarly we can prove that $|P_u(a,s) d^T(a,s)|\le C|d^T(a,s)|$ for $0<|s|\le \epsilon$. Combining (4.29), (4.31) and (4.32), we have shown that $(\mu _s(a_+,s), \mu _u(a_-,s))$ are holomorphically extendable over $s=0$, and satisfies (4.30).

If $s=0$ were not singular for the projections $P_s,P_u$, then from (4.27) we could prove that $\hat{Y} \in H^{2,1}_0(\xi \le a)$ and $\hat{Y} \in H^{2,1}_0(\xi \ge a)$ just like [11]. The idea of the proof still works under the restriction $|s|\le \epsilon$ for a small $\epsilon >0$. In particular, part (2) of Lemma 3.1 in [11] implies that

$$\begin{aligned} |T(\xi , a,s )P_u^-(a,s)(\hat{Y}(a,s),\hat{Z}(a,s))|_{L^2(\xi \le a)} \le {C} |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}. \end{aligned}$$

The proof of Lemma 3.8 in [11] implies that the $L^2(\xi \le a)$ norms of the two terms

$$\begin{aligned} \int _{-\infty }^\xi T(\xi ,\zeta ,s) P^-_s(\zeta ,s) (\hat{h}(\zeta ,s))d\zeta \text { and } \int _a^\xi T(\xi ,\zeta ,s )P^-_u(\zeta ,s) (\hat{h}(\zeta ,s)) d\zeta \end{aligned}$$

are also bounded by $C |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}$. Therefore

$$\begin{aligned} |\hat{Y}|_{L^2(\xi \le a)} \le C |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}, \quad |s|\le \epsilon . \end{aligned}$$

Similar estimates can be obtained for $\xi \ge a$ from the second half of (4.27). This proves (4.25).

Now consider the three terms in (4.27) for $\xi \le a, \; |s| \le \epsilon$ again. By (4.30), we have

$$\begin{aligned} |(\hat{Y}(a_-,s),\hat{Z}(a_-,s))|_{E^{0.72\times 0.25}}(\gamma )&\le C |\hat{\phi }_a|_{E^{0.72\times 0.25}}(\gamma ),\\ |T(\xi , a,s )P_u^-(a,s)(\hat{Y}(a_-,s),\hat{Z}(a_-,s))^\tau |_{E^{0.72\times 0.25}}(\gamma )&\le Ce^{-\alpha |\xi -a|} |\hat{\phi }_a|_{E^{0.72\times 0.25}}(\gamma ). \end{aligned}$$

Using the fact $0<\alpha <\alpha _1$, it is easy to check that for $|s| \le \epsilon$,

$$\begin{aligned}&|\hat{h}(\zeta ,s)|_{E^{0.72\times 0.25}(s)} \le C e^{-\alpha _1|\zeta -a|} |\hat{\phi }_a|_{E^{0.72\times 0.25}(s)},\\&\left| \int _{-\infty }^\xi T(\xi ,\zeta ,s) P_s^-(\zeta ,s) (\hat{h}(\zeta ,s))d\zeta + \int _a^\xi T(\xi ,\zeta ,s )P_u^-(\zeta ,s) (\hat{h}(\zeta ,s)) d\zeta \right| _{E^{0.72\times 0.25}(s)} \\&\le Ce^{-\alpha |\xi -a|} |\hat{\phi }_a|_{E^{0.72\times 0.25}(s)}. \end{aligned}$$

This proves (4.26) for $\xi \le a$. The proof for $\xi \ge a$ is similar.$\square$

Proof (The proof of Theorem 4.2 continued.)

For $|s|=\epsilon$, the functions $(\hat{Y},\hat{Z})$ have been constructed two times – converted from $(\hat{u},\hat{v})$ obtained in Lemma 4.4, and directly from Lemma 4.5. However, the solution $(\hat{Y},\hat{Z})$ is unique for any given $s \in \Sigma (-\eta ,\theta )$. This proves that $(\hat{Y},\hat{Z})$ is analytic in the entire region $s\in \Sigma (-\eta ,\theta )$.

Combining (4.24) and (4.25), we have for $\xi \le a$,

$$\begin{aligned} |\hat{Y}|_{L^2(\xi \le a)}&\le \frac{C}{(1+|s|)} |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}, \quad \text {if } s\in \Sigma (-\eta , \theta ). \\ \int _{-\infty }^\infty (1+|s|)^2 |\hat{Y}|_{L^2(\xi \le a)}^2 d\omega&\le C \int _{-\infty }^\infty |\hat{\phi }_a|_{E^{0.75\times 0.25}(s)}^2 d\omega \le C |\hat{\phi }_a|^2_{\mathcal {H}^{0.75\times 0.25}(\gamma )}. \end{aligned}$$

Similar results can be obtained for $\xi \ge a$. The inverse Laplace transform shows that both for $\xi \ge a$ and $\xi \le a$, $Y\in H^{2,1}_0(\gamma )$ for some $-\eta <\gamma <0$.

By combining (4.24) and (4.26), and using the inverse Laplace transform, we have

$$\begin{aligned} |(\hat{Y}, \hat{Z})|_{E^{0.75\times 0.25}(s)}&\le Ce^{-\alpha |\xi -a|} |\hat{\phi }_a|_{E^{0.75\times 0.25}}(s), \quad s\in \Sigma (-\eta , \theta ),\\ |(Y, Z)|_{H_0^{0.75\times 0.25}(\gamma )}&\le Ce^{-\alpha |\xi -a|} |\phi _a|_{H_0^{0.75\times 0.25}}(\gamma ). \end{aligned}$$

The distance of $\Gamma _j$ to $M^\pm _j$ is greater than $x_j - y_j -N$. So $(Y,Y_\xi )$ at $\Gamma _j$ is bounded by $C e^{-\alpha |x_j - y_j -N|}|\phi _a|$. Recall that $(u_j, u_{j\xi }) = (Y,Z) + (\beta (t)q^\prime _j, \beta (t) q^{\prime \prime }_j)$, which is also bounded by $C e^{-\alpha |x_j - y_j -N|}|\phi _a|$ at $\Gamma _j$.

Using the result of Part B, we can eliminate the jump errors along $M_j^\pm , 1\le j \le m$. The process will induce exponentially small errors along $\Gamma _j$ again. Repeating the process, the jump error along $\Gamma _j$ and $M_j^\pm$ can be eliminated. We introduce a function $\beta _j(t)$ in each iteration, which is added up to form the final $\beta _j(t)$ for each $u_j$. $\square$

5 Solution of the Nonlinear System

In Sect. 4, we solved the nonhomogeneous linear system (2.6), rewritten here for the reader’s convenience:

$$\begin{aligned} \begin{aligned}&u_{jt}= u_{j,xx}+ Df(q_j)u_j + h_j, \; uj(x,0) = u_{j0}(x),\text { for }(x,t)\in \Omega _j, \\&[(u_j,u_{jx})](\Gamma _j)=J_j(\Gamma _j),\\&[u_{j0},u_{j0,x}]=J_j(\Gamma _j)|_{t=0}. \end{aligned} \end{aligned}$$

(5.1)

where $h_j \in L^2(\Gamma _j,\gamma )$, $u_{j0}(x) \in H^1(x_{j-1},x_j)$, and $J_j(\Gamma _j) \in H^{0.75\times 0.25}(\gamma )$ are temporarily given functions, independent of $(\{u_j\},\{r_j\})$.

We obtained the solution in the form $u_j(x,t)= u_j^{(1)}(x,t) + u_j^{(2)}(x,t)$ where $u_j^{(1)}$ is the solution of a nonhomogeneous initial value problem (4.1) without jump conditions, and $u_j^{(2)}$ is the solution of (4.8) with nonzero jump conditions along $\Gamma _j$.

We now prove the main result of the paper – Theorem 1.1. To obtain the solution to the nonlinear problem, as in (2.7), we set $h_j= B(r_j) u_j + R(r_j,u_j)$, $u_{j0}(x) =\bar{u}_{j0}(x)-r_j q^\prime _j(\xi ) + g_j(\xi ,r_j)$ and $J_j(\Gamma _j)= J_j(\Gamma _j,\{r_j\})=J_{j0} + G_j(\{r_j\})$ in (5.1). In the resulting nonlinear system, we look for $\{r_j\}$, so that (5.1) has a solution $u_j\in H^{2,1}(\Omega _j,\gamma ), 1\le j \le m$.

The solution $u_j^{(1)}(x,t)$ in $\Omega _j$ can be expressed as $U=\beta _j^{(1)}(t) q^\prime _j(\xi _j) + Y_j^{(1)}(\xi ,t)$. To simplify the notation, the inner product for $L^2$ functions $\int <a(\xi ), b(\xi )>d\xi$ will be denoted by $<a,b>$. Before restricting to $\Omega _j$, the equations for $\beta _j^{(1)}$ and $Y_j^{(1)}$ are

$$\begin{aligned} Y^{(1)}_{jt}&= L_j Y_j^{(1)} + Q_j \tilde{h}_j,\\ \dot{\beta }_j^{(1)}(t)&= \langle z_j, \tilde{h}_j\rangle ,\\ \beta _j^{(1)}(0)&= \langle z_j, \bar{u}_{j0}\rangle - r_j + \langle z_j, g_j(\cdot ,r_j)\rangle . \end{aligned}$$

Let $\mathcal {K}_j$ be the integral operator as in (4.4) and $\left( \cdot \right) _{\Omega _j}$ be the restriction of a function to $\Omega _j$. Then in $\Omega _j$,

$$\begin{aligned} \beta _j^{(1)}(t)&= \beta _j^{(1)}(\infty ) + \int _\infty ^t \langle z_j,\tilde{h}_j \rangle dt,\\ Y^{(1)}_j&= \left( \mathcal {K}_jQ_j( -\tilde{h}_j) + e^{t L_j} Q_j(\bar{u}_{j0} + g_j(\xi ,r_j))\right) _{\Omega _j}\!,\\ r_j&= \langle z_j,\bar{u}_{j0}\rangle + \langle z_j, g_j(\cdot ,r_j)\rangle - \beta _j^{(1)}(0). \end{aligned}$$

We have $\dot{\beta }_j^{(1)} \in L^2(\gamma ),\; \beta _j^{(1)} \in X^1(\gamma )$.

The solution $u^{(2)}(x,t)=\left( u_1^{(2)},\dots ,u^{(2)}_m\right)$ can be expressed by operators

$$\begin{aligned} F_j: \{J_j(\Gamma _j,\{r_j\})-([u^{(1)}],[u^{(1)}_x])(\Gamma _j)\}_{j=1}^{m-1} \rightarrow u_j^{(2)}, \;1\le j\le m. \end{aligned}$$

In process in Sect. 4.2 yields the solution of the jump problem in the form $u_j^{(2)}= \beta _j^{(2)}(t)q^\prime _j+Y_j^{(2)}(x,t)$. Define $F_j^\sharp (\{J_j\}):= \beta _j^{(2)}(t)q^\prime _j$ and $F_j^\flat (\{J_j\}) := Y_j^{(2)}(x,t)$. Then

$$\begin{aligned} u_j^{(2)}=F_j(\{J_j\})= F_j^\sharp (\{J_j\}) + F_j^\flat (\{J_j\}),\quad J_j:=J_j(\Gamma _j,\{r_j\})-([u^{(1)}],[u^{(1)}_x])(\Gamma _j) \end{aligned}$$

We look for a solution of (5.1): $u_j = \beta _j(t)q^\prime _j + Y_j,1\le j\le m$, with $\beta _j(\infty )=0$. Notice that $\beta _j^{(2)}(0)=0$. From $\beta _j(t) =\beta _j^{(1)}(t) + \beta _j^{(2)}(t)$, we obtain $\beta _j^{(1)}(\infty )= -\beta _j^{(2)}(\infty )$ and $\beta _j^{(1)}(0)= -\beta _j^{(2)}(\infty )+ \int _\infty ^0 \langle z_j,\tilde{h}_j \rangle dt$. Thus

$$\begin{aligned} \beta _j(t)= \int _\infty ^t \langle z_j,\tilde{h}_j \rangle dt - \beta _j^{(2)}(\infty ) +\beta _j^{(2)}(t) . \end{aligned}$$

It is easy to check that $\beta _j^{(2)}= \langle z_j,F^\sharp _j(\{J_j\}) \rangle \in X^1(\gamma )$ with $J_j=J_{j0}+G_j(\{r_j\})-([u^{(1)}],[u^{(1)}_x])(\Gamma _j)$. Together, we consider a system for $r_j$ and $u_j=\beta _j(t)q^\prime _j+ Y_j$:

$$\begin{aligned} \begin{aligned} \beta _j(t)&= \int _\infty ^t \langle z_j, \tilde{h}_j \rangle dt +\beta _j^{(2)}(t) - \beta _j^{(2)}(\infty ).\\ Y_j&=\left( \mathcal {K}_j Q_j \tilde{h}_j + e^{t L} Q_j(\bar{u}_{j0} + g_j(\xi ,r))\right) _{\Omega _j}+ F_j^\flat (\{J_{j}),\\ r_j&=\langle z_j,\bar{u}_{j0}\rangle + \langle z_j, g_j(\cdot , r_j)\rangle +\int _0^\infty \langle z_j,\tilde{h}_j \rangle dt + \beta _j^{(2)}(\infty ). \end{aligned} \end{aligned}$$

(5.2)

System (5.2) can be expressed as

$$\begin{aligned} \{\beta _j, Y_j,r_j\} = \Phi (\{\bar{u}_{j0}\}, \{J_{j0}\}, \{\beta _j\}, \{Y_j\}, \{r_j\}),\quad 1\le j \le m. \end{aligned}$$

(5.3)

We shall solve this as a fixed point problem by the contraction mapping principle on the unknown variables $(\beta _j, Y_j, r_j)$. Let $B(\epsilon )$ be an $\epsilon$-ball in

$$\begin{aligned}&\prod _1^m X^1(\gamma ) \times \prod _1^m H^{2,1}(\Omega _j,\gamma ) \times \mathbb {R}^m. \\&B(\epsilon ):= \left\{ (\{\beta _j\}, \{Y_j\}, \{r_j\}) : \sum _{1\le j\le m}(|\beta _j| + |Y_j| + |r_j| ) \le \epsilon \right\} . \end{aligned}$$

To ensure that $\Phi$ is a contraction mapping on $B(\epsilon )$, it suffices to have

• (1) $|\Phi (\{\bar{u}_{j0}\}, \{J_{j0}\}, 0,0,0)| \le \epsilon /2$, and

• (2) the Lipschitz numbers of $h_j, g_j$ and $J_j(r_j)$ with respect to $(\beta _j, Y_j,r_j)$ are sufficiently small on $B(\epsilon )$ so that

  $$\begin{aligned} |\Phi (\{\bar{u}_{j0}\}, \{J_{j0}\}, \{\beta _j\}, \{Y_j\}, \{r_j\})-\Phi (\{\bar{u}_{j0}\}, \{J_{j0}\}, 0,0,0)| \le \epsilon /2. \end{aligned}$$

Condition (1) is satisfied if $\min \{|y_{j+1}-y_j|:1\le j \le m-1\}$ is sufficiently large and if for $1\le j\le m,\;|\bar{u}_{j0}|<\rho , |\{J_{j0}\}|<C\rho$ are sufficiently small, that is, if $\min \{|y_{j+1}-y_j|:1\le j \le m-1\}$ and $\rho$ satisfies conditions specified in Theorem 1.1.

To ensure that (2) is satisfied, and $\Phi$ is a contraction mapping on $(\beta , Y_j,r_j)$, recall

$$\begin{aligned} h_j&= B(r_j)u_j + {R(r_j,u_j)}, \quad g_j= q_j(\xi _j) - q_j(\xi _j+r_j) + r_j q^\prime _j(\xi _j),\\ G_j(\{r_j\})&= W_{j+1}(\Gamma _j)-W_{j+1}(\Gamma _j+r_{j+1}) +W_j(\Gamma _j + r_j) - W_j( \Gamma _j). \end{aligned}$$

It is straightforward to check that $h_j, g_j$ are all small terms in the sense that:

• (1) $|h_j| + |g_j| \le C(|u_j|^2 + |r_j|^2)$,

• (2) the derivatives of $h_j$ and $g_j$ with respect to $r_j,u_j$ are small.

It remains to verify that under the conditions of Theorem 1.1, the the jumps $G_j$ and $dG_j/dr_k$ are small for all $1 \le j \le m-1, 1\le k \le m$.

Along the line $\Gamma _j$, $G_j(\{r_j\}) = \mathcal {O}(|\{W_{jx}\}||\{r_j\}|)$. Therefore,

$$\begin{aligned} |G_j(\{r_j\})| \le C \max \{e^{-\eta |x_j- y_j|}:1\le j \le m-1 \}|\{r_j\}| <<\epsilon \end{aligned}$$

For $k \ne j,j+1$, $dJ_j/d r_k=0$, while for $k=j$ or $j+1$,

$$\begin{aligned} |dG_j/dr_k| \le C \max \{e^{-\eta |x_j- y_j|}:1\le j \le m-1 \}<<1. \end{aligned}$$

Therefore the Lipschitz number of $\{G_j(\{r_j\})\}$ with respect to $\{r_k\}$ is exponentially small if $\min \{|y_{j+1}-y_j|:1\le j \le m-1\}>\ell$ is sufficiently large. The constant $\ell$ is independent of $\delta _0$ as in Theorem 1.1 and Remark 1.1.

We have proved that system (5.2) can be solved by the contraction mapping principle on $\{r_j\}, \{Y_j\}$ and $\{\beta _j\}$, and $u_j\in H^{2,1}(\Omega _j,\gamma )$. The solution $u_j$ is a continuous function $t \in \mathbb {R}^+ \rightarrow H^1(\Omega _j)$. To check estimates (2) of Definition (1.1), let the solution of the linear problem be

$$\begin{aligned} (\{\beta _j\}, \{Y_j\}, \{r_j\})^{(0)}=\Phi (\{\bar{u}_{j0}\}, \{J_{j0}\}, 0,0,0). \end{aligned}$$

(5.4)

From Sect. 4, $|(\{Y_j\}, \{\beta _j\},\{r_j\})^{(0)}|\le C \rho$. If the rate of the contraction map $\Phi$ is $0<k<1$, from (5.3) and (5.4), we have

$$\begin{aligned}&|(\{Y_j\}, \{\beta _j\},\{r_j\})-(\{Y_j\}, \{\beta _j\},\{r_j\})^{(0)}|\le k |(\{Y_j\}, \{\beta _j\},\{r_j\}) |,\\&|(\{Y_j\}, \{\beta _j\},\{r_j\})|\le (1-k)^{-1} |(\{Y_j\}, \{\beta _j\},\{r_j\})^{(0)} | \le C\rho . \end{aligned}$$

Thus, $|Y_j|_{H^{2,1}(\Omega _j,\gamma )} + |\beta _j|_{X^1(\gamma )} \le C\rho$. So $u_j$ is a continuous function $t \in \mathbb {R}^+ \rightarrow H^1(\Omega _j)$ and $|e^{-\gamma t} u_j|_{H^1(\Omega _j)}\le C(|Y_j| + |\beta _j|)\le C\rho$. This proves estimate (2) of Definition (1.1).

6 Generalized Fisher/KPP Equations and Final Remarks

In this section we briefly consider the concatenation of two traveling waves of the generalized Fisher/KPP equation where our assumptions H1 and H2 are not satisfied. We hope to show that concatenation of waves and spatial dynamics can be useful in dealing with such nonstandard case.

The Fisher-KPP equation $u_t=u_{xx} + 2u(1-u)$ has a traveling wave solution $u(x-3t)$ connecting $u=1$ to $u=0$. The change of variable $u \rightarrow 1-u$ yields $u_t= u_{xx} -2u(1-u)$, which has has a traveling wave $u(x-3t)$ connecting $u=0$ to $u=1$. We now consider the generalized Fisher-KPP equation and the associated first order system satisfied by the traveling wave $u(\xi )=u(x-3t)$:

$$\begin{aligned} \begin{aligned} u_t&= u_{xx} -2u^n(1-u),\quad n\in \mathbb {N},\\ u'&=v,\quad v'=-3v + 2 u^n(1-u). \end{aligned} \end{aligned}$$

(6.1)

Denote the traveling wave $u(x-3t)$ by $q_2(x-c_2 t)$. Let $q_1(x-c_1 t)$ be a traveling wave that moves to the left with the speed $c_1<0$. (One such example is to flip the axis $x \rightarrow -x$ so that $q_1(x-c_1 t) = q_2(-x-c_2 t)$ and $c_1 = -c_2$.) For each fixed $t$, as $x$ increases from $-\infty$ to $\infty$, $q_1(x-c_1t)$ (or $q_2(x-c_2t)$) connects $u=1$ to $u=0$ (or $u=0$ to $u=1$).

Define the concatenated wave $u(x,t)^{con}$ separated by $\Gamma =\{x=0, t\ge 0\}$ as in (1.8). Let $u(\xi ,t)= q_j(\xi ) + u_j(\xi ,t)$ be the exact solution near $u^{con}$, where $j=1$ for $x<0$ and $j=2$ for $x>0$. For $n\in \mathbb {N}$, each single wave $q_1$ (or $q_2$) is stable only under some weighted norms applied to large $\xi$ and/or large $-\xi$. Let $w_j(\xi ) \ge 1$ be a suitable weight function. The weighted norms are designed to limit the allowed perturbations to $q_1$ and $q_2$ by requiring that $\Vert u_j\Vert _{H^k_{w}}:= \Vert w_j u_j\Vert _{H^k}<\infty$.

For $n=1$, the traveling wave $q_1$ is a node to saddle connection and $q_2$ is a saddle to node connection. As in [23], we can choose $w_1(\xi )=e^{c_1\xi /2}$ for $\xi < 0$ and $w_1(\xi )=1$ for $\xi \ge 0$; and choose $w_2(\xi )$ similarly. See Fig. 3 for the spectrum before and after adding the weighted norms. Observe that $w_1(\xi ) \rightarrow \infty$ as $\xi \rightarrow -\infty$, and $w_2(\xi ) \rightarrow \infty$ as $\xi \rightarrow \infty$, those are the left end and right end of the concatenated wave. Therefore the same weights can be applied to $u_j(x,t), j=1,2$, to put restriction on perturbations of the initial data of the concatenated wave to ensure its stability.

Fig. 3

The spectrum for the wave $q_2$ when $n=1$. a Without the weight function the spectrum is bounded to the right by a parabola with the vertex at $B=Df(1)>0$. b With the weight function the spectrum is bounded to the right by a parabola with the vertex at $A=Df(0)$, plus the line segment $\overline{AC}$, where $C=Df(1)-c_2^2/4<0$

For $n \ge 2$, $(u,v)=(0,0)$ is non-hyperbolic with eigenvalues $\uplambda _1=0, \uplambda _2\ne 0$. The traveling wave $q_1$ connects $(1,0)$ to the center manifold of $(0,0)$ and $q_2$ connects the center manifold of $(0,0)$ to $(1,0)$. The system looks similar to that studied by Wu, Xing and Ye [27], but is not the same. For the initial data of $u_1(x,t), x<0$ (or $u_2(x,t), x >0$), we can use the same exponential weight functions $w_j(\xi )$ as when $n=1$. However, if $n \ge 2$, it is known that the linear variational system around $q_1(\xi ), \xi \ge 0$ (or $q_2(\xi ), \xi \le 0$) has an algebraic dichotomy (rather than an exponential dichotomy), see [27]. To restrict the perturbations of each traveling wave, for $u_1(x,t), x>0$ (or $u_2(x,t), x<0$), we may use $w_j(\xi ) = c_j (1+|\xi |)^\gamma ,\;\gamma >0$ for $\xi >0,\;j=1$ (or $\xi <0,\;j=2$), as in [13, 27]. However, for the concatenated wave, since $u_1$ exists only for $x<0$ and $u_2$ exists only for $x>0$ so the boundedness of the weighted norms does not put any restriction on the initial values of $u_1$ for large $x$ (or initial values of $u_2$ for large $-x$).

In comparison, our method of eliminating jumps between the waves does not depend on evolution operators in time. It depends on evolution operators in space $x$, so it is more flexible to deal with weights or jumps in $x$ direction. As in [14], we might be able to replace the weighted norms by some boundary conditions to the left and right of $\Gamma$, which also helps to restrict the allowed perturbations of $q_1$ and $q_2$.

To summarize, the main ideas of our method, as outlined in Sect. 1, should work both for bistable, and generalized Fisher/KPP type traveling waves. In our future work, we hope to find suitable function spaces so that the linear variational system may have exponential dichotomies and the stability of the concatenated wave may be proved by method similar to that used in this paper.