Keywords

Introduction

Numbers are more or less omnipresent in everyday life. On a typical day, we may be confronted with numbers as soon as the alarm clock rings at 06.00 o’clock. One may then pick it up to read the time and estimate whether there is still enough time to put the alarm on snooze for another 8 min when one has to catch tube number 4 leaving from platform 2 which one usually takes to get to the office. On the way, one may evaluate whether there is still enough money in one’s wallet to pay for the expensive coffee at the train station. These scenes nicely illustrate the prevalence of numerical information in our everyday life.

Accordingly, there is accumulating empirical evidence indicating that success in managing modern life at the beginning of the twenty-first century is associated substantially with the ability to appropriately deal with and handle numbers (e.g. Parsons & Bynner, 2005). Deficits in numerical competencies can entail both considerable personal handicaps (e.g. Dowker, 2005) and socio-economic costs (e.g. Gross, Hudson, & Price, 2009). Generally, there is now evidence that the ability to reason with numbers seems even more important than literacy for individual life and career prospects (see Butterworth, Varma, & Laurillard, 2011 for a review).

Therefore, it is of particular importance to investigate the processes underlying numerical cognition from its neuronal correlates to its developmental trajectories and how it can be acquired best. This chapter aims at providing a brief overview of these aspects. In the first part, we will summarize current research on the neural correlates of numerical cognition with a specific focus on the neural fibre pathways connecting the involved brain areas, as well as the neural correlates of numerical learning. In part two we will then describe related approaches for numerical learning using embodied and interactive training methods for numerical competencies drawing on the metaphor of a mental number line (henceforth: MNL ) representation. Finally, by integrating these two lines of research, we open up a new perspective on the possible origins of numerical cognition as redeployed neural correlates from physical experiences.

Neural Correlates of Numerical Cognition

Considering the scenes from daily life described above, it is obvious that they require an adequate understanding of numbers. However, there seem to be different aspects of numbers that are meaningful in different situations. For example, reading the time requires knowledge of Arabic number symbols. Estimating the money left in our wallet as well as time needed requires understanding the meaning of number magnitude and computational processes. Finally, for the mere naming of number words, but also for the use of numerical labels (i.e. tube number 4), verbal processes are involved. From a scientific point of view, these processes are specified by the currently most influential model of numerical cognition, the Triple-Code Model (Dehaene, 1992; Dehaene, Piazza, Pinel, & Cohen, 2003).

The Triple-Code Model

As already reflected in its name, this model assumes three numerical codes or representations underlying our numerical and mathematical competencies. The codes comprise (1) a visual Arabic number form necessary for identifying number symbols, (2) a verbal representation for processing spoken number words and storing arithmetic facts such as multiplication tables, and (3) an analogue representation of number magnitude (Dehaene & Cohen, 1995). This analogue magnitude representation is assumed to be essential for our understanding of (numerical) magnitudes. Interestingly, the analogue magnitude code was also hypothesized to contain a spatial component reflected in a left-to-right ordering of numbers along the MNL (e.g. Dehaene, Bossini, & Giraux, 1993; Fischer & Shaki, 2014 for a review; see below for a more elaborate discussion on the MNL ).

Importantly, however, the TCM not only provides a theoretical differentiation of representations involved in numerical cognition but gained its high influence on the field because of its unique integration of behavioural and neuro-functional aspects—making it an anatomo-functional model. This means that the three representational codes introduced above can be associated with specific brain regions: (1) The visual number form representation was attributed to the fusiform gyrus (e.g. Klein et al., 2014). (2) The verbal representation of numbers and with it the representation of arithmetic facts seems to be associated with left-lateralized perisylvian language areas and the angular gyrus in particular (e.g. Klein, Willmes, et al., 2010). Finally, (3) the analogue magnitude representation is supposed to be situated in the bilateral intraparietal sulci (IPS, Arsalidou & Taylor, 2011 for a meta-analysis) as well as additional posterior parietal areas associated with navigating upon the MNL (e.g. Dehaene et al., 2003)—reflecting a spatial representation of number magnitude.

The most important content-wise postulate of the triple-code model is the general distinction between a mental representation of number magnitude on the one side and rather verbally mediated retrieval processes for arithmetic facts on the other side. It is important to note that these two representational codes (e.g. number magnitude vs. verbal code for arithmetic facts) can dissociate. For instance, patients suffering from a stroke in the left hemisphere can present with a selective deficit of rote verbal knowledge (including multiplication facts) with preserved semantic knowledge of numerical quantities. On the other hand, patients with intraparietal lesions can show specific impairments of quantitative numerical knowledge (e.g. in subtraction), whereas knowledge of rote arithmetic facts is preserved (Dehaene & Cohen, 1997). Such double dissociations corroborate that numerical information is processed in different formats within distinct cerebral areas (for reviews, see Nuerk, Klein, & Willmes, 2012; Willmes & Klein, 2014). These two dissociable systems have also been substantiated by recent neuroimaging studies (i.e. left-hemispheric perisylvian areas and angular gyrus for arithmetic facts: e.g. Delazer et al., 2003, Klein, Willmes et al., 2010, bilateral IPS for number magnitude information: e.g. Klein, Nuerk, Wood, Knops, & Willmes, 2009; Klein, Moeller, Nuerk, & Willmes, 2010; Klein, Mann, et al., 2013).

In this context, it is important to note, however, that the vast majority of existing studies investigating the neural correlates of numerical cognition in general and numerical learning in particular focused on grey matter activation patterns and their changes. In contrast, knowledge on how these observed brain areas work together considering their connectivity is still rather patchy.

Adding Neural Connectivity to the Triple-Code Model

Already in its initial form, the TCM assumed that mental arithmetic requires the close interplay of parietal as well as additional (pre)frontal processes (Dehaene & Cohen, 1995). Therefore, numerical cognition and mental arithmetic are a clear case of multi-modular and distributed processing within the human brain (i.e. involving different number-specific representations as well as number-unspecific processes associated with different brain regions). However, even though numerous neuroimaging studies localized grey matter cortical structures recruited during number processing (see Arsalidou & Taylor, 2011; Dehaene et al., 2003 for reviews), the white matter pathways connecting these areas have largely been neglected so far. Thus, the TCM so far does not take into account the connecting fibre pathways underlying its multi-modular organization of numerical cognition. Accordingly, this approach has been criticized as “corticocentric myopia ” (Parvizi, 2009) because it does not take into account that any given brain function depends on the integrity of a widespread network integrating cortical areas across the entire brain. Therefore, attempts to explain typical and atypical cognitive functioning in general and numerical cognition in particular should combine (1) localized neural correlates of cognitive functions in circumscribed grey matter areas and (2) the connectivity of these cortical areas via white matter pathways to other cortical and subcortical areas .

However, hodology, the science of connectional anatomy (Catani & ffytche, 2005), has only recently become accessible to evaluation in the living brain by using DTI (diffusion tensor imaging). While functional magnetic resonance imaging (fMRI) identifies functionally defined cortical areas, DTI tractography also indicates the white matter tracts connecting these areas. This provides a powerful non-invasive tool to study brain connectivity patterns underlying cognitive functions. Employing diffusion tensor tractography, perisylvian language networks (e.g. Saur et al., 2008) but also networks underlying attentional processes (e.g. Umarova et al., 2010) have already been specified. In contrast, research interest into brain connectivity underlying numerical cognition has increased only recently (see Matejko & Ansari, 2015; Moeller, Willmes, & Klein, 2015 for reviews).

Importantly, there are currently only two studies worldwide which systematically investigated white matter connections of the representational codes suggested by the TCM (Klein, Moeller, Glauche et al., 2013, Klein et al., 2014, see Fig. 2.1). In these studies, we showed that the representations of arithmetic facts and number magnitude were subserved by two largely distinct neural networks, which do not share common neural pathways. This is of particular interest because the TCM proposes a contribution of both magnitude manipulations and arithmetic fact retrieval to complex arithmetic. However, our recent results further add to answering the question how magnitude manipulations and arithmetic fact retrieval actually interact. In the latter study by Klein et al. (2014) we suggested the idea that it might not be a question of either magnitude manipulation or fact retrieval. Instead, both networks will contribute to numerical cognition in a 'more or less' manner. Thus, it seems reasonable to assume that single digit multiplications or additions with summands up to five are primarily solved by processes of fact retrieval. However, there is also evidence for magnitude-related influences on these very easy tasks (e.g. Thevenot et al., 2007). The other way around, multiplying two three-digit numbers requires calculation and thus the manipulation of number magnitudes. Nevertheless, column-wise processing (i.e. unit digit * unit digit, tens digit * tens digit, etc.) involves single digit multiplications so that intermediate steps can be solved using arithmetic fact retrieval. Even though this idea seems to work for what is going on cognitively, we still can only speculate on the neural structures at which the two networks might interact. From an anatomical point of view, this might most probably be at the junction of the left angular gyrus and the IPS. These structures are not only anatomically close but are also well connected via association fibres and most probably via U-fibres as well (Caspers et al., 2011). However, future studies will have to evaluate this claim .

Fig. 2.1
figure 1

Overlay of fibre tracts identified for magnitude manipulations (red) and arithmetic fact retrieval (blue). Panel A gives a detailed view on the course of the fibre tracts in axial orientation. Two anatomically largely distinct dorsal vs. ventral fibre pathway profiles for magnitude manipulations (red) and arithmetic fact retrieval (blue) can be observed. Importantly, the two networks differ not only in localization of activation but also in the connections between associated cortex areas. Additionally, the connection between the visual number form area (VNF) and the number magnitude representation (IPS/pIPS) is displayed in red. Panel B again reflects the identified pathways in a 3D volume rendering. Finally, Panel C depicts a detailed view on the course of the fibre tracts in coronal orientation

Full size image

Furthermore, there is also evidence extending the TCM by means of identifying new structures and their connectivity involved in numerical cognition. Only recently, studies on functional/effective connectivity also indicated a specific role of the hippocampus in numerical development (Qin et al., 2014; Supekar et al., 2013). In children, hippocampal-prefrontal as well as hippocampal-parietal connectivity was found to be associated with the acquisition of retrieval-based solution strategies, while in adults hippocampal-parietal connectivity was associated with the retrieval of arithmetic facts. This latter finding was corroborated by our structural connectivity analyses (Klein et al., 2014) but also by a recent intervention study evaluating the neural correlates of multiplication fact learning in adults (Bloechle et al., 2016).

In summary, it can be said that our structural connectivity results not only updated the TCM by considering fibre pathways for the representations of magnitude (manipulations) and verbally driven arithmetic fact retrieval (Klein et al., 2014). Additionally, we were able to specify how brain structures associated with long-term memory processes (such as the hippocampus) are involved in the fronto-parietal network of numerical cognition. However, describing the neural networks subserving numerical cognition is only the first step. In a next step, it is important to evaluate the changes within these networks through numerical development and learning .

Neural Correlates of Numerical Learning

After initial scepticism, the majority of researchers are now confident that neuro-scientific research offers new approaches to investigate brain plasticity—a necessary prerequisite for both numerical instruction/education and rehabilitation—because it is able to specify the functional relationship between brain and behaviour (e.g. Ansari, De Smedt, & Grabner, 2012; Goswami, 2008). Recent research indicates that this can not only be achieved on the theoretical but also on the empirical level.

Importantly, there are now first studies investigating the neural correlates of numerical learning by means of evaluating changes in activation patterns within the above described neural networks. On an ontogenetic level, the meta-analyses of Kaufmann et al. (2011) indicated that numerical development in children is reflected by a frontal-to-parietal shift of activation associated with the processing of numerical information. This shift of activation within the fronto-parietal network of number processing is usually argued to indicate that the processing of numerical activation gets more specific and automated with increasing age and experience. Accordingly, neural activation in frontal brain areas associated with domain-general processes such as working memory and executive control (e.g. Nee et al., 2013) decreases while activation in parietal areas primarily associated with the processing of numerical content increases.

A more specific and controlled evaluation of the neural correlates of numerical learning was pursued by intervention studies. As regards the processing of arithmetic facts, Zaunmüeller et al. (2009) evaluated the effects of a training of arithmetic facts for a stroke patient. Following a left-hemispheric lesion, he showed a severe multiplication deficit (see also Klein, Moeller, & Willmes, 2013). An intensive training of multiplication tables restored the patient’s ability to directly retrieve results from memory instead of having to calculate results. On the neural level, the authors observed a specific increase in activation of right-hemispheric areas (e.g. the angular gyrus) homologue to those of the lesioned left hemisphere which are usually associated with the processing of arithmetic facts. This indicated that the intact right hemisphere seemed to have taken over arithmetic fact retrieval—at least to some degree. Moreover, Bloechle et al. (2016) measured brain activation in healthy participants before and after an extensive multiplication training to evaluate the neural correlates of arithmetic fact acquisition more specifically. When comparing activation patterns for trained and untrained problems in the post-training fMRI session, the authors replicated a higher activation of the left AG for trained problems as observed previously (Delazer et al., 2003; Ischebeck et al., 2007). However, in a pre-post comparison of activation for trained problems and the same problems in the pretraining fMRI session, no signal change in the AG was observed. Instead, we observed changes in neural activation through the training in hippocampal, parahippocampal, and retrosplenial structures suggesting the involvement of these areas associated with long-term memory in arithmetic fact retrieval.

With respect to the representation of number magnitude and its spatial dimension, Kucian et al. (2011) evaluated the effects of a number line estimation training for children at both the behavioural and the neural level. The authors found that the training not only improved children’s performance in number line estimation, but also led to functionally related remediation of neural activation in number-related parietal brain areas. For children with mathematics learning difficulties in particular, the training led to a specific change in the brain activation pattern: differences between the activation of children with and without mathematics learning difficulties in number-specific parietal cortex areas were reduced after the training.

Thereby, these studies demonstrated that it is possible to directly associate effects of numerical learning with changes in brain activation patterns (see also Delazer et al., 2003; Ischebeck et al., 2006). The effects of the spatial-numerical training of number line estimation in children as found by Kucian et al. (2011) seem of particular importance. These fit nicely with the suggestion of Dehaene et al. (2003) that apart from the content-wise differentiation between magnitude manipulations and arithmetic fact retrieval, spatial processes associated with the internal navigation on the MNL have a specific neural correlate in the posterior superior parietal lobules. Following this rationale and considering the results of Kucian et al. (2011), an association of numbers with physical space should be observable at the neural level.

Spatial-Numerical Associations at the Neural Level

First evidence for spatial-numerical associations to be represented at the neural level comes from observations of patients with hemi-spatial neglect (see Umiltà, Priftis, & Zorzi, 2009 for a review). These patients treat any objects, people, etc. in the neglected hemi-field (most often the left one following a right-hemispheric stroke) as if they did not exist at all (Bisiach, Capitani, Luzzatti, & Perani, 1981; Guariglia, Palermo, Piccardi, Iaria, & Incoccia, 2013). Accordingly, in case there is a spatial representation of number magnitude (in terms of a left-to-right oriented MNL ), it should be affected in patients suffering from neglect. And indeed, the characteristic rightward bias observed in neglect patients for spatial tasks such as line bisection (see Jewell & McCourt, 2000 for a review) was found to generalize to numerical tasks. Accordingly, neglect patients not only misplaced the midpoint of a physical line towards the right, but also the middle of a numerical interval (e.g. indicating 7 as the middle between 1 and 9; Zorzi, Priftis, & Umiltà, 2002, see also Hoeckner et al., 2008 for two-digit numbers). These results demonstrated that spatial neglect influences the representation of number magnitude and its mapping onto physical space (see also Mihulowicz, Klein, Nuerk, Willmes, & Karnath, 2015).

Further corroboration for the claim of spatial-numerical associations on the neural level is provided by the results of Knops, Thirion, Hubbard, Michel, and Dehaene (2009). These authors investigated the interrelation between addition and subtraction and saccadic eye movements. In particular, the authors used the brain activation associated with either left- or rightward saccades to predict whether participants were performing either addition or subtraction problems. The authors observed that participants’ completion of addition problems was predicted reliably by the neural activity observed for rightward saccades, whereas the completion of subtraction problems was predicted by neural activation associated with leftward saccades. Interestingly, this nicely fits with the idea of the operational momentum effect (McCrink, Dehaene, & Dehaene-Lambertz, 2007), which assumes that addition reflects a rightward movement on the MNL , whereas subtraction reflects a leftward movement. Knops et al. (2009) argue that the association of leftward saccades with subtraction and of rightward saccades with addition indicates systematic navigation upon the MNL during subtraction and addition.

Taken together, these findings indicate a reliable association of the neural representation of number magnitude and physical space as reflected by the conceptual metaphor of the MNL . Importantly, the idea of a spatial representation of number magnitude is not restricted to basic research on the neural underpinnings of numerical cognition but generalizes to research on children’s numerical development and has already been applied in intervention studies.

Development and Applications of Spatial-Numerical Associations

The metaphor of a MNL is a well-established theoretical concept (1) investigated in research on children’s numerical development in general but also (2) used successfully as an instructional tool to corroborate numerical development in primary school years. In the following part of this chapter we will elaborate on these points in more detail.

Spatial-Numerical Associations in Children’s Numerical Development

Research on the development of numerical abilities in infants suggests that an innate sensitivity to magnitudes exists (e.g. Xu, Spelke, & Goddard, 2005). This means that only a few months old infants already seem to recognize differences in number—an interpretation that is supported by an increasing number of studies (e.g. De Hevia, Izard, Coubart, Spelke, & Streri, 2014; McCrink & Wynn, 2004). Moreover, infants have even been reported to be able to perform simple arithmetic (e.g. McCrink & Wynn, 2004, 2009). For instance, in one of the first studies on the topic, Wynn (1992) used a habituation paradigm considering infants’ looking times as an indicator of their number-related cognitive processing. The author placed one object behind a screen and then added a second object while the infant was watching the scene. The screen was then removed to reveal either one or two objects. Infants looked longer at the display when there was only one instead of two objects. Wynn (1992) interpreted this to indicate that infants were surprised about the outcome because it violated their expectation to see two objects. This was observed not only for addition but also subtraction problems and thus indicates infants’ innate sensitivity to numerical magnitude. Likewise, there is also first evidence on systematic spatial-numerical associations early in numerical development.

First systematic evidence for a left-to-right oriented association of number and physical space came from the Spatial Numerical Association of Response Codes (SNARC) effect (Dehaene et al., 1993; see also Wood et al., 2008, for a meta-analysis). This effect describes the phenomenon that in Western cultures, participants tend to react faster to smaller numbers with their left hand and to larger numbers with their right hand (Dehaene et al., 1993). Initially, the fact that the effect was not observed before primary school was interpreted to indicate that it is driven by culture (e.g. Cohen-Kadosh, Lammertyn, & Izard, 2008; Zebian, 2005). This hypothesis, however, seems outdated as spatial-numerical associations other than the SNARC effect have already been observed for kindergartners (e.g. Ebersbach, 2015; Patro & Haman, 2012) and even infants (de Hevia et al., 2014, see Patro, Nuerk, Cress, & Haman, 2014 for a review). In the study by de Hevia et al. (2014), 7-months-old infants were found to associate the dimensions of physical space and number, as indicated by infants preference in looking times for left-to-right oriented increasing numerical sequences. This indicates that the analogue magnitude representation described in the TCM (Dehaene & Cohen, 1995) might be innately associated with physical space (de Hevia & Spelke, 2010).

Although this indicates a very early association of physical space and number, which is preserved through life (de Hevia & Spelke, 2009), a precise mapping of number magnitude onto space (reflecting a number line) nevertheless takes time to develop, as indicated by children’s number line estimation performance (e.g. Siegler & Booth, 2004). For instance, when asked to estimate the position of a target number on a given number line, young children tend to systematically overestimate the spatial positions of small numbers (i.e. placing 10 where 40 should be on an number line ranging from 0 to 100, e.g. Moeller, Pixner, Kaufmann, & Nuerk, 2009).

However, an accurate number-to-space mapping was argued to be an important building block for the development of later arithmetic skills. In line with this notion, there is convincing evidence showing that children’s number line estimation accuracy is correlated reliably with their arithmetic performance (e.g. Link et al., 2014; Schneider, Grabner, & Paetsch, 2009; Siegler & Booth, 2004). Even more so, children with mathematics learning difficulties were observed to present with particularly worse number line estimation performance (e.g. Geary, Hoard, Nugent, & Byrd-Craven, 2008; Landerl, 2013). Accordingly, there have even been attempts to identify subtypes of mathematics learning difficulties that suggest the existence of a specific weak MNL subtype (e.g. Wilson & Dehaene, 2007; see also Bartelet, Ansari, Vaessen, & Blomert, 2014 for a data-driven approach).

However, the argument on the importance of a MNL representation also works the other way around. Not only is the MNL influential in numerical development, it can also be trained successfully by approaches specifically strengthening children’s spatial-numerical associations .

Towards an Embodied Training of the Mental Number Line

In recent years, an increasing number of trainings have been developed to train number magnitude understanding in general (e.g. The Number Race , Wilson, Revkin, Cohen, Cohen, & Dehaene, 2006) and spatial-numerical associations in particular (e.g. Ramani & Siegler, 2008). Some approaches even address the MNL metaphor explicitly and directly train the association between numbers and physical space. For example, a preliminary version of the now commercially available Dybuster® Calcularis program (for an evaluation see Käser et al., 2013) specifically trained children in the number line estimation task. In this study, Kucian et al. (2011) found their number line estimation training to be effective. Children with and without mathematics learning difficulties improved significantly not only in number line estimation but also arithmetic problem solving. Considering recent theoretical developments on embodied cognition in general (e.g. Barsalou, 2008; Wilson, 2002) and embodied representations of numbers in particular (e.g. Fischer & Brugger, 2011; Myachikov et al., 2013 for theoretical considerations), we aimed to increase the effects of number line trainings by allowing for an embodied interaction and experience of the trained spatial-numerical association through movement-based elements.

In a new training approach building on the concept of embodied numerosity (Domahs, Moeller, Huber, Willmes, & Nuerk, 2010), we evaluated the benefits of incorporating whole-body movement into the training of spatial-numerical associations. The rationale behind this idea were findings of other types of number-related physical movement such as finger counting that influenced spatial-numerical associations (Fischer, 2008). However, not just finger counting has been associated with numerical processing. In recent years, accumulating evidence suggested a link between whole-body movement and numerical processing (Hartmann, Farkas, & Mast, 2012; Hartmann, Grabherr, & Mast, 2012; Shaki & Fischer, 2014). For example, Shaki and Fischer (2014) showed that the magnitude of numbers that participants should generate randomly while walking influenced their decision whether to turn left or right after some steps. When the last generated number was relatively small, this led to a significant increase of left turns, whereas relatively large numbers were associated with reliably more right turns.

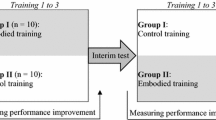
In line with the results of this and other previous studies, we developed an embodied spatial-numerical training on a digital dance mat (Fischer, Moeller, Bientzle, Cress, & Nuerk, 2011). In this training, kindergarteners had to perform number magnitude comparisons in a set-up in which one number was presented on a number line, and another number had to be classified as either larger or smaller than the first one. Children’s responses had to be made by jumping from the central field of the dance mat to the left for a smaller decision and to the right for a larger decision (see Fig. 2.2). This training was compared to a similar training performed on a tablet PC. In a randomized crossover design, each child received both trainings in a balanced order, and improvements over the two training phases were compared against each other. Importantly, we observed that children not only improved their number line estimation performance more through the experimental than the control training, but also showed more pronounced improvements in their understanding of counting principles.

Fig. 2.2
figure 2

Schematic illustrations of embodied trainings: Panel A depicts a training set-up with the digital dance mat as in Fischer et al. (2011). Panel B shows a simplified version of the training set-up used by Link, Moeller, Huber, Fischer, and Nuerk (2013), with the green screen indicating from which end of the number line the child should start walking

Full size image

Follow-up studies were conducted using different digital media and training different numerical concepts (Fischer et al., 2015; Link et al., 2014; Link et al., 2013; see Fischer et al., 2014; Dackermann et al., 2016 for overviews). For instance, in another study (Link et al., 2013), we trained first-graders to perform the number line estimation task with their entire body. On an up to 3 m long number line taped on the floor, children marked their estimates by walking to the estimated location of the target numbers on the number line (see Fig. 2.2). We used a Kinect™ sensor to record children’s estimates. Results following a randomized crossover design revealed that the embodied training was equally effective compared to a PC training of the very same content. However, the embodied training led to more pronounced improvements of children’s performance on simple addition problems and addition problems involving a carry operation. What is more, we observed that children with lower general cognitive abilities and visual working memory capacity specifically benefitted from the embodied training.

In a recent study (Fischer et al., 2015), we used an interactive whiteboard to train the number line estimation task. Due to the width of the whiteboard (about 1.5 m), second-graders had to move left or right to mark their estimates on the presented number line. Compared to a number line training on a PC and a non-numerical training on the interactive whiteboard (controlling for the motivational appeal of this medium), the experimental training again led to more pronounced improvement in children ’s number line estimation but also their addition performance.

In another innovative approach, promising results were obtained when training children’s understanding of the equidistant spacing of numbers upon the number line in an embodied fashion (Dackermann, Fischer, Cress, Nuerk, & Moeller, 2016). In this study, the embodied training condition required children to walk a certain distance in a given number of equally spaced steps. In the control training children had to subdivide a given line—presented on a tablet PC—into equally spaced segments without any embodied experience of the equidistance principle. Importantly, results indicated that children not only improved more strongly through the embodied training condition in their ability to divide distances into equally spaced segments. Additionally, their performance on an unbounded number line estimation task also increased more strongly after the embodied compared to a control training.

Taken together, these promising results indicate that embodied numerical trainings are effective in corroborating children’s basic numerical concepts. In light of current numbers of about 6 % of children who suffer from mathematics learning difficulties (e.g. Fischbach et al., 2013; see Moeller, Fischer, Cress, & Nuerk, 2012 for an overview), our next step will be a training specifically addressing these children. Since our trainings are designed to promote basic numerical competencies, and children with mathematics learning difficulties are facing problems already at this level of competencies, this seems a reasonable and promising starting point for applying embodied intervention methods.

Overlapping Brain Activation for Numbers and Space

An additional benefit of such embodied trainings addressing basic numerical competencies is that these basic competencies have been associated with specific brain areas (see above, e.g. Arsalidou & Taylor, 2011; Dehaene et al., 2003). Thus, it should be possible to evaluate changes of the way in which numerical information is processed in the brain through training as previously attempted by Kucian et al. (2011). Therefore, neuro-scientific methods such as fMRI may not only be used to evaluate specificities of brain activation associated with number processing but also changes in brain activation due to numerical training and instruction in particular.

As described above, there is now accumulating evidence corroborating the idea that the underpinnings of numerical cognition but also the effects of specific (embodied) spatial-numerical trainings can be evaluated on the neural level. Interestingly however, when it comes to spatial-numerical associations, the evidence also suggests a major involvement of brain areas not primarily associated with the processing of number magnitude. For example, an involvement of areas associated with attentional shifts in physical space reflected by saccades (Knops et al., 2009, see above) or mental navigation (Dehaene et al., 2003) was observed. Moreover, there are empirical findings suggesting an involvement of further brain areas in numerical cognition more broadly such as areas associated with specific motoric functioning and finger movements in particular (e.g. Kaufmann et al., 2008; Tschentscher, Hauk, Fischer, & Pulvermüller, 2012). Furthermore, there is even more specific empirical evidence indicating overlapping neural activation in (intra)parietal cortex areas for the processing of numbers, the execution of saccades , but also grasping and pointing movements (Simon, Mangin, Cohen, Le Bihan, & Dehaene, 2002; Simon et al., 2004). Importantly, these prominent co- and overlapping activations of brain areas associated with the mental representation of physical space and the representation of the body (as required for saccades and grasping/pointing movements) raise the question how and why these areas are specifically related to the processing of numerical information. In the following, we will discuss a neuro-functional account on this question.

Numerical Cognition: Reused Neural Circuits for Physical Experiences

The question how and why specific brain areas are co-activated for or show overlapping activation with the processing of numerical information addresses the issue of how specific observed neural correlates reflect specific cognitive functions such as motor abilities, spatial cognition, attention, and also numerical cognition. However, while it is reasonable to assume that neural circuits for motor abilities and also the processing of spatial information are necessary phylogenetic developments to allow interactions with the environment, this does not hold for the human ability to use symbol systems such as Arabic numbers for numerical cognition. In fact, such cultural acquisitions are far too recent to evolve their specific brain mechanisms (with Arabic numbers being used for about 1000 years, cf. Menninger, 1957, see also Chrisomalis, 2004). Instead, it was suggested that the capacity of numerical cognition (and also other cultural competencies such as reading) may have evolved through a specific form of cortical plasticity unique to humans termed neural recycling (Dehaene, 2005). Following the neural recycling hypothesis, “the human ability to acquire new cultural objects relies on a process […] whereby those novel objects invade cortical territories initially devoted to similar or sufficiently close functions. According to this view, our evolutionary history, and therefore our genetic organization, has created a cerebral architecture that is both constrained and partially plastic, and that delimits a space of learnable cultural objects. New cultural acquisitions are therefore possible only inasmuch as they are able to fit within the pre-existing” (Dehaene, 2005, p. 126).

For the case of numerical cognition, it was suggested that even for tasks with symbolic Arabic numbers humans rely on an analogue magnitude code, also described as a MNL (Dehaene et al., 2003). Importantly, this analogue magnitude code does not seem to be specific to the processing of number magnitude but may generalize to the processing of physical and temporal magnitudes (i.e. spatial distances and time durations, e.g. Bueti & Walsh, 2009; Santiago & Lakens, 2015; Walsh, 2003). This indicates that the cultural acquisition of processing number magnitude may have invaded the phylogenetically older circuits for processing physical space and time. This seems reasonable as all three domains share and build upon a generalized representation of magnitude. Accordingly, this might not only account for spatial-numerical associations on the behavioural level such as the SNARC effect but also explain co-activation and overlapping activation of brain areas associated with grasping and saccades (which require the integration of spatial and temporal information) and numerical processing (e.g. Simon et al., 2002, 2004).

Related to the neural recycling hypothesis and providing a more specific account on the involvement of brain areas associated with finger movements in numerical cognition (e.g. Kaufmann et al., 2008; Tschentscher et al., 2012), Penner-Wilger and Anderson (2008, 2011; see also Anderson & Penner-Wilger, 2013) suggested what they termed the massive redeployment hypothesis . This hypothesis suggests that at least parts of the neural circuitry originally subserving finger use may have been redeployed to support the representation of number. Because this part serves both functions now, this neural circuit should be commonly activated in tasks requiring finger use or number processing. Thereby, the massive redeployment hypothesis also accounts for the finding that finger gnosis (i.e. the ability to recognize one’s fingers without visual control) is a reliable predictor of children’s numerical development with those children presenting with better finger gnosis also showing better numerical performance (e.g. Noël, 2005; Wyschkon, Poltz, Höse, von Aster, & Esser, 2015).

Although very similar at first glance, there is an important difference between this hypothesis and the neural recycling hypothesis. The massive redeployment hypothesis proposes that existing components are reused and thus lower level circuits are combined to evolve more complex cognitive functions. In contrast, the neuronal recycling hypothesis suggests that novel cultural acquisitions such as number invade and change existing neural circuits that show sufficient proximity (cf. the idea of a generalized magnitude representation, e.g. Walsh, 2003).

Coming back to the idea of our embodied numerical training, both of these hypotheses on the neuro-functional organisation and integration of the neural circuits underlying numerical cognition may actually account for (parts of) the beneficial effects of the embodied training approach. As these trainings require participants to move their whole body in physical space to perform a numerical task, the respective correlated or even overlapping brain areas should be activated jointly. Thereby, the systematic association of physical space and number magnitude (following the neural recycling hypothesis) and/or the systematic involvement of bodily movements (following the massive redeployment hypothesis) should provide an additional access to the relevant representation of numerical magnitude.

Taken together, we have come full circle from embodied interaction beneficial for numerical learning to the neural correlates of numerical cognition and its integration into brain circuits originally subserving spatial and motor-related processes, which substantiate the idea of systematically training spatial-numerical associations in an embodied way.