Computational Performance of Echo State Networks with Dynamic Synapses

Abstract

The echo state network is a framework for temporal data processing, such as recognition, identification, classification and prediction. The echo state network generates spatiotemporal dynamics reflecting the history of an input sequence in the dynamical reservoir and constructs mapping from the input sequence to the output one in the readout. In the conventional dynamical reservoir consisting of sparsely connected neuron units, more neurons are required to create more time delay. In this study, we introduce the dynamic synapses into the dynamical reservoir for controlling the nonlinearity and the time constant. We apply the echo state network with dynamic synapses to several benchmark tasks. The results show that the dynamic synapses are effective for improving the performance in time series prediction tasks.

1 Introduction

The echo state network (ESN) is a computational framework for processing time series data, consisting of two parts: the dynamical reservoir (DR) and the readout [1]. The DR is often constructed with sparsely connected recurrent neural networks (RNNs), which play the role to map the input time series into nonlinear spatiotemporal dynamics generated by the DR. The dynamics of the DR is a function of the input history, and therefore, the activation states in the DR contain the information of the input data. The readout is used to make a mapping from the activation states in the DR to the output time series. In the readout, the outputs of the ESN are often created by a linear combination of the activation states of the DR.

The feature of the ESN is that only the connection weights in the readout part are trained. The input connection weights and the internal connection weights in the DR are all fixed in advance. Therefore, in terms of computation time, the ESN is advantageous compared with the RNNs where all the weights are adjusted [2]. Particularly when the readout is a linear transformation, it is easy to obtain the weights that minimize the difference between the network output sequence and the desired output sequence by any linear regression method.

The ESNs have been successfully applied to a variety of tasks such as time series prediction, system identification, system control, adaptive filtering, noise reduction, function generation, and pattern classification. However, the ESN with the neuron-based reservoir is not good at dealing with slowly changing time series data whose time constant is smaller than that of the neuron unit. A time delay is required to handle the slow dynamics in the sample data. Although a delay line can be realized by connecting neurons in a chain in an unidirectional way, more time delay requires more neurons. Here, to change the nonlinearity and the time constant of the DR in another way, we introduce dynamic synapses into the DR.

Dynamic synapse, also called short-term synaptic plasticity, refers to the synapse in which the efficiency of synaptic transmission changes transiently due to the changes in the calcium concentration and the release of neurotransmitters [3]. The short-term synaptic plasticity persists for only several hundred milliseconds. Mongillo et al. theoretically showed that short-term facilitation in the prefrontal cortex is implicated in working memory [4]. Their simulations indicate that a population activity can be reactivated by weak nonspecific excitatory inputs as long as the synapses remain facilitated. Thus, dynamic synapses can store the history of the past neural activities for about one second as the changes in the synaptic transmission efficiency. Therefore, they can process information in accordance with the past neural activity. Hence dynamic synapses may play an important functional role in time series processing in the brain.

In this study, we propose the ESN with dynamic synapses and investigate its computational performance in time series prediction and memory capacity. We perform numerical experiments on several benchmark tasks to evaluate the effectiveness of the dynamic synapses in information processing. This research is important for understanding the dynamical behavior of the brain as well as realizing bio-inspired / energy-efficient information processing systems.

2 Methods

2.1 Models

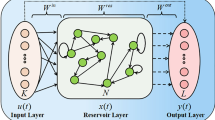
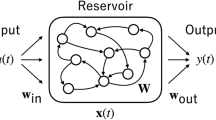
(1) Echo State Network. In this study, we use the ESN with dynamic synapses. Our ESN consists of ${ K}$ input layer neurons $\mathbf{I}(t)=[I_{i}(t)]_{1\le i \le K}$, randomly connected ${ N}$ hidden layer neurons $\mathbf{H}(t)=[h_{i}(t)]_{1\le i \le N}$ (dynamical reservoir), and L output layer neurons $\mathbf{Y}(t)=[y_{i}(t)]_{1\le i \le L}$. The ${ N} \times { K}$ input weight matrix $\mathbf{W}^{in}=[w^{in}_{i,j}]$ is created as an uniform random matrix in the range [−0.5, 0.5], and the ${ N} \times { N}$ internal weight matrix $\mathbf{W}=[w_{ij}]$ is created as an uniform sparse random matrix in the range [−0.5, 0.5]. $\mathbf{W}$ is normalized by the spectral radius represented as $\alpha _{sd}(<1)$. We set the sparseness of the internal weight matrix $\mathbf{W}$ at 15 %. The reservoir state $\mathbf{H}(t)$ is generated by the following difference equation:

$$\begin{aligned} \mathbf{H}(t+1) = \mathbf{f}(\mathbf{W}^{in}{} \mathbf{I}(t+1)+\mathbf{W}{} \mathbf{H}(t)), \end{aligned}$$

(1)

where $\mathbf{f}$ denotes the component-wise application of the unit’s activation function f. We use the sigmoid function $f(s)=1/(1+\exp (-s))$, the hyperbolic tangent $f(s)=\tanh (s)$, and the linear function $f(s)=s$. The output $\mathbf{Y}(t)$ is generated by the following difference equation:

$$\begin{aligned} \mathbf{Y}(t+1) = \mathbf{f}^{out}(\mathbf{W}^{out}{} \mathbf{H}(t)), \end{aligned}$$

(2)

where $\mathbf{W}^{out}$ is an ${ L} \times ({ K+N+L})$ output weight matrix calculated by using input-output training data pairs [2]. We use the output activation function $f^{out}(s)=\tanh (s)$.

(2) Dynamic Synapse. The short-term plasticity of dynamic synapses is caused by quantitative alteration of the releasable neurotransmitters and the calcium concentration [5, 6]. The dynamics of dynamic synapses are described by the following two equations for the variables $x_{i}$ representing the ratio of the releasable neurotransmitters and $u_i$ representing the calcium concentration of neuron $i (i=1,...,N)$:

$$\begin{aligned} x_{i}(t+1)= & {} x_{i}(t)+\frac{1-x_{i}(t)}{\tau _{D}}-x_{i}(t)u_{i}(t)h_{i}(t),\end{aligned}$$

(3)

$$\begin{aligned} u_{i}(t+1)= & {} u_{i}(t)+\frac{U_{se}-u_{i}(t)}{\tau _{F}}+U_{se}(1-u_{i}(t))h_{i}(t), \end{aligned}$$

(4)

where $\tau _{D}$ and $\tau _{F}$ are time constants for the dynamics of $x_i$ and $u_i$, respectively. If no action potential comes to the presynaptic terminal, $x_{i}$ and $u_{i}$ recover to the steady state level 1 and $U_{se}$, respectively. Here, the efficiency of synaptic transmission is proportional to $x_{j}(t)u_{j}(t)$. Therefore, when we innovate dynamic synapses, the strength of the connection from the jth neuron to the ith neuron is redefined as $D_{ij}(t)=w_{ij}x_{j}(t)u_{j}(t)/U_{se}$. This standard dynamic synapse model requires $0<h_{i}$. Therefore, this model cannot use tanh units and linear units, and instead we use the sigmoid units in this model.

The standard dynamic synapse model reproduces faithfully the experimental results. However, this model is not necessarily suitable for the neural network. For example, (1) this dynamic synapse model is not superset of the static synapse. (2) Dynamics of synaptic efficacy is not monotonic. (3) Dynamic synapse is complex because it includes two variables. To solve these problem, I devised a new univariate dynamic synapse model as follows:

$$\begin{aligned} e_{i}(t+1) = e_{i}(t)+\frac{1-e_{i}(t)}{\tau _{i}}+a_{i}(e_{i}(t)-m_{i})(M_{i}-e_{i}(t))h_{i}(t), \end{aligned}$$

(5)

where $e_{i}(t)$ is the synaptic efficacy of neuron i, and $a_{i}$ determines the rate of change of synaptic efficacy, $m_{i}$ and $M_{i}$ are the minimum and maximum values of synaptic efficacy, respectively ($0<m_{i}<1$, $1<M_{i}$). Now $w_{ij}$ can be described by $D_{ij}(t)=w_{ij}e_{j}(t)$. In this model, if $a_{i}>0$, then the short-term facilitation occurs. If $a_{i}<0$, then the short-term depression occurs. If $a_{i}=0$, then synapses become static. This model can use tanh units.

2.2 Tasks

(1) Memory Capacity. In order to evaluate the short-term memory capacity of ESN with dynamic synapses, we calculated the Memory Capacity (MC) [2, 7] of the network. We consider an ESN with a single input unit I(t) and many output units $\{y_{k}(t);k=1,2,...\}$. The input I(t) is a random signal generated by sampling from a uniform distribution in the interval [−0.5, 0.5]. Training signal $d_{k}(t)=I(t-k)$ are delayed versions of input signal I(t). Memory Capacity (MC) of an ESN is defined as follows:

$$\begin{aligned} \mathrm{MC} = \sum _{k=1}^{\infty }\max _{\mathbf{w}^{out}} r^{2}(I(t-k), y_{k}(t)), \end{aligned}$$

(6)

where

$$\begin{aligned} r^{2}(I(t-k), y_{k}(t)) = \frac{cov^{2}(I(t-k), y_{k}(t))}{\sigma ^{2}(I(t-k))\sigma ^{2}(y_{k}(t))} \end{aligned}$$

(7)

is the determination coefficient (cov denotes the covariance and $\sigma ^{2}$ denotes the variance).

(2) NARMA 10 Time Series. NARMA (Nonlinear autoregressive moving average) is a generalized version of the autoregressive moving average model, where the regression is nonlinear. NARMA is often used in many studies to evaluate the performance of time series processing of RNNs. The NARMA 10 time series, which includes 10 steps time lag, is generated by the following recurrence relation:

$$\begin{aligned} y(t) = \alpha y(t-1) + \beta y(t-1)\sum _{i=1}^{n}y(t-i) + \gamma I(t-n)I(t-1) + \delta , \end{aligned}$$

(8)

where $\alpha =0.3$, $\beta =0.05$, $\gamma =1.5$, $\delta =0.1$, $n=10$ [8]. The input I(t) is a signal generated by randomly sampling from a uniform distribution in [0, 0.5]. The task is to predict y(t) from I(t).

(3) NARMA 20 Time Series. The NARMA 20 time series includes 20 steps time lag. This is a more difficult task than the NARMA10 because of the longer history. The NARMA 20 has an additional nonlinear transformation by tanh to confine the signal in a finite range. The NARMA 20 is generated by the following recurrence relation:

$$\begin{aligned} y(t) = \tanh \left( \alpha y(t-1) + \beta y(t-1)\sum _{i=1}^{n}y(t-i) + \gamma I(t-n)I(t-1) + \delta \right) , \end{aligned}$$

(9)

where $n=20$ and the rest of conditions are the same as NARMA 10.

Fig. 1.

Comparison of Memory Capacity between the static synapse and the dynamic synapse. We set $N=400$ and $\alpha _{sd}=0.99$. We use the standard dynamic synapse model in A–B, and the univariate dynamic synapse model in C–F. A, B. Dependence of Memory Capacity on the time constant. We ran 20 trials with different initial weights, and we calculate the average value. We use the standard dynamic synapse model C. Forgetting curves of linear DR with static synapses. D. Forgetting curves of the tanh DR with static synapses. E. Forgetting curves of the linear DR with dynamic synapses. F. Forgetting curves of the tanh DR with dynamic synapses.

Table 1. Comparison of the performance between the static synapse and the dynamic synapse. We ran 20 trials with different initial weights, and we calculate the average value and the standard deviation. In these tasks, we use the univariate dynamic synapse model. A. Memory Capacity of the ESN. We set $\alpha _{sd}=0.99$, $N=400$, $a_{i}\in [0, 0.1]$ (random), $\tau _{i}\in [1, 20]$ (random), $m_{i}\in [0, 0.1]$ (random), and $M_{i}\in [1, 4]$ (random). B. NARMA task. We set $\alpha _{sd}=0.8$, and use the tanh units. The rest of conditions are the same as those in A.

3 Results

First, the memory capacity of the ESN with dynamic synapses was evaluated in comparison with the ESN without static synapses. In this task, we set $\alpha _{sd}=0.99$, $N=400$, and $w_{ij}^{in}\in [-0.1, 0.1]$. The activation function of the neuron units in the dynamic reservoir is given by the linear type, the tanh type or the sigmoid type. Figure 1 shows the results of the numerical experiments on the memory capacity task. Figures 1A and B show how the memory capacity depends on the delay parameters $\tau _D$ and $\tau _F$ in the dynamic synapses when using sigmoid units. These results show that a smaller value of $\tau _D$ gives a larger memory capacity and the value of $\tau _F$ is not influential on the capacity. Figures 1C–F show the forgetting curves which indicate how much input history can be embedded in the spatiotemporal dynamics of the dynamic reservoir. As the length of the delay k is increased, the determination coefficient tends to decrease. In this task, we use the univariate dynamic synapse model. We set $a_{i}\in [0, 0.1]$ (random) , $\tau _{i}\in [1, 20]$ (random), $m_{i}\in [0, 0.1]$ (random), and $M_{i}\in [1, 4]$ (random). Figures 1C and D for linear units show that the memory capacity is much decreased by introducing the dynamic synapses. This means that the linearity of the original dynamic reservoir, which is favorable for the transmission of the input data without transformation, is lost by the nonlinearity of the dynamic synapses. In the case of tanh units, the decrease in the memory capacity is relatively small as shown in Figs. 1E and F. Table 1A summarizes the statistical results for 20 trials in the above four cases. Overall, the dynamic synapses are not effective for improving the memory capacity due to their highly nonlinear property.

Next, NARMA time series prediction performance of the ESN with dynamic synapses was evaluated in comparison with the ESN without static synapses. In this task, we use the univariate dynamic synapse model. We set $\alpha _{sd}=0.8$, $N=400$, $w_{ij}^{in}\in [-0.3, 0.3]$, $a_{i}\in [0, 0.1]$ (random) , $\tau _{i}\in [1, 20]$ (random), $m_{i}\in [0, 0.1]$ (random), and $M_{i}\in [1,4]$ (random). Table 1B summarizes the statistical results for 20 trials. In the NARMA 10 task, we normalize output to range [−0.5, 0.5]. As a result, we found that the dynamic synapse reduce the prediction error about 39.3–47.1 % in NARMA 10 and about 9.5–14.2 % in NARMA 20. Figure 2 shows the time series of training signals (NARMA 10, NARMA 20) and output signals.

Fig. 2.

Training signal (the dotted line) vs Output signal (the solid line). The activation function of the internal units is given by $f=\tanh$. A. NARMA10 time series with the static synapses. B. NARMA10 time series with the dynamic synapses. C. NARMA20 time series with static synapses. D. NARMA20 time series with the dynamic synapses

4 Conclusion

We have proposed an echo state network incorporating dynamic synapses which can change the nonlinearity and the time constant of the dynamic reservoir. Numerical experiments were performed to evaluate the effect of dynamic synapses on the computational ability of the echo state network. In the memory capacity task, the dynamic synapses are not effective for improving the performance. This is because the linear dynamics, which is advantageous for the memory capacity task, is broken by the dynamic synapses. In the time series prediction tasks with NARMA 10 and NARMA 20, the dynamic synapses can reduce the prediction error. These tasks require highly nonlinear dynamics, which can be brought about by the dynamic synapses. In this way, the dynamic synapses are suited for relatively difficult tasks that require a dynamical reservoir generating highly nonlinear dynamics. Further numerical experiments for other tasks, however, are necessary to fully reveal the effect of the dynamic synapses on computational ability of the echo state network. In particular, the prediction of time series with slow dynamics is an interesting task to understand how dynamic synapses control the time constant.