Leveraging Structural Hierarchy for Scalable Network Comparison

Abstract

K-core decomposition is a popular method that segments a network revealing the underlying hierarchy. We explore the propensity of this decomposition method for structural discrimination among networks by extracting features from each level of the hierarchy. We propose a novel algorithm for Network Comparison using k-core Decomposition (NCKD). The method is effective, efficient and scalable, with computational complexity of $O(|{\mathcal E}|)$, where ${\mathcal E}$ is the set of edges in the network. The low computational complexity of the method makes it attractive for scalable network comparison.

NCKD algorithm decomposes networks and extracts features from the resulting shells. Jensen-Shannon distance between extracted features quantifies structural differences between networks. We establish that probability distributions of coreness and intra/inter-shell edges are capable of characterizing different genres of networks and capturing finer structural differences between networks of the same genre. We experiment with synthetic and real-life networks up to eight million edges on a single PC. Comparison with two recent state-of-the-art network comparison methods affirms that NCKD outperforms in terms of effectiveness and scalability.

1 Introduction

Complex networks have attracted immense attention because of their ability to model social relations, power grids, transportation links, biological processes etc. [7]. One of the challenging tasks in network analytics is to assess and quantify similarity between two networks. Applications of network comparison include construction of phylogenetic trees and function prediction in biological networks, studying evolution in social networks, analysing semantic structure in natural languages, detecting code theft by comparing two executable objects etc. [7, 9].

Similarity between two networks is a function of similarities between their orders, sizes, and topological features. While similarities in orders and sizes are trivial to assess, capturing topological and structural similarities is the core challenge in the task of network¹ comparison. Comparison of two networks essentially entails analogizing structural properties such as nature of hierarchy, clustering tendency, neighborhood characterization, correlation between topological attributes etc. Networks may be compared either at a local or global level depending upon the application. For example, construction of a phylogenetic tree using biological networks involves clustering organisms with similar biological evolution. This task demands a global comparison of networks. On the other hand, comparison of two metabolic networks for the purpose of discovering causal factors for functional differences calls for local level comparison.

Extraction of global features like diameter, average clustering coefficient, characteristic path length, betweenness centrality etc. for comparison purpose is unattractive because of high computational complexity even for medium-sized graphs. Computation of local features, on the other hand, involves examining configuration and properties of small subgraphs, conferring scale independence to the comparison method. Hence, it is tempting to adopt local properties for structural comparison of massive networks. Earlier approaches for network comparison pursued this trend and deployed local features including degree, clustering coefficient, degree centrality, triad census, graphlet distribution etc. [10]. Lamentably, these approaches fail to capture underlying structural hierarchy prevailing in real-life networks.

Therefore, it is desirable to devise methods that summarize network structure both locally and globally. Since hierarchical k-core decomposition promotes the local feature degree to the global feature coreness, we explore k-core decomposition as a tool to quantify the structural similarity between two networks. K-core decomposition has been recognized as an important technique for understanding complex networks by decomposing them in hierarchy [2, 12, 24]. We posit that hierarchical segmentation using k-core decomposition method has potential to reveal structural differences between networks at all levels of hierarchy.

1.1 Motivation

Motivational factors for using hierarchical k-core decomposition approach for scalable network comparison are listed below.

• i. Real-life networks exhibit structural hierarchy and comparing analogous signals at all levels of hierarchies has potential to reveal the structural disparity between networks.

• ii. The proposed algorithm is particularly appealing for comparing large and sparse graph since k-core decomposition method has computational complexity of $O(|{\mathcal E}|)$, ${\mathcal E}$ being the set of edges [4].

• iii. Massive networks that cannot fit in main memory can be decomposed using distributed k-core decomposition [22].

1.2 Contributions

In this paper, we propose a novel and scalable method for Network Comparison using k-core Decomposition (NCKD). According to Faust [10], network comparison studies are designed to answer two questions. First, does a pair of networks exhibit common structural tendencies?, and second, which structural features distinguish among different relations between nodes? We demonstrate that node distribution in shells of the network is an effective and efficient implement to answer the first question. Augmenting node distribution in shells with edge distribution boosts its power to cogently answer the second question. Research contributions of the paper are listed below:

• i. A novel algorithm (NCKD) that uses k-core decomposition to quantify network similarity through network signatures generated using probability distribution of nodes and edges in shells respectively (Sect. 4).

• ii. Comparison of NCKD with two state-of-the-art network comparison algorithms (Sect. 5.2).

• iii. Extensive experimentation to demonstrate effectiveness, scalability and robustness of NCKD (Sects. 5.3 and 5.4).

2 Related Work

Several decent algorithms for network comparison, that quantify similarity between networks, have been proposed in recent years. A related but different problem is network alignment, addressed in bio-informatics, where the goal is to map nodes of one network to the nodes of another. Our focus is on recent representative network comparison algorithms followed by a brief overview of applications of k-core decomposition.

2.1 Network Comparison

Popular approaches for comparing networks include (i) graph isomorphism, (ii) graph edit distance, (iii) iterative methods, and (iv) feature extraction [6].

Graph isomorphism, a theoretically sound approach, has been traditionally employed to establish exact matching between two graphs [15]. Approximate matching is commonly obtained by graph edit distance, which essentially is an error-tolerant method [11]. Iterative methods compute the pairwise similarity between nodes by capturing similarity/dissimilarity of their neighborhoods [21]. These three approaches lead to algorithms with high computational complexity and are hence non-scalable [18]. This deters their applicability to large networks.

Feature extraction approach has recently found favour with the community interested in analyzing massive graphs. The strategy involves constructing features from the compared graphs and computing distance between them to quantify differences. Banerjee [3] used eigenvalues of normalized graph Laplacian spectra to capture global topological properties for computing pairwise networks similarity. Recently, Lu et al. [18] compared complex networks using the heat content estimated by lazy random walk.

Macindoe et al. [19] considered all induced subgraphs of a parametrized radius centered on each vertex and computed three socially relevant structural features, Leadership, Bonding, and Diversity (L,B,D), driven by social theories for each subgraph. Earth mover’s distance between LBD distributions of networks quantifies their similarity. Netsimile [6] algorithm composes network signature from moments of distributions of selected local topological properties of the network. The pairwise similarity score of networks is computed using Canberra distance between their signatures. Scale-independent nature of selected properties renders a computational complexity of O(N), where N is the order of the graph.

These algorithms make use of either local or global features, each of which is individually ineffective and non-scalable for network discrimination. NCKD algorithm plugs the gap as it is scalable and exploits local feature while taking into account the global hierarchical structure of the network.

2.2 K-Core Decomposition

Seidman [24] introduced k-core decomposition for characterizing network structure.The k-core of a network is a maximal subgraph in which every node is connected to at least k other nodes. Batagelj et al. [4] present an $O(|\mathcal E)|$ algorithm for k-core decomposition of a graph ${\mathcal G}$ with $|\mathcal E|$ edges. Analysis of the k-core structure of a graph has been effectively used in identification of social cores and influential nodes in social networks, acceleration of community detection, evaluation of co-operation in communities, and as a visualization tool to highlight the topological and hierarchical structure of graphs [2, 12, 23]. Recently proposed k-truss decomposition method also presents a hierarchical view of the network yielding the largest subgraph in which every edge is contained in at least (k-2) triangles within it [25]. The method is effective for focusing on smaller and cohesive areas, which are subgraphs of k-core. However higher computational complexity of order $O(|{\mathcal E|}^{1.5})$ for k-truss decomposition is a discouraging factor. Hence, we chose to use k-core decomposition method for network comparison.

To the best of authors’ knowledge, NCKD is first-ever application of k-core decomposition for scalable network comparison using single PC.

3 Preliminaries and Notation

We introduce formal notation and definitions used in the paper. Let $\mathcal G$ be a simple, undirected graph $\mathcal {G=(V,E)}$, where $\mathcal V$ is the set of vertices and $\mathcal E$ is the set of edges. An edge $\mathsf {e}_{ij} \in {\mathcal E}$ if it connects vertices $\mathsf {v}_i$ and $\mathsf {v}_j$; $\mathsf {v}_i,\mathsf {v}_j \in \mathcal V$. The order of $\mathcal G$ is $|\mathcal V|$ and its size is $|\mathcal E|$. The degree of a vertex $\mathsf {v}$ is denoted by $\rho (\mathsf {v})$. The k-core decomposition algorithm iteratively prunes vertices of degree less than k resulting in a hierarchy of nested k-core sub-graphs, within which each node is connected to at least k other nodes. Formal definitions as adapted from [2] follow.

Definition 3.1

A subgraph, ${\mathcal G}^\prime _k= ({\mathcal V}^\prime _k,{\mathcal E}^\prime _k )$ of $\mathcal {G=(V,E)}$, induced by the set ${\mathcal V}^\prime _k \subseteq {\mathcal V}$ is a k-core (core of order k) of $\mathcal G$ if $\forall \mathsf {v} \in {\mathcal V}^{\prime }_k$: $\rho (\mathsf {v}) \ge k$, ($k \ge 0$) and ${\mathcal G}^\prime _k$ is a maximal connected subgraph with this property. $\square$

Definition 3.2

Coreness $\zeta (\mathsf {v})$ of vertex $\mathsf {v}$ is k if it belongs to a k-core but not to any (k+1)-core. Coreness of a graph $\mathcal {G=(V,E)}$ is ${max} \{\zeta (\mathsf {v}) \,\forall \mathsf {v} \in {\mathcal V}\}$.$\square$

Definition 3.3

A k-shell ($\mathcal S_k$) of $\mathcal {G=(V,E)}$ is the set of all vertices with coreness k, i.e., $\mathcal S_k = \{\mathsf {v} \vert \mathsf {v} \in \mathcal V \wedge \zeta (\mathsf {v}) = \text{ k }\}$. $\square$

The k-core decomposition reflects the structure of a network by faithfully capturing the inherent hierarchy as nested cores. The lower bound on number of nodes in a k-core is (k+1) and a loose upper bound is $|{\mathcal V}|$. The lower bound on the number of edges is $\left( {\begin{array}{c}\text{ k }+1\\ 2\end{array}}\right)$, while a loose upper bound is $|\mathcal E|$ [5]. If both endpoints of an edge have the same coreness, the edge is termed as an intra-shell edge, otherwise it is an inter-shell edge.

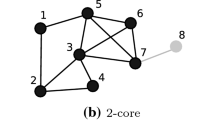
Example 3.1

Figure 1 shows graph $\mathcal {G}$ with $|\mathcal {V}|=32$ and $|\mathcal {E}|=47$. Dashed circles, marked $\mathrm {k}=i$, demarcate the cores. Nodes within a dashed circle and having same color denote shell ${\mathcal S_k}$. Shell ${\mathcal S}_4$, the highest order shell induces the 4-core of $\mathcal {G}$. Subgraph induced by ${\mathcal S}_3 \cup {\mathcal S}_4$ is the 3-core of $\mathcal {G}$. $\square$

Fig. 1.

K-core decomposition of $\mathcal {G}$. Nodes with same color constitute a shell. (Color figure online)

4 Characterizing Networks Using K-Core Decomposition

Adaptation of k-core decomposition for designing a similarity measure is non-trivial because two networks with the same hierarchical structure can have vastly different topology. The challenge is to identify and extract suitable features of the decomposed graph for effective and scalable network discrimination. We hypothesize that differences in the node/edge distribution of shells in the decomposed graph are effective discriminators for the overall structure of underlying networks. We first explain a simple and effective network feature i.e. node distribution followed by the statement of its limitation, and reasoning behind inclusion of edges arrangements.

4.1 Coreness Distribution

Distribution of nodes within shells captures the spread of nodes and reflects the underlying structure [24]. It is synonymous with the distribution of coreness of nodes in the decomposed graph.

Consider a graph $\mathcal {G=(V,E)}$ with coreness $\mathsf {k}$ and shells $\{\mathcal {S}_0, \ldots , \mathcal {S_\mathsf {k}}\}$. Let X be a discrete random variable denoting coreness of a node in $\mathcal {G}$ and defined on the sample space $\varLambda =\{0, \ldots , {\mathsf k} \}$. We define probability mass function for X as $p(x) = p(X=x) = \frac{|\mathcal S_x|}{|\mathcal V|}$, where $|\mathcal S_x|$ is the cardinality of shell $\mathcal S_x$. It is clear that $\sum _{x=0}^{\mathsf k}{|\mathcal S_x|=|\mathcal V|}$. Here, p(x) denotes the probability that a node has coreness value x. Alternatively, p(x) is the probability of an arbitrary node lying in shell $\mathcal S_x$. Following example explains computation of probability distribution (p) of nodes (coreness) in the shell.

Example 4.1

Graph $\mathcal {G}$ in Fig. 1 has 32 nodes and 5 shells. Probability distribution (p) of nodes in $\mathcal G$, is given by $p = \langle$0/32, 17/32, 4/32, 6/32, 5/32$\rangle$.

We studied probability distribution of coreness for several synthetic and real-life networks (Table 1) to test its propensity for network comparison. We show the plot of coreness distribution of six metabolic and five co-author networks in Figs. 2a and b. The striking similarity between the coreness probability distributions of graphs belonging to the same genre strongly indicates its utility as a discriminating network feature. Preliminary experimentation (not reported due to space constraint) however quickly revealed the inadequacy of this feature to effectively capture structural differences arising in the real world networks.

Fig. 2.

Plots for probability distribution of coreness for two genres of real-life networks.

This insufficiency arises because the arrangement of edges in a graph, which is the cause of topological variations, is completely ignored by the coreness distribution. Extreme topologies of star and chain with n nodes having identical hierarchical structure and probability distribution of coreness, present a very clear example to substantiate the argument. Since coreness is inadequate to capture finer structural differences between networks, it is myopic to depend on it as a sole distinguishing feature.

4.2 Edges Distribution

Theoretically, a graph of order n with coreness $\mathsf k$ and coreness distribution p is a random sample from the family $\mathcal {F}_{\mathsf {k},p,n}$ of graphs [14]. Graph $\mathcal G$ in question is one realization from this family. All graphs in $\mathcal {F}_{\mathsf {k},p,n}$ will have similar coreness distribution, even though they may be topologically different. This is unacceptable in both theory and practice. Rewiring and swapping lemmas stated in [5] reinforce this argument.

According to the rewiring lemma, two adjacent nodes in a shell can disconnect and connect independently to nodes with higher coreness, and vice versa without changing the coreness distribution of the graph. The swapping lemma allows non-adjacent nodes in the same shell to swap end-nodes without altering the coreness distribution of the graph. It is reasonable to conclude that coreness distribution is inadequate to capture finer structural differences between networks. For better discrimination between the members of $\mathcal {F}_{\mathsf {k},p,n}$ family, we incorporate arrangements of edges influencing the network structure in addition to nodes distribution.

Let $\mathcal G$ be a graph with coreness $\mathsf k$. Then, $E^l$ denotes the lower triangular matrix representing the arrangement of edges of G. $E^l_{ij}$ is the count of inter-shell links between shells ${\mathcal S}_i$ and ${\mathcal S}_j$. $E^l_{ii}$ is the count of intra-shell links in shell ${\mathcal S}_i$. Clearly $\sum _i \sum _j E^l_{ij} = \vert \mathcal {E}\vert$, $(0 \le i \le \mathsf {k}, 0 \le j \le i)$. Example 4.2 clarifies the idea of intra- and inter-shells links using matrix representation used in [5].

Example 4.2

The count of intra- and inter-shell edges in $\mathcal G$ of Fig. 1 is shown below in the lower triangular matrix ($E^l$). Shell $\mathcal S_2$ has one intra-shell link indicated by $E^l_{22}=1$. It also has six inter-shell links with $\mathcal S_1$ indicated by $E^l_{21}=6$.

$$E^l= \left( {\begin{array}{ccccc} 0 &{} &{} &{} &{} \\ 0 &{} 4 &{} &{} &{} \\ 0 &{} 6 &{} 1 &{} &{} \\ 0 &{} 5 &{} 2 &{} 9 &{} \\ 0 &{} 1 &{} 5 &{} 4 &{} 10 \\ \end{array} } \right) $$

We vectorize matrix $E^l$ to a vector V of size $\frac{({\mathsf k}+1)({\mathsf k}+2)}{2}$ such that $V=[E_{00}^l, E_{10}^l, E_{11}^l, E_{20}^l, \ldots , E_{{\mathsf k}{\mathsf k}}^l]$. Index r in V for $E_{ij}^l$ is obtained by using the following rule.

$$\begin{aligned} r \longleftarrow j+\frac{i*(i+1)}{2} \end{aligned}$$

(1)

Clearly, the vectorization expresses isomorphism between V and $E^l$. Let R be a discrete random variable defined on sample space $\varLambda ^\prime =\Big (0,1,\ldots ,\frac{(\mathsf {k}+1)(\mathsf {k}+2)}{2}-1\Big )$ denoting linkage count within and between shells in the graph. When $R=r$, it denotes linkage between shells ${\mathcal S}_i$ and ${\mathcal S}_j$, with the mapping defined by Eq. 1. The probability mass function u(r) of random variable R is defined as $u(r) = p(R=r) = \frac{E^l_{ij}}{\vert \mathcal {E}\vert }$. Here u(r) denotes the probability that an arbitrary edge in $\mathcal G$ connects a node in ${\mathcal S}_i$ to a node in ${\mathcal S}_j$. It is easy to show that u corresponds to probability distribution of intra-shell and inter-shell links. Following example shows the edge probability distribution u for the lower triangular matrix given in Example 4.2.

Example 4.3

Given 47 edges in $\mathcal G$, probability distribution of edges (u) is computed as: $\langle$ 0/47, 0/47, 4/47, 0/47, 6/47, 1/47, 0/47, 5/47, 2/47, 9/47, 0/47, 1/47, 5/47, 4/47, 10/47 $\rangle$. $\square$

If the number of nodes and edges in two graphs with identical coreness distribution are same, structural differences between them arise due to rewiring of edges. To examine the sensitivity of $E^l$ towards rewiring, we focus on the cases that do not alter the coreness of the involved nodes post-rewiring. There are two possibilities for rewiring of a node. It can either connect to a node in the same shell or to a node in a higher shell. Rewiring of a node in a lower shell can be considered as the former situation from the viewpoint of the node in the lower shell. We explain these cases below.

Fig. 3.

Example for edge rewiring. $\mathcal S_i, \mathcal S_j, \mathcal S_k$ are the shells.

R1. Rewiring an inter-shell edge: Consider nodes $\mathsf {u},\mathsf {v}, \mathsf {w} \in {\mathcal V}$, located in distinct shells $\mathcal {S}_i$, $\mathcal {S}_j$, $\mathcal {S}_k$ respectively, s.t. $i \ne j \ne k$ and $i < j,k$. Let edges $(\mathsf {u},\mathsf {v}) \in {\mathcal E}$ and $(\mathsf {u},\mathsf {w}) \notin {\mathcal E}$ Then R1 leads to

$$\begin{aligned} {\mathcal E} :={\mathcal E} \setminus (\mathsf {u},\mathsf {v}) \cup (\mathsf {u},\mathsf {w}) \end{aligned}$$

(2)

Figure 3(a) exhibits this case. Since node $\mathsf {u}$ lies in shell $\mathcal {S}_i$, it has at least i links with nodes in higher shells. After deleting edge $(\mathsf {u},\mathsf {v})$ and adding edge $(\mathsf {u},\mathsf {w})$, link count of $\mathsf {u}$ in higher shell remains same. Consequently, coreness of $\mathsf {u}$ remains unchanged. Coreness of $\mathsf {v}$ and $\mathsf {w}$ remains unchanged since links to lower shells do not impact coreness (by Definition 3.1). Consequently, post-rewiring coreness distribution remains unchanged. In the edge distribution matrix, two entries change as follows: $E^l_{ik}$ is incremented and $E^l_{ij}$ is decremented by 1. Hence altered structure of the graph is captured by the edge distribution.

R2. Rewiring an intra-shell edge: Consider nodes $\mathsf {u},\mathsf {v}, \mathsf {u}^\prime , \mathsf {v}^\prime \in \mathcal V$ s.t. $\mathsf {u},\mathsf {v} \in \mathcal {S}_i$, $\mathsf {u}^\prime \in \mathcal {S}_j$, $\mathsf {v}^\prime \in \mathcal {S}_k$ and $i \ne j \ne k$, $i< j,k$. Let edges $(\mathsf {u},\mathsf {v}) \in {\mathcal E}$, $(\mathsf {u},\mathsf {u}^\prime ) \notin {\mathcal E}$, $(\mathsf {v},\mathsf {v}^\prime ) \notin {\mathcal E}$. Then R2 leads to

$$\begin{aligned} {\mathcal E} :={\mathcal E} \setminus (\mathsf {u},\mathsf {v}) \cup (\mathsf {u},\mathsf {u}^\prime ) \cup (\mathsf {v},\mathsf {v}^\prime ) \end{aligned}$$

(3)

Figure 3(b) exhibits this case. Following similar arguments as in R1, intra-shell rewiring does not alter coreness distribution, but is reflected in edge distribution.

4.3 NCKD Algorithm

The proposed algorithm for Network Comparison using k-core Decomposition (NCKD) uses probability distribution of nodes as well as intra-shell/inter-shell edges. The problem of pair-wise network comparison reduces to computing the statistical distance between probability distributions representing signatures of the networks. We use Jensen-Shannon Distance (JSD) as it is a popular metric for comparing probability distributions due to its property of non-negativity, identity, symmetry, and boundedness [17]. Equation 4 gives JSD between two probability distributions p and q, with respective weights $w_1 \text{ and } w_2$ ($w_1,w_2 \ge 0 \text{ and } w_1+w_2=1$).

$$\begin{aligned} JSD(p,q) = {[H(w_1*p + w_2*q)-w_1*H(p) -w_2*H(q)]}^{\frac{1}{2}} \end{aligned}$$

(4)

Here, H is the Shannon entropy function. Equipped with a tool to capture finer distinctions of graph topologies, we quantify the structural difference (distance) between two networks as average of differences (distance) between the (i) distribution of coreness and (ii) distribution of edges.

Let p and q respectively denote the probability distributions of coreness of graphs ${\mathcal G}_1$ and ${\mathcal G}_2$. Further, u and v denote the edge probability distributions of graphs ${\mathcal G}_1$ and ${\mathcal G}_2$. Applying JSD on these distributions and averaging the result gives the net distance between two networks. Equation 5 formally defines distance between networks.

$$\begin{aligned} {\mathcal D}({\mathcal G_1}, {\mathcal G_2})= avg(JSD(p,q),JSD(u,v)) \end{aligned}$$

(5)

Algorithm 1 summarizes the steps for NCKD. Please note that in all experiments reported in paper, we assign equal weights to the distributions while computing JSD. We are conscious that weights can be constructively manipulated to capture preference for one graph over other during the comparison.

5 Experiments

The experimental study is designed to assess and compare effectiveness, scalability and robustness of NCKD algorithm against two recent network comparison algorithms Netsimile [6] and LBD [19]. We implemented NCKD algorithm in Python (64 bits, v 2.7.3) and executed on Intel Core i5-3201M CPU @2.50 GHz with 8 GB RAM, running UBUNTU 12.04.

5.1 About Datasets

We performed experiments with both synthetic and real-life datasets (Table 1). Synthetic datasets allow controlled variation of data characteristics and hence enable close scrutiny of algorithmic behaviour. Real-life datasets expose the strengths and weakness of the algorithm in practical scenarios.

Table 1. Characteristics of synthetic and real-life networks used; D: Diameter, C: Connected components, GCC: Global clustering coefficient, $\alpha$: Parameter for power law distribution

Synthetic datasets were generated using igraph package of R. Erdös-Rényi (E), Forest-Fire (F), Watts-Strogatz (W), and Barabási-Albert (B) models were used for analysis. Order (number of nodes) of the network in thousands (K) is included in nomenclature. Since each network is one probabilistic realization of the model parameters, we generated multiple networks with same parameters. Thus, B10K-n meant $n^{th}$ realization of Barabási-Albert network of order 10K. Three real-life genres include (i) Co-author (CA), (ii) Autonomous Systems (A), and (iii) Metabolic (M) networks. Large datasets used for scalability experiment are described in Sect. 5.4.

5.2 Effectiveness of NCKD

We compute effectiveness of NCKD by comparing ${\mathcal D}({\mathcal G}_1, {\mathcal G}_2)$ (Eq. 5) with distance measures defined in two state-of-the-art algorithms LBD and Netsimile. We compute pairwise distances for networks given in Table 1, using distance measures used in three algorithms. LBD algorithm was unable to generate network signatures for large graphs even after running for more than 24 h. We, therefore, restrict experiment to 14/32 graphs that LBD algorithm was able to process in reasonable time (<4 h) and cluster the networks using hierarchical agglomerative clustering². We compute purity, precision, recall, accuracy, and Normalized Mutual Information (NMI) measures [20] to assess the quality of clustering (Table 2).

Table 2. Quality metrics for hierarchical clustering of 14 small networks and all 32 networks.

It is clear from Table 2 that resultant clustering of 14 small networks by NCKD is better than those delivered by Netsimile and LBD algorithms. Timings (averaged over 3 runs) for generating network signatures (Table 3) for small networks show that NCKD is also faster. We dropped LBD algorithm for further experimentation since it was patently non-scalable and the clustering, as evidenced by NMI, was also poorer in quality.

Table 3. Signature generation time (in seconds) for NCKD, Netsimile and LBD on selected networks from Table 1. A - indicates that the algorithm did not complete even after running for 24 h.

Next, we execute Netsimile and NCKD on all networks mentioned in Table 1. Figures 4a and b show the dendrograms generated from pairwise distances computed by two algorithms. It is evident that NCKD algorithm performs better grouping than Netsimile. Cluster quality metrics of 32 networks (Table 2) for two algorithms vindicate the visual observation. Comparison of execution time of two algorithms reveals that NCKD is several orders faster than Netsimile (See Large synthetic and real-life networks in Table 3). The swift execution of NCKD indicates its scalability.

Fig. 4.

Dendrogram for networks described in Table 4. Networks belonging to same genre have same color. (Color figure online)

In order to capture finer distinctions between networks of the same genre, we selected eleven metabolic networks in two sub-categories (six Archaea (A) and five Eukaryotes (E)) whose order ranges from 490 to 1511 and size ranges from 1148 to 3807 [13]. We performed hierarchical agglomerative clustering of these networks from distance matrices generated by NCKD and NetSimile (Fig. 5). Algorithm NCKD is able to identify one pure group of Eukaryotes, which Netsimile missed. The clustering quality metrics for metabolic networks shown in Table 4 confirm the effectiveness of NCKD over Netsimile.

Fig. 5.

Metabolic networks in two sub-categories - A: Archaea, and E: Eukaryote.

Table 4. Quality metrics for dendrograms shown in Fig. 5

5.3 Handling of Missing Data

We compare effectiveness of NCKD and Netsimile towards missing data. For this experiment, we compared networks with themselves after applying random edge deletion systematically. For network G, we created $G^{'}_{x_1}, G^{'}_{x_2} \cdots G^{'}_{x_k}$ variations by deleting $x_i\%$ of edges from it. Intuitively, both algorithms should yield similarity score (SS) of 1 while comparing G with $G^{'}_{0}$, with the score falling as deleted edges increase. Fall in SS is expected to be different for different graphs due to structural differences. In order to beat the effect of randomness, reported results are averaged over three runs.

Three real-life networks (A-1, DC-1, CA-1) and one synthetic network (E10K-1) were perturbed by deleting edges from 0 % to 20 % (in steps of 2) and compared using two algorithms. Similarity scores obtained by NCKD and Netsimile are plotted in Figs. 6a and b. Netsimile registered a fall of maximum 10 % for the real-life datasets even after deleting 20 % edges while NCKD revealed significant differences in networks. This observation indicates superior ability of NCKD to suitably react to missing data.

Fig. 6.

Comparison of robustness towards missing data - NCKD vs. Netsimile.

Fig. 7.

Feature generation time of NCKD for synthetic networks

Fig. 8.

Feature generation time of NCKD for massive real-life networks. n/w: Network

5.4 Scalability w.r.t Large Datasets

Networks generated from different models allow convenient variations in the order of graphs to examine scalability of NCKD. We generated 10 graphs for each generative model (description in Table 1) with varying number of nodes 100K to 1000K in steps of 100K, and edges proportionally depending on the model. Netsimile was unable to process graphs of order >100K even after running for more than 24 h. Hence, it was dropped for scalability analysis. NCKD was executed five times for each graph to average out the timing observations. Figure 7 shows approximately sublinear growth in timings for each model. The increase in timings for the models varies with the number of edges in the corresponding networks. Edges increase fastest in FF model and slowest in BA model, which is faithfully reflected by the timings for two models.

Figure 8 shows execution timings of NCKD for five real-life large datasets downloaded from SNAP³, which strengthens the claim of scalability. Since k-core decomposition algorithm is $O({\mathcal E})$, time increases linearly with edges.

6 Conclusion

Each large-scale network is unique at the microscopic level. However, at different levels of resolutions, commonalities emerge among different pairs of graphs. Discovery of these commonalities and their quantification is the goal of the proposed algorithm NCKD (Network Comparison using k-core Decomposition), which is intuitive, effective and scalable. The algorithm decomposes the graph into cores, analyses shells and constructs node and edge related probability distributions, which serve as network signatures. Jensen-Shannon distance is applied on these signatures to find distance between networks. We establish that node and edge distributions adequately discriminate networks.

Extensive experimentation and comparison of NCKD with Netsimile and LBD algorithms establish its superiority in terms of effectiveness and scalability. Execution timings for large synthetic and real-life networks affirm its scalability. We also demonstrate that NCKD is sensitive to the underlying topological structure of the graph, but needs to be improved to take cognizance of size and order of the network. The agenda for future is to overcome its deficiency to clearly segregate networks of the same genre by including more shell features.