1 Introduction

Due to the rapid development of information technology, we are witnessing the proliferation of graph data based applications over recent years. This has led to huge research efforts devoted to real-world network analytics [2, 4,5,6, 10, 16, 23, 27]. Among them, identifying cohesive subgraphs to characterize the structure of real-world networks has been extensively studied. Observing that the cohesive subgraph models are often computed globally and fail to detect sparser regions if the network contains distinct regions of different densities, Govindan et al. proposed a new model named k-Peak recently [7]. By conducting the k-Peak decomposition (compute the k-Peak for all possible k values in the graph), [7] can divide the graph into separate ’mountains’ and can find the centers of distinct regions in the graph.

Motivation. The k-Peak decomposition addresses the issue of neglecting sparser regions in the existing cohesive subgraph model [7], however, since k-Peak only considers the edge connection (i.e., degree) between nodes in the subgraph, the returned results are often not that cohesive [5, 14, 28]. The returned loose structure restricts the effectiveness of the k-Peak decomposition. On the other hand, triangles are higher-order connectivity structure than degree [3, 19] and are known as fundamental building blocks of a network [12, 17, 18]. Therefore, triangles are commonly treated as the building blocks for the cohesive subgraph model in the literature [5, 8, 16, 27]. Motivated by this, in this paper, we propose a new model named k-TriPeak based on the triangles and study the k-TriPeak decomposition problem. The model inherits the ability to find the centers of distinct regions of k-Peak model and avoids the problem of incohesiveness for the returned result. Formally, given a graph G, the support of an edge is the number of triangles containing it. A k-TriContour of G is the largest subgraph of G such that (i) the support of edges in it is at least \(k-2\); (ii) the k-TriContour does not include edges from a higher TriContour. The k-TriPeak of G is the union of j-TriContours, where \(j \ge k\). And k-TriPeak decomposition computes the k-TriPeak for all possible k values.

Fig. 1.
figure 1

k-Peak vs k-TriPeak

Full size image

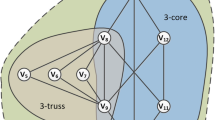
Example 1

Consider the graph in Fig. 1, we show the 3-Peak and 5-TriPeak of G (The counterpart of 3-Peak is 5-TriPeak since the support of edges is at least \(k-2\) in the definition of k-TriContour). As shown in Fig. 1, since 3-Peak only considers the edge connection between nodes, the incohesive subgraph induced by \(v_{11}, \dots , v_{15}\) is also returned. On the contrary, this incohesive subgraph is filtered out by the 5-TriPeak. In the literature, another similar cohesive subgraph model defined based triangles, k-truss, is also studied [5]. It is defined as the largest subgraph of G in which every edge is contained in at least \((k-2)\) triangles within the subgraph. The problem of k-truss is that it is unable to find the centers of distinct regions in the graph. As shown in Fig. 1, two centers of regions exist in G, namely \(\{v_1, \dots , v_{5}\}\), \(\{v_5, \dots , v_{10}\}\). For k-truss model, if we return the 6-truss, the center \(\{v_1, \dots , v_{5}\}\) will be missed; if we return 5-truss, the two centers are returned but the returned result also contains node \(v_{11}\) and \(v_{16}\) and these two nodes are loosely connected with each other and are not what we want. On the contrary, 5-TriPeak can find these two centers.

Applications. k-TriPeak decomposition can be used in many applications. For example, in the community detection, since k-TriPeak model can find central regions with different densities, those sparser communities in the graph will not be missed if the k-TriPeak model is adopted [8, 14]. Similar to k-Peak decomposition, k-TriPeak decomposition can also be used to visualize the graph through the mountain plot technique presented in [7]. Moreover, understanding the hierarchical structure facilitates graph-topology analysis [1, 22]. The k-TriPeaks of a graph for all k values form a hierarchical structure. It is clear that k-TriPeak decomposition is helpful for understanding the hierarchical structure in a graph.

Our Approach. To perform the k-TriPeak decomposition, a direct approach is following the idea of k-Peak decomposition in [7]. In [7], the k-Peak decomposition is achieved by iteratively computing the k-core with maximum k value in the graph through the k-core decomposition algorithm [2] and removing the computed k-core until the graph is empty. Following the idea, we can implement the k-TriPeak decomposition through k-truss decomposition algorithm [15] in a similar way. However, as analysed in Sect. 3, lots of unnecessary edges will involve in the expensive k-truss decomposition procedure, which leads to the inefficiency of this direct approach. To address the drawback of this approach, in this paper, we propose a new algorithm for the k-TriPeak decomposition. Our new algorithm adopts a top-down decomposition paradigm in which k is explored in decreasing order. Based on this top-down decomposition paradigm, we design two effective but lightweight upper bounding techniques. Using these two upper bounding techniques, we can prune the unpromising edges involving in the expensive k-truss decomposition procedure and the unnecessary computation in the direct approach can be significantly reduced.

Contribution. In this paper, we make the following contributions:

  • (1) The k-TriPeak model to find the centers of distinct regions in the graph. We investigate the drawbacks of existing k-Peak model and propose a new model, namely k-TriPeak. Based on the k-TriPeak model, we study the problem of k-TriPeak decomposition. To the best of our knowledge, this is the first work to study the problem of efficient k-TriPeak decomposition.

  • (2) An efficient algorithm for k-TriPeak decomposition. We present an efficient algorithm to perform the k-TriPeak decomposition. In our algorithm, we adopt a top-down decomposition paradigm and devise a static upper bound and a dynamic upper bound to reduce the unnecessary computation. Moreover, we also explore efficient techniques with which we can maintain the dynamic upper bound in O(1) time for each update during the decomposition process.

  • (3) Extensive performance studies on large real-world datasets. We conduct extensive performance studies using large real-world datasets. The experimental results demonstrate the effectiveness of our proposed model and the efficiency and scalability of the devised decomposition algorithm.

2 Preliminaries

We model a undirected graph as G(V, E), where V(G) represents the set of nodes and E(G) represents the set of edges in G. We denote the number of nodes as n and the number of edges as m, i.e., \(n = |V(G)|\) and \(m = |E(G)|\). We define the size of G, denoted by |G|, as \(|G| = m + n\). For a node \(u \in V(G)\), we use \({\mathsf {nbr}} (u, G)\) to denote the neighbor set of u in G, i.e., \({\mathsf {nbr}} (u, G) = \{ v \in V(G) | (u, v) \in E(G) \} \). The degree of a node \(u \in V(G)\), denoted by \({\mathsf {deg}} (u, G)\), is the number of neighbors of u, i.e., \({\mathsf {deg}} (u, G) = |{\mathsf {nbr}} (u, G)|\). A triangle in G is a cycle of length 3. In this paper, we omit G in the notations when it is explicit in context.

Definition 1

(Support). Given a graph G, the support of an edge \(e \in E(G)\), denoted by \({\mathsf {sup}} (e, G)\), is the number of triangles that contain e in G.

Definition 2

(k-TriContour). Given a graph G, a subgraph S is the k-TriContour of G, denoted by \(C_k(G)\), if (i) \({\mathsf {sup}} (e, S) \ge k - 2\) for every edge \(e \in S\); (ii) the k-TriContour does not include edges from a higher TriContour; (iii) S is maximal, i.e., any subgraph \(S' \supset S\) is not a k-TriContour.

Definition 3

(k-TriPeak). Given a graph G, a k-TriPeak, denoted by \(P_k(G)\), is the union of j-TriContours, where \(j \ge k\).

Definition 4

(TriPeak Number). The TriPeak number of an edge e in G, denoted by \(\kappa (e, G)\), is the value k such that e is contained in the k-TriContour.

Problem Statement. In this paper, we study the problem of k-TriPeak decomposition that computes the k-TriPeak for all possible k values in the given graph. Since the k-TriPeak consists of the edges with TriPeak number at least k. The k-TriPeak decomposition problem equals to compute the TriPeak number for each edge in the given graph. Therefore, in this paper, we aim to design an efficient algorithm to perform the assignment of TriPeak number to each edge.

Fig. 2.
figure 2

An example graph G

Full size image

Example 2

Consider the graph G illustrated in Fig. 2, we also show its corresponding k-TriContour and k-TriPeak in Fig. 2. For example, for the edge \((v_8, v_9)\), its support is 3 since it is contained in triangles \( \{v_8, v_9, v_6\}, \{v_8, v_9, v_{10}\}, \{v_8, v_9, v_{11}\}\). The 5-TriContour of G is the subgraph induced by nodes \(\{v_5, v_6, v_8 \dots v_{15}\}\) except edge \((v_5, v_6)\) and \((v_{10}, v_{13})\) as this is the maximal subgraph such that the support for each edge in it is 3 and it does not contain any edges from a k-TriContour with \(k > 5\). Note that although \((v_{1}, v_{7})\) has support 3, it is not in the 5-TriContour of G. This is because \((v_{1}, v_{7})\) is contained in \( \{v_1, v_7, v_2\}, \{v_1, v_7, v_{3}\}, \{v_1, v_7, v_{4}\}\) but edges \((v_7, v_2)\), \((v_7, v_3)\) and \((v_7, v_4)\) are in the 6-TriContour of G. After the TriPeak decomposition, all the TriPeak number of edge can be obtained. For example, \(\kappa ((v_6, v_7)) = 6\) as it is in the 6-TriContour and \(\kappa ((v_{10}, v_{13}))\) is 3 as it is in the 3-TriContour.

3 Baseline k-TriPeak Decomposition Algorithm

Inspired by the solution proposed in [7] to perform the Peak decomposition, we present a baseline solution for the TriPeak decomposition problem in this section. In [7], to conduct the Peak decomposition, it iteratively computes the k-core with maximum k value in the graph by the k-core decomposition algorithm [2] and removing the computed k-core until the graph is empty. Following the same idea, we can perform the TriPeak decomposition through the k-truss decomposition [15] based on the following lemma:

Lemma 1

Given a graph G, let \(k_{max}\) be the maximum value such that the corresponding k-truss in G, denoted by \(T_{k_{max}}(G)\), is not empty, then \(T_{k_{max}}(G) = P_{k_{max}}(G)\).

Proof

According to Definition 2, \(C_{k_{max}}(G) = T_{k_{max}}(G)\) since there doesn’t exist \(C_k(G)\) with \(k > k_{max}\), otherwise such \(C_k(G)\) is also a \(T_k(G)\) that \(k > k_{max}\). And by Definition 3, \(P_{k_{max}}(G)\) is the union of \(C_j(G)\) where \(j \ge k_{max}\). Thus \(P_{k_{max}}(G) = C_{k_{max}}(G) = T_{k_{max}}(G)\).

Based on Lemma 1, for a given graph G, the \(k_{max}\)-truss and \(k_{max}\)-TriPeak in G are the same, which means the TriPeak number of edges in \(T_{k_{max}}(G)\) equals to \(k_{max}\) exactly. Moreover, based on Definitions 2 and 4, the edges with TriPeak number k have no impact on the TriPeak number of edges whose TriPeak number is \(k'\), where \(k' < k\). In other words, for a graph G, if we remove the edges with TriPeak number k from G, the edges with TriPeak number \(k'\) in G and the new generated graph \(G'\) after the edge removal are the same. Therefore, we can conduct the TriPeak decomposition by iteratively computing the k-truss with the maximum k value and removing the edges in the graph until the graph is empty.

figure a

Algorithm. Based on the above analysis, the baseline algorithm, \(\mathsf {Baseline}\), is shown in Algorithm 1. The baseline algorithm iteratively computes and removes the k-truss with the maximum k value of G at each iteration (line 2–5). If an edge is contained in k-truss with the maximum k value of G at current iteration, the TriPeak number of it will be assigned (line 4) and it will be removed from G then (line 5). This process is carried out until all edges in G are removed (line 1).

Procedure \(\mathsf {maxTruss}\) computes the k-truss with the maximum k value in G. It first computes the support of each edge in G by the triangle counting algorithm [9] (line 7). Then it sorts all the edges in ascending order of their supports and keep them in an array (line 8). After that, the algorithm iteratively removes the edge e with the lowest support, which is the first edge in the sorted edge array, and add e into the result set of \(\varPhi _{k_{max}}\) (line 11–14). When removing e, the supports of all other edges that form a triangle with e should be decreased, and their new positions in the sorted edge array should be updated (line 15–20). This algorithm terminates after all edges in G are removed (line 10) and returns the k-truss with the maximum k value (line 21). [15] shows that the time complexity of procedure \(\mathsf {maxTruss}\) is \(O(m^{1.5})\).

Drawbacks of the Baseline Solution. In the baseline algorithm, we conduct the TriPeak decomposition through k-truss decomposition iteratively. In each iteration, the edges with \(\kappa (e) = k_{max}\) are assigned by computing the k-truss of G with the maximum k value in current iteration (line 4). For a specific iteration, an ideal algorithm is that the computation in this iteration only involves the edges with \(\kappa (e) = k_{max}\). However, in the baseline algorithm, all the edges in the remaining graph are taken as the input for the k-truss decomposition algorithm (line 2). Assume that there is an edge e with a small TriPeak number \(k'\) in G, it will participate in all iterations computing k-truss where \(k \ge k'\) in the baseline algorithm. Therefore, lots of redundant computation exist in the baseline algorithm and it is inefficient to conduct TriPeak decomposition considering the time complexity of k-truss decomposition is \(O(m^{1.5})\).

Fig. 3.
figure 3

A running example of Algorithm 1

Full size image

Example 3

Figure 3 shows a running example of Algorithm 1 on the graph G in Fig. 2. It first performs k-truss decomposition on the whole graph and finds 6-TriPeak. Then, it removes edges in the 6-TriPeak and performs k-truss decomposition on all remaining edges to find the 5-TriContour on the remaining graph. The procedure terminates when all the edges are removed. As shown in Fig. 3, although the TriPeak number of edges incident to \(v_1\), \(v_{16}\), \(v_{17}\), \(v_{18}\) and \((v_{10}, v_{13})\) is not 5, all of these edges involve the k-truss decomposition to compute 5-TriContour on the remaining graph, which leads to the inefficiency of Algorithm 1.

4 Our New Approach

To overcome the drawbacks of the baseline solution, we propose a new paradigm for the TriPeak decomposition problem. In this section, we first present an overview of the new paradigm in Sect. 4.1. Then, we show our concrete techniques in Sects. 4.2 and  4.3, respectively.

4.1 A New Top-Down Decomposition Paradigm

In the baseline algorithm (Algorithm 1), in a specific iteration, we compute the TriPeak number for the edges with \(\kappa (e) = k_{max}\), where \(k_{max}\) is the maximum k value such that the corresponding k-truss exists in the remaining graph of current iteration. Since the \(k_{max}\) for current iteration cannot be determined in advance, it has to conduct the truss decomposition on the graphs consisting of the edges with \(\kappa (e) \le k_{max}\), which leads to the inefficiency of the baseline algorithm for the TriPeak decomposition problem. On the other hand, based on Lemma 1, we know the maximum TriPeak number for all edges in G equals to the maximum k value such that the k-truss exists in the original input graph. For brevity, we denote it as \(\kappa _{max}\). In other words, we know the TriPeak number for all edges of G is in the range from 1 to \({\kappa _{max}}\). According to the definition of TriPeak decomposition, the essence of the problem is to determine the TriPeak number for each edge. Therefore, to perform the TriPeak decomposition, we can iterate all the possible TriPeak number of the graph in decreasing order based on their values and compuate the edges whose TriPeak number equals to the specific TriPeak number. The benefit of this paradigm is that it is possible to prune the edge with \(\kappa (e) < k\) in a specific iteration as we know the TriPeak number k to be handled in each iteration in advance. In this way, we can reduce the redundant computation in the baseline algorithm caused by edges with small TriPeak number involving truss decomposition many times.

Fig. 4.
figure 4

The new paradigm

Full size image

Algorithm Framework. Following the above analysis, the new TriPeak decomposition paradigm is illustrated in Fig. 4. Staring from \(\kappa _{max}\), the paradigm computes the TriPeak number for the edges in decreasing order of k. For a specific k, the edges with \(\kappa (e) = k\) are computed. As analysed above, we aim to limit the edges involving the truss computation in this step to the edges with \(\kappa (e) = k\). However, this goal is hard to achieve. Therefore, we compute upper bounds of TriPeak number for the edges and use these upper bounds to prune the useless edges. Specifically, when processing a specific k (without loss of generality, we denote the input graph regarding k as \(G_k\)), it first prunes the edges whose upper bound of TriPeak number is less than k, i.e., \(\overline{\kappa (e)} < k\). We denote the pruned graph as \(G'_k\). Then, we determine the edges with \(\kappa (e) = k\) by computing the k-truss on \(G'_k\). After that, the edges with \(\kappa (e) = k\) are removed from \(G_k\) and the remaining graph are treated as the input graph for the next iteration. The process terminates when \(G_k\) is empty.

4.2 Upper Bounding Techniques

As analysed in Sect. 4.1, the key point for the efficiency of the new paradigm is tight upper bounds of \(\kappa (e)\). To achieve this goal, in this part, we will introduce two kinds of upper bounding techniques for \(\kappa (e)\).

A Static Upper Bound. Based on the definition of TriPeak number, a direct upper bound of the TriPeak number of the edges in G can be obtained by the truss number:

Definition 5

(Truss Number). Given a graph G, the truss number of an edge e in G, denoted by \(\phi (e)\), is the maximal number of k such that e is contained in a k-truss.

Lemma 2

Let e be an edge in G, \(\phi (e)\) is the truss number of e, and \(\kappa (e)\) is the TriPeak number of e, then \(\phi (e) \ge \kappa (e)\).

Proof

By the definition of k-TriContour, every edge in k-TriContour has no less than \(k-2\) triangles inside k-TriContour, which indicates that the k-TriContour is a part of k-truss. Thus if e is in k-TriContour, it must also be in k-truss. Hence \(\phi (e) \ge \kappa (e)\) holds.

The truss number for each edge can be easily obtained through the k-truss decomposition algorithm. However, since k-TriContour does not consider the support from triangles in higher TriContours, as our decomposition paradigm progresses, the pruning power of truss number weakens and the edges with \(\phi (e) > \kappa (e)\) accumulate more and more. Therefore, we propose another tight but lightweight upper bound for \(\kappa (e)\). The upper bound is defined based on \(G_k\) (the input graph of our paradigm when processing a specific k, i.e., the graph after removing all the edges with \(\kappa (e) > k\)) and is dynamically maintained as our decomposition paradigm progresses.

A Dynamic Upper Bound. Given an edge \((u, v) \in E(G_k)\), \({\mathsf {sup}} ((u, v), G_k)\) be the support of \(e = (u, v)\) in \(G_k\). For a node \(u \in V(G_k)\), let \(h(u, G_k)\) returns the maximum value h such that there exist at least h neighbours v of u with \({\mathsf {sup}} ((u, v), G_k) \ge h\). We define \(\lambda (e, G_k) = \min \{{\mathsf {sup}} (e, G_k), h(u, G_k), h(v, G_k)\}\,+\,2\). And we can prove that for any arbitrary valid k in our paradigm, \(\lambda (e, G_k)\) is an upper bound of \(\kappa (e, G)\), which is shown in the following lemma:

Lemma 3

Let e be an edge in G, then \(\lambda (e, G_k) \ge \kappa (e, G)\).

Proof

Since \(e = (u, v)\) is still remained in \(G_k\), we know \(C_{\kappa (e, G)}(G) \subseteq G_k\). And within \(C_{\kappa (e, G)}(G)\), we know that \({\mathsf {sup}} (e, C_{\kappa (e, G)}(G)) + 2 \ge \kappa (e, G)\), \(h(u, C_{\kappa (e, G)}(G)) + 2 \ge \kappa (e, G)\) and \(h(v, C_{\kappa (e, G)}(G)) + 2 \ge \kappa (e, G)\). Thus \(\lambda (e, G_k) = \min \{{\mathsf {sup}} (e, G_k), \) \( h(u, G_k), h(v, G_k)\} + 2 \) \(\ge \min \{{\mathsf {sup}} (e, C_{\kappa (e, G)}(G)), h(u, C_{\kappa (e, G)}(G)), h(v, C_{\kappa (e, G)}(G))\} + 2 \) \(\ge \kappa (e, G)\).

4.3 Our k-TriPeak Decomposition Algorithm

In this part, we present our algorithm to conduct the TriPeak decomposition. With the new decomposition paradigm and upper bounding techniques, the only challenge is integrating the upper bounding techniques into decomposition paradigm efficiently, especially the maintenance of upper bound \(\lambda (e, G_k)\). This part addresses this challenge.

figure b

Algorithm. Our algorithm, \(\mathsf {TriPeakDecom}\), is shown in Algorithm 2. It first computes the \(\kappa _{max}\) and initializes the auxiliary information for the upper bounds (line 1–5). Then, it conduct the TriPeak decomposition following the new top-down paradigm until the graph is empty (line 6–23).

Specifically, it first invokes procedure \(\mathsf {maxTruss}\) in Algorithm 1 to compute \(\kappa _{max}\), \({\mathsf {sup}} (e)\) and \(\phi (e)\) for each edge e (\(\phi (e)\) equals to \(k_{max}\) when e is removed from G in line 20 of Algorithm 1). Then it computes h(u) for each node u based on the supports of edges incident to u (line 2). At last, \(\lambda (e)\) for each edge e is assigned according to its definition and \(\overline{\kappa (e)}\) of each edge e is initialized as \(\min \{\lambda (e), \phi (e)\}\) (line 4–5).

Then, it conducts the TriPeak decomposition iteratively starting with \(k = \kappa _{max}\) and \(G_k = G\) (line 6) and the decomposition terminates when \(G_k\) is empty (line 7). In a specific iteration processing k, it first extracts \(G'_k\) from \(G_k\) with edges of which the upper bound \(\overline{\kappa (e)}\) is no less than k (line 8). This step filters out the unpromising edges. Then it computes the \(C_{k'}\) of \(G'_k\) by the \(\mathsf {maxTruss}\) procedure (line 9). If \(k' = k\), for each edge \(e=(u, v) \in C_k'\), it assigns \(\kappa (e) = k\) and removes the edge from \(G_k\) (line 13). The remaining work is to maintain the incorrect \(\overline{\kappa (e)}\) caused by the removal of edges. As \(\phi (e)\) is fixed in the whole process, we only need to find the edges whose \(\lambda (e)\) changes after the edge removal. To achieve this goal, \(\mathsf {TriPeakDecom}\) uses a set S to store the nodes u that h(u) has changed in the iteration since this change may influence \(\lambda (e)\) of any edges incident to u (line 11). Regarding a removed edge (u, v), for u, v and each common neighbor w of u and v, it decreases the support of (u, w) and (v, w) (line 18), updates h(u), h(v) and h(w) (line 14, 19) and \(\lambda ((u, w))\) and \(\lambda ((v, w))\) (line 19). If a node u whose h(u) is changed, adds u into S (line 15, 20). At the end of iteration, for each node \(w \in S\), it updates \(\overline{\kappa (e)}\) for all edges incident to w, since the change of h(w) may change \(\overline{\kappa (e)}\) (line 21–22). When an iteration finishes, k is decreased and the remaining edges are be taken as the input graph for the next iteration (line 23).

Efficient Maintenance of \(\lambda (e, G_k)\). In Algorithm 2, we maintain \(\lambda (e, G_k)\) dynamically as the decomposition processes (line 19, 22). Based on the definition of \(\lambda (e, G_k)\), for an edge \(e = (u, v)\), the key to obtain \(\lambda (e, G_k)\) is to compute \(h(u, G_k)\) and \(h(v, G_k)\). However, the time complexity to compute \(h(u, G_k)\) and \(h(v, G_k)\) on the fly based on the edge support maintained in Algorithm 2 is at least \(O(\max \{{\mathsf {deg}} (u, G_k), {\mathsf {deg}} (v, G_k)\})\). Since \(h(u, G_k)\) is recomputed frequently in Algorithm 2 (line 14, 19), this approach is inefficient. To improve the efficiency to maintain h(u), for each node u, besides h(u), we maintain the number of edges incident to u with different support values, respectively, i.e., \(cnt^{u}_{i}\), which represents the number of edges incident to u with support equals i. Moreover, we also maintain \(cnt^{u}_{\ge h(u)}\) that stores the number of edges incident to u with support not less than h(u). During the decomposition, when the support of an edge \(e = (u, v)\) decrease from i to j, we just decrease \(cnt^{u}_{i}\) and \(cnt^{v}_{i}\) by 1 and increase \(cnt^{u}_{j}\) and \(cnt^{v}_{j}\) by 1. And for the node u (the same as v), if \(i \ge h(u)\), \(j < h(u)\) and if \(cnt^{u}_{\ge h(u)} > h(u)\), we decrease \(cnt^{u}_{\ge h(u)}\) by 1; and if \(cnt^{u}_{\ge h(u)} = h(u)\), we decrease h(u) by 1 and update \(cnt^{u}_{\ge h(u)}\) as \(cnt^{u}_{\ge h(u)} + cnt^{u}_{h(u)} - 1\). Otherwise, we just keep h(u) and \(cnt^{u}_{\ge h(u)}\) unchanged. In this way, for the operation updating h(u) regarding a node u in line 14 and 19 in Algorithm 2, we can finish it in O(1) time. As a result, for each edge e, the \(\lambda (e, G_k)\) are maintained in O(1) in the decomposition procedure.

Fig. 5.
figure 5

A running example of Algorithm 2

Full size image

Example 4

Figure 5 shows a running example of Algorithm 2 on the graph G in Fig. 2. Similar to Algorithm 1, it first performs truss decomposition and finds 6-TriPeak. Then, it removes edges in the 6-TriPeak and performs truss decomposition to find the 5-TriContour. Different from Algorithm 1, when performing the k-truss decomposition to find 5-TriContour, it first prunes the edges with \(\overline{\kappa (e)} < 5\). For example, the edge \((v_{10}, v_{13})\) is pruned by static upper bound as \(\phi ((v_{10}, v_{13})) < 5\) though \(\lambda ((v_{10}, v_{13})) \ge 5\); edge \((v_1, v_7)\) is pruned by dynamic upper bound as \(\lambda ((v_1, v_7)) < 5\) though \(\phi ((v_1, v_7)) \ge 5\). As illustrated in Fig. 5, Algorithm 2 significantly reduces the number of unnecessary edges involving the procedure of truss decomposition compared with Algorithm 1.

Theorem 1

Given a graph G, the running time of Algorithm 2 can be bounded by \(O(\kappa _{max} \cdot m^{1.5})\).

Proof

The whole algorithm can be divided into two stages, the initialization stage (line 1–6) and the main iteration stage (line 7–23). Line 1 invokes \(\mathsf {maxTruss}\) procedure using \(O(m^{1.5})\) time. Line 2–5 can be done in O(m) time. In the main iteration stage, line 9 takes \(O(m^{1.5})\) time. Line 13–15 and line 18–20 can be done in constant time, and line 21–22 requires O(m) time. Now the only question left is what is the number of loops in line 12 and 16. For a certain node u, line 16 is bounded by \({\mathsf {deg}} (u)\), and line 12 is bounded by \(|{\mathsf {nbr}} _{\ge u}|\), which is the number of neighbors of u whose degree is not smaller than u. Thus line 12–20 can be done in \(O(\sum _{u \in G_k}{({\mathsf {deg}} (u) \cdot |{\mathsf {nbr}} _{\ge u}|)})\) time, which is bounded by \(O(m^{1.5})\). This is because if \({\mathsf {deg}} (u) \le \sqrt{m}\), \(|{\mathsf {nbr}} _{\ge u}| \le {\mathsf {deg}} (u) \le \sqrt{m}\) and \(\sum _{u \in G_k}{({\mathsf {deg}} (u) \cdot |{\mathsf {nbr}} _{\ge u}|)} \le m^{1.5}\). If \({\mathsf {deg}} (u) > \sqrt{m}\), \(|{\mathsf {nbr}} _{\ge u}| \le \sqrt{m}\) as well for \({\mathsf {deg}} (u) \cdot |{\mathsf {nbr}} _{\ge u}| \le \sum _{v \in |{\mathsf {nbr}} _{\ge u}|}{{\mathsf {deg}} (v)} < 2m\), and \(\sum _{u \in G_k}{({\mathsf {deg}} (u) \cdot |{\mathsf {nbr}} _{\ge u}|)} \le m^{1.5}\). The number of iterations is bounded by \(\kappa _{max}\). Thus, the the running time of Algorithm 2 can be bounded by \(O(\kappa _{max} \cdot m^{1.5})\).

5 Performance Studies

In this section, we evaluate the effectiveness of our model and the efficiency and scalability of our proposed algorithm. The experiments are conducted on a machine with an Intel Xeon 2.20 GHz CPU and 128 GB memory running Red Hat Linux 4.8.5, 64 bit.

Table 1. Datasets used in experiments
Full size table

Datasets. In our experiments, we evaluate the algorithms on six publicly available real-world datasets as listed in Table 1. Of these, DBLP and LiveJournal are downloaded from SNAPFootnote 1, and the others are downloaded from KONECTFootnote 2.

Algorithms. We implement and compare the following four algorithms:

  • \(\mathsf {Baseline}\): Algorithm 1

  • \(\mathsf {TriPeakDecom_s}\): TriPeak decomposition algorithm with static upper bound only.

  • \(\mathsf {TriPeakDecom_d}\): TriPeak decomposition algorithm with dynamic upper bound only.

  • \(\mathsf {TriPeakDecom}\): Algorithm 2

Fig. 6.
figure 6

Effectiveness of k-TriPeak and k-Peak

Full size image

All algorithms are implemented in C++ and compiled with GNU GCC 4.8.5 using optimization level 2. The time cost of the algorithm is measured as the amount of elapsed wall-clock time during the program execution.

Exp-1: Effectiveness. We evaluate the effectiveness of k-TriPeak and k-Peak by examining the quality of detected subgraph via the clustering coefficient [18] metric. Clustering coefficient (CC) indicates the tendency of nodes in a subgraph to cluster together. Thus, high clustering coefficient means high probability that the connections inside the detected subgraph are dense. In this experiment, we find all k-TriPeaks and k-Peaks with different k values and compute the clustering coefficient of them. Since the distributions of k in findings of k-TriPeak and k-Peak are quite different, here we compare the clustering coefficient of \(k_1\)-TriPeak and \(k_2\)-Peak of similar size even if \(k_1 \ne k_2\). The results are shown in Fig. 6. In Fig. 6, the horizontal coordinate denotes the size of k-TriPeak (k-Peak) as a persentage of total graph.

As shown in Fig. 6, as the size of k-TriPeak (k-Peak) increases, the value of clustering coefficient for both of them generally decreases. However, it can be observed that, of similar size, the k-TriPeak is much denser than k-Peak. For example, in Flixster dataset, the k-TriPeak of which the size is around 30% of the total graph has clustering coefficient of 0.7, while the k-Peak of similar size only have 0.1. This is because k-TriPeak takes a high-order connectivity structure as the building blocks while k-Peak only considers degree. These results indicate that compared with the k-Peak model, the returned result of k-TriPeak are more cohesive and k-TriPeak is better cohesive subgraph model compared with k-Peak.

Table 2. Running time on real-world datasets
Full size table

Exp-2: Efficiency. In this experiment, we compare the total processing time of those four algorithms on six real-world datasets. The results are reported in Table 2.

Generally, the processing time increases as the size of the graph increases. \(\mathsf {Baseline}\) takes the most time on all six datasets. It spends more than 8 hours to perform the TriPeak decomposition on LiveJournal dataset. The reason for \(\mathsf {Baseline}\)’s long running time is that edges with small TriPeak number, which make up a large portion of the whole graph, take participate in the k-truss decomposition for the big TriPeak number many times. The algorithms solely adopting static or dynamic upper bounding technique run much faster than \(\mathsf {Baseline}\). \(\mathsf {TriPeakDecom_s}\) is faster than \(\mathsf {TriPeakDecom_d}\) on Livemocha, Flixster and Skitter and the opposite on DBLP, Flickr and LiveJournal, for they play to their strength on different stages in a decomposition. \(\mathsf {TriPeakDecom}\) algorithm, which adopts both upper bounding techniques, achieves the best performance on all six datasets. For example, on LiveJournal, it achieves an order of magnitude faster than \(\mathsf {Baseline}\).

Fig. 7.
figure 7

Scalability testing

Full size image

Exp-3: Scalability. We study the scalability of the four algorithms in this experiment. To test the scalability, we randomly sample the nodes and edges respectively of two largest datasets Skitter and LiveJournal from 20% to 100% and take the induced subgraph as the input graph. The results are shown in Fig. 7.

As shown in Fig. 7, as the size of the graph increases, the processing times of four algorithms increase due to the increasing of the number of iterations and the number of involved edges in each iteration. Moreover, as the size of the graph increases, the gap in processing times between \(\mathsf {Baseline}\) and other three algorithms increases. This is because the unnecessary computation on edges, which are reduced by other three algorithms but remained in \(\mathsf {Baseline}\), make up larger portion of computation when the size of the graph grows. The gap in processing times between \(\mathsf {TriPeakDecom_s}\) and \(\mathsf {TriPeakDecom_d}\) remains small on both datasets. The \(\mathsf {TriPeakDecom}\) algorithm consumes the least time and its processing time grows the most stably on all datasets. The results show the good scalability of our proposed algorithm.

6 Related Work

The most related works to k-TriPeak are k-Peak [7] and k-truss [5], which have been introduced in Sect. 1. Since k-Peak is defined based on degree, the returned results of k-Peak are often not that cohesive [5, 14, 28] compared with the k-TriPeak [14]. The difference between k-TriPeak and k-truss is that in a k-truss, triangles containing edges from the higher k-truss are taken into consideration while in a k-TriPeak, all these edges are filtered out. This difference leads to it that k-TriPeak is able to find the centers of distinct regions in a graph as k-Peak [7].

Besides k-Peak and k-truss, there are many different models proposed in the literature. One of the most intuitive cohesive subgraph models is the clique model in which each node is adjacent to every other node [4]. More complex models based on the clique model [20, 21, 25] are also studied in the literature. However, clique is often too restrictive for many applications, thus, more clique relaxation models have been proposed, such as the k-plex [13], n-clan and n-club [11]. Nevertheless, these models always face the problem of computational intractability. To address this problem, more polynomial time solvable cohesive subgraph models are proposed recently, such as k-core [2], triangle k-core [27], (k, s)-core [26], DN-Graph [16], k-edge connected component [22, 24] and k-mutual-friend subgraph model [28].

7 Conclusion

Motivated by the recent proposed k-Peak model, in this paper, we propose a new k-TriPeak model based on the triangles in the graph and study the k-TriPeak decomposition problem. To perform the k-TriPeak decomposition, we first present an approach following the idea of k-Peak decomposition. However, this approach involves lots of unnecessary computation. Therefore, we propose a new top-down paradigm to conduct the decomposition. Based on the new paradigm, we devise two effective upper bounds to prune the unnecessary edges involving computation in the baseline approach. Moreover, we explore efficient techniques to maintain the upper bounds during the decomposition. We conduct experiments on large real-world datasets and the experimental results demonstrate the efficiency and effectiveness of our proposed algorithm.