Input-State-Output Representations of Concatenated 2D Convolutional Codes

Abstract

In this paper we investigate a novel model of concatenation of a pair of two-dimensional (2D) convolutional codes. We consider finite-support 2D convolutional codes and choose the so-called Fornasini-Marchesini input-state-output (ISO) model to represent these codes. More concretely, we interconnect in series two ISO representations of two 2D convolutional codes and derive the ISO representation of the obtained 2D convolutional code. We provide necessary condition for this representation to be minimal. Moreover, structural properties of modal reachability and modal observability of the resulting 2D convolutional codes are investigated.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Codes derived by combining two codes (an inner code and an outer code) form an important class of error-correcting codes called concatenated codes. This class, originally introduced by David Forney in 1965, became widely used in communications due to fact that they can achieve excellent performance with reasonable complexity. Although the first construction of concatenated codes used block codes, NASA started to use a short-constraint-length (64-state) convolutional code as an inner code, decoded by the optimal Viterbi algorithm, because it had been realized that convolutional codes are superior to block codes from the point of view of performance versus complexity. Indeed, it was in 1993 that the field of coding theory was revolutionized by the invention of turbo codes (concatenation of two convolutional codes) by Berrou et al.

Roughly speaking one dimensional (1D) convolutional codes can be seen as a generalization of block codes in the sense that a block code is a convolutional code with no delay, i.e., block codes are basically 0D convolutional codes. In this way, two-dimensional (2D) convolutional codes extend the 1D convolutional codes. These codes have a practical potential in applications as they are very suitable to encode data recorded in 2 dimensions, e.g., pictures, storage media, wireless applications, etc. However, in comparison to 1D convolutional codes, little research has been done in the area of 2D convolutional codes.

In this paper the authors further investigate the concatenation properties of 2D convolutional codes, and therefore extend their previous results presented in [1]. In this case we study a new type of concatenation that has not been analysed before in the context of 2D convolutional codes. In particular, we derive conditions for the minimality of an input-state-output representation of the concatenated code. Furthermore, we show that this concatenation of two 2D convolutional codes results in another 2D convolutional code and we explicitly compute an ISO representation. Finally, we investigate under which conditions fundamental properties such as modal observability and reachability of ISO representations of two 2D convolutional codes carry over after serial concatenation.

2 Preliminaries

Denote by $\mathbb {F}[z_1,z_2]$ the ring of polynomials in two indeterminates with coefficients in $\mathbb {F}$, by $\mathbb {F}(z_1z_2)$ the field of fractions of $\mathbb {F}[z_1,z_2]$ and by $\mathbb {F}[[z_1,z_2]]$ the ring of formal powers series in two indeterminates with coefficients in $\mathbb {F}$.

In this section we start by giving some preliminaries on matrices over $\mathbb {F}[z_1,z_2]$.

Definition 1

A matrix $G(z_1,z_2) \in \mathbb {F}[z_1,z_2]^{n \times k}$, with $n \ge k$ is,

• 1. unimodular if $n=k$ and $\det (G(z_1,z_2)) \in \mathbb {F} \backslash \{0\}$;

• 2. right factor prime (rFP) if for every factorization

  $$G(z_1,z_2)=\overline{G}(z_1,z_2)T(z_1, z_2),$$

  with $\overline{G}(z_1,z_2)\in \mathbb {F}[z_1,z_2]^{n \times k}$ and $T(z_1,z_2)\in \mathbb {F}[z_1,z_2]^{k \times k}$, $T(z_1,z_2)$ is unimodular;

• 3. right zero prime (rZP) if the ideal generated by the $k \times k$ minors of $G(z_1,z_2)$ is $\mathbb {F}[z_1,z_2]$.

A matrix is left factor prime ($\ell FP$)/left zero prime ($\ell ZP$) if its transpose is rFP/rZP, respectively. Moreover, zero primeness implies factor primeness, but the contrary does not happen. The following lemmas give characterizations of right factor primeness and right zero primeness that will be needed later.

Lemma 1

([2, 3]) Let $G(z_1,z_2) \in \mathbb F[z_1,z_2]^{n \times k}$, with $n \ge k$. Then the following are equivalent:

• 1. $G(z_1,z_2)$ is right factor prime;

• 2. for all $\hat{u}(z_1,z_2)\in \mathbb F(z_1,z_2)^k$, $G(z_1,z_2) \hat{u}(z_1,z_2)\in \mathbb F[z_1,z_2]^{n}$ implies that $\hat{u}(z_1,z_2) \in \mathbb F[z_1,z_2]^k$.

• 3. the $k \times k$ minors of $G(z_1,z_2)$ have no common factor.

Lemma 2

([2, 3]) Let $G(z_1,z_2) \in \mathbb F[z_1,z_2]^{n \times k}$, with $n \ge k$. Then the following are equivalent:

• 1. $G(z_1,z_2)$ is right zero prime;

• 2. $G(z_1,z_2)$ admits a polynomial left inverse;

• 3. $G(\lambda _1,\lambda _2)$ is full column rank, for all $\lambda _1,\lambda _2\in \overline{\mathbb {F}}$, where $\overline{\mathbb {F}}$ denotes the algebraic closure of $\mathbb {F}$.

It is well known that given a full column rank polynomial matrix $G(z_1,z_2)$ in $\mathbb F[z_1,z_2]^{n \times k}$, there exists a square polynomial matrix $V(z_1,z_2) \in \mathbb F[z_1,z_2]^{k \times k}$ and a rFP matrix $\bar{G}(z_1,z_2) \in \mathbb F[z_1,z_2]^{n \times k}$ such that

$$G(z_1,z_2)=\bar{G}(z_1,z_2)V(z_1,z_2).$$

The following lemma will be needed in the sequel. Let $G(z_1,z_2) \in \mathbb F[z_1,z_2]^{n\times k}$, $H(z_1,z_2) \in \mathbb F[z_1,z_2]^{(n-k) \times n}$, $n>k$, $c_i$ the ith column of $H(z_1,z_2)$ and $r_j$ the jth row of $G(z_1,z_2)$. We say that the full size minor of $H(z_1,z_2)$ constituted by the columns $c_{i_1},\ldots ,c_{i_{n-k}}$ and the full size minor of $G(z_1,z_2)$ constituted by the rows $r_{j_1},\ldots ,r_{j_k}$ are corresponding maximal order minors of $H(z_1,z_2)$ and $G(z_1,z_2)$, if $\{ i_{1},\ldots ,i_{n-k} \} \cup \{ j_{1},\ldots ,j_{k}\}= \{ 1,\ldots ,n \}$ and $\{ i_{1},\ldots ,i_{n-k} \} \cap \{ j_{1},\ldots ,j_{k} \} = \emptyset .$

Lemma 3

([4]) Let $G(z_1,z_2) \in \mathbb F[z_1,z_2]^{n \times k}$ and $H(z_1,z_2) \in \mathbb F[z_1,z_2]^{(n-k) \times n}$ be a rFP and a $\ell FP$ matrices, respectively, such that $H(z_1,z_2)G(z_1,z_2)=0$. Then the corresponding maximal order minors of $H(z_1,z_2)$ and $G(z_1,z_2)$ are equal, modulo a unit of the ring $\mathbb F[z_1,z_2]$.

Next we give preliminaries on 2D linear systems, which we will use to construct 2D finite support convolutional codes. In particular we consider the Fornasini-Marchesini state space model representation of 2D systems ([5]). In this model a first quarter plane 2D linear system, denoted by $\varSigma \!=\!\left( A_1,A_2,B_1,B_2,C,D\right)$, is given by the updating equations

$$\begin{aligned} \begin{array}{rcl} x(i\!+\!1,j\!+1\!) &{} = &{} A_1 x(i,j\!+\!1) + A_2 x(i\!+\!1,j) + B_1 u(i,j\!+\!1) + B_2 u(i\!+\!1,j) \\ y(i,j) &{} = &{} C x(i,j) + D u(i,j), \end{array} \end{aligned}$$

(1)

where $A_1, A_2 \in \mathbb F^{\delta \times \delta }$, $B_1, B_2 \in \mathbb F^{\delta \times k}$, $C \in \mathbb F^{(n-k) \times \delta }$, $D \in \mathbb F^{(n-k) \times k}$, $\delta , n , k \in \mathbb {N}$, $n > k$ and with past finite support of the input and of the state and zero initial conditions (i.e., $u(i,j)=x(i,j)=0$ for $i <0$ or $j<0$ and $x(0,0)=0$). We say that $\varSigma =(A_1,A_2,B_1,B_2,C,D)$ has dimension $\delta$, local state x(i, j), input u(i, j) and output y(i, j), at (i, j).

The input, state and output 2D sequences (trajectories), $\{u(i,j)\}_{(i,j)\in \mathbb {N}^2}$, $\{x(i,j)\}_{(i,j)\in \mathbb {N}^2}$, $\{y(i,j)\}_{(i,j)\in \mathbb {N}^2}$, respectively, can be represented as formal power series,

$$\hat{u}(z_1,z_2)\!=\!\!\!\sum _{(i,j) \in \mathbb N^2}\!\!\! u(i,j) z_1^i z_2^j \in \mathbb F[[z_1,z_2]]^k$$

$$ \hat{x}(z_1,z_2)\!=\!\!\!\sum _{(i,j) \in \mathbb N^2}\!\!\! x(i,j) z_1^i z_2^j \in \mathbb F[[z_1,z_2]]^{\delta }$$

$$\hat{y}(z_1,z_2)\!=\! \sum _{(i,j) \in \mathbb N^2} \!\!\!y(i,j) z_1^i z_2^j \in \mathbb F[[z_1,z_2]]^{n-k}$$

We will use the sequence and the corresponding series interchangeably. Given an input trajectory $\hat{u}(z_1,z_2)$ with corresponding state $\hat{x}(z_1,z_2)$ and output $\hat{y}(z_1,z_2)$ trajectories obtained from (1), the triple $(\hat{x}(z_1,z_2), \hat{u}(z_1,z_2), \hat{y}(z_1,z_2))$ is called an input-state-output trajectory of $\varSigma =(A_1,A_2,B_1,B_2,C,D)$. The set of input-state-output trajectories of $\varSigma$ is given by

$$ \ker _{\mathbb {F}[[z_1,z_2]]}X(z_1,z_2)= \left\{ \hat{r}(z_1,z_2) \in \mathbb {F}[[z_1,z_2]]^{n + \delta } \ | \ X(z_1,z_2)\hat{r}(z_1,z_2)=0\right\} $$

where

$$\begin{aligned} X(z_1,z_2) = \begin{bmatrix} I_{\delta }-A_1 z_1 - A_2 z_2&-B_1 z_1 - B_2 z_2&0 \\ -C&-D&I_{n-k} \end{bmatrix}. \end{aligned}$$

(2)

Next we present the modal reachability and observability properties of such systems.

Definition 2

([1, 5]) Let $\varSigma =(A_1,A_2,B_1,B_2,C,D)$ be a 2D linear system with dimension $\delta$.

• 1. $\varSigma$ is modally reachable if the matrix $\begin{bmatrix} I_{\delta }-A_1z_1-A_2z_2&B_1z_1+B_2z_2\end{bmatrix}$ is $\ell FP$. Moreover $\varSigma$ is modally reachable if and only if the corresponding matrix $X(z_1,z_2)$ defined in (2) is $\ell FP$.

• 2. $\varSigma$ is modally observable if the matrix $\begin{bmatrix} I_{\delta }-A_1z_1-A_2z_2 \\ C \end{bmatrix}$ is rFP.

3 Input-State-Output Representations of 2D Finite Support Convolutional Codes

Definition 3

([6]) A 2D (finite support) convolutional code $\mathcal { C}$ of rate k / n is a free $\mathbb {F}[z_1,z_2]$-submodule of $\mathbb {F}[z_1,z_2]^n$, where k is the rank of $\mathcal {C}$. A full column rank matrix $G(z_1,z_2) \in \mathbb {F}[z_1,z_2]^{n \times k}$ whose columns constitute a basis for $\mathcal C$, i.e., such that

$$ \mathcal {C} = \text {Im}_{\mathbb {F}[z_1,z_2]} G(z_1,z_2) = \big \{ \hat{v}(z_1,z_2) =G(z_1,z_2) \hat{u}(z_1,z_2) \ | \ \hat{u}(z_1,z_2) \in \mathbb {F}[z_1,z_2]^{k}\big \}, $$

is called an encoder of $\mathcal C$. The elements of $\mathcal C$ are called codewords.

Two full column rank matrices $G(z_1,z_2)$ and $\bar{G}(z_1,z_2)$ in $\mathbb {F}[z_1,z_2]^{n \times k}$ are equivalent encoders if they generate the same 2D convolutional code, i.e., if

$$\text {Im}_{\mathbb F[z_1,z_2]}G(z_1,z_2) = \text {Im}_{\mathbb {F}[z_1,z_2]} \bar{G}(z_1,z_2),$$

which happens if and only if there exists a unimodular matrix $U(z_1,z_2)$ in $\mathbb {F}[z_1,z_2]^{k \times k}$ such that $G(z_1,z_2) U(z_1,z_2)=\bar{G}(z_1,z_2)$ (see [6]).

Note that the fact that two equivalent encoders differ by unimodular matrices also implies that the primeness properties of the encoders of a code are preserved, i.e., if $\mathcal C$ admits a rFP (rZP) encoder then all its encoders are rFP (rZP). A 2D finite support convolutional code $\mathcal {C}$ that admits rFP encoders is called noncatastrophic and is named basic if all its encoders are rZP. Moreover, if $\mathcal {C}$ admits an encoder $G(z_1,z_2)=\begin{bmatrix}I_k \\ \tilde{G}(z_1,z_2)\end{bmatrix}$, up to a row permutation, $\mathcal {C}$ is called systematic.

Let us now consider a first quarter plane 2D linear system $\varSigma$ defined in (1). For $(i,j) \in \mathbb N^2$, define

$$ v(i,j) = \begin{bmatrix} y(i,j)\\ u(i,j)\end{bmatrix} \in \mathbb {F}^{n} $$

to be the code vector. We will only consider the finite support input-output trajectories, $(v(i,j))_{(i,j) \in \mathbb N^2}$ of (1). We will not consider such trajectories with corresponding state trajectory $\hat{x}(z_1,z_2)$ having infinite support, since this would make the system remain indefinitely excited. Thus, we will restrict ourselves to finite support input-output trajectories $(\hat{u}(z_1,z_2), \hat{y}(z_1,z_2))$ with corresponding state $\hat{x}(z_1,z_2)$ also having finite support. We call such trajectories $( \hat{u}(z_1,z_2), \hat{y}(z_1,z_2))$ finite-weight input-output trajectories and the triple $( \hat{x}(z_1,z_2), \hat{u}(z_1,z_2), \hat{y}(z_1,z_2))$ finite-weight trajectories. Note that not all finite support input-output trajectories have finite weight. The following result asserts that the set of finite-weight trajectories of (1) forms a 2D finite support convolutional code.

Theorem 1

([7]) The set of finite-weight input-output trajectories of (1) is a 2D finite support convolutional code of rate k / n.

We denote by $\mathcal{C}(A_1,A_2,B_1,B_2,C,D)$ the 2D finite support convolutional code whose codewords are the finite-weight input-output trajectories of the 2D linear system $\varSigma =(A_1,A_2,B_1,B_2,C,D)$. Moreover, $\varSigma$ is called an input-state-output (ISO) representation of $\mathcal{C}(A_1,A_2,B_1,B_2,C,D)$ (see [7]).

Next theorem shows how the modal reachability and observability properties of ISO representations reflect on the structure of the corresponding code.

Theorem 2

([1, 7]) Let $\varSigma \!=\!(A_1,A_2,B_1,B_2,C,D)$ be a 2D linear system.

• 1. If $\varSigma$ is modally observable then $\mathcal{C}(A_1,A_2,B_1,B_2,C,D)$ is noncatastrophic and its codewords are the finite support input-output trajectories of $\varSigma$.

• 2. Assume that $\varSigma$ is modally reachable then $\varSigma$ is modally observable if and only if $\mathcal{C}(A_1,A_2,B_1,B_2,C,D)$ is noncatastrophic.

In the 1D case, ISO representations of a convolutional code of minimal dimension are usually used to define the code. This is due the fact that they have good structural properties that provide important tools in the analysis of the code. Such representation are called minimal and they are completely characterized. However it does not exist a characterization of minimal representations for 2D convolutional codes. Next theorem gives a sufficient condition for minimality.

Theorem 3

([7]) Let $\varSigma \!=\!(A_1,A_2,B_1,B_2,C,D)$ be a modally reachable 2D linear system with k inputs, $n-k$ outputs and dimension $\delta$. Suppose that $X(z_1,z_2)$, defined in (2), has a $(\delta +n-k)\times (\delta +n-k)$ minor with degree $\delta$, computed by picking up necessarily its first $\delta$ columns. Then $\varSigma$ is a minimal ISO representation of $\mathcal {C}(A_1,A_2,B_1,B_2,C,D)$.

4 Input-State-Output Representations of Concatenated 2D Convolutional Codes

In this section we will study 2D convolutional codes that result from a series interconnection of two systems representations of other 2D convolutional codes. We will consider the second interconnection model defined in [8] for 1D systems.

Let

$$\varSigma _1=\left( A_1^{(1)},A_2^{(1)},B_1^{(1)},B_2^{(1)}, C^{(1)}, D^{(1)}\right) $$

and

$$\varSigma _2=\left( A_1^{(2)},A_2^{(2)},B_1^{(2)},B_2^{(2)}, C^{(2)}, D^{(2)}\right) $$

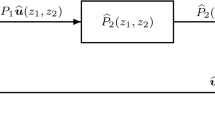
be two ISO representations of the 2D convolutional codes $\mathcal {C}_1$ and $\mathcal {C}_2$, of rate k / m and $(m-k)/(n-k)$, respectively. Represent by $u^{(1)}$ and $u^{(2)}$ the input vectors of $\varSigma _1$ and $\varSigma _2$, by $x^{(1)}$ and $x^{(2)}$ the state vectors of $\varSigma _1$ and $\varSigma _2$ and by $y^{(1)}$ and $y^{(2)}$ the output vectors of $\varSigma _1$ and $\varSigma _2$, respectively. Let us consider the series interconnection of $\varSigma _1$ and $\varSigma _2$ by feeding the output vectors $y^{(1)}$ of $\varSigma _1$ as inputs of $\varSigma _2$ as represented in Fig. 1.

Fig. 1

Series concatenation of $\mathcal {C}_1$ and $\mathcal {C}_2$

Theorem 4

Let consider $\mathcal {C}_1 = \mathcal {C}\left( A_1^{(1)},A_2^{(1)},B_1^{(1)},B_2^{(1)}, C^{(1)}, D^{(1)}\right)$ and $\mathcal {C}_2 = \mathcal {C}\left( A_1^{(2)},A_2^{(2)},B_1^{(2)},B_2^{(2)}, C^{(2)}, D^{(2)}\right)$ two 2D convolutional codes of rate k / m and $(m-k)/(n-k)$, respectively.

Then the series interconnection of $\varSigma _1=\left( A_1^{(1)},A_2^{(1)},B_1^{(1)},B_2^{(1)}, C^{(1)}, D^{(1)}\right)$ and $\varSigma _2=\left( A_1^{(2)},A_2^{(2)},B_1^{(2)},B_2^{(2)}, C^{(2)}, D^{(2)}\right)$ by considering the inputs of $\varSigma _2$ to be the output vectors of $\varSigma _1$ and with code vector $v=\begin{bmatrix} y^{(2)} \\ v^{(1)} \end{bmatrix}$, where $v^{(1)}$ is the code vector of $\varSigma _1$, is a 2D convolutional code with ISO representation $\varSigma = (A_1,A_2,B_1,B_2,C,D)$, given by

$$ A_1=\begin{bmatrix} A_1^{(2)}&\,&B_1^{(2)} C^{(1)} \\ 0&\,&A_1^{(1)} \end{bmatrix}, \; \; A_2=\begin{bmatrix} A_2^{(2)}&\,&B_2^{(2)} C^{(1)} \\ 0&\,&A_2^{(1)} \end{bmatrix}, \; \; B_1=\begin{bmatrix} B_1^{(2)} D^{(1)} \\ B_1^{(1)}\end{bmatrix}, $$

$$ B_2=\begin{bmatrix} B_2^{(2)} D^{(1)} \\ B_2^{(1)}\end{bmatrix}, \; \; C=\begin{bmatrix} C^{(2)}&\,&D^{(2)} C^{(1)} \\ 0&\,&C^{(1)} \end{bmatrix}, \;\; D=\begin{bmatrix} D^{(2)} D^{(1)} \\ D^{(1)} \end{bmatrix}. $$

The next theorem gives conditions to ensure the modal observability of the code obtained by concatenation. We will not present the proof here for lack of space. The proof follows a similar reasoning than Theorem IV.2. of [1].

Theorem 5

Consider two 2D systems $\varSigma _1=\left( A_1^{(1)},A_2^{(1)},B_1^{(1)},B_2^{(1)}, C^{(1)}, D^{(1)}\right)$ and $\varSigma _2=\left( A_1^{(2)},A_2^{(2)},B_1^{(2)},B_2^{(2)}, C^{(2)}, D^{(2)}\right)$ of dimension $\delta _1$ and $\delta _2$, respectively. If $\varSigma _1$ and $\varSigma _2$ are modally observable, then the series interconnection of $\varSigma _1$ and $\varSigma _2$ (defined as in Theorem 4) is modally observable.

The next example shows that it is not sufficient that the 2D linear systems $\varSigma _1$ and $\varSigma _2$ are modally reachable to get the system obtained by series interconnection also modally reachable.

Example 1

Let $\alpha$ be a primitive element, with $\alpha ^3+\alpha +1=0$, of the Galois field $\mathbb F=GF(8)$. Consider the 2D linear systems $\varSigma _1=\left( A_1^{(1)},A_2^{(1)},B_1^{(1)},B_2^{(1)}, C^{(1)}, D^{(1)}\right)$ and $\varSigma _2=\left( A_1^{(2)},A_2^{(2)},B_1^{(2)},B_2^{(2)}, C^{(2)}, D^{(2)}\right)$, where

$$A_1^{(1)}=A_2^{(1)}=\begin{bmatrix}0\end{bmatrix}, \quad B_1^{(1)}=B_2^{(1)}=\begin{bmatrix}1 \end{bmatrix}, \quad C^{(1)}=\begin{bmatrix}\alpha ^4\end{bmatrix}, \quad D^{(1)}=\begin{bmatrix}\alpha ^3\end{bmatrix},$$

$$A_1^{(2)}=A_2^{(2)}=\begin{bmatrix}\alpha \end{bmatrix}, \quad B_1^{(2)}=B_2^{(2)}=\begin{bmatrix}1\end{bmatrix}, \quad C^{(2)}=\begin{bmatrix}\alpha ^4\end{bmatrix}, \quad D^{(2)}=\begin{bmatrix}1\end{bmatrix}.$$

Then $\varSigma _1$ and $\varSigma _2$ are modally reachable. In fact, it is easy to see that the matrices $\begin{bmatrix}I_{1}-A_1^{(1)}z_1-A_2^{(1)}z_2&B_1^{(1)}z_1+B_2^{(1)}z_2\end{bmatrix}$ and $\begin{bmatrix} I_{1}-A_1^{(2)}z_1-A_2^{(2)}z_2&B_1^{(2)}z_1+B_2^{(2)}z_2\end{bmatrix}$ are $\ell FP$.

Let $\varSigma =(A_1,A_2,B_1,B_2,C,D)$ be the 2D system obtained by series interconnection of $\varSigma _1$ and $\varSigma _2$ as defined in Theorem 4; then

$$ A_1=A_2=\!\!\begin{bmatrix} \alpha&\alpha ^4 \\ 0&0\end{bmatrix}, \quad B_1=B_2=\!\!\begin{bmatrix} \alpha ^3 \\ 1 \end{bmatrix}, \quad C=\!\!\begin{bmatrix} \alpha ^4&\alpha ^4\\ 0&\alpha ^4 \end{bmatrix} \quad D=\!\!\begin{bmatrix} \alpha ^3 \\ \alpha ^3 \end{bmatrix} $$

The matrix $\begin{bmatrix} I_{2}-A_1z_1-A_2z_2&B_1z_1+B_2z_2\end{bmatrix}$ is not $\ell FP$. In fact, there exists

$$ \hat{u}(z_1,z_2)=\frac{1}{1+\alpha (z_1+z_2)} \begin{bmatrix} 1+\alpha ^2(z_1+z_2)&\alpha +(1+\alpha ^2)(z_1+z_2) \end{bmatrix} $$

which is not polynomial, such that $\hat{u}(z_1,z_2) \begin{bmatrix} I_{2}-A_1z_1-A_2z_2&B_1z_1+B_2z_1\end{bmatrix}$ is polynomial. Then $\begin{bmatrix} I_{2}-A_1z_1-A_2z_2&B_1z_1+B_2z_2\end{bmatrix}$ is not $\ell FP$, which means that $\varSigma$ is not modally reachable.

The following theorem gives conditions on $\varSigma _1$ and $\varSigma _2$ to obtain the corresponding series interconnection modally reachable.

Theorem 6

Consider two 2D systems $\varSigma _1=\left( A_1^{(1)},A_2^{(1)},B_1^{(1)},B_2^{(1)}, C^{(1)}, D^{(1)}\right)$ and $\varSigma _2=\left( A_1^{(2)},A_2^{(2)},B_1^{(2)},B_2^{(2)}, C^{(2)}, D^{(2)}\right)$ of dimension $\delta _1$ and $\delta _2$, respectively. If $\varSigma _1$ is modally reachable and the matrix $I_{\delta _2}-A_1^{(2)}z_1-A_2^{(2)}z_2$ is unimodular, then the series interconnection of $\varSigma _1$ and $\varSigma _2$ (defined as in Theorem 4) is modally reachable.

Proof

Assume that $\varSigma _1$ is modally reachable and the matrix $I_{\delta _2}-A_1^{(2)}z_1-A_2^{(2)}z_2$ is unimodular. Attending to Definition 2, we have to prove that the matrix

$$\begin{aligned} T(z_1,z_2)\!=\!\begin{bmatrix} I_{\delta _2} - A_1^{(2)}z_1 - A_2^{(2)}z_2&-B_1^{(2)} C^{(1)}z_1 - B_2^{(2)} C^{(1)}z_2&B_1^{(2)} D^{(1)}z_1 + B_2^{(2)} D^{(1)}z_2 \\ 0&I_{\delta _1} - A_1^{(1)}z_1 - A_2^{(1)}z_2&B_1^{(1)}z_1 + B_2^{(1)}z_2 \end{bmatrix} \end{aligned}$$

is $\ell FP$.

Let $\hat{u}(z_1,z_2)\!\in \!\mathbb F(z_1,z_2)^{1\times (\delta _1+\delta _2)}$ be such that $\hat{u}(z_1,z_2) T(z_1,z_2)\!\in \!\mathbb F[z_1,z_2]^{1\times (\delta _1+\delta _2+k)}$. Suppose that $\hat{u}(z_1,z_2) = \begin{bmatrix} \hat{u}_2(z_1,z_2)^T&\hat{u}_1(z_1,z_2)^T \end{bmatrix}$ with $\hat{u}_2(z_1,z_2)\in \mathbb F(z_1,z_2)^{\delta _2}$. Then

$$ \hat{u}_2(z_1,z_2)^T \begin{bmatrix} I_{\delta _2} - A_1^{(2)}z_1 - A_2^{(2)}z_2 \end{bmatrix} \in \mathbb F[z_1,z_2]^{1\times \delta _2} $$

and, since $I_{\delta _2}-A_1^{(2)}z_1-A_2^{(2)}z_2$ is unimodular, $\hat{u}_2(z_1,z_2)\in \mathbb F[z_1,z_2]^{\delta _2}.$

On the other hand,

$$\begin{aligned}&\hat{u}_{2}(z_1,z_2)^T \begin{bmatrix} -B_1^{(2)} C^{(1)}z_1 - B_2^{(2)} C^{(1)}z_2&B_1^{(2)} D^{(1)}z_1 + B_2^{(2)} D^{(1)}z_2 \end{bmatrix} \\&+ \hat{u}_{1}(z_1,z_2)^T \begin{bmatrix} I_{\delta _1} - A_1^{(1)}z_1 - A_2^{(1)}z_2&B_1^{(1)}z_1 + B_2^{(1)}z_2 \end{bmatrix} \in \mathbb {F}[z_1,z_2]^{1\times (\delta _1+k)} \end{aligned}$$

which implies that

$$ \hat{u}_{1}(z_1,z_2)^T \begin{bmatrix} I_{\delta _1} - A_1^{(1)}z_1 - A_2^{(1)}z_2&B_1^{(1)}z_1 + B_2^{(1)}z_2 \end{bmatrix}\in \mathbb {F}[z_1,z_2]^{1\times (\delta _1+k)} $$

and, since $\varSigma _1$ is modally reachable, $\hat{u}_1(z_1,z_2)\in \mathbb F[z_1,z_2]^{\delta _1}$.

Therefore $\hat{u}(z_1,z_2)$ is in $\mathbb F[z_1,z_2]^{1\times (\delta _1+\delta _2)}$ and, by Lemma 1, $T(z_1,z_2)$ is $\ell FP$ and thus $\varSigma$ is modally reachable.

Remark 1

Note that if the matrix $I_{\delta _2}-A_1^{(2)}z_1-A_2^{(2)}z_2$ is unimodular then $\varSigma _2$ is modally reachable. Moreover, this means that the code $\mathcal {C}_2$ admits an encoder of the form $\begin{bmatrix}I\\ \tilde{G}(z_1,z_2) \end{bmatrix}$ and therefore is systematic.

We will now considered the concatenation of a 2D convolutional code $\mathcal {C}_1$ of rate 1 / 2 and degree $\delta _1$ with a 2D convolutional code $\mathcal {C}_2$ of rate $1/(n-1)$ and degree $\delta _2$ and we will derive conditions on the ISO representations of $\mathcal {C}_1$ and $\mathcal {C}_2$ that will produce a minimal representation of concatenation code of $\mathcal {C}_1$ and $\mathcal {C}_2$.

Theorem 7

Let $\varSigma _1=\left( A_1^{(1)},A_2^{(1)},B_1^{(1)},B_2^{(1)}, C^{(1)}, D^{(1)}\right)$ be a ISO system with 1 input and 1 output and degree $\delta _1$ and let $\varSigma _2=\left( A_1^{(2)},A_2^{(2)},B_1^{(2)},B_2^{(2)}, C^{(2)}, D^{(2)}\right)$ be a ISO system with 1 input and $n-2$ outputs and degree $\delta _2$ such that

$$ A_1^{(1)}=diag\left( a_1,\ldots ,a_{\delta _1}\right) , \, A_2^{(1)}=diag\left( b_1,\ldots ,b_{\delta _1}\right) , \, B_1^{(1)}=\begin{bmatrix}p_1 \\ \vdots \\ p_{\delta _1}\end{bmatrix}, \, B_2^{(1)}=\begin{bmatrix}m_1 \\ \vdots \\m_{\delta _1}\end{bmatrix} $$

$$ A_1^{(2)}=diag\left( c_1,\ldots ,c_{\delta _2}\right) , \, A_2^{(2)}=diag\left( d_1,\ldots ,d_{\delta _2}\right) , \, B_1^{(2)}=\begin{bmatrix}s_1 \\ \vdots \\s_{\delta _2}\end{bmatrix}, \, B_2^{(2)}=\begin{bmatrix}t_1 \\ \vdots \\t_{\delta _2}\end{bmatrix} $$

with $a_i,b_i,p_i,m_i,c_k,d_k,s_k,t_k\in \mathbb {F}{\setminus }\{0\}$ and

• (a) $a_ib_j=a_jb_i$, $a_i\ne a_j$ and $b_i\ne b_j$, for $i\ne j$,

• (b) $c_kd_l=c_ld_k$, $c_k\ne c_l$ and $d_k\ne d_l$, for $k\ne l$,

• (c) $a_id_k=b_ic_k$, $a_i\ne c_k$ and $b_i\ne d_k$, for all i and for all k,

• (d) $a_im_i=b_il_i$, for all i,

• (e) $c_kt_k=d_ks_k$, for all k,

with $i,j\in \{1,\ldots ,\delta _1\}$, $k,l\in \{1,\ldots ,\delta _2\}$. Then $\varSigma _1$ and $\varSigma _2$ are a minimal representation of $\mathcal {C}_1$ and $\mathcal {C}_2$, respectively, and the series interconnection $\varSigma$ of $\varSigma _1$ and $\varSigma _2$ is a minimal representation of the concatenation code of $\mathcal {C}_1$ and $\mathcal {C}_2$.

Proof

Consider $X_1(z_1,z_2)$, $X_2(z_1,z_2)$ and $X(z_1,z_2)$ the matrices defined in (2) for the 2D linear systems $\varSigma _1$, $\varSigma _2$ and $\varSigma$, respectively, and let

$$Y_1(z_1,z_2)=\begin{bmatrix} I_{\delta _1}-A_1^{(1)}z_1-A_2^{(1)}z_2&-B_1^{(1)}z_1-B_2^{(1)}z_2\end{bmatrix}.$$

Conditions (a) and (d) imply that $Y_1(\lambda _1,\lambda _2)$ is full row rank for all $\lambda _1,\lambda _2\in \overline{\mathbb {F}}$. Thus $Y_1(z_1,z_2)$ is $\ell ZP$, which implies that $X_1(z_1,z_2)$ is $\ell FP$. Applying the same reasoning, we show that $X_2(z_1,z_2)$ and $X(z_1,z_2)$ are also $\ell FP$. Moreover, it is easy to see that $\det \left( I_{\delta _i}-A_1^{(i)}z_1-A_2^{(i)}z_2\right)$ has degree $\delta _i$, $i=1,2$, and $\det \left( I_{\delta _1+\delta _2}-A_1z_1-A_2z_2\right)$ has degree $\delta _1+\delta _2$. The result follows from Theorem 3.

The distance of a code determines its robustness in terms of error correction. It can be shown that the code obtained by the concatenation of two convolutional codes $\mathcal {C}_1$ and $\mathcal {C}_2$ defined as in Theorem 7 has higher distance than $\mathcal {C}_2$. More investigation must be done to determine at what extent this distance can be improved.