Keywords

1 Introduction

The class of convolutional codes generalizes the class of linear block codes in a natural way. In comparison to the literature on linear block codes, there are only relatively few algebraic constructions of convolutional codes which have a good designed distance. There are several methods for constructing convolutional codes, for example by extending the constructions known for block codes to convolutional codes, such as the ones based on cyclic or quasi-cyclic constructions on block codes [7, 8, 10, 19].

Combining known codes is a powerful method to obtain new codes with better error correction capability avoiding the exponential increase of decoding complexity. For convolutional codes, we can find in the literature some powerful combining methods as woven convolutional codes [21, 22] and turbo codes [18]. More recently, as a natural extension of the direct product codes introduced by Elias [3], Bossert, Medina and Sidorenko [1] introduce the product of convolutional codes and they show that every convolutional product code can be represented as a woven convolutional code (see also [11]).

On the other hand, it is well-known that there exists a close connection between linear systems over finite fields and convolutional codes. Rosenthal [13] provides an excellent survey of the different points of view about convolutional codes. By using the input-state-output representation of convolutional codes introduced by Rosenthal and York [16], Climent, Herranz and Perea [2] and Herrnaz [4] introduce the input-state-output representation of different serial and parallel concatenated convolutional codes, and by using them, they also present a construction of new codes with prescribed distance.

The rest of the paper is structured as follows. In Sect. 2 we present the basic notions and previous results related to convolutional codes and convolutional product codes. Then, in Sect. 3, we introduce two input-state-output representations of a convolutional product code and prove that none of them is minimal. Moreover we introduce a lower bound on the free distance of the convolutional product code.

2 Preliminaries

Let \(\mathbb{F}\) be a finite field and denote by \(\mathbb{F}[z]\) the polynomial ring on the variable z with coefficients in \(\mathbb{F}\). A convolutional code \(\mathcal{C}\) of rate k∕n is a submodule of \(\mathbb{F}[z]^{n}\) that can be described as (see [17, 20])

$$\displaystyle{\mathcal{C} =\mathop{ \mathrm{im}}\nolimits _{\mathbb{F}[z]}(G(z)) =\{ \mathbf{\mathit{v}}(z) \in \mathbb{F}[z]^{n}\ \vert \ \mathbf{\mathit{v}}(z) = G(z)\mathbf{\mathit{u}}(z)\ \text{with}\ \mathbf{\mathit{u}}(z) \in \mathbb{F}[z]^{k}\}}$$

where u(z) is the information vector, v(z) is the corresponding codeword and G(z)is an n × k polynomial matrix with rank k called generator or encoder matrix of \(\mathcal{C}\). Two full column rank matrices \(G_{1}(z),G_{2}(z) \in \mathbb{F}[z]^{n\times k}\) are said to be equivalent encoders if and only if there exists a unimodular matrix \(P(z) \in \mathbb{F}[z]^{k\times k}\) such that \(G_{2}(z)\,=\,G_{1}(z)P(z)\). The complexity of a convolutional code \(\mathcal{C}\) is the highest degreeof the full size minors of any encoder of \(\mathcal{C}\). A generator matrix of a convolutional code is called minimal if and only if the complexity is equal to the sum of the column degrees.

A generator matrix is said to be catastrophic [6] if there exists some input sequence u(z) with infinite nonzero entries which generates a codeword v(z) = G(z)u(z) with a finite nonzero entries. A convolutional code \(\mathcal{C}\) is observable if one, and therefore any, generator matrix G(z) is right prime (see [14]). Furthermore, if G(z) is a generator matrix of an observable convolutional code, then G(z) is a noncatastrophic generator matrix (see [14]).

Let \(\mathbf{\mathit{v}}(z) \in \mathcal{C}\) and assume that \(\mathbf{\mathit{v}}(z) = \mathbf{\mathit{v}}_{0}z^{\gamma } + \mathbf{\mathit{v}}_{1}z^{\gamma -1} + \cdots + \mathbf{\mathit{v}}_{\gamma -1}z + \mathbf{\mathit{v}}_{\gamma }\) with \(\mathbf{\mathit{v}}_{t} \in \mathbb{F}^{n}\), for \(t = 0,1,\ldots,\gamma -1,\gamma\). If we consider \(\mathbf{\mathit{v}}_{t} = \left (\begin{array}{*{10}c} \mathbf{\mathit{y}}_{t} \\ \mathbf{\mathit{u}}_{t}\end{array} \right )\), where \(\mathbf{\mathit{y}}_{t} \in \mathbb{F}^{n-k}\) and\(\mathbf{\mathit{u}}_{t}\,\in \,\mathbb{F}^{k}\), then the convolutional code \(\mathcal{C}\) is equivalently described by the (A, B, C, D) representation (see [13, 16, 17, 20])

$$\displaystyle{\left.\begin{array}{rcl} \mathbf{\mathit{x}}_{t+1} & =&A\mathbf{\mathit{x}}_{t} + B\mathbf{\mathit{u}}_{t}, \\ \mathbf{\mathit{y}}_{t}& =&C\mathbf{\mathit{x}}_{t} + D\mathbf{\mathit{u}}_{t}, \end{array} \right \},\quad t = 0,1,2,\ldots,\quad \mathbf{\mathit{x}}_{0} = \mathbf{0}.}$$

For each instant t, we say that x t is the state vector, u t is the information vector, y t is the parity vector, and v t  is the codeword. In the linear systems theory, this representation is known as the input-state-output (ISO) representation.

If \(\mathcal{C}\) is a rate k∕n convolutional code with complexity δ, we call \(\mathcal{C}\) an (n, k, δ)-code, and in that case, it is possible (see [9]) to choose matrices A, B, C and D of sizes δ ×δ, δ × k, (n − k) ×δ and (n − k) × k, respectively. In convolutional coding theory, an ISO representation (A, B, C, D) having the above sizes is called a minimal representation and it is characterized through the condition that the pair (A, B) is controllable, that is (see [16]),

$$\displaystyle{\mathop{\mathrm{rank}}\nolimits \left (\begin{array}{*{10}c} B &AB &\cdots &A^{\delta -1}B \end{array} \right ) =\delta.}$$

Moreover, if (A, B) is controllable, then the convolutional code defined by the matrices (A, B, C, D) is an observable code if and only if (A, C) is an observable pair (see [12]). Recall that (A, C) is an observable pair if \((A^{T},C^{T})\) is a controllable pair.

The free distance of a convolutional code \(\mathcal{C}\) can be characterized (see [5]) as

$$\displaystyle\begin{array}{rcl} d_{\mathit{free}}(\mathcal{C}) =\min \left (\sum _{t=0}^{\infty }\mathop{\mathrm{wt}}\nolimits (\mathbf{\mathit{u}}_{ t}) +\sum _{ t=0}^{\infty }\mathop{\mathrm{wt}}\nolimits (\mathbf{\mathit{y}}_{ t})\right )& & {}\\ \end{array}$$

where the minimum has to be taken over all possible nonzero codewords and where wt denotes the Hamming weight. The free distance of an (n, k, δ)-code \(\mathcal{C}\) is always upper-bounded (see [15]) by the generalized Singleton bound

$$\displaystyle{d_{\mathit{free}}(\mathcal{C}) \leq (n - k)\left (\left \lfloor \frac{\delta } {k}\right \rfloor + 1\right ) +\delta +1.}$$

In addition, the convolutional code \(\mathcal{C}\) is called maximum-distance separable (MDS) if its free distance is equal to the generalized Singleton bound.

To finish this section, we introduce the product of two convolutional codes called “horizontal” and “vertical” codes respectively. Assume that \(\mathcal{C}_{h}\) and \(\mathcal{C}_{\mathit{v}}\) are horizontal \((n_{h},k_{h},\delta _{h})\) and vertical \((n_{\mathit{v}},k_{\mathit{v}},\delta _{\mathit{v}})\) codes respectively. Then, the product convolutional code (see [1, 11]) \(\mathcal{C} = \mathcal{C}_{h} \otimes \mathcal{C}_{\mathit{v}}\) is defined to be the convolutional code whose codewords consist of all \(n_{\mathit{v}} \times n_{h}\) matrices in which columns belong to \(\mathcal{C}_{\mathit{v}}\) and rows belongs to \(\mathcal{C}_{h}\). It is an \((n_{h}n_{\mathit{v}},k_{h}k_{\mathit{v}},\delta _{h}k_{\mathit{v}} + k_{h}\delta _{\mathit{v}})\).

Encoding of the product convolutional code \(\mathcal{C}\) can be done as follows (see [1, 11]). Let G v (z) and G h (z) be generator matrices of the component convolutional codes \(\mathcal{C}_{\mathit{v}}\) and \(\mathcal{C}_{h}\), respectively. Denote by U(z) a k v × k h information matrix. Now, we can apply row-column encoding; i.e., every column of U(z) is encoded using G v (z), and then every row of the resulting matrix G v (z)U(z) is encoded using G h (z) as \((G_{\mathit{v}}(z)U(z))G_{h}(z)^{T}\). We can also apply column-row encoding; i.e., every row of U(z) is encoded using G h (z), and then every column of the resulting matrix \(U(z)G_{h}(z)^{T}\) is encoding using G v (z) as \(G_{\mathit{v}}(z)(U(z)G_{h}(z)^{T})\). As a consequence of the associativity of the product of matrices, we get the same matrix in both cases. So, the codeword matrix V (z) is given by

$$\displaystyle{V (z) = G_{\mathit{v}}(z)\,U(z)\,G_{h}(z)^{T},}$$

and by using properties of the Kronecker product, we have

$$\displaystyle{\mathop{\mathrm{vect}}\nolimits \left (V (z)\right ) = \left (G_{h}(z) \otimes G_{\mathit{v}}(z)\right )\mathop{\mathrm{vect}}\nolimits \left (U(z)\right )}$$

where \(\mathop{\mathrm{vect}}\nolimits \left (\cdot \right )\) is the operator that transforms a matrix into a vector by stacking the column vectors of the matrix below one another. So, the generator matrix G(z) of the product convolutional code \(\mathcal{C}\) is the Kronecker product

$$\displaystyle{G(z) = G_{h}(z) \otimes G_{\mathit{v}}(z)}$$

of the generator matrices of the horizontal and vertical codes.

3 ISO Representation of a Product Convolutional Code

Assume that \((A_{h},\!\!\,B_{h},\!\!\,C_{h},\!\!\,D_{h})\) and \((A_{\mathit{v}},\!\!\,B_{\mathit{v}},\!\!\,C_{\mathit{v}},\!\!\,D_{\mathit{v}})\) are the ISO representations of the\((n_{h},k_{h},\delta _{h})\) horizontal and \((n_{\mathit{v}},k_{\mathit{v}},\delta _{\mathit{v}})\) vertical codes \(\mathcal{C}_{h}\) and \(\mathcal{C}_{\mathit{v}}\), respectively. Assume also that the \(k_{\mathit{v}} \times k_{h}\) matrix \(U_{t}\) is the information matrix of the product code \(\mathcal{C} = \mathcal{C}_{h} \otimes \mathcal{C}_{\mathit{v}}\).

By using the ISO representation of the horizontal code \(\mathcal{C}_{h}\) we can encode the information vector \(\mathbf{\mathit{u}}_{t} =\mathop{ \mathrm{vect}}\nolimits \left (U_{t}\right )\) as

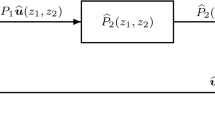
$$\displaystyle{ \left.\begin{array}{rcl} \mathbf{\mathit{x}}_{t+1}^{h}& = & (A_{h} \otimes I_{k_{\mathit{v}}})\mathbf{\mathit{x}}_{t}^{h} + (B_{h} \otimes I_{k_{\mathit{v}}})\mathbf{\mathit{u}}_{t} \\ \mathbf{\mathit{y}}_{t}^{h}& = & (C_{h} \otimes I_{k_{\mathit{v}}})\mathbf{\mathit{x}}_{t}^{h} + (D_{h} \otimes I_{k_{\mathit{v}}})\mathbf{\mathit{u}}_{t} \end{array} \right \},\quad \mathbf{\mathit{v}}_{t}^{h} = \left (\begin{array}{*{10}c} \mathbf{\mathit{y}}_{t}^{h} \\ \mathbf{\mathit{u}}_{t} \end{array} \right ),\quad t = 0, 1, 2,\ldots,\quad \mathbf{\mathit{x}}_{0}^{h} = \mathbf{0}. }$$
(1)

Analogously, by using the ISO representation of the vertical code \(\mathcal{C}_{\mathit{v}}\) we can encode the same information vector u t as

$$\displaystyle{ \left.\begin{array}{rcl} \mathbf{\mathit{x}}_{t+1}^{\mathit{v}} & = & (I_{k_{h}} \otimes A_{\mathit{v}})\mathbf{\mathit{x}}_{t}^{\mathit{v}} + (I_{k_{h}} \otimes B_{\mathit{v}})\mathbf{\mathit{u}}_{t} \\ \mathbf{\mathit{y}}_{t}^{\mathit{v}} & = & (I_{k_{h}} \otimes C_{\mathit{v}})\mathbf{\mathit{x}}_{t}^{\mathit{v}} + (I_{k_{h}} \otimes D_{\mathit{v}})\mathbf{\mathit{u}}_{t} \end{array} \right \},\quad \mathbf{\mathit{v}}_{t}^{\mathit{v}} = \left (\begin{array}{*{10}c} \mathbf{\mathit{y}}_{t}^{\mathit{v}} \\ \mathbf{\mathit{u}}_{t} \end{array} \right ),\quad t = 0, 1, 2,\ldots,\quad \mathbf{\mathit{x}}_{0}^{\shortmid} = \mathbf{0}, }$$
(2)

Then we encode the parity vector \(\mathbf{\mathit{y}}_{t}^{h}\) (respectively, \(\mathbf{\mathit{y}}_{t}^{\mathit{v}}\)) by using the vertical code \(\mathcal{C}_{\mathit{v}}\) (respectively, the horizontal code \(\mathcal{C}_{\mathit{h}}\)) as

$$\displaystyle\begin{array}{rcl} \left.\begin{array}{rcl} \mbox{ $\mathfrak{x}$}_{t+1}^{\mathit{v}} & =&(I_{n_{h}-k_{h}} \otimes A_{\mathit{v}})\mbox{ $\mathfrak{x}$}_{t}^{\mathit{v}} + (I_{n_{h}-k_{h}} \otimes B_{\mathit{v}})\mathbf{\mathit{y}}_{t}^{h} \\ \mbox{ $\mathfrak{y}$}_{t}^{\mathit{v}} & =&(I_{n_{h}-k_{h}} \otimes C_{\mathit{v}})\mbox{ $\mathfrak{x}$}_{t}^{\mathit{v}} + (I_{n_{h}-k_{h}} \otimes D_{\mathit{v}})\mathbf{\mathit{y}}_{t}^{h} \end{array} \right \},\quad \mbox{ $\mathfrak{v}$}_{t}^{\mathit{v}} = \left (\begin{array}{*{10}c} \mbox{ $\mathfrak{y}$}_{t}^{\mathit{v}} \\ \mathbf{\mathit{y}}_{t}^{h} \end{array} \right ),\quad t = 0,1,2,\ldots,\quad \mbox{ $\mathfrak{x}$}_{0}^{\mathit{v}} = \mathbf{0},& &{}\end{array}$$
(3)
$$\displaystyle\begin{array}{rcl} \left.\begin{array}{rcl} \mbox{ $\mathfrak{x}$}_{t+1}^{h}& =&(A_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}})\mbox{ $\mathfrak{x}$}_{t}^{h} + (B_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}})\mathbf{\mathit{y}}_{t}^{\mathit{v}} \\ \mbox{ $\mathfrak{y}$}_{t}^{h}& =&(C_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}})\mbox{ $\mathfrak{x}$}_{t}^{h} + (D_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}})\mathbf{\mathit{y}}_{t}^{\mathit{v}} \end{array} \right \},\quad \mbox{ $\mathfrak{y}$}_{t}^{h} = \left (\begin{array}{*{10}c} \mbox{ $\mathfrak{y}$}_{t}^{h} \\ \mathbf{\mathit{y}}_{t}^{\mathit{v}} \end{array} \right ),\quad t = 0,1,2,\ldots,\quad \mbox{ $\mathfrak{x}$}_{0}^{h} = \mathbf{0},& &{}\end{array}$$
(4)

Then, by using properties of the Kronecker product we obtain the following result.

Theorem 1

For the vectors \(\mbox{ $\mathfrak{y}$}_{t}^{\mathit{v}}\) and \(\mbox{ $\mathfrak{y}$}_{t}^{h}\) defined by expressions (3) and (4) respectively, it follows that \(\mbox{ $\mathfrak{y}$}_{t}^{\mathit{v}} = \mbox{ $\mathfrak{y}$}_{t}^{h}\) , for \(t = 0,1,2,\ldots\)

Proof

By induction over t. □ 

Next result establishes that the ISO representations defined by matrices in expressions (1)–(4) are minimal ISO representations.

Theorem 2

Let us assume that \((A_{h},B_{h},C_{h},D_{h})\) and \((A_{\mathit{v}},B_{\mathit{v}},C_{\mathit{v}},D_{\mathit{v}})\) are minimal ISO representations of the \((n_{h},k_{h},\delta _{h})\) horizontal and \((n_{\mathit{v}},k_{\mathit{v}},\delta _{\mathit{v}})\) vertical codes \(\mathcal{C}_{h}\) and \(\mathcal{C}_{\mathit{v}}\) , respectively. Then

  1. 1.

    The matrices \((A_{h} \otimes I_{k_{\mathit{v}}},B_{h} \otimes I_{k_{\mathit{v}}},C_{h} \otimes I_{k_{\mathit{v}}},D_{h} \otimes I_{k_{\mathit{v}}})\) in expression (1) define a minimal ISO representation of an \((n_{h}k_{\mathit{v}},k_{h}k_{\mathit{v}},\delta _{h}k_{\mathit{v}})\) convolutional code \(\mathcal{C}_{h}(k_{\mathit{v}})\) .

  2. 2.

    The matrices \((I_{k_{h}} \otimes A_{\mathit{v}},I_{k_{h}} \otimes B_{\mathit{v}},I_{k_{h}} \otimes C_{\mathit{v}},I_{k_{h}} \otimes D_{\mathit{v}})\) in expression (2) define a minimal ISO representation of an \((k_{h}n_{\mathit{v}},k_{h}k_{\mathit{v}},k_{h}\delta _{\mathit{v}})\) convolutional code \(\mathcal{C}_{\mathit{v}}(k_{h})\) .

  3. 3.

    The matrices \((I_{n_{h}-k_{h}} \otimes A_{\mathit{v}},I_{n_{h}-k_{h}} \otimes B_{\mathit{v}},I_{n_{h}-k_{h}} \otimes C_{\mathit{v}},I_{n_{h}-k_{h}} \otimes D_{\mathit{v}})\) in expression (3) define a minimal ISO representation of an \(((n_{h} - k_{h})n_{\mathit{v}},(n_{h} - k_{h})k_{\mathit{v}},(n_{h} - k_{h})\delta _{\mathit{v}})\) convolutional code \(\mathcal{C}_{\mathit{v}}(n_{h} - k_{h})\) .

  4. 4.

    The matrices \((A_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}},B_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}},C_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}},D_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}})\) in expression (4) define a minimal ISO representation of an \((n_{h}(n_{\mathit{v}} - k_{\mathit{v}}),k_{h}(n_{\mathit{v}} - k_{\mathit{v}}),\delta _{h}(n_{\mathit{v}} - k_{\mathit{v}}))\) convolutional code \(\mathcal{C}_{h}(n_{\mathit{v}} - k_{\mathit{v}})\) .

Proof

The result follows from the fact that \((A_{h},B_{h},C_{h},D_{h})\) and \((A_{\mathit{v}},B_{\mathit{v}},C_{\mathit{v}},D_{\mathit{v}})\) are minimal ISO representations and the properties of the Kronecker product of matrices. □ 

It is not difficult to show that the codes \(\mathcal{C}_{h}(k_{\mathit{v}})\) and \(\mathcal{C}_{h}(n_{\mathit{v}} - k_{\mathit{v}})\) (respectively, \(\mathcal{C}_{\mathit{v}}(k_{h})\) and \(\mathcal{C}_{\mathit{v}}(n_{h} - k_{h})\)) correspond to the block parallel concatenation of convolutional codes described in [4, Section 5.3], and therefore

$$\displaystyle\begin{array}{rcl} & & d_{\mathit{free}}\left (\mathcal{C}_{h}(k_{\mathit{v}})\right ) = d_{\mathit{free}}\left (\mathcal{C}_{h}(n_{\mathit{v}} - k_{\mathit{v}})\right ) = d_{\mathit{free}}\left (\mathcal{C}_{h}\right ), \\ & & d_{\mathit{free}}\left (\mathcal{C}_{\mathit{v}}(k_{h})\right ) = d_{\mathit{free}}\left (\mathcal{C}_{\mathit{v}}(n_{h} - k_{h})\right ) = d_{\mathit{free}}\left (\mathcal{C}_{\mathit{v}}\right ).{}\end{array}$$
(5)

Now, by using the second model of serial concatenated convolutional codes introduced in [2, 4] we have the following result.

Theorem 3

With the same notation as in Theorem 2 .

  1. 1.

    If \(\mathcal{S}_{1}\) is the rate \(k_{h}k_{\mathit{v}}/((n_{h} - k_{h})n_{\mathit{v}} + k_{h}k_{\mathit{v}})\) convolutional code defined by the serial concatenation of \(\mathcal{C}_{h}(k_{\mathit{v}})\) and \(\mathcal{C}_{\mathit{v}}(n_{h} - k_{h})\) , then \((\mathbf{A}_{1},\mathbf{B}_{1},\mathbf{C}_{1},\mathbf{D}_{1})\) , with

    $$\displaystyle\begin{array}{rcl} \mathbf{A}_{1} = \left [\begin{array}{cc} I_{n_{h}-k_{h}} \otimes A_{\mathit{v}} & C_{h} \otimes B_{\mathit{v}} \\ O &A_{h} \otimes I_{k_{\mathit{v}}}\end{array} \right ],\qquad \mathbf{B}_{1} = \left [\begin{array}{c} D_{h} \otimes B_{\mathit{v}} \\ B_{h} \otimes I_{k_{\mathit{v}}}\end{array} \right ],& & {}\\ \mathbf{C}_{1} = \left [\begin{array}{cc} I_{n_{h}-k_{h}} \otimes C_{\mathit{v}} & C_{h} \otimes D_{\mathit{v}} \\ O &C_{h} \otimes I_{k_{\mathit{v}}}\end{array} \right ],\qquad \mathbf{D}_{1} = \left [\begin{array}{c} D_{h} \otimes D_{\mathit{v}} \\ D_{h} \otimes I_{k_{\mathit{v}}}\end{array} \right ],& & {}\\ \end{array}$$

    is an ISO representation of \(\mathcal{S}_{1}\) .

  2. 2.

    If \(\mathcal{S}_{2}\) is the rate \(k_{h}k_{\mathit{v}}/(n_{h}(n_{\mathit{v}} - k_{\mathit{v}}) + k_{h}k_{\mathit{v}})\) convolutional code defined by the serial concatenation of \(\mathcal{C}_{\mathit{v}}(k_{h})\) and \(\mathcal{C}_{h}(n_{\mathit{v}} - k_{\mathit{v}})\) , then \((\mathbf{A}_{2},\mathbf{B}_{2},\mathbf{C}_{2},\mathbf{D}_{2})\) , with

    $$\displaystyle\begin{array}{rcl} \mathbf{A}_{2} = \left [\begin{array}{ccc} A_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}} & B_{h} \otimes C_{\mathit{v}} \\ O &I_{k_{h}} \otimes A_{\mathit{v}}\end{array} \right ],\qquad \mathbf{B}_{2} = \left [\begin{array}{c} B_{h} \otimes D_{\mathit{v}} \\ I_{k_{h}} \otimes B_{\mathit{v}}\end{array} \right ],& & {}\\ \mathbf{C}_{2} = \left [\begin{array}{cc} C_{h} \otimes I_{n_{\mathit{v}}-k_{\mathit{v}}} & D_{h} \otimes C_{\mathit{v}} \\ O &I_{k_{h}} \otimes C_{\mathit{v}}\end{array} \right ],\qquad \mathbf{D}_{2} = \left [\begin{array}{c} D_{h} \otimes D_{\mathit{v}} \\ I_{k_{h}} \otimes D_{\mathit{v}}\end{array} \right ],& & {}\\ \end{array}$$

    is an ISO representation of \(\mathcal{S}_{2}\) .

Proof

The result follows from Theorem 9 of [2]. □ 

In general the ISO representations \((\mathbf{A}_{1},\mathbf{B}_{1},\mathbf{C}_{1},\mathbf{D}_{1})\) and \((\mathbf{A}_{2},\mathbf{B}_{2},\mathbf{C}_{2},\mathbf{D}_{2})\) introduced in the above theorem are not minimal (see [2, 4]). In [2, 4] we can find some sufficient conditions to ensure the minimality of the above ISO representations.

Now, by Theorem 15 of [2] we have that

$$\displaystyle{ d_{\mathit{free}}\left (\mathcal{S}_{1}\right ) \geq d_{\mathit{free}}\left (\mathcal{C}_{h}\right )\quad \text{and}\quad d_{\mathit{free}}\left (\mathcal{S}_{2}\right ) \geq d_{\mathit{free}}\left (\mathcal{C}_{\mathit{v}}\right ). }$$
(6)

As a consequence of Theorem 1, by using the second model of parallel concatenation (see [4, Section 5.2]) we have the following result.

Theorem 4

With the same notation as in Theorems 2 and 3 .

  1. 1.

    If \(\mathcal{P}_{1}\) is the rate \((k_{h}k_{\mathit{v}}/n_{h}n_{\mathit{v}})\) convolutional code defined by the parallel concatenation of \(\mathcal{S}_{1}\) and \(\mathcal{C}_{\mathit{v}}(k_{h})\) , then \((\mathfrak{A}_{1},\mathfrak{B}_{1},\mathfrak{C}_{1},\mathfrak{D}_{1})\) with

    is an ISO representation of \(\mathcal{P}_{1}\) .

  2. 2.

    If \(\mathcal{P}_{2}\) is the rate \((k_{h}k_{\mathit{v}}/n_{h}n_{\mathit{v}})\) convolutional code defined by the parallel concatenation of \(\mathcal{S}_{2}\) and \(\mathcal{C}_{h}(k_{\mathit{v}})\) , then \((\mathfrak{A}_{2},\mathfrak{B}_{2},\mathfrak{C}_{2},\mathfrak{D}_{2})\) with

    is an ISO representation of \(\mathcal{P}_{2}\) .

Note that, according to expressions (1)–(4) and Theorem 1, \(\mathcal{P}_{1}\) is the product convolutional code \(\mathcal{C} = \mathcal{C}_{h} \otimes \mathcal{C}_{\mathit{v}}\). Moreover, since \(\mathfrak{A}_{1}\) is a matrix of size \((n_{h}\delta _{\mathit{v}} +\delta _{h}k_{\mathit{v}}) \times (n_{h}\delta _{\mathit{v}} +\delta _{h}k_{\mathit{v}})\) and the complexity of \(\mathcal{C}\) is \(k_{h}\delta _{\mathit{v}} +\delta _{h}k_{\mathit{v}}\), we can ensure that the ISO representation \((\mathfrak{A}_{1},\mathfrak{B}_{1},\mathfrak{C}_{1},\mathfrak{D}_{1})\) provided by part 1 of Theorem 4 is nonminimal. By an analogous argument \(\mathcal{P}_{2}\) is the product convolutional code \(\mathcal{C} = \mathcal{C}_{h} \otimes \mathcal{C}_{\mathit{v}}\) and the ISO representation \((\mathfrak{A}_{2},\mathfrak{B}_{2},\mathfrak{C}_{2},\mathfrak{D}_{2})\) provided by part 2 of Theorem 4 is nonminimal.

Next result introduces a lower bound on the free distance \(d_{\mathit{free}}\) of the convolutional product code in terms of the constituent convolutional codes.

Theorem 5

If \(\mathcal{C}_{h}\) and \(\mathcal{C}_{\mathit{v}}\) are \((n_{h},k_{h},\delta _{h})\) and \((n_{\mathit{v}},k_{\mathit{v}},\delta _{\mathit{v}})\) codes, respectively, then,

$$\displaystyle\begin{array}{rcl} d_{\mathit{free}}(\mathcal{C}_{h} \otimes \mathcal{C}_{\mathit{v}}) \geq \max \left \{d_{\mathit{free}}(\mathcal{C}_{\mathit{v}}),d_{\mathit{free}}(\mathcal{C}_{h})\right \}.& & {}\\ \end{array}$$

Proof

With the same notation as in Theorem 4, as a consequence of Theorem 5.8 of [4] we have that

$$\displaystyle\begin{array}{rcl} & & d_{\mathit{free}}\left (\mathcal{P}_{1}\right ) \geq \max \left \{d_{\mathit{free}}\left (\mathcal{S}_{1}\right ),d_{\mathit{free}}\left (\mathcal{C}_{\mathit{v}}\right )\right \}, {}\\ & & d_{\mathit{free}}\left (\mathcal{P}_{2}\right ) \geq \max \left \{d_{\mathit{free}}\left (\mathcal{S}_{2}\right ),d_{\mathit{free}}\left (\mathcal{C}_{h}\right )\right \}. {}\\ \end{array}$$

The result follows now by expressions (5) and (6) an the fact that \(\mathcal{P}_{1} = \mathcal{P}_{2} = \mathcal{C}_{h} \otimes \mathcal{C}_{\mathit{v}}\). □