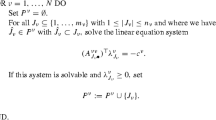Algorithmic Principle of Least Revenue for Finding Market Equilibria

Abstract

In analogy to extremal principles in physics, we introduce the Principle of Least Revenue for treating market equilibria. It postulates that equilibrium prices minimize the total excessive revenue of market’s participants. As a consequence, the necessary optimality conditions describe the clearance of markets, i.e. at equilibrium prices supply meets demand. It is crucial for our approach that the potential function of total excessive revenue be convex. This facilitates structural and algorithmic analysis of market equilibria by using convex optimization techniques. In particular, results on existence, uniqueness, and efficiency of market equilibria follow easily. The market decentralization fits into our approach by the introduction of trades or auctions. For that, Duality Theory of convex optimization applies. The computability of market equilibria is ensured by applying quasi-monotone subgradient methods for minimizing nonsmooth convex objective—total excessive revenue of the market’s participants. We give an explicit implementable algorithm for finding market equilibria which corresponds to real-life activities of market’s participants.

1 Introduction

We start with a celebrated quotation of Leonhard Euler (1744): “Nothing in the world takes place without optimization, and there is no doubt that all aspects of the world that have a rational basis can be explained by optimization methods.” Rephrasing this in modern terms, the laws of nature can be derived by using extremal (or variational) principles. Indeed, the laws are often first-order necessary optimality conditions for minimizing (or maximizing) a properly chosen potential function. To illustrate this idea, let us consider the Newton law

$$\displaystyle{ m\ddot{r} = F, }$$

(1)

where r(t) is the particle’s position at time t, F the acting force, and m the particle’s mass. The goal of classical mechanics is to solve this differential equation for various forces: gravity, electromagnetism, friction, etc. For conservative forces (gravity, electrostatics, but not friction), the force can be expressed as

$$\displaystyle{ F = -\nabla V, }$$

(2)

where the potential energy V (r) depends on the particle’s position. For this case, let us define the potential function called action:

$$\displaystyle{ A(r)\mathop{ =}\limits^{\mathrm{ def}}\int _{t_{1}}^{t_{2} }\left (\frac{m\dot{r}^{2}} {2} - V (r)\right )dt. }$$

(3)

The action represents the difference between the kinetic and potential energy of a particle. The integrand in ( 3) is called Lagrangian

$$\displaystyle{L(r)\mathop{ =}\limits^{\mathrm{ def}}\frac{m\dot{r}^{2}} {2} - V (r).}$$

Now, the Principle of Least Action says:

The true path taken by the particle is an extremum of the action.

In fact, it is an easy exercise from the calculus of variations to show that an extremum of the action satisfies the Newton law. Note that Newton law comes from the first-order variation of the action. Second derivative of the trajectory appears just because of the integration by parts. So, Newton law for conservative forces can be viewed as a first-order potential system. The least action principle (or Lagrangian method) became extremely fruitful in all of physics, not just mechanics. Many fundamental laws of physics can be expressed in terms of a least action principle, e.g. electromagnetism, optics, special and general relativity, particle physics etc. (see [1]). Recently in [21], the principle of least action has been applied to supply chains linking variation in production to variation in net-inventory.

From the optimization perspective, the introduction of extremal principles highlights the algorithmic aspects of laws. Instead of solving the law’s systems of equations, we may consider iterative schemes for minimizing the corresponding potential function. Of course, regarding physical laws it sounds like a philosophical paradox: who minimizes the action, and by using what method? However, having in mind the application of extremal principles in social sciences, this point of view could be valuable. Namely, optimization methods for minimizing a potential function provide behavioral dynamics. They explain how a social system eventually arrives at a state which is described by the corresponding law. Although, Isaac Newton remarked in 1720: “I can calculate the motion of heavenly bodies, but not the madness of people,”—we pursue exactly this goal, at least in some particular economic setting. It will turn out that the economic behavior of people is not as mad as it may look like.

In this paper we introduce and exploit extremal principles for the economic law of supply and demand. The latter says that at a competitive market supply meets demand at an appropriate price, i.e.

$$\displaystyle{ \sum _{k}^{}\tilde{y}_{k} =\sum _{ i}^{}\tilde{x}_{i}, }$$

(4)

where $\tilde{y}_{k}$ is kth producer’s and $\tilde{x}_{i}$ is ith consumer’s bundle of goods, respectively. It is also common to refer to ( 4) as the market clearing condition. Here, $\tilde{y}_{k} \in S_{k}(p)$ is kth producer’s supply operator, and $\tilde{x}_{i} \in D_{i}(p)$ is ith consumer’s demand operator at a price p. Hence, the law of supply and demand can be equivalently written as an inclusion problem

$$\displaystyle{ 0 \in \sum _{k}^{}S_{k}(p) -\sum _{i}^{}D_{i}(p). }$$

(5)

Solutions of ( 5) are called equilibrium prices. Together with corresponding production and consumption bundles, they form market equilibrium (e.g., [8]).

The role of prices in balancing supply and demand is well-known in economics since Adam Smith. As Milton Friedman pointed out in [2]: “Adam Smith’s flash of genius was his recognition that the prices …in a free market could coordinate the activity of millions of people, each seeking his own interest, in such a way as to make everyone better off.” Mathematically, this coordination may be explained by the fact that prices act as dual or Lagrange multipliers for the market clearance. In accordance with the latter, our main assumption states that supply and demand operators can be expressed as convex subdifferentials:

$$\displaystyle{ S_{k}(p) = \partial \mathcal{E}_{k}(p),\quad D_{i}(p) = -\partial \mathcal{E}_{i}(p). }$$

(6)

$\mathcal{E}_{k}(p)$ is kth producer’s excessive profit, and $\mathcal{E}_{i}(p)$ ith consumer’s excessive wealth. Note that the subdifferentiability assumption ( 6) has the same mathematical meaning as the assumption of dealing with a conservative force ( 2). Let us define the potential function called total excessive revenue:

$$\displaystyle{ \mathcal{E}(p)\mathop{ =}\limits^{\mathrm{ def}}\sum _{k}^{}\mathcal{E}_{k}(p) +\sum _{ i}^{}\mathcal{E}_{i}(p). }$$

(7)

In our framework, the total excessive revenue represents the Lagrangian w.r.t. the market clearance. Now, we are ready to state the Principle of Least Revenue:

Equilibrium prices minimize the total excessive revenue of market’s participants.

In fact, the first-order necessary optimality conditions for minimizing the total excessive revenue give us the law of supply and demand ( 5). The latter is due to the subdifferentiability assumption ( 6). Further, it is crucial for our approach that the potential function of total excessive revenue is convex. This opens up for structural and algorithmic analysis of market equilibria by using convex optimization techniques. E.g., the Walrasian tâtonnement, as suggested in [19], states that prices change proportionally to the excess demand, i.e.

$$\displaystyle{\dot{p} \in \sum _{i}^{}D_{i}(p) -\sum _{k}^{}S_{k}(p).}$$

Under assumption ( 6) the Walrasian tâtonnement becomes a subgradient system

$$\displaystyle{\dot{p} \in -\partial \mathcal{E}(p).}$$

Its discretized version is

$$\displaystyle{p[t + 1] = p[t] - h[t]\nabla \mathcal{E}\left (p[t]\right ),}$$

with time t, step-sizes h[t], and excess supplies $\nabla \mathcal{E}\left (p[t]\right ) \in \partial \mathcal{E}\left (p[t]\right )$. This corresponds to the standard subgradient scheme for the convex minimization of $\mathcal{E}$. In absence of assumption ( 6), the Walrasian tâtonnement is fraught with severe problems. These relate, on one side, to communication, implementation, interpretation, organization and, on the other side, to stability and definiteness, see e.g. [8] for details.

The paper is organized as follows. In Sect. 2 we describe the excessive revenue model for a competitive market from [14]. We show that the least revenue principle applies to the excessive revenue model. Based on this fact, existence, uniqueness and efficiency results for market equilibrium follow. In order to minimize the total excessive revenue, quasi-monotone subgradient methods for nonsmooth convex minimization from [13] are presented in Sect. 3. They guarantee the best possible rate of convergence for the whole sequence of test points rather than of their averages. This fact allows us to prevent uncontrollable jumps of the function values at some iterations. Moreover, the sequence of record values does not enter the complexity bound. This is crucial for the applicability of quasi-monotone subgradient methods in our economic setting. Indeed, the values of the total excessive revenue are not available to market’s participants. By using quasi-monotone subgradient methods, we explain in Sect. 4 how equilibrium prices can be successively adjusted. For that, we concentrate on

• the regulation design: regulator settles and updates prices which are taken by producers and consumers;

• the trade design: producers settle and update their individual prices, and consumers buy at the lowest purchase price;

• the auction design: consumers settle and update their individual prices, and producers sell at the highest offer price.

Notation.

Our notation is quite standard. We denote by $\mathbb{R}^{n}$ the space of n-dimensional column vectors x = (x ⁽¹⁾, …, x ⁽ⁿ⁾)^T, and by $\mathbb{R}_{+}^{n}$ the set of all vectors with nonnegative components. For x and y from $\mathbb{R}^{n}$, we introduce the standard scalar product and the Hadamard product

$$\displaystyle{\langle x,y\rangle =\sum \limits _{ i=1}^{n}x^{(i)}y^{(i)},\quad x \circ y = \left (x^{(i)}y^{(i)}\right )_{ i=1}^{n} \in \mathbb{R}^{n}.}$$

Finally, a ₊ denotes the positive part of the real value $a \in \mathbb{R}$: $a_{+} =\mathop{ \mathrm{max}}\limits \{a,0\}$. For $x = (x^{(1)},\ldots,x^{(n)})^{T} \in \mathbb{R}^{n}$ we denote $x_{+} = \left (x_{+}^{(1)},\ldots,x_{+}^{(n)}\right )^{T}$. For vectors $p_{1},\ldots,p_{K} \in \mathbb{R}^{n}$, denote by $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k} \in \mathbb{R}^{n}$ the vector with coordinates

$$\displaystyle{\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}\right )^{(j)} =\mathop{ \mathrm{min}}\limits _{ k=1,\ldots,K}p_{k}^{(j)},\quad j = 1,\ldots,n.}$$

For the vectors $p_{1},\ldots,p_{I} \in \mathbb{R}^{n}$, we denote by $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i} \in \mathbb{R}^{n}$ the vector with coordinates

$$\displaystyle{\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}\right )^{(j)} =\mathop{ \mathrm{max}}\limits _{ i=1,\ldots,I}p_{i}^{(j)},\quad j = 1,\ldots,n.}$$

2 Excessive Revenue Model

Let us present the excessive revenue model of competitive market from [14].

2.1 Producers and Consumers

Consider a market with K producers, which are able to produce n different goods. Given a vector of prices $p \in \mathbb{R}_{+}^{n}$, the kth producer forms the supply operator S _k (p) of production bundles $\tilde{y}_{k} \in \mathbb{R}_{+}^{n}$. For that, the kth producer maximizes the profit with respect to the variable cost, subsequently trying to cover the fixed cost. Namely,

• Producer k ∈ { 1, …, K} chooses first the tentative production bundle $y_{k} \in \mathbb{R}_{+}^{n}$ by solving the profit maximization problem:

  $$\displaystyle{ \pi _{k}(p)\mathop{ =}\limits^{\mathrm{ def}}\mathop{\mathrm{max}}\limits _{y_{k}\in \mathcal{Y}_{k}}\left \langle p,y_{k}\right \rangle - c_{k}(y_{k}). }$$

  (8)

  Here, $\mathcal{Y}_{k} \subset \mathbb{R}_{+}^{n}$ is the production set, assumed to be nonempty, compact and convex. The producer’s yield is $\left \langle p,y_{k}\right \rangle$. The variable cost of producing y _k is denoted by c _k (y _k ). We assume that c _k is a convex function on $\mathbb{R}_{+}^{n}$. Clearly, the profit π _k (p) is convex in p as the maximum of linear functions. By $\mathcal{Y}_{k}^{{\ast}}(p)$ we denote the set of optimal solutions of ( 8), i.e. $y_{k} \in \mathcal{Y}_{k}^{{\ast}}(p)$. Note that the profit maximization problem ( 8) appears already in Marshallian partial equilibrium analysis, see e.g. [8].

• Secondly, the kth producer compares the profit π _k (p) with the fixed cost of maintaining the technological set $\mathcal{Y}_{k}$, denoted by $\kappa _{k} \equiv \kappa _{k}(\mathcal{Y}_{k}) \in \mathbb{R}_{+}$. The latter can include the interest paid to the bank, different charges for renting the equipment, land use, etc. By this comparison, a participation level α _k  ≡ α _k (p) ∈ [0, 1] of kth producer is properly adjusted:

  $$\displaystyle{ \alpha _{k}(p)\mathop{ =}\limits^{\mathrm{ def}}\left \{\begin{array}{ll} 1,&\mbox{ if }\pi _{k}(p)>\kappa _{k}, \\ 0,&\mbox{ if }\pi _{k}(p) <\kappa _{k}.\end{array} \right. }$$

  (9)

  In case π _k (p) = κ _k , α _k (p) ∈ [0, 1] is not unique and may vary. We call producers’ participation levels satisfying the relation ( 9) proper.

• Finally, the supply operator $S_{k}: \mathbb{R}_{+}^{n} \rightrightarrows \mathbb{R}_{+}^{n}$ of kth producer is given by

  $$\displaystyle{ S_{k}(p)\mathop{ =}\limits^{\mathrm{ def}}\left \{\tilde{y}_{k} =\alpha _{k}y_{k}\,\left \vert \,\alpha _{k} \equiv \alpha _{k}(p)\mbox{ and }y_{k} \in \mathcal{Y}_{k}^{{\ast}}(p)\right.\right \}. }$$

  (10)

  Here, the production bundles are

  $$\displaystyle{\tilde{y}_{k}\mathop{ =}\limits^{\mathrm{ def}}\alpha _{k}y_{k},}$$

  where α _k  ≡ α _k (p) is the proper participation level of the kth producer, and $y_{k} \in \mathcal{Y}_{k}^{{\ast}}(p)$ is the tentative production.

Let I consumers be active at the market. The ith consumer has to decide on the consumption bundle $\tilde{x}_{i} \in \mathbb{R}_{+}^{n}$. These consumption bundles form the demand D _i (p), given the price $p \in \mathbb{R}_{+}^{n}$. The ith consumer minimizes the expenditure with an aim to guarantee the desirable utility level. Then he tries to cover this expenditure by the available wealth. Namely,

• Consumer i ∈ { 1, …, I} decides first on the tentative consumption bundle $x_{i} \in \mathbb{R}_{+}^{n}$ by minimizing expenditure:

  $$\displaystyle{ e_{i}(p)\mathop{ =}\limits^{\mathrm{ def}}\mathop{\mathrm{min}}\limits _{\begin{array}{c} x_{i} \in X_{i} \\ u_{i}(x_{i}) \geq \underline{ u}_{i}\end{array} }\left \langle p,x_{i}\right \rangle =\mathop{ \mathrm{min}}\limits _{\begin{array}{c} x_{i} \in \mathcal{X}_{i}\end{array} }\left \langle p,x_{i}\right \rangle, }$$

  (11)

  where the ith consumption set is

  $$\displaystyle{\mathcal{X}_{i}\mathop{ =}\limits^{\mathrm{ def}}\left \{x_{i} \in X_{i}\,\vert \,u_{i}(x_{i}) \geq \underline{ u}_{i}\right \}.}$$

  Here, $X_{i} \subset \mathbb{R}_{+}^{n}$ is assumed to be nonempty, compact and convex. By $u_{i}: X_{i} \rightarrow \mathbb{R}_{+}$ we denote the utility function of the ith consumer, assumed to be concave. The utility level $\underline{u}_{i} \in \mathbb{R}_{+}$ is desirable by ith consumer. The consumer’s expenditure e _i (p) is concave in p as the minimum of linear functions. By $\mathcal{X}_{i}^{{\ast}}(p)$ we denote the set of optimal solutions of ( 11), i.e. $x_{i} \in \mathcal{X}_{i}^{{\ast}}(p)$. The minimization of expenditure in ( 11) is well-known in economics as a dual problem for utility maximization. The desirable utility level u _i mainly reflects the consumer’s standards on qualities of goods. In [18] the agent who faces the expenditure minimization problem ( 11) is called the dual consumer. The dual consumer usually acts on regular basis, thus, generating the flows of consumption. We also refer to [5, Chap. 10] and [7] for more details on the dual theory of consumption. The compactness assumption on X _i refers to the fact that the consumption is bounded. Naturally, there are physical limits to what people can consume in order to satisfy their basic needs. The unbounded desire for wealth is not an issue here, since the wealth w _i is a primitive in our model (see below and confer the discussion on this assumption in [17]).

• Secondly, the ith consumer compares the expenditure e _i (p) with the available wealth $w_{i} \in \mathbb{R}_{+}$. The latter can include the budget, salary and rent payments, etc. By this comparison, a participation level β _i  ≡ β _i (p) ∈ [0, 1] of ith consumer is properly adjusted:

  $$\displaystyle{ \beta _{i}(p)\mathop{ =}\limits^{\mathrm{ def}}\left \{\begin{array}{ll} 1,&\mbox{ if }e_{i}(p) <w_{i}, \\ 0,&\mbox{ if }e_{i}(p)> w_{i}.\end{array} \right. }$$

  (12)

  In case e _i (p) = w _i , β _i (p) ∈ [0, 1] is not unique and may vary. We call consumers’ participation levels satisfying the relation ( 12) proper.

• Finally, the demand operator $D_{i}: \mathbb{R}_{+}^{n} \rightrightarrows \mathbb{R}_{+}^{n}$ of ith consumer is given by

  $$\displaystyle{ D_{i}(p)\mathop{ =}\limits^{\mathrm{ def}}\left \{\tilde{x}_{i} =\beta _{i}x_{i}\,\left \vert \,\beta _{i} \equiv \beta _{i}(p)\mbox{ and }x_{i} \in \mathcal{X}_{i}^{{\ast}}(p)\right.\right \}. }$$

  (13)

  Here, the consumption bundles are

  $$\displaystyle{\tilde{x}_{i}\mathop{ =}\limits^{\mathrm{ def}}\beta _{i}x_{i},}$$

  where β _i  ≡ β _i (p) is the proper participation level of the ith consumer, and $x_{i} \in \mathcal{X}_{i}^{{\ast}}(p)$ is the tentative consumption.

For the sake of convenient navigation along the text, we list model’s data and variables:

Table 1

There are two non-standard ingredients in our model which need to be explained and thoroughly justified. The first concerns the expenditure minimization problem ( 11) with the given level u _i of desirable utility. The second deals with the proper adjustment of participation levels α _k and β _i in ( 9) and ( 12), respectively.

• (1) Expenditure minimization and responsible consumer

The minimization of expenditure in ( 11) is well-known in economics as a dual problem for utility maximization (e.g. [8]):

$$\displaystyle{ v_{i}(p,w_{i})\mathop{ =}\limits^{\mathrm{ def}}\mathop{\mathrm{max}}\limits _{\begin{array}{c} x_{i} \in X_{i} \\ \left \langle p,x_{i}\right \rangle \leq w_{i} \end{array} }u_{i}(x). }$$

(14)

Namely, under some technical assumptions if x _i solves ( 14) then it also solves ( 11) with u _i  = v _i (p, w _i ). Conversely, if x _i solves ( 11) then it also solves ( 14) with $w_{i} = \left \langle p,x_{i}\right \rangle$. In our setting the desirable utility level u _i is given, thus, it is a primitive of the model. It mainly reflects the consumer’s standards on qualities of life. Hence, it does not explicitly depend on the wealth w _i as in the classical setting. Note that we model wealth effects by subsequent comparison of w _i with expenditure e _i (p) rather than by the usual budget constraint $\left \langle p,x_{i}\right \rangle \leq w_{i}$ as in ( 14) (cf. also the discussion in (2) below). The introduction of desirable utility levels u _i as primitives is the main departure from the usual consumption model ( 14). This is the crucial point in our market modeling which postulates in the sense that consumer’s objectives become monetary, hence transferable. As we shall see in Sect. 2.3 below, this fact implies that supply and demand operators can be expressed as convex subdifferentials, i.e. assumption ( 6) be valid.

Now, let us explain why in some interesting situations the desirable utility level u _i is explicitly available to consumers. For many daily goods there are physical standards to be satisfied. They constitute the so-called minimum standards of life. Additionally, some consumers often accept standards imposed by the society, e.g. through advertisement, their friends or family members. E.g., it became evident that some consumers use to shrink their usual consumption motivated by ecological reasons. Also experienced consumers, who go shopping in a supermarket say on a weekly basis, know the standards of their living. Overall, we may think of a responsible consumer who does care about the own expenditure. Namely, the consumer is not willing to spend more than necessary to satisfy the given standards. Thus, such a consumer tries to minimize the expenditure while guaranteeing the standards.

• (2) Adjustment of participation levels and long-term behavior

Note that there is evidence from behavioral economics that consumer’s choices need not be consistent with the maximization of a preference relation (see [9] and references therein). The reason for that is usually referred to as consumers’ bounded rationality. Classic examples include status-quo biases, attraction, compromise and framing effects, temptation and self-control, consideration sets, and choice overload. Due to the proposed approach, the demand operator is consistent with the long-term behavior of responsible consumers. In our model, the production and consumption bundles, the consumer’s wealths, and producers’ costs are considered as constant flows. This means that we get the same amount of corresponding objects in each standard interval of time (say, 1 week). Thus, our economy can be seen as stationary. If the income of a person or a firm during this interval is greater than the expenses, then he/she can ensure a constant rate of growth of the own capital. In this profitable case, we have: α _k (p) = β _i (p) = 1, i.e. producers and consumers implement their tentative bundles. If the income is strictly less than expenses, then the producer/consumer must leave the market sooner or later, i.e. α _k (p) = β _i (p) = 0. This is true both for producers (bankruptcy), and for consumers (emigration from this market). We refer to those agents as being bankrupt. If the regular income is equal to the regular expenses, then tentative production and consumption bundles may shrink due to participation levels α _k (p), β _i (p). In this marginal case, producers and consumers usually have α _k (p), β _i (p) ∈ (0, 1). With probability one they neither fully participate in economic activities nor quit the market. In what follows, we give a behavioral explanation on how α _k (p), β _i (p) are adjusted. Note that marginal agents reach their break-even point at current prices p, hence, they make neither a profit nor a loss. For a marginal producer it means that the corresponding profit is equal to the fixed costs: π _k (p) = κ _k . Net saving of a marginal consumer is zero, i.e. the own wealth is equal to the minimal possible expenditure: w _i  = e _i (p). Hence, for $\hat{p} \approx p$ the break-even point will be mainly shifted either to profitability or bankruptcy. This reflects the existence of poverty in the society. Marginal producers face at nearby prices $\hat{p} \approx p$

$$\displaystyle{\mbox{ either }\quad \pi _{k}(\hat{p})>\kappa _{k}\quad \mbox{ or }\quad \pi _{k}(\hat{p}) <\kappa _{k},}$$

and marginal consumers face

$$\displaystyle{\mbox{ either }\quad w_{i}> e_{i}(\hat{p})\quad \mbox{ or }\quad w_{i} <e_{i}(\hat{p}).}$$

Hence, sometimes marginal producers/consumers can implement their tentative bundles, i.e.

$$\displaystyle{\alpha _{k}(\hat{p}) = 1,\quad \beta _{i}(\hat{p}) = 1,}$$

and sometimes it is not possible, i.e.

$$\displaystyle{\alpha _{k}(\hat{p}) = 0,\quad \beta _{i}(\hat{p}) = 0.}$$

The particular 0–1 values of $\alpha _{k}(\hat{p})$ and $\beta _{i}(\hat{p})$ depend on the individual history of successes and failures for producers and consumers, respectively. To be more concrete, let us consider some price adjustment process $\hat{p}(t) \rightarrow p$ with discrete time t → ∞. Now, the participation levels α _k (p), β _i (p) can be viewed as frequencies of agents’ successful and failed attempts. Indeed, by averaging and taking the limit we obtain the participation levels:

$$\displaystyle{\frac{1} {t}\sum \limits _{s=1}^{t}\alpha _{ k}(\hat{p}(s)) \rightarrow \alpha _{k}(p),\quad \frac{1} {t}\sum \limits _{s=1}^{t}\beta _{ i}(\hat{p}(s)) \rightarrow \beta _{i}(p)\quad \mbox{ for }t \rightarrow \infty.}$$

This interpretation of participation levels as frequencies is based on the long-term behavior of the agents. Our analysis of the price adjustment process from Sect. 4 confirms this interpretation. Namely, the limits above actually define α _k (p), β _i (p) as frequencies obtained during the price adjustment.

Let us address the question why marginal agents do not quit the market although they eventually implement only a share of their tentative production/consumption bundles. As a consequence marginal producers do not fully exploit their available capacities and cannot cover the fixed costs. Marginal consumers do not spend all their available wealths and cannot reach the desirable levels of utility. Nevertheless, these agents stay at the market since they actually do not know that they are marginal. During the price adjustment, the only available information is their individual history of successes and failures while attempting to produce and to consume. With above notation, at time t they know a 0–1 sequence of $\alpha _{k}(\hat{p}(s))$ and $\beta _{i}(\hat{p}(s))$, s = 1, …, t. This particular history depends on many factors, as their luck, current prices, particular actions of other agents, etc. From time to time, marginal agents succeed to implement their tentative production/consumption bundles, but occasionally they fail. This unsure market environment causes marginal agents to temporally reduce consumption and to wait for “fair prices”. Such a behavior is typical for poor people, and we can treat their fractional participation levels α _k (p) and β _i (p) as a measure of poverty. A hidden, but very important, consequence of this marginal behavior is a possibility to clear the market as we shall see in Sect. 2.2. We conclude that the marginal agents play a crucial role in our approach to market modeling.

Overall, the participation levels α _k (p), β _i (p) are indicators of economic viability. These items account for most important, but non-standard features of our market model. Their inclusion is one of the chief novelties of the paper.

2.2 Equilibrium Market Flows

In accordance to the previous notations, we eventually say that the market flow

$$\displaystyle{\widetilde{F} = \left (\left (\tilde{y}_{k} =\alpha _{k}y_{k}\right )_{k=1}^{K},\left (\tilde{x}_{ i} =\beta _{i}x_{i}\right )_{i=1}^{I}\right )}$$

is defined by the triple (p, F, γ). Here, $p \in \mathbb{R}_{+}^{n}$ is the vector of prices,

$$\displaystyle{F = \left (\left (y_{k}\right )_{k=1}^{K},\left (x_{ i}\right )_{i=1}^{I}\right ) \in \prod _{ k=1}^{K}\mathcal{Y}_{ k} \times \prod _{i=1}^{I}\mathcal{X}_{ i}}$$

is the tentative market flow, and

$$\displaystyle{\gamma = \left (\left (\alpha _{k}\right )_{k=1}^{K},\left (\beta _{ i}\right )_{i=1}^{I}\right ) \in [0,1]^{K+I}}$$

is the proper system of participation levels (w.r.t. p and F), i.e.

$$\displaystyle{\alpha _{k} = \left \{\begin{array}{ll} 1,&\mbox{ if }\left \langle p,y_{k}\right \rangle - c_{k}(y_{k})>\kappa _{k}, \\ 0,&\mbox{ if }\left \langle p,y_{k}\right \rangle - c_{k}(y_{k}) <\kappa _{k} \end{array} \right.,\quad \beta _{i} = \left \{\begin{array}{ll} 1,&\mbox{ if }\left \langle p,x_{i}\right \rangle <w_{i}, \\ 0,&\mbox{ if }\left \langle p,x_{i}\right \rangle> w_{i}. \end{array} \right.}$$

Now we define the partial market equilibrium in the standard way.

Definition 1 (Market Equilibrium).

We say that $p^{{\ast}}\in \mathbb{R}^{n}$ is the equilibrium price if there exists a market flow

$$\displaystyle{\widetilde{F}^{{\ast}} = \left (\left (\tilde{y}_{ k}^{{\ast}} =\alpha _{ k}^{{\ast}}y_{ k}^{{\ast}}\right )_{ k=1}^{K},\left (\tilde{x}_{ i}^{{\ast}} =\beta _{ i}^{{\ast}}x_{ i}^{{\ast}}\right )_{ i=1}^{I}\right ) \in \prod _{ k=1}^{K}S_{ k}(p^{{\ast}}) \times \prod _{ i=1}^{I}D_{ i}(p^{{\ast}}),}$$

satisfying the market clearing condition

$$\displaystyle{ p^{{\ast}}\geq 0,\quad \sum _{ k=1}^{K}\tilde{y}_{ k}^{{\ast}}-\sum _{ i=1}^{I}\tilde{x}_{ i}^{{\ast}}\geq 0,\quad \left \langle p^{{\ast}},\sum _{ k=1}^{K}\tilde{y}_{ k}^{{\ast}}-\sum _{ i=1}^{I}\tilde{x}_{ i}^{{\ast}}\right \rangle = 0. }$$

(15)

In this case, $\widetilde{F}^{{\ast}}$ is called the equilibrium market flow. Setting

$$\displaystyle{\gamma ^{{\ast}} = \left (\left (\alpha _{ k}^{{\ast}}\right )_{ k=1}^{K},\left (\beta _{ i}^{{\ast}}\right )_{ i=1}^{I}\right ),}$$

we call $\left (p^{{\ast}},\gamma ^{{\ast}},\widetilde{F}^{{\ast}}\right )$ the market equilibrium.

The market clearing condition ( 15) states that the consumption never exceeds the production, and the markets of goods with positive prices (p ^(j) > 0) are perfectly cleared:

$$\displaystyle{\sum _{k=1}^{K}\tilde{y}_{ k}^{{\ast}(j)} =\sum _{ i=1}^{I}\tilde{x}_{ i}^{{\ast}(j)}.}$$

2.3 Principle of Least Revenue

Given a vector of prices $p \in \mathbb{R}_{+}^{n}$, producers maximize their profits and consumers minimize their expenditures. Afterwards, both properly adjust their participation levels by comparing the profits with the fixed costs, in case of producers, or by comparing the expenditures with the wealths, in case of consumers. Exactly the same behavior can be obtained by maximizing their excessive profits and excessive wealths, respectively.

The excessive profit of the kth producer is set as

$$\displaystyle{ \mathcal{E}_{k}(p)\mathop{ =}\limits^{\mathrm{ def}}\left (\pi _{k}(p) -\kappa _{k}\right )_{+} =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} y_{k} \in \mathcal{Y}_{k} \end{array} }\left (\left \langle p,y_{k}\right \rangle - c_{k}(y_{k}) -\kappa _{k}\right )_{+}. }$$

(16)

Using the substitution $\tilde{y}_{k} =\alpha _{k}y_{k}$, we obtain

$$\displaystyle{\mathcal{E}_{k}(p) = \left (\pi _{k}(p) -\kappa _{k}\right )_{+} =\mathop{ \mathrm{max}}\limits _{\alpha _{k}\in [0,1]}\alpha _{k}\left (\pi _{k}(p) -\kappa _{k}\right ) =}$$

$$\displaystyle{\mathop{\mathrm{max}}\limits _{\begin{array}{c} \alpha _{k} \in [0, 1] \\ y_{k} \in \mathcal{Y}_{k}\end{array} }\alpha _{k}\left (\left \langle p,y_{k}\right \rangle - c_{k}(y_{k}) -\kappa _{k}\right ) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \alpha _{k} \in [0, 1] \\ \tilde{y}_{k} \in \alpha _{k}\mathcal{Y}_{k} \end{array} }\left \langle p,\tilde{y}_{k}\right \rangle -\alpha _{k}c_{k}\left (\tilde{y}_{k}/\alpha _{k}\right )-\alpha _{k}\kappa _{k}.}$$

Note that the maximization problem

$$\displaystyle{\mathcal{E}_{k}(p) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \alpha _{k} \in [0, 1] \\ \tilde{y}_{k} \in \alpha _{k}\mathcal{Y}_{k} \end{array} }\left \langle p,\tilde{y}_{k}\right \rangle -\alpha _{k}c_{k}\left (\tilde{y}_{k}/\alpha _{k}\right )-\alpha _{k}\kappa _{k}}$$

is convex, and its set of optimal solutions consists of proper participation levels α _k and production bundles $\tilde{y}_{k}$. Moreover, $\mathcal{E}_{k}(p)$ is convex in p as the maximum of linear functions. Hence, the convex subdifferential of the excessive profit $\mathcal{E}_{k}$ gives the supply S _k of the kth producer, i.e.

$$\displaystyle{ \partial \mathcal{E}_{k}(p) = S_{k}(p). }$$

(17)

The latter follows e.g. from [22, Theorem 2.4.18] on the convex subdifferential of a max-type function.

Analogously, we define the excessive wealth of the ith consumer as follows:

$$\displaystyle{ \mathcal{E}_{i}(p)\mathop{ =}\limits^{\mathrm{ def}}\left (w_{i} - e_{i}(p)\right )_{+} =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} x_{i} \in \mathcal{X}_{i} \end{array} }\left (w_{i} -\left \langle p,x_{i}\right \rangle \right )_{+}. }$$

(18)

Using the substitution $\tilde{x}_{i} =\beta _{i}x_{i}$, we obtain

$$\displaystyle{\mathcal{E}_{i}(p) = \left (w_{i} - e_{i}(p)\right )_{+} =\mathop{ \mathrm{max}}\limits _{\beta _{i}\in [0,1]}\beta _{i}\left (w_{i} - e_{i}(p)\right ) =}$$

$$\displaystyle{\mathop{\mathrm{max}}\limits _{\begin{array}{c} \beta _{i} \in [0, 1] \\ x_{i} \in \mathcal{X}_{i}\end{array} }\beta _{i}\left (w_{i} -\left \langle p,x_{i}\right \rangle \right ) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \beta _{i} \in [0, 1] \\ \tilde{x}_{i} \in \beta _{i}\mathcal{X}_{i} \end{array} }\beta _{i}w_{i}-\left \langle p,\tilde{x}_{i}\right \rangle.}$$

Note that $\tilde{x}_{i} \in \beta _{i}\mathcal{X}_{i}$ means

$$\displaystyle{\tilde{x}_{i} \in \beta _{i}X_{i}\mbox{ and }u_{i}\left (\tilde{x}_{i}/\beta _{i}\right ) \geq \underline{ u}_{i}.}$$

In particular, the so-called perspective function $\beta _{i}u_{i}\left (\tilde{x}_{i}/\beta _{i}\right )$ is jointly concave in $\left (\tilde{x}_{i},\beta _{i}\right )$, e.g. [4]. The maximization problem

$$\displaystyle{\mathcal{E}_{i}(p) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \beta _{i} \in [0, 1] \\ \tilde{x}_{i} \in \beta _{i}\mathcal{X}_{i} \end{array} }\beta _{i}w_{i}-\left \langle p,\tilde{x}_{i}\right \rangle }$$

is convex, and its set of optimal solutions consists of proper participation levels β _i and consumption bundles $\tilde{x}_{i}$. Moreover, $\mathcal{E}_{i}(p)$ is convex in p as the maximum of linear functions. Hence, the convex subdifferential of the excessive wealth $\mathcal{E}_{i}$ gives the opposite demand D _i of the ith consumer, i.e.

$$\displaystyle{ \partial \mathcal{E}_{i}(p) = -D_{i}(p). }$$

(19)

The latter follows also from [22, Theorem 2.4.18].

Overall, we define the total excessive revenue as the sum of excessive profits and excessive wealths:

$$\displaystyle{ \mathcal{E}(p)\mathop{ =}\limits^{\mathrm{ def}}\sum _{k=1}^{K}\mathcal{E}_{ k}(p) +\sum _{ i=1}^{I}\mathcal{E}_{ i}(p). }$$

(20)

Note that function $\mathcal{E}(\cdot )$ is convex since it is a sum of convex functions. Moreover, its convex subdifferential represents the excess supply due to ( 17) and ( 19).

Remark 1 (Homogeneous Case).

For the homogeneous case we can give yet another explanation why marginal producers and consumers still stay at the market. Let us assume the homogeneity of the kth producer’s cost function c _k (⋅ ), and the homogeneity of the fixed cost κ _k (⋅ ), i.e.

$$\displaystyle{\kappa _{k}(\alpha \mathcal{Y}_{k}) =\alpha \kappa _{k}(\mathcal{Y}_{k}),\quad \alpha \in [0,1].}$$

Then,

$$\displaystyle{\mathcal{E}_{k}(p) =\mathop{ \mathrm{max}}\limits \limits _{\begin{array}{c} \alpha _{k} \in [0, 1],\tilde{y}_{k} \in \alpha _{k}\mathcal{Y}_{k} \end{array} }\left \langle p,\tilde{y}_{k}\right \rangle -c_{k}\left (\tilde{y}_{k}\right )-\kappa _{k}(\alpha _{k}\mathcal{Y}_{k}).}$$

For a marginal producer with $\mathcal{E}_{k}(p) = 0$, this means that his activity, even within the maximal technological set $\mathcal{Y}_{k}$ does not generate any profit. The situation is not changing if the production activities (the set $\mathcal{Y}_{k}$) will be proportionally reduced by a factor α _k  ∈ [0, 1]. Thus, it is natural to admit that in this marginal situation the producer can work with a reduced technological set $\alpha _{k}\mathcal{Y}_{k}$ by producing $\tilde{y}_{k} \in \alpha _{k}\mathcal{Y}_{k}$. By doing so, he cannot cover the share (1 −α _k )κ _k of the fixed cost. However, his unused capacities amounting to $(1 -\alpha _{k})\mathcal{Y}_{k}$ can be eventually exploited at other markets.

Now, we assume the homogeneity of the ith consumer’s utility function u _i (⋅ ), and that $X_{i} = \mathbb{R}_{+}^{n}$. Then,

$$\displaystyle{\mathcal{E}_{i}(p) =\mathop{ \mathrm{max}}\limits \limits _{\begin{array}{c} \beta _{i} \in [0, 1],\,\tilde{x}_{i} \geq 0 \\ u_{i}\left (\tilde{x}_{i}\right ) \geq \beta _{i}\underline{u}_{i} \end{array} }\beta _{i}w_{i}-\left \langle p,\tilde{x}_{i}\right \rangle.}$$

If the excessive wealth of a consumer is zero, then again, there is no special reason to allocate all the wealth w _i to this expensive market. The consumer can admit to spend here only a part of it, namely β _i w _i with some β _i  ∈ [0, 1], which is sufficient to guarantee the share β _i u _i of his desirable utility level. Note that this does not change the zero level of the excessive wealth. The remaining part (1 −β _i )w _i of the wealth can be used then at other markets. □ 

By application of [15, Theorem 23.8] on the subdifferential of the sum of convex functions, we obtain:

Theorem 1 (Excess Supply and Total Excessive Revenue).

For $p \in \mathbb{R}_{+}^{n}$ it holds:

$$\displaystyle{\partial \mathcal{E}(p) =\sum _{ k=1}^{K}S_{ k}(p) -\sum _{i=1}^{I}D_{ i}(p).}$$

Proof.

We apply [15, Theorem 23.8] on the subdifferential of the sum of convex functions in order to obtain

$$\displaystyle{\partial \mathcal{E}(p) =\sum _{ k=1}^{K}\partial \mathcal{E}_{ k}(p) -\sum _{i=1}^{I}\partial \mathcal{E}_{ i}(p).}$$

Together with ( 17) and ( 19) the assertion follows. □ 

Theorem 1 allows us to characterize equilibrium prices as minimizers of $\mathcal{E}$.

Theorem 2 (Principle of Least Revenue).

$p \in \mathbb{R}_{+}^{n}$ is a system of equilibrium prices if and only if it solves the following convex minimization problem:

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p). }$$

(P)

Proof.

• 1. Assume that $p^{{\ast}}\in \mathbb{R}^{n}$ is an equilibrium prices. Then, in view of Definition 1, there exists an equilibrium market flow

  $$\displaystyle{\widetilde{F}^{{\ast}} = \left (\left (\tilde{y}_{ k}^{{\ast}}\right )_{ k=1}^{K},\left (\tilde{x}_{ i}^{{\ast}}\right )_{ i=1}^{I}\right ) \in \prod _{ k=1}^{K}S_{ k}(p^{{\ast}}) \times \prod _{ i=1}^{I}D_{ i}(p^{{\ast}}),}$$

  satisfying the market clearing condition

  $$\displaystyle{p^{{\ast}}\geq 0,\quad \sum _{ k=1}^{K}\tilde{y}_{ k}^{{\ast}}-\sum _{ i=1}^{I}\tilde{x}_{ i}^{{\ast}}\geq 0,\quad \left \langle p^{{\ast}},\sum _{ k=1}^{K}\tilde{y}_{ k}^{{\ast}}-\sum _{ i=1}^{I}\tilde{x}_{ i}^{{\ast}}\right \rangle = 0.}$$

  Denote $\zeta ^{{\ast}} =\sum _{ k=1}^{K}\tilde{y}_{k} -\sum _{i=1}^{I}\tilde{x}_{i}$. In view of Theorem 1, $\zeta ^{{\ast}}\in \partial \mathcal{E}(p^{{\ast}})$. Since $\mathcal{E}$ is convex in p, for all $p \in \mathbb{R}_{+}^{n}$ we have:

  $$\displaystyle{\mathcal{E}(p) -\mathcal{E}(p^{{\ast}}) \geq \left \langle \zeta ^{{\ast}},p - p^{{\ast}}\right \rangle = \left \langle \zeta ^{{\ast}},p\right \rangle \geq 0.}$$

  Thus, p ^∗ minimizes the total excessive revenue.

• 2. Assume that $p^{{\ast}}\in \mathbb{R}_{+}^{n}$ is optimal for the minimization problem ( P). Then there exists $\zeta ^{{\ast}}\in \partial \mathcal{E}(p^{{\ast}})$ such that

  $$\displaystyle{\left \langle \zeta ^{{\ast}},p - p^{{\ast}}\right \rangle \geq 0,\quad \mbox{ for all }p \in \mathbb{R}_{ +}^{n}.}$$

  Considering p = 0 and p = 2p ^∗, we conclude that $\left \langle \zeta ^{{\ast}},p^{{\ast}}\right \rangle = 0$. Consequently, $\zeta ^{{\ast}}\in \mathbb{R}_{+}^{n}$. Again due to Theorem 1, there exists a market flow

  $$\displaystyle{\widetilde{F}^{{\ast}} = \left (\left (\tilde{y}_{ k}^{{\ast}}\right )_{ k=1}^{K},\left (\tilde{x}_{ i}^{{\ast}}\right )_{ i=1}^{I}\right ) \in \prod _{ k=1}^{K}S_{ k}(p^{{\ast}}) \times \prod _{ i=1}^{I}D_{ i}(p^{{\ast}}),}$$

  such that

  $$\displaystyle{\zeta ^{{\ast}} =\sum _{ k=1}^{K}\tilde{y}_{ k}^{{\ast}}-\sum _{ i=1}^{I}\tilde{x}_{ i}^{{\ast}}.}$$

  Hence, $\widetilde{F}^{{\ast}}$ satisfies the market clearing condition, meaning that it is actually an equilibrium market flow. In view of Definition 1, p ^∗ is an equilibrium price. □ 

2.4 Existence

Theorem 2 says that equilibrium prices correspond to optimal solutions for the minimization problem:

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p). }$$

(P)

This is the key to provide existence results for equilibrium prices. We denote by P ^∗ the set of equilibrium prices. Let us introduce productive markets, at which the set of equilibrium prices P ^∗ turns out to be nonempty and bounded.

Definition 2 (Productive Market).

A market is called productive if there exist subsets of producers $\mathcal{K}\subset \{ 1,\ldots,K\}$ and consumers $\mathcal{L}\subset \{ 1,\ldots,L\}$, such that the corresponding production and consumption flows

$$\displaystyle{\left (\left \{\bar{y}_{k}\right \}_{k\in \mathcal{K}},\left \{\bar{x}_{i}\right \}_{i\in \mathcal{L}}\right ) \in \prod \limits _{k\in \mathcal{K}}\mathcal{Y}_{k} \times \prod \limits _{i\in \mathcal{L}}\mathcal{X}_{i}}$$

establish positive balances for goods:

$$\displaystyle{ \begin{array}{rcl} \sum _{k\in \mathcal{K}}\bar{y}_{k}&>&\sum _{i\in \mathcal{L}}\bar{x}_{i}. \end{array} }$$

(21)

The market productivity means that there are some producers who can oversupply some consumers’ needs.

Theorem 3 (Existence and Boundedness of Equilibrium Prices).

At the productive markets, the set of equilibrium prices P ^∗ is nonempty and bounded.

Proof.

Due to Theorem 2, equilibrium prices in P ^∗ form the set of optimal solutions of the minimization problem ( P). We show that the latter set is bounded. For that, it is sufficient to prove that the level sets of function $\mathcal{E}(\cdot )$ are bounded. Denote $\bar{\xi }=\sum \limits _{k\in \mathcal{K}}\bar{y}_{k} -\sum \limits _{i\in \mathcal{L}}\bar{x}_{i}$. For all $p \in \mathbb{R}_{+}^{n}$ we have

$$\displaystyle{\begin{array}{rcl} \mathcal{E}(p)& =&\sum \limits _{k=1}^{K}\left [\pi (p) -\kappa _{k}\right ]_{+} +\sum \limits _{ i=1}^{L}\left [w_{i} - e_{i}(p)\right ]_{+}\\ \\ & \geq &\sum \limits _{k\in \mathcal{K}}\left [\pi (p) -\kappa _{k}\right ]_{+} +\sum \limits _{i\in \mathcal{L}}\left [w_{i} - e_{i}(p)\right ]_{+}\\ \\ & \geq &\sum \limits _{k\in \mathcal{K}}\pi (p) -\kappa _{k} +\sum \limits _{i\in \mathcal{L}}w_{i} - e_{i}(p)\\ \\ & \geq &\sum \limits _{k\in \mathcal{K}}\left (\langle p,\bar{y}_{k}\rangle - c_{k}(\bar{y}_{k}) -\kappa _{k}\right ) +\sum \limits _{i\in \mathcal{L}}\left (w_{i} -\langle p,\bar{x}_{i}\rangle \right )\\ \\ & =& -\sum \limits _{k\in \mathcal{K}}\left (\kappa _{k} + c_{k}(\bar{y}_{k})\right ) +\sum \limits _{i\in \mathcal{L}}w_{i} + \left \langle \bar{\xi },p\right \rangle. \end{array} }$$

Since $\bar{\xi }> 0$, the intersection of the level sets of function $\mathcal{E}$ with $\mathbb{R}_{+}^{n}$ is bounded.

As a direct consequence of Theorem 2, we state the following result.

Theorem 4 (Convexity of Equilibrium Prices).

The set of equilibrium prices P ^∗ is convex.

Further, we formulate additional assumptions in order to guarantee that our market indeed works, i.e. the equilibrium prices do not vanish. Due to Theorem 2, we need to ensure that the optimal solution p ^∗ of the minimization problem ( P) is not at the origin. For that, we introduce the following condition rejecting the Zero-Cost Production (ZCP):

$$\displaystyle{ \mbox{ If $\alpha _{k}\kappa _{k} +\alpha _{k}c_{k}\left (\tilde{y}_{k}/\alpha _{k}\right ) = 0$ with $\tilde{y}_{k} \in \alpha _{k}\mathcal{Y}_{k}$ and $\alpha _{k} \in [0,1]$, then $\tilde{y}_{k} = 0$.} }$$

(22)

This condition is automatically satisfied for κ _k  > 0. If κ _k  = 0, then ( 22) implies that for the kth producer there is no nonzero production plan with zero production cost. Recall that

$$\displaystyle{ \mathcal{E}_{k}(p) =\mathop{ \mathrm{max}}\limits \limits _{\begin{array}{c} \alpha _{k} \in [0, 1] \\ \tilde{y}_{k} \in \alpha _{k}\mathcal{Y}_{k} \end{array} }\left \langle p,\tilde{y}_{k}\right \rangle -\alpha _{k}c_{k}\left (\tilde{y}_{k}/\alpha _{k}\right )-\alpha _{k}\kappa _{k}, }$$

(23)

Therefore, condition ( 22) implies that $\partial \mathcal{E}_{k}(0) =\{ 0\}$. Note that $\tilde{y}_{k} = 0$ if α _k  = 0 in ( 23), hence, the term $\alpha _{k}c_{k}\left (\tilde{y}_{k}/\alpha _{k}\right )$ is set to vanish in this case.

Assume now that the wealth w _i of ith consumer is positive. Since

$$\displaystyle{\mathcal{E}_{i}(p) =\mathop{ \mathrm{max}}\limits \limits _{\begin{array}{c} \beta _{i} \in [0, 1] \\ \tilde{x}_{i} \in \beta _{i}\mathcal{X}_{i} \end{array} }[\beta _{i}w_{i}-\left \langle p,x_{i}\right \rangle,}$$

we conclude that $\partial \mathcal{E}_{i}(0) = -\mathcal{X}_{i}$. Thus, we have proved the following statement.

Lemma 1.

Let all producers satisfy ZCP-condition, and the wealths of all consumers be positive. Then,

$$\displaystyle{ \begin{array}{rcl} \partial \mathcal{E}(0)& =& -\sum \limits _{i=1}^{L}\mathcal{X}_{i}. \end{array} }$$

(24)

Corollary 1 (Nonzero Equilibrium Prices).

Existence of a consumer with nonzero life standard is sufficient for having p ^∗ ≠ 0.

Proof.

Indeed, assume that p ^∗ = 0. In view of the first-order optimality conditions for ( P), there exists $\xi ^{{\ast}} \in \partial \mathcal{E}(0)$ such that

$$\displaystyle{\begin{array}{rcl} \left \langle \xi ^{{\ast}},p\right \rangle & \geq &0\quad \forall p \geq 0. \end{array} }$$

Hence, $\xi ^{{\ast}} = -\sum \limits _{i=1}^{L}x_{i}^{{\ast}}\geq 0$ for some $x_{i}^{{\ast}}\in \mathcal{X}_{i}$. Therefore, all x _i ^∗ = 0, implying zero life standards for all consumers.

It is interesting that the last statement is formulated only in terms of consumption standards. This confirms the primary role of demand in generating supply.

2.5 Efficiency

Let us present the first welfare theorem for equilibrium market flow. We are going to prove that any equilibrium market flow is efficient in the sense of Pareto optimality. This means that no producers or consumers can improve the gain (excessive profits and excessive wealths, respectively) without worsening the gain of some others. Let us start from the definition of feasible market flows.

We recall that for a given vector of prices $p \in \mathbb{R}_{+}^{n}$ and a tentative market flow

$$\displaystyle{F = \left (\left \{y_{k}\right \}_{k=1}^{K},\left \{x_{ i}\right \}_{i=1}^{L}\right ) \in \prod _{ k=1}^{K}\mathcal{Y}_{ k} \times \prod _{i=1}^{L}\mathcal{X}_{ i},}$$

the system of participation levels $\gamma = \left (\left \{\alpha _{k}\right \}_{k=1}^{K},\left \{\beta _{i}\right \}_{i=1}^{L}\right ) \in [0,1]^{K+L}$ is called proper (with respect to π and F) if it satisfies the following conditions:

$$\displaystyle{\begin{array}{lcl} \alpha _{k}& =&\left \{\begin{array}{ll} 1,&\mathrm{if}\ \langle p,y_{k}\rangle - c_{k}(y_{k})>\kappa _{k}, \\ 0,&\mathrm{if}\ \langle p,y_{k}\rangle - c_{k}(y_{k}) <\kappa _{k}, \end{array} \right.\\ & & \\ \beta _{i} & =&\left \{\begin{array}{ll} 1,&\mathrm{if}\ \langle p,x_{i}\rangle <w_{i}, \\ 0,&\mathrm{if}\ \langle p,x_{i}\rangle> w_{i}.\\ \end{array} \right. \end{array}}$$

Such a triple (p, F, γ) defines a real market flow

$$\displaystyle{\widetilde{F} = \left (\left \{\tilde{y}_{k} =\alpha _{k}y_{k}\right \}_{k=1}^{K},\left \{\tilde{x}_{ i} =\beta _{i}x_{i}\right \}_{i=1}^{L}\right ).}$$

Definition 3 (Feasible Market Flow).

The real market flow

$$\displaystyle{\widetilde{F} = \left (\left \{\tilde{y}_{k}\right \}_{k=1}^{K},\left \{\tilde{x}_{ i}\right \}_{i=1}^{L}\right ),}$$

defined by the triple (p, F, γ), is called feasible if it satisfies the market clearing condition:

$$\displaystyle{p \geq 0,\quad \sum _{k=1}^{K}\tilde{y}_{ k} -\sum _{i=1}^{I}\tilde{x}_{ i} \geq 0,\quad \left \langle p,\sum _{k=1}^{K}\tilde{y}_{ k} -\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle = 0.}$$

Note that an equilibrium market flow is in particular feasible.

Definition 4 (Pareto Optimal Market Flow).

A feasible market flow $\widetilde{F}$, defined by the triple

$$\displaystyle{\begin{array}{c} \left (p,F = \left (\left \{y_{k}\right \}_{k=1}^{K},\left \{x_{i}\right \}_{i=1}^{L}\right ),\gamma \right ), \end{array} }$$

is called Pareto optimal if there is no feasible market flow $\widetilde{F}'$ defined by another triple

$$\displaystyle{\begin{array}{c} \left (p',F' = \left (\left \{y_{k}'\right \}_{k=1}^{K},\left \{x_{i}'\right \}_{i=1}^{L}\right ),\gamma '\right ) \end{array} }$$

such that all inequalities

$$\displaystyle{ \begin{array}{rcl} (\left \langle p',y_{k}'\right \rangle - c_{k}(y_{k}') -\kappa _{k})_{+} & \geq &(\left \langle p,y_{k}\right \rangle - c_{k}(y_{k}) -\kappa _{k})_{+},k = 1\ldots K,\\ \\ (w_{i} -\left \langle p',x_{i}'\right \rangle )_{+} & \geq &(w_{i} -\left \langle p,x_{i}\right \rangle )_{+},\,i = 1\ldots L,\\ \end{array} }$$

(25)

are satisfied, and at least one of them is strict.

Note that we define Pareto optimality with respect to excessive profits and excessive wealths. In our model they play a role of objective functions of the agents.

Theorem 5 (Efficiency of Equilibrium Market Flows).

Any equilibrium market flow is Pareto optimal.

Proof.

Using notation of Definition 4, let $\widetilde{F}^{{\ast}}$ be the equilibrium market flow defined by the triple (p ^∗, F ^∗, γ ^∗). Assume that the inequalities ( 25) are all valid for some feasible market flow $\widetilde{F}'$ defined by the triple (p′, F′, γ′). And let at least one of these inequalities be strict. For $p \in \mathbb{R}_{+}^{n}$ and $F \in \varOmega \mathop{=}\limits^{\mathrm{ def}}\prod _{k=1}^{K}\mathcal{Y}_{k} \times \prod _{i=1}^{L}\mathcal{X}_{i}$, define the function

$$\displaystyle{\varphi (p,F) =\sum \limits _{ k=1}^{K}(\left \langle p,y_{ k}\right \rangle - c_{k}(y_{k}) -\kappa _{k})_{+} +\sum \limits _{ i=1}^{L}(w_{ i} -\left \langle p,x_{i}\right \rangle )_{+}.}$$

In view of our assumption, φ(p′, F′) > φ(p ^∗, F ^∗). Since p ^∗ is an equilibrium price, in view of Theorem 2 and definitions ( 16), ( 18) we have:

$$\displaystyle{\varphi (p^{{\ast}},F^{{\ast}}) =\mathop{ \mathrm{min}}\limits \limits _{ p\geq 0} \mathop{ \mathrm{max}}\limits \limits _{F\in \varOmega }\varphi (p,F) =\mathop{ \mathrm{max}}\limits \limits _{F\in \varOmega } \mathop{\mathrm{min}}\limits \limits _{p\geq 0}\varphi (p,F) \geq \mathop{\mathrm{min}}\limits \limits _{p\geq 0}\varphi (p,F').}$$

It remains to note that the market clearance condition for the flow $\widetilde{F}'$ is exactly the necessary and sufficient characterization of point p′ as the optimal solution to the latter minimization problem. Therefore, φ(p ^∗, F ^∗) ≥ φ(p′, F′), a contradiction.

In view of Theorem 2, equilibrium prices minimize the total excessive revenue. Let us prove a very intuitive result that its optimal value is equal to the difference of the real consumers’ wealths and the real producers’ costs.

Theorem 6 (Total Excessive Revenue of the Market).

Let p ^∗ be an equilibrium price, and

$$\displaystyle{\widetilde{F}^{{\ast}} = \left (\left (\tilde{y}_{ k}^{{\ast}} =\alpha _{ k}^{{\ast}}y_{ k}^{{\ast}}\right )_{ k=1}^{K},\left (\tilde{x}_{ i}^{{\ast}} =\beta _{ i}^{{\ast}}x_{ i}^{{\ast}}\right )_{ i=1}^{I}\right )}$$

be an equilibrium market flow defined by the triple (p ^∗ ,F ^∗ ,γ ^∗ ). Then,

$$\displaystyle{\mathcal{E}(p^{{\ast}}) =\sum \limits _{ i=1}^{I}\beta _{ i}^{{\ast}}w_{ i} -\sum \limits _{k=1}^{K}\alpha _{ k}^{{\ast}}(c_{ k}(y_{k}^{{\ast}}) +\kappa _{ k}) \geq 0.}$$

Proof.

It holds:

$$\displaystyle{\begin{array}{rcl} \mathcal{E}(p^{{\ast}})& =&\sum \limits _{k=1}^{K}\left (\left \langle p^{{\ast}},y_{k}^{{\ast}}\right \rangle - c_{k}(u_{k}^{{\ast}}) -\kappa _{k}\right )_{+} +\sum \limits _{ i=1}^{I}\left (w_{i} -\left \langle p^{{\ast}},x_{i}^{{\ast}}\right \rangle \right )_{+}\\ \\ & =&\sum \limits _{k=1}^{K}\alpha _{k}^{{\ast}}\left (\left \langle p^{{\ast}},y_{k}^{{\ast}}\right \rangle - c_{k}(u_{k}^{{\ast}}) -\kappa _{k}\right ) +\sum \limits _{ i=1}^{I}\beta _{i}^{{\ast}}\left (w_{i} -\left \langle p^{{\ast}},x_{i}^{{\ast}}\right \rangle \right )\\ \\ & =&\left \langle p^{{\ast}},\sum \limits _{k=1}^{K}\alpha _{k}^{{\ast}}y_{k}^{{\ast}}-\sum \limits _{i=1}^{I}\beta _{i}^{{\ast}}x_{i}^{{\ast}}\right \rangle -\sum \limits _{k=1}^{K}\alpha _{k}^{{\ast}}(c_{k}(y_{k}^{{\ast}}) +\kappa _{k}) +\sum \limits _{ i=1}^{I}\beta _{i}^{{\ast}}w_{i}^{{\ast}}. \end{array} }$$

In view of the market clearance condition, we have

$$\displaystyle{\begin{array}{c} \left \langle p^{{\ast}},\sum \limits _{k=1}^{K}\alpha _{k}^{{\ast}}y_{k}^{{\ast}}-\sum \limits _{i=1}^{I}\beta _{i}^{{\ast}}x_{i}^{{\ast}}\right \rangle = 0. \end{array} }$$

This gives us the desired expression for optimal value of $\mathcal{E}$. It is nonnegative since all terms in its definition ( 20) are nonnegative.

Note that the nonnegative value

$$\displaystyle{ \begin{array}{rcl} \mathcal{E}(p^{{\ast}}) =\sum \limits _{ i=1}^{I}\beta _{i}^{{\ast}}w_{i} -\sum \limits _{k=1}^{K}\alpha _{k}^{{\ast}}(c_{k}(y_{k}^{{\ast}}) +\kappa _{k}) \end{array} }$$

(26)

represents the total rate of accumulation of the capital within the market. In general, equilibrium prices, market flows, and participation levels are not unique. Nevertheless, all of them ensure the same value of $\mathcal{E}^{{\ast}}\mathop{ =}\limits^{\mathrm{ def}}\mathcal{E}(p^{{\ast}})$. We call it the total excessive revenue of the market.

2.6 Welfare Maximization

In order to state the adjoint problem for ( P), we set

$$\displaystyle{\alpha \mathop{=}\limits^{\mathrm{ def}}\left \{\alpha _{k}\right \}_{k=1}^{K},\tilde{y}\mathop{ =}\limits^{\mathrm{ def}}\left \{\tilde{y}_{ k}\right \}_{k=1}^{K},\beta \mathop{=}\limits^{\mathrm{ def}}\left \{\beta _{ i}\right \}_{i=1}^{I},\tilde{x}\mathop{ =}\limits^{\mathrm{ def}}\left \{\tilde{x}_{ i}\right \}_{i=1}^{I},}$$

$$\displaystyle{\mathcal{Y}\mathop{ =}\limits^{\mathrm{ def}}\prod _{k=1}^{K}\mathcal{Y}_{ k},\alpha \mathcal{Y}\mathop{ =}\limits^{\mathrm{ def}}\prod _{k=1}^{K}\alpha _{ k}\mathcal{Y}_{k},\mathcal{X}\mathop{ =}\limits^{\mathrm{ def}}\prod _{i=1}^{I}\mathcal{X}_{ i},\beta \mathcal{X}\mathop{ =}\limits^{\mathrm{ def}}\prod _{i=1}^{I}\beta _{ i}\mathcal{X}_{i}.}$$

Here, α, β represent participation levels, and $\tilde{y}$, $\tilde{x}$ represent production and consumption bundles, respectively. Moreover, $\alpha \mathcal{Y}$, $\beta \mathcal{X}$ represent production and consumption sets given the participation levels α, β, respectively.

The feasible set of the adjoint problem is formed by participation levels and corresponding production and consumption bundles, i.e.

$$\displaystyle{\mathcal{A}\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (\alpha,\tilde{y},\beta,\tilde{x}\right )\,\left \vert \,\begin{array}{l} \left (\alpha,\tilde{y}\right ) \in [0,1]^{K} \times \alpha \mathcal{Y} \\ \left (\beta,\tilde{x}\right ) \in [0,1]^{I} \times \beta \mathcal{X} \end{array} \right.\right \}.}$$

Note that the set A is convex. Further, the following market feasibility constraint needs to be satisfied:

$$\displaystyle{ \sum _{k=1}^{K}\tilde{y}_{ k} \geq \sum _{i=1}^{I}\tilde{x}_{ i}, }$$

(27)

meaning that the aggregate consumption does not exceed the aggregate production. The objective function of the adjoint problem is

$$\displaystyle{\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\mathop{ =}\limits^{\mathrm{ def}}\sum _{i=1}^{I}\beta _{ i}w_{i} -\sum _{k=1}^{K}\alpha _{ k}c_{k}\left (\tilde{y}_{k}/\alpha _{k}\right ) +\alpha _{k}\kappa _{k},}$$

expressing the difference between the aggregate wealth spent for consumption and producers’ costs. Finally, we consider the welfare maximization problem

$$\displaystyle{ \mathop{\mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A}\end{array} }\left \{\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\,\left \vert \,\begin{array}{l} \sum _{k=1}^{K}\tilde{y}_{k} \geq \sum _{i=1}^{I}\tilde{x}_{i} \end{array} \right.\right \}. }$$

(A)

In ( A) the central authority assigns production and consumption bundles, as well as agents’ participation levels. Moreover, it maximizes the welfare of the society while ensuring the market feasibility. In order to state ( A), the central authority needs to know agents’ cost and utility functions, production and consumption sets, etc. Obviously, this information about the agents is hardly observable to the central authority. Consequently, it cannot be justified in general that the welfare maximization problem is tackled directly. Nevertheless, note that the prices of goods play the role of Lagrange or dual multipliers for the market feasibility constraint ( 27), cf. already [3, 16] for similar interpretations. Hence, due to the duality theory of convex programming, the welfare maximization ( A) is the adjoint problem for ( P).

Theorem 7 (Adjoint for ( P)).

The welfare maximization ( A ) is adjoint for the total revenue minimization ( P ):

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A} \end{array} }\left \{\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\,\left \vert \,\begin{array}{l} \sum _{k=1}^{K}\tilde{y}_{k} \geq \sum _{i=1}^{I}\tilde{x}_{i} \end{array} \right.\right \}.}$$

We note that the productivity of the market from Definition 2 implies the standard Slater condition for the adjoint problem ( A).

We emphasize that the adjoint problem ( A) of the welfare maximization can hardly be solved directly. In order to construct its feasible set $\mathcal{A}$ and its objective function Φ, a central authority should acquire the knowledge on producers’ costs and their production sets, on consumers’ utility functions and their consumption sets. It is clear that this is implementable only within a planned economy. Even in this case, as we know e.g. from the history of communistic countries, producers and consumers are reluctant to report their market constants to the authority. In fact, they feel rather antagonistic about each other and about the authority, thus, trying to keep their information private. In turn, our approach concentrates on the total revenue minimization problem ( P). By doing so, we explain how the free market provides a welfare maximizing solution by a decentralized price adjustment. Here, producers and consumers report only their individual supplies and demands to each other while trading or auctioning. There is no need in a central authority, since the price updates are performed by producers, in case of trade, and by consumers, in case of auction. Finally, the price adjustment balances agents’ antagonistic behavior leading to a market equilibrium.

3 Quasi-Monotone Subgradient Method

We first present quasi-monotone subgradient methods for nonsmooth convex minimization from [13]. For that, we consider the following minimization problem:

$$\displaystyle{ f^{{\ast}}\mathop{ =}\limits^{\mathrm{ def}}\mathop{\mathrm{min}}\limits _{ x\in X}f(x), }$$

(28)

where $X \subset \mathbb{R}^{n}$ is a closed convex set with nonempty interior int X, and f is a convex function on $\mathbb{R}^{n}$. Moreover, let f be representable as a maximum of concave functions, i.e.

$$\displaystyle{ f(x) =\mathop{ \mathrm{max}}\limits _{a\in A}\varPhi (a) +\varphi (x,a), }$$

(29)

where $A \subset \mathbb{R}^{m}$ is a compact convex set, φ(⋅ , a) is a convex function on $\mathbb{R}^{n}$ for every a ∈ A, and Φ, φ(x, ⋅ ) are concave functions on $\mathbb{R}^{m}$ for every x ∈ X. Denote by a(x) one of the optimal solutions of the maximization problem in ( 29). Then,

$$\displaystyle{ \nabla f(x)\mathop{ =}\limits^{\mathrm{ def}}\nabla _{x}\varphi (x,a(x)) }$$

(30)

denotes a subgradient of f at x. This formula follows from the result on the subdifferential of a max-type function, e.g. [22, Theorem 2.4.18]. Recall that for an arbitrary subgradient ∇f(x) at x ∈ X of a convex function f we have:

$$\displaystyle{ f(y) \geq f(x) +\langle \nabla f(x),y - x\rangle,\quad y \in X. }$$

(31)

Using the representation ( 29), we also have:

$$\displaystyle{f^{{\ast}} =\mathop{ \mathrm{min}}\limits _{ x\in X}f(x) =\mathop{ \mathrm{min}}\limits _{x\in X}\mathop{ \mathrm{max}}\limits _{a\in A}\left [\varPhi (a) +\varphi (x,a)\right ] =\mathop{ \mathrm{max}}\limits _{a\in A}\left [\varPhi (a) +\mathop{ \mathrm{min}}\limits _{x\in X}\varphi (x,a)\right ].}$$

The latter maximization problem

$$\displaystyle{ \mathop{\mathrm{max}}\limits _{a\in A}\left [\varPhi (a) +\mathop{ \mathrm{min}}\limits _{x\in X}\varphi (x,a)\right ] }$$

(32)

is called adjoint for ( 28) with the adjoint variable a ∈ A.

For the set X, we assume to be known a prox-function d(x).

Definition 5.

$d: X\mapsto \mathbb{R}$ is called a prox-function for X if the following holds:

• d(x) ≥ 0 for all x ∈ X and d(x[0]) = 0 for certain x[0] ∈ X;

• d is strongly convex on X with convexity parameter one:

  $$\displaystyle{ d(y) \geq d(x) +\langle \nabla d(x),y - x\rangle + \frac{1} {2}\|y - x\|^{2},\quad x,y \in X, }$$

  (33)

  where ∥ ⋅ ∥ is a norm on $\mathbb{R}^{n}$.

• Auxiliary minimization problem

  $$\displaystyle{ \mathop{\mathrm{min}}\limits _{x\in X}\left \{\langle z,x\rangle +\chi d(x)\right \} }$$

  (34)

  is easily solvable for $z \in \mathbb{R}^{n},\chi> 0$.

As a simple consequence of Definition 5, we have for x ∈ X:

$$\displaystyle{ d(x) \geq d(x[0]) + \left \langle \nabla d(x[0]),x - x[0]\right \rangle + \frac{1} {2}\|x - x[0]\|^{2} \geq \frac{1} {2}\|x - x[0]\|^{2}. }$$

(35)

For a sequence of positive parameters $\left \{\chi [t]\right \}_{t\geq 0}$, we consider the following iteration:

$$\displaystyle{ \begin{array}{|c|}\hline\\ \begin{array}{c} \mathbf{Quasi-monotone\ Subgradient\ Method} \end{array}\\\hline \\ \begin{array}{ll} \mathbf{1.}\ \text{Take a current subgradient}\ \nabla f(x[t]) = \nabla _{x}\varphi (x[t],a(x[t])).\\ \\ \mathbf{2.}\ \text{Accumulate subgradients}\ z[t] = z[t - 1] + \nabla f(x[t]),z[-1] = 0.\\ \\ \mathbf{3.}\ \text{Compute the forecast}\ x^{+}[t] = \mbox{ arg}\mathop{\mathrm{min}}\limits _{ x\in X}\left \{\left \langle z[t],x\right \rangle +\chi [t]d(x)\right \}.\\ \\ \mathbf{4.}\ \text{Update by combining}\ x[t + 1] = \frac{t + 1} {t + 2}x[t] + \frac{1} {t + 2}x^{+}[t]. \\ \end{array}\\ \\\hline \end{array} }$$

(SM)

Note that from ( SM) we have

$$\displaystyle{z[t] =\sum _{ r=0}^{t}\nabla f(x[r]),\quad x[t + 1] = \frac{1} {t + 2}\left (x[0] +\sum _{ r=0}^{t}x^{+}[r]\right ).}$$

Next Lemma 2 is crucial for the convergence analysis of the quasi-monotone subgradient method ( SM). It estimates the dual gap for the minimization problem ( 28) and its adjoint problem ( 32) evaluated at the historical averages.

For that, we define the penalty term δ _t and the remainder term ρ _t , t ≥ 0, as follows:

$$\displaystyle{\begin{array}{lcl} \delta _{t}(a)&\mathop{ =}\limits^{\mathrm{ def}}& -\mathop{\mathrm{min}}\limits _{x\in X}\left \{\varphi (x,a) + \frac{\chi [t]} {t + 1}d(x)\right \},\quad a \in A, \\ \rho _{t} &\mathop{ =}\limits^{\mathrm{ def}}& \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {2\chi [r - 1]}\left \|\nabla f(x[r])\right \|_{{\ast}}^{2},\quad \chi [-1] =\chi [0]. \\ \end{array} }$$

Here, ∥ ⋅ ∥ _∗ is the conjugate norm to ∥ ⋅ ∥ , i.e.

$$\displaystyle{ \|s\|_{{\ast}}\mathop{ =}\limits^{\mathrm{ def}}\mathop{\mathrm{max}}\limits _{s\in \mathbb{R}^{n}}\left \{\langle s,x\rangle:\| x\| \leq 1\right \},\quad s \in \mathbb{R}^{n}. }$$

(36)

Further, we define the average adjoint state

$$\displaystyle{a[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}a(x[r]),\quad t \geq 0.}$$

Note that a[t] ∈ A, since A is convex.

Lemma 2 is motivated by the estimate sequence technique (e.g., Sect. 2.2.1 in [10]) and is due to [13]. For the readers’ convenience its proof is postponed to Appendix.

Lemma 2.

Let the sequence $\left \{x[t]\right \}_{t\geq 0}$ be generated by ( SM ) with nondecreasing parameters

$$\displaystyle{ \chi [t + 1] \geq \chi [t],\quad t \geq 0. }$$

(37)

Then, for all t ≥ 0 it holds:

$$\displaystyle{ f(x[t]) -\varPhi (a[t]) +\delta _{t}(a[t]) \leq \rho _{t}. }$$

(38)

We apply the quasi-monotone subgradient method ( SM) in the following setup ( S1)–( S3). Let $X = \mathbb{R}_{+}^{n}$ be equipped with the Euclidean prox-function

$$\displaystyle{ d(x)\mathop{ =}\limits^{\mathrm{ def}}\frac{1} {2}\sum _{j=1}^{n}\left (x^{(j)}\right )^{2},\quad x \in X = \mathbb{R}_{ +}^{n}. }$$

(S1)

Note that the corresponding norm in Definition 5 and its conjugate according to ( 36) are

$$\displaystyle{\|x\|^{2} =\sum _{ j=1}^{n}\left (x^{(j)}\right )^{2},\quad \|s\|_{ {\ast}}^{2} =\sum _{ j=1}^{n}\left (s^{(j)}\right )^{2}.}$$

Further, we assume that φ is linear w.r.t. x:

$$\displaystyle{ \varphi (x,a) = -\sum _{j=1}^{n}x^{(j)}h_{ j}(a), }$$

(S2)

where $h = \left (h_{j}(\cdot ),j = 1,\ldots,n\right )$, are convex functions on $\mathbb{R}^{m}$. Then, the adjoint problem ( 32) takes the form

$$\displaystyle{ f^{{\ast}} =\mathop{ \mathrm{max}}\limits _{ \begin{array}{c} a \in A \end{array} }\left \{\varPhi (a)\,\left \vert \,h_{j}(a) \leq 0,\quad j = 1,\ldots,n\right.\right \}. }$$

(39)

The maximization problem ( 39) is assumed to satisfy the Slater condition (e.g., [15]), i.e.

$$\displaystyle{ \mbox{ there exists }\bar{a} \in A\mbox{ such that }h_{j}(\bar{a}) <0\mbox{ for all }j = 1,\ldots,n. }$$

(S3)

Under ( S1)–( S3) we have in ( SM):

$$\displaystyle{\begin{array}{rcl} \nabla f(x[t])& =& - h(a(x[t])), \\ z[t]& =& -\sum _{r=0}^{t}h(a(x[r])), \\ x^{+}[t]& =& \frac{1} {\chi [t]}\left (-z[t]\right )_{+} = \frac{1} {\chi [t]}\left (\sum _{r=0}^{t}h(a(x[r]))\right )_{ +}. \end{array} }$$

Here, the forecast x ⁺[t] is chosen to be proportional to the historical infeasibility.

Now we are ready to proceed with the convergence analysis of the method ( SM) under ( S1)–( S3). Next Lemma 3 estimates the dual gap for the minimization problem ( 28) and its adjoint problem ( 39) evaluated at the historical averages.

Lemma 3.

Let the sequence $\left \{x[t]\right \}_{t\geq 0}$ be generated by ( SM ) under ( S1 )–( S3 ) with nondecreasing parameters

$$\displaystyle{\chi [t + 1] \geq \chi [t],\quad t \geq 0.}$$

Then, for all t ≥ 0 it holds:

$$\displaystyle{ f(x[t])-f^{{\ast}}+C_{ 1} \frac{\chi [t]} {t+1} \leq f(x[t])-\varPhi (a[t])+\frac{t+1} {\chi [t]} \sum _{j=1}^{n}\left (h_{ j}(a[t])\right )_{+}^{2}\leq C_{ 2} \frac{1} {t+1} \sum _{r=0}^{t} \frac{1} {\chi [r-1]} }$$

(40)

with positive constants C ₁ ,C ₂ > 0.

The proof of Lemma 3 is postponed to Appendix. For the precise dependence of constants C ₁ and C ₂ on the market’s data see ( 75) and ( 76) in Appendix.

In order for ( SM) to converge, the parameters $\left \{\chi [t]\right \}_{t\geq 0}$ need to be properly chosen. Next Lemma 4 identifies successful adjustment strategies of parameters. Namely, the parameters monotonically increase over time, but by decreasing increments.

Lemma 4.

Let nondecreasing parameters satisfy

$$\displaystyle{ \chi [t] -\chi [t - 1] \rightarrow 0,\quad \chi [t] \rightarrow \infty. }$$

(41)

Then,

$$\displaystyle{ \frac{\chi [t]} {t + 1} \rightarrow 0,\quad \mbox{ and}\quad \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {\chi [r - 1]} \rightarrow 0. }$$

(42)

Moreover, the best achievable order of convergence in ( 42 ) is $O\left ( \frac{1} {\sqrt{t}}\right )$.

For the proof of Lemma 4 see Appendix.

Remark 2.

As in the proof of Lemma 4, nondecreasing parameters can be written in the cumulative form:

$$\displaystyle{\chi [t] =\sum _{ r=0}^{t}\iota [r] +\chi [-1]}$$

with increments ι[t] ≥ 0. Then, the convergence condition ( 41) means that increments tend to zero and sum up to infinity, i.e.

$$\displaystyle{\iota [t] \rightarrow 0,\quad \sum _{t=0}^{\infty }\iota [t] = \infty.}$$

The latter coincides with the usual condition imposed on the step-sizes of the subgradient method for nonsmooth convex minimization (e.g., [10]). However, in our setting ι[t] play the role of incremental step-sizes. This gives rise to suppose that the parameters χ[t] can be formed by incremental learning (cf. [20]). In fact, the parameter χ[t] increases over time, however, by decreasing increments ι[t]. □ 

Now, we are ready to prove the main convergence result for ( SM) under ( S1)–( S3).

Theorem 8 (Convergence of ( SM)).

Let the sequence $\left \{x[t]\right \}_{t\geq 0}$ be generated by ( SM ) under ( S1 )–( S3 ) with nondecreasing parameters satisfying

$$\displaystyle{\chi [t] -\chi [t - 1] \rightarrow 0,\quad \chi [t] \rightarrow \infty.}$$

Then, $\left \{x[t]\right \}_{t\geq 0}$ converges to the solution set of the minimization problem ( 28 ). Moreover, the average adjoint states $\left \{a[t]\right \}_{t\geq 0}$ converge to the solution set of its adjoint problem ( 39 ). The achievable rate of convergence is of the order $O\left ( \frac{1} {\sqrt{t}}\right )$.

Proof.

From Lemma 3 we obtain:

$$\displaystyle{f(x[t])-f^{{\ast}}+C_{ 1} \frac{\chi [t]} {t+1} \leq f(x[t])-\varPhi (a[t])+\frac{t+1} {\chi [t]} \sum _{j=1}^{n}\left (h_{ j}(a[t])\right )_{+}^{2}\leq C_{ 2} \frac{1} {t+1} \sum _{r=0}^{t} \frac{1} {\chi [r-1]}.}$$

This inequality is composed by the objective function f of the primal problem ( 28), computed at the current iterates x[t], objective function Φ of its adjoint problem ( 39), computed at historical averages a[t], and the quadratic penalty $\sum _{j=1}^{n}\left (h_{j}(a[t])\right )_{+}^{2}$ for violation of the constraints:

$$\displaystyle{h_{j}(a[t]) \leq 0,\quad j = 1,\ldots,n}$$

Due to the choice of parameters χ[t], Lemma 4 provides:

$$\displaystyle{ \frac{\chi [t]} {t + 1} \rightarrow 0,\mbox{ and } \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {\chi [r - 1]} \rightarrow 0.}$$

Hence, the assertion follows. □ 

Now, we turn our attention to the case of constant and linear parameters.

Remark 3 (Constant Parameters).

Let the constant parameters be applied in ( SM). Let ɛ > 0 denote the tolerance for convergence of x[t] towards a solution of the primal problem ( 28), and a[t] towards a solution of its adjoint problem ( 39). Our goal is to indicate the number of steps t(ɛ) and the parameters χ(ɛ), in order to guarantee the tolerance ɛ for this primal-adjoint process. For that, we apply constant confidence parameters χ[t] = χ to obtain

$$\displaystyle{ \frac{\chi [t]} {t + 1} = \frac{\chi } {t + 1},\quad \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {\chi [r - 1]} = \frac{1} {\chi }.}$$

Recalling ( 40), the order of convergence for the primal-adjoint process is

$$\displaystyle{\mathop{\mathrm{max}}\limits \left \{ \frac{\chi } {t + 1}, \frac{1} {\chi } \right \}.}$$

Choosing

$$\displaystyle{t(\varepsilon ) = O\left (\frac{1} {\varepsilon ^{2}} \right ),\chi (\varepsilon ) = O\left (\frac{1} {\varepsilon } \right ),}$$

we have

$$\displaystyle{\mathop{\mathrm{max}}\limits \left \{ \frac{\chi (\varepsilon )} {t(\varepsilon ) + 1}, \frac{1} {\chi (\varepsilon )}\right \} = O(\varepsilon ).}$$

 □ 

Remark 4 (Linear Growth of Parameters).

Let us define the parameters in ( SM) as follows

$$\displaystyle{\chi [t] = (t + 1)\sigma,}$$

where σ > 0 can be seen as a growth rate of parameters. For the forecast we have then:

$$\displaystyle{x^{+}[t] = \frac{1} {\sigma } \left ( \frac{1} {t + 1}\sum _{r=0}^{t}h(a(x[r]))\right )_{ +}.}$$

Here, the forecast x ⁺[t] is formed proportional to the average infeasibility. We turn our attention to the convergence of ( SM) for this case. Recalling ( 40), the order of convergence for the primal-adjoint process is

$$\displaystyle{\mathop{\mathrm{max}}\limits \left \{\sigma, \frac{1} {\sigma } \cdot \frac{1} {t + 1}\left (1 +\sum _{ r=1}^{t}\frac{1} {r}\right )\right \},}$$

or equivalently,

$$\displaystyle{\mathop{\mathrm{max}}\limits \left \{\sigma, \frac{1} {\sigma } \cdot \frac{\ln t} {t + 1}\right \}.}$$

Thus, the primal-adjoint process converges up to a residuum $O\left (\sigma \right )$. □ 

4 Decentralization of Prices

Theorem 2 reveals the origin of equilibrium prices at the market. Namely, in order to reach an equilibrium price one needs to solve the minimization problem:

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p). }$$

(P)

Our goal is to explain how agents can efficiently tackle this nonsmooth convex minimization problem by successively updating prices. This can be implemented by introducing various price designs. In this paper, we focus on

• the regulation design: regulator settles and updates prices which are taken by producers and consumers;

• the trade design: producers settle and update their individual prices, and consumers buy at the lowest purchase price;

• the auction design: consumers settle and update their individual prices, and producers sell at the highest offer price.

4.1 Regulation

It is crucial for our approach that the updates of prices correspond to subgradient-type methods for solving ( P). Due to Theorem 1, the subgradients $\nabla \mathcal{E}(p)$ represent the excess supply, i.e.

$$\displaystyle{ \nabla \mathcal{E}(p) =\sum _{ k=1}^{K}y_{ k} -\sum _{i=1}^{I}x_{ i},\mbox{ where }y_{k} \in S_{k}(p),x_{i} \in D_{i}(p). }$$

(43)

It can be seen from ( 43) that the subgradients of $\mathcal{E}$ are not known to individual agents. Indeed, $\nabla \mathcal{E}(p)$ represents the aggregate excess supply. For getting access to its value, one would assume the existence of a market regulator who collects the information about agents’ production and consumption bundles, and aggregates them over the whole market. Here, the full information about production and consumption over the market must be available to the regulator. Besides, the prices need to be updated by the latter, thus, leading to the price regulation. Clearly, these assumptions can be justified within a centrally planned economy. This allows to suppose that the regulator uses the subgradients $\nabla \mathcal{E}(p)$ for updating prices. In what follows, the quasi-monotone subgradient method for solving ( P) from Sect. 3 is applied to this end.

Let the regulator choose a sequence of positive confidence parameters $\left \{\chi [t]\right \}_{t\geq 0}$. We consider the following iteration:

$$\displaystyle{ \mathbf{Price\ Regulation} }$$

(REG)

• 1. Regulator determines the aggregated excess supply $\nabla \mathcal{E}(p[t])$:

  • (a) kth producer computes an optimal tentative production bundle

    $$\displaystyle{y_{k}(p[t]) \in \mathcal{Y}_{k}^{{\ast}}(p[t]),}$$

    and participation level

    $$\displaystyle{\alpha _{k}(p[t]) = \left \{\begin{array}{ll} 1,&\mbox{ if }\pi _{k}(p[t]) \geq \kappa _{k}, \\ 0,&\mbox{ if }\pi _{k}(p[t]) <\kappa _{k},\end{array} \right.}$$

    indicating whether y _k (p[t]) is implemented.

    The production bundle is α _k (p[t])y _k (p[t]), i.e. either y _k (p[t]) or zero.

  • (b) ith consumer computes an optimal tentative consumption bundle

    $$\displaystyle{x_{i}(p[t]) \in \mathcal{X}_{i}^{{\ast}}(p[t]),}$$

    and participation level

    $$\displaystyle{\beta _{i}(p[t]) = \left \{\begin{array}{ll} 1,&\mbox{ if }e_{i}(p[t]) \leq w_{i}, \\ 0,&\mbox{ if }e_{i}(p[t]) <w_{i},\end{array} \right.}$$

    indicating whether x _i (p[t]) is implemented.

    The consumption bundle is β _i (p[t])x _i (p[t]), i.e. either x _i (p[t]) or zero.

  • (c) regulator observes the current excess supplies

    $$\displaystyle{ \nabla \mathcal{E}(p[t]) =\sum _{ k=1}^{K}\alpha _{ k}(p[t])y_{k}(p[t]) -\sum _{i=1}^{I}\beta _{ i}(p[t])x_{i}(p[t]). }$$

    (44)

• 2. Regulator accumulates the excess supplies

  $$\displaystyle{ z[t] = z[t - 1] + \nabla \mathcal{E}(p[t]),\quad z[-1] = 0. }$$

  (45)

• 3. Regulator computes the price forecast w.r.t. the confidence parameter χ[t]:

  $$\displaystyle{ p^{+(j)}[t] = \frac{\zeta ^{(j)}} {\chi [t]} \left (-z^{(j)}[t]\right )_{ +},\quad j = 1,\ldots,n, }$$

  (46)

  where ζ ^(j) are positive scaling coefficients.

• 4. Regulator updates

  $$\displaystyle{ p[t + 1] = \frac{t + 1} {t + 2}p[t] + \frac{1} {t + 2}p^{+}[t] }$$

  (47)

  by combining the previous price with the forecast. □ 

First, we give an interpretation for the price forecast ( 46). Recall that z ^(j)[t] represents the aggregated excess supply for good j accumulated up to time t. If z ^(j)[t] ≥ 0, i.e. supply exceeds demand, then p ^+(j)[t] = 0 for good j. In case of z ^(j)[t] < 0, the price forecast p ^+(j)[t] is proportional to the accumulated and aggregated excess demand with positive scaling coefficients ζ ^(j). Here, χ[t] plays the role of a confidence parameter. Namely, χ[t]’s express to which extent the regulator takes into account the excess demands while forecasting prices.

Secondly, let us interpret the price update ( 47). Due to the latter, the next price is a convex combination of the previous price and the price forecast. With time advancing, the proportion of the previous price becomes nearly one, but the fraction of the forecast vanishes. Hence, we conclude that our price update corresponds to a behavior of an experienced regulator. Such regulator credits the experience much more than the current forecast. Further, from ( 47) we have

$$\displaystyle{ p[t + 1] = \frac{1} {t + 2}\left (p[0] +\sum _{ r=0}^{t}p^{+}[r]\right ). }$$

(48)

The latter means that the prices generated by ( REG) can be viewed as historical averages of preceding forecasts. This averaging pattern is also quite natural to assume for regulator’s behavior while adjusting prices. Moreover, as it will be shown later, this price adjustment based on averaging successively leads to equilibrium prices.

Along with the prices $\left \{\left (p_{1}[t],\ldots,p_{K}[t]\right )\right \}_{t\geq 0}$ generated by method ( TRA), we consider the corresponding historical averages of participation levels:

$$\displaystyle{\alpha _{k}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\alpha _{ k}(p_{k}[r]),\quad \beta _{i}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\beta _{ i}(p[r]).}$$

Note that α _k [t] ∈ [0, 1] is the frequency of successful production attempts by kth producer up to time t. Analogously, β _i [t] ∈ [0, 1] is the frequency of successful consumption attempts by ith consumer up to time t. We denote by

$$\displaystyle{\gamma [t] = \left (\alpha [t],\beta [t]\right )\mathop{ =}\limits^{\mathrm{ def}}\left (\left \{\alpha _{k}[t]\right \}_{k=1}^{K},\left \{\beta _{ i}[t]\right \}_{i=1}^{I}\right )}$$

the system of average participation levels. The historical averages of production and consumption bundles are defined as follows:

$$\displaystyle{\tilde{y}_{k}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\alpha _{ k}(p_{k}[r])y_{k}(p_{k}[r]),\quad \tilde{x}_{i}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\beta _{ i}(p[r])x_{i}(p[r]).}$$

Due to convexity, $\tilde{y}_{k}[t] \in \alpha _{k}[t]\mathcal{Y}_{k}$ and $\tilde{x}_{i}[t] \in \beta _{i}[t]\mathcal{X}_{i}$. We denote by

$$\displaystyle{\widetilde{F}[t] = \left (\tilde{y}[t],\tilde{x}[t]\right )\mathop{ =}\limits^{\mathrm{ def}}\left (\left \{\tilde{y}_{k}[t]\right \}_{k=1}^{K},\left \{\tilde{x}_{ i}[t]\right \}_{i=1}^{I}\right )}$$

the average market flow. Overall, the sequence

$$\displaystyle{\left (\alpha [t],\tilde{y}[t],\beta [t],\tilde{x}[t]\right ) \in \mathcal{A},\quad t \geq 0,}$$

is feasible for the adjoint problem ( A).

Now, we are ready to prove the main convergence result for ( REG).

Theorem 9 (Convergence of Price Regulation).

At a productive market, let the regulator apply in ( REG ) nondecreasing confidence parameters satisfying

$$\displaystyle{\chi [t] -\chi [t - 1] \rightarrow 0,\quad \chi [t] \rightarrow \infty.}$$

Then, the sequence of prices, average participation levels, and the average market flow

$$\displaystyle{\left (p[t],\gamma [t],\widetilde{F}[t]\right )}$$

converges toward the set of market equilibria. The achievable rate of convergence is of the order $O\left ( \frac{1} {\sqrt{t}}\right )$.

Proof.

The iteration scheme ( REG) is a variant of the quasi-monotone subgradient method ( SM). Hence, we may obtain the convergence for ( REG) by means of Theorem 8. For that, let us discuss the applicability of conditions ( S1)–( S3).

• On ( S1 ): The price forecast ( 57) can be derived by means of the Euclidean prox-function for $\mathbb{R}_{+}^{n}$:

  $$\displaystyle{d(p)\mathop{ =}\limits^{\mathrm{ def}}\frac{1} {2}\sum _{j=1}^{n} \frac{1} {\zeta ^{(j)}}\left (p^{(j)}\right )^{2}.}$$

  In fact, for $z[t] \in \mathbb{R}^{n},\chi [t]> 0$ we consider the minimization problem as from step 3. in ( SM):

  $$\displaystyle{\mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\left \{\langle z[t],p\rangle +\chi [t]d(p)\right \}.}$$

  Its unique solution is the price forecast ( 46) as from step 3. in ( REG):

  $$\displaystyle{p^{+(j)}[t] = \frac{\zeta ^{(j)}} {\chi [t]} \left (-z^{(j)}[t]\right )_{ +},\quad j = 1,\ldots,n.}$$

• On ( S2 ): It follows from Theorem 7 that the total excessive revenue is representable as a maximum of concave functions:

  $$\displaystyle{\mathcal{E}(p) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\in \mathcal{A}\\ \end{array} }\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )+\varphi \left (p,\tilde{y},\tilde{x}\right ),}$$

  where

  $$\displaystyle{\varphi \left (p,\tilde{y},\tilde{x}\right ) = \left \langle p,\sum _{k=1}^{K}\tilde{y}_{ k} -\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle.}$$

  Note that φ is linear w.r.t. p. In particular, due to Theorem 7, the adjoint problem for the total revenue minimization ( P) is the welfare maximization ( A).

• On ( S3 ): The welfare maximization problem ( A) satisfies the Slater condition in view of the market productivity (cf. Definition 2).

Overall, we apply Theorem 8 to deduce that p[t] converges toward the solution set of ( P), and $\left (\gamma [t],\widetilde{F}[t]\right )$ converges toward the solution set of ( A) by order $O\left ( \frac{1} {\sqrt{t}}\right )$. In view of the duality from Theorem 7, the assertion follows. □ 

4.2 Trade

Aiming to avoid the assumption of price regulation, we decentralize prices by introducing the trade design:

kth producer settles and updates individual prices p _k ,

and consumers buy at the lowest purchase price $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}$.

Recall that for vectors $p_{1},\ldots,p_{K} \in \mathbb{R}^{n}$, we denote by $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k} \in \mathbb{R}^{n}$ the vector with coordinates

$$\displaystyle{\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}\right )^{(j)} =\mathop{ \mathrm{min}}\limits _{ k=1,\ldots,K}p_{k}^{(j)},\quad j = 1,\ldots,n.}$$

The trade design incorporates the feature of Bertrand competition, namely, that consumers search for lowest prices, e.g. [8]. Following the framework of Bertrand competition, we assume that consumers are able to undertake global price search across the producers.

For the trade design, the total excessive revenue depends on the producers’ prices $\left (p_{k}\right )_{k=1}^{K}$ as follows:

$$\displaystyle{\mathcal{E}(p_{1},\ldots,p_{K})\mathop{ =}\limits^{\mathrm{ def}}\sum _{k=1}^{K}\mathcal{E}_{ k}\left (p_{k}\right ) +\sum _{ i=1}^{I}\mathcal{E}_{ i}\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}\right ) =}$$

$$\displaystyle{ \sum _{k=1}^{K}\mathop{ \mathrm{max}}\limits _{ y_{k}\in \mathcal{Y}_{k}}\left (\left \langle p_{k},y_{k}\right \rangle - c_{k}(y_{k})\right )_{+} +\sum _{ i=1}^{I}\mathop{ \mathrm{max}}\limits _{ x_{i}\in \mathcal{X}_{i}}\left (w_{i} -\left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},x_{i}\right \rangle \right )_{+}. }$$

(49)

The decentralization of prices makes the corresponding subdifferential information about excess demands available to producers. In fact, note that the total excessive revenue $\mathcal{E}$ from ( 49) is convex in the variables $\left (p_{k}\right )_{k=1}^{K}$. Let us obtain an expression for its convex subgradients $\nabla _{p_{k}}\mathcal{E}(p_{1},\ldots,p_{K})$ w.r.t. p _k :

$$\displaystyle{ \nabla _{p_{k}}\mathcal{E}(p_{1},\ldots,p_{K}) =\tilde{ y}_{k} -\sum _{i=1}^{I}\mu _{ ik} \circ \tilde{ x}_{i},\quad k = 1,\ldots,K, }$$

(50)

where $\mu _{ik} \circ \tilde{ x}_{i} = \left (\mu _{ik}^{(j)}\tilde{x}_{i}^{(j)}\right )_{j=1}^{(n)}$. Here, $\tilde{y}_{k} \in S_{k}(p_{k})$ is the supply of kth producer w.r.t. the individual price p _k , and $\tilde{x}_{i} \in D_{i}\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}\right )$ is the demand of ith consumer w.r.t. the lowest purchase price $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}$. Moreover,

$$\displaystyle{\left (\mu _{ik}\right )_{k=1}^{K} \in M\left (p_{ 1},\ldots,p_{K}\right ),}$$

where

$$\displaystyle{M\left (p_{1},\ldots,p_{K}\right )\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (\mu _{k}\right )_{k=1}^{K} \in [0,1]^{n\times K}\,\left \vert \,\begin{array}{c} \sum _{k=1}^{K}\mu _{ k}^{(j)} = 1, \\ \mu _{k}^{(j)} = 0\mbox{ if }p_{ k}^{(j)}\not =\mathop{\mathrm{min}}\limits _{ k=1,\ldots,K}p_{k}^{(j)} \\ j = 1,\ldots,n,k = 1,\ldots,K \end{array} \right.\right \}.}$$

Note that μ _ik ^(j) can be interpreted as the share of ith consumer’s demand from kth producer for good j. Indeed, the shares μ _ik ^(j) for good j sum up to 1 over all producers k = 1, …, K. Moreover, the share μ _ik ^(j) vanishes if the kth producer’s price p _k ^(j) exceeds the lowest purchase price $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}^{(j)}$ for good j.

We claim that the subdifferential information in ( 50) is known to kth producer. First, note that $\tilde{y}_{k}$ is kth producer’s production. Despite of the fact that the shares μ _ik and the demands $\tilde{x}_{i}$ cannot be estimated by kth producer, their aggregated product $\sum _{i=1}^{I}\mu _{ik} \circ \tilde{ x}_{i}$ is perfectly available to him. Indeed, $\sum _{i=1}^{I}\mu _{ik} \circ \tilde{ x}_{i}$ forms the bundle of goods demanded by all consumers from kth producer. Altogether, the subgradients $\nabla _{p_{k}}\mathcal{E}(p_{1},\ldots,p_{K})$ represent the individual excess of kth producer’s supply over all consumers’ demands. Overall, we obtain:

Theorem 10 (Producers’ Excess Supply and Total Excessive Revenue).

$$\displaystyle{\partial _{p_{k}}\mathcal{E}(p_{1},\ldots,p_{K}) = S_{k}(p_{k}) -\sum _{i=1}^{I}\mu _{ ik} \circ D_{i}\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}\right ),\quad k = 1,\ldots,K,}$$

with demand shares $\left (\mu _{ik}\right )_{k=1}^{K} \in M\left (p_{1},\ldots,p_{K}\right ).$

Due to Theorem 10, the subdifferential of $\mathcal{E}(p_{1},\ldots,p_{K})$ is completely available to kth producer. This fact suggests to adjust prices by solving the minimization problem

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{K}). }$$

(PD)

Note that the minimization problem ( PD) is stated w.r.t. the decentralized producers’ prices $\left (p_{k}\right )_{k=1}^{K}$, while previously in ( P) one minimizes over the common prices p.

We relate the minimization problem ( PD) to ( P). For that, let us call function f(x), $x \in \mathbb{R}^{n}$, nondecreasing (nonincreasing) in x if f(x) ≥ f(y) (f(x) ≤ f(y)) for any x ≥ y.

Lemma 5 (Decentralization I).

Let function of K + 1 vector variables

$$\displaystyle{F(p_{0},p_{1},\ldots,p_{K}),\quad p_{k} \in \mathbb{R}^{n},k = 0,\ldots,K,}$$

be (a) nonincreasing in p ₀ , and (b) nondecreasing in all other variables p _k , k = 1,…,K. Then,

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}F\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},p_{1},\ldots,p_{K}\right ) =\mathop{ \mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}F(p,\ldots,p).}$$

Proof.

Indeed,

$$\displaystyle{\begin{array}{c} \mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}F\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},p_{1},\ldots,p_{K}\right )\mathop{ =}\limits^{\mathrm{ a)}} \\ \mathop{\mathrm{min}}\limits _{p,p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\left \{F\left (p,p_{1},\ldots,p_{K}\right )\,\left \vert \,p_{k} \geq p,k = 1,\ldots,K\right.\right \}\mathop{ =}\limits^{\mathrm{ b)}} \\ \mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}F(p,\ldots,p).\end{array} }$$

 □ 

Next Theorem 11 states that the minimization of the total excessive revenue remains invariant under the trade design.

Theorem 11 (Total Revenue and Trade).

Problems ( P ) and ( PD ) are equivalent, i.e.

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{K}) =\mathop{ \mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p). }$$

(51)

Moreover,

• (i) if $\left (p_{k}\right )_{k=1}^{K}$ solves ( PD ), then $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}$ solves ( P ),

• (ii) if p solves ( P ), then (p,…,p) solves ( PD ).

Proof.

We set

$$\displaystyle{F(p_{0},p_{1},\ldots,p_{K})\mathop{ =}\limits^{\mathrm{ def}}\sum _{k=1}^{K}\mathcal{E}_{ k}\left (p_{k}\right ) +\sum _{ i=1}^{I}\mathcal{E}_{ i}\left (p_{0}\right ).}$$

Note that F is nonincreasing in p ₀, and nondecreasing in p _k , k = 1, …, K. Applying Lemma 5 and in view of

$$\displaystyle{F\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},p_{1},\ldots,p_{K}\right ) = \mathcal{E}(p_{1},\ldots,p_{K}),\quad F(p,\ldots,p) = \mathcal{E}(p),}$$

( 51) holds.

Let $\left (p_{k}\right )_{k=1}^{K}$ solve ( PD). Then,

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p) \leq \mathcal{E}\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}\right )\mathop{ \leq }\limits^{ (59)}\mathcal{E}(p_{1},\ldots,p_{K}).}$$

By using ( 51), $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}$ solves ( P).

Now, let p solve ( P). Then,

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{K}) \leq \mathcal{E}(p,\ldots,p) = \mathcal{E}(p),}$$

By using ( 51), (p, …, p) solves ( PD). □ 

Further, we show that the welfare maximization problem ( A) turns out to be adjoint not only for ( P), but also for ( PD). The proof of this fact uses the following Lemma 6.

Lemma 6.

For $y_{k},x \in \mathbb{R}_{+}^{n}$ , k = 1,…,K, the inequality

$$\displaystyle{ \sum _{k=1}^{K}y_{ k} \geq x }$$

(52)

is equivalent to

$$\displaystyle{ \sum _{k=1}^{K}\left \langle p_{ k},y_{k}\right \rangle \geq \left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},x\right \rangle \,\mbox{ for all }p_{k} \in \mathbb{R}_{+}^{n},k = 1,\ldots,K. }$$

(53)

Proof.

• (i) Let ( 52) be satisfied. For $p_{k} \in \mathbb{R}_{+}^{n}$, k = 1, …, K, we have

  $$\displaystyle{\sum _{k=1}^{K}\left \langle p_{ k},y_{k}\right \rangle \geq \left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},\sum _{k=1}^{K}y_{ k}\right \rangle \geq \left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},x\right \rangle.}$$

  The first inequality is due to $y_{k} \in \mathbb{R}_{+}^{n}$, and $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k} \geq p_{k}$, k = 1, …, K. The second inequality is due to ( 52) and $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k} \in \mathbb{R}_{+}^{n}$.

• (ii) Let ( 53) be satisfied. Setting there $p_{k} = p \in \mathbb{R}_{+}^{n}$, we get

  $$\displaystyle{\left \langle p,\sum _{k=1}^{K}x_{ k}\right \rangle \geq \left \langle p,y\right \rangle \,\mbox{ for all }p \in \mathbb{R}_{+}^{n}.}$$

  Hence, ( 52) is fulfilled. □ 

The welfare maximization ( A) remains adjoint for the total revenue minimization ( PD) under the trade design.

Theorem 12 (Adjoint for ( PD)).

The welfare maximization ( A ) is adjoint for the total revenue minimization ( PD ):

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{K}) =}$$

$$\displaystyle{ \mathop{\mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A}\end{array} }\left \{\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\,\left \vert \,\begin{array}{l} \sum _{k=1}^{K}\tilde{y}_{k} \geq \sum _{i=1}^{I}\tilde{x}_{i} \end{array} \right.\right \}. }$$

(54)

Proof.

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{K}) =}$$

$$\displaystyle{\begin{array}{ll} =&\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A}\end{array} }\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) +\sum _{ k=1}^{K}\left \langle p_{ k},\tilde{y}_{k}\right \rangle -\left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle, \\ =&\mathop{\mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A}\end{array} }\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) +\mathop{ \mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\sum _{k=1}^{K}\left \langle p_{ k},\tilde{y}_{k}\right \rangle -\left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle, \\ =&\mathop{\mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\in \mathcal{A}\\ \end{array} }\left \{\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\,\left \vert \,\begin{array}{l} \sum _{k=1}^{K}\left \langle p_{ k},\tilde{y}_{k}\right \rangle \geq \left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle \\ \mbox{ for all }p_{k} \in \mathbb{R}_{+}^{n},k = 1,\ldots,K \end{array} \right.\right \}.\end{array}}$$

Applying Lemma 6, we get the assertion ( 54). □ 

We describe how producers may efficiently adjust their individual prices $\left (p_{k}\right )_{k=1}^{K}$ to arrive at an equilibrium price. This price adjustment corresponds to the quasi-monotone subgradient method from Sect. 3. It is applied to the minimization of the total excessive revenue ( PD) under the trade design.

Let kth producer choose a sequence of positive confidence parameters $\left \{\chi _{k}[t]\right \}_{t\geq 0}$, k = 1, …, K. We consider the following iteration:

$$\displaystyle{ \mathbf{Pricing\ via\ Trade} }$$

(TRA)

• 1. Producers determine their current excess supplies $\nabla _{p_{k}}\mathcal{E}(p_{1}[t],\ldots,p_{K}[t])$:

  • (a) kth producer computes an optimal tentative production bundle

    $$\displaystyle{y_{k}(p_{k}[t]) \in \mathcal{Y}_{k}^{{\ast}}(p_{ k}[t]),}$$

    and participation level

    $$\displaystyle{\alpha _{k}(p_{k}[t]) = \left \{\begin{array}{ll} 1,&\mbox{ if }\pi _{k}(p_{k}[t]) \geq \kappa _{k}, \\ 0,&\mbox{ if }\pi _{k}(p_{k}[t]) <\kappa _{k},\end{array} \right.}$$

    indicating whether y _k (p _k [t]) is implemented.

    The production bundle is α _k (p _k [t])y _k (p _k [t]), i.e. either y _k (p _k [t]) or zero.

  • (b) ith consumer identifies the lowest purchase prices

    $$\displaystyle{p[t] =\mathop{ \mathrm{min}}\limits _{k=1,\ldots,K}p_{k}[t],}$$

    computes an optimal tentative consumption bundle

    $$\displaystyle{x_{i}(p[t]) \in \mathcal{X}_{i}^{{\ast}}(p[t]),}$$

    and participation level

    $$\displaystyle{\beta _{i}(p[t]) = \left \{\begin{array}{ll} 1,&\mbox{ if }e_{i}(p[t]) \leq w_{i}, \\ 0,&\mbox{ if }e_{i}(p[t]) <w_{i},\end{array} \right.}$$

    indicating whether x _i (p[t]) is implemented.

    The consumption bundle is β _i (p[t])x _i (p[t]), i.e. either x _i (p[t]) or zero.

  • (c) ith consumer decides on demand shares

    $$\displaystyle{\left (\mu _{ik}[t]\right )_{k=1}^{K} \in M\left (p_{ 1}[t],\ldots,p_{K}[t]\right ),}$$

    and demands from kth producer the bundle

    $$\displaystyle{\mu _{ik}[t] \circ \beta _{i}(p[t])x_{i}(p[t]),\quad k = 1,\ldots,K.}$$

  • (d) kth producer computes the current excess supply

    $$\displaystyle{ \nabla _{p_{k}}\mathcal{E}(p_{1}[t],\ldots,p_{K}[t]) =\alpha _{k}(p_{k}[t])y_{k}(p_{k}[t]) -\sum _{i=1}^{I}\mu _{ ik}[t] \circ \beta _{i}(p[t])x_{i}(p[t]). }$$

    (55)

• 2. kth producer accumulates the excess supplies

  $$\displaystyle{ z_{k}[t] = z_{k}[t - 1] + \nabla _{p_{k}}\mathcal{E}(p_{1}[t],\ldots,p_{K}[t]),\quad z_{k}[-1] = 0. }$$

  (56)

• 3. kth producer computes the price forecast w.r.t. the confidence parameter χ _k [t]:

  $$\displaystyle{ p_{k}^{+(j)}[t] = \frac{\zeta _{k}^{(j)}} {\chi _{k}[t]} \left (-z_{k}^{(j)}[t]\right )_{ +},\quad j = 1,\ldots,n, }$$

  (57)

  where ζ _k ^(j) are positive scaling coefficients.

• 4. kth producer updates

  $$\displaystyle{ p_{k}[t + 1] = \frac{t + 1} {t + 2}p_{k}[t] + \frac{1} {t + 2}p_{k}^{+}[t] }$$

  (58)

  by combining the previous individual price with the forecast. □ 

Along with the prices $\left \{\left (p_{1}[t],\ldots,p_{K}[t]\right )\right \}_{t\geq 0}$ generated by method ( TRA), we consider the corresponding historical averages of participation levels:

$$\displaystyle{\alpha _{k}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\alpha _{ k}(p_{k}[r]),\quad \beta _{i}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\beta _{ i}(p[r]).}$$

Note that α _k [t] ∈ [0, 1] is the frequency of successful production attempts by kth producer up to time t. Analogously, β _i [t] ∈ [0, 1] is the frequency of successful consumption attempts by ith consumer up to time t. We denote by

$$\displaystyle{\gamma [t] = \left (\alpha [t],\beta [t]\right )\mathop{ =}\limits^{\mathrm{ def}}\left (\left \{\alpha _{k}[t]\right \}_{k=1}^{K},\left \{\beta _{ i}[t]\right \}_{i=1}^{I}\right )}$$

the system of average participation levels. The historical averages of production and consumption bundles are defined as follows:

$$\displaystyle{\tilde{y}_{k}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\alpha _{ k}(p_{k}[r])y_{k}(p_{k}[r]),\quad \tilde{x}_{i}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\beta _{ i}(p[r])x_{i}(p[r]).}$$

Due to convexity, $\tilde{y}_{k}[t] \in \alpha _{k}[t]\mathcal{Y}_{k}$ and $\tilde{x}_{i}[t] \in \beta _{i}[t]\mathcal{X}_{i}$. We denote by

$$\displaystyle{\widetilde{F}[t] = \left (\tilde{y}[t],\tilde{x}[t]\right )\mathop{ =}\limits^{\mathrm{ def}}\left (\left \{\tilde{y}_{k}[t]\right \}_{k=1}^{K},\left \{\tilde{x}_{ i}[t]\right \}_{i=1}^{I}\right )}$$

the average market flow. Overall, the sequence

$$\displaystyle{\left (\alpha [t],\tilde{y}[t],\beta [t],\tilde{x}[t]\right ) \in \mathcal{A},\quad t \geq 0,}$$

is feasible for the adjoint problem ( A).

Now, we are ready to prove the main convergence result for ( TRA).

Theorem 13 (Convergence of Pricing via Trade).

At a productive market, let producers apply in ( TRA ) nondecreasing confidence parameters satisfying

$$\displaystyle{\chi _{k}[t] -\chi _{k}[t - 1] \rightarrow 0,\quad \chi _{k}[t] \rightarrow \infty,\quad k = 1,\ldots,K.}$$

Then, the sequence of lowest purchase prices, average participation levels, and the average market flow

$$\displaystyle{\left (\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}[t],\gamma [t],\widetilde{F}[t]\right )}$$

converges toward the set of market equilibria. The achievable rate of convergence is of the order $O\left ( \frac{1} {\sqrt{t}}\right )$.

Proof.

The iteration scheme ( TRA) is a variant of the quasi-monotone subgradient method ( SM). Hence, we may obtain the convergence for ( TRA) by means of Theorem 8. For that, let us discuss the applicability of conditions ( S1)–( S3).

• On ( S1 ): The price forecast ( 57) can be derived by means of the Euclidean prox-functions for $\mathbb{R}_{+}^{n}$:

  $$\displaystyle{d_{k}(p)\mathop{ =}\limits^{\mathrm{ def}}\frac{1} {2}\sum _{j=1}^{n} \frac{1} {\zeta _{k}^{(j)}}\left (p^{(j)}\right )^{2},\quad k = 1,\ldots,K.}$$

  In fact, for $z_{k}[t] \in \mathbb{R}^{n},\chi _{k}[t]> 0$ we consider the minimization problem as from step 3. in ( SM):

  $$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{K}\in \mathbb{R}_{+}^{n}}\left \{\sum _{k=1}^{K}\langle z_{ k}[t],p_{k}\rangle +\chi _{k}[t]d_{k}(p_{k})\right \}.}$$

  Its unique solution is the price forecast ( 57) as from step 3. in ( TRA):

  $$\displaystyle{p_{k}^{+(j)}[t] = \frac{\zeta _{k}^{(j)}} {\chi _{k}[t]} \left (-z_{k}^{(j)}[t]\right )_{ +},\quad j = 1,\ldots,n,k = 1,\ldots,K.}$$

• On ( S2 ): It follows from Theorem 12 that the total excessive revenue is representable as a maximum of concave functions:

  $$\displaystyle{\mathcal{E}(p_{1},\ldots,p_{K}) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\in \mathcal{A}\\ \end{array} }\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )+\varphi \left (p_{1},\ldots,p_{K},\tilde{y},\tilde{x}\right ),}$$

  where

  $$\displaystyle{\varphi \left (p_{1},\ldots,p_{K},\tilde{y},\tilde{x}\right ) =\sum _{ k=1}^{K}\left \langle p_{ k},\tilde{y}_{k}\right \rangle -\left \langle \mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k},\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle.}$$

  Although φ is not linear w.r.t. $\left (p_{1},\ldots,p_{K}\right )$, but it is partially linear, i.e.

  $$\displaystyle{\varphi \left (p,\ldots,p,\tilde{y},\tilde{x}\right ) = \left \langle p,\sum _{k=1}^{K}\tilde{y}_{ k} -\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle.}$$

  The partial linearity of φ suffices for the analogous convergence analysis as in Sect. 3 (see [11] for details). In particular, due to Theorem 12, the adjoint problem for the total revenue minimization ( PD) remains unchanged under the trade design, i.e. it is the welfare maximization ( A).

• On ( S3 ): The welfare maximization problem ( A) satisfies the Slater condition in view of the market productivity (cf. Definition 2).

Overall, we apply Theorem 8 to deduce that the sequence $\left (p_{k}[t]\right )_{k=1}^{K}$ converges toward the solution set of ( PD), and $\left (\gamma [t],\widetilde{F}[t]\right )$ converges toward the solution set of ( A) by order $O\left ( \frac{1} {\sqrt{t}}\right )$. Due to Theorem 11, $\mathop{\mathrm{min}}\limits _{k=1,\ldots,K}p_{k}[t]$ converges toward the solution set of ( P). In view of the duality from Theorem 12, the assertion follows. □ 

4.3 Auction

Analogously, we proceed with the auction design:

ith consumer settles and updates his individual prices p _i ,

and producers sell at the highest offer price $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}$.

Recall that for vectors $p_{1},\ldots,p_{I} \in \mathbb{R}^{n}$, we denote by $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i} \in \mathbb{R}^{n}$ the vector with coordinates

$$\displaystyle{\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}\right )^{(j)} =\mathop{ \mathrm{max}}\limits _{ i=1,\ldots,I}p_{i}^{(j)},\quad j = 1,\ldots,n.}$$

The auction design incorporates the dominant aspect in auction theory that highest bidders are first served [6]. Following the auction framework, we assume that producers are able to undertake global price search across the consumers.

Here, the total excessive revenue depends on the consumers’ prices $\left (p_{i}\right )_{i=1}^{I}$ as follows:

$$\displaystyle{\mathcal{E}(p_{1},\ldots,p_{I})\mathop{ =}\limits^{\mathrm{ def}}\sum _{k=1}^{K}\mathcal{E}_{ k}\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}\right ) +\sum _{ i=1}^{I}\mathcal{E}_{ i}\left (p_{i}\right ) =}$$

$$\displaystyle{ \sum _{k=1}^{K}\mathop{ \mathrm{max}}\limits _{ y_{k}\in \mathcal{Y}_{k}}\left (\left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},y_{k}\right \rangle - c_{k}(y_{k})\right )_{+} +\sum _{ i=1}^{I}\mathop{ \mathrm{max}}\limits _{ x_{i}\in \mathcal{X}_{i}}\left (w_{i} -\left \langle p_{i},x_{i}\right \rangle \right )_{+}. }$$

(59)

The decentralization of prices makes the corresponding subdifferential information about excess demands available to consumers. In fact, note that the total revenue $\mathcal{E}$ from ( 59) is convex in the variables $\left (p_{i}\right )_{i=1}^{I}$. Let us obtain an expression for its convex subgradients $\nabla _{p_{i}}\mathcal{E}(p_{1},\ldots,p_{I})$ w.r.t. p _i :

$$\displaystyle{ \nabla _{p_{i}}\mathcal{E}(p_{1},\ldots,p_{I}) =\sum _{ k=1}^{K}\lambda _{ ik} \circ \tilde{ y}_{k} -\tilde{ x}_{i},\quad k = 1,\ldots,K. }$$

(60)

where $\lambda _{ik} \circ \tilde{ y}_{k} = \left (\lambda _{ik}^{(j)}\tilde{y}_{k}^{(j)}\right )_{j=1}^{(n)}$. Here, $\tilde{x}_{i} \in D_{i}(p_{i})$ is the demand of ith consumer w.r.t. his individual price p _i , and $\tilde{y}_{k} \in S_{k}\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}\right )$ is the supply of kth producer w.r.t. the highest offer price $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}$. Moreover,

$$\displaystyle{\left (\lambda _{ik}\right )_{i=1}^{I} \in L\left (p_{ 1},\ldots,p_{I}\right ),}$$

where

$$\displaystyle{L\left (p_{1},\ldots,p_{I}\right )\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (\lambda _{i}\right )_{i=1}^{I} \in [0,1]^{n\times I}\,\left \vert \,\begin{array}{c} \sum _{i=1}^{I}\lambda _{ i}^{(j)} = 1, \\ \lambda _{i}^{(j)} = 0\mbox{ if }p_{ i}^{(j)}\not =\mathop{\mathrm{max}}\limits _{ i=1,\ldots,I}p_{i}^{(j)} \\ j = 1,\ldots,n,i = 1,\ldots,I \end{array} \right.\right \}.}$$

Note that λ _ik ^(j) can be interpreted as the share of kth producer’s supply to ith consumer for good j. Indeed, the shares λ _ik ^(j) for good j sum up to 1 over all consumers i = 1, …, I. Moreover, the share λ _ik ^(j) vanishes if the ith consumer’s price p _i ^(j) is less than the highest offer price $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}^{(j)}$ for good j.

We claim that the subdifferential information in ( 50) is known to ith consumer. First, note that $\tilde{x}_{i}$ is his consumption bundle. Despite of the fact that the shares λ _ik and the supplies $\tilde{y}_{k}$ cannot be estimated by ith consumer, their aggregated product $\sum _{k=1}^{K}\lambda _{ik} \circ \tilde{ y}_{k}$ is perfectly available to him. Indeed, $\sum _{k=1}^{K}\lambda _{ik} \circ \tilde{ y}_{k}$ forms the bundle of goods supplied by all producers to ith consumer. Altogether, the subgradients $\nabla _{p_{i}}\mathcal{E}(p_{1},\ldots,p_{I})$ represent the individual excess of ith consumer’s supply over his demands.

Theorem 14 (Consumers’ Excess Supply and Total Excessive Revenue).

$$\displaystyle{\partial _{p_{i}}\mathcal{E}(p_{1},\ldots,p_{I}) =\sum _{ k=1}^{K}\lambda _{ ik} \circ S_{k}\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{I}\right ) - D_{i}\left (p_{i}\right ),\quad i = 1,\ldots,I,}$$

with supply shares $\left (\lambda _{ik}\right )_{i=1}^{I} \in L\left (p_{1},\ldots,p_{I}\right ).$

Due to Theorem 14, the subdifferential of $\mathcal{E}(p_{1},\ldots,p_{I})$ is completely available to ith consumer. This fact suggests to adjust prices by solving the minimization problem

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{I}). }$$

(PA)

Note that the minimization problem ( PA) is stated w.r.t. the decentralized consumers’ prices $\left (p_{i}\right )_{i=1}^{I}$, while previously in ( P) one minimizes over the common prices p.

We relate the minimization problem ( PA) to ( P). For that, let us call function f(x), $x \in \mathbb{R}^{n}$, nondecreasing (nonincreasing) in x if f(x) ≥ f(y) (f(x) ≤ f(y)) for any x ≥ y.

Lemma 7 (Decentralization II).

Let function of I + 1 vector variables

$$\displaystyle{G(p_{0},p_{1},\ldots,p_{I}),\quad p_{i} \in \mathbb{R}^{n},i = 0,\ldots,I,}$$

be (a) nondecreasing in p ₀ , and (b) nonincreasing in all other variables p _i , i = 1,…,I. Then,

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}G\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},p_{1},\ldots,p_{I}\right ) =\mathop{ \mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}G(p,\ldots,p).}$$

Proof.

Indeed,

$$\displaystyle{\begin{array}{c} \mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}G\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},p_{1},\ldots,p_{I}\right )\mathop{ =}\limits^{\mathrm{ a)}} \\ \mathop{\mathrm{min}}\limits _{p,p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\left \{G\left (p,p_{1},\ldots,p_{I}\right )\,\left \vert \,p_{i} \leq p,i = 1,\ldots,I\right.\right \}\mathop{ =}\limits^{\mathrm{ b)}} \\ \mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}G(p,\ldots,p).\end{array} }$$

 □ 

Next Theorem 15 states that the minimization of the total excessive revenue remains invariant under the auction design.

Theorem 15 (Total Revenue and Auction).

Problems ( P ) and ( PA ) are equivalent, i.e.

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{I}) =\mathop{ \mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p). }$$

(61)

Moreover,

• (i) if $\left (p_{i}\right )_{i=1}^{I}$ solves ( PA ), then $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}$ solves ( P ),

• (ii) if p solves ( P ), then (p,…,p) solves ( PA ).

Proof.

We set

$$\displaystyle{G(p_{0},p_{1},\ldots,p_{I})\mathop{ =}\limits^{\mathrm{ def}}\sum _{k=1}^{K}\mathcal{E}_{ k}\left (p_{0}\right ) +\sum _{ i=1}^{I}\mathcal{E}_{ i}\left (p_{i}\right ).}$$

Note that G is nondecreasing in p ₀, and nonincreasing in p _i , i = 1, …, I. Applying Lemma 7 and in view of

$$\displaystyle{G\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},p_{1},\ldots,p_{I}\right ) = \mathcal{E}(p_{1},\ldots,p_{I}),\quad G(p,\ldots,p) = \mathcal{E}(p),}$$

( 61) holds.

Let $\left (p_{i}\right )_{i=1}^{I}$ solve ( PA). Then,

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p\in \mathbb{R}_{+}^{n}}\mathcal{E}(p) \leq \mathcal{E}\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}\right )\mathop{ \leq }\limits^{ (49)}\mathcal{E}(p_{1},\ldots,p_{I}).}$$

By using ( 61), $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{k}$ solves ( P).

Now, let p solve ( P). Then,

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{I}) \leq \mathcal{E}(p,\ldots,p) = \mathcal{E}(p),}$$

By using ( 61), (p, …, p) solves ( PA). □ 

Further, we show that the welfare maximization problem ( A) turns out to be adjoint not only for ( P), but also for ( PA). The proof of this fact uses the following Lemma 8.

Lemma 8.

For $x_{i},y \in \mathbb{R}_{+}^{n}$ , i = 1,…,I, the inequality

$$\displaystyle{ \sum _{i=1}^{I}x_{ i} \leq y }$$

(62)

is equivalent to

$$\displaystyle{ \sum _{i=1}^{I}\left \langle p_{ i},x_{i}\right \rangle \leq \left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},y\right \rangle \,\mbox{ for all }p_{i} \in \mathbb{R}_{+}^{n},i = 1,\ldots,I. }$$

(63)

Proof.

• (i) Let ( 62) be satisfied. For $p_{i} \in \mathbb{R}_{+}^{n}$, i = 1, …, I, we have

  $$\displaystyle{\sum _{i=1}^{I}\left \langle p_{ i},x_{i}\right \rangle \leq \left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},\sum _{i=1}^{I}x_{ i}\right \rangle \leq \left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},y\right \rangle.}$$

  The first inequality is due to $x_{i} \in \mathbb{R}_{+}^{n}$, and $p_{i} \leq \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}$, i = 1, …, I. The second inequality is due to ( 62) and $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I} \in \mathbb{R}_{+}^{n}$.

• (ii) Let ( 63) be satisfied. Setting there $p_{i} = p \in \mathbb{R}_{+}^{n}$, we get

  $$\displaystyle{\left \langle p,\sum _{i=1}^{I}x_{ i}\right \rangle \leq \left \langle p,y\right \rangle \,\mbox{ for all }p \in \mathbb{R}_{+}^{n}.}$$

  Hence, ( 62) is fulfilled. □ 

Theorem 16 (Adjoint for ( PA)).

The welfare maximization ( A ) is adjoint for the total revenue minimization ( PA ):

$$\displaystyle{ \mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{I}) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A} \end{array} }\left \{\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\,\left \vert \,\begin{array}{l} \sum _{k=1}^{K}\tilde{y}_{k} \geq \sum _{i=1}^{I}\tilde{x}_{i} \end{array} \right.\right \}. }$$

(64)

Proof.

We obtain:

$$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\mathcal{E}(p_{1},\ldots,p_{I}) =}$$

$$\displaystyle{\begin{array}{ll} =&\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A}\end{array} }\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) + \left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},\sum _{k=1}^{K}\tilde{y}_{ k}\right \rangle -\sum _{i=1}^{I}\left \langle p_{ i},\tilde{x}_{i}\right \rangle, \\ =&\mathop{\mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) \in \mathcal{A}\end{array} }\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right ) +\mathop{ \mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},\sum _{k=1}^{K}\tilde{y}_{ k}\right \rangle -\sum _{i=1}^{I}\left \langle p_{ i},\tilde{x}_{i}\right \rangle, \\ =&\mathop{\mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\in \mathcal{A}\\ \end{array} }\left \{\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\,\left \vert \,\begin{array}{l} \sum _{i=1}^{I}\left \langle p_{ i},\tilde{x}_{i}\right \rangle \leq \left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},\sum _{k=1}^{K}\tilde{y}_{ k}\right \rangle \\ \mbox{ for all }p_{i} \in \mathbb{R}_{+}^{n},i = 1,\ldots,I \end{array} \right.\right \}.\end{array}}$$

Applying Lemma 8, we get the assertion ( 64). □ 

Analogously, we describe how consumers may efficiently adjust their individual prices $\left (p_{i}\right )_{i=1}^{I}$ to arrive at an equilibrium price. This price adjustment also corresponds to the quasi-monotone subgradient method from Sect. 3. It is applied to the minimization of the total excessive revenue ( PA) under the auction design.

Let ith producer choose a sequence of positive confidence parameters $\left \{\chi _{i}[t]\right \}_{t\geq 0}$, i = 1, …, I. We consider the following iteration:

$$\displaystyle{ \mathbf{Pricing\ via\ Auction} }$$

(AUC)

• 1. Consumers determine their current excess supplies $\nabla _{p_{i}}\mathcal{E}(p_{1}[t],\ldots,p_{i}[t])$:

  • (a) ith consumer computes an optimal tentative consumption bundle

    $$\displaystyle{x_{i}(p_{i}[t]) \in \mathcal{X}_{i}^{{\ast}}(p_{ i}[t]),}$$

    and participation level

    $$\displaystyle{\beta _{i}(p_{i}[t]) = \left \{\begin{array}{ll} 1,&\mbox{ if }e_{i}(p_{i}[t]) \leq w_{i}, \\ 0,&\mbox{ if }e_{i}(p_{i}[t]) <w_{i},\end{array} \right.}$$

    indicating whether x _i (p _i [t]) is implemented.

    The consumption bundle is β _i (p _i [t])x _i (p _i [t]), i.e. either x _i (p _i [t]) or zero.

  • (b) kth producer identifies the highest offer prices

    $$\displaystyle{p[t] =\mathop{ \mathrm{max}}\limits _{i=1,\ldots,I}p_{i}[t],}$$

    and computes an optimal tentative production bundle

    $$\displaystyle{y_{k}(p[t]) \in \mathcal{Y}_{k}^{{\ast}}(p[t]),}$$

    and participation level

    $$\displaystyle{\alpha _{k}(p[t]) = \left \{\begin{array}{ll} 1,&\mbox{ if }\pi _{k}(p[t]) \geq \kappa _{k}, \\ 0,&\mbox{ if }\pi _{k}(p[t]) <\kappa _{k},\end{array} \right.}$$

    indicating whether y _k (p[t]) is implemented.

    The production bundle is α _k (p[t])y _k (p[t]), i.e. either y _k (p[t]) or zero.

  • (c) kth producer decides on supply shares

    $$\displaystyle{\left (\lambda _{ik}[t]\right )_{i=1}^{I} \in L\left (p_{ 1}[t],\ldots,p_{I}[t]\right ),}$$

    and supplies to ith consumer the bundle

    $$\displaystyle{\lambda _{ik}[t] \circ \alpha _{k}(p[t])y_{k}(p[t]).}$$

  • (d) ith consumer computes the current excess supply

    $$\displaystyle{ \nabla _{p_{i}}\mathcal{E}(p_{1}[t],\ldots,p_{I}[t]) =\sum _{ k=1}^{K}\lambda _{ ik}[t] \circ \alpha _{k}(p[t])y_{k}(p[t]) -\beta _{i}(p_{i}[t])x_{i}(p_{i}[t]). }$$

    (65)

• 2. ith consumer accumulates the excess supplies

  $$\displaystyle{ z_{i}[t] = z_{i}[t - 1] + \nabla _{p_{i}}\mathcal{E}(p_{1}[t],\ldots,p_{I}[t]),\quad z_{i}[-1] = 0. }$$

  (66)

• 3. ith consumer computes the price forecast w.r.t. the confidence parameter χ _i [t]:

  $$\displaystyle{ p_{i}^{+(j)}[t] = \frac{\zeta _{i}^{(j)}} {\chi _{i}[t]} \left (-z_{i}^{(j)}[t]\right )_{ +},\quad j = 1,\ldots,n, }$$

  (67)

  where ζ _i ^(j) are positive scaling coefficients.

• 4. ith consumer updates

  $$\displaystyle{ p_{i}[t + 1] = \frac{t + 1} {t + 2}p_{i}[t] + \frac{1} {t + 2}p_{i}^{+}[t] }$$

  (68)

  by combining the previous individual price with the forecast. □ 

Along with the prices $\left \{\left (p_{i}[t]\right )\right \}_{t\geq 0}$, i = 1, …, I, generated by method ( AUC), we consider the corresponding historical averages of participation levels:

$$\displaystyle{\alpha _{k}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\alpha _{ k}(p[r]),\quad \beta _{i}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\beta _{ i}(p_{i}[r]).}$$

Note that α _k [t] ∈ [0, 1] is the frequency of successful production attempts by kth producer up to time t. Analogously, β _i [t] ∈ [0, 1] is the frequency of successful consumption attempts by ith consumer up to time t. We denote by

$$\displaystyle{\gamma [t] = \left (\alpha [t],\beta [t]\right )\mathop{ =}\limits^{\mathrm{ def}}\left (\left \{\alpha _{k}[t]\right \}_{k=1}^{K},\left \{\beta _{ i}[t]\right \}_{i=1}^{I}\right )}$$

the system of average participation levels. The historical averages of production and consumption bundles are defined as follows:

$$\displaystyle{\tilde{y}_{k}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\alpha _{ k}(p[r])y_{k}(p[r]),\quad \tilde{x}_{i}[t]\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {t + 1}\sum _{r=0}^{t}\beta _{ i}(p_{i}[r])x_{i}(p_{i}[r]).}$$

Due to convexity, $\tilde{y}_{k}[t] \in \alpha _{k}[t]\mathcal{Y}_{k}$ and $\tilde{x}_{i}[t] \in \beta _{i}[t]\mathcal{X}_{i}$. We denote by

$$\displaystyle{\widetilde{F}[t] = \left (\tilde{y}[t],\tilde{x}[t]\right )\mathop{ =}\limits^{\mathrm{ def}}\left (\left \{\tilde{y}_{k}[t]\right \}_{k=1}^{K},\left \{\tilde{x}_{ i}[t]\right \}_{i=1}^{I}\right )}$$

the average market flow. Overall, the sequence

$$\displaystyle{\left (\alpha [t],\tilde{y}[t],\beta [t],\tilde{x}[t]\right ) \in \mathcal{A},\quad t \geq 0,}$$

is feasible for the adjoint problem ( A).

Now, we are ready to prove the main convergence result for ( AUC).

Theorem 17 (Convergence of Pricing via Auction).

At a productive market, let consumers apply in ( AUC ) nondecreasing confidence parameters satisfying

$$\displaystyle{\chi _{i}[t] -\chi _{i}[t - 1] \rightarrow 0,\quad \chi _{i}[t] \rightarrow \infty,\quad i = 1,\ldots,I.}$$

Then, the sequence of highest offer prices, average participation levels, and the average market flow

$$\displaystyle{\left (\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}[t],\gamma [t],\widetilde{F}[t]\right )}$$

converges toward the set of market equilibria. The achievable rate of convergence is of the order $O\left ( \frac{1} {\sqrt{t}}\right )$.

Proof.

The iteration scheme ( AUC) is a variant of the quasi-monotone subgradient method ( SM). Hence, we may obtain the convergence for ( AUC) by means of Theorem 8. For that, let us discuss the applicability of conditions ( S1)–( S3).

• On ( S1 ): The price forecast ( 67) can be derived by means of the Euclidean prox-functions for $\mathbb{R}_{+}^{n}$:

  $$\displaystyle{d_{i}(p)\mathop{ =}\limits^{\mathrm{ def}}\frac{1} {2}\sum _{j=1}^{n} \frac{1} {\zeta _{i}^{(j)}}\left (p^{(j)}\right )^{2},\quad i = 1,\ldots,I.}$$

  In fact, for $z_{i}[t] \in \mathbb{R}^{n},\chi _{i}[t]> 0$ we consider the minimization problem as from step 3. in ( SM):

  $$\displaystyle{\mathop{\mathrm{min}}\limits _{p_{1},\ldots,p_{I}\in \mathbb{R}_{+}^{n}}\left \{\sum _{i=1}^{I}\langle z_{ i}[t],p_{i}\rangle +\chi _{i}[t]d_{i}(p_{i})\right \}.}$$

  Its unique solution is the price forecast ( 67) as from step 3. in ( AUC):

  $$\displaystyle{p_{i}^{+(j)}[t] = \frac{\zeta _{i}^{(j)}} {\chi _{i}[t]} \left (-z_{i}^{(j)}[t]\right )_{ +},\quad j = 1,\ldots,n,i = 1,\ldots,I.}$$

• On ( S2 ): It follows from Theorem 16 that the total excessive revenue is representable as a maximum of concave functions:

  $$\displaystyle{\mathcal{E}(p_{1},\ldots,p_{I}) =\mathop{ \mathrm{max}}\limits _{\begin{array}{c} \left (\alpha,\tilde{y},\beta,\tilde{x}\right )\in \mathcal{A}\\ \end{array} }\varPhi \left (\alpha,\tilde{y},\beta,\tilde{x}\right )+\varphi \left (p_{1},\ldots,p_{I},\tilde{y},\tilde{x}\right ),}$$

  where

  $$\displaystyle{\varphi \left (p_{1},\ldots,p_{I},\tilde{y},\tilde{x}\right ) = \left \langle \mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i},\sum _{k=1}^{K}\tilde{y}_{ k}\right \rangle -\left \langle p_{i},\tilde{x}_{i}\right \rangle.}$$

  Although φ is not linear w.r.t. $\left (p_{1},\ldots,p_{I}\right )$, but it is partially linear, i.e.

  $$\displaystyle{\varphi \left (p,\ldots,p,\tilde{y},\tilde{x}\right ) = \left \langle p,\sum _{k=1}^{K}\tilde{y}_{ k} -\sum _{i=1}^{I}\tilde{x}_{ i}\right \rangle.}$$

  The partial linearity of φ suffices for the analogous convergence analysis as in Sect. 3 (see [12] for details). In particular, due to Theorem 16, the adjoint problem for the total revenue minimization ( PA) remains unchanged under the auction design, i.e. it is the welfare maximization ( A).

• On ( S3 ): The welfare maximization problem ( A) satisfies the Slater condition in view of the market productivity (cf. Definition 2).

Overall, we apply Theorem 8 to deduce that the sequence $\left (p_{i}[t]\right )_{i=1}^{I}$ converges toward the solution set of ( PA), and $\left (\gamma [t],\widetilde{F}[t]\right )$ converges toward the solution set of ( A) by order $O\left ( \frac{1} {\sqrt{t}}\right )$. Due to Theorem 15, $\mathop{\mathrm{max}}\limits _{i=1,\ldots,I}p_{i}[t]$ converges toward the solution set of ( P). In view of the duality from Theorem 16, the assertion follows. □ 

5 Conclusions

We presented the excessive revenue model of a competitive market. Its crucial advantage is that it can be written in potential form. The convex potential is the total excessive revenue of market’s participants. Equilibrium prices, which balance supply and demand, arise as the minimizers of the total excessive revenue. The latter constitutes the least revenue principle in analogy to extremal principles in physics. The least revenue principle allowed us to efficiently adjust prices by application of Convex Analysis. For that, we used quasi-monotone methods for nonsmooth convex minimization of the total excessive revenue. They represent implementable behavioral schemes for the real-life activities of producers and consumers due to the trade or auction. Thus, the main features of our price adjustment are as follows:

• Reliability refers to the fact that the price adjustment leads to equilibrium prices, and corresponding supply equals demand on average.

• Computability of price adjustment means that we can guarantee the convergence of the proposed price adjustment mechanisms at an explicitly stated (nonasymptotic) rate, which in fact is the best convergence rate achievable in large-scale nonsmooth convex minimization.

• Decentralization explains how market participants can successively update prices by themselves via trade or auction rather than by relying on a central authority.

Appendix

Proof of Lemma 2:.

We define the average linearization terms ℓ _t and ψ _t for f:

$$\displaystyle{\begin{array}{lcl} \ell_{t}(x)&\mathop{ =}\limits^{\mathrm{ def}}&\sum _{r=0}^{t}f(x[r]) + \left \langle \nabla f(x[r]),x - x[r]\right \rangle, \\ \psi _{t} &\mathop{ =}\limits^{\mathrm{ def}}&\mathop{\mathrm{min}}\limits _{x\in X}\left \{\ell_{t}(x) +\chi [t]d(x)\right \}.\\ \end{array} }$$

First, we show by induction that for all t ≥ 0 it holds:

$$\displaystyle{ f(x[t]) - \frac{\psi _{t}} {t + 1} \leq \rho _{t}. }$$

(69)

Let us assume that condition ( 69) is valid for some t ≥ 0. Then,

$$\displaystyle{\psi _{t+1} =\mathop{ \mathrm{min}}\limits _{x\in X}\left \{\ell_{t}(x) + f(x_{t+1}) + \left \langle \nabla f(x[t + 1]),x - x[t + 1]\right \rangle +\chi [t + 1]d(x)\right \}}$$

$$\displaystyle{\mathop{\geq }\limits^{ (37)}\mathop{\mathrm{min}}\limits _{x\in X}\left \{\ell_{t}(x) +\chi [t]d(x) + f(x[t + 1]) + \left \langle \nabla f(x[t + 1]),x - x[t + 1]\right \rangle \right \}}$$

$$\displaystyle{\mathop{\geq }\limits^{ (33)}\mathop{\mathrm{min}}\limits _{x\in X}\left \{\psi _{t} + \frac{1} {2}\chi [t]\left \|x - x^{+}[t]\right \|^{2} + f(x[t + 1]) + \left \langle \nabla f(x[t + 1]),x - x[t + 1]\right \rangle \right \}}$$

$$\displaystyle{\mathop{\geq }\limits^{ (69)}\mathop{\mathrm{min}}\limits _{x\in X}\left \{\begin{array}{l} (t + 1)f(x[t]) - (t + 1)\rho _{t} \\ + \frac{1} {2}\chi [t]\left \|x - x^{+}[t]\right \|^{2} + f(x[t + 1]) + \left \langle \nabla f(x[t + 1]),x - x[t + 1]\right \rangle \end{array} \right \}}$$

$$\displaystyle{\mathop{\geq }\limits^{ (31)}\mathop{\mathrm{min}}\limits _{x\in X}\left \{\begin{array}{l} (t + 1)\left [f(x[t + 1]) + \left \langle \nabla f(x[t + 1]),x[t] - x[t + 1]\right \rangle \right ] - (t + 1)\rho _{t} \\ + \frac{1} {2}\chi [t]\left \|x - x^{+}[t]\right \|^{2} + f(x[t + 1]) + \left \langle \nabla f(x[t + 1]),x - x[t + 1]\right \rangle \end{array} \right \}.}$$

Since (t + 2)x[t + 1] = (t + 1)x[t] + x ⁺[t], we obtain

$$\displaystyle{\psi _{t+1} \geq (t + 2)f(x[t + 1]) - (t + 1)\rho _{t}}$$

$$\displaystyle{+\mathop{\mathrm{min}}\limits _{x\in X}\left \{\left \langle \nabla f(x[t + 1]),x - x^{+}[t]\right \rangle + \frac{1} {2}\chi [t]\left \|x - x^{+}[t]\right \|^{2}\right \}}$$

$$\displaystyle{\geq (t + 2)f(x[t + 1]) - (t + 1)\rho _{t} - \frac{1} {2\chi [t]}\left \|\nabla f(x[t + 1])\right \|_{{\ast}}^{2}.}$$

$$\displaystyle{= (t + 2)f(x[t + 1]) - (t + 2)\rho _{t+1}.}$$

It remains to note that

$$\displaystyle{\psi _{0} =\mathop{ \mathrm{min}}\limits _{x\in X}\left \{f(x[0]) + \left \langle \nabla f(x[0]),x - x[0]\right \rangle +\chi [0]d(x)\right \}\mathop{ \geq }\limits^{ (35)}f(x[0]) -\rho _{0}.}$$

Now, we relate the term $\frac{\psi _{t}} {t + 1}$ from ( 69) to the adjoint problem ( 32). It holds due to convexity of φ(⋅ , a), a ∈ A:

$$\displaystyle{f(x[r]) + \left \langle \nabla f(x[r]),x - x[r]\right \rangle =}$$

$$\displaystyle{\mathop{=}\limits^{ (29),\ (30)}\varPhi \left (a(x[r])\right ) +\varphi \left (x[r],a(x[r])\right ) + \left \langle \nabla _{x}\varphi \left (x[r],a(x[r])\right ),x - x[r]\right \rangle }$$

$$\displaystyle{\leq \varPhi \left (a(x[r]\right ) +\varphi \left (x,a(x[r])\right ).}$$

Hence, we obtain due to concavity of Φ and φ(x, ⋅ ), x ∈ X:

$$\displaystyle{\ell_{t}(x) \leq \sum _{r=0}^{t}\varPhi \left (a(x[r]\right ) +\varphi \left (x,a(x[r])\right ) \leq (t + 1)\left [\varPhi \left (a[t]\right ) +\varphi \left (x,a[t]\right )\right ].}$$

Finally, we get

$$\displaystyle{ \frac{\psi _{t}} {t + 1} \leq \varPhi \left (a[t]\right ) +\mathop{ \mathrm{min}}\limits _{x\in X}\left \{\varphi \left (x,a[t]\right ) + \frac{\chi [t]} {t + 1}d(x)\right \} =\varPhi \left (a[t]\right ) -\delta _{t}(a[t]). }$$

(70)

Altogether, ( 69) and ( 70) provide the formula ( 38). □ 

The following result on the quadratic penalty for the maximization problem ( 39) will be needed.

Lemma 9.

Under ( S1 )–( S3 ) it holds for κ > 0:

$$\displaystyle{\mathop{\mathrm{max}}\limits _{\begin{array}{c} a \in A\end{array} }\left [\varPhi (a) - \frac{\kappa } {2}\sum _{j=1}^{n}\left (h_{ j}(a)\right )_{+}^{2}\right ] \leq f^{{\ast}}+\frac{1} {2\kappa }\sum _{j=1}^{n}x^{{\ast}(j)},}$$

where x ^∗ solves the minimization problem ( 28 ).

Proof.

Let a ^∗ be an optimal solution of ( 39). Due to the Slater condition, there exist some Lagrange multipliers x ^∗(j), j = 1, …, n such that

$$\displaystyle{ \left \langle \nabla \varPhi (a^{{\ast}}) -\sum _{ j=1}^{n}x^{{\ast}(j)}\nabla h_{ j}(a^{{\ast}}),a^{{\ast}}- a\right \rangle \geq 0,\quad \mbox{ for all }a \in A, }$$

(71)

$$\displaystyle{ x^{{\ast}(j)} \geq 0,\quad h_{ j}(a^{{\ast}}) \leq 0,\quad \sum _{ j=1}^{n}x^{{\ast}(j)}h_{ j}(a^{{\ast}}) = 0. }$$

(72)

Note that the vector of Lagrange multipliers $x^{{\ast}} = \left (x^{{\ast}(j)},j = 1,\ldots,n\right )$ solves the minimization problem ( 28). Due to the concavity of Φ and the convexity of h _j , j = 1, …, n, it holds for all a ∈ A:

$$\displaystyle{ \varPhi (a) \leq \varPhi (a^{{\ast}}) + \left \langle \nabla \varPhi (a^{{\ast}}),a - a^{{\ast}}\right \rangle, }$$

(73)

$$\displaystyle{ h_{j}(a) \geq h_{j}(a^{{\ast}}) + \left \langle \nabla h_{ j}(a^{{\ast}}),a - a^{{\ast}}\right \rangle. }$$

(74)

We estimate

$$\displaystyle{\begin{array}{rcl} \varPhi (a)&\mathop{ \leq }\limits^{ (73)}&\varPhi (a^{{\ast}}) + \left \langle \nabla \varPhi (a^{{\ast}}),a - a^{{\ast}}\right \rangle \mathop{\leq }\limits^{ (71)}f^{{\ast}} +\sum _{ j=1}^{n}x^{{\ast}(j)}\left \langle \nabla h_{ j}(a^{{\ast}}),a - a^{{\ast}}\right \rangle \\ &\mathop{\leq }\limits^{ (74)}&f^{{\ast}} +\sum _{ j=1}^{n}x^{{\ast}(j)}\left (h_{ j}(a) - h_{j}(a^{{\ast}})\right )\mathop{ =}\limits^{ (72)}f^{{\ast}} +\sum _{ j=1}^{n}x^{{\ast}(j)}h_{ j}(a),\quad a \in A.\\ \end{array}}$$

Hence,

$$\displaystyle{\begin{array}{rcl} \mathop{\mathrm{max}}\limits _{\begin{array}{c} a \in A \end{array} }\left [\varPhi (a) - \frac{\kappa } {2}\sum _{j=1}^{n}\left (h_{ j}(a)\right )_{+}^{2}\right ]& \leq &f^{{\ast}} +\mathop{ \mathrm{max}}\limits _{\begin{array}{c} a \in A \end{array} }\sum _{j=1}^{n}\left [x^{{\ast}(j)}h_{ j}(a) - \frac{\kappa } {2}\left (h_{j}(a)\right )_{+}^{2}\right ] \\ & \leq &f^{{\ast}} +\sum _{ j=1}^{n}\mathop{ \mathrm{max}}\limits _{\begin{array}{c} b_{j} \in \mathbb{R} \end{array} }\sum _{j=1}^{n}\left [x^{{\ast}(j)}b_{ j} - \frac{\kappa } {2}\left (b_{j}\right )_{+}^{2}\right ] \\ & =&f^{{\ast}} +\sum _{ j=1}^{n}\frac{1} {2\kappa }x^{{\ast}(j)}. \\ \end{array} }$$

 □ 

Proof of Lemma 3:.

First, we estimate the penalty term δ _t and the remainder term ρ _t , t ≥ 0 under (S1)–(S3). It holds:

$$\displaystyle{\begin{array}{lcl} \delta _{t}(a[t])& =& -\mathop{\mathrm{min}}\limits _{x\in X}\left \{\varphi (x,a[t]) + \frac{\chi [t]} {t + 1}d(x)\right \} \\ & =& -\mathop{\mathrm{min}}\limits _{x\in \mathbb{R}_{+}^{n}}\left \{-\sum _{j=1}^{n}x^{(j)}h_{ j}(a[t]) + \frac{\chi [t]} {t + 1} \cdot \frac{1} {2}\sum _{j=1}^{n}\left (x^{(j)}\right )^{2}\right \} \\ & =&\frac{t + 1} {\chi [t]} \sum _{j=1}^{n}\left (h_{ j}(a[t])\right )_{+}^{2}, \\ \rho _{t} & =& \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {2\chi [r - 1]}\left \|\nabla f(x[r])\right \|_{{\ast}}^{2} \\ & =& \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {2\chi [r - 1]}\sum _{j=1}^{n}\left (h_{ j}(a[r])\right )^{2} \\ & \leq &C_{2} \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {\chi [r - 1]}. \end{array} }$$

The latter inequality follows due to the compactness of the adjoint set A and the convexity of h _j , j = 1, …, n with

$$\displaystyle{ C_{2} = \frac{1} {2}\mathop{\mathrm{max}}\limits _{a\in A}\sum _{j=1}^{n}\left (h_{ j}(a)\right )^{2}. }$$

(75)

Substituting into ( 38), we get the right-hand side of ( 40):

$$\displaystyle{f(x[t]) -\varPhi (a[t]) + \frac{t + 1} {\chi [t]} \sum _{j=1}^{n}\left (h_{ j}(a[t])\right )_{+}^{2} \leq C_{ 2} \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {\chi [r - 1]}.}$$

Now, we estimate this dual gap from below by using

$$\displaystyle{\begin{array}{rcl} \varPhi \left (a[t]\right ) -\frac{t + 1} {\chi [t]} \sum _{j=1}^{n}\left (h_{ j}(a[t])\right )_{+}^{2} & \leq &\mathop{\mathrm{max}}\limits _{\begin{array}{c} a \in A \end{array} }\left [\varPhi (a) -\frac{t + 1} {\chi [t]} \sum _{j=1}^{n}\left (h_{ j}(a)\right )_{+}^{2}\right ] \\ &\mathop{ \leq }\limits^{\mbox{ Lemma 9}}&f^{{\ast}} + C_{ 1} \frac{\chi [t]} {t + 1},\end{array} }$$

where

$$\displaystyle{ C_{1} = \frac{1} {4}\sum _{j=1}^{n}x^{{\ast}(j)} }$$

(76)

and x ^∗ is a solution of the minimization problem ( 28).

Finally, we get the left-hand side of ( 40)

$$\displaystyle{f(x[t]) -\varPhi (a[t]) + \frac{t + 1} {\chi [t]} \sum _{j=1}^{n}\left (h_{ j}(a[t])\right )_{+}^{2} \geq f(x[t]) - f^{{\ast}}- C_{ 1} \frac{\chi [t]} {t + 1}.}$$

 □ 

Proof of Lemma 4:.

Since χ[t] −χ[t − 1] → 0, it holds by averaging that $\frac{1} {t + 1}\sum _{r=0}^{t}\chi [r] -\chi [r - 1] \rightarrow 0$. Thus,

$$\displaystyle{ \frac{1} {t + 1}\chi [t] = \frac{1} {t + 1}\sum _{r=0}^{t}\chi [r] -\chi [r - 1] + \frac{1} {t + 1}\chi [-1] \rightarrow 0.}$$

From χ[t] → ∞ we have $\frac{1} {\chi [t]} \rightarrow 0$, and also by averaging, $\frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {\chi [r - 1]} \rightarrow 0.$

The convergence of the order $O\left ( \frac{1} {\sqrt{t}}\right )$ can be achieved in ( 42) by choosing $\chi [t] = O(\sqrt{t})$. In fact, we obtain:

$$\displaystyle{ \frac{1} {t + 1}\sum _{r=0}^{t} \frac{1} {\chi [r - 1]} = \frac{1} {t + 1}\left ( \frac{1} {\chi [-1]} + \frac{1} {\chi [0]}\right ) + \frac{1} {t + 1}\sum _{r=1}^{t} \frac{1} {\sqrt{r}}.}$$

Immediately, we see that $\frac{1} {t+1}\left ( \frac{1} {\chi [-1]} + \frac{1} {\chi [0]}\right ) \rightarrow 0$ as of the order $O\left (\frac{1} {t} \right )$. Note that for a convex univariate function ξ(r), $r \in \mathbb{R}$, and integer bounds a, b, we have

$$\displaystyle{ \sum _{r=a}^{b}\xi (r) \leq \int \limits _{ a-1/2}^{b+1/2}\xi (s)\mathrm{d}s. }$$

(77)

Hence, we get

$$\displaystyle{ \frac{1} {t + 1}\sum _{r=1}^{t} \frac{1} {\sqrt{r}}\mathop{ \leq }\limits^{ (77)} \frac{1} {t + 1}\int \limits _{1-1/2}^{t+1/2} \frac{1} {\sqrt{s}}\mathrm{d}s}$$

$$\displaystyle{= \frac{2} {t + 1}\sqrt{s}\,\Big\vert _{1/2}^{t+1/2} = \frac{2} {t + 1}\left (\sqrt{t + 1/2} -\sqrt{1/2}\right ) \rightarrow 0.}$$

Here, the order of convergence is $O\left ( \frac{1} {\sqrt{t}}\right )$. By assuming $\chi [t] = O(\sqrt{t})$, the convergence $\frac{\chi [t]} {t + 1} = \frac{\sqrt{t}} {t + 1} \rightarrow 0$ is also of the order $O\left ( \frac{1} {\sqrt{t}}\right )$. □