Switched-Capacitor Power-Converter Topology Overview and Performance Comparison

Abstract

Switched-capacitor power converters are interesting candidates to realize integrated power converters with acceptable power efficiencies. Depending on the input and output voltage ranges to be accommodated at a desired efficiency, certain voltage conversion ratio(s) need(s) to be implemented. Though the theoretical minimum number of floating capacitors to realize a desired voltage conversion ratio is known, how to actually synthesize the corresponding topologies and what impact these topologies have on circuit performance is less trivial. Besides two-clock-phase topologies, multiple-clock-phase topologies have recently been introduced. This paper gives an overview of various methods to implement desired voltage conversion ratios with two or multiple clock phases and compares their performance under given boundary conditions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In our modern society, the use of data-centric electronic devices has become ubiquitous. Due to the consumer demand of being able to use these devices anywhere, a multitude of battery-powered devices exists, including laptops, smart phones, smart watches and other so-called wearable electronic devices. Depending on the usage demands, energy storage in these devices can be implemented with a variety of different battery chemistries, where either primary (non-rechargeable) or secondary (rechargeable) batteries are used. In many cases, Li-ion batteries are used due to their superior energy density. Depending on the used battery chemistry for energy storage, the input voltage to the electronic device spans a relatively large range. At the same time, a large number of different load voltages for internal supply and for accommodating external interfaces need to be derived from the input voltage in the electronic device [1]. Bridging the gap between the input voltage range and the necessary load voltages in the electronic device can be accommodated by the power management block in Fig. 13.1 [2]. As can be seen in the figure, both voltage up and down conversion may be needed to bridge the voltage gap.

Fig. 13.1

Mismatch between energy storage voltage and load voltage [2]

Voltage conversion in the power management block in Fig. 13.1 can be implemented in three different ways, i.e. with a continuous-time voltage regulator, an inductive or a switched-capacitor power converter (SCPC) [3]. In a continuous-time voltage regulator a dissipative pass device only allows implementing voltage down conversion from input voltage V _in to a lower output voltage V _out at a maximum efficiency of V _out /V _in . Despite their favorable Electro-Magnetic-Interference (EMI) behavior, in cases where V _out is much lower than V _in , the low efficiency may become a problem, especially at high power levels. Switched-mode circuits using reactive component(s) for temporal energy storage can implement both up and down DC/DC conversion at higher efficiency. If the primary reactive energy-storage component is an inductor, an inductive DC/DC converter can be implemented with two power switches and an inductor. Depending on how the switches and inductor are connected, either a down, an up, or an inverting up-down DC/DC converter can be constructed [4]. The ratio between input and output voltage is controlled by the duty cycle at which the power switches are operated. If the primary reactive energy-storage component is a capacitor, an SCPC can be implemented with a set of power switches and one or more so-called floating capacitors. As this paper will discuss in detail, the topology in which these switches and capacitor(s) are connected determines the ratio between input and output voltage. The output impedance of the converter is controlled to maintain a fixed output voltage when output current and/or input voltage vary.

Besides maximizing the run time of the battery-powered electronic devices by increasing the energy density of batteries and increasing the efficiency of voltage conversion, reducing the power consumption of the load is also important. For digital loads, increasing the power efficiency while maintaining the performance has led to the introduction of fine-grained power-management schemes, such as scaling the digital supply voltage with the activity of the connected block [5]. This need for local supply-voltage generation has sparked the development of DC/DC converters that are integrated with the load [1, 3].

Various methods exist to integrate the inductor with an inductive DC/DC converter [1, 3]. First, the inductor can be integrated on the same die as the converter power switches, converter control block and load, either as an air-core inductor [6, 7], or as post-processed thin-film inductor with magnetic core, e.g. based on CoZrTa alloys [8]. Alternatively, the inductor can be integrated elsewhere in the package, e.g. using bondwires [9] or package-trace air-core inductors [10], or realizing the inductor on a separate passive-integration die co-packaged with the active CMOS die [11]. In all cases, integrated inductive converters are used for relatively high output powers above 100 mW [3], because the efficiency performance of integrated inductive DC/DC converters decreases when realized for lower output power in smaller areas, in contrast to that of their integrated capacitive counterparts [12]. This makes SCPCs an attractive candidate for monolithic integration in the power range below 100 mW, but even when external SMD capacitors are used to realize higher output powers, competitive power densities compared to inductive DC/DC converters with external inductor can be shown [13].

Several monolithic capacitor integration possibilities exist for SCPCs, such as using the gate capacitance of MOSTs (MOSCAPs), using inter-metal capacitance in fringe capacitors (usually placed on top of MOSCAPs), or, when available, using Metal-Insulator-Metal (MIM) capacitors [1, 3]. Higher power densities can be obtained when non-standard capacitor realizations such as trench capacitors are used [14]. Besides purely inductive or switched-capacitor DC/DC converters, intermediate solutions are also appearing. On the one hand, floating capacitors are added to integrated inductive converters to create multiple voltage levels at the switching node [15, 16]. This reduces the ripple current in the inductor and the blocking voltage in the switches and therefore increases efficiency. On the other hand, inductors are added to integrated capacitive converters to reduce losses associated with (dis)charging the capacitors [17].

This paper deals with the fundamental aspect in SCPCs of how to realize the needed voltage conversion ratios in different ways, and how the resulting different topologies compare in performance. Section 13.2 gives a basic theoretical background on switched-capacitor power conversion. Sections 13.3 and 13.4 describe two-clock-phase and multi-clock-phase topology examples and how to synthesize these. A performance comparison of the various topologies in Sects. 13.3 and 13.4 is made in Sect. 13.5. Finally, conclusions are drawn in Sect. 13.6.

2 Theoretical Considerations for Switched-Capacitor Power Converters

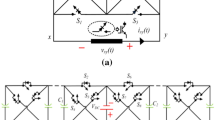
The basic model of an SCPC is shown in Fig. 13.2a [3]. An ideal DC transformer multiplies the input voltage V _in with voltage conversion ratio M. As will be described in more detail in Sects. 13.3 and 13.4, this ratio M depends on the used circuit topology, i.e. how the capacitors are connected during the different clock phases of the converter. The average equivalent output impedance of the converter is modelled by R _out . As shown in Fig. 13.2b, R _out shows asymptotic behavior for both low and high values of switching frequency, f _s [18]. For low values of f _s , the asymptote is the Slow-Switching Limit (SSL), whereas for high f _s values the Fast-Switching Limit (FSL) defines the asymptote. In the SSL, the currents flowing into capacitors are impulsive and reach zero at the end of each clock phase, and R _out depends on f _s and the used floating capacitance. In the FSL, the voltage across the capacitors does not change during the conductance phase and R _out depends on the resistance in the charge and discharge path of the floating capacitors, i.e. mostly the on-resistance of the power switches. The asymptotes cross at corner frequency, f _c . The overall curve for R _out can now be approximated by:

Fig. 13.2

(a) Averaged model of an SCPC, (b) equivalent output impedance R_out as function of switching frequency f_s

$$ {R}_{out}=\sqrt{R_{FSL}^2+{R}_{SSL}^2} $$

(13.1)

As can be seen from Fig. 13.2a, the maximum possible efficiency of an SCPC equals V _out /MV _in . However, since the averaged model does not consider the switching nature of the converter, in reality the achieved efficiency will be lower due to the occurrence of switching losses. These losses are caused by charging and discharging the parasitic capacitances associated with the plates of each floating capacitor in the converter, also known as bottom-plate losses, and by driver losses from turning the power switches on and off. Besides switching losses, conduction losses occur with a value of (MV _in  − V _out )I _out , as can be inferred from Fig. 13.2a.

In order to maintain a relatively high efficiency in cases where either V _in or V _out or both, have a large range, multiple values of M need to be used. In a multi-ratio SCPC, these multiple values of M can be generated using a single circuit [3]. A recent example of using eight values of M to maintain an efficiency above 90 % across the full range of a Li-ion battery as input source is given in [13]. Another important aspect in the design of any switched-mode power converter is the output voltage ripple. As with inductive DC/DC converters, interleaving can be applied in SCPCs as well to reduce output voltage ripple [3, 19]. This can be achieved by splitting up a large converter that delivers charge packets Q to the output at time instants T _s  = 1/f _s apart, in N identical parallel converters or modules, each delivering a charge packet Q/N to the output consecutively at time instants T _s /N apart. For integrated converters, splitting up a converter in parallel modules is not an issue. Scaling a converter for higher or lower output power then entails placing more or fewer of these modules in parallel. Finally, the control of output voltage V _out involves selecting the correct value of M (in case a multi-ratio converter is used), which usually is implemented open-loop using a look-up table, and modulating the value of R _out in a closed control loop [3]. Modulation of R _out is mostly done by varying f _s (in the SSL), but can also be achieved by varying the floating capacitance (in the SSL) or modulating the on-resistance or the duty cycle of the power switches (in the FSL).

For a given number of floating capacitors, all possible values of M that can be realized using these capacitors can be calculated based on the Fibonacci number series [3, 20]. This is illustrated in Table 13.1 [3].

Table 13.1 All possible values of M in relation to number of floating capacitors

Though Table 13.1 shows which values of M can be realized, the systematic synthesis of each of these values has not been addressed so far. In many cases, the ratios given in Table 13.1 can be realized in multiple ways, leading to different performance tradeoffs. This paper describes the different ways that exist to realize a desired value of M, using either two clock phases (Sect. 13.3) or more than two clock phases (Sect. 13.4), and their performances are compared in Sect. 13.5.

3 Two-Clock-Phase Topologies

In two-clock-phase SCPCs, the floating capacitors are charged and discharged in two consecutive clock phases, both clock phases fitting within one switching period, T _s . In steady state, the charging and discharging in the two clock phases are balanced. Section 13.3.1 gives an overview of the historically used two-clock-phase topologies, while Sect. 13.3.2 describes a synthesis method for two-clock-phase SCPC topologies.

3.1 Overview of Known Topologies

As described in Sect. 13.1, SCPCs can accommodate both voltage up and down conversion. In fact, a converter designed for a voltage conversion ratio M can also be used for the voltage conversion ratio 1/M by swapping input and output connections. As Table 13.1 shows, for each M that is realizable with a given number of floating capacitors, there is a corresponding 1/M value. Therefore, only voltage down conversion is considered in this section, but the five basic topologies shown also hold for up conversion [21, 22]. The five most well-known switched-capacitor power conversion topologies for M = 1/8 are shown in Fig. 13.3. For each topology, the circuit constellations in the two clock phases ϕ ₁ and ϕ ₂ are depicted, without showing the switch topology necessary to achieve these two states in a single circuit. The floating capacitors are denoted by C _i and the DC voltage across them is indicated as normalized to V _out , whereas the output buffer capacitor is C _out with voltage V _out  = V _in /8 across it.

Fig. 13.3

Most well-known SCPC topologies for M = 1/8: (a) Dickson, (b) ladder, (c) series-parallel, (d) fractional-1, (e) recursive [24]

The Dickson topology is shown in Fig. 13.3a. This topology was inspired by the Greinacher or Cockroft-Walton topology, which effectively implements an AC/DC voltage conversion and therefore is not considered here. The Dickson topology is primarily applied in voltage up converters, since one of the switches in the charging path of each floating capacitor can be replaced with a diode, which simplifies converter control. To accommodate a voltage conversion ratio of M or 1/M, M − 1 floating capacitors are needed, leading to seven floating capacitors in Fig. 13.3a. The ladder topology consists of two chains of series-connected floating capacitors that slide up and down along each other, which sets it apart from the other four topologies, since within each string the floating capacitors remain connected in the same order in both clock phases. To accommodate a voltage conversion ratio of M or 1/M, 2M − 3 floating capacitors are needed, corresponding to thirteen floating capacitors in Fig. 13.3b. This inefficient use of the available capacitance makes the ladder topology less practical, but since all intermediate voltages are available at the ladder taps, it can be used as auxiliary converter to realize the needed drive voltages in a main SCPC [23].

The series-parallel topology shown in Fig. 13.3c uses M − 1 floating capacitors to achieve a voltage ratio of M or 1/M. In contrast to the Dickson topology, each floating capacitor has the same DC voltage across it in steady state. Figure 13.3d shows one example of a fractional topology using the minimum possible number of capacitors to realize M = 1/8 according to Table 13.1, i.e., four floating capacitors. Due to this most efficient use of capacitance compared to the other four topologies, many examples of fractional SCPCs can be found in the literature. However, though Table 13.1 shows what ratios are possible, in practice a fractional topology to realize a desired value of M is usually derived by trial and error.

A larger number of capacitors compared to the fractional topology of Fig. 13.3d can be used to achieve equally spaced voltage conversion ratios using a modular approach [24], as shown in Fig. 13.3e. With the smart reconfiguration of multiple replicas of the same 2:1 unit cell (M = 1/2) consisting of two floating capacitors, 2^N − 1 voltage ratios can be achieved using N unit cells, so 2N floating capacitors. Though less voltage ratios are possible for a given number of floating capacitors compared to Table 13.1, the recursive approach of placing the same unit cell in series or parallel makes this topology easily reconfigurable. This can be an advantage compared to the fractional topology, especially when a multi-ratio converter is needed to maintain efficiency over a wider input or output voltage range.

3.2 Topology Synthesis

To break away from the trial and error aspect for the topology synthesis in Fig. 13.3d, a generic iterative algorithm for synthesizing SCPC topologies was developed [25]. A short summary of the method is given in this section. Figure 13.4 shows a conceptual block diagram of a two-clock-phase SCPC consisting of n _c floating capacitors with three external terminals.

Fig. 13.4

Conceptual SCPC with n_c floating capacitors

The Fibonacci limit for the achievable conversion gains of SCPCs was introduced in Table 13.1. According to this limit, with n _c floating capacitors all conversion ratios given by Eq. (13.2) can be realized:

$$ M(n_c)=\frac{V_{out}}{V_{in}}=\frac{1\le P\le {F}_{n_c+1}}{1\le Q\le {F}_{n_c+1}} $$

(13.2)

where P and Q are integers and F _n is the n _cth Fibonacci number. The synthesis algorithm for a target conversion ratio, M = P/Q, is divided into two steps:

• I) Iterative generation of configuration pairs: In this step, all valid configuration pairs (without considering connections to the external terminals) with the required number of floating capacitors, as given by the Fibonacci limit of Eq. (13.2), are generated through iteration. For each configuration pair, n _c floating capacitor voltages and the output voltage V _out need to be resolved, so valid configuration pairs are the ones that yield n _c  + 1 valid KVL(Kirchoff Voltage Law) equations while maintaining charge balance for each floating capacitor. These valid configuration pairs are depicted in Table 13.2, where c _i denote the floating capacitors, and q _Φ1 and q _Φ2 are the effective charge coefficients during the two clock phases, and q _sum  = q _Φ1 + q _Φ2. A configuration pair describes charge flow through the floating capacitors and corresponds to the set of KVL equations for each clock phase.

  Table 13.2 Valid configuration pairs for n_c = 2, 3 and 4 (redundant pairs omitted)

• II) Terminal assignment: A converter with a desired voltage conversion ratio, M = V _out /V _in  = P/Q has charge conversion ratio q _out /q _in  = 1/M = Q/P. After normalization, q _out  = Q and q _in  = P. With terminal assignment, the three external terminals are connected to the configuration pairs with q _sum  ≥ max(P,Q) such that the charge conversion ratio is satisfied over the two phases Φ ₁ and Φ ₂.

A more detailed example of applying the two synthesis steps is given in [25]. To further illustrate the application of this algorithm, consider M = 1/8, which implies P = 1, and Q = 8. Following the steps of the algorithm:

• 1) n _c  = 4 from the Fibonacci limit on the possible conversion ratios, see Table 13.1.

• 2) Table 13.2 gives all possible configuration pairs for n _c  = 4. The exact explanation of this table can be found in [25].

• 3) Out of 11 possible configuration pairs, only the configuration pair (4.4) satisfies q _sum  ≥ max(P,Q), since it has a value q _sum  = 8. Its charge flow diagram is shown in Fig. 13.5a. The terminal assignment with P = 1 and Q = 8 can be done in two different ways resulting in two different topologies with the same M. Figure 13.3d shows the results of polarity assignment to the capacitors corresponding to assignment (1) and Fig. 13.5b shows it for assignment (2).

  Fig. 13.5

  

  (a) Charge flow diagram for configuration pair (4.4) in Table 13.2, (b) synthesized alternative fractional-2 SCPC topology to realize M = 1/8

It should be noted that the floating capacitors of the two topologies with M = 1/8 have identical charge coefficients as defined in [18], hence the same SSL and FSL impedances. However, they differ in the capacitor and switch blocking voltages, hence one topology can be better suited over the other in a given application. This point will be developed further in Sect. 13.5.

4 Multi-Clock-Phase Topologies

The Fibonacci constraint on the minimum required number of floating capacitors can be extended by employing additional clock phases within each switching period T _s . In these multi-clock-phase topologies, the charge balance of the capacitors can occur over more than two clock phases. Two recent examples of multi-clock-phase SCPCs are given in Sect. 13.4.1, while Sect. 13.4.2 shows examples of alternative synthesized multi-clock-phase topologies.

4.1 Overview of Known Topologies

An example of a topology using three clock phases achieving a voltage up-conversion ratio M = 6 using three floating capacitors is shown in Fig. 13.6 [26]. By exploiting an additional clock phases, this topology uses one less floating capacitor to realize M = 6. The operation of the converter is as follows:

Fig. 13.6

SCPC topology using three clock phases for M = 6 [26]

• Φ₁: C ₁ and C ₂ are charged to V _in while C ₃ is unconnected: normalized charge coefficients q _c1 = 2, q _c2 = 2, q _c3 = 0.

• Φ₂: C ₁ and C ₂ are placed in series with V _in and C ₃ is charged to 3V _in : charge coefficients q _c1 = −1, q _c2 = −1, q _c3 = 1.

• Φ₃: C ₁, C ₂ and C ₃ are in series with V _in to charge C _out to 6V _in : charge coefficients q _c1 = −1, q _c2 = −1, q _c3 = −1.

The charge coefficients in the three clock phases reveal an important difference between multi-clock-phase and two-clock-phase topologies: in multi-clock-phase topologies, the amount of (dis)charge supplied to a floating capacitor does not need to be the same during each clock phase unlike the two-clock-phase topologies. The charge balancing of the floating capacitors occurs over more than two clock phases, with some capacitors potentially being inactive during certain phase(s). This feature will result in different output impedance characteristics for a multi-clock-phase topology compared to a two-clock-phase topology. In the realization of the switched-capacitor up converter using this topology, the capacitance values of C ₂ and C ₃ were increased to enable the reduction of the capacitance of C ₁ and hence its full integration, leaving only two SMD floating capacitors. Therefore, the potential of this multi-clock-phase topology to realize the desired M with a lower number of capacitors than prescribed by Table 13.1 was fully exploited to yield a high-efficiency, low-volume DC/DC converter.

Another approach to realizing multi-clock-phase converters is based on binary topologies [27]. The binary topologies employ ${2}^{n_c}$ clock phases with n _c floating capacitors to provide the binary conversion ratios given by:

$$ M=\frac{1\le P\le {2}^{n_c}-1}{2^{n_c}} $$

(13.3)

Figure 13.7 shows an example with M = 1/2³ = 1/8 that uses three floating capacitors with eight clock phases. A unit charge is supplied to V _out during each clock phase, resulting in a total of eight units of charge over a complete switching period. Therefore, the charge coefficient of each floating capacitor, when it is used, is always 1/8, the minimum possible. This minimum charge coefficient will result in the lowest SSL impedance as will be discussed in Sect. 13.5 (given the same total amount of floating capacitance and the same switching frequency). In [27], this topology has been implemented using a cascade of N 2:1 unit cells (M = 1/2) operating in successively doubling frequencies, which is the same as having a single switching frequency with 2^N clock phases. This approach has the advantage of modularity, similar to the two-clock-phase variant in Fig. 13.3e.

Fig. 13.7

Binary eight-clock-phase topology providing M = 1/8 [27]

Two observations can be made about this topology: (1) from the charge-flow point of view, the configurations in the phases Φ ₂, Φ ₄, Φ ₆, and Φ ₈ are identical to each other, just as the configurations in phases Φ ₃, and Φ ₇ are identical to each other, (2) each configuration has only one KVL loop. This means that there are actually only four unique configurations in this topology. This is consistent with the requirement of four linearly independent loops to uniquely resolve the voltages across the capacitors and the output voltage V _out [25].

4.2 Topology Synthesis

By combining the configurations with identical charge flow in Fig. 13.7 in a single phase, a multi-clock-phase fractional topology using four clock phases instead of eight clock phases can be made as shown in Fig. 13.8. The (dis)charging behavior of this topology is depicted in the table shown in the inset, normalized to q _in  = q _out /8.

Fig. 13.8

Alternative M = 1/8 topology with four clock phases, including charging behaviour

By manipulating the table in Fig. 13.8, other multi-clock-phase topologies can be generated. As an example, consider a target conversion ratio of M = 1/7. This converter delivers a normalized total charge of 7q _in to V _out over one switching period. To achieve this, the last two rows of the table in Fig. 13.8 can be adapted, resulting in the (dis)charging behavior of the table in Fig. 13.9. The (dis)charging of the floating capacitors has also been changed to maintain charge balance. The resulting topology is shown in Fig. 13.9 resulting in a four-clock-phase topology with M = 1/7. In general, with n _c floating capacitors, topologies with a conversion ratio given by:

Fig. 13.9

Four-clock-phase topology to generate M = 1/7 including charging behavior

$$ M=\frac{1\le P\le {2}^{n_c}}{1\le Q\le {2}^{n_c}} $$

(13.4)

can be realized using a maximum of n _c  + 1 clock phases (discounting repetition of configurations with identical charge flow, as in the case of binary multi-clock-phase topologies).

5 Topology Performance Comparison

5.1 Comparison Between Alternative Two-Clock-Phase Topologies

As described in previous sections, there are many different topologies that can provide the same conversion ratio M. However, they might present different advantages or disadvantages that makes them more or less suitable for different applications. From the functionality point of view of an SCPC, the most important parameter besides M, is the amount of output impedance R _out (see Fig. 13.2). In the SSL region, the output impedance R _SSL can be computed as follows:

$$ {R}_{SSL}=\frac{m}{f_s{C}_T} $$

(13.5)

where f _s is the switching frequency, C _T is the total amount of floating capacitance and m is a topology-dependent parameter that is determined by circuit analysis [18].

In the FSL region, the output impedance R _FSL only depends on the on-resistance of the switches (neglecting the interconnect parasitic resistances) and the topology, and can be expressed as follows:

$$ {R}_{FSL}=p\frac{k_{sw}}{A_{swT}} $$

(13.6)

where p is a topology-dependent parameter obtained by circuit analysis [18], A _swT is the total area of the switches in [mm²], and k _sw is a technology-related parameter that states the on-resistance of the switches per unit of silicon area (assuming the same voltage rating for all the devices), in [Ω⋅mm²]. Therefore, the inverse ratio A _swT /k _sw describes the amount of conductance that is used by the design.

Table 13.3 shows the values of the p and m parameters for a number of different topologies that provide the same conversion ratio (M = 1/8) with a different number of floating capacitors n _c . As shown, all the different two-clock-phase topologies (A–E) have the same m and p values, which means that actually all the considered topologies will present the same output impedance provided that they operate at the same switching frequency, use the same amount of total floating capacitance and the same total amount of area for the switches.

Table 13.3 Performance parameter comparison of various M = 1/8 topologies

Topologies F and G in Table 13.3 represent the two different multi-clock-phase topologies that were introduced in Sect. 13.4, also providing M = 1/8. However, because of their multi-clock-phase nature, conclusions from the comparison with the two-clock-phase topologies cannot be derived directly. This will be commented in Sect. 13.5.2, along with the content of the last two columns.

In more detail, the parameters shown in Table 13.3 can be described as follows:

• n _c  → the number of required floating capacitors.

• n _sw  → the number of power switches.

• m → product of R _SSL , the switching frequency and the total amount of floating capacitance (given the optimum relative sizing of all the floating capacitors), see Eq. (13.5).

• p → ratio between R _FSL and the amount of conductance, given the optimum relative sizing of all the power switches, see Eq. (13.6).

• l → this parameter can be used as an indication of the bottom-plate power losses that a topology suffers from. If all the energy spent to charge and discharge the parasitic bottom-plate capacitors is considered lost (pessimistic approach), the l parameter is calculated as:

$$ l={\displaystyle \sum_{i=1}^{n_C}{C}_{Ri}{V}_{Ri}^2} $$

(13.7)

where C _Ri is the value of each floating capacitor normalized to the total amount of floating capacitance C _T , and V _Ri is the voltage across each floating capacitor, normalized to the input voltage V _in . From the l parameter definition in Eq. (13.7), it becomes straightforward to compute the total amount of bottom-plate losses:

$$ {P}_{bot}={V}_{in}^2{f}_s\alpha {C}_Tl $$

(13.8)

where α is a technology-dependent ratio representing the average of both top-plate and bottom-plate parasitics of the floating capacitors relative to their capacitance.

• The summation of the g⋅V _off ² (conductance g and blocking voltage V _off ) values of all the power switches. The blocking voltage is squared because conceptually, the on-resistance of a power switch increases with the square of its blocking voltage. This parameter provides an intuitive indication about the size of the switches, and as a result, also about the energy that needs to be spent to drive their gates.

• The summation of V _ci ⋅q _ci for all the floating capacitors. This parameter becomes especially relevant in fully integrated solutions, since the relative sizes of the floating capacitors is proportional to the amount of charge flowing through them and the operating voltage across them.

• V _Ci  → The voltage across each of the floating capacitors C _i (normalized to the output voltage V _out  = V _in /8), as shown in Sects. 13.3 and 13.4.

• q _Ci  → The amount of charge flowing through each of the floating capacitors C _i (normalized to the amount of input charge per switching period q _in  = q _out /8 = I _out ⋅T _s /8).

Based on comparing only the p and m parameters of two-clock-phase topologies A–E, it could be concluded that all the different topologies would provide the same performance. However, looking at the rest of the table content, substantial advantages could be obtained by making a proper topology choice for a particular application-technology combination. Below, different possible scenarios will be discussed.

5.1.1 Scenario 1: Floating Capacitors Realized with External SMDCapacitors

For this scenario, the most interesting options would be the fractional topologies (D and E), because they require the smallest number of capacitors and pins. Since the amount of bottom-plate parasitics of SMD capacitors is normally negligible, in case of a high-voltage application, the fractional-1 topology (D) would represent a better fit since the operating voltage across the floating capacitors is smaller. On the other hand, if this becomes irrelevant, e.g. because of the relatively low voltage of the application, then the fractional-2 topology (E) would be preferred because of the lower combination of conductance and blocking voltage of the power switches, which would likely result in lower switching losses.

5.1.2 Scenario 2: Fully Integrated Switched-Capacitor PowerConverter

In the fully-integrated scenario, the relative importance of the different parameters changes quite significantly. In the integrated domain, the number of floating capacitors is not a problem by itself, but their total size is. If the application is sufficiently low-voltage enough, so that the voltage across the capacitors does not impact their implementation towards a lower capacitance density, then a Dickson topology (A) would clearly be the best choice due to its extremely low bottom-plate losses, and low area required for the switches. On the other hand, when a particular application runs at a relatively high voltage, a series-parallel topology (B) could become interesting due to the minimization of the voltage across all the floating capacitors, despite the significantly larger amount of bottom-plate and switching losses. The fractional-2 topology (E) shows a good trade-off between blocking voltage and conductance of the required switches, as well as very low bottom-plate power losses and applied voltage across the floating capacitors. Despite not standing out in any of the main converter parameters, the recursive topology (C) provides a very interesting modular approach to implement a multi-ratio SCPC by means of smart interconnection of unit cells that implement M = 1/2. This implies that a single cell could be designed, replicated and smartly used to easily create a large range of conversion ratios (though not all the possible ones). Unfortunately, in cases where extremely high or low ratios are needed, the number of needed unit cells and therefore floating capacitors would make a design based on external components (scenario 1) unpractical.

It is important to take into account that all parameter values shown in Table 13.3 are merely indicative of a trend, and would only apply to cases where the voltage rating of devices (both floating capacitors and power switches) could be gradually adjusted in a continuous way. Unfortunately, most technology processes provide devices with very specific voltage ratings that change in discrete steps. This clearly precludes the existence of an absolute optimum choice for every different application-technology combination.

5.2 Comparison Between Two-Clock-Phase and Multi-Clock-Phase Topologies

In this section, the more conventional two-clock-phase topologies will be compared to multi-clock-phase topologies, in terms of the achievable gains and performance considering similar parameters to the ones used in Sect. 13.5.1.

Although parameters related to output impedance (p and m) and the possible conversion ratios are common to all the two-clock-phase topologies (besides the ladder topology of Fig. 13.3b), this is not the case with topologies operating with multiple clock phases. As a result, the two-clock-phase topologies will be compared to the approach presented in [27] (as illustrated by the binary multi-clock-phase topology F, Fig. 13.7), since this is the finest example of a multi-ratio multi-clock-phase topology that the authors are aware of. This particular approach allows for a systematic way to synthesize a different number of binary-scaled conversion ratios that operate in multi-clock-phase, with a small number of floating capacitors. As introduced in Sect. 13.4.1, a smart connection of voltage-halver stages is used that each operate at twice the frequency of its precedent, resulting in a particular case of multi-clock-phase design (with ${2}^{n_c}$ clock phases for n _c floating capacitors).

Figure 13.10 shows the achievable number of conversion ratios M (up/down) that can be obtained from a fractional two-clock-phase (see Table 13.1) and a binary multi-clock-phase topology, as a function of the number of floating capacitors. As expected from Sect. 13.4, multi-clock-phase topologies are able to achieve a higher maximum ratio for a given number of floating capacitors than fractional two-clock-phase ones. However, it is the density of available ratios in a particular gain range that allows multi-ratio designs to keep a high power efficiency over a certain range of input or output voltage.

Fig. 13.10

Comparison between achievable voltage conversion ratios M for fractional two-clock-phase and binary multi-clock-phase topologies

As observed from Fig. 13.10, a fractional two-clock-phase design could provide more conversion ratios in a particular gain range than the binary multi-phase approach, eventually resulting in a higher average power efficiency. As an example of that, Fig. 13.11 compares the theoretical maximum power efficiency (V _out /MV _in ) available from multi-ratio designs using four floating capacitors based on either a two-clock-phase or a binary multi-clock-phase topology. In this example an output voltage of 5 V has been considered for an input voltage range corresponding to Li-ion batteries (2.6–4.2 V), as in [13]. In this example, the two-clock-phase fractional topology delivers an average efficiency across the input voltage range of 96.4 %, compared to 95.4 % for the binary multi-clock-phase topology. However, the more evenly distributed ratios from the binary multi-clock-phase topology makes the ratio control easier by increasing the linearity.

Fig. 13.11

Impact of achievable voltage conversion ratios with fractional two-clock-phase and binary multi-clock-phase topologies in practical multi-ratio converters

Besides the conversion ratios that can be generated from a particular approach (either using two or multiple clock phases), the performance of an SCPC is also strongly determined by its output impedance and switching losses. Figure 13.12a shows, as a function of the step-down conversion ratio M, the ratio between the switching frequency of a multi-clock-phase design (f _mph ) and a two-clock-phase (f _2ph ) design. Both designs provide the same R _SSL with the same total amount of floating capacitance C _T . It is clearly noticeable that multi-clock-phase topologies require a lower f _s to provide the same amount of impedance, although they have a higher number of switching events due to their higher number of clock phases within each switching period T _s . From Eq. (13.5), for a given value of R _SSL , the value of m varies with that of f _s . Therefore, the ratio of switching frequency coincides with the ratio of m values of each family of topologies.

Fig. 13.12

Comparison of two-clock-phase vs. binary multi-clock-phase topologies in terms of (a) switching frequency, (b) switch area and (c) switching losses indication, as a function of the step-down conversion ratio M

Both binary multi-clock-phase and two-clock-phase topologies can also be compared based on their R _FSL value. Figure 13.12b shows the ratio of the total amount of area spent on implementing the power switches for the multi-clock-phase case (A _mph ) and for the two-clock-phase designs (A _2ph ), as a function of the implemented conversion ratio M. From this graph it becomes clear that the two-clock-phase topologies will require less area spent in the switches, thus making them more appealing when implementing an SCPC with external floating capacitors, especially when high output power is needed and a lower switch area leads to a lower cost [13]. Similar to the m ratio corresponding to the f _s ratio in Fig. 13.12a, the switch-area ratio in Fig. 13.12b coincides with the ratio of p values according to Eq. (13.6).

Considering that multi-clock-phase topologies require larger power switches (for the same R _FSL ) but require lower f _s (for the same R _SSL and C _T ) albeit with having more switching events per cycle, it is relevant to compare their expected amount of switching losses. An indication of the amount of switching losses that can be expected from either design approach could be computed as the product of the switching frequency and the amount of area that is switched per cycle. In case of two-clock-phase topologies, the amount of area that switches per cycle is the same as the total amount of area spent in switches (A _swT ). However, in multi-clock-phase designs, some switches might be turned-on/off more than once per switching period T _s , meaning that the amount of area that switches is bigger than A _swT by a factor switching_events/n _sw (if all the switches are equally sized, as in the binary multi-clock-phase topology). To address this issue, the following parameter is defined as an indicative parameter of the amount of switching losses:

$$ H={f}_s{A}_{swT}\frac{{switching\hbox{\_}events}}{n_{sw}}\left\{\begin{array}{c}\hfill 2\ phases\to switching\hbox{\_}events={n}_{sw}\hfill \\ {}\hfill mult. ph\to switching\hbox{\_}events>{n}_{sw}\hfill \end{array}\right. $$

(13.9)

Figure 13.12c shows the ratio of this parameter for both the multi-clock-phase and two-clock-phase topology (H _mph /H _2ph ), as a function of the conversion ratio M. It is observed that in general higher switching losses should be expected from multi-clock-phase designs providing the same conversion ratio and output impedance, despite the lower switching frequency. As in previous results, both approaches coincide for M = 1/2, for which a single floating capacitor is used and only two clock phases are possible.

Unfortunately, the amount of bottom-plate losses and the blocking voltage of the different devices could not be included in the results of Fig. 13.12b, c without loss of generality, due the wide variety of two-clock-phase topologies that could be implemented, providing the same conversion ratio. In case that not all the devices of a particular design could have the same voltage rating, this should also be taken into account when considering the different design strategies.

For completeness, the multi-clock-phase designs of Figs. 13.7 and 13.8, providing M = 1/8, have also been included in Table 13.3 (topologies F and G, respectively). For the particular case of M = 1/8, the different two-clock-phase topologies A–E can be compared to multi-clock-phase designs F and G, including the blocking voltages of the devices as well as bottom-plate losses. The relative amount of bottom-plate losses is obtained from the ml product which takes into account the difference in switching frequency. To compute the relative amount of switching losses taking into account the blocking voltage of the power switches (last column of the table), which switch is used more than once needs to be carefully considered for the multi-clock-phase topologies, as well as their relatively lower f _s (represented by the m value). From the Table 13.3, the following is observed:

• Multi-clock-phase topologies are clearly an interesting solution for designs with discrete floating capacitors, where reducing the number of components and pins is important.

• Multi-clock-phase topologies operate at lower f _s , although their bottom-plate losses are not necessarily smaller. However, when using discrete floating capacitors, this may be irrelevant.

• Multi-clock-phase designs require a larger amount of area for the switches, which is relevant for high-power designs [13, 27].

• Despite operating at lower f _s , no lower switching losses result from multi-clock-phase designs since they have more switching events per cycle.

6 Conclusions

Various SCPC topologies are possible to realize a desired voltage conversion ratio M. A major distinction between possible topologies is the number of clock phases that is used within a switching cycle. Within the group of two-clock-phase SCPCs, different topologies are possible that use different numbers of floating capacitors to realize a desired value of M. The fractional topology uses the minimum number of floating capacitors to realize a given M value according to the Fibonacci limit, but the synthesis of such a fractional topology is usually performed by trial and error. Instead, this paper gives an example of systematic derivation of two-clock-phase topologies. Comparing the performance of various two-clock-phase topologies to each other, the output impedance is the same given the same switching frequency, total floating capacitance and total switch area. However, this paper has shown that depending on the application, performance differences e.g. in the amount of bottom-plate losses, the voltages appearing across the floating capacitors or the blocking voltages of power switches, different topologies come out favorably for different applications.

Using more than two clock phases allows the extension of the achievable range of M values of two-clock-phase converters. This allows realizing a target M with a lower number of floating capacitors, which can be advantageous in applications using external floating capacitors. A comparison between two-clock-phase and binary multi-clock-phase topologies shows that though the range of M values is smaller, the density of available M values in a certain needed range is higher in two-clock-phase topologies. This increases the achievable average efficiency across e.g. the desired input voltage range compared to binary multi-clock-phase topologies. Moreover, two-clock-phase topologies use less area to implement the power switches, which may be favorable for high-power applications. However, the modular approach to generate different conversion ratios with the binary multi-clock-phase reduces complexity in generating a larger number of conversion ratios.