Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In computational engineering analysis, one frequently faces the challenges involved in solving flow problems with moving boundaries and interfaces (MBI). This wide class of problems include fluid–structure interaction (FSI), fluid–object interaction (FOI), fluid–particle interaction (FPI), free-surface and multi-fluid flows, and flows with solid surfaces in fast, linear, or rotational relative motion. The computational challenges still being addressed include accurately representing the small-scale flow patterns, which require a reliable multiscale method. They also include contact or near contact between moving solid surfaces and other cases of topology change (TC) or near TC, such as those in flapping-wing aerodynamics, wind-turbine aerodynamics, cardiovascular fluid mechanics, and thermo-fluid analysis of ground vehicle tires. These four classes of problems played a key role in motivating the development of the space–time (ST) computational methods discussed in this article.

A method for flows with MBI can be viewed as an interface-tracking (moving-mesh) technique or an interface-capturing (nonmoving-mesh) technique, or possibly a combination of the two. In interface-tracking methods, as the interface moves, the mesh moves to follow (i.e., “track”) the interface. The Arbitrary Lagrangian–Eulerian (ALE) finite element formulation [1] is the most widely used moving-mesh technique. It has been used for many flow problems with MBI, including FSI (see, for example, [2–6]). The Deforming-Spatial-Domain/Stabilized ST (DSD/SST) method [4, 7–11], introduced in 1992, is also a moving-mesh method. The costs and benefits of moving the fluid mechanics mesh to track a fluid–solid interface were articulated in many papers (see, for example, [8]).

Moving-mesh methods require mesh update methods. Mesh update consists of moving the mesh for as long as possible and remeshing as needed. With the key objectives being to maintain the element quality near solid surfaces and to minimize frequency of remeshing, a number of advanced mesh update methods [9, 12, 13] were developed in conjunction with the DSD/SST method, including those that minimize the deformation of the layers of small elements placed near solid surfaces.

Perceived challenges in mesh update are quite often given as reasons for avoiding interface-tracking methods in classes of problem that can be, and actually have been, solved with such methods. A robust moving-mesh method with effective mesh update can handle FSI or other MBI problems even when the solid surfaces undergo large displacements (see, for example, FPI [14, 15] with the number of particles reaching 1,000 [15], parachute FSI [9, 16], flapping-wing aerodynamics [17–22]), and wind-turbine rotor and tower aerodynamics [21, 23]. It can handle FSI or other MBI problems also even when the solid surfaces are in near contact or create near TC, if the “nearness” is sufficiently “near” for the purpose of solving the problem. Examples of such problems are FPI with collision between the particles [14, 15], parachute-cluster FSI with contact between the parachutes of the cluster [16], flapping-wing aerodynamics with the forewings and hindwings crossing each other very close [17–21], and wind-turbine rotor and tower aerodynamics with the blades passing the tower close [21, 23].

No method is a panacea for all classes of MBI problems. Some interfaces, such as those in splashing, might be too complex for an interface-tracking technique, requiring an interface-capturing technique. The Mixed Interface-Tracking/Interface-Capturing Technique (MITICT) [15] was introduced for computations that involve both fluid–solid interfaces that can be accurately tracked with a moving-mesh method and fluid–fluid interfaces that are too complex to be tracked. Those fluid–fluid interfaces are captured over the mesh tracking the fluid–solid interfaces. The MITICT was successfully tested in 2D computations with solid circles and free surfaces [24] and in 3D computation of ship hydrodynamics [25].

In some MBI problems with contact between the solid surfaces, the “nearness” that can be modeled with a moving-mesh method without actually bringing the surfaces into contact might not be “near” enough for the purpose of solving the problem. Cardiovascular FSI with heart valves is an example. The Fluid–Solid Interface-Tracking/Interface-Capturing Technique (FSITICT) [26] was motivated by such FSI problems. In the FSITICT, we track the interface we can with a moving mesh, and capture over that moving mesh the interfaces we cannot track, specifically the interfaces where we need to have an actual contact between the solid surfaces. Two versions of the FSITICT were proposed, one with fixed-partitioning (FSITICT-FP), and one with adaptive-partitioning (FSITICT-AP). In the FSITICT-FP, the tracked/captured partitioning of the fluid–solid interface will be fixed during the computation. In the FSITICT-AP, the mesh will stop tracking the parts that have become too difficult to track, leaving them to be captured. This does not require remeshing. If any of the captured parts become suitable for tracking, a new mesh that is boundary-conforming for those parts will be generated and the tracking of those parts will start. An application of the FSITICT-FP was presented in [27], where an ALE method was used for interface-tracking, and a fully Eulerian approach for interface capturing, with some 2D test computations. This specific application was extended in [28] to 2D FSI models with flapping and contact. The FSITICT-FP was successfully extended in [29] to 3D FSI computation of a bioprosthetic heart valve. In that case the interface-tracking technique was an ALE method, and the interface-capturing technique was a variational immersed-boundary method.

Since its inception, the DSD/SST method has been applied to some of the most challenging flow problems with MBI. The classes of problems solved include the free-surface and multi-fluid flows [7, 24], FOI [7, 24], aerodynamics of flapping wings [17–22, 30], flows with solid surfaces in fast, linear, or rotational relative motion [14, 15, 23], compressible flows [14, 31], shallow-water flows [15, 32], FPI [14, 15], and FSI [16, 20, 30, 31, 33]. Much of the success with the DSD/SST method in recent years has been due to the new directions we have taken the ST methods in bringing solution and analysis to different classes of computationally challenging engineering problems.

The original DSD/SST method is based on the SUPG/PSPG stabilization, where “SUPG” and “PSPG” stand for the Streamline-Upwind/Petrov-Galerkin [34] and Pressure-Stabilizing/Petrov-Galerkin [7] methods. Starting in its early years, the DSD/SST method also included the “LSIC” (least-squares on incompressibility constraint) stabilization. The ST-VMS method [4, 10, 11] is the variational multiscale version of the DSD/SST method. It was called “DSD/SST-VMST” (i.e., the version with the VMS turbulence model) when it was first introduced in [10]. The VMS components are from the residual-based VMS method given in [35, 36]. We have been using the ST-VMS method since its inception in most of our computations. The original DSD/SST method was named “DSD/SST-SUPS” in [10] (i.e., the version with the SUPG/PSPG stabilization), which was also called “ST-SUPS” in [4].

The ST methods give us the option of using higher-order basis functions in time, including the NURBS, which have been used very effectively as spatial basis functions (see [37, 38]). We started using that option with the methods and concepts introduced in [10]. This of course increases the order of accuracy in the computations [39], and the desired accuracy can be attained with larger time steps, but there are positive consequences beyond that. The ST context provides us better accuracy and efficiency in temporal representation of the motion and deformation of the moving interfaces and volume meshes, and better efficiency in remeshing. This has been demonstrated in a number of 3D computations, specifically, flapping-wing aerodynamics [17–21], separation aerodynamics of spacecraft [40], and wind-turbine aerodynamics [21, 23]. The mesh update method based on using NURBS basis functions in mesh motion and remeshing was named “ST/NURBS Mesh Update Method (STNMUM)” in [23].

There are some advantages in using a discontinuous temporal representation in ST computations. For a given order of temporal representation, we can reach a higher-order accuracy than one would reach with a continuous representation of the same order. When we need to change the spatial discretization (i.e., remesh) between two ST slabs, the temporal discontinuity between the slabs provides a natural framework for that change. There are advantages also in continuous temporal representation. We obtain a smooth solution, NURBS-based when needed. We also can deal with the computed data in a more efficient way, because we can represent the data with fewer temporal control points, and that reduces the computer storage cost. These advantages motivated the development of the ST computation techniques with continuous temporal representation (ST-C) [41].

There are different types of nonmoving-mesh methods that can compute MBI problems involving an actual contact between solid surfaces or other cases of TC. Some of those methods give up on the accurate representation of the interface, and most give up on the consistent representation of the interface motion. The DSD/SST formulation does not need to give up on either, even where we have an actual contact or some other TC, provided that we can update the mesh even there. Using an ST mesh that is unstructured both in space and time, as proposed for contact problems in [15], would give us such a mesh update option. However, that would require a fully unstructured 4D mesh generation, and that is not easy in computing real-world problems. An ST interface-tracking method that can deal with TC was introduced in [42], and it is called ST-TC. It is a practical alternative to using unstructured ST meshes, but without giving up on the accurate representation of the interface or the consistent representation of the interface motion, even where there is an actual contact between solid surfaces or other TC. The ST-TC method is based on special mesh generation and update, and a master–slave system that maintains the connectivity of the “parent” mesh when there is a TC.

The ST Slip Interface (ST-SI) method [43] is the ST version of the ALE-VMS sliding-interface method [44]. It is for FSI and other MBI problems where one or more of the subdomains contain spinning structures, and the mesh covering a spinning structure spins with it, thus maintaining the high-resolution representation of the boundary layers near the structure. The subdomains are covered by meshes that do not match at the interface and have slip between them, and the ST-SI method carefully accounts for, in the ST context, the compatibility conditions for the velocity and stress between the two sides.

In Section 2 we briefly review the ST basis functions. The ST-VMS method is described in Section 3, and the STNMUM in Section 4. The ST-C, ST-TC, and ST-SI methods are described in Sections 5, 6, and 7. The examples are given in Section 8, and the concluding remarks in Section 9.

2 ST Basis Functions

The concept of using NURBS basis functions, in conjunction with the ST methods, in temporal representation of the unknown variables and motion of the solid surfaces and fluid meshes was introduced in [10]. An ST basis function can be written as a product of its spatial and temporal parts:

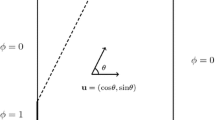
$$\displaystyle\begin{array}{rcl} N_{a}^{\alpha } = T^{\alpha }\left (\theta \right )N_{ a}\left (\boldsymbol{\xi }\right ),& & a = 1,2,\ldots,n_{\mathrm{en}}, \\ & & \alpha = 1,2,\ldots,n_{\mathrm{ent}},{}\end{array}$$
(1)

where θ ∈ [−1, 1] is the temporal element coordinate, and n en and n ent are the number of spatial and temporal element nodes. Figure 1 shows an example. Temporal NURBS basis functions can be used in an ST slab for the representation of the unknown variables and test functions as well as the spatial coordinates. As pointed out in [4, 10, 11, 23], different components (i.e., unknowns), and the corresponding test functions, can be discretized with different sets of temporal basis functions. This was shown in [4, 10, 11, 23] by introducing a secondary mapping Θ ζ (θ) ∈ [−1, 1], where Θ ζ (θ) is a strictly increasing function, and rewriting the generalized ST basis function for the element indices \(\left (a,\ \alpha \right )\) as

$$\displaystyle{ \left (N_{a}^{\alpha }\right )_{\zeta } = T^{\alpha }\left (\varTheta _{\zeta }(\theta )\right )N_{ a}\left (\boldsymbol{\xi }\right ). }$$
(2)

For example, we can discretize time and position as

$$\displaystyle\begin{array}{rcl} t =\sum _{ \alpha =1}^{n_{\mathrm{ent}} }T^{\alpha }(\varTheta _{t}(\theta ))t^{\alpha },& &{}\end{array}$$
(3)
$$\displaystyle\begin{array}{rcl} \mathbf{x} =\sum _{ \alpha =1}^{n_{\mathrm{ent}} }T^{\alpha }(\varTheta _{x}(\theta ))\mathbf{x}^{\alpha }.& &{}\end{array}$$
(4)

Here Θ t (θ) and Θ x (θ) are the secondary mappings for time and position, and t α and x α are the time and position values corresponding to the basis function T α.

Fig. 1
figure 1

Temporal NURBS basis functions.

Full size image

3 ST-VMS Method

The ST-VMS method can be written as

$$\displaystyle\begin{array}{rcl} & & \int _{Q_{n}}\mathbf{w}^{h} \cdot \rho \left (\frac{\partial \mathbf{u}^{h}} {\partial t} + \mathbf{u}^{h} \cdot \boldsymbol{\nabla }\mathbf{u}^{h} -\mathbf{f}^{h}\right )\mathrm{d}Q +\int _{ Q_{n}}\boldsymbol{\varepsilon }(\mathbf{w}^{h}):\boldsymbol{\sigma } (\mathbf{u}^{h},p^{h})\mathrm{d}Q \\ & & \ \ \ -\int _{\left (P_{n}\right )_{\mathrm{h}}}\mathbf{w}^{h} \cdot \mathbf{h}^{h}\mathrm{d}P +\int _{ Q_{n}}q^{h}\boldsymbol{\nabla }\cdot \mathbf{u}^{h}\mathrm{d}Q +\int _{\varOmega _{ n}}(\mathbf{w}^{h})_{ n}^{+} \cdot \rho \left ((\mathbf{u}^{h})_{ n}^{+} - (\mathbf{u}^{h})_{ n}^{-}\right )\mathrm{d}\varOmega \\ & & \ \ \ +\sum _{e=1}^{(n_{\mathrm{el}})_{n} }\int _{Q_{n}^{e}}\frac{\tau _{\mathrm{SUPS}}} {\rho } \left [\rho \left (\frac{\partial \mathbf{w}^{h}} {\partial t} + \mathbf{u}^{h} \cdot \boldsymbol{\nabla }\mathbf{w}^{h}\right ) +\boldsymbol{ \nabla }q^{h}\right ] \cdot \mathbf{r}_{\mathrm{ M}}(\mathbf{u}^{h},p^{h})\mathrm{d}Q \\ & & \ \ \ +\sum _{e=1}^{(n_{\mathrm{el}})_{n} }\int _{Q_{n}^{e}}\nu _{\mathrm{LSIC}}\boldsymbol{\nabla }\cdot \mathbf{w}^{h}\rho r_{\mathrm{ C}}(\mathbf{u}^{h})\mathrm{d}Q -\sum _{ e=1}^{(n_{\mathrm{el}})_{n} }\int _{Q_{n}^{e}}\tau _{\mathrm{SUPS}}\mathbf{w}^{h} \cdot \left (\mathbf{r}_{\mathrm{ M}}(\mathbf{u}^{h},p^{h}) \cdot \boldsymbol{\nabla }\mathbf{u}^{h}\right )\mathrm{d}Q \\ & & \ \ \ -\sum _{e=1}^{(n_{\mathrm{el}})_{n} }\int _{Q_{n}^{e}}\frac{\tau _{\mathrm{SUPS}}^{2}} {\rho } \mathbf{r}_{\mathrm{M}}(\mathbf{u}^{h},p^{h}) \cdot \left (\boldsymbol{\nabla }\mathbf{w}^{h}\right ) \cdot \mathbf{r}_{\mathrm{ M}}(\mathbf{u}^{h},p^{h})\mathrm{d}Q = 0, {}\end{array}$$
(5)

where

$$\displaystyle\begin{array}{rcl} \mathbf{r}_{\mathrm{M}}(\mathbf{u}^{h},p^{h}) =\rho \left (\frac{\partial \mathbf{u}^{h}} {\partial t} + \mathbf{u}^{h} \cdot \boldsymbol{\nabla }\mathbf{u}^{h} -\mathbf{f}^{h}\right ) -\boldsymbol{\nabla }\cdot \boldsymbol{\sigma } (\mathbf{u}^{h},p^{h}),& &{}\end{array}$$
(6)
$$\displaystyle\begin{array}{rcl} r_{\mathrm{C}}(\mathbf{u}^{h})& =\boldsymbol{ \nabla }\cdot \mathbf{u}^{h}&{}\end{array}$$
(7)

are the residuals of the momentum equation and incompressibility constraint. Here, ρ, u, p, f, \(\boldsymbol{\sigma }\), \(\boldsymbol{\varepsilon }\), and h are the density, velocity, pressure, external force, stress tensor, strain rate tensor, and the traction specified at the boundary. The test functions associated with the velocity and pressure are w and q. A superscript “h” indicates that the function is coming from a finite-dimensional space. The symbol Q n represents the ST slice between time levels n and n + 1, \(\left (P_{n}\right )_{\mathrm{h}}\) is the part of the lateral boundary of that slice associated with the traction boundary condition h, and Ω n is the spatial domain at time level n. The superscript “e” is the ST element counter, and n el is the number of ST elements. The functions are discontinuous in time at each time level, and the superscripts “−” and “+” indicate the values of the functions just below and just above the time level. There are various ways of defining the stabilization parameters τ SUPS and ν LSIC. We use the following expressions:

$$\displaystyle\begin{array}{rcl} \tau _{\mathrm{SUPS}} = \left ( \frac{1} {\tau _{\mathrm{SUGN12}}^{2}} + \frac{1} {\tau _{\mathrm{SUGN3}}^{2}} + \frac{1} {\tau _{\mathrm{SUGN4}}^{2}}\right )^{-\frac{1} {2} },& &{}\end{array}$$
(8)
$$\displaystyle\begin{array}{rcl} \tau _{\mathrm{SUGN12}} = \left (\sum _{\alpha =1}^{n_{\mathrm{ent}} }\sum _{a=1}^{n_{\mathrm{ens}} }\left \vert \frac{\partial N_{a}^{\alpha }} {\partial t} + \mathbf{u}^{h} \cdot \boldsymbol{\nabla }N_{ a}^{\alpha }\right \vert \right )^{-1},& &{}\end{array}$$
(9)
$$\displaystyle\begin{array}{rcl} \tau _{\mathrm{SUGN3}} = \frac{h_{\mathrm{RGN-MIN}}^{2}} {4\nu },& &{}\end{array}$$
(10)
$$\displaystyle\begin{array}{rcl} \tau _{\mathrm{SUGN4}} = \left \|\boldsymbol{\nabla }\mathbf{u}^{h}\right \|_{ F}^{-1},& &{}\end{array}$$
(11)
$$\displaystyle\begin{array}{rcl} \nu _{\mathrm{LSIC}} = \frac{h_{\mathrm{RGN-MIN}}^{2}} {4\tau _{\mathrm{SUPS}}},& &{}\end{array}$$
(12)

where n ens and n ent are the number of spatial and temporal element nodes, N a α is the basis function associated with spatial and temporal nodes a and α, ∥ ⋅ ∥  F represents the Frobenius norm,

$$\displaystyle\begin{array}{rcl} h_{\mathrm{RGN-MIN}} = 2\left \|\left \{\boldsymbol{\nabla }N_{a}^{\alpha }\right \}\right \|_{ 2}^{-1} \equiv 2\left (\lambda _{\mathrm{ max}}\left (\sum _{\alpha =1}^{n_{\mathrm{ent}} }\sum _{a=1}^{n_{\mathrm{ens}} }\boldsymbol{\nabla }N_{a}^{\alpha }\boldsymbol{\nabla }N_{ a}^{\alpha }\right )\right )^{-\frac{1} {2} },& &{}\end{array}$$
(13)

and λ max(⋅ ) represents the maximum eigenvalue of the symmetric tensor.

Remark 1.

Most of these stabilization parameters originate from [8, 9].

Remark 2.

The component τ SUGN4, given by Eq. (11), was introduced in [45]. It was introduced based on the reasoning that the \(\tau _{\mathrm{SUPS}}\mathbf{w}^{h} \cdot \left (\mathbf{r}_{\mathrm{M}} \cdot \boldsymbol{\nabla }\mathbf{u}^{h}\right )\) term should not overwhelm the \(\mathbf{w}^{h} \cdot \rho (\mathbf{u}^{h} \cdot \boldsymbol{\nabla }\mathbf{u}^{h})\) term.

Remark 3.

A symmetric version of that τ SUGN4 was also introduced in [45]:

$$\displaystyle\begin{array}{rcl} \tau _{\mathrm{SUGN4}}& =\|\boldsymbol{\varepsilon } (\mathbf{u}^{h})\|_{F}^{-1}.&{}\end{array}$$
(14)

4 STNMUM

4.1 Mesh Computation and Representation

Given the fluid mechanics mesh on a moving solid surface, we compute the fluid mechanics volume mesh using the mesh moving methods [9, 12, 13] developed in conjunction with the DSD/SST method. As proposed in [46] and also described in [4], these mesh moving methods are used in computing the meshes that will serve as temporal control points. This allows us to do mesh computations with longer time in between, but get the mesh-related information, such as the coordinates and their time derivatives, from the temporal representation whenever we need. Of course this also reduces the storage amount and access associated with the meshes.

Remark 4.

Getting the meshes used in the computations from the temporal representation can be done independent of which time direction was used in computing the control meshes. For example, in flapping-wing aerodynamics, the control meshes can be computed while the wings are flapping forward or backward in time.

4.2 Remeshing

In many computations remeshing becomes unavoidable. Two choices were proposed in [46] and also described in [4]. To explain those choices, let us assume that when we try to move from control mesh M c β to M c β+1, we find the quality of M c β+1 to be less than desirable. In the first choice, called “trimming,” we remesh going back to M c β−p+1, where p is the order of the NURBS basis functions. Then whenever our solution process needs a mesh, depending on the time, we use the control meshes belonging to either only the un-remeshed set or only the remeshed set (Figure 2). In the second choice, we perform knot insertion p times in the temporal representation of the surface at the right-most knot before the maximum value of the basis function corresponding to t c β+1, making that knot a new patch boundary. Then we do the mesh moving computation for the control meshes associated with the newly defined basis functions, not only the one at the new patch boundary, but also going back (p − 1) basis functions (Figure 3). We favor the second choice, because we believe that in many cases the need for remeshing is generated by a topological change, which we can avoid going over with a large step if we use the knot insertion process.

Fig. 2
figure 2

Remeshing and trimming NURBS. A set of un-remeshed meshes (top). A set of remeshed meshes (middle). Common basis functions (bottom).

Full size image
Fig. 3
figure 3

Remeshing with knot insertion. For the set of un-remeshed meshes, there are p newly defined basis functions and the corresponding control points are marked “New.” We carry out the mesh moving computations for those meshes.

Full size image

5 ST-C Method

We describe, from [41], the version of the ST-C method used in extracting continuous temporal representation from computed data. This is essentially a post-processing method, and can also be seen as a data compression method. For the version used in direct computation of the solution with continuous temporal representation, see [41].

5.1 Least-Squares Projection for Full Temporal Domain

When we have the complete sequence of computed data, we can project that to a smooth representation, with basis functions that provide us that smooth representation, such as NURBS basis functions. As an example, Figure 4 shows the goal continuous data ϕ C and its basis functions, where ϑ denotes the parametric temporal coordinate. The projection for each spatial node can be done independently from the other nodes. Consider the time-dependent, typically discontinuous computed data ϕ D for a node. We define the basis functions as T C α, where α = 0, 1, …, and the coefficients to be determined in the projection as ϕ α. We use a standard least-squares projection: given ϕ D, find the solution \(\phi _{\mathrm{C}} \in \mathcal{S}_{\mathrm{C}}\), such that for all test functions \(w_{\mathrm{C}} \in \mathcal{V}_{\mathrm{C}}\):

$$\displaystyle\begin{array}{rcl} \int _{0}^{T}w_{\mathrm{ C}}\left (\phi _{\mathrm{C}} -\phi _{\mathrm{D}}\right )\mathrm{d}t = 0,& &{}\end{array}$$
(15)

where T represents time period of the computation, and \(\mathcal{S}_{\mathrm{C}}\) and \(\mathcal{V}_{\mathrm{C}}\) are the solution and test function spaces constructed from the basis functions. This approach requires that we store all the computed data before the projection, and that would be a significant computer storage cost when the number of time steps is large.

Fig. 4
figure 4

Continuous solution (top) and its basis functions (bottom); ϑ is the parametric coordinate.

Full size image

5.2 Successive-Projection Technique

In ST-C with the successive-projection technique (ST-C-SPT), we extract the continuous solution shown in Figure 4 without storing all the computed data. We describe the technique here for the special case with quadratic B-splines. To explain the successive nature of the SPT, let us suppose that we have the continuous solution extracted up to t n  = 4. 0, as shown in Figure 5. We assume that this continuous solution, which we will call \(\overline{\phi }_{\mathrm{C}}\), has already replaced ϕ D up to t n  = 4. 0. With that, we describe how we extract the continuous solution up to t n+1 = 5. 0, as shown in Figure 6. With the newly computed data ϕ D between t n  = 4. 0 and t n+1 = 5. 0, we solve the following projection equation: given ϕ D on t ∈ (4. 0, 5. 0), \(\overline{\phi }_{\mathrm{C}}\) on t ∈ [2. 0, 4. 0], and ϕ C α, α = 2, 3, find \(\phi _{\mathrm{C}} \in \mathcal{S}_{\mathrm{C}}\), such that \(\forall w_{\mathrm{C}} \in \mathcal{V}_{\mathrm{C}}\):

$$\displaystyle\begin{array}{rcl} \int _{2.0}^{4.0}w_{\mathrm{ C}}\left (\phi _{\mathrm{C}} -\overline{\phi }_{\mathrm{C}}\right )\mathrm{d}t +\int _{ 4.0}^{5.0}w_{\mathrm{ C}}\left (\phi _{\mathrm{C}} -\phi _{\mathrm{D}}\right )\mathrm{d}t = 0.& &{}\end{array}$$
(16)

Equation (16) is essentially used for defining the coefficients ϕ C α, α = 4, 5, 6, which correspond to the basis functions T C α. How to deal with the initial part of the extraction, description of the ST-C-SPT for the general case (i.e., beyond quadratic B-splines), and comments on efficient implementation of the SPT can be found in [41].

Fig. 5
figure 5

Continuous solution up to t n  = 4. 0 (top) and its basis functions (bottom).

Full size image
Fig. 6
figure 6

Continuous solution up to t n+1 = 5. 0 (top) and its basis functions (bottom). The bold part of the top curve indicates the part of the solution that does not change. The empty squares denote the temporal control values to be determined. The dashed lines denote the modified and new basis functions, which correspond to those control values.

Full size image

6 ST-TC Method

6.1 TC

We consider two hypothetical cases of two bars to provide a context for TC. In the first case, shown in Figure 7, the bars are initially coinciding, with just one hole in the fluid mechanics domain. Then the red bar starts moving upward, creating a second hole. In the second case, shown in Figure 8, the bars are initially aligned with connected ends, again with a single hole in the domain. Then the red bar starts a flapping motion, up and down, creating a second hole in the domain, except when their ends become connected periodically during the flapping motion. When the red bar is in the upper position, the part of the domain below it is connected to the part of the domain above the blue bar. When the red bar is in the lower position, the part of the domain above it is connected to the part of the domain below the blue bar. These two cases are representatives of the typical TC challenges we expect to see in the classes of MBI problems we are targeting. Especially the first case is really not possible to treat in a consistent way without using an ST method.

Fig. 7
figure 7

Hypothetical case of two bars that are initially coinciding, with one hole in the domain (left). The red bar starts moving upward, creating a second hole in the domain (right).

Full size image
Fig. 8
figure 8

Hypothetical case of two bars that are initially aligned with connected ends, with one hole in the domain (left). The red bar starts a flapping motion, up (middle) and down (right), creating a second hole in the domain, except when their ends become connected periodically.

Full size image

6.2 Master–Slave System

We propose a very simple technique in the ST context. Having a constraint between nodes in a finite element formulation is quite common. These constraints reduce the number of unknowns, but in our implementation we delay that unknown elimination until the iterative solution of the linear systems encountered at nonlinear iterations of a time step. The iterative solution of the linear systems is performed with reduced number of unknowns. The technique is easy to manage in a parallel-computing environment, especially if the preconditioner is simple enough. Typically we assign a master node to each slave node, and we use only the unknowns of the master nodes in iterative solution of the linear systems. We can use different master–slave relationships at different time levels. This is a practical alternative to, but less general than, using ST meshes that are unstructured in time. Still, we can use this concept to deal with the TC cases considered above, and the important point is that the connectivity of the “parent” mesh does not change. Consequently, the distribution model in the parallel-computing environment does not change during the computations.

With this technique, we need to implement one more functionality. We exclude certain elements from the integration of the finite element formulation. The exclusion principles are given below.

  • Exclude all spatial elements with zero volume from the spatial integration.

  • Exclude all ST elements with zero ST volume from the ST integration.

  • We assume that checking if an ST element has zero ST volume is equivalent to checking if all the spatial elements associated with that ST element have zero volume. Therefore, for this purpose, we check the spatial-element volumes.

  • To identify the spatial elements with zero volume, which should have zero Jacobian at all the integration points, instead of evaluating the Jacobians, we make the determination for a given spatial element from the master–slave relationship of its nodes. The method is explained more in [42].

7 ST-SI Method

In describing the ST-SI formulation, we will use the labels “Side A” and “Side B” to represent the two sides of the SI. In the ST-SI version of the formulation given by Eq. (5), we will have added boundary terms corresponding to the SI. The boundary terms for the two sides will be added separately, using test functions w A h and q A h and w B h and q B h. Here we give only the boundary terms for Side B:

$$\displaystyle\begin{array}{rcl} & & -\int _{\left (P_{n}\right )_{\mathrm{SI}}}q_{\mathrm{B}}^{h}\mathbf{n}_{\mathrm{ B}} \cdot \mathbf{u}_{\mathrm{B}}^{h}\mathrm{d}P -\int _{\left (P_{n}\right )_{\mathrm{SI}}}\rho \mathbf{w}_{\mathrm{B}}^{h} \cdot \left (\mathbf{n}_{\mathrm{ B}} \cdot \left (\mathbf{u}_{\mathrm{B}}^{h} -\mathbf{v}_{\mathrm{ B}}^{h}\right )\right )\mathbf{u}_{\mathrm{ B}}^{h}\mathrm{d}P \\ & & +\int _{\left (P_{n}\right )_{\mathrm{SI}}}q_{\mathrm{B}}^{h}\mathbf{n}_{\mathrm{ B}} \cdot \frac{1} {2}\left (\mathbf{u}_{\mathrm{B}}^{h} + \mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P \\ & & +\int _{\left (P_{n}\right )_{\mathrm{SI}}}\rho \mathbf{w}_{\mathrm{B}}^{h} \cdot \frac{1} {2}\left (\left (\mathbf{n}_{\mathrm{B}} \cdot \left (\mathbf{u}_{\mathrm{B}}^{h} -\mathbf{v}_{\mathrm{ B}}^{h}\right ) +\alpha ^{h}\right )\mathbf{u}_{\mathrm{ B}}^{h} -\left (\mathbf{n}_{\mathrm{ A}} \cdot \left (\mathbf{u}_{\mathrm{A}}^{h} -\mathbf{v}_{\mathrm{ A}}^{h}\right ) +\alpha ^{h}\right )\mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P \\ & & -\int _{\left (P_{n}\right )_{\mathrm{SI}}}\mathbf{w}_{\mathrm{B}}^{h} \cdot \frac{1} {2}\left (\mathbf{n}_{\mathrm{B}} \cdot \boldsymbol{\sigma }_{\mathrm{B}}^{h} -\mathbf{n}_{\mathrm{ A}} \cdot \boldsymbol{\sigma }_{\mathrm{A}}^{h}\right )\mathrm{d}P -\int _{\left (P_{n}\right )_{\mathrm{SI}}}\mathbf{n}_{\mathrm{B}} \cdot \mu \boldsymbol{\varepsilon }\left (\mathbf{w}_{\mathrm{B}}^{h}\right ) \cdot \left (\mathbf{u}_{\mathrm{ B}}^{h} -\mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P \\ & & +\int _{\left (P_{n}\right )_{\mathrm{SI}}} \frac{\mu C} {h} \mathbf{w}_{\mathrm{B}}^{h} \cdot \left (\mathbf{u}_{\mathrm{ B}}^{h} -\mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P, {}\end{array}$$
(17)

where

$$\displaystyle\begin{array}{rcl} \alpha ^{h}& =& \max \left (\left \vert \mathbf{n}_{\mathrm{ B}} \cdot \left (\mathbf{u}_{\mathrm{B}}^{h} -\mathbf{v}_{\mathrm{ B}}^{h}\right )\right \vert,\left \vert \mathbf{n}_{\mathrm{ A}} \cdot \left (\mathbf{u}_{\mathrm{A}}^{h} -\mathbf{v}_{\mathrm{ A}}^{h}\right )\right \vert \right ),{}\end{array}$$
(18)
$$\displaystyle\begin{array}{rcl} h =\min (h_{\mathrm{B}},h_{\mathrm{A}}),& &{}\end{array}$$
(19)
$$\displaystyle\begin{array}{rcl} h_{\mathrm{B}}& = 2\left (\sum _{\alpha =1}^{n_{\mathrm{ent}}}\sum _{a=1}^{n_{\mathrm{ens}}}\left \vert \mathbf{n}_{\mathrm{B}} \cdot \boldsymbol{\nabla }N_{a}^{\alpha }\right \vert \right )^{-1}\text{(for Side B)},&{}\end{array}$$
(20)
$$\displaystyle\begin{array}{rcl} h_{\mathrm{A}}& = 2\left (\sum _{\alpha =1}^{n_{\mathrm{ent}}}\sum _{a=1}^{n_{\mathrm{ens}}}\left \vert \mathbf{n}_{\mathrm{A}} \cdot \boldsymbol{\nabla }N_{a}^{\alpha }\right \vert \right )^{-1}\text{(for Side A)}.&{}\end{array}$$
(21)

Here, \(\left (P_{n}\right )_{\mathrm{SI}}\) is the SI in the ST domain, n is the unit normal vector, and v is the mesh velocity. Side A counterpart of Eq. (17) can be written by simply interchanging subscripts A and B.

Remark 5.

The first and third integrations set the volumetric flow rate at the boundary to \(\mathbf{n}_{\mathrm{B}} \cdot \frac{1} {2}\left (\mathbf{u}_{\mathrm{B}}^{h} + \mathbf{u}_{\mathrm{ A}}^{h}\right )\).

Remark 6.

The second and fourth integrations set the advective flux at the boundary to the Lax–Friedrichs flux.

Remark 7.

The fifth integration contains the average traction.

Remark 8.

The sixth integration is the adjoint consistent term [47].

Remark 9.

The seventh integration is a penalty term, where C is a nondimensional penalty constant, and usually C = 1 is large enough for stability.

For notation convenience, we introduce the symbols

$$\displaystyle\begin{array}{rcl} \mathcal{F}_{\mathrm{B}}^{h}& = \mathbf{n}_{\mathrm{ B}} \cdot \left (\mathbf{u}_{\mathrm{B}}^{h} -\mathbf{v}_{\mathrm{ B}}^{h}\right ),&{}\end{array}$$
(22)
$$\displaystyle\begin{array}{rcl} \mathcal{F}_{\mathrm{A}}^{h}& = \mathbf{n}_{\mathrm{ A}} \cdot \left (\mathbf{u}_{\mathrm{A}}^{h} -\mathbf{v}_{\mathrm{ A}}^{h}\right ).&{}\end{array}$$
(23)

With that, we replace the momentum flux as follows:

$$\displaystyle\begin{array}{rcl} & & -\int _{\left (P_{n}\right )_{\mathrm{SI}}}q_{\mathrm{B}}^{h}\mathbf{n}_{\mathrm{ B}} \cdot \mathbf{u}_{\mathrm{B}}^{h}\mathrm{d}P -\int _{\left (P_{n}\right )_{\mathrm{SI}}}\rho \mathbf{w}_{\mathrm{B}}^{h} \cdot \mathcal{F}_{\mathrm{ B}}^{h}\mathbf{u}_{\mathrm{ B}}^{h}\mathrm{d}P \\ & & +\int _{\left (P_{n}\right )_{\mathrm{SI}}}q_{\mathrm{B}}^{h}\mathbf{n}_{\mathrm{ B}} \cdot \frac{1} {2}\left (\mathbf{u}_{\mathrm{B}}^{h} + \mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P \\ & & +\int _{\left (P_{n}\right )_{\mathrm{SI}}}\rho \mathbf{w}_{\mathrm{B}}^{h} \cdot \frac{1} {2}\left (\left (\mathcal{F}_{\mathrm{B}}^{h} + \left \vert \mathcal{F}_{\mathrm{ B}}^{h}\right \vert \right )\mathbf{u}_{\mathrm{ B}}^{h} + \left (\mathcal{F}_{\mathrm{ B}}^{h} -\left \vert \mathcal{F}_{\mathrm{ B}}^{h}\right \vert \right )\mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P \\ & & -\int _{\left (P_{n}\right )_{\mathrm{SI}}}\mathbf{w}_{\mathrm{B}}^{h} \cdot \frac{1} {2}\left (\mathbf{n}_{\mathrm{B}} \cdot \boldsymbol{\sigma }_{\mathrm{B}}^{h} -\mathbf{n}_{\mathrm{ A}} \cdot \boldsymbol{\sigma }_{\mathrm{A}}^{h}\right )\mathrm{d}P -\int _{\left (P_{n}\right )_{\mathrm{SI}}}\mathbf{n}_{\mathrm{B}} \cdot \mu \boldsymbol{\varepsilon }\left (\mathbf{w}_{\mathrm{B}}^{h}\right ) \cdot \left (\mathbf{u}_{\mathrm{ B}}^{h} -\mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P \\ & & +\int _{\left (P_{n}\right )_{\mathrm{SI}}} \frac{\mu C} {h} \mathbf{w}_{\mathrm{B}}^{h} \cdot \left (\mathbf{u}_{\mathrm{ B}}^{h} -\mathbf{u}_{\mathrm{ A}}^{h}\right )\mathrm{d}P. {}\end{array}$$
(24)

Remark 10.

Assuming that the discrete boundaries on the two sides of the interface are the same, n B = −n A. With that, we see the traction h B h ≡ −h A h as

$$\displaystyle\begin{array}{rcl} \mathbf{h}_{\mathrm{B}}^{h}& = -\frac{1} {2}\left (p_{\mathrm{B}}^{h} + p_{\mathrm{ A}}^{h}\right )\mathbf{n}_{\mathrm{ B}} + \frac{1} {2}\mathbf{n}_{\mathrm{B}} \cdot \left (2\mu \boldsymbol{\varepsilon }(\mathbf{u}_{\mathrm{B}}^{h}) + 2\mu \boldsymbol{\varepsilon }(\mathbf{u}_{\mathrm{ A}}^{h})\right ) -\frac{\mu C} {h} \left (\mathbf{u}_{\mathrm{B}}^{h} -\mathbf{u}_{\mathrm{ A}}^{h}\right ).&{}\end{array}$$
(25)

8 Examples

The first two examples are from [48] for the ST-TC method and from [45] for the ST-C method. The third example is a 2D test computation based on the combination of ST-TC and ST-SI methods. For all computations presented, the core technology is the ST-VMS method. More examples for the ST-TC method can be found in [22, 42, 48]. Examples for the STNMUM can be found in [17–21] for flapping-wing aerodynamics, in [40] for separation aerodynamics of spacecraft, and in [21, 23] for wind-turbine aerodynamics. Examples for the ST-SI method can be found in [43].

8.1 Aortic-Valve Model with Coronary Arteries

We created a typical aortic-valve model, which has three leaflets with two outlets, corresponding to coronary arteries, and one main outlet, corresponding to the beginning of the aorta. Figure 9 shows the velocity magnitude when the valve is open and is about to close. For more on this computation, see [48].

Fig. 9
figure 9

Aortic-valve model with coronary arteries. Volume rendering of the velocity magnitude (m/s) at t∕T = 0.4 and 0.5, where T is the cardiac period.

Full size image

8.2 Thermo-Fluid Analysis of a Ground Vehicle and Its Tires

First the thermo-fluid computation is carried out over the full domain, with a reasonable mesh refinement. The large amount of time-history data from that computation is stored using the ST-C-SPT method. This is followed by a higher-resolution computation over the local domain containing the tires we focus on. This gives us increased accuracy in the thermo-fluid analysis, including increased accuracy in the heat transfer rates from the tires. Figure 10 shows the temperature patterns from the local computation. Figure 11 shows the Nusselt number from the global and local computations. For more on this computation, see [45].

Fig. 10
figure 10

Thermo-fluid analysis of a ground vehicle and its tires. Temperature volume rendering from the local computation. Colors from red to yellow indicate temperature from low to high.

Full size image
Fig. 11
figure 11

Time and circumferentially averaged Nusselt number from the global (left) and local (right) computations.

Full size image

8.3 2D Model of Flow Past a Tire in Contact with the Road

This is an example of how the ST-TC and ST-SI methods can be used in combination for computational analysis of a challenging problem. The computation is challenging because the tire does not have circular symmetry and is in rotational contact with the road. The first challenge is addressed with the ST-SI method, which enables flow computations with spinning structures while maintaining the high-resolution representation of the boundary layers near the structure. The second challenge is addressed with the ST-TC method, which enables flow computations with contact between moving solid surfaces while maintaining the high-resolution representation of the boundary layers near the solid surfaces. Figure 12 shows the mesh and the velocity magnitude. More on this type of computations and the combined method and its implementation will be presented in a future paper.

Fig. 12
figure 12

2D model of flow past a tire in contact with the road. Velocity magnitude superimposed over the mesh. Colors from blue to red indicate values from low to high.

Full size image

9 Concluding Remarks

We have presented an overview of some of the new directions we have taken the ST methods since 2010 in bringing solution and analysis to different classes of computationally challenging engineering problems. The new directions include a) the VMS version of the DSD/SST method, which is called ST-VMS, b) ST methods based on using NURBS basis functions in temporal representation of the unknown variables and motion of the solid surfaces and fluid meshes, including the mesh update method STNMUM, c) ST techniques with continuous representation in time, which is called ST-C, d) ST interface-tracking with topology change, which is called ST-TC, and e) ST-VMS method for flow computations with slip interfaces, which is called ST-SI. We described the new directions and presented a few examples.