Keywords

1 Introduction

In industry, to transport heavy payloads to desired positions, cranes systems, including overhead cranes, tower cranes, boom cranes, and offshore cranes [1], are widely used. To simplify the mechanical structure and reduce the cost, the payload is usually linked to the trolley or the boom by a rope, which leads to the fact that the payload cannot be controlled directly. This kind of design usually results in the fact that the number of control inputs of crane systems is less than to-be-controlled degrees of freedom. Systems with this behavior are known as underactuated systems [2], which are more difficult to be controlled properly compared with full actuated systems, due to the unactuated property. As a typical underactuated system, the overhead crane system is always operated by experienced workers. However, long time working may cause fatigue and operation errors, which is very dangerous. Therefore, automatic control design for overhead crane systems is very important.

So far, the control problem of overhead crane systems has attracted attentions of researchers with a series of control methods presented. For example, Singhose et al. [3–5] propose a series of open loop methods based on the idea of input shaping, which can suppress the payload swing with few sensors. By deeply analyzing the system energy, Sun et al. present some passivity based control methods which can achieve asymptotically stable results in [6, 7]. To deal with unknown disturbance/uncertainties, in [8–10], some sliding mode control methods are proposed, which show great robustness. Considering that system parameters cannot be obtained accurately, researchers propose some adaptive methods, which can obtain satisfactory performance w.r.t. parameter uncertainties [11, 12]. Trajectory planning methods are also used to control overhead crane systems, which can treat various of constraints conveniently [13, 14].

In recent years, intelligent control methods are developing quickly and a lot of intelligence based control methods, such as fuzzy control methods [16], genetic algorithm (GA)-based methods [17], and neural network-based methods [18–21], have been proposed for overhead crane systems. For example, in [18], a novel control method is proposed by combining the principles of neural networks and variable structure systems, which can drive the cart smoothly, rapidly and with limited payload swing. [20] proposes a recurrent neural network control method with a hybrid evolutionary algorithm to achieve the control objective of a three dimension tower crane system. An anti-sway position control method is design for an automated transfer crane in [21], which uses the neural network method to tune the PID parameters.

These methods stated above can achieve the transportation objective of overhead crane systems. However, in practice, the working environment of an overhead crane may be very complex and some emergency situations may occur. To deal with this, overhead cranes may need to brake emergently to avoid accidents like collision. As far as we are concerned, the common used braking method in industry is directly set the actual force to zero. It should be noted that there exists high coupling between the trolley motion and the payload swing and irrelevant operation to the trolley can cause large payload swing which is very dangerous. Due to the lack of consideration for the payload swing angle, the crane braking method in industry can only ensure the stop of the trolley while the objective of swing suppression is ignored. To deal with the emergency braking problem, only few methods have been presented. In [22], Ma et al. propose a switching based braking method to deal with this problem, however, the trolley braking and the swing suppression still cannot be dealt with simultaneously.

To achieve the objectives of fast trolley braking and payload swing suppression at the same time, we propose a novel emergency braking method in this paper. In particular, by deep analysis, we first divide the control objective into two parts. Then corresponding controllers are designed for both parts to ensure the sub-objectives separately. After that, a novel emergency braking method is proposed by combing these two controllers together. At last, the performance of our method is verified by simulation tests. Different from the existing method, the proposed method can ensure the trolley being within safe domain (never exceeding the safe limit) and the payload swing suppression simultaneously, which can make sure safety as much as possible.

The rest of this paper is organized as follows. The crane dynamics, as well as the control objectives of emergency braking, are described in Sect. 2. In Sect. 3, we show the main design process of the proposed method. Section 4 exhibits some numerical simulation results to illustrate the effectiveness of this method. The main work is finally concluded and summarized in Sect. 5.

2 Problem Statement

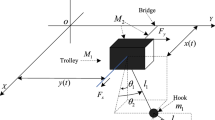
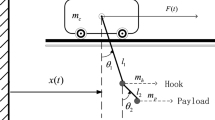
In this paper, we focus on the emergency braking problem of overhead crane systems, whose dynamics are shown as follows:

$$\begin{aligned} (M+m)\ddot{x}+ml\ddot{\theta }\cos \theta -ml\dot{\theta }^2\sin \theta =F, \end{aligned}$$
(1)
$$\begin{aligned} ml^2\ddot{\theta }+ml\cos \theta \ddot{x}+mgl\sin \theta =0, \end{aligned}$$
(2)

where M and m denote the trolley mass and the payload mass, respectively; x(t) is the trolley displacement while \(\theta (t)\) represents the payload swing angle; l is the length of the massless rope; g is the gravity acceleration constant. From the system dynamics, it is seen that there exist two system states, x(t) and \(\theta (t)\), and only one control input F(t), which leads to the fact that the overhead crane system is a typical underactuated system. We can also find that strong coupling exists between the trolley motion and the payload swing. In summary, it is difficult to control overhead crane systems properly.

The control objective of the emergency braking problem is to develop a proper control strategy to regulate the trolley velocity, together with the payload swing angle and swing angular velocity, to zero. Thus we have

$$\begin{aligned} \dot{x}(t)\rightarrow 0,~\theta (t)\rightarrow 0,~\dot{\theta }(t)\rightarrow 0, \end{aligned}$$
(3)

At the same time, during the entire braking process, the trolley displacement should not exceed the safe limit, in the sense that,

$$\begin{aligned} x(t)<\lambda , \end{aligned}$$
(4)

wherein \(\lambda \) represents the safe limit.

Considering the emergency braking problem, the trolley should stop as soon as possible to avoid collision while the payload swing should be as small as possible to ensure safety. Based on this, the control objective of emergency braking can be divided into two parts, known as fast trolley braking and payload swing suppression. Due to the coupling behavior, sudden braking of the trolley may probably cause large swing of the payload which is very dangerous. Therefore, it is difficult to achieve these two parts simultaneously, and it is very important and useful to design a proper emergency braking control method for overhead cranes. Subsequently, we will design a suitable control method for each part and then combine them together to propose a combined method to achieve the entire control objective.

3 Controller Design and Analysis

In this section, a novel emergency braking controller is proposed for overhead crane systems to achieve fast trolley braking, as well as payload swing suppression. Specifically, control objectives of trolley braking and payload swing suppression are considered separately with suitable control methods being designed. Then we combine the designed controllers together to obtain a novel emergency braking controller.

3.1 Braking Control for the Trolley

To regulate the trolley velocity to zero, we can design the following controller directly:

$$\begin{aligned} F_{1a}=-k_1\dot{x}, \end{aligned}$$
(5)

where \(k_1\in \mathbf {R}\) represents a positive control gain. Though controller (5) can regulate the trolley velocity to zero successfully, it cannot ensure the constraint in (4). Based on this fact, a potential-function-like item is added into the controller with the following expression:

$$\begin{aligned} F_{1p}=-\frac{k_2\dot{x}}{(\lambda -x_b)^2-(x-x_b)^2}, \end{aligned}$$
(6)

where \(\lambda \) is the safe position and \(x_b\) denotes the trolley position when emergency braking begins. \(k_2\in \mathbf {R}\) is a positive control gain. From the structure of (6), it is seen that if the trolley gets too close to the safe limit, this part can provide a large braking force to make the trolley decelerate fast.

Then we can design the trolley braking controller as follows:

$$\begin{aligned} F_1&=F_{1a}+F_{1_p}\nonumber \\&=-k_1\dot{x}-\frac{k_2\dot{x}}{(\lambda -x_b)^2-(x-x_b)^2}. \end{aligned}$$
(7)

Using (7), we can ensure that the trolley can brake fast and will not reach the safe limit.

3.2 Swing Suppression Control for the Payload

Though the controller in (7) can achieve the objective of trolley braking, it may also cause large payload swing which can be very dangerous and may lead to accidents. Therefore, the objective of payload swing suppression needs also to be taken into consideration. Then, the following controller is proposed to suppress the payload swing:

$$\begin{aligned} F_2=k_3\theta +k_4\dot{\theta }, \end{aligned}$$
(8)

where \(k_3,~k_4\in \mathbf {R}\) represent positive control gains. Utilizing this controller, the payload swing angle, as well as the swing angular velocity, will converge to zero.

3.3 Emergency Braking Control with Swing Suppression

Using (7) and (8), the objective of trolley braking and swing suppression can be achieved respectively. To achieve these objectives simultaneously, (7) and (8) are combined to obtain a novel emergency braking controller as follows:

$$\begin{aligned} F=F_1+F_2=-k_1\dot{x}-\frac{k_2\dot{x}}{(\lambda -x_b)^2-(x-x_b)^2}+k_3\theta +k_4\dot{\theta }. \end{aligned}$$
(9)

Utilizing (9), the objective of emergency braking, shown in (3) and (4), can be achieved.

4 Simulation Results

To illustrate the effectiveness of the proposed method, some simulation tests are carried out in the environment of MATLAB/Simulink. The system parameters are set the same as the actual self-built crane test-bed:

$$\begin{aligned} m=1~\mathrm{{kg}},~M=6.5~\mathrm{{kg}},~l=0.75~\mathrm{{m}}. \end{aligned}$$

Without loss of generality, the initial trolley position and the initial payload swing angle are both set as zero, in the sense that,

$$\begin{aligned} x(0)=0,\theta (0)=0. \end{aligned}$$

To test the proposed emergency braking method, the original target position of the trolley is selected as \(x_d=0.8~\mathrm {m}\) and we choose an eleven-order polynomial based trajectory planning method as the original crane control method. The expression of the planned trajectory is shown as follows:

$$\begin{aligned} x_r(t)=x_d \left( x_p + \frac{l}{g}\ddot{x}_p\right) , \end{aligned}$$
(10)

where g is the gravity acceleration constant which is chosen as \(g=9.8~{\mathrm{m}/\mathrm{s}^2}\). \(x_p\) represents an auxiliary trajectory with the following expression:

$$\begin{aligned} x_p=-252 \tau ^{11}+1386 \tau ^{10}-3080 \tau ^9+3456 \tau ^8-1980\tau ^7+462\tau ^6, \end{aligned}$$
(11)

wherein \(\tau =\frac{t}{T}\) and T denotes the designed transportation time which is chosen as \(T=6~\mathrm{{s}}\).

Emergency braking begins at \(3~\mathrm{{s}}\) and the controller is switched to the proposed emergency braking controller. The trolley position at this time is \(x_b=0.4~\mathrm{{m}}\). To verify the performance, in the simulation test, we choose two safe limits as \(\lambda =0.6~\mathrm{{m}}\) and \(\lambda =0.5~\mathrm{{m}}\). The control gains are chosen as \(k_1=1,~k_2=1,~k_3=20,~k_4=10\) when \(\lambda =0.6~\mathrm{{m}}\), and \(k_1=1,~k_2=2,~k_3=200,~k_4=50\) when \(\lambda =0.5~\mathrm{{m}}\).

The simulation results are shown in Figs. 1 and 2. From these figures, it is seen that using the proposed emergency braking controller, we can make the trolley brake quickly and during the entire process, the trolley position never exceeds the given safe limits. At the same time, the controller can suppress the payload swing obviously, which can avoid large payload swing and make the braking process safer. In summary, it is concluded that the proposed controller can achieve the objectives of fast trolley braking and payload swing suppression.

Fig. 1.
figure 1

Simulation results for emergency braking control. Solid line: proposed method; Dashed line: safe limit \(\lambda =0.6~\mathrm{{m}}\).

Full size image
Fig. 2.
figure 2

Simulation results for emergency braking control. Solid line: proposed method; Dashed line: safe limit \(\lambda =0.5~\mathrm{{m}}\).

Full size image

5 Summary and Conclusion

In this paper, a novel emergency braking control strategy, which can ensure trolley braking and payload swing suppression simultaneously, is proposed for overhead crane systems. In particular, by deeply analyzing the control objective, it is divided into two parts which are considered separately. For each part, a proper controller is designed, and then a novel emergency braking control method is obtained by combined these two controllers together. Different from the common used braking method that directly makes the trolley stop, the proposed method can also achieve the objective of payload swing suppression which ensures safety. Simulation results are included to illustrate the satisfactory performance of the proposed controller in the sense of fast trolley braking and payload swing suppression. In our further work, we will concentrate on design intelligent control methods, for example, neural network-based control method, to finish the emergency braking objective. Also, we will try to use the neural network method to optimize the control gains of this proposed method to obtain better performance.