1 Introduction

Underactuated system is a kind of nonlinear system whose number of independent control variables is less than the number of system degrees of freedom. It is superior to fully actuated system in saving energy, reducing cost, reducing weight and enhancing system flexibility. The underactuated system, such as robot manipulator [1], underactuated surface (USV) vessels [2, 3], autonomous underwater vehicles (AUVs) [4,5,6] and cranes [7,8,9], has simple structure and is convenient for overall dynamic analysis and test.

Due to the underactuated characteristics of the crane system, the payload swing can only be controlled indirectly by controlling the motion of the trolley due to the underactuated nature of the cranes. Conventional control methods of cranes are mainly dependent on the experience of the operator, which seriously degrades the efficiency of transportation and is, to a certain extent, risky. Therefore, in recent decades, numerous scholars have focused on researching crane control methods for a wide variety of control requirements. The main control methods can be divided into the following categories: optimal control method [10], nonlinear control [11,12,13,14,15], adaptive control [16] and intelligent algorithms [17, 18].

To be more specific, the analysis of these control strategies is as follows. According to the shaper parameters and cable length, Maghsoudi et al. put forward an improved shaper, which achieved better control effect than the conventional input shaping method by experiment [19]. An adaptive tracking control strategy was provided by Zhang et al. [20], which has validity in tracking error and uncertainties of model parameters. Giacomelli et al. designed an input-output inverse control method to address the problem of the residual hook and load swing [21]. Sun et al. put forward an optimal controller for the bridge crane with double pendulum effect [22]. On the one hand, the method realizes the target of driving trolley to the desired destination and anti-swing, on the other hand, it considers the system state and control input constraints. An optimal control strategy applied to a 3D crane system was put forward by Maghsoudi et al [23]. The control method also combined with a Zero Vibration shaper. It has confirmed that the control method can display superior positioning performance. For sake of solving the problem of actuator saturation, Sun et al. come up with a nonlinear output feedback controller with saturation by constructing a new energy function [24]. This method does not need difference operation to obtain the swing angle velocity signal. It is robust to the change of model parameters as well as external interference while realizing the positioning and swing angle suppression of the trolley. Tang et al. put forward the method of combining two kinds of motion trajectories for the load swing caused by trolley motion and external wind interference in the double swing bridge crane, that is, one is used to restrain the swing caused by trolley motion and the other is used to restrain the swing caused by wind interference [25]. Maleki et al. put forward a two-stage mode specific insensitive input shaper, which is used to solve the problem of the hook and load swing angle components in the rotary crane [26]. Compared with the two-stage mode zero swing input shaper, the validity of the control scheme was verified, and the robustness of the method to the change of rotation angle speed and angular acceleration of the cantilever was also proved.

Through the analysis of the existing literature, scholars mainly focused on the positioning and anti-swing control of two-dimensional double pendulum crane or three-dimensional single pendulum crane system. However, in practical engineering, it is not only necessary to realize the transportation of goods in three-dimensional space, but also the double pendulum phenomenon caused by the hook mass or the shape of goods can not be ignored, which increases the difficulty of controller design. On the other hand, the changes of cargo mass, rope length, actuator friction and other parameters will also reduce the robustness of traditional controller. In addition, the selection of controller parameters often depends on the experience of engineers, which greatly reduces the design efficiency of the control system.

Hence, a fuzzy adaptive nonlinear controller, which cannot only accomplish anticipated control goal efficaciously, but also has better robust control performance for three-dimensional double-pendulum overhead cranes (3DDPOC), will be put forward. The specific contributions are as follows:

  1. 1.

    This method can realize the accurate positioning performance of the trolley, and improve the transient control performance because more signals related to the swing of hook and load is added into the control input.

  2. 2.

    The proposed fuzzy method and adaptive law of the controller cannot only improve the robustness of the system, but also reduce the selection time of controller parameters, so as to greatly improve the efficiency of the overall design of the system.

The remaining structure of this paper is as follows: In Sect. 2, the mathematical model of 3DDPOC is established. Then, Sect. 3 describes the design of the proposed controller. The adaptive controller is designed according to the energy equation, in order to enhance the real-time control, a fuzzy controller is added, and the two are combined into the proposed controller to further improve the positioning and sway reduction performance. Section 4 introduces the self-built overhead crane platform and the discussion and analysis of the experimental results, which proves the superiority of the proposed controller. Section 5 summarizes the main work of this paper.

Fig. 1
figure 1

Overhead crane model

Full size image

2 Problem statement

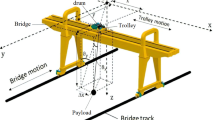
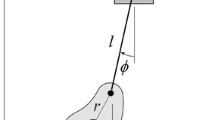
According to the structural diagram shown in Fig. 1, the mathematical model of crane studied in this paper can be derived as follows [27]:

$$\begin{aligned}&({M_1} + {m_1} + {m_2})\ddot{x} + ({m_1}{l_1}{C_1}{C_2} + {m_2}{l_1}{C_1}{C_2}){{\ddot{\theta }}_1} \nonumber \\&\qquad - ({m_1}{l_1}{S_1}{S_2} + {m_\mathrm{{2}}}{l_1}{S_1}{S_2}){{\ddot{\theta }}_2} + {m_2}{l_2}{C_3}{C_4}{{\ddot{\theta }}_3}\nonumber \\&\qquad - {m_2}{l_2}{S_3}{S_4}{{\ddot{\theta }}_4} - 2({m_1} + {m_2}){l_1}{C_1}{S_2}{{\dot{\theta }}_1}{{\dot{\theta }}_2}\nonumber \\&\qquad - 2{m_2}{l_2}{C_3}{S_4}{{\dot{\theta }}_3}{{\dot{\theta }}_4} - ({m_1} + {m_2}){l_1}{S_1}{C_2}\dot{\theta }_1^2\nonumber \\&\qquad - ({m_1} + {m_2}){l_1}{S_1}{C_2}\dot{\theta }_2^2 - {m_2}{l_2}{S_3}{C_4}\dot{\theta }_3^2\nonumber \\&\qquad - {m_2}{l_2}{S_3}{C_4}\dot{\theta }_4^2 = {F_x} - {F_{rx}} \end{aligned}$$
(1)
$$\begin{aligned}&({M_2} + {m_1} + {m_2})\ddot{y} + ({m_1}{l_1}{C_2} + {m_\mathrm{{2}}}{l_1}{C_2}){{\ddot{\theta }}_2}\nonumber \\&\qquad + {m_2}{l_2}{C_4}{{\ddot{\theta }}_4} - ({m_1} + {m_2}){l_1}{S_2}\dot{\theta }_2^2 - {m_2}{l_2}{S_4}\dot{\theta }_4^2\nonumber \\&\qquad = {F_y} - {F_{ry}} \end{aligned}$$
(2)
$$\begin{aligned}&({m_1} + {m_2}){l_1}{C_1}{C_2}\ddot{x} + ({m_1} + {m_2})l_1^2C_2^2{{\ddot{\theta }}_1}\nonumber \\&\qquad + {m_2}{l_1}{l_2}({C_1}{C_2}{C_3}{C_4} + \left. {{C_2}{C_4}{S_1}{S_3}} \right) {{\ddot{\theta }}_3}\nonumber \\&\qquad + {m_2}{l_1}{l_2}\left( {{C_2}{C_3}{S_1}{S_4}} \right. \left. { - {C_1}{C_2}{S_3}{S_4}} \right) {{\ddot{\theta }}_4}\nonumber \\&\qquad + {m_2}{l_1}{l_2}({C_2}{C_3}{C_4}{S_1} - {C_1}{C_2}{C_4}{S_3})\dot{\theta }_3^2\nonumber \\&\qquad - {m_2}{l_1}{l_2}({C_1}{C_2}{C_4}{S_3} + {C_2}{C_3}{C_4}{S_1})\dot{\theta }_4^2\nonumber \\&\qquad - 2({m_1} + {m_2})l_1^2{S_2}{C_2}{{\dot{\theta }}_1}{{\dot{\theta }}_2} - 2{m_2}{l_1}{l_2}\nonumber \\&\qquad \times {({C_1}{C_2}{C_3}{S_4} + {S_1}{C_2}{S_3}{S_4})}{{\dot{\theta }}_3}{{\dot{\theta }}_4}\nonumber \\&\qquad + ({m_1} + {m_2})g{l_1}{S_1}{C_2} = 0 \end{aligned}$$
(3)
$$\begin{aligned}&\qquad - ({m_1} + {m_2}){l_1}{S_1}{S_2}\ddot{x} + ({m_1} + {m_2}){l_1}{C_2}\ddot{y}\nonumber \\&\qquad + ({m_1} + {m_2})l_1^2{{\ddot{\theta }}_2} + {m_2}{l_1}{l_2}({C_1}{C_4}{S_2}{S_3}\nonumber \\&\qquad - {S_1}{S_2}{C_3}{C_4}){{\ddot{\theta }}_3} + {m_2}{l_1}{l_2}({C_2}{C_4} + {C_1}{C_3}{S_2}{S_4}\nonumber \\&\qquad + {S_1}{S_2}{S_3}{S_4}){{\ddot{\theta }}_4} + ({m_1} + {m_2})l_1^2{C_2}{S_2}\dot{\theta }_1^2\nonumber \\&\qquad + {m_2}{l_1}{l_2}({C_1}{C_3}{C_4}{S_2} + {S_1}{S_2}{S_3}{C_4})\dot{\theta }_3^2\nonumber \\&\qquad - {m_2}{l_1}{l_2}({C_2}{S_4} + {C_1}{C_3}{C_4}{S_2} + {S_1}{S_2}{S_3}{C_4})\dot{\theta }_4^2\nonumber \\&\qquad + 2{m_2}{l_1}{l_2}({S_1}{S_2}{S_4}{C_3} - {C_1}{S_2}{S_3}{S_4}){{\dot{\theta }}_3}{{\dot{\theta }}_4}\nonumber \\&\qquad + ({m_1} + {m_2})g{l_1}{C_1}{S_2} = 0 \end{aligned}$$
(4)
$$\begin{aligned}&{m_2}{l_2}{C_3}{C_4}\ddot{x} + {m_2}{l_1}{l_2}({C_1}{C_2}{C_3}{C_4} + {S_1}{S_3}{C_2}{C_4}){{\ddot{\theta }}_1}\nonumber \\&\qquad + {m_2}{l_1}{l_2}({C_1}{C_4}{S_2}{S_3} - {S_1}{S_2}{C_3}{C_4}){{\ddot{\theta }}_2} + {m_2}l_2^2C_4^2{{\ddot{\theta }}_3}\nonumber \\&\qquad + {m_2}{l_1}{l_2}({C_1}{C_2}{C_4}{S_3} - {S_1}{C_2}{C_3}{C_4})\dot{\theta }_1^2 + {m_2}{l_1}{l_2}\nonumber \\&\qquad ({C_1}{C_2}{C_4}{S_3}{-}{S_1}{C_2}{C_3}{C_4})\dot{\theta }_2^2{-}2{m_2}{l_1}{l_2}({C_1}{C_3}{C_4}{S_2}\nonumber \\&\qquad + {S_1}{S_2}{S_3}{C_4}){{\dot{\theta }}_1}{{\dot{\theta }}_2} - 2{m_2}l_2^2{S_4}{C_4}{{\dot{\theta }}_3}{{\dot{\theta }}_4}\nonumber \\&\qquad + {m_2}g{l_2}{S_3}{C_4} = 0 \end{aligned}$$
(5)
$$\begin{aligned}&\qquad - {m_2}{l_2}{S_3}{S_4}\ddot{x} + {m_2}{l_2}{C_4}\ddot{y} + {m_2}{l_1}{l_2}({C_2}{C_3}{S_1}{S_4}\nonumber \\&\qquad - {C_1}{C_2}{S_3}{S_4}){{\ddot{\theta }}_1} + {m_2}{l_1}{l_2}({C_2}{C_4} + {S_1}{S_2}{S_3}{S_4}\nonumber \\&\qquad + {C_1}{C_3}{S_2}{S_4}){{\ddot{\theta }}_2} + {m_2}l_2^2{{\ddot{\theta }}_4} + {m_2}{l_1}{l_2}({C_1}{C_2}{C_3}{S_4}\nonumber \\&\qquad + {C_2}{S_1}{S_3}{S_4})\dot{\theta }_1^2 + {m_2}{l_1}{l_2}({C_1}{C_2}{C_3}{S_4}\nonumber \\&\qquad + {S_1}{C_2}{S_3}{S_4} - {C_4}{S_2})\dot{\theta }_2^2 + {m_2}l_2^2{S_4}{C_4}\dot{\theta }_3^2\nonumber \\&\qquad + 2{m_2}{l_1}{l_2}({C_1}{S_2}{S_3}{S_4} - {C_3}{S_1}{S_2}{S_4}){{\dot{\theta }}_1}{{\dot{\theta }}_2}\nonumber \\&\qquad + {m_2}g{l_2}{C_3}{S_4} = 0 \end{aligned}$$
(6)

The detailed definition of the parameters in (1)–(6) can be found in Table 1.

Table 1 Parameters of the system
Full size table

Besides, the following friction model in [27] is used:

$$\begin{aligned}&{F_{rx}} = {f_{rox}}\tanh \left( {\frac{{\dot{x}}}{{{\varepsilon _x}}}} \right) - {k_{rx}}\left| {\dot{x}} \right| \dot{x}, \end{aligned}$$
(7)
$$\begin{aligned}&{F_{ry}} = {f_{roy}}\tanh \left( {\frac{{\dot{y}}}{{{\varepsilon _y}}}} \right) - {k_{ry}}\left| {\dot{y}} \right| \dot{y}, \end{aligned}$$
(8)

where \({f_{rox}}\), \({f_{roy}}\), \({{\varepsilon _x}}\), \({{\varepsilon _y}}\), \({k_{rx}}\) and \({k_{ry}}\) represent the friction-related parameters.

For the sake of facilitating the subsequent design and analysis, the following assumption is reasonable [24, 25, 27].

  • The rope and the rigging can be seen as massless rigid links, and their flexibility and torsion can be neglected.

  • The hook and load swing angle of the crane system always meet the following constraints:

    $$\begin{aligned}&-\frac{\pi }{2}< \theta _1, \theta _2, \theta _3, \theta _4 < \frac{\pi }{2} \end{aligned}$$
    (9)

2.1 Control objective

The control objective is that, on the one hand, the trolley can reach the target position accurately, and on the other hand, it can eliminate the swing angle of the hook and load efficiently. It can be elaborated as the following expressions:

  1. 1)

    To reach their desired positions, the trolley is driven to track some suitable reference trajectories, therefore the mathematical expressions is as follows:

    $$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } {e_x} = 0,\mathop {\lim }\limits _{t \rightarrow \infty } {e_y} = 0 \end{aligned}$$
    (10)

    where \(e_x\) and \(e_y\) represent the positioning errors, \(x_{d}\), \(y_{d}\) are the designed destinations. At the same time, the following formulations are introduced to represent the positioning error variables:

    $$\begin{aligned}&e_x=x-x_{d}, e_y=y-y_{d} \end{aligned}$$
    (11)
    $$\begin{aligned}&\dot{e}_x=\dot{x}, \dot{e}_y=\dot{y} \end{aligned}$$
    (12)
  2. 2)

    Meanwhile, the elimination of the swing angles in all levels are expressed as follows:

    $$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _1} = 0,\;\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _2} = 0,\nonumber \\&\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _3} = 0,\;\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _4} = 0 \end{aligned}$$
    (13)

3 Controller development and stability analysis

3.1 Adaptive controller design

As shown in Fig. 1, the total mechanical energy of the overhead cranes system is formulated as:

$$\begin{aligned} {E_m}= & {} \frac{1}{2}\dot{q}_{}^TM(q)\dot{q} + ({m_1}+m_2)g{l_1}(1 - {C_1}{C_2}) \nonumber \\&+{m_2}g{l_2}(1 - {C_3}{C_4}) \end{aligned}$$
(14)

Taking the derivative of system energy \(E_m\), it is easy to get the expression as follows:

$$\begin{aligned} {{\dot{E}}_m}= & {} {{\dot{q}}^T}M(q)\ddot{q} \!+\! \frac{1}{2}{{\dot{q}}^T}\dot{M}(q)\dot{q} \!+\! \left( {{m_1} \!+\! {m_2}} \right) \nonumber \\\times & {} g{l_1}({S_1}{C_2}{{\dot{\theta }}_1} \!+\! {C_1}{S_2}{{\dot{\theta }}_2}) \mathrm{{ }}\!+\! {m_2}g{l_2}({S_3}{C_4}{{\dot{\theta }}_3} \!+\! {C_3}{S_4}{{\dot{\theta }}_4})\nonumber \\= & {} \left( {{F_x} \!-\! {F_{rx}}} \right) \dot{x} \!+\! \left( {{F_y} \!-\! {F_{ry}}} \right) \dot{y} \end{aligned}$$
(15)

which implies that passivity of the crane system, with \({F_x} - {F_{rx}}\) and \({F_y} - {F_{ry}}\) being the inputs, \(\dot{x}\) and \(\dot{y}\) being the outputs.

As mentioned in the previous section, the coefficients related to friction in Eqs. (7) and (8) are difficult to determine. Therefore, an adaptive control strategy is applied to estimate the values of these unknown parameters. Then, the following expression can be derived from Eq. (15):

$$\begin{aligned} {{\dot{E}}_m}=\left( {{F_x} \!-\! \varepsilon _x^T{\omega _x}} \right) \dot{x} \!+\! \left( {{F_y} \!-\! \varepsilon _y^T{\omega _y}} \right) \dot{y} \end{aligned}$$
(16)

where the vectors \(\varepsilon _x\), \(\varepsilon _y\), \(\omega _x\) and \(\omega _y\) can be defined as:

$$\begin{aligned}&{\varepsilon _x} = {\left[ {\begin{array}{*{20}{c}} {\tanh \left( {\frac{{\dot{x}}}{{{\varepsilon _x}}}} \right) }&{\left| {\dot{x}} \right| \dot{x}} \end{array}} \right] ^T},{\omega _x} = \left[ {\begin{array}{*{20}{c}} {{f_{rox}}}&{ - {k_{rx}}} \end{array}} \right] \nonumber \\&{\varepsilon _y} = {\left[ {\begin{array}{*{20}{c}} {\tanh \left( {\frac{{\dot{y}}}{{{\varepsilon _y}}}} \right) }&{\left| {\dot{y}} \right| \dot{y}} \end{array}} \right] ^T},{\omega _x} = \left[ {\begin{array}{*{20}{c}} {{f_{roy}}}&{ - {k_{ry}}} \end{array}} \right] \end{aligned}$$
(17)
Fig. 2
figure 2

Fuzzy controller structure diagram

Full size image

Considering the structure of Eq. (14) and the control objective in Eqs. (10) and (13), we designed a Lyapunov candidate function:

$$\begin{aligned} V= & {} \frac{1}{2}\dot{q}_{}^TM(q)\dot{q} + {m_1}g{l_1}(1 - {C_1}{C_2}) \nonumber \\&+ {m_2}g[{l_1}(1 - {C_1}{C_2}) + {l_2}(1 - {C_3}{C_4})]\nonumber \\&{+}\frac{1}{2}{k_{px}}e_x^2\mathrm{{ {+} }}\frac{1}{2}{k_{py}}e_y^2 {+} \frac{1}{2}{{\tilde{\omega }}} _x^T\varphi _x^{ - 1}{{{{\tilde{\omega }}} }_x} {+} \frac{1}{2}{{\tilde{\omega }}} _y^T\varphi _y^{ - 1}{{{{\tilde{\omega }}} }_y}\nonumber \\ \end{aligned}$$
(18)

where \({k_{px}},{k_{py}} \in {R^ + }\) are controller gains, \(\varphi _x\) and \(\varphi _y\) are positive definite diagonal matrices which have adjustable elements, and \({{{{\tilde{\omega }}} }_x},{{{{\tilde{\omega }}} }_y}\) are estimation error which can be presented as follows:

$$\begin{aligned}&{{{{\tilde{\omega }}} }_x} = {{{{\hat{\omega }}} }_x} - {\omega _x},{{\tilde{\omega }}_y} = {{{{\hat{\omega }}} }_y} - {\omega _y} \end{aligned}$$
(19)
$$\begin{aligned}&{{\dot{\tilde{\omega }} }_x} = {\dot{{{\hat{\omega }}}}_x},{{\dot{{{\tilde{\omega }}}} }_y} = {\dot{{{\hat{\omega }}} }_y} \end{aligned}$$
(20)

The following equation can be derived from Eqs. (1)–(6), (15) and V constructed in Eq. (18):

$$\begin{aligned} \dot{V}= & {} {{\dot{E}}_m}\mathrm{{ + }}{k_{px}}{e_x}\dot{x}\mathrm{{ + }}{k_{py}}{e_y}\dot{y} + {{\tilde{\omega }}} _x^T\varphi _x^{ - 1}{\dot{{{\hat{\omega }}} }_x} + {{\tilde{\omega }}} _y^T\varphi _y^{ - 1}{\dot{\hat{\omega }}_y}\nonumber \\= & {} \left( {{F_x} - \varepsilon _x^T{\omega _x} + {k_{px}}{e_x}} \right) \dot{x} + \left( {{F_y} - \varepsilon _y^T{\omega _y} + {k_{py}}{e_y}} \right) \dot{y}\nonumber \\&+ \tilde{\omega }_x^T\varphi _x^{ - 1}{\dot{{{\hat{\omega }}} }_x} + {{\tilde{\omega }}} _y^T\varphi _y^{ - 1}{\dot{{{\hat{\omega }}} }_y} \end{aligned}$$
(21)

Combining with the above conclusions and enhancing swing angle suppression effect, the adaptive controllers based on Lyapunov stability theory can be proposed as follows:

$$\begin{aligned}&{F_x} = - {k_{px}}e_x^{} - {k_{dx}}\dot{x} + \varepsilon _x^T{{{{\hat{\omega }}} }_x} \nonumber \\&- ({k_{11}}\theta _1^2 + {k_{12}}\theta _2^2 + {k_{13}}\theta _3^2 + {k_{14}}\theta _4^2)\dot{x} \end{aligned}$$
(22)
$$\begin{aligned}&{F_y} = - {k_{py}}e_y^{} - {k_{dy}}\dot{y} + \varepsilon _y^T{{{{\hat{\omega }}} }_y} \nonumber \\&- ({k_{21}}\theta _1^2 + {k_{22}}\theta _2^2 + {k_{23}}\theta _3^2 + {k_{24}}\theta _4^2)\dot{y} \end{aligned}$$
(23)

where \(k_{dx}\), \(k_{dy}\), \({k_{1i}}\) and \({k_{2i}} \in {R^ + }(i = 1,2,3,4)\) are also controller gains, which need to be determined. The adaptive law can be designed as follows:

$$\begin{aligned}&{\dot{{{\hat{\omega }}} }_x} = - {\varphi _x}{\varepsilon _x}\dot{x} \end{aligned}$$
(24)
$$\begin{aligned}&{\dot{{{\hat{\omega }}} }_y} = - {\varphi _y}{\varepsilon _y}\dot{y} \end{aligned}$$
(25)

where \(\varphi _x\) and \(\varphi _y\) are also gains to be determined.

Remark 1

In this paper, on the basis of establishing the dynamic model of the overhead crane, we consider the energy function of the system as the basis of the designed Lyapunov function. Then, considering the positioning performance of the trolley and the compensation performance of friction, two auxiliary functions are designed to form the final Lyapunov function. Finally, the proposed controller is designed according to Lyapunov stability theorem and swing angle suppression performance.

3.2 Fuzzy controller design

Based on the frequency and complexity of the actual operation of the crane, in order to complete the control requirements more effectively, we added a fuzzy control method to adjust its parameters \({k_{px}}\), \({k_{dx}}\), \({k_{py}}\) and \({k_{dy}}\) online to achieve stronger real-time performance and higher control accuracy.

Two fuzzy controllers are added in the adaptive controller. Considering the similarity of the fuzzy controller in \({F_x }\) and \({F_y}\), the controller with \({F_x }\) in Eq. (22) is taken as an example. Taking the displacement and speed error of x as input, the output signals are the corrected \(\varDelta {k_{px}}\) and \(\varDelta {k_{dx}}\).

In Fig. 2, NB (negative big), NM (negative medium), NS (negative small), ZE (zero), PS (positive small), PM (positive medium) and PB (positive big) are chosen for \({e_x }\), \({{\dot{e}}_x }\), \(\varDelta {k_{px}}\) and \(\varDelta {k_{dx}}\). Among them, the basic domain of the trolley displacement and velocity errors are all \(x \in \) [-3, 3]. The basic domains of revision are \(\varDelta {k_{px}}\in \) [1, 12] and \(\varDelta {k_{dx}}\in \) [3, 12]. Their quantization factors are 0.25, 20, 10 and 10 respectively and use trimf and gaussmf type functions as membership functions. According to the rules in Fig. 3, the adaptive adjustment of \({k_{px}}\) and \({k_{dx}}\) parameters are:

$$\begin{aligned} {k_{px}}= & {} k_{px}^0 + \varDelta {k_{px}} \end{aligned}$$
(26)
$$\begin{aligned} {k_{dx}}= & {} k_{dx}^0 + \varDelta {k_{dx}} \end{aligned}$$
(27)

where \(k_{px}^0\) and \(k_{dx}^0\) are the initial values of the controller parameter, and \(\varDelta {k_{px}}\), \(\varDelta {k_{dx}}\) are the two modified values.

Fig. 3
figure 3

Fuzzy control rules

Full size image

The fuzzy rules for tuning the control gains are expressed generally as:

$$\begin{aligned} \mathrm{{If }}\,E\,\mathrm{{ is }}\,{M_{i1}}\,\mathrm{{and}}\,EC\mathrm{{ is }}\,{M_{j1}}\mathrm{{then }}\,{k_{px}}\,\mathrm{{ is }}\,{Q_{i1}}\,\mathrm{{and}}\,{k_{dx}}\,\mathrm{{ is }}\,{Q_{j1}}\nonumber \\ \end{aligned}$$
(28)

where \({M_{i1}}\), \({M_{j1}}\), \({Q_{i1}}\) and \({Q_{j1}}\) represent different membership curves. In addition, set two inputs and seven fuzzy sets, the total rule is forty nine, as given in Fig. 3.

3.3 Stability analysis

This section will illustrate the theoretical proof through the following theorem.

Theorem 1

The nonlinear adaptive controllers Eqs. (22) and (23) with update laws in Eqs. (24) and (25) were proposed, which can simultaneously realize the positioning of the trolley as well as the suppression of double-pendulum effect.

$$\begin{aligned}&\lim _{t \rightarrow \infty }\left[ x \quad y \quad \theta _1 \quad \theta _2 \quad \theta _3 \quad \theta _4 \right] ^T\nonumber \\&\quad = \left[ {{x_{d}}} \quad {{y_{d}}} \quad 0 \quad 0 \quad 0 \quad 0 \right] ^T \end{aligned}$$
(29)
$$\begin{aligned}&\lim _{t \rightarrow \infty }\left[ \dot{x} \quad \dot{y} \quad {\dot{\theta }}_1 \quad {\dot{\theta }}_2 \quad {\dot{\theta }}_3 \quad {\dot{\theta }}_4 \right] ^T \nonumber \\&\quad =\left[ 0 \quad 0 \quad 0 \quad 0 \quad 0 \quad 0 \right] ^T \end{aligned}$$
(30)

Proof

The V designed in Eq. (18) as previously mentioned, is adopted as the candidate function of Lyapunov. Combining the controllers in Eqs. (22) and (23) with the update laws in Eqs. (24) and (25), the following result can be derived from Eq. (21):

$$\begin{aligned} \dot{V}= & {} - {k_{dx}}{{\dot{x}}^2} - {k_{dy}}{{\dot{y}}^2} \nonumber \\&- ({k_{11}}\theta _1^2 + {k_{12}}\theta _2^2 + {k_{13}}\theta _3^2 + {k_{14}}\theta _4^2){{\dot{x}}^2}\nonumber \\&- ({k_{21}}\theta _1^2 + {k_{22}}\theta _2^2 + {k_{23}}\theta _3^2 + {k_{24}}\theta _4^2){{\dot{y}}^2} \le 0 \end{aligned}$$
(31)

Therefore, it can be proved that the closed-loop system is stable at the desired equilibrium point. In other words, V(t), the candidate function of Lyapunov, is non increasing. Therefore, we can obtain that

$$\begin{aligned}&V \in {L_\infty } \Rightarrow e_x^{},e_y^{}, \theta _1^{}, \theta _2^{}, \theta _3^{}, \nonumber \\&\quad \theta _4^{},{{{\tilde{\omega }}} _x},{{{\tilde{\omega }}} _y},{{{\hat{\omega }}} _x},{{{\hat{\omega }}} _y},{F_x},{F_y} \in {L_\infty } \end{aligned}$$
(32)

Further, S is introduced as an invariant and compact set as follows:

$$\begin{aligned} S\mathop = \limits ^\varDelta \left\{ {\left( {q,\dot{q}} \right) \left| {\dot{V}\left( x \right) = 0} \right. } \right\} \end{aligned}$$
(33)

Then, \(\varOmega \) is defined as the largest invariant set in S. In view of this, we can derive the following conclusions from the \(\varOmega \):

$$\begin{aligned} \dot{x}= & {} 0,\dot{y} = 0 \Rightarrow \ddot{x} = 0,\ddot{y} = 0,{{\dot{e}}_x} = 0,\dot{e}_y^{} = 0 \nonumber \\\Rightarrow & {} e_x^{} = {\lambda _1},e_y^{} = {\lambda _2}\nonumber \\\Rightarrow & {} x = {\lambda _1} + {x_d},y = {\lambda _2} + {y_d} \end{aligned}$$
(34)

where \(\lambda _1\) and \(\lambda _2\) are constants. Therefore, the controller \(F_x\) and \(F_y\) can be represented as follows in the set S:

$$\begin{aligned} {F_x} = - {k_{px}}{\lambda _1},{F_y} = - {k_{py}}{\lambda _2} \end{aligned}$$
(35)

Substituting Eq. (33) into Eqs. (7) and (8), we can obtain that:

$$\begin{aligned} {F_{rx}} = 0,{F_{ry}} = 0 \end{aligned}$$
(36)

Combining with the above equation (35), then, substituting Eq. (33) into Eq. (1) and simplify it mathematically, the following expression can be obtained:

$$\begin{aligned}&\frac{d}{{dt}}\left\{ {{\alpha _1}\left[ {\beta \left( {{C_1}{C_2}{{\dot{\theta }}_1} \!-\! {S_1}{S_2}{{\dot{\theta }}_2}} \right) \!+\! \left( {{C_3}{C_4}{{\dot{\theta }}_3} \!-\! {S_3}{S_4}{{\dot{\theta }}_4}} \right) } \right] } \right\} \nonumber \\&\quad =\frac{1}{{{m_x}}}{F_x} \end{aligned}$$
(37)

Meanwhile, we define that

$$\begin{aligned}&\beta \buildrel \varDelta \over = \frac{{\left( {{m_1} + {m_2}} \right) {l_1}}}{{{m_2}{l_2}}}, {m_x} \buildrel \varDelta \over = {M_1} + {m_1} + {m_2}, {\alpha _1}\mathrm{{ = }}\frac{{{m_2}{l_2}}}{{{m_x}}}\nonumber \\ \end{aligned}$$
(38)

Then, the following equation can be obtained by integrating Eq. (37):

$$\begin{aligned}&{\alpha _1}\left[ {\beta \left( {{C_1}{C_2}{{\dot{\theta }}_1} - {S_1}{S_2}{{\dot{\theta }}_2}} \right) + \left( {{C_3}{C_4}{{\dot{\theta }}_3} - {S_3}{S_4}{{\dot{\theta }}_4}} \right) } \right] \nonumber \\&\quad = \frac{1}{{{m_x}}}\int {\left( {{F_x}} \right) } {\hbox {d}}t + {\rho _1} \end{aligned}$$
(39)

with \({\rho _1}\) being a constant.

Considering the expression of Eq. (35), if \({\rho _1} \ne 0\) is satisfied, the following result can be obtained when \(t \rightarrow \infty \), that is

$$\begin{aligned} \frac{1}{{{m_x}}}\int {\left( {{F_x}} \right) } {\hbox {d}}t\mathrm{{ = }}\frac{1}{{{m_x}}}\left( { - {k_{px}}{\lambda _1}t} \right) \rightarrow \infty \end{aligned}$$
(40)

At the same time, we can obtain that:

$$\begin{aligned} {\alpha _1}\left[ {\beta \left( {{C_1}{C_2}{{\dot{\theta }}_1} \!-\! {S_1}{S_2}{{\dot{\theta }}_2}} \right) \!+\! \left( {{C_3}{C_4}{{\dot{\theta }}_3} \!-\! {S_3}{S_4}{{\dot{\theta }}_4}} \right) } \right] \rightarrow \infty \nonumber \\ \end{aligned}$$
(41)

However, this contradicts the previous conclusion, which is \({F_x} \in {L_\infty }\) in Eq. (32).

Hence, only the following result can be obtained:

$$\begin{aligned}&{\lambda _1}\mathrm{{ = }}0 \Rightarrow {F_x}\mathrm{{ = 0}} \end{aligned}$$
(42)

Then, combining the expression Eq. (22) of controller and the conclusion of Eq. (42), we can obtain the following result:

$$\begin{aligned}&{e_x} = 0 \Rightarrow x = {x_d} \end{aligned}$$
(43)

Using methods similar to those in the above analysis process, we can obtain the following conclusion:

$$\begin{aligned} F_y= & {} 0 \\ \nonumber {e_y}= & {} 0 \Rightarrow y = {y_d} \end{aligned}$$
(44)

According to Eqs. (36), (42)–(44), the following equations can be obtained:

$$\begin{aligned}&({m_1}{l_1} \!+\! {m_2}{l_1}){{\ddot{\theta }}_1} \!+\! {m_2}{l_2}{{\ddot{\theta }}_3} \!=\! \mathrm{{0}} \end{aligned}$$
(45)
$$\begin{aligned}&({m_1}{l_1} \!+\! {m_\mathrm{{2}}}{l_1}){{\ddot{\theta }}_2} \!+\! {m_2}{l_2}{{\ddot{\theta }}_4} \!=\! \mathrm{{0}} \end{aligned}$$
(46)
$$\begin{aligned}&({m_1} \!+\! {m_2})l_1^2{{\ddot{\theta }}_1} \!+\! {m_2}{l_1}{l_2}{{\ddot{\theta }}_3} \!+\! ({m_1} \!+\! {m_2})g{l_1}{\theta _1} \!=\! 0\mathrm{{ }} \end{aligned}$$
(47)
$$\begin{aligned}&({m_1} \!+\! {m_2})l_1^2{{\ddot{\theta }}_2} \!+\! {m_2}{l_1}{l_2}{{\ddot{\theta }}_4} \!+\! ({m_1} \!+\! {m_2})g{l_1}{\theta _2} \!=\! 0 \end{aligned}$$
(48)
$$\begin{aligned}&{m_2}{l_1}{l_2}{{\ddot{\theta }}_1} \!+\! {m_2}l_2^2{{\ddot{\theta }}_3} \!+\! {m_2}g{l_2}{\theta _3} \!=\! 0 \end{aligned}$$
(49)
$$\begin{aligned}&{m_2}{l_1}{l_2}{{\ddot{\theta }}_2} \!+\! {m_2}l_2^2{{\ddot{\theta }}_4} \!+\! {m_2}g{l_2}{\theta _4} \!=\! 0 \end{aligned}$$
(50)

Substituting Eq. (45) into Eq. (47), the following result can be obtained:

$$\begin{aligned}&g{\theta _1} = 0 \Rightarrow {\theta _1} = 0 \Rightarrow {\ddot{\theta }_1} = 0 \Rightarrow {\ddot{\theta }_3} = 0 \end{aligned}$$
(51)

Substituting Eq. (46) into Eq. (48), it can be obtained as follows:

$$\begin{aligned}&g{\theta _2} = 0 \Rightarrow {\theta _2} = 0 \Rightarrow {\ddot{\theta }_2} = 0 \Rightarrow {\ddot{\theta }_4} = 0 \end{aligned}$$
(52)

Then, substituting the results of Eqs. (51) and (52) into Eqs. (49) and (50), respectively.

$$\begin{aligned}&{{\ddot{\theta }}_1} = 0,{{\ddot{\theta }}_3} = 0 \Rightarrow g{\theta _3} = 0 \Rightarrow {\theta _3} = 0 \end{aligned}$$
(53)
$$\begin{aligned}&{{\ddot{\theta }}_2} = 0,{{\ddot{\theta }}_4} = 0 \Rightarrow g{\theta _4} = 0 \Rightarrow {\theta _4} = 0 \end{aligned}$$
(54)

From Eqs. (43), (44) and (51)–(54), it is shown that all systems are included in the largest balance invariant set \(\varOmega \), using LaSalle’s invariance principle to prove Theorem 1 [27].

Remark 2

The fuzzy controller only adjusts the parameters online and does not affect the stability of the controller, hence there is not much explanation here.

4 Experimental results and discussion

This section will be divided into three parts. The first part is the introduction of the self-built overhead crane experiment platform, the second part presents experimental conditions, and the third part is the comparative experiment and analysis with the existing controllers. The comparative controllers are chosen linear-quadratic-regulator (LQR) [28] and enhanced coupling controller (ECC) [11].

4.1 Experimental setup

Figure 4 describes the structure of the overhead crane hardware platform, whose nominal value is shown in Table 2. For the experiments implemented in this section, two absolute encoders (16384 PPR) are used to observe the values of \({\theta _1}\)-\({\theta _4}\). In addition, an absolute encoder (550 PPR) is also utilized to feedback the position of the trolley to complete the regulation control. For the drive section, DC drivers are used to drive the trolley on the guide rail for x and y direction operation. The control signals are generated by MATLAB simulation and the data interaction between the platform and the IPC is performed by a motion control board.

Fig. 4
figure 4

Experimental setup

Full size image
Table 2 Nominal value of overhead crane parameters
Full size table

4.2 Reference trajectory and proposed controller gains

In order to verify the effectiveness of the method and compare the control performance with the traditional method, the following equations are used as the reference input signal for the trolley in x and y directions, respectively:

$$\begin{aligned} {\varvec{q}}(i) _r = \left\{ {\begin{array}{l} \begin{array}{l} ({\varvec{q}}(i) _d - {\varvec{q}}(i) _0)\left( {\frac{t}{{{t_{\varvec{q}}(i) d}}} - \frac{1}{{2\pi }}\sin \left( \frac{{2\pi t}}{{{t_{q(i) d}}}}\right) } \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {\varvec{q}}(i) _0,\,t \in [0,\,{t_{\varvec{q}}(i) d}) \end{array}\\ {{\varvec{q}}(i) _d,\,t \in [{t_{\varvec{q}}(i) d},{{ + }}\,\infty )} \end{array}} \right. \end{aligned}$$
(55)

where \(q(i) _0\), \(q{(i)_d}\) and \({t_{q(i )d}}\) (\(i=1,2\)) represent the initial target position, the final target position, and the reaching time, respectively. In addition, \(q{(i )_0} = 0\)[m], \({t_{q(i )d}} = 5\)[s], \(q{(1)_d} = {x_d} = 0.4\)[m] and \(q{(2)_d} = {y_r} = 0.4\)[m].

Aiming at the problem that the selection of parameters in the traditional controller only depends on the experience of engineers, this paper proposes an auxiliary selection of main parameters in the controller combined with fuzzy control algorithm. The initial fuzzy controller gains of \({F_x }\) and \({F_y}\) are:

$$\begin{aligned} k_{px}^0 = 5, k_{dx}^0 = 10,k_{py}^0= 5,k_{dy}^0= 15 \end{aligned}$$
(56)

According to the time response of the crane system, the remaining parameters are selected as: \(k_{11}=400, k_{12}=800, k_{13}=800, k_{14}=400\) and \(k_{21}=300, k_{22}=500, k_{23}=400, k_{24}=800\), respectively.

4.3 Comparative experiments

To verify the effectiveness of the proposed method, the following two traditional control methods are used for comparative experiments:

4.3.1 LQR controller [28]

In order to design the LQR controller, we need to linearize the crane system model and select a cost function \(J = \int _0^\infty {\left[ {{x^T}\left( t \right) Qx\left( t \right) + {u^T}\left( t \right) Ru\left( t \right) } \right] } dt\), where Q and R are semi-positive definite matrices. Combined with the state feedback control method, the following expression can be obtained:

$$\begin{aligned} {F_x}= & {} - {\kappa _{p1}}{e_x} - {\kappa _{d1}}\dot{x} - {\kappa _1}{\theta _1} - {\kappa _2}{\theta _3} \nonumber \\&- {\kappa _3}{{\dot{\theta }}_1} - {\kappa _4}{{\dot{\theta }}_3} + {F_{rx}} \end{aligned}$$
(57)
$$\begin{aligned} {F_y}= & {} - {\kappa _{p2}}{e_y} - {\kappa _{d2}}\dot{y} - {\kappa _5}{\theta _2} - {\kappa _6}{\theta _4} \nonumber \\&- {\kappa _7}{{\dot{\theta }}_2} - {\kappa _8}{{\dot{\theta }}_4} + {F_{ry}} \end{aligned}$$
(58)

with \(\kappa _{p1}\), \(\kappa _{p2}\), \(\kappa _{d1}\), \(\kappa _{d2}\), \(\kappa _1\), \(\kappa _2\), \(\kappa _3\), \(\kappa _4\), \(\kappa _5\), \(\kappa _6\), \(\kappa _7\), \(\kappa _8\) \( \in R\) representing control gains. According to the design experience, we choose

\(Q=\) diag \( \left( 200\mathrm{{ }}\quad 100\mathrm{{ }}\quad 20\mathrm{{ }}\quad 20\mathrm{{ }}\quad 20\mathrm{{ }} \quad 20\mathrm{{ }}\quad 5\mathrm{{ }}\quad 5\mathrm{{ }}\quad 5\mathrm{{ }} \right. \left. 5\mathrm{{ }}\quad 5\mathrm{{ }}\quad 5 \right) \) and \(R = {\left[ {1\mathrm{{ }}\quad 1} \right] ^T}\). Then, we have \(\kappa _{px}=6.3246, \kappa _{py}=6.3246, \kappa _{dx}=-2.9873, \kappa _{dy}=-2.0433, \kappa _{1}=0.9480, \kappa _{2}=0.5145, \kappa _{3}=10.6964, \kappa _{4}=15.2723, \kappa _{5}=-0.9062, \kappa _{6}=-1.4450, \kappa _{7}=0.1921, \kappa _{8}=0.2921\).

Table 3 Quantified analysis results
Full size table

4.3.2 Enhanced coupling controller (ECC) [11]

To apply the control method in [11] to the research object of this paper, we designed similar composite functions \(\varXi _x={\dot{x}}-k_1\theta _1-k_2\theta _3\) and \(\varXi _y={\dot{y}}+k_3\theta _2+k_4\theta _4\). Then, the controllers are obtained as follows:

$$\begin{aligned} {F_x}= & {} - {k_{p1}}(\int _0^t {\left( {\dot{x} - {k_1}{\theta _1} - {k_2}{\theta _3}} \right) d\tau - } {x_d}) \nonumber \\&- {k_{d1}}\left( {\dot{x} - {k_1}{\theta _1} - {k_2}{\theta _3}} \right) \nonumber \\&- ({M_1} + {m_1} + {m_2})\left( {{k_1}{{\dot{\theta }}_1} + {k_2}{{\dot{\theta }}_3}} \right) + {F_{rx}} \end{aligned}$$
(59)
$$\begin{aligned} {F_y}= & {} - {k_{p2}}(\int _0^t {\left( {\dot{y} + {k_3}{\theta _2} + {k_4}{\theta _4}} \right) d\tau - } {y_d}) \nonumber \\&- {k_{d2}}\left( {\dot{y} + {k_3}{\theta _2} + {k_4}{\theta _4}} \right) \nonumber \\&+ ({M_2} + {m_1} + {m_2})({k_3}{{\dot{\theta }}_2} + {k_4}{{\dot{\theta }}_4}) + {F_{ry}} \end{aligned}$$
(60)

with \(k_{p1}\), \(k_{d1}\), \(k_{p2}\), \(k_{d2}\), \(k_1\), \(k_2\), \(k_3\), \(k_4\) \( \in R\) representing control gains, where \(k_{p1}=38\), \(k_{d1}=7.6\), \(k_{p2}=38\), \(k_{d1}=8.6\), \(k_1=-0.04\), \(k_2=-0.012\), \(k_3=-0.023\), \(k_4=-0.020\).

Fig. 5
figure 5

Comparative experimental results

Full size image

In order to facilitate the analysis and discussion of the experimental results, we draw the results of the three methods in the same figure, namely Fig. 5. At the same time, the trolley positioning time, the maximum swing angle and the input force are also shown in Table 3. According to the results shown in Fig. 5 and Table 3, in terms of trolley positioning, although LQR method can make the trolley start faster, the actual time to reach the target position is the longest. At the same time, not only the maximum swing angle in four directions is the largest, but also there is obvious residual swing. On the other hand, although the swing angle suppression performance of ECC is similar to that of the proposed method, it still takes a long time to locate the trolley.

Remark 3

It is worth noting that the reasons for selecting the above two methods as the comparison controller are: 1. The LQR controller is a typical design method based on the linear model of the controlled object. At the same time, the selection of control parameters Q and R completely depends on human experience. Therefore, it can reflect the superiority of the parameter selection method based on fuzzy control proposed in this paper. 2. The method in [11] is originally a nonlinear control method for the design of two-dimensional single pendulum crane system. Although it can be extended to three-dimensional double pendulum crane system, the control effect is slightly worse than that proposed one in this paper because the coupling characteristics of the system are ignored in the design.

4.4 Robust performance

This section verifies the robustness of the proposed method from two aspects. 1) Change the crane system parameters, such as the load mass \(M_2\) becomes 1 kg or 2 kg; The rope length \(l_2\) becomes 0.3 m or 0.25 m. 2) The system is disturbed by non-zero initial swing angle. The results are shown in Figs. 6 and 7. As can be seen from Fig. 6 , no matter whether the load mass becomes larger or smaller, and the rope length becomes longer or shorter, we have obtained good trolley positioning and swing angle suppression performance. On the other hand, it can be seen from Fig. 7 that although the maximum swing angle increases due to the influence of the initial swing angle disturbance, it eventually converges to zero. The reason why this result can be obtained is that the proposed controller is independent of the crane system parameters, and it does not need to linearize the nonlinear crane system model in the design process.

Fig. 6
figure 6

Experimental results with different system parameter

Full size image
Fig. 7
figure 7

Experimental results with non-zero initial sway angles

Full size image

5 Conclusion

A fuzzy adaptive nonlinear controller, which can realize not only the positioning performance, but also the suppression of hook and load angle components, was designed for the complex dynamic model of the double-pendulum overhead crane. With the Lyapunov technique and the LaSalle’s invariance principle, a rigorous mathematical demonstration was carried out on the stability of the whole control system at the equilibrium point. Finally, the comparative experimental results revealed that the presented control strategy is superior to systems subjected to alternative control strategies. Meanwhile, the controller obtained great control performance under the condition of uncertain model parameters and non-zero initial hook and load angles.