Systems of Partial Differential Equations in ExaSlang

Abstract

As HPC systems are becoming increasingly heterogeneous and diverse, writing software that attains maximum performance and scalability while remaining portable as well as easily composable is getting more and more challenging. Additionally, code that has been aggressively optimized for certain execution platforms is usually not easily portable to others without either losing a great share of performance or investing many hours by re-applying optimizations. One possible remedy is to exploit the potential given by technologies such as domain-specific languages (DSLs) that provide appropriate abstractions and allow the application of technologies like automatic code generation and auto-tuning. In the domain of geometric multigrid solvers, project ExaStencils follows this road by aiming at providing highly optimized and scalable numerical solvers, specifically tuned for a given application and target platform. Here, we introduce its DSL ExaSlang with data types for local vectors to support computations that use point-local vectors and matrices. These data types allow an intuitive modeling of many physical problems represented by systems of partial differential equations (PDEs), e.g., the simulation of flows that include vector-valued velocities.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The solution of PDEs is a part of many problems that arise in science and engineering. Often, a PDE cannot be solved analytically but must be solved numerically. As a consequence, the first step towards a solution is to discretize the equation, which results in a system of (linear) equations. However, depending on the size of the problem and the targeted numerical accuracy, the systems can grow quite large and result in the need for large clusters or supercomputers. These execution platforms are increasingly heterogeneous for reasons such as performance and energy efficiency. Today, a compute cluster consists of hundreds of nodes, where each node may contain multiple CPU cores—sometimes even of different type—and one or more accelerators, e.g., a GPU or some other manycore accelerator such as the Xeon Phi.

A common approach to enabling performance portability for a variety of platforms is the separation of algorithm and implementation via a domain-specific language (DSL). In a DSL, domain experts can specify an algorithm to solve a certain problem without having to pay attention to implementation details. Instead, they can rely on the DSL compiler to generate a program with good—or even near optimal—performance. Usually, the execution of hand-written program code is faster than that of automatically generated code. However, rather than putting hardware and optimization knowledge individually into each application’s implementation in isolation, in the DSL approach, all these efforts are put into the compiler and, consequently, every program benefits. Thus, for a new execution platform, only the compiler must be adapted, not individual application programs. This enhances performance portability.

In contrast, library-based approaches require updates of the library to make use of new technologies. This may potentially break backward compatibility and incur changes to the application program which often lead to laborious re-programming efforts. Often, a new technology comes with a new programming paradigm which is not easily captured using a library that was developed with a previous technology and paradigm in mind.

An additional advantage of DSLs is that users can be more productive by composing a new algorithm much more quickly, since it requires only a short specification. Yet another advantage of generative approaches is the ability to validate models. By providing language elements with corresponding constraints, a great number of invalid models become non-specifiable. Furthermore, since the DSL compiler has some knowledge about the application domain and works at a much higher level of abstraction, it can perform semantic validations, avoiding the generation of invalid programs and helping end-users in the correction of errors.

2 Multigrid Methods

In this section, we give a short introduction to multigrid methods. For a more in-depth review, we refer to the respective literature [6, 23].

In scientific computing, multigrid methods are a popular choice for the solution of large systems of linear equations that stem from the discretization of PDEs. The basic multigrid method cycle is shown in Algorithm 1. Here, by modifying the parameter γ that controls the number of recursive calls, one can choose between the V-cycle (γ = 1), and the W-cycle (γ = 2). There exist additional cycle types that provide higher convergence rates for certain problems [23].

In the pre- and post-smoothing steps, high-frequency components of the error are damped by smoothers such as the Jacobi or the Gauss-Seidel method. In Algorithm 1, ν ₁ and ν ₂ denote the number of smoothing steps that are applied. Low-frequency components are transformed to high-frequency components by restricting them to a coarser level, making them good targets for smoothers once again.

At the coarsest level, the small number of unknowns makes a direct solution for the remaining unknowns feasible. In the special case of a single unknown, the single smoother iteration corresponds to solving the problem directly. When moving to large-scale clusters, parallel efficiency can be potentially improved by stopping at a few unknowns per compute node and relying on specialized coarse grid solvers such as the conjugate gradient (CG) and generalized minimal residual (GMRES) methods.

Algorithm 1 Recursive multigrid algorithm to solve $u_{h}^{(k\,+\,1)}\,=\,\mathop{\mathrm{MG}}\nolimits _{h}\left (u_{h}^{(k)},A_{h},f_{h},\gamma,\nu _{1},\nu _{2}\right )$

3 The ExaStencils Approach

ExaStencils¹ [9] is a basic research project focused on a single application domain: geometric multigrid. The implementation of large simulations involving a great diversity of different mathematical models or complex work flows is out of ExaStencils’ scope. The project’s goal is to explore how to obtain optimal performance on highly heterogeneous HPC clusters automatically. By employing a DSL for the specification of algorithms and, therefore, separating it from the implementation, we are able to operate on different levels of abstraction that we traverse during code generation. As a consequence, we can apply appropriate optimizations in every code refinement step, i.e., algorithmic optimizations, parallelization and communication optimizations down to low-level optimizations, resulting in a holistic optimization process. One key element in this optimization chain, working mainly at the algorithmic level, is local Fourier analysis (LFA) [2, 25] to obtain a-priori convergence predictions of iterative schemes. This helps to select adequate solver components—if not specified by the user—and to fine-tune numerical parameters. Another central feature of the ExaStencils approach is software product line (SPL) technology [21], which treats an application program not as an individual but as a member of a family with commonalities and variabilities. Based on machine learning from previous code-generation and benchmark runs, this supports the automatic selection of the optimization strategy that is most effective for the given combination of algorithm and target hardware. Embedded into the ExaStencils compiler, the techniques of LFA and SPL are sources of domain knowledge that is available at compile time.

4 The ExaStencils DSL ExaSlang

When creating a new programming language—especially a DSL—it is of utmost importance to pay attention to the user’s experience. A language that is very complex will not be used by novices, whereas a very abstract language will not be used by experts. For our DSL ExaSlang—short for ExaStencils language—we identified three categories of users: domain experts, mathematicians, and computer scientists.

Each category of users focuses on a different aspect of the work flow resulting in the numerical solver software, starting with the system of equations to be solved. Whereas the domain expert cares about the underlying problem, and to some extent, about the discretization, the mathematician focuses on the discretization and components of the multigrid-based solver implementation. Finally, the computer scientist is mainly interested in the numerical solver implementation, e.g., parallelization and communication strategies.

The following subsections highlight a number of concepts and features of ExaSlang. A more detailed description can be found elsewhere [18].

4.1 Multi-layered Approach

As pictured in Fig. 1, ExaSlang consists of four layers that address the needs of the different user groups introduced previously. We call them ExaSlang 1–4; higher numbers offer less abstraction and more language features.

Fig. 1

Multi-layered approach of ExaSlang [18]

In ExaSlang 1, the problem is defined in the form of an energy functional to be minimized or a partial differential equation to be solved, with a corresponding computational domain and boundary definitions. In any case, this is a continuous description of the problem. We propose this layer for use by scientists and engineers that have little or no experience in programming. The problem specification might be on paper or also in LaTeX or the like.

In ExaSlang 2, details of the discretization of the problem are specified. We deem this layer suitable for more advanced scientists and engineers as well as mathematicians.

In ExaSlang 3, algorithmic components, settings and parameters are modeled. Since they build on the discretized problem specified in ExaSlang 2, this is the first layer at which the multigrid method is discernible. At this layer, it is possible to define smoothers and to select the multigrid cycle. Computations are specified with respect to the complete computational domain. Since this is already a very advanced layer in terms of algorithm and discretization details, we see mainly mathematicians and computer scientists working here.

In ExaSlang 4, the most concrete language layer, user-relevant parts of the parallelization become visible. Data structures can be adapted for data exchange and communication patterns can be specified via simple statements. We classify this layer as semi-explicitly parallel and see only computer scientists using it. A detailed description of its key elements is given in the next subsection. Note that, even though this is the least abstract layer, it is still quite a bit more abstract than the solver implementation generated in, e.g., C++.

Orthogonal to the functional program description is the target platform description language (TPDL), which specifies not only the hardware components of the target system such as CPUs, memory hierarchies, accelerators, and the cluster topology, but also available software such as compilers or MPI implementations.

Unavailable to the user and, thus, not illustrated in Fig. 1 is what we call the intermediate representation (IR). It forms a bridge between the code in ExaSlang 4 and the target code in, e.g., C++ and contains elements of both. This is the stage at which most of the compiler-internal transformations take place, i.e., parallelization efforts such as domain partitioning, and high-level and low-level optimizations such as polyhedral optimizations and vectorization. Finally, the IR is transformed to target source code, e.g., in C++, that is written to disk and available for the user to transfer to the designated hardware to compile and run.

4.2 Overview of ExaSlang 4

As explained in Sect. 4.1, ExaSlang 4 is the least abstract layer of ExaSlang and has been extended to host the data types for local vectors that form a crucial part of ExaSlang 3. This section highlights a number of keywords and data types. A more thorough overview of ExaSlang 4 is available elsewhere [18].

4.2.1 Stencils

Stencils are crucial for the application domain and approach of project ExaStencils. They are declared by specifying the offset from the grid point that is at the center of the stencil and a corresponding coefficient. Coefficients may be any numeric expression, including global variables and constants, binary expressions and function calls. Since access is via offsets, the declarations of coefficients do not need to be ordered. Furthermore, unused coefficients, which would have a value of 0, can be omitted. An example declaration using constant coefficients is provided in Listing 1.

Listing 1 Example 3D stencil declaration

4.2.2 Fields and Layouts

From the mathematical point of view, fields are vectors that arise, for example, in the discretization of functions. Therefore, a field may form the right-hand side of a partial differential equation, the unknown to be solved, or represent any other value that is important to the algorithm, such as the residual. As such, different boundary conditions can be specified. Currently, Neumann, Dirichlet, and no special treatment are supported. Values of fields may either be specified by the users via constants or expressions, or calculated as part of the program. Multiple copies of the same fields can be created easily via our slotting mechanism that works similarly to a ring buffer and can be used for intuitive specifications of Jacobi-type updates and time-stepping schemes. To define a field, a layout is mandatory. It specifies a data type and location of the discretized values in the grid, e.g., grid nodes or cells, and communication properties such as the number of ghost layers. In case the special field declaration external Field is detected, data exchange functions are generated for linked fields. They can be used to interface generated solvers as part of larger projects.

4.2.3 Data Types, Variables, and Values

As a statically-typed language, ExaSlang 4 provides a number of data types which are grouped into three categories. The first category are simple data types, which consist of Real for floating-point values, Integer for whole numbers, String for the definition of character sequences, and Boolean for use in conditional control flow statements. Additionally, the Unit type is used to declare functions that do not return any value. The second category are aggregate data types, a combination of simple data types, namely for complex numbers and the new data types for local vectors and matrices which are introduced in Sect. 6. Finally, there are algorithmic data types that stem from the domain of numerical calculations. Apart from the aforementioned data types stencil, field and layout, the domain type belongs to this category and is used to specify the size and shape of the computational domain.

Note that variables and values using algorithmic data types can only be declared globally. Other data types can also be declared locally, i.e., inside functions bodies or nested local scopes such as conditional branch bodies or loop bodies. Additionally, to keep variable content in sync across program instances running on distributed-memory parallel systems, they can be declared as part of a special global declaration block.

The syntax of variable and constant declarations is similar to that of Scala, with the keywords Variable and Value or, in short, Var and Val. Followed by the user-specified name, both definitions require specification of the data type, which can be of either simple or aggregate. Optionally for variables—mandatory for values—an initial value is specified via the assignment operator.

4.2.4 Control Flow

Functions can take an arbitrary number of parameters of simple or aggregate types and return exactly one value of a simple or aggregate type, or nothing. In the latter case, the return type is Unit. If the compiler detects a function with the signature Function Application(): Unit, a C++ function main() is generated and the compilation process is switched to the generation of a standalone program. A lot of the ExaSlang 4 syntax is like Scala, but there are additional features. In ExaSlang 4, functions are introduced with the keyword Function, or shorter, Func. An example declaration, which additionally uses the concept of level specifications presented later, is depicted in Listing 2.

The syntax and semantics of conditionals in ExaSlang 4 corresponds to Scala.

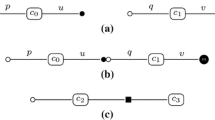
An important concept in ExaSlang 4 are loops, which are available in two main types: temporal (i.e., sequential in time) and spatial (i.e., parallel across the computational domain). The temporal loop has the keyword repeat and comes as a post-test loop (repeat until <condition>) or a counting loop (repeat <integer> times). Spatial loops iterate across the computational domain. Since ExaSlang 4 is explicitly parallel, a loop over <field> can be nested inside a loop over fragments loop. Fragments are entities that arise during domain partitioning. Fragments aggregate to blocks, which in turn form the computational domain. This hierarchy is depicted in Fig. 2, where the computational domain is divided into four blocks, each consisting of six fragments. Each fragment consists of 16 data values at chosen discretization locations. The reasoning behind this strategy is to connect primitives with different parallelization concepts such as distributed- and shared-memory parallelism. One example is to map blocks to MPI ranks and fragments to OpenMP threads.

Fig. 2

Example partitioning of the computational domain into 4 blocks (green) of 6 fragments (brown) each, with 16 data values (blue) per fragment

4.2.5 Level Specifications

Function, as well as layout, field, stencil, variable and value declarations can be postfixed by an @ symbol, followed by one or more integers or keywords. We call them level specifications, as they bind a certain program entity to one or several specific multigrid levels. This feature is unique to ExaSlang 4. A common usage example is to end the multigrid recursion at the coarsest level, as depicted in Listing 2. Level specifications support a number of keywords that are mapped to discrete levels during code generation. To write ExaSlang 4 programs without the explicit definition of the multigrid cycle size—and, thus, enable the application of domain knowledge at compile time—aliases such as coarsest and finest can reference bottom and top levels of the multigrid algorithm. For declarations, the keyword all marks an element to be available at all multigrid levels. Inside a function, relative addressing is possible by specifying coarser and finer, or by specifying simple expressions. Here, decreasing level numbers corresponds to decreasing (coarsening) the grid size, with 0 being the coarsest level if not defined otherwise by the compiler’s domain knowledge. Structures at the current multigrid level are referenced by current. Level specifications are resolved at compile time. Thus, general specifications such as all are overridden by more specific ones. For example, line 5 of Listing 2 could also be declared as Function VCycle @all, since the definition at the coarsest level would be overridden by the definition on line 1.

Listing 2 Specifying direct solving on the coarsest multigrid level to exit recursion using level specifications

5 Code Generation

Our transformation and code generation framework, which forms the basis for all transformations that drive the compilation process towards the various target platforms, is written in Scala [13, 19]. Because of its flexible object-functional nature, we deem Scala a suitable language for the implementation of DSLs and corresponding compilers. Scala features the powerful technique of pattern matching that is used to identify object instances based on types or values at run time, making it easy and elegant to find and replace parts of the program during the compilation process.

Since ExaStencils is meant to support high-performance computing, our target platforms include clusters and supercomputers such as SuperMUC, TSUBAME and JUQUEEN. We used especially the latter to validate our scaling efforts [18]. However, while scalability is one thing, run-time performance is what users are interested in. Thus, during code generation, a number of high-level optimizations based on polyhedral transformations are applied [8], such as loop tiling to enable parallelization. Another optimization is the increase of data locality by tiling and modifying the schedule of loops. Additionally, low-level optimizations such as CPU-specific vectorization have been implemented. Furthermore, we demonstrated that our compilation framework and code generation approach is flexible enough to generate specialized hardware designs from the abstract algorithm description given in ExaSlang 4 [20].

6 Data Types for Systems of Partial Differential Equations

This section highlights the advantages of local vectors and matrices for systems of PDEs and sketches their usage in ExaSlang 3 and ExaSlang 4.

Listing 3 Definition of layout and field of vectors with Neumann boundary conditions

6.1 Motivation

Systems of PDEs can always be expressed in ExaSlang 4 by splitting up components since, this way, only scalar data types are required. However, to implement computations of coupled components, data structures require multiple scalar values per point. We call such data types vectors or matrices, respectively, and have just recently incorporated them in ExaSlang 4, as a preparation step for code specified in ExaSlang 3.

One added benefit of specialized data types for the specification of systems of PDEs is the much increased readability of the source code—for us, of ExaSlang 4 code. Especially for domain experts, who should not have to be experts in programming, they correspond to a more natural representation of the mathematical problem which will help when checking or modifying ExaSlang 3 and 4 code that has been generated from more abstract layers of ExaSlang, i.e., ExaSlang 2.

6.2 The ExaSlang Data Types

In ExaSlang 4, the new data types Vector and Matrix belong to the category of aggregate data types and can be given a fixed dimensionality. Additionally, a ColumnVector (short: CVector) can be specified to explicitly set the vector type when the direction cannot be derived from assigned values. The element types of these aggregated data types can be simple numeric data types, i.e., integers, reals or complex numbers. As is the case for other declarations in ExaSlang 4, it is possible to use a short-hand notation by specifying the designated inner data type, followed by the corresponding number of elements in each direction. An example is shown in Listing 4, where lines 1 and 2 are equivalent.

Anonymous constant vectors default to row vectors. The suffix T transposes vector and matrix expression, thus defines the second vector to be a column vector expression in line 3 of Listing 4.

As part of the optimization process, the ExaStencils compiler applies transformations such as constant propagation and folding also to expressions containing vectors and matrices. Beside the standard operators such as addition, subtraction and multiplication that consider the vector and matrix data types in a mathematical sense, there are element-wise operators. Example calculations are depicted in Listing 4, for both vector-wise and element-wise operators. Of course, vector and matrix entries do not need to be constant, but can be any valid expression evaluating to a numeric value.

Listing 4 Example declarations and calculations using vectors and matrices

7 Modifications to the Code Generator

In ExaSlang 4, the dimensionality of a field equals the dimensionality of the problem. That is, fields may have up to three dimensions. However, with our new data types, each grid point in the field may have a non-zero dimensionality as well. At present we work with vectors and 2D matrices, but our implementation can also handle higher dimensionalities.

In order to support the new data types in the generated C++ code, one could simply store multiple scalar values inside a structure to represent a local vector (or matrix) at a certain grid point, such that a field becomes an array of structures. However, arrays of structures potentially introduce run-time overhead caused, for one, by the dynamic memory management applied to instances of the structure and, for another, because custom compilers like for CUDA and OpenCL generate inferior target code if they can handle arrays of structures at all. Also, high-level synthesis (HLS) tools, which emit hardware descriptions for FPGAs, provide limited or no support for arrays of structures.

To overcome these limitations and to enable optimizations such as tiling a field for parallelization or, for hybrid target platforms, distribution across different devices, we linearize fields and the structures in them. This exposes the size and memory layout of a field and provides the possibility to modify them. The dimensionality of the array that represents a field with non-scalar grid points is the sum of the dimensionality of the field and that of the structure at the grid points. For example, a three-dimensional field of 2 × 2 matrices becomes a five-dimensional array. At each grid point, one matrix consisting of four scalar values is stored, resulting in a total of 4 ⋅ n ⋅ m values for a field of size n × m. Each value has five coordinates as depicted in Fig. 3: the d _i denote the coordinates of the grid point, the c _i those of the structure at the grid point.

Fig. 3

Access to one element of three-dimensional matrix field consists of the index to field’s grid point (d _i ) and of the matrix element (c _i )

During code generation, special care is necessary for non-scalar variables that appear on both sides of an assignment involving a multiplication such as A = A B with A and B being matrices or vectors of appropriate shape. The assignment is refined to two separate assignments: first, the operation is applied and the result is saved into a temporary variable (A′ = A B), then the original variable is reassigned (A = A′). This guarantees that no intermediate result is used to calculate subsequent vector or matrix entries while, at the same time, resulting in code that can be vectorized easily.

8 Example Application

To demonstrate the application of the new data types, we choose the calculation of the optical flow detection. In contrast to solving the incompressible Navier-Stokes equations, it does not need specialized smoothers and also exhibits acceptable convergence rates when solved without the use of systems of PDEs, making it an excellent example to compare code sizes of the two approaches. The optical flow approximates the apparent motion of patterns such as edges, surfaces or objects in a sequence of images, e.g., two still images taken by a camera or a video stream. Note that this approximation does not need to necessarily describe the physical motion; the actual motion of an object is not always reflected in intensity changes in the images. To be more precise, we actually calculate the displacement field between two images.

8.1 Theoretical Background

Among the numerous approaches to approximate the optical flow, we opt for a multigrid-based algorithm [7].

Our goal is to approximate the 2D motion field (u, v) between two images that are part of an image sequence I. An image point I(x, y, t) has, aside from the two spatial coordinates x and y, a temporal coordinate t. As an example, a certain value of t can correspond to one frame of a video stream. We assume that a moving object does not change in intensity in time, i.e., we neglect changes in illumination. We call this the constant brightness assumption, which can be written as follows:

$$\displaystyle\begin{array}{rcl} \tfrac{d\mathbf{I}} {dt} = 0\;.& &{}\end{array}$$

(1)

For small movements, i.e., for small time differences between two images, the movement of an intensity value at a pixel (x, y, t) can be described by:

$$\displaystyle{ I(x,y,t) = I(x + dx,y + dy,t + dt)\;. }$$

(2)

Taylor expansion of this term around (x, y, t) and reordering results in:

$$\displaystyle{ \tfrac{\partial \mathbf{I}} {\partial x} \tfrac{dx} {dt} + \tfrac{\partial \mathbf{I}} {\partial y} \tfrac{dy} {dt} + \tfrac{\partial \mathbf{I}} {\partial t} \approx 0\;. }$$

(3)

We now can define the partial image derivatives $I_{x}:= \tfrac{\partial \mathbf{I}} {\partial x}$, $I_{y}:= \tfrac{\partial \mathbf{I}} {\partial y}$, $I_{t}:= \tfrac{\partial \mathbf{I}} {\partial t}$, the spatio-temporal gradient $\nabla _{\theta }\mathbf{I}:= \left (I_{x},I_{y},I_{t}\right )^{\mathrm{T}}$ and the optical flow vector $(u,v):= \left (\tfrac{dx} {dt}, \tfrac{dy} {dt} \right )$.

After more transformation steps, we end up with a two-dimensional system of PDEs:

$$\displaystyle\begin{array}{rcl} -\alpha \varDelta u + I_{x}(I_{x}u + I_{y}v) = -I_{x}I_{t}& &{}\end{array}$$

(4)

$$\displaystyle\begin{array}{rcl} -\alpha \varDelta v + I_{y}(I_{x}u + I_{y}v) = -I_{y}I_{t}\;.& &{}\end{array}$$

(5)

After discretization using finite differences (FD) for constant coefficient operators and image derivatives and finite volumes (FV) for variable operators, we obtain the following linear system:

$$\displaystyle{ \left (\begin{array}{*{10}c} \alpha +\left (\begin{array}{*{10}c} &-1&\\ -1 & 4&-1 \\ &-1& \end{array} \right ) + I_{x}^{2} & I_{x}I_{y} \\ I_{x}I_{y} &\alpha +\left (\begin{array}{*{10}c} &-1&\\ -1 & 4&-1 \\ &-1& \end{array} \right ) + I_{y}^{2} \end{array} \right )\left (\begin{array}{*{10}c} u\\ v \end{array} \right ) = \left (\begin{array}{*{10}c} -I_{x}I_{t} \\ -I_{y}I_{t} \end{array} \right )\;. }$$

(6)

For simplification purposes, we disregard the time gradient I _t and fix it to 1. After more transformations, we obtain the following 5-point stencil to use in our iterative scheme:

$$\displaystyle{ \left (\begin{array}{*{10}c} &\left (\begin{array}{*{10}c} -1&\\ &-1 \end{array} \right )& \\ \left (\begin{array}{*{10}c} -1&\\ &-1 \end{array} \right )&\left (\begin{array}{*{10}c} 4\alpha + I_{x}^{2}& I_{x}I_{y} \\ I_{x}I_{y} &4\alpha + I_{y}^{2} \end{array} \right )&\left (\begin{array}{*{10}c} -1&\\ &-1 \end{array} \right ) \\ &\left (\begin{array}{*{10}c} -1&\\ &-1 \end{array} \right )& \end{array} \right )\;. }$$

(7)

An extension in 3D space to detect the optical flow of volumes is trivial and omitted here because of space constraints.

Listing 5 Declaration of the smoothing stencil for the optical flow in 2D

Listing 6 Smoother definition using slots for the flow field

8.2 Mapping to ExaSlang 4

Mapping the introduced algorithm to ExaSlang 4 is straight-forward thanks to the new local vector data types. In Listing 5, code corresponding to (7) is depicted. Here, we first defined the central coefficient, followed by the four directly neighboring values with offsets ± 1 in x and y direction. Each stencil coefficient consists of two components, as our system of PDEs is to be solved for the velocities in x and y direction of the image.

The smoother function using the previously introduced stencil is shown in Listing 6. As we will also use the smoother for coarse-grid solution, it has been defined for all multigrid levels using @all. For the computations, we loop over the flow field, calculating values based on the active field slot and writing them into the next slot. After calculations are done, we set the next field slot to be active using advance. Effectively, both slots are swapped, as only two slots have been defined.

Note the function calls inverse(diag(SmootherStencil@current)) which are used to invert the 2 × 2 matrix that is the central stencil element without further user intervention.

In Listing 7, the ExaSlang 4 implementation of a V(3,3)-cycle is depicted. This corresponds to Algorithm 1 with parameters γ = 1 and ν ₁ = ν ₂ = 3. The function has been defined for all multigrid levels except the coarsest one, with a separate function declaration a few lines below for the coarsest level. This function exits the multigrid recursion by omitting the recursive call. As highlighted previously, it calls the smoother once to solve the system of PDEs on the coarsest grid.

Listing 7 V(3,3)-cycle function in ExaSlang 4

In our optical flow implementation, application of stencils on coarser grids works by coarsening the gradient fields using full weighting restriction. Then, the discrete stencil is composed based on the coefficients—including level-dependent accesses to fields—specified by the user.

One big advantage of the local vector data types is that many existing multigrid component implementations can be re-used. For example, in this application no changes are needed for inter-grid operators such as restriction and prolongation, as they are based on scaling or adding values at discretization points regardless of whether these are represented by scalars or local vectors. During code generation, our framework detects the underlying data type the operators are working on and emits corresponding code. Consequently, it is very easy to adapt existing solver implementations to the new data types: Most often, only field layout definitions and stencils computing components of the system of PDEs need to be changed.

8.3 Results

In Fig. 4, the resulting flow field for the standard example of a rotating sphere is depicted. Fig. 5 shows the optical flow of a driving car. Because the scene has not been filmed using a fixed camera, there is also a movement of the background. In both result plots, a number of vectors has been omitted to improve clearness and reduce file size.

Fig. 4

Optical flow of rotating sphere

Fig. 5

Optical flow of an image sequence showing a driving car

Figure 6 shows the code sizes in lines of code for a few optical flow implementations, among them the implementation yielding the depicted flow fields. Both serial and parallel version have been generated from the exact same ExaSlang file. OpenMP has been used as the underlying parallelization technology. For both 2D cases, using local vectors instead of computing each component separately reduces the ExaSlang 4 program sizes by around 16 %. In 3D, stencils are larger and a third component must be computed, so with the use of the new data types, the savings increase to around 28 %. Consequently, the generated C++ source is smaller, since fewer loops are generated. However, expressions involving the new data types are not yet being optimized by our code generation framework. For the driving car test case, the average time per V(3,3)-cycle using Jacobi smoothers on an Intel i7-3770 increases from 31.6 ms to 36.3 ms with the new data types, due to slightly higher efforts at run time and optimization steps still missing. For two OpenMP threads using the new data types, average time decreases to 18.9 ms. As memory bandwidth seems to be already saturated, adding more threads does not yield further speedup. Input images are 512 × 512 pixels large, which results in a V-cycle consisting of nine levels, each with three pre- and post-smoothing steps. For the solution on the coarsest grid consisting of one unknown, another smoother iteration is applied. As our focus is on the introduction of the new data types and their advantages with respect to modeling of algorithms, we deliberately postpone the dissemination and discussion of further performance results.

Fig. 6

Comparison of code sizes in lines of code LoC of user-specified ExaSlang 4 and generated code for different implementations of optical flow detection using a V(3,3)-cycle with Jacobi resp. red-black Gauss-Seidel (RBGS) smoothers and direct solution on the coarsest grid level (one unknown) by a single smoother iteration

9 Related Work

In previous work, the benefits of domain-specific optimization have been demonstrated in various domains. The project closest in spirit to ExaStencils has been SPIRAL [14], a widely recognized framework for the generation of hard- and software implementations of digital signal processing algorithms (linear transformations, such as FIR filtering, FFT, and DCT). It takes a description in a domain-specific language and applies domain-specific transformations and auto-tuning techniques to optimize run-time performance specifically for a given target hardware platform. Since it operates at the level of linear algebra, it directly supports vectors and matrices.

Many languages and corresponding compilers have been customized for the domain of stencil computations. Examples include Liszt [4], which adds abstractions to Java to ease stencil computations for unstructured problems, and Pochoir [22], which offers a divide-and-conquer skeleton on top of the parallel C extension Cilk to make stencil computations cache-oblivious. PATUS [3] uses auto-tuning techniques to improve performance. Other than ExaStencils, they support only vectors of fixed lengths, operate at a lower level of abstraction and do not provide language support for multigrid methods.

SDSLc [17] is a compiler for the Stencil DSL (SDSL), a language that is embedded in C, C++ and MATLAB, and used to express stencil expressions. Given such input, the SDSL compiler can emit shared-memory parallel CPU code and CUDA code for NVIDIA GPUs. Furthermore, it can generate FPGAs-based hardware descriptions by emitting code for a C-based HLS tool. During code generation, SDSLc applies a number of high-level optimizations, such as data layout transformations and tiling, based on polyhedral transformations, to enable low-level optimizations such as vectorization. In contrast to ExaStencils, automatic distributed-memory parallelization is not supported. Furthermore, SDSL is an embedded DSL without features specific to multigrid algorithms.

Mint [24] and STELLA (STEncil Loop LAnguage) [5] are DSLs embedded in C, respectively C++, and consider stencil codes on structured grids. Mint’s source-to-source compiler transforms special annotations to high-performance CUDA code, whereas STELLA supports additionally OpenMP for parallel CPU execution. At present, neither offers distributed-memory parallelization.

In the past, several approaches to the generation of low-level stencil code from abstract descriptions have been pursued. However, to the best of our knowledge, most do not target multigrid methods for exascale machines.

Julia [1] centers around the multiple dispatch concept to enable distributed parallel execution. It builds on a just-in-time (JIT) compiler and can also be used to write stencil codes in a notation similar to Matlab. It works at a level of abstraction lower than ExaStencils.

HIPAcc [11] is a DSL for the domain of image processing and generates OpenCL and CUDA from a kernel specification embedded into C++. It provides explicit support for image pyramids, which are data structures for multi-resolution techniques that bear a great resemblance to multigrid methods [12]. However, it supports only fixed length vectors of size four and only supports 2D data structures. Furthermore, it does not consider distributed-memory parallelization such as MPI.

The finite element method library FEniCS [10] provides a Python-embedded DSL, called Unified Form Language (UFL), with support of vector data types. Multigrid support is available via PETSc, which provides shared-memory and distributed-memory parallelization via Pthreads and MPI, as well as support for GPU accelerators. The ExaStencils approach and domain-specific language aim at another class of users and provide a much more abstract level of programming.

PyOP2 [16] uses Python as the host language. It targets mesh-based simulation codes over unstructured meshes and uses FEniCS to generate kernel code for different multicore CPUs and GPUs. Furthermore, it employs run-time compilation and scheduling. FireDrake [15] is another Python-based DSL employing FEniCS’ UFL and uses PyOP2 for parallel execution. While PyOP2 supports vector data types, it does not feature the extensive, domain-specific, automatic optimizations that are the goals of project ExaStencils.

10 Future Work

In future work, we will embed the data types introduced here in our code generator’s optimization process in order to reach the same performance as existing code. For example, the polyhedral optimization stages must be aware of the sizes of data of these types when calculating calculation schedules. Consequently, low-level optimizations, especially data pre-fetching and vectorization transformations, must be adapted.

Additionally, we will showcase more applications using the new local vector and matrix data types. One application domain that will benefit greatly is that of solvers for coupled problems occurring, e.g., in computational fluid dynamics such as the incompressible Navier-Stokes equations. Here, the components of a vector field can be used to express unknowns for various physical quantities such as velocity components, pressure and temperature. The vector and matrix data types will greatly simplify the way in which such problems, and their solvers, can be expressed. Furthermore, not solving for each component separately but for the coupled system in one go allows for increased numerical stability and faster convergence. Of course, this may require the specification of specialized coarsening and interpolation strategies for unknowns and stencils. Moreover, specialized smoothers, such as Vanka-type ones, are crucial for optimal results.

11 Conclusions

We reviewed ExaSlang 4, the most concrete layer of project ExaStencils’ hierarchical DSL for the specification of geometric multigrid solvers. To ease description of solvers for systems of PDEs, we introduced new data types that represent vector and matrices. The benefits of these data types, such as increased programmer productivity and cleaner code, were illustrated by evaluating program sizes of an example application computing the optical flow.

The new data types are also a big step towards an implementation of ExaSlang 3, since functionality that is available at the more abstract ExaSlang layers must be available at the more concrete layers as well. Furthermore, they expand the application domain of project ExaStencils, e.g., towards computational fluid dynamics.