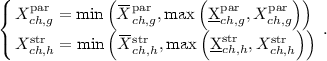Keywords

1 Introduction

The problem of designing control systems is well known in science [1]. This is due to the fact that the quality of work of individual parts or even of entire machines mainly depends on the characteristics of the used controller. It should be noted that in this context, the design of the control system is not only the selection of parameters for a known controller structure. On the contrary, it is a much broader concept. Namely, the design of the control system consists of the following elements:

  • indication of measurable signals, which can be used in a feedback loop,

  • selection of the controller structure,

  • tuning of controller parameters,

  • implementation in target hardware platform with fulfillment of requirements of real-time work.

Usually these steps are performed in the presented order. If this approach does not lead to achieve the desired effect (that is, to obtain a satisfactory quality of work), then the whole procedure must be repeated starting from the second step. The controller structure needs to be modified (or completely changed) and the tuning procedure must be carried out starting from the beginning.

In the literature there are known controller structures which are typically used, they are: controllers structures based on the combination of linear correction terms, e.g. PID controllers (optionally with gain scheduling algorithm, with feed-forward path or with additional low-pass filters [2], state feedback controllers, nonlinear controllers based on computational intelligence and hybrid controllers, in which are combined approaches from other groups. However, in practice PID controllers are used the most often [1]. It is a result of widespread knowledge of how they work and their relatively simple implementation in a microprocessor-based control systems.

It is important to point out that the control system design process is difficult and time consuming. Sometimes, in order to obtain a better quality of control, an engineer, basing on his experience, has to modify the controller structure. Modification of the controller structure, usually performed by means of trial and error method, causes the process of controller design much more difficult.

Among the experimental methods for the design of control systems, methods based on artificial intelligence [17, 20–22, 25–28, 31, 38–43, 56, 63, 64] and in particular the methods of evolution [32–34] are becoming more common. The effectiveness of these methods is proven by their diversity. They include, among others, fuzzy systems [8–14, 36, 53, 54], optimization methods [5–7, 19, 22–24, 29, 30, 37, 44–52], decision trees [3, 4] and can be used in wide area of problems [15, 16, 18, 57–62, 65, 67–74]. These methods make the design of the control system easier. However, in many cases the obtained controller is sensitive to interference, which commonly occurs in the real-world conditions. The measurement noise and limited resolution of the digital word used to carry information about the measured values can lead to unstable controller operation.

In this paper it is proposed the use of low-pass finite-impulse-response filters (FIR) with programmable characteristics for each of the measurement signals used in the feedback loop. These filters are designed to suppress interference that could disrupt the work of the control system. So, it is possible to find the structure and parameters of the controller, which makes it immune to this type of interference. We suggest the use of an universal initial structure which in the process of evolution will be adjusted in a way that the designed controller fulfills the control objective in the best way possible. This elastic structure consists of basic functional blocks and filters, both with programmable connections and parameters. Due to this approach the design of the control system can be regarded as one continuous process, unlike the commonly used method of trial and error. As a result, the process of controller design is performed easier and faster. Details of the proposed method are described in Sect. 3.

This paper is organized into 5 sections. Section 2 contains a description of the extended PID controller structure, while Sect. 3 shows the proposed evolutionary algorithm used to design control system. Simulation results are presented in Sect. 4. Conclusions are drawn in Sect. 5.

2 Description of Proposed PID Controller

Proposed controller is based on elastic structure, which among the others, depends from number of controller input signals \(fb_i\), \(i=1,...,FB\), FB stands for number of feedback signals (see Fig. 1). In proposed structure assumptions that \(fb_1\) stands for desired value of \(fb_2\) and the rest of the feedback signals stand for additional measurable signals were made. Moreover, the control blocks (CB) and finite impulse response filters (FIR) can be dynamically switched off or on by changing controller parameters. Due to that, the design of the controller should not only consider selecting the real parameters of the controller but also integer parameters encoding its structure.

Proposed controller (see Fig. 1) uses typical P, I and D elements (see. respectively Fig. 2(a), (b) and (c)). These elements can be part of typical control block CB (see Fig. 2(d)). The output value of typical control block takes the following form:

$$\begin{aligned} u\left( t \right) = {K^\mathrm{{P}}}e\left( t \right) + {K^\mathrm{{I}}}\int \limits _0^t {e\left( t \right) dt + } {K^\mathrm{{D}}}\frac{{de\left( t \right) }}{{dt}}, \end{aligned}$$
(1)

where \({K^\mathrm{{P}}}\), \({K^\mathrm{{I}}}\) and \({K^\mathrm{{D}}}\) stand respectively for parameters of P, I and D elements of control block. The proposed CB structure allows for additional reduction of P, I, D elements by using integer values \(C^\mathrm{{P}}\), \(C^\mathrm{{I}}\), \(C^\mathrm{{D}}\) and reduction of whole control block by integer value \(C^\mathrm{{CB}}\). The reduction takes place if the integer values are set to 0. The output of the proposed CB takes the following form:

$$\begin{aligned} u\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {{C^\mathrm{{P}}} \cdot {K^\mathrm{{P}}}e\left( t \right) + {C^\mathrm{{I}}} \cdot {K^\mathrm{{I}}}\int \limits _0^t {e\left( t \right) dt + } {C^\mathrm{{D}}} \cdot {K^\mathrm{{D}}}\frac{{de\left( t \right) }}{{dt}}}&{}{\mathrm{{for}}}&{}{{C^{\mathrm{{CB}}}} = 1}\\ {e(t)}&{}{\mathrm{{for}}}&{}{{C^{\mathrm{{CB}}}} = 0} \end{array}} \right. . \end{aligned}$$
(2)
Fig. 1.
figure 1

Proposed controller structure: (a) with any number of FB feedback signals, (b) with 3 feedback signals.

Full size image
Fig. 2.
figure 2

Typical structure of: (a) element P, (b) element I, (c) element D, (d) control block CB, (e) filter FIR, \(z^{-1}\) stands for values from previous time step.

Full size image

The proposed FIR filters used in controller are based on typical FIR filters (see Fig. 2(e)) with using an additional integer parameter \(C^\mathrm{{F}}\) to reduction of the filter (in case of reduction the output of the filter is exact to input of the filter). Thus, the output of the proposed filter takes the following form:

$$\begin{aligned} u\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {\sum \limits _{s = 1}^S {{b_s}e\left( {t - s - 1} \right) } }&{}{\mathrm{{for}}}&{}{{C^\mathrm{{F}}} = 1}\\ {e(t)}&{}{\mathrm{{for}}}&{}{{C^\mathrm{{F}}} = 0} \end{array}} \right. \end{aligned}$$
(3)

where e(t) stands for input value, \(e(t-i)\) stands for input value from \(t-i\) time step, \(b_s\) stands for weights of filter, \(s=1,...,S\), S stands for length of the filter (S has to be an odd number). The weights of the filter are calculated using filter parameters: transition frequency ft and lenght of the filter S, which are a part of the elastic structure of the controller and should be selected by learning algorithm as well. The weights values \(b_s\) are calculated as follows:

$$\begin{aligned} {b_s} = \left\{ {\begin{array}{*{20}{c}} {\frac{{\sin \left( {2\pi ft\left| {s - \frac{1}{2}(S - 1)} \right| } \right) }}{{\pi \left| {s - \frac{1}{2}(S - 1)} \right| }}}&{}{\mathrm{{for}}}&{}{s = \frac{1}{2}(S - 1)}\\ {2\,ft}&{}{\mathrm{{for}}}&{}{s \ne \frac{1}{2}(S - 1)} \end{array}} \right. . \end{aligned}$$
(4)

The proposed controller structure is characterized by the following advantages: (a) it is able to process any number of feedback signals \(fb_i\), (b) it uses cascade control blocks configuration which allows us to obtain good accuracy of the controller, (c) the structure is dynamic, each CB block, CB block elements (P,I,D) and filter FR can be switched off or on, (d) it has great capabilities of learning due to many selectable parameters (e) it is able to minimize the impact of feedback signals noises by use of the FIR filters.

3 Description of the Proposed Algorithm

A new hybrid evolutionary algorithm is presented to select the proposed controller parameters and parameters encoding controller structure. It is based on an ensemble of genetic algorithm (to select controller structure) and evolutionary strategy (to select controller parameters). This ensemble was proposed in our previous work [33, 67] and it achieved good results. In this paper we propose a number of improvements (introduced by our experience) that may allow us to obtain even better results. These improvements are based on iteration-dependent parameters of learning algorithm, using multiple learning parameters and operators, and new encoding of the controller parameters.

3.1 Encoding of the Controller Parameters

The parameters and the structure of the proposed controller are encoded in chromosome \({\mathbf{{X}}_{ch}}\) defined as follows:

$$\begin{aligned} {\mathbf{{X}}_{ch}} = \left\{ {\mathbf{{X}}_{ch}^{\mathrm{{par}}},\mathbf{{X}}_{ch}^{\mathrm{{str}}}} \right\} , \end{aligned}$$
(5)

where part \({\mathbf{{X}}_{ch}^{\mathrm{{par}}}}\) encodes the real parameters of the controller and part \({\mathbf{{X}}_{ch}^{\mathrm{{str}}}}\) encodes integer parameters of the controller. The part \({\mathbf{{X}}_{ch}^{\mathrm{{par}}}}\) is defined as follows:

$$\begin{aligned} \mathbf{{X}}_{ch}^{\mathrm{{par}}} = \left\{ {\begin{array}{*{20}{c}} {{K^\mathrm{{P}}_1},{K^\mathrm{{I}}_1},{K^\mathrm{{D}}_1},...,{K^\mathrm{{P}}_M},{K^\mathrm{{I}}_M},{K^\mathrm{{D}}_M},}\\ {f{t_1},...,f{t_R}} \end{array}} \right\} = \left\{ {X_{ch,1}^{\mathrm{{par}}},...,X_{ch,{L^{\mathrm{{par}}}}}^{\mathrm{{par}}}} \right\} , \end{aligned}$$
(6)

where \(K^\mathrm{{P}}_m\in [0, 20],K^\mathrm{{I}}_m\in [0,50],K^\mathrm{{D}}_m\in [0,5]\) stand for CB P, I, D parameters, \(m=1,...,M\), M stands for number of CB blocks, \(ft_r\in [0.1,0.5]\) stands for transition frequency, \(r=1,...,R\), R stands for number of filters, \(L^{\mathrm{{par}}}=3M+R\) stands for number of genes in part \({\mathbf{{X}}_{ch}^{\mathrm{{par}}}}\). The part \({\mathbf{{X}}_{ch}^{\mathrm{{str}}}}\) is defined as follows:

$$\begin{aligned} {\mathbf{X}^{\mathrm{str}}_{{ch}}} = \left\{ {\begin{array}{*{20}{c}} {C_1^{\mathrm{P}},C_1^{\mathrm{I}},C_1^{\mathrm{D}},...,C_M^{\mathrm{P}},C_M^{\mathrm{I}},C_M^{\mathrm{D}},}\\ {C_1^{\mathrm{CB}},...,C_M^{\mathrm{CB}},C_1^{\mathrm{F}},...,C_R^{\mathrm{F}}}\\ {{F_1},...,{F_R}} \end{array}} \right\} = \left\{ {X_{ch,1}^{\mathrm{str}},...,X_{ch,{L^{\mathrm{str}}}}^{\mathrm{str}}} \right\} , \end{aligned}$$
(7)

where \(C^\mathrm{{P}}_m\in \{0,1\},C^\mathrm{{I}}_m\in \{0,1\},C^\mathrm{{D}}_m\in \{0,1\}\) stand for activation of CB PID elements (values equal to 1 stands for active element), \(C^\mathrm{{CB}}_m\in \{0,1\}\) stands for activation of m-th control block, \(C^\mathrm{{F}}_r\in \{0,1\}\) stands for activation of r-th filter (values equal to 1 stands for active element), \(F_r\in \{0,...,9\}\) stands for lenght of the filter (real lenght of the filter is calculated as \(S_r = 5+2F_r\)), \(L^{\mathrm{{str}}}=4M+2R\) stands for number of genes in part \({\mathbf{{X}}_{ch}^{\mathrm{{str}}}}\).

3.2 Proposed Algorithm Description

Proposed algorithm is based on new iteration-dependent mutation and crossover from genetic algorithm and evolutionary strategy. The algorithm works according to the following steps:

  • Step 1. Initialization. In this step the value iteration is set to 0. Next the N individuals (each individual \({\mathbf{{X}}_{ch}}\) represents controller encoded by chromosome (5)) are randomly initialized and stored in population \(\mathbf {P}\). The initialization of individuals’ genes is realized as follows:

    (8)

    where \(U^\mathrm{{g}}(a,b)\) returns a random real value from the range [a, b]. and stand respectively for minims and maxims values of genes \(X_{ch,g}^{\mathrm{{par}}}\), \(g=1,...,L^\mathrm{{par}}\), \(U^\mathrm{{h}}(a,b)\) returns random integer value from the range [a, b]. and stand respectively for minims and maxims values of genes \(X_{ch,h}^{\mathrm{{str}}}\), \(h=1,...,L^\mathrm{{str}}\).

  • Step 2. Evaluation. In this step each individual is evaluated by fitness function defined as follows:

    $$\begin{aligned} \mathrm{{ff}}\left( {{\mathbf{{X}}_{ch}}} \right) = \sum \limits _{f = 1}^F{{\mathrm{{w}}_f} \cdot \mathrm{{ffco}}{\mathrm{{m}}_f}\left( {{\mathbf{{X}}_{ch}}} \right) }, \end{aligned}$$
    (9)

    where \({\mathrm{{ffco}}{\mathrm{{m}}_f}\left( {{\mathbf{{X}}_{ch}}} \right) }\) stands for fitness function components which depend from simulation problem (see Sect. 4.1), \(w_f\) stands for weights of fitness function components, \(f=1,...,F\), F stands for number of fitness function components.

  • Step 3. Probabilities calculation. In this step the value iteration is incremented. Next, the dynamic parameters for mutation and crossover are calculated as follows:

    $$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{p_1} = 0.2 + 0.2 \cdot \alpha }\\ {{p_2} = 0.2 \cdot \alpha }\\ {{p_3} = 0.5 \cdot \alpha }\\ {{p_4} = 0.1 \cdot \alpha }\\ {{p_5} = 0.2 \cdot \alpha \cdot \alpha } \end{array}} \right. , \end{aligned}$$
    (10)

    where \(p_1\) stands for gene mutation probability, \(p_2\) stands for gene mutation range, \(p_3\) stands for chance of select gene directly from one of parents while crossover, \(p_4\) stands for integer gene mutation probability (this value is small due to higher impact on the system), \(p_5\) stands for chance of assign random integer value into integer gene (all parameters p were estimated experimentally on the basis of experience of authors), \(\alpha \) stands for iteration-dependent value calculated as:

    $$\begin{aligned} \alpha = 1 - \frac{{iteration}}{{iteratio{n^{\max }}}}. \end{aligned}$$
    (11)

    where \(iteration^{\max }\) stands for maximum number of iteration of the algorithm.

  • Step 4. Reproduction. In this step a N new individuals are created and stored in population \(\mathbf {P'}\). For each individual the condition \(U^\mathrm{{g}}(0,1)<p_c\) is checked (where \(p_c\) stands for crossover probability). If this condition is met, new individual is created as a result of crossover between two individuals selected by the roulette wheel method [55] from population \(\mathbf {P}\). Otherwise, the individual is created as a result of cloning and mutating of one individual selected by the roulette wheel method [55] from population \(\mathbf {P}\). The mutation is performed according to Eq. (13) described in detail in Step 5. The genes obtained from crossover are calculated as:

    (12)

    where \({X_{ch,*1}^{\mathrm{{A,*2}}}}\) and \({X_{ch,*}^{\mathrm{{B,*}}}}\) stand respectively for genes from the first and second parent, \(*1\) stands for ‘par’ or ‘str’, \(*2\) stands for ‘g’ or ‘h’. The purpose of Eq. (12) is to increase chance to select gene values directly from parents or in the other case to select gene values between gene values of parents (if condition \({{U^\mathrm{{g}}}\left( {0,1} \right) \ge {p_3}}\) is met).

  • Step 5. Mutation. In this step genes of individuals from population \(\mathbf {P'}\) are mutated. For each individual the condition \(U^\mathrm{{g}}(0,1)<p_m\) is checked (where \(p_m\) stands for mutation probability). If this condition is met, genes of the individual are modified as follows:

    (13)

    Next, if condition \(U^\mathrm{{g}}(0,1)<p_t\) is met (where \(p_t\) stands for integer mutation probability, which also depends from the iteration number \(p_t=p_o\cdot \alpha \), where \(p_o\) stands for integer mutation factor) additional integer mutation is performed:

    (14)

  • Step 6. Repair. This step purpose is to repair (cut to specified ranged) gene values of individuals from population \(\mathbf {P'}\) which is calculated as follows:

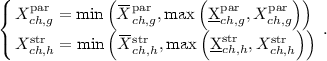    (15)

  • Step 7. Evaluation. In this step all individuals from population \(\mathbf {P'}\) are evaluated according to fitness function (9).

  • Step 8. Merging. This step aim is to select the best N individuals from merged populations \(\mathbf {P}\) and \(\mathbf {P'}\). Selected individuals replace population \(\mathbf {P}\).

  • Step 9. Stopping condition. In this step the stop condition is checked (iteration \( \ge iteration^{\max }\)). If this condition is met, algorithm stops and the best individual according to the fitness function value is presented. Otherwise, the algorithm goes back to Step 3.

4 Simulations Results

In our simulations a problem of designing controller structure and tuning parameters for double spring-mass-damp object was considered (see Fig. 3). More details about this model can be found in our previous paper [67]. Object parameters were set as follows: spring constant \(k=10\) N/m, coefficient of friction \(\mu =0.5\), masses \({m_1=m_2=0.2}\) kg. Initial values of: \({s^1}\), \({v^1}\), \({s^2}\) i \({v^2}\) were set to zero, and \(s^*\) is a desired position of mass \(m_1\) (see Fig. 3), simulation length \(T^\mathrm{{all}}\) was set to 10 s, output signal of the controller was limited to the range \(u \in \left( {-2,+2} \right) \), quantization resolution for the output signal y of the controller as well as for the position sensor for \(s^1\) and \(s^2\) was set to 8 bit, time step in the simulation was equal to \(T = 0.1\) ms, while interval between subsequent controller activations were set to twenty simulation steps, number of model iteration is calculated as \(Z={T^\mathrm{{all}}/ T}\). The feedback signals for the controller was chosen as: \(fb_1=s^*\), \(fb_2=s^1\), \(fb_3=s^2\) (\(FB=3\)).

Fig. 3.
figure 3

Simulated spring-mass-damp object.

Full size image

4.1 Problem Evaluation

For problem under consideration a trapezoidal shape of desired signal \(s^*\) was used (see Fig. 4). Moreover, for considered simulation problem, a following fitness function components (9) were used:

  • Complexity of the controller:

    $$\begin{aligned} {\mathrm{ffcom}}_1\left( {{{\mathbf{X}}_{ch}}} \right) = \frac{{\sum \limits _{m = 1}^M {\left( {{\mathbf{X}}_{ch}^{{\mathrm{str}} }\left\{ {C_m^{\mathrm{P}}} \right\} + {\mathbf{X}}_{ch}^{{\mathrm{str}} }\left\{ {C_m^{\mathrm{I}}} \right\} + {\mathbf{X}}_{ch}^{{\mathrm{str}} }\left\{ {C_m^{\mathrm{D}}} \right\} + {\mathbf{X}}_{ch}^{{\mathrm{str}} }\left\{ {C_m^{{\mathrm{CB}}}} \right\} } \right) } }}{{4M}}, \end{aligned}$$
    (16)

    where notation \({\mathbf{X}}_{ch}^{{\mathrm{str}} }\left\{ a \right\} \) stands for using gene a from chromosome \({\mathbf{X}}_{ch}\).

  • RMSE standing for accuracy of the controlled object:

    $$\begin{aligned} \mathrm{{ffcom}_2}\left( \mathbf{{X_{ch}}} \right) = RMSE = \sqrt{\frac{1}{Z}\cdot \sum \limits _{i = 1}^Z {{\varepsilon ^2_{i}}} } = \sqrt{\frac{1}{Z}\cdot \sum \limits _{i = 1}^Z {{{\left( {s_{i}^* - s_{i}^1} \right) }^2}} } , \end{aligned}$$
    (17)

  • Overshooting of the controller:

    $$\begin{aligned} \mathrm{{ff}}{\mathrm{{com}}_\mathrm{{3}}}\left( {{\mathbf{{X}}_{\mathbf{{ch}}}}} \right) = \mathop {\max }\limits _{i = 1,...,Z} \left\{ {{s^1_i}} \right\} . \end{aligned}$$
    (18)

  • Oscillations of the output of the controller:

    $$\begin{aligned} \mathrm{{ffco}}{\mathrm{{m}}_\mathrm{{4}}}\left( {{\mathbf{{X}}_{\mathbf{{ch}}}}} \right) \mathrm{{ = }}\sum \limits _{\mathrm{{o = 1}}}^{\mathrm{{O - 1}}} {\sqrt{\left| {{\mathrm{{r}}_\mathrm{{o}}}\mathrm{{ - }}{\mathrm{{r}}_{\mathrm{{o + 1}}}}} \right| } } , \end{aligned}$$
    (19)

    where \(r_o\) stands for each local minims and maxims of the output values of the controller (those minims and maxims were selected with ignoring noise influence on the signals), \(o=1,...,O\), O stands for number of minims and maxims of osculations.

4.2 Simulation Parameters

In the simulations the following values of parameters were set experimentally: fitness function components weights \(w_1 = 0.1\), \(w_2 = 10\), \(w_3 = 0.01\), \(w_4 = 0.1\), crossover probability \(p_c = 0.75\), mutation probability \(p_m = 0.75\), integer mutation factor \(p_o = 0.50\), number of algorithm iterations \(iteration^{\max }=1000\), number of individuals in populations \(N = 100\).

Fig. 4.
figure 4

Best simulations results for: (a) case 0, (b) case 1, (c) case 2, (d) case 3. \(s^1\) stands for position of the mass \(m_1\), \(|s^*-s^1|\) stands for difference with desired position of mass \(m_1\) (\(s^*\)) and \(s^1\), u stands for output of the controller.

Full size image
Table 1. Averaged simulation results.
Full size table

4.3 Simulation Cases

In the simulations four cases were tested to show the effectiveness of the proposed controller and learning algorithm:

  • Case 0 - case without filters and noise of the feedback signals (to present possibilities of learning algorithm).

  • Case 1 - case without filters and with 1 % of noise of \(s^1\) and \(s^2\) feedback signals (to show how noise of the signals affect the results).

  • Case 2 - case with filters and with 1 % of noise of \(s^1\) and \(s^2\) feedback signals (to show impact of the filters on the results).

  • Case 3 - case with static filters (\(C^\mathrm{{F}}\) were set to 1) and with 1 % of noise of \(s^1\) and \(s^2\) feedback signals (to show impact of the filters on the results).

For each case simulations were repeat 100 times and results were averaged.

4.4 Obtained Results

The averaged simulations results are presented in Table 1, the best simulations results are presented in Tables 2, 3, Figs. 4 and 5.

Table 2. The best simulation results (by fitness function value).
Full size table
Fig. 5.
figure 5

Best simulations structures obtained for: (a) case 0, (b) case 1, (c) case 2, (d) case 3. Gray rectangles stands for reduced elements of the controller.

Full size image
Table 3. Parameters of controllers obtained for the best simulation results, ’-’ stands for parameters reduced by the corresponding integer parameters.
Full size table

4.5 Simulation Results

Conclusions from the simulation are as follows: (a) including noise of feedback signals significantly degrade the performance of controller (see Fig. 4(a) and (b) and \(\mathrm{{ff}}(\cdot )\) values in Table 1); (b) adding filters allowed us to reduce impact of noise (see Fig. 4(c) and (d) and \(\mathrm{{ff}}(\cdot )\) values in Table 1); (c) using dynamic reduction of filters in learning process (case 2) led to obtain 0.7 (in average) active filters in the controller, which allowed us to obtain 5.6 % accuracy improvement and 7.8 % oscillations improvement of the system (see Fig. 4(b) and (c) and Table 1); (d) using static active filters led to obtain 11.1 % accuracy improvement and 56.6 % oscillations improvement (see Fig. 4(b) and (d) and Table 1); (e) obtained structures are simple and the average reduction of controller elements is close to 50 % (see Fig. 5 and Table 3); (f) the best obtained accuracy of the controller (see Table 2) without noise of feedback signals is better than accuracy obtained by hybrid multi-population algorithms [35]; (g) the best obtained accuracy of the controller (see Table 2) with noise of feedback signals and with use of filters (case 2 and case 3) is close to accuracy obtained by hybrid population algorithms without noise of feedback signals [66].

5 Summary

The proposed elastic structure of the controller containing proposed CB blocks and FIR filters allowed us to obtain accurate and simple controllers, with reduced impact of feedback signals noise on the performance of the controller. Moreover, the proposed training algorithm, which allows reduction of any component of the controller and simultaneously selection of its parameters, allowed us to obtain a very good results in terms of accuracy, superior to the results presented in the literature. In the future, the authors plan to use the proposed controller and learning algorithm in a more complex control problems.