Optimal Growth with Polluting Waste and Recycling

Abstract

We study an optimal AK-like model of capital accumulation and growth in the presence of a negative environmental externality in the tradition of Stokey (Int Econ Rev 39(1):1–31, 1998). Both production and consumption activities generate polluting waste. The economy exerts a recycling effort to reduce the stock of waste. Recycling also generates income, which is fully devoted to capital accumulation. The whole problem amounts to choosing the optimal control paths for consumption and recycling to maximize a social welfare function that notably includes the waste stock and disutility from the recycling effort. We provide a mathematical analysis of both the asymptotic behavior of the optimal trajectories and the shape of transition dynamics. Numerical exercises are performed to illustrate the analysis and to highlight some of the economic implications of the model. The results suggest that when recycling acts as an income generator, (1) a contraction of both the consumption and capital stock is observed in the long run after an expansion phase; (2) whether polluting waste is predominantly due to production or consumption, greater consumption and lower capital stock are obtained in the long run compared with the situation when recycling does not create additional income; (3) greater recycling effort and lower stock of waste are resulted in the long run.

The authors acknowledge constructive comments from two anonymous referees. The usual disclaimer applies.

1 Introduction

Since the Meadows report (1972), economic research on the limits of the contemporaneous growth regime and the design of optimal sustainable policies has been central to many agendas. While the very first attempts along these investigation lines have been directed at the issue of non-renewable resources (see for example, Stiglitz 1974, or Hartwick 1977), substantial efforts have been devoted to studying the impact of pollution on growth and social welfare, especially since the ‘90s. A fundamental theoretical contribution to this topic is that of Stokey (1998). Within various optimal growth settings, Stokey studied the implications of pollution externalities for optimal capital accumulation (and therefore for optimal growth). A remarkable outcome of this study is the analysis of the AK economy with and without pollution externalities. In the latter case, the economy optimally starts on exponentially growing balanced growth paths with strictly positive growth rates. When pollution produces negative welfare losses, the economy no longer follows these virtuous paths; rather, it converges to optimal steady states (therefore, with zero growth). In other words, pollution drastically limits (optimal) growth. Several authors have extended Stokey (1998)’s framework to account for more technological or ecological ingredients; Boucekkine et al. (2013) is one of the most recent extensions. When pollution is irreversible (that is, when the environmental absorption capacity irreversibly declines above a certain pollution stock level), these authors show that the optimal relationship between income and pollution can take a much richer set of forms, although optimal exponential growth invariably vanishes under pollution externalities.

This paper incorporates polluting waste and recycling into this type of optimal relationship analysis. More precisely, we are interested in polluting waste for which natural absorption takes extremely long. A characteristic example of such pollution is that of plastic waste, that is, bags, bottles, etc., which can be absorbed by the environment only after four to six centuries. Because of this extremely long time, no natural amenities can be reasonably assumed, and recycling efforts are required to avoid massive accumulation with harmful consequences in the long run. In the case of plastic waste, it seems that insufficient efforts have been deployed to prevent such a scenario, as evidenced by the emergence of several plastic vortexes in the oceans (Kaiser 2010). Jambeck et al. (2015) calculated that 275 million metric tons of plastic was generated in 192 coastal countries in 2010, with 4.8–12.7 million metric tons entering the ocean. In spite of the significant development of recycling and energy recovery activities, post-consumer plastic waste predominantly goes to landfill (PlasticsEurope 2015). Jambeck et al. (2015) consider that without waste management infrastructure improvements, the cumulative quantity of plastic waste available to enter the ocean from land is predicted to reach 80 million metric tons by 2025.

Several authors have already modeled waste generation and recycling activities within economic frameworks. Of course, these models are largely found in the industrial organization literature (see for example, Martin 1982, or Grant 1999). Nonetheless, waste and recycling are increasingly being examined from a more macroeconomic perspective. The recent macroeconomic literature contains studies of the impact of recycling on aggregate fluctuations (see De Beir et al. 2010, for example). There have also been several attempts to incorporate waste and recycling in a sustainability analysis, as we are doing in our paper, most often in decentralized equilibrium frameworks with technological progress (see for example, the recent paper by Fagnart and Germain 2011).

Below we provide a first-best central planner analysis in line with Stokey’s seminal paper incorporating waste (both from consumption and production) and recycling. Perhaps the work that is most closely related to ours is that of Lusky (1976). Lusky (1976) also solved a central planner problem regarding waste and recycling. However, our problem differs from his along three essential dimensions. First, Lusky (1976) has strictly concave production functions with labor as a unique input, whereas capital accumulation is an essential feature of our model and we use an AK production technology as in Stokey (1998). Second, recycling is modeled differently in Lusky (1976): recycling produces a consumable good (so it increases consumption possibilities), while in our model recycling output goes to capital accumulation given that our focus is sustainable growth via capital accumulation, to which recycling contributes. Third, the social welfare functions are not the same. In particular, while in both papers waste produces negative externalities, recycling increases instantaneous utility in Lusky (1976) via the recycled consumption good whereas the recycling effort supposes a strictly concave welfare loss in our set-up.

The problem we consider is an infinite time horizon problem with two control variables (consumption and recycling effort) and two states (capital and stock of waste). The state equations are linear mainly due to the linearity of the production function and of waste generation processes. Using a version of the maximum principle, we can extract the (necessary and sufficient) optimality conditions, and study the asymptotic properties of the optimal paths. The economic implications of this analysis are then evaluated in light of the sustainability literature à la Stokey.

Our results suggest that when recycling acts as an income generator, (1) a contraction of both the consumption and capital stock is observed in the long run after an expansion phase; (2) whether polluting waste is predominantly due to production or consumption, greater consumption and lower capital stock are obtained in the long run compared with the situation when recycling does not create additional income; (3) greater recycling effort and lower stock of waste are resulted in the long run.

The paper is organized as follows. Section 2 gives the specifications of our central planner problem with waste and recycling. Section 3 analyzes the mathematical properties of the model. In Section 4, we perform some quantitative exercises and we bring out the main lessons we can draw from the point of view of sustainability. Section 5 concludes the paper.

2 Model

Assume that the social planner owns a stock of productive capital that provides a continuous flow of revenue, aK(t), where $K(t)\ge 0$ denotes the capital stock at time t, and $a>0$, the constant marginal unit of revenue generated by the productive capital stock. The production function is linear in the stock of capital, as in Stokey (1998) and Boucekkine et al. (2013). The flow of revenue allows for a certain consumption level, $c(t)>0$. The revenue generation process and the consumption decisions are both assumed to generate polluting waste, $w(t)\ge 0$, where $w(t)=\alpha aK(t)+\beta c(t)$, $\alpha, \beta >0$ being the marginal wasting impact of the revenue generation process and the current consumption, respectively.

Though most of the polluting waste is generally related to productive processes (Klassen 2001), it is not clear whether the consumption process generates more waste than the revenue generation process. In the case of the plastics industry, polluting waste is predominant in either process depending on the market segment and the polymer type (PlasticsEurope 2015). In this regard, we assume that $\alpha \frac{>}{<}\beta$. By construction (no capital accumulation), waste is generated only by consumption in Lusky (1976). The same is assumed in the macroeconomic literature in line with De Beir et al. (2010), which relies heavily on the related industrial organization (e.g., Martin 1982): waste produced from consumption is used one period ahead as an input in the recycling sector. In this paper, waste can come from both consumption and production (or capital utilization), and some of the essential properties of optimal paths may depend on whether $\alpha \frac{>}{<}\beta$.

To reduce the stock of polluting waste, denoted by $W(t)\ge 0$, the social planner may invest in recycling efforts $v(t)\ge 0$ over time. We assume that the waste generating processes and recycling operations are mutually independent so that the recycling efforts are non-proportional to the waste emissions (e.g., El Ouardighi et al. 2015). This assumption allows for unbounded recycling efforts, i.e., $v(t)\frac{<}{>}w(t)$, to account for the possibility of reduction of past waste emissions. The environmental absorption capacity of polluting waste is approximated by zero. This approximation is consistent with the extremely long time needed for natural absorption of plastic waste. In economic terms, it implies that the social planner cannot benefit from any natural abatement of pollution waste.¹

Finally, a fixed proportion of recycled waste is supposed to generate additional revenues, φv(t), and therefore to positively influence the capital accumulation process, $1\ge \varphi \ge 0$ being the marginal proportion of the recycled waste that adds to capital accumulation. An illustration of this assumption is related to the plastics industry, where 60 million tons of plastics diverted from landfills are equivalent to over 60 billion euros (PlasticsEurope 2015).

In more elaborated industrial organization models of recycling, the recycling sector may produce profits (as in Martin 1982), which are later redistributed to the owners. In our central planner setting, the idea is pretty much the same: recycling not only decreases the level of polluting waste, but it also generates an income, which contributes to capital accumulation. Both functions of recycling help alleviate the sustainability problem faced by the economy. Only abatement plays this role in Stokey (1998) for example. If $\varphi =0$, the income generation channel of recycling is shut down, and we are closer to Stokey’s framework regarding the impact of pollution control instruments.

Based on these assumptions, the endogenous capital accumulation process is described as follows:

$$ \overset{.}{K}=aK(t)-c(t)+\varphi v(t),\kern1em K(0)={K}_0>0 $$

where a positive difference between the total revenues from capital and recycled waste, and current consumption results in investment in productive capital, while a negative difference leads to disinvestment. The initial endowment in productive capital is given by ${K}_0>0$.

The dynamics of polluting waste are given by:

$$ \overset{.}{W}=\alpha aK(t)+\beta c(t)-v(t),\kern1em W(0)={W}_0>0 $$

where the recycling efforts are such that $\overset{.}{W}\frac{>}{<}0$, $\forall t>0$, for a given initial stock of waste,${W}_0>0$.

Regarding the objective function of the social planner, we make the following assumptions. At each period, the instantaneous social utility is given as the difference between the utility drawn from current consumption and the costs incurred from the stock of waste and the recycling efforts, respectively. The instantaneous utility from current consumption is a concave function, that is, ln c(t). In addition, the stock of waste entails negative externalities such as environmental pollution and destruction of the biomass (e.g., Barnes 2002). These negative externalities are valued as an increasing convex function of the stock of waste, that is, eW(t)²/2, $e>0$. Lastly, the recycling effort generates an increasing quadratic cost, denoted by fv(t)²/2, $f>0$. Without loss of generality, we set $f=1$.

Denoting the discounting rate by $r>0$, and assuming an infinite planning horizon, the social planner’s optimal control problem is:

$$ U={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-rt}\left( \ln c(t)-\frac{eW{(t)}^2}{2}-\frac{v{(t)}^2}{2}\right)}\mathrm{d}t $$

(1)

subject to:

$$ \overset{.}{K}=aK(t)-c(t)+\varphi v(t),\kern1em K(0)={K}_0>0 \vspace*{-1.8pc}$$

(2)

$$ \overset{.}{W}=\alpha aK(t)+\beta c(t)-v(t),\kern1em W(0)={W}_0>0 $$

(3)

As mentioned in the introduction, our social welfare function differs from Lusky (1976)’s in that it includes a welfare loss due to the recycling effort and has no additional (recycled) consumption term. Note that we consider a pollution (via aggregate waste) negative externality while the macroeconomic literature of recycling and fluctuations does not (see for example De Beir et al. 2010). The same comparison holds with the ecological sustainability literature (see Fagnart and Germain 2011).

We now come to the mathematical resolution of the optimal control problem considered. We limit our presentation to the case of an interior solution.

3 Analysis

Skipping the time index for convenience, the current-value Hamiltonian is:

$$ H= \ln c-\frac{e{W}^2}{2}-\frac{v^2}{2}+\lambda \left(aK-c+\varphi v\right)+\mu \left(\alpha aK+\beta c-v\right) $$

(4)

where $\lambda \equiv \lambda (t)$ and $\mu \equiv \mu (t)$ are costate variables, $j=1,2$, that evolve according to:

$$ \overset{.}{\lambda }=\left(r-a\right)\lambda -\mu \alpha a \vspace*{-1.8pc}$$

(5)

$$ \overset{.}{\mu }=r\mu +eW $$

(6)

Necessary conditions for optimality are:

$$ {H}_c=\frac{1}{c}-\lambda +\mu \beta =0\Rightarrow c=\frac{1}{\lambda -\mu \beta } \vspace*{-1.8pc}$$

(7)

$$ {H}_v=-v+\lambda \varphi -\mu =0\Rightarrow v=\lambda \varphi -\mu $$

(8)

Because the stock of polluting waste has a negative marginal influence on the social planner’s objective function, its implicit price should be non-positive, i.e., $\mu \le 0$. Along with $\lambda >0$, this should result in strictly positive consumption and recycling effort respectively in (7) and (8).

The Legendre-Clebsch condition of concavity of the Hamiltonian with respect to the control variables is satisfied, as the Hessian:

$$ \left[\begin{array}{cc}\hfill {H}_{cc}\hfill & \hfill {H}_{cv}\hfill \\ {}\hfill {H}_{vc}\hfill & \hfill {H}_{vv}\hfill \end{array}\right]=\left[\begin{array}{ll}\hfill -{c}^{-2}\hfill & \hfill 0\hfill \\ ~~\, 0\hfill & \hfill -1\hfill \end{array}\right] $$

is negative definite. This guarantees a maximum of the Hamiltonian.

Lemma 1

The necessary conditions are sufficient for optimality.

Plugging the respective expressions of c and v from (7) and (8) in (4) results in the maximized Hamiltonian:

$$ {H}^0= \ln \left(\frac{1}{\lambda -\mu \beta}\right)-1+\frac{{(\lambda \varphi -\mu )}^2}{2}+\left(\lambda +\mu \alpha \right)aK-\frac{e{W}^2}{2} $$

from which the Hessian matrix:

$$ \left[\begin{array}{cc}\hfill {H}_{KK}\hfill & \hfill {H}_{KW}\hfill \\ {}\hfill {H}_{WK}\hfill & \hfill {H}_{WW}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill -e\hfill \end{array}\right] $$

is negative semi-definite. This ensures that the necessary conditions are also sufficient for optimality. □

Plugging the value of c and v from (7) and (8) in (2) and (3), respectively, the equations:

$$ \overset{.}{K}=aK-\frac{1}{\lambda -\mu \beta }+\varphi (\lambda \varphi -\mu ) \vspace*{-1.8pc}$$

(9)

$$ \overset{.}{W}=\alpha aK+\frac{\beta }{\lambda -\mu \beta }-\lambda \varphi +\mu $$

(10)

along with (5) and (6), form the canonical system in the state-costate space.

We now prove that as in Stokey (1998), the dynamic system will not converge to a balanced growth path despite the assumed impacts of recycling on the stock of pollution and on income generation. We first show the existence of steady states and then assess stability.

Proposition 1

In the case of a patient social planner, i.e., $r<a$, and $\beta \varphi <1$, the steady state is unique and given by:

$$\begin{array}{lll}\displaystyle {\left({K}^S\kern1em {W}^S\kern1em {c}^S\kern1em {v}^S\right)}^T=&\displaystyle \left(\frac{\left(1-\beta \varphi \right)\sqrt{\left(1+\varphi \alpha \right)a-r}}{a\sqrt{\left(1+\alpha \varphi \right)\left(\alpha +\beta \right)\varPhi }}\right.\\[1.5pc] &\left. \times \displaystyle\frac{r\left(a-r\right)\sqrt{\alpha +\beta }}{e\sqrt{\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]\varPhi }}\right.\\[1.5pc] &\left. \times\displaystyle\sqrt{\frac{\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]}{\left(\alpha +\beta \right)\varPhi }}\right.\\[1.5pc] &\left. \times\displaystyle\sqrt{\frac{\left(\alpha +\beta \right)\left[\left(1+\varphi \alpha \right)a-r\right]}{\left(1+\varphi \alpha \right)\varPhi }}\right)\end{array} $$

(11)

where $\varPhi =\left[a\left(\alpha +\beta \right)-r\beta \right]$, and the superscript ‘S’ stands for steady state.

Proof

Equating the RHS of (9)-(10)-(5)-(6) to 0 and solving by identification and substitution, we get:

$$ {\lambda}^S=\frac{\alpha a\sqrt{\alpha +\beta }}{\sqrt{\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]\varPhi }} \vspace*{-1.2pc}$$

$$ {\mu}^S=-\frac{\left(a-r\right)\sqrt{\alpha +\beta }}{\sqrt{\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]\varPhi }} $$

and K ^S and W ^S as given in (11). Note that $r<a$ implies that $r<\left(1+\varphi \alpha \right)a<\left(\alpha +\beta \right)a/\beta$, which allows for a feasible steady state stock of waste. Conversely, for any $r>a$, the steady state stock of waste is not feasible. Plugging the above expressions in (7) and (8), respectively, and simplifying, yields c ^S and v ^S in (11).

From (11), it can be shown that the limiting transversality conditions are satisfied for the saddle-paths because:

$$ \underset{t\mapsto +\infty }{ \lim }{e}^{-rt}\lambda (t)K(t)=\underset{t\mapsto +\infty }{ \lim}\left[\frac{\left(1-\beta \varphi \right)\alpha {e}^{-rt}}{\left(1+\varphi \alpha \right)\varPhi}\right]=0 \vspace*{-1.2pc}$$

$$ \underset{t\mapsto +\infty }{ \lim }{e}^{-rt}\mu (t)W(t)=\underset{t\mapsto +\infty }{ \lim}\left\{-\frac{r\left(\alpha +\beta \right){\left(a-r\right)}^2{e}^{-rt}}{e\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]\varPhi}\right\}=0 $$

This ensures the uniqueness of the globally optimal solution. □

In the case where $r<a$, and $\beta \varphi <1$, a zero steady state is obtained which is not optimal. The reason is the following. To be steady, zero waste and capital require zero recycling and consumption, which with respect to costate Eqs. (5) and (6), implies that the corresponding costate variables must be zero as well. Substituting zero costates into the optimality condition (7), we find that the optimal consumption tends to infinity rather than to zero. Consequently, a zero waste and capital is steady but not optimal. This indeed does not affect the results as they are derived for a non-zero steady state.

From the canonical system (5)-(6)-(9)-(10), the isoclines of $\overset{.}{K}=0$ and $\overset{.}{W}=0$ are given by:

$$ {K}_{\left|\overset{.}{K}=0\right.}^S=\frac{r\left(a-r\right)}{a\varPhi e{W}^S}-\frac{\varphi \left[\left(1+\alpha \varphi \right)a-r\right]e{W}^S}{ra\left(a-r\right)} \vspace*{-1.2pc}$$

(12)

$$ {K}_{\left|\overset{.}{W}=0\right.}^S=\frac{1}{\alpha a}\left[\frac{\left[\left(1+\alpha \varphi \right)a-r\right]e{W}^S}{r\left(a-r\right)}-\frac{r\beta \left(a-r\right)}{\varPhi e{W}^S}\right] $$

(13)

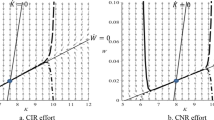
Using (12)–(13) and (11), Fig. 1 describes the sensitivity of the state variables at the steady state to the parameters.

Fig. 1

Sensitivity of the steady state to the parameter values

From Fig. 1, the marginal wasting impact of both the revenue generation process (α) and the consumption process (β) on the capital stock is negative. In contrast, the influence of these processes on the stock of waste is different because an increase in the marginal wasting impact of the revenue generation (consumption) process results in less (more) waste stock. In contrast, an increase in the marginal impact of the recycling effort on the capital accumulation process (φ) reduces both the capital stock and the waste stock. Note that the influence of the discounting rate and the marginal revenue coefficient on the stock of capital and of waste is similar to that of the marginal polluting impact of revenue generation (α) and the marginal impact of the recycling effort on the capital accumulation process (φ). The marginal revenue coefficient (a) has a similar impact on the stock of capital and the stock of waste as the marginal wasting impact of the consumption process (β). Finally, a greater cost coefficient of the waste stock (e) lowers the waste stock and does not affect the capital stock, and vice-versa.

We now move to the stability analysis and investigate the structure of the associated stable manifolds.

Proposition 2

The steady state exhibits a (local) two-dimensional stable manifold if the social planner is moderately patient (i.e., $r<\left(1+\varphi \alpha \right)a$), and a one-dimensional stable manifold otherwise.

Proof

To analyze the stability of the steady state, we compute the Jacobian matrix of the canonical system (9)-(10)-(5)-(6), that is:

$$ \begin{array}{lll} \left|J\right|&=&ae\left\{\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]+\frac{\left(\alpha +\beta \right)\varPhi }{{\left(\lambda -\beta \mu \right)}^2}\right\}\\&=&2ae\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right] \end{array} $$

Given that λ and μ are evaluated at their steady state value, we compute the determinant:

$$ \begin{array}{lll} \left|J\right|&=&ae\left\{\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]+\frac{\left(\alpha +\beta \right)\varPhi }{{\left(\lambda -\beta \mu \right)}^2}\right\}\\&=&2ae\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right] \end{array} $$

which has a positive value for a moderately patient social planner ($r<\left(1+\varphi \alpha \right)a$), and negative otherwise. As shown in Dockner and Feichtinger (1991), a negative determinant is a necessary and sufficient condition for the Jacobian matrix to have one negative eigenvalue and either three positive eigenvalues or one positive eigenvalue and two with positive real parts. In terms of dynamic behavior, this corresponds to the case of a one-dimensional stable manifold.

In the case of a moderately patient social planner ($r<\left(1+\varphi \alpha \right)a$), we use Dockner’s formula (Dockner 1985) to determine the sum of the principal minors of J of order 2 minus the squared discounting rate, that is:

$$ \begin{array}{lll} \varPsi &=&-a\left(a-r\right)-e\left[\frac{\beta^2}{{\left(\lambda -\beta \mu \right)}^2}+1\right]\\&=&-a\left(a-r\right)-e\left[\frac{\beta^2\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]}{\left(\alpha +\beta \right)\varPhi }+1\right] \end{array}$$

The necessary and sufficient conditions that ensure that two eigenvalues have negative real parts and two have positive real parts, which corresponds to the case of a two-dimensional stable manifold, are $\left|J\right|>0$ and $\varPsi <0$. The sign of Ψ is negative, which implies that a two-dimensional stable manifold (saddle-point) exists in the case of a moderately patient social planner. □

According to Proposition 2, if the social planner is relatively impatient, the zero steady state cannot be reached from some or all initial states, which confirms that it is not optimal. Conversely, if the social planner is moderately patient, the positive saddle-point exists that can be reached. We may dig deeper in the analysis and draw further properties of the optimal paths, in particular about the existence of oscillatory transitions to the steady states. This gives a rough idea of the ability of the model to generate non-monotonic optimal trajectories and fluctuations, a central issue in the recent recycling-related macroeconomic literature (De Beir et al. 2010).

Proposition 3

Assuming a patient social planner (i.e., $r<a$), for any given a, e, and $\beta \varphi <1$, there exists a threshold $\tilde{\alpha}>0$ such that for any $\alpha >\tilde{\alpha}$, the convergence to the steady state is oscillatory.

Proof

To determine whether the optimal path is monotonic or follows cyclical motions, we compute the expression (Dockner 1985):

$$ \begin{array}{lll} \varOmega &=&{\varPsi}^2-4\left|J\right|={\left\{a\left(a-r\right)+e\left[\frac{\beta^2\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]}{\left(\alpha +\beta \right)\varPhi }+1\right]\right\}}^2\\&&-8ae\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right] \end{array}$$

A positive (negative) sign of Ω indicates that convergence to the saddle-point is monotonic (spiraling) near the steady state. Because the sign of Ω is ambiguous, a limit value analysis highlights the role played by a, e, φ, α and β in the sign of Ω for a given $r<a$ (Table 1).

Table 1 Limit value analysis

The results suggest that Ω is generally positive, which implies that convergence to the saddle-point is monotonic near the steady state in general. However, given that $\underset{\alpha \mapsto {0}^{+}}{ \lim}\varOmega >0$ and $\underset{\alpha \mapsto \infty }{ \lim}\varOmega =-\infty$, it can be shown that $\partial \varOmega /\partial \alpha <0$.

Therefore, we conclude that there exists a threshold $\tilde{\alpha}>0$ such that for any $\alpha >\tilde{\alpha}$, we have $\varOmega <0$. □

According to Proposition 3, if the social planner is patient, convergence to the locally stable steady state is either monotonic or oscillatory, depending on the magnitude of the wasting impact of the revenue generation process. That is, if the wasting impact of the revenue generation process is excessively high, the optimal policy follows a spiralling path which has the effect of reducing both the long run stock of capital and stock of waste, as suggested in Fig. 1. Therefore, a monotonic convergence is less detrimental to the capital stock but also more detrimental to the environment than a spiralling convergence.

Proposition 4

The saddle paths of the control and state variables in the neighborhood of the steady state are:

$$ c(t)=\frac{1}{\lambda^S-\beta {\mu}^S+\left({B}_1-\beta {B}_3\right){e}^{\chi_1t}+\left({B}_2-\beta {B}_4\right){e}^{\chi_3t}} \vspace*{-20pt}$$

(14)

$$ v(t)=\varphi {\lambda}^S-{\mu}^S+\left(\varphi {B}_1-{B}_3\right){e}^{\chi_1t}+\left(\varphi {B}_2-{B}_4\right){e}^{\chi_3t} \vspace*{-20pt}$$

(15)

$$ K(t)={K}^S+{B}_5{e}^{\chi_1t}+{B}_6{e}^{\chi_3t} \vspace*{-20pt}$$

(16)

$$ W(t)={W}^S+{B}_7{e}^{\chi_1t}+{B}_8{e}^{\chi_3t} $$

(17)

where B ₁, …, B ₈ are constants of integration and ${\chi}_1,{\chi}_3<0$.

Proof

The linear approximation of the system (5)-(6)-(9)-(10) around the steady state is:

$$ \overset{.}{\lambda }=\left(r-a\right)\lambda -\mu \alpha a \vspace*{-15pt}$$

$$ \overset{.}{\mu }=r\mu +eW \vspace*{-15pt}$$

$$ \overset{.}{K}=aK+\frac{\lambda -\beta \mu -2\left(\lambda -\beta \mu \right)}{{\left(\lambda -\beta \mu \right)}^2}+\varphi (\lambda \varphi -\mu ) \vspace*{-15pt}$$

$$ \overset{.}{W}=\alpha aK-\frac{\beta \left[\lambda -\beta \mu -2\left(\lambda -\beta \mu \right)\right]}{{\left(\lambda -\beta \mu \right)}^2}-(\lambda \varphi -\mu ) $$

Using Dockner’s formula (1985), the four eigenvalues associated with the Jacobian matrix of the canonical system are:

$$ {\fontsize{9}{11}{\selectfont\begin{array}{lll} {}_1{}^3\chi_2^4&=&\frac{r}{2}\pm \sqrt{\frac{r^2}{4}-\frac{\Psi}{2}\pm \frac{1}{2}\sqrt{\Psi^2-4\left|J\right|}}\\&=&\frac{r}{2}\pm \sqrt{\frac{r^2}{4}+\frac{1}{2}\left\{a\left(a-r\right)+e\left[\frac{\beta^2\left(1+\varphi \alpha \right)\left[\left(1+\varphi \alpha \right)a-r\right]}{\left(\alpha +\beta \right)\Phi}+1\right]\right\}\pm \frac{\sqrt{\Omega}}{2}} \end{array}}}$$

and λ ^S and μ ^S are given in the proof of Proposition 1. As expected, two eigenvalues, χ ₁ and χ ₃, have a negative sign and two have a positive sign, χ ₂ and χ ₄. Choosing the negative roots for convergence, the time paths of the costate and state variables are written as:

$$ \lambda (t)={\lambda}^S+{B}_1{e}^{\chi_1t}+{B}_2{e}^{\chi_3t} \vspace*{-1.2pc}$$

$$ \mu (t)={\mu}^S+{B}_3{e}^{\chi_1t}+{B}_4{e}^{\chi_3t} \vspace*{-1.2pc}$$

$$ K(t)={K}^S+{B}_5{e}^{\chi_1t}+{B}_6{e}^{\chi_3t} \vspace*{-1.2pc}$$

$$ W(t)={W}^S+{B}_7{e}^{\chi_1t}+{B}_8{e}^{\chi_3t} $$

These equations involve 10 unknowns (i.e., B ₁, …, B ₈,λ(0), μ(0)) that can be solved with the 10 following equations, which are drawn from the above expressions and the linearized versions of (5)-(6)-(9)-(10):

$$ \lambda (0)={\lambda}^S+{B}_1+{B}_2 \vspace*{-1.2pc}$$

$$ \mu (0)={\mu}^S+{B}_3+{B}_4 \vspace*{-1.2pc}$$

$$ {K}_0={K}^S+{B}_5+{B}_6 \vspace*{-1.2pc}$$

$$ {W}_0={W}^S+{B}_7+{B}_8 \vspace*{-1.2pc}$$

$$ \left(r-a\right){\lambda}^S+\left(r-a-{\chi}_1\right){B}_1+\left(r-a-{\chi}_3\right){B}_2-\alpha a\left({\mu}^S+{B}_3+{B}_4\right)=0 \vspace*{-1.2pc}$$

$$ r{\mu}^S+\left(r-{\chi}_1\right){B}_3+\left(r-{\chi}_3\right){B}_4+e\left({W}^S+{B}_7+{B}_8\right)=0 \vspace*{-1.2pc}$$

$$ \begin{array}{lll} a{K}^S-\frac{\lambda^S-\beta {\mu}^S-{B}_1-{B}_2+\beta \left({B}_3+{B}_4\right)}{{\left({\lambda}^S-\beta {\mu}^S\right)}^2}+\left(a-{\chi}_1\right){B}_5+\left(a-{\chi}_3\right){B}_6\\+\varphi \left[\varphi \left({\lambda}^S+{B}_1+{B}_2\right)-{\mu}^S-{B}_3-{B}_4\right]=0 \vspace*{-1.2pc}\end{array}$$

$$ \begin{array}{lll} \alpha a\left({K}^S+{B}_5+{B}_6\right)+\frac{\beta \left[{\lambda}^S-\beta {\mu}^S-{B}_1-{B}_2+\beta \left({B}_3+{B}_4\right)\right]}{{\left({\lambda}^S-\beta {\mu}^S\right)}^2}\\-\varphi \left({\lambda}^S+{B}_1+{B}_2\right)+{\mu}^S+{B}_3+{B}_4-{\chi}_1{B}_7-{\chi}_3{B}_8=0 \vspace*{-1.2pc}\end{array} $$

$$ \begin{array}{lll} {\left(r-a\right)}^2{\lambda}^S+\left[{\left(r-a\right)}^2-{\chi}_1^2\right]{B}_1+\left[{\left(r-a\right)}^2-{\chi}_3^2\right]{B}_2\\+\alpha a\left[\left(a-2r\right)\left({\mu}^S+{B}_3+{B}_4\right)-e\left({W}^S+{B}_7+{B}_8\right)\right]=0 \vspace*{-1.5pc}\end{array} $$

$$ {r}^2{\mu}^S+\left({r}^2-{\chi_1}^2\right){B}_3+\left({r}^2-{\chi_3}^2\right){B}_4+e\left[r{W}^S+\left(r+{\chi}_1\right){B}_7+\left(r+{\chi}_3\right){B}_8\right]=0 $$

This system of equations can be solved numerically. Finally, using (7), and (8) yields (14), (15), (16), and (17).

4 Numerical Example

We now give a numerical example to suggest the economic insight that could be gained from our model. To this end, we use the following parameter values (Table 2).

The parameter values in Table 2 reflect a configuration characterized by players’ relative patience with a discounting rate, r, similar to the market interest in normal time (that is, 5 %), and lower than the marginal revenue from the productive capital stock, a, which is set at an intermediate value (that is, 10 %). By varying parameters α, β and φ, we show that various structurally different solutions are possible. The numerical solutions were computed with Maple 18.0.

Table 2 Parameter values

The induced steady state values are reported in the following table (Table 3).

Table 3 State and control steady state values under various configurations

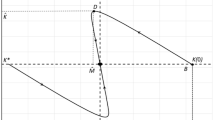
The main relationship to be investigated is that between the optimal stocks of capital and pollution to uncover a possible environmental Kuznets curve as in Stokey (1998) or Boucekkine et al. (2013). Regarding this relationship, the results of our experiments are reported in Fig. 2 below. Several remarkable features can be deduced from these figures.

Fig. 2

Phase-planes of stock of capital and stock of waste. (a) Production more wasteful than consumption; (b) Consumption more wasteful than production

The first result is that the relationship between capital (or income) and pollution is non-monotonic, if recycling generates additional income (that is $\varphi >0$). This is true when production is more wasteful than consumption (Fig. 2a) and in the opposite case (Fig. 2). In both cases, we observe that the stock of pollution decreases while capital rises initially, but in the last stage of convergence to the steady state both stocks go down. In contrast, also in both cases, the relationship is permanently monotonic if recycling does not generate income (that is, $\varphi =0$): the pollution stock decreases to its steady state value whereas capital increases to its corresponding stationary value. No turning point is observed in such cases.

It is worth pointing out two interesting connected outcomes at this stage. First, the kind of non-monotonicity we get is not of the environmental Kuznets curve kind, which is therefore not the rule in our optimal recycling model. Second, this non-monotonicity only arises when recycling generates additional income. To understand these remarkable properties, it is useful to have a look at the optimal control time paths. They are reported in Fig. 3.

Fig. 3

Time paths of control variables (logarithmic time scale). (a) Consumption; (b) Recycling effort

In all the parametric configurations, optimal consumption starts at a relatively low level, in contrast to recycling. We are therefore in a situation where both controls act as substitutes. In our calibrated economy, priority is given to pollution control in the short run to decrease the stock of polluting waste as quickly as possible. In the transition to the steady states, consumption increases steadily to its corresponding stationary value when recycling has no additional income ($\varphi =0.1$) or rises then decreases to the steady state value when recycling does generate income ($\varphi >0$). Whatever the parameterization, recycling effort always starts at a high value and follows an unambiguous monotonically decreasing path to its steady state value.

With these elements in hand, one can rationalize the optimal relationship between income and pollution we have uncovered. When recycling generates income, capital increases markedly in the initial stage of transitional dynamics because recycling is highest at this stage, and income from recycling goes entirely to capital accumulation. This significant increment in the stock of capital ends up boosting production and therefore consumption (notably with respect to the case where recycling does not generate income). In the medium term, consumption is quite high while recycling drops sharply. In the last stage of the transitional dynamics, the consumption level is still markedly higher than in the case $\varphi =0$, while income from recycling is much lower than in the initial stage of the transition dynamics (because the amount recycled in also much lower). The conjunction of the two latter forces pushes capital down in the ultimate adjustment stage given the law of motion of capital (2), generating the turning point observed and described above.

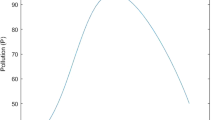
Therefore, the non-monotonicity observed is mainly due to the timing of optimal recycling, which massively takes place in the initial periods. The welfare implications of such timing can be seen in Fig. 4, where the social welfare function is computed for different time horizons. The initial sharp drop in social welfare is due to the initial intense recycling period.

Fig. 4

Overall social utility

5 Conclusion

In this paper, we have studied the sustainability of a Stokey-inspired AK model, one that considers a negative environmental externality that arises both from production and consumption. Instead of the typical abatement technologies, we present novel recycling modelling where recycling also generates income that is fully devoted to capital accumulation.

We have studied the qualitative properties of the resulting optimal control problem, notably in terms of optimal asymptotic states, stability and transition. We have also worked out a numerical example and got some highly interesting economic results in comparison with the seminal framework of Stokey, both in terms of the optimal pace of recycling and the relationship between income and pollution.

In particular, the role played by recycling as an income generator is crucial in the sense that it gives rise to a contraction of both the consumption and capital stock in the long run after an expansion phase. Whether polluting waste is predominantly due to production or consumption, when recycling generates additional income, greater consumption and lower capital stock are obtained in the long run compared with the situation when recycling does not create additional income. In parallel, when recycling generates additional income, greater recycling effort and lower stock of waste are resulted in the long run than when recycling has no additional income.

Of course, this is just a preliminary investigation; further analyses involving control-state constraints and alternative specifications within the same class of models along with alternative calibrations are needed to corroborate and complement this study.