Efficient Subsequence Join Over Time Series Under Dynamic Time Warping

Abstract

Joining two time series in their similar subsequences of arbitrary length provides useful information about the synchronization of the time series. In this work, we present an efficient method to subsequence join over time series based on segmentation and Dynamic Time Warping (DTW) measure. Our method consists of two steps: time series segmentation which employs important extreme points and subsequence matching which is a nested loop using sliding window and DTW measure to find all the matching subsequences in the two time series. Experimental results on ten benchmark datasets demonstrate the effectiveness and efficiency of our proposed method and also show that the method can approximately guarantee the commutative property of this join operation.

1 Introduction

Time series data occur in so many applications of various domains: from business, economy, medicine, environment, meteorology to engineering. A problem which has received a lot of attention in the last decade is the problem of similarity search in time series databases.

The similarity search problem is classified into two kinds: whole sequence matching and subsequence matching. In the whole sequence matching, it is supposed that the time series to be compared have the same length. In the subsequence matching, the result of this problem is a consecutive subsequence within the longer time series data that best matches the query sequence.

Besides the two above-mentioned similarity search problems, we have the problem of subsequence join over time series. Subsequence join finds pairs of similar subsequences in two long time series. Two time series can be joined at any locations and for arbitrary length. Subsequence join is a symmetric operation and produces many-to-many matches. It is a generalization of both whole sequence matching and subsequence matching. Subsequence join can bring out useful information about the synchronization of the time series. For example, in the stock market, it is crucial to find correlation among two stocks so as to make trading decision timely. In this case, we can perform subsequence join over price curves of stocks in order to obtain their common patterns or trends. Figure 1 illustrates the results of subsequence join on two time series. This join operation is potentially useful in many other time series data mining tasks such as clustering, motif discovery and anomaly detection.

Fig. 1

Two time series are joined to reveal some pairs of matching subsequences

There have been surprisingly very few works on subsequence join over time series. Lin et al. in 2010 [5, 6] proposed a method for subsequence join which uses a non-uniform segmentation and finds joining segments based on a similarity function over a feature-set. This method is difficult-to-implement and suffers high computational complexity that makes it unsuitable for working in large time series data. Mueen et al. [7] proposed a different approach for subsequence join which is based on correlation among subsequences in two time series. This approach aims to maximizing the Pearson’s correlation coefficient when finding the most correlated subsequences in two time series. Due to this specific definition of subsequence join, their proposed algorithm, Jocor, becomes very expensive computationally. Even though the authors incorporated several speeding-up techniques, the runtime of Jocor is still unacceptable even for many time series datasets with moderate size. These two previous works indicate that subsequence join problem is more challenging than subsequence matching problem.

In this work, we present an efficient method to subsequence join over time series based on segmentation and Dynamic Time Warping measure. Our method consists of two steps: (i) time series segmentation which employs important extreme points [1, 8] and (ii) subsequence matching which is a nested loop using sliding window and DTW measure to find all the matching subsequences in the two time series. DTW distance is used in our proposed method since so far it is the best measure for various kinds of time series data even though its computational complexity is high. We tested our method on ten pairs of benchmark datasets. Experimental results reveal the effectiveness and efficiency of our proposed method and also show that the method can approximately guarantee the commutative property of this join operation.

2 Related Work

2.1 Dynamic Time Warping

Euclidean distance is a commonly used measure in time series data mining. But one problem with time series data is the probable distortion along the time axis, making Euclidean distance unsuitable. This problem can be effectively handled by Dynamic Time Warping. This distance measure allows non-linear alignment between two time series to accommodate series that are similar in shape but out of phase. Given two time series Q and C, which have length m and length n, respectively, to compare these two time series using DTW, an n-by-n matrix is constructed, where the (ith, jth) element of the matrix is the cumulative distance which is defined as

$$ \gamma \left( {i,\,j} \right) = d\left( {q_{i} ,\,c_{j} } \right) + { \hbox{min} }{\{ }\gamma \left( {i - 1,\,j} \right),\,\gamma \left( {i,\,j - 1} \right),\,\gamma \left( {i - 1,\,j - 1} \right){\} } $$

That means $\gamma (i,\,j)$ is the summation between $d(i,\,j) = (q_{i} - c_{j} )^{2}$, a square distance of q _i and c _j , and the minimum cumulative distance of the adjacent element to (i, j).

A warping path P is a contiguous set of matrix elements that defines a mapping between Q and C. The tth element of P is defined as $p_{t} = (i,\,j)_{t}$, so we have:

$$ P = p_{1} ,p_{2} , \ldots ,p_{t} , \ldots ,p_{T} \quad \quad \hbox{max} (m,n) \le T < m + n - 1 $$

Next, we choose the optimal warping path which has minimum cumulative distance defined as

$$ DTW(Q,C) = { \hbox{min} }\left\{ {\sqrt {\sum\limits_{t = 1}^{T} {p_{t} } } } \right\} \, $$

The DTW distance between two time series Q and C is the square root of the cumulative distance at cell (m, n).

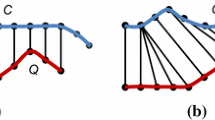
To accelerate the DTW distance calculation, we can constrain the warping path by limiting how far it may stray from the diagonal. The subset of matrix that the warping path is allowed to traverse is called warping window. Two of the most commonly used global constraints in the literature are the Sakoe-Chiba band proposed by Sakoe and Chiba 1978 and Itakura Parallelogram proposed by Itakura 1975 [2]. Sakoe-Chiba band is the area defined by two straight lines in parallel with the diagonal (see Fig. 2).

Fig. 2

(Left) Two time series Q and C which are similar in shape but out of phase: Using euclidean distance (top left) and DTW distance (bottom left). Note that Sakoe-Chiba band with width R is used to limit the warping path (right) [9]

In this work, we use the Sakoe-Chiba Band with width R and assume that all the time series subsequences in subsequence matching under DTW are of the same length.

2.2 Important Extreme Points

Important extreme points in a time series contain important change points of the time series. Based on these important extreme points we can segment the time series into subsequences. The algorithm for identifying important extreme points was first introduced by Pratt and Fink [8]. Fink and Gandhi [1] proposed the improved variant of the algorithm for finding important extreme points. In [1] Fink and Gandhi give the definition of strict, left, right and flat minima as follows.

Definition 1

(Minima) Given a time series $t_{1} ,\, \ldots ,\,t_{n}$ and t _i is its point such that $1 < i < n$

• t _i is a strict minimum if $t_{i} < t_{i - 1}$ and $t_{i} < t_{i + 1}$.

• t _i is a left minimum if $t_{i} < t_{i - 1}$ and there is an index right > i such that $t_{i} = t_{i + 1} = \ldots = t_{right} < t_{right + 1}$.

• t _i is a right minimum if $t_{i} < t_{i + 1}$ and there is an index left < i such that $t_{left - 1} > t_{left} = \ldots = t_{i - 1} = t_{i}$.

• t _i is a flat minimum if there are indices left < i and right > i such that $t_{left - 1} > t_{left} = \ldots = t_{i} = \ldots = t_{right} < t_{right + 1}$

The definition for maxima is similar. Figure 3 shows an example of a time series and its extrema. Figure 4 illustrates the four types of minima.

Fig. 3

Example of a time series and its extrema. The importance of each extreme point is marked with an integer greater than 1 [1]

Fig. 4

Four types of important minima [1]. a Strict minimum. b Left and right minima. c Flat minimum

We can control the compression rate with a positive parameter R; an increase of R leads to the selection of fewer points. Fink and Gandhi [1] proposed some functions to compute the distance between two data values a, b, in a time series. In this work we use the distance $dist(a,\,b) = \left| {a - b} \right|$.

For a given distance function dist and a positive value R, Fink and Gandhi [1] gave the definition of important minimum as follows.

Definition 2

(Important minimum) For a given distance function dist and positive value R, a point t _i of a series $t_{1} ,\, \ldots ,\,t_{n}$ is an important minimum if there are indices il and ir, where $il < i < ir$, such that t _i is a minimum among $t_{il} ,\, \ldots ,\,t_{ir}$, and dist $\left( {t_{i} ,\,t_{il} } \right) \ge R$ and dist $\left( {t_{i} ,\,t_{ir} } \right) \ge R$.

The definition for important maxima is similar.

Given a time series T of length n, starting at the beginning of the time series, all important minima and maxima of the time series are identified by using the algorithm given in [1]. The algorithm takes linear computational time and constant memory. The algorithm requires only one scan through the whole time series and, it can process new coming points as they arrive one by one, without storing the time series in memory.

After having all the extrema, we can select only strict, left and right extrema and discard all flat extrema.

In this work, we apply this algorithm for finding all important extrema from time series before extracting subsequences on them.

3 Subsequence Join Over Time Series Based on Segmentation and Matching

Our proposed method for subsequence join over time series is based on some main ideas as follows. Given two time series, first a list of subsequences is created for each time series by applying the algorithm for finding important extreme points in each time series [1]. Afterwards, we apply a nested loop join approach which uses a sliding window and DTW distance to find all the matching subsequences in the two time series. We call our subsequence join method EP-M (Extreme Points and Matching).

3.1 The Proposed Algorithm

The proposed algorithm EP-M for subsequence join over time series consists of the following steps.

Step 1::

We compute all important extreme points of the two time series T ₁ and T ₂ . The results of this step are two lists of important extreme points $EP1 = \left( {ep1_{1} ,ep1_{2} , \ldots ,ep1_{m1} } \right)$ and $EP2 = \left( {ep2_{2} ,ep2_{2} , \ldots ,ep2_{m2} } \right)$ where m1 and m2 are the numbers of important extreme points in T ₁ and T ₂ , respectively. In the next steps, when creating subsequences from a time series (T ₁ or T ₂ ), we extract the subsequence bounded by the two extreme points ep _i and ep _i+2

Step 2::

We keep time series T ₁ fixed and for each subsequence s extracted from T ₁ we find all its matching subsequences in T ₂ by shifting a sliding window of the length equal to the length of s along T ₂ one data point at a time. We store all the resulting subsequences in the result set S ₁

Step 3::

We keep time series T ₂ fixed and for each subsequence s extracted from T ₂ we find all its matching subsequences in T ₁ by shifting a sliding window of the length equal to the length of s along T ₁ one data point at a time. We store all the resulting subsequences in the result set S ₂

In Step 1, for the algorithm that identifies all the important extreme points in the time series, we have to determine the parameter R, the compression rate. According to Pratt and Fink [8], they only suggested that R should be greater than 1. In this work, we apply the following heuristic for selecting value for R. This heuristic is very intuitive. Let SD be the standard deviation of the time series. We set R to 1.5 * SD.

The pseudo-code for describing Step 2 and Step 3 in EP-M is given as follows.

Notice that Procedure Subsequence_Matching invokes the procedure DTW_EA which computes DTW distance. The DTW_EA procedure applies Early Abandoning technique as mentioned in the following subsection.

3.2 Some Other Issues

• Normalization

  In order to make meaningful comparisons between two time series, both must be normalized. In our subsequence join method, before applying EP-M algorithm we use min-max normalization to transform the scale of one time series to the scale of the other time series based on the maximum and minimum values in each time series.

  Min-max normalization can transform a value v of a numeric variable A to v’ in the range [min_A, max_A] by computing:

  $$ v' = \frac{{v - \text{min}_{A} }}{{\text{max}_{A} - \text{min}_{A} }}(new\_{ \hbox{max} }_{A} - new\_{ \hbox{min} }_{A} ) + new\_{ \hbox{min} }_{A} $$

• Speeding-up DTW distance computation

  To accelerate the calculation of DTW distance, a number of approaches, such as using global constraints like Sakoe-Chiba band or Itakura parallelogram and using some lower bounding techniques have been proposed. Besides, Li and Wang [4] proposed the method which applies an early abandoning technique to accelerate the exact calculation of DTW. The main idea of this technique is described as follows. The method checks if values of the neighboring cells in the cumulative distance matrix exceed the tolerance, and if so, it will terminate the calculation of the related cell. Li and Wang 2009, called their proposed method EA_DTW (Early Abandon DTW). The details of the EA_DTW algorithm are given in [4].

4 Experimental Evaluation

We implemented all the comparative methods with Microsoft C#. We conducted the experiments on an Intel(R) Core(TM) i7-4790, 3.6 GHz, 8 GB RAM PC. The experiments aim to three goals. First, we compare the quality of EP-M algorithm in the two cases: using Euclid distance and using DTW distance. Second, we test the accuracy and time efficiency of EP-M algorithm. Finally, we check whether the EP-M algorithm can approximately guarantee the commutative property of the join operation. For simplicity, we always use equal size time series (i.e. $n_{1} = n_{2}$) to join although our method is not limited to that.

4.1 Datasets

Our experiments were conducted over the datasets from the UCR Time Series Data Mining archive [3]. There are 10 datasets used in these experiments. The names and lengths of 10 datasets are as follows: Chromosome-1 (128 data points), Runoff (204 data points), Memory (6874 data points), Power-Demand-Italia (29931 data points), Power (35450 data points), Koski-ECG (144002 data points), Chromosome (999541 data points), Stock (2119415 data points), EEG (10957312 data points).

Since the subsequence join has to work on the two time series of some degree of similarity, we need a method to generate the synthetic dataset T ₂ (inner time series in Step 2) for each test dataset T ₁ (outer time series in Step 2). The synthetic dataset is generated by applying the following rule:

$$ x_{i} = x_{i - 1} \pm |x_{i - 1} - \varepsilon |\quad \quad {\text{where}}\;\varepsilon = \frac{{\sum\nolimits_{i = 1}^{6} {x_{i} } }}{6} $$

In the above formula, + or − is determined by a random process. The synthetic dataset is created after the correspondent dataset has been normalized, therefore, the noisy values does not affect to the generated dataset. Specifically for Runoff dataset (from The Be River in Southern Vietnam) we use the real datasets (monthly data from 1977 to 1993) at two measurement stations Phuoc Long and Phuoc Hoa. The dataset at Phuoc Long Station will play the role of time series T ₁ and the dataset at Phuoc Hoa Station will be time series T ₂ .

4.2 DTW Versus Euclidean Distance in EP-M Algorithm

In time series data mining, distance measure is crucial factor which has a huge impact on the performance of the data mining task. Here we need to know between DTW and Euclidean distance which measure is more suitable for our proposed subsequence join method. We conducted the experiment to compare the performance of EP-M algorithm using each of the two distance measures in terms of the number of pairs of matching subsequences found by the algorithm. Table 1 reports the experimental results over 8 datasets. The experimental results show that with Euclidean distance, EP-M can miss several pairs of matching subsequences in the two time series (see the last column). That means EP-M with Euclidean Distance can not work well in subsequence join as EP-M with DTW. The experiment recommends that we should use DTW distance in the EP-M algorithm even though DTW incurs much more computational time than Euclidean distance.

Table 1 Experimental results in comparing DTW to euclidean distance

4.3 Accuracy of EP-M Algorithm

Now we turn our discussion to the accuracy of EP-M algorithm. Following the tradition established in previous works, the accuracy of a similarity search algorithm is basically based on human analysis of the matching subsequences discovered by that algorithm. That means through human inspection we can check if the matching subsequences of a query in question identified by the proposed algorithm in a given time series have almost the same shape as the query pattern. If the check result is positive in most of the test datasets, we can conclude that the proposed algorithm brings out the accurate similarity search.

Through our experiment, we found out that the result sets provided by our EP-M algorithm are quite accurate over all the test datasets.

4.4 Time Efficiency of EP-M

The names and runtimes (in minutes) of 9 datasets by EP-M are as follows: Chromosome-1 (0.003), Runoff (0.007), Memory (3.227), Power-Demand-Italia (10.8), Power (82), Koski-ECG (106.2), Chromosome (64.4), Stock (34.7), EEG (30.45).

The maximum length of these datasets is 30000. The execution time of EP-M on the Koski-ECG dataset with 30,000 data points is about 1 h 46 min. So, the runtimes reported are acceptable in practice.

4.5 The Commutative Property of Join Operation by EP-M

The reader may wonder if subsequence join achieved by EP-M can satisfy the commutative property of join operation, i.e. $T_{1} { \triangleright \triangleleft }T_{2} = T_{2} { \triangleright \triangleleft }T_{1}$. We can check this theoretic property through experiments over 10 datasets with the maximum length 5000. For $T_{1} { \triangleright \triangleleft }T_{2}$, time series T ₁ is considered in the outer loop and time series T ₂ is considered in the inner loop of Step 2 in EP-M. For $T_{2} { \triangleright \triangleleft }T_{1}$, the order of computation is in the opposite. Table 2 reports the experimental results on commutative property of join operation by EP-M in terms of the number of pairs of matching subsequences found by the algorithm in two cases $T_{1} { \triangleright \triangleleft }T_{2}$ and $T_{2} { \triangleright \triangleleft }T_{1}$. The experimental results reveal that the difference between two cases is small enough to confirm that the EP-M method can approximately guarantee the commutative property of this join operation.

Table 2 Experimental results on commutative property of join operation by EP-M

5 Conclusions

Subsequence join on time series data can be used as a useful analysis tool in many domains such as finance, health care monitoring, environment monitoring. In this paper, we have introduced an efficient and effective algorithm to perform subsequence join on two time series based on segmentation and Dynamic Time Warping measure.

As for future works, we intend to extend our subsequence join method for the context of streaming time series. Besides, we plan to adapt our EP-M method with Compression Rate Distance [10], a new distance measure that is better than DTW, but with O(n) computational complexity. Future work also includes considering the utility of EP-M algorithm for the problem of time series clustering, classification, motif discovery and anomaly detection.