Fault Localization of Timed Automata Using Maximum Satisfiability

Abstract

Timed automata are formal models for systems whose real-time behavior is a major concern, and practical model checking tools are available for them. Although these tools are effective to detect faulty behavior, localizing root causes of faulty timed automata requires a costly manual task of studying counter-examples. This paper presents an automatic fault localization problem. The proposed approach follows the Reiter’s model-based diagnosis theory to employ the consistency-based method, and details the method to show how the Reiter’s general theory is applicable to timed automata. In particular, the proposed method introduces a modest assumption on the failure. The paper discusses how the failure model and properties to be checked affect the formula used in the consistency-based fault localization method.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Timed or hybrid systems are employed as a modeling tool for a wide variety of non-functional concerns such as real-time timing properties or energy consumption [16]. Their formal models, especially linear hybrid systems [2] including timed automata [1], are well studied and industrial-strength verification tools for the timed automata are developed (e.g. [10]). These tools check the behavioral aspects automatically, but require a costly manual study of generated counter-example traces to identify root causes of the failure.

Automatic fault localization methods are successful for the case of VLSI circuit designs [19, 21] or imperative programs [5, 7–9]. These consistency-based approaches adapt the model-based diagnosis (MBD) theory [18] and use Boolean satisfiablity [4] as in the bounded model checking (BMC) [3], or specifically the maximum satisfiability (MaxSAT). In the MBD theory, an artifact and its property or an assertion are encoded in a logic formula. The whole formula is unsatisfiable if the artifact is faulty in that it violates the property. The fault localization problem is finding a subset of clauses in the formula to make it satisfiable if they are removed. This subset of clauses is a minimal correction subset (MCS) of the unsatisfiable formula [12].

This paper proposes a consistency-based fault localization method for timed automata using the MaxSAT. The method adopts the Boolean encoding of timed automata proposed in [20]. The contributions of this paper are as follows. (1) We introduce a framework of fault localization methods that details the MBD theory [18], which constitutes the main body of Sect. 4. The framework makes explicit the relationship between the failure model, the trace formula, and the property to be checked. (2) For timed automata, an important class of fault localization problems is reduced to solving a set of clock constraints. Since the constraints are expressed in linear real arithmetic theory [1], the problem is decidable. (3) This paper demonstrates the feasibility of the proposed method with experiments on small example cases using the Yices-1 [6], a partial MaxSAT solver.

Although the work is still at a feasibility study stage, it is, as far as we know, the first report on the automatic fault localization of timed automata using the maximum satisfiability.

2 Preliminaries

This section introduces the basic concepts. We use the term SAT to refer to both pure Boolean satisfiability and satisfiability modulo theories (SMT) methods.

Scope-Bounded Analysis. The SAT method is a basis of various automatic analysis methods such as bounded model checking (BMC) [3]. Given a system, we encode potential execution paths of the system in a logic formula ${\varphi }_{TF}$. We let ${\varphi }_{AS}$ be a formula of the property to be checked. Because ${\lnot }({\varphi }_{TF}~{\Rightarrow }~{\varphi }_{AS})$ $=$ ${\varphi }_{TF}~{\wedge }~{\lnot }{\varphi }_{AS}$, a BMC problem is to see whether ${\varphi }_{TF}~{\wedge }~{\lnot }{\varphi }_{AS}$ is satisfiable. The formula is satisfied if the system (${\varphi }_{TF}$) violates the given property (${\varphi }_{AS}$). The obtained assignments constitute counter-examples to demonstrate this failure. In the following, ${\varphi }_{CE}$ refers to a formula encoding these counter-example assignments.

Fault Localization Problem. Let a formula ${\varphi }_{FL}$ be ${\varphi }_{EI}~{\wedge }~{\varphi }_{TF}~{\wedge }~{\varphi }_{AS}$ for the above mentioned ${\varphi }_{TF}$ and ${\varphi }_{AS}$, and ${\varphi }_{EI}$ that encodes error-inducing formula; ${\varphi }_{FL}={\varphi }_{EI}~{\wedge }~{\varphi }_{TF}~{\wedge }~{\varphi }_{AS}$. We construct ${\varphi }_{EI}$ as a sub-formula of ${\varphi }_{CE}$ so that ${\varphi }_{EI}$ provides necessary comditions for the failing situation. From these, ${\varphi }_{FL}$ is unsatisfiable.

If the system fails for a particular set of input data values, ${\varphi }_{CE}$ includes a sub-formula to encode such a set of data values. In this case, ${\varphi }_{EI}$ is simple enough to represent that the specific variables take particular values that lead the system to such a failing execution. In the fault localization of an imperative program [5, 7–9], ${\varphi }_{EI}$ encodes a set of input data values that make the program violating ${\varphi }_{AS}$. However, ${\varphi }_{EI}$ may have further information that reflects the characteristics of the target system. Finding appropriate ${\varphi }_{EI}$ for TAs will be discussed in Sect. 4.2.

The fault localization problem is finding clauses in ${\varphi }_{TF}$ that are responsible for the unsatisfiability of ${\varphi }_{FL}$. These clauses, if found, constitute a conflict, which is an erroneous situation containing root causes of the failure. By definition, ${\varphi }_{EI}$ and ${\varphi }_{AS}$ are supposed to be satisfiable. Therefore, it is exactly the problem in which we search for root causes of the faulty system.

In what follows, C refers to a set of clauses that constitute a given formula ${\varphi }$ in conjunctive normal form (CNF). We use C and ${\varphi }$ interchangeably. For details about the basic concepts, we refer to the standard literature (e.g. [4]).

Minimal Unsatisfiable Subset. A set of clauses M, $M~{\subseteq }~C$, is a minimal unsatisfiable subset (MUS) iff M is unsatisfiable and ${\forall }{c}{\in }M{:}{M}{\backslash }\{c\}$ is satisfiable.

Maximal Satisfiable Subset. A set of clauses M, $M~{\subseteq }~C$, is a maximal satisfiable subset (MSS) iff M is satisfiable and ${\forall }{c}{\in }({C}{\backslash }{M}){:}{M}{\cup }\{c\}$ is unsatisfiable.

Minimal Correction Subset. A set of clauses M, $M~{\subseteq }~C$, is a minimal correction subset (MCS) iff ${C}{\backslash }{M}$ is satisfiable and ${\forall }{c}{\in }M{:}({C}{\backslash }{M}){\cup }\{c\}$ is unsatisfiable. By definition, an MCS is a complement of an MSS. MCS is sometimes called coMSS.

Hitting Set. Let $\varOmega$ be a set of sets from some finite domain D. A hitting set of $\varOmega$, H, is a set of elements from D that covers every set in $\varOmega$ by having at least one element in common with it. Formally, H is a hitting set of $\varOmega$ iff ${H}{\subseteq }{D}$ and ${\forall }S{\in }{\varOmega }{:}{H}{\cap }{S}{\ne }{\emptyset }$. A minimal hitting set is a hitting set from which no element can be removed without losing the hitting set property.

Partial Maximum Satisfiability. A maximum satisfiability (MaxSAT) problem for a CNF formula is finding an assignment that maximizes the number of satisfied clauses. Partial MaxSAT (pMaxSAT) is a variant of the MaxSAT, in which some clauses are marked soft or relaxable, and the others are marked hard or non-relaxable. A pMaxSAT problem is finding an assignment that satisfies all the hard clauses and maximizes the number of satisfied soft clauses.

An Example. Here is a simple example to illustrate the basic concepts [11].

$$\begin{aligned} \begin{array}{lllllllll} &{} &{} {C}_{1} &{} &{} {C}_{2} &{} &{} {C}_{3} &{} &{} {C}_{4} \\ \varphi &{} = &{} (a) &{} \wedge &{} ({\lnot }a) &{} \wedge &{} ({\lnot }a{\vee }b) &{} \wedge &{} ({\lnot }b) \\ \\ \end{array} \end{aligned}$$

Its MUSes, MCSes, and MSSes are the following.

•    MUSes($\varphi$) = $\{~\{{C}_{1},{C}_{2}\},~ \{{C}_{1},{C}_{3},{C}_{4}\}~\}$

•    MCSes($\varphi$) = $\{~\{{C}_{1}\},~~~~~~~~~~\{{C}_{2},{C}_{3}\},~\{{C}_{2},{C}_{4}\}~\}$

•    MSSes($\varphi$) = $\{~\{{C}_{2},{C}_{3},{C}_{4}\},~\{{C}_{1},{C}_{4}\},~\{{C}_{1},{C}_{3}\}~\}$

MUSes($\varphi$) and MCSes($\varphi$) are related by a hitting set relationship.

Next, if we mark ${C}_{3}$ as hard and all the rest to be soft, a set of two MCS elements, $\{~\{{C}_{1}\},~\{{C}_{2},{C}_{4}\}~\}$, is obtained as MCSes. This illustrates that there are two possible repairs to make the formula $\varphi$ satisfiable under the assumption that ${C}_{3}$ is believed to be correct. We may remove either ${C}_{1}$ or both ${C}_{2}$ and ${C}_{4}$. Note that we must decide which candidate we choose to repair. This decision requires a piece of information beyond the fault localization method. The repair is not the focus of this paper.

Model-Based Diagnosis. Fault localization is finding a subset of clauses, called diagnosis, in the unsatisfiable formula ${\varphi }_{FL}$ to make it satisfiable if they are removed. The model-based diagnosis framework [18] presents a way to calculate diagnoses from conflicts. Note that a conflict is an erroneous situation and a diagnosis refers to root causes. Formally, diagnoses are MCSes, a set of MCS elements, while conflicts are MUSes, a set of MUS elements. MCSes are calculated from MUSes by a hitting set relationship [12]. The consistency-based approach [7, 8, 19], adopted in this paper, calculates an MSS to obtain an MCS by complementing the MSS, and repeats this process to collect MCSes. Any solution to MaxSAT problem is also an MSS, although every MSS is not always a solution to MaxSAT [15]. We use MaxSAT to obtain MCSes (e.g. [13]).

The fault localization problem needs a method to represent the fact that ${\varphi }_{EI}$ and ${\varphi }_{AS}$ are to be satisfiable and that some clauses in ${\varphi }_{TF}$ are suspicious. The pMaxSAT approach fits well this requirement [7–9, 21]. The clauses in ${\varphi }_{EI}$ and ${\varphi }_{AS}$ are marked hard. Suspicious clauses in ${\varphi }_{TF}$ are soft. The other clauses in ${\varphi }_{TF}$ that are assumed to be bug-free are hard. This decision, in which clauses are marked soft, is dependent on the adopted failure model (see Sect. 4.2).

3 Scope-Bounded Analysis

3.1 Timed Automata

Timed automata are finite state transition systems that have a finite number of non-negative real-valued clocks [1]. We follow the standard definitions.

Formal Model. A timed automaton $\mathcal{A}$ is a tuple ${\langle }~{Loc},{\ell }_{0},{X},{Edg},{Inv}~{\rangle }$.

• 1. Loc is a non-empty finite set of locations.

• 2. ${\ell }_{0}$ is the initial location, ${\ell }_{0}{\in }Loc$.

• 3. X is a finite set of clock variables. For a positive natural number $n ({\in }~\mathcal{N}$) and an operator ${\bowtie }~{\in }~\{{<},{\le },{=},{\ge },{>}\}$, constraints of the form ${x}~{\bowtie }~{n}$ and ${x}_{1}-{x}_{2}~{\bowtie }~{n}$ constitute a set of primitive clock constraints. We denote Z(X) to be a set of formulas constructing from these primitive constraints possibly using logical connectives of ${\wedge }$, ${\vee }$ and ${\lnot }$.

• 4. Edg represents a set of transitions. It is a finite set ${Loc}{\times }{Z(X)}{\times }{2}^{X}{\times }{Loc}$. An element of Edg, $({l},{g},{r},{l'})$, is written as ${l}~{\mathop {\longrightarrow }\limits ^{g,r}}~{l'}$, where g is a guard condition in Z(X) and r refers to a set of clock variables (${\in }~{2}^{X}$) to reset.

• 5. Inv is a mapping from Loc to clock constraints, ${Inv} : {Loc}{\rightarrow }{Z(X)}$.

Parallel Composition of Timed Automata. We represent a complex system as a parallel composition of timed automata, where two timed automata are synchronized on a same event. The definition of timed automata now contains a finite set of events $\varSigma$ and an empty symbol $\epsilon$, ${\langle }~{Loc},{\ell }_{0},{X},{\varSigma }{\cup }\{{\epsilon }\},{Edg},{Inv}~{\rangle }$. Particularly, Edg is ${Loc}{\times }({\varSigma }{\cup }\{{\epsilon }\}){\times }{Z(X)}{\times }{2}^{X}{\times }{Loc}$, and its element $({l},{a},{g},{r},{l'})$ is written as ${l}~{\mathop {\longrightarrow }\limits ^{a,g,r}}~{l'}$.

Parallel composition is defined for given two timed automata $\mathcal{A}^{(1)}$ and $\mathcal{A}^{(2)}$, where ${\varSigma }^{(1)}{\cap }{\varSigma }^{(2)}{\ne }{\emptyset }$. Locations of the composed automaton are pairs of locations, ${\langle }{l}^{(1)},~{l}^{(2)}{\rangle }~{\in }~{Loc}^{(1)}{\times }{Loc}^{(2)}$. Its invariant at each location is a conjunction, ${Inv}^{(1)}({l}^{(1)}){\wedge }{Inv}^{(2)}({l}^{(2)})$. Symbols common to both alphabets (${a}{\in }{\varSigma }^{(1)}{\cap }{\varSigma }^{(2)}$) synchronize two automata. $\mathcal{A}^{(1)}$ and $\mathcal{A}^{(2)}$ take transitions simultaneously. The parallel composition can be extended to cases where more than two automata are involved.

3.2 Boolean Encoding

Fault localization as well as bounded model checking needs Boolean encoding of a trace formula ${\varphi }_{TF}$. We follow the encoding method presented in [20].

Trace Formula. A state of a timed automaton $\mathcal{A}$ is characterized by a location variable (at) and clock variables (${x}_{1},~{\ldots }~,{x}_{n}$). Below, we use an abbreviation such as $\hat{x}$ to refer to a vector of variables $({x}_{1},~{\ldots }~,{x}_{n})~{\in }~{X}^{n}$. We introduce a set ${V}{=}\{{at},~\hat{x}\}$. A timed automaton $\mathcal{A}$ is defined as ${\langle }{I},{T}{\rangle }$ over V. We use j-indexed state variable such that ${V}_{j}{=}\{{at}_{j},~{\hat{x}}_{j}\}$.

• 1. Initial State : I is defined on V.

  ${I}{=}({at}={\ell }_{0}~{\wedge }~\hat{x}=0)$

• 2. Discrete Transition Step : T(e) is a relation on V and $V'$ where ${e}={l}~{\mathop {\longrightarrow }\limits ^{g,r}}~{l'}$ and ${z}_{i}=0$ if ${x}_{i}~{\in }~{r}$, ${z}_{i}={x}_{i}$ otherwise.

  ${T(e)}{=}({at}={l}~{\wedge }~{at'}={l'}~{\wedge }~{g}~{\wedge }$ $\hat{x}'=\hat{z}$ ${\wedge }~Inv({l'})(\hat{x}'))$

• 3. Delay Transition Step :

  D is a relation on V and $V'$. Inv(S) is the set of locations that have an invariant different from true. Clock variables are updated by an amount of ${\delta }$.

  ${D}{=}~{\exists }~{\delta }~{>}{0}~.$ $~(({\bigwedge }_{{l}{\in }{Inv(S)}}~({at}={l}){\Rightarrow }Inv(l)(\hat{x}'))$ ${\wedge }~{at'}={at}~{\wedge }~\hat{x}'=\hat{x}+{\delta }$)

• 4. Transition Relation : T is a relation on V and $V'$.  ${T}{=}~({\bigvee }_{e{\in }Edg}T(e))~{\vee }{D}$

• 5. K-step Unfolding of Timed Automaton : ${\varphi }_{TF}^{K}$ is a trace formula to encode potential K-step execution paths. Let ${V}_{j}$ be a set of j-indexed variables $\{{at}_{j}, {\hat{x}}_{j}\}$. V in I is ${V}_{0}$. V and $V'$ in ${T}_{j}$ are ${V}_{j-1}$ and ${V}_{j}$ respectively.

  ${\varphi }_{TF}^{K}~=~{I}~{\wedge }~({\bigwedge }_{j=1..K}~{T}_{j})$

Now, we consider parallel composition cases. In order to define a delay transition step, we introduce a special symbol delay to represent that the automaton takes a delay transition. The input alphabet is ${\varSigma }{\cup }\{{\epsilon },~delay\}$. The set V is extended to include a variable act referring to an input symbol ($\{at,~\hat{x}\}~{\cup }~\{act\}$).

• 1. Inactivity Transition : ${F}{=}({at'=at}~{\wedge }~({\bigwedge }_{x{\in }X}{x'=x})~{\wedge }~({\bigwedge }_{\alpha {\in }{\varSigma }{\cup }\{delay\}}{act{\ne }{\alpha }}))$

• 2. Discrete Transition Step for ${e}={l}~{\mathop {\longrightarrow }\limits ^{a,g,r}}~{l'}$ : A discrete transition of a single timed automaton for ${e}={l}~{\mathop {\longrightarrow }\limits ^{g,r}}~{l'}$ is a special case of a being $\epsilon$.

  ${T(e)} = ({at}={l}~{\wedge }~{at'}={l'}~{\wedge }~{act=a}~{\wedge }~{g}$ ${\wedge }~\hat{x}'=\hat{z}$ ${\wedge }~Inv({l'})(\hat{x}'))$

• 3. Delay Transition Step :

  ${D}{=}~{\exists }~{\delta }~{>}{0}~.$

    $~(({\bigwedge }_{{l}{\in }{Inv(S)}}~({at}={l}){\Rightarrow }Inv(l)(\hat{x}'))$ ${\wedge }~{at'}={at}~{\wedge }~\hat{x}'=\hat{x}+{\delta }$ ${\wedge }~{act=delay}$)

• 4. Transition Relation : ${T}{=}~({\bigvee }_{e{\in }Edg}T(e))~{\vee }~{D}~{\vee }~{F}$

• 5. K-step Unfolding of N number of Timed Automata : There are N number of timed automata ${A}^{(1)}~{\ldots }~{A}^{(N)}$ composed, where ${A}^{(i)}$ is ${\langle }{I}^{(i)},{T}^{(i)}{\rangle }$. ${I}^{(i)}$ and ${T}^{(i)}$ are the initial state and transition relation for the i-th automaton respectively. ${T}^{(i)}_{j}$ is j-th transition of i-th automaton.

  ${\varphi }_{TF}^{K}~=~{\bigwedge }_{i=1..N}({I}^{(i)}~{\wedge }~({\bigwedge }_{j=1..K}~{T}^{(i)}_{j}))$, which is rewritten as ${I}~{\wedge }~({\bigwedge }_{j=1..K}~{T}_{j})$ where ${I}={\bigwedge }_{i=1..N}~{I}^{(i)}$ and ${T}_{j}={\bigwedge }_{i=1..N}~{T}^{(i)}_{j}$.

Bounded Model Checking. We introduce a labeling function Lab from each location to a set of atomic propositions, ${Lab}~{:}~{Loc} {\rightarrow } {2}^{Prop}$. Prop is defined over state variables of a timed automaton, $\{{at},~\hat{x}\}$. $Lab(\ell )$ is a set of propositions that are true at the location $\ell$.

Specifically, p ($p{\in }Prop$) takes a form of equality or dis-equality on the location variable (at), and of primitive clock constraints for clock variables (${x}_{j}$). Clock constraints are represented in linear real arithmetic (LRA). We do not consider propositions involving act ($act{\in }{\varSigma }$) because the event symbol is concerned with transition synchronization.

Although a BMC problem is usually defined for arbitrary formulas of linear temporal logic (LTL) [20], we restrict to consider only two cases, safety properties and guarantee [14]. Let ${\psi }(\hat{v})$ be a propositional formula constructed from Prop. Each ${\hat{v}}_{j}$ stands for a vector of state variables in ${V}_{j}$. A safety property is expressed in LTL as ${\Box }{\psi }$, and a guarantee property is ${\Diamond }{\psi }$. Recall a BMC problem is checking the satisfiability of ${\varphi }_{TF}~{\wedge }~{\lnot }{\varphi }_{AS}$. As a negation of ${\Box }{\psi }$ is ${\Diamond }{\lnot }{\psi }$ and a negation of ${\Diamond }{\psi }$ is ${\Box }{\lnot }{\psi }$ respectively, a whole formula for the K-unfolded case is

${\varphi }_{safety}~=~$ ${I}({\hat{v}}_{0})~{\wedge }~({\bigwedge }_{j=1..K}~{T}_{j}({\hat{v}}_{j-1},{\hat{v}}_{j}))~{\wedge }~({\bigvee }_{j=1..K}~{\lnot }{\psi }({\hat{v}}_{j}))$,

or

${\varphi }_{guarantee}~=~$ ${I}({\hat{v}}_{0})~{\wedge }~({\bigwedge }_{j=1..K}~{T}_{j}({\hat{v}}_{j-1},{\hat{v}}_{j}))~{\wedge }~({\bigwedge }_{j=1..K}~{\lnot }{\psi }({\hat{v}}_{j}))$

                  ${\wedge }~~({\bigvee }_{j=0..K-1}({\hat{v}}_{k}={\hat{v}}_{j}))$.

The formula ${\varphi }_{guarantee}$ has an auxiliary constraint that we check ${\lnot }{\psi }$ against the paths to contain loops [4]. Since the check is done in a bounded scope, ${\Box }{\lnot }{\psi }$ can be satisfied only when loops exist.

4 Fault-Localization of Timed Automata

4.1 The Framework

The problem of fault localization using the pMaxSAT is formulated as finding MCSes for an unsatisfiable formula ${\varphi }_{FL}$ of the form ${\varphi }_{EI}~{\wedge }~{\varphi }_{TF}~{\wedge }~{\varphi }_{AS}$. Recall that ${\varphi }_{EI}$ expresses a failing situation, ${\varphi }_{TF}$ encodes all potential execution paths, and ${\varphi }_{AS}$ is a property to be checked. We need to determine the following three aspects so as to define the fault localization problem precisely.

The first aspect concerns with the property to be checked, which is common to BMC problems. We, indeed, conduct the BMC to see if the system is correct or not with respect to a given property. As discussed in Sect. 3.2, we adopt Prop defined over state variables of a timed automaton, $\{{at},~\hat{x}\}$. Specifically, p ($p{\in }Prop$) takes a form of equality or dis-equality on the location variable (at), and of primitive clock constraints for clock variables (${x}_{j}$).

The second is the failure model we assume. The formula ${\varphi }_{TF}$ is a Boolean encoding of operational semantics of timed automata and expresses all potential execution paths. Although all the elements can, in principle, be suspicious, we look for some particular clauses in ${\varphi }_{TF}$ to account for the failure. We will introduce a modest assumption on the failure model, which Sect. 4.2 will explain in detail.

The third aspect is what to encode in ${\varphi }_{EI}$. Basically, the formula demonstrates a failing situation. A conjunction ${\varphi }_{EI}~{\wedge }~{\varphi }_{TF}$ encodes a subset of all potential execution paths. ${\varphi }_{EI}$ acts as a filter to extract appropriate paths from those represented by ${\varphi }_{TF}$. The encoding of these paths has impact on the efficiency and precision of identifying MCS elements. Therefore, ${\varphi }_{EI}$ is sensitive to the fault localization problem, and is related to the property formula ${\varphi }_{AS}$. We will explain in details in Sect. 4.2.

4.2 Fault Localization Method

Failure Model. Timed automata are finite state transition systems that have non-negative real-valued clocks. Now we assume that a given set of timed automata can be composed, which means that they are not deadlocked due to inappropriate parallel compositions. Then, faulty behavior in timed automata is originated from some bugs in using clock variables. Since timed automata refer to clocks in invariants, transition guards, and resets, we consider that potential root causes are in them; invariants Inv(l), and g and r on an edge of ${l}~{\mathop {\longrightarrow }\limits ^{a,g,r}}~{l}$. These are suspicious elements in faulty systems consisting of timed automata. The fault localization problem is now checking a conjunction of clock constraints that are collected from a failing trace with respect to a given property ${\varphi }_{AS}$.

In the fault localization problem using the pMaxSAT method, those suspicious elements are marked soft or relaxable. Because an initial state is usually definite, all elements in the formula I are hard or non-relaxable. The inactivity transition F, for the case of composing automata, is also definite because it encodes situations that a constituent automaton does not take any transition.

We will look at the discrete transition T(e) and delay transition D in detail. The elements concerning with invariants, guards and resets are marked soft. Below ${p}^{H}$ shows that p is hard while ${p}^{S}$ is p marked soft.

• 1. Discrete Transition Step :

  ${T(e)}~{=}~(~{({at}={l})}^{H}~{\wedge }~{({at'}={l'})}^{H}~{\wedge }~{(act=a)}^{H}~{\wedge }~{(g)}^{S}$

              ${\wedge }$ ${(\hat{x}'=\hat{z})}^{S}$ ${\wedge }~{(Inv({l'})(\hat{x}'))}^{S}~)$

• 2. Delay Transition Step :

  ${D}~{=}~{\exists }~{\delta }~{>}{0}~.$ $~(({\bigwedge }_{{l}{\in }{Inv(S)}}~{at}={l}{\Rightarrow }{(Inv(l)(\hat{x}'))}^{S})$

              ${\wedge }~{({at'}={at})}^{H}~{\wedge }~{(\hat{x}'=\hat{x}+{\delta })}^{H}$ ${\wedge }~{(act=delay)}^{H}$)

In addition, we mark discrete transition steps themselves soft, ${(T(e))}^{S}$. Relaxing a clause that corresponds to a discrete transition step is a situation in which we identify a particular transition to be a potential root cause. Contrarily, delay transition steps must be hard ${(D)}^{H}$, because the notion of the time elapse is essential in timed automata. If they are relaxed, the automaton looses time-dependent behavior.

Multiple Transitions. A timed automaton usually has multiple edges ${e}_{i}$ that share a common source location ${l}_{s}$; ${e}_{i}={l}_{s}{\mathop {\longrightarrow }\limits ^{{a}_{i},{g}_{i},{r}_{i}}}{{l}_{i}}$. They include an empty transition¹ as a special case; ${e}_{\epsilon }={l}_{s}{\mathop {\longrightarrow }\limits ^{{\epsilon }}}~{{l}_{i}}$. Furthermore, a timed automaton has a delay transition D at the same source location ${l}_{s}$. Some of these transitions are non-deterministic that are competing to fire at the same time. For a given location ${l}_{s}$, we introduce a set $E({l}_{s})$ to include all the edges, either discrete, delay, or empty transitions, that share the location ${l}_{s}$ as their source.

Multiple transitions make the fault localization method complicated. The consistency-based fault localization method relies on the fact that MCSes can be calculated from the unsatisfiability of ${\varphi }_{FL}$ where ${\varphi }_{EI}$ induces erroneous situations. However, if a system has multiple transitions, especially non-deterministic transitions, it can take transitions other than the one in the failing execution, and some of the paths may be successful. Consequently, ${\varphi }_{FL}$ can be satisfiable for these alternative transitions. We are unable to calculate MCSes.

The above observation implies that we cannot use full flow-sensitive trace formula, which is succeeded in the case of imperative programs [8]. Such a trace formula faithfully represents all potential execution paths and thus contains non-deterministic transitions if a similar encoding method is used for timed automata. Note that imperative programs are deterministic, and that this issue does not appear.

Sliced Transition Sequence. Given a property formula ${\varphi }_{AS}$, we first conduct a K-scoped BMC to obtain a counter-example, $c.e.~{\models }~{\varphi }_{TF}~{\wedge }~{\lnot }{\varphi }_{AS}$. The counter-example² contains a transition sequence leading to the violation of ${\varphi }_{AS}$ (${\langle }~I,~T({e}^{1}),~\ldots ,~T({e}^{K})~{\rangle }$) and the other information involving a set of delay values (${\delta }^{i}={d}^{i}$). $T({e}^{j})$ is a j-th executed instance of a transition e (${e}{\in }Edg$).

For a safety property (${{\varphi }_{safety}}$), there is an index L (${L}{\le }{K}$) such that L is a state at which ${\psi }({\hat{v}}_{j})$ violates for the first time, a minimum of such indices. For a guarantee property (${{\varphi }_{guarantee}}$), a counter-example takes a form of the lasso structure [3]. A lasso consists of a prefix sequence followed by a loop. At all the states on a lasso, the property ${\lnot }{\psi }({\hat{v}}_{j})$ is true. Therefore, L is chosen to be the length of the prefix plus the circumference of the loop part. Now, the transition sequence up to L contains enough information leading to the violation of the condition. We construct a truncated sequence up to the L state, ${I}~{\wedge }~({\bigwedge }_{j=1..L}{T({e}^{j})})$. This formula faithfully represents an executed path to the violation, which indeed defines a failing situation.

We encode the situation in the error inducing formula ${\varphi }_{EI}$ as follows. For a source location ${l}_{s}^{j}$ of each transition instance $T({e}^{j})$ appearing in a counter-example trace, we obtain $E({l}_{s}^{j})$ representing a set of transitions that share a common source location ${l}_{s}^{j}$. For each element ${e}^{i}{\in }E({l}_{s}^{j}){/}\{T({e}^{j})\}$, we introduce its Boolean encoding of transition step ${\tau }({e}^{i})$; ${\tau }({e}^{i})$ is either a discrete, delay or inactivity transition step whose source location is ${l}_{s}^{j}$. If we let $T({l}_{s}^{j})$ be a transition step fired at ${l}_{s}^{j}$, then $T({l}_{s}^{j})=T({e}^{j}){\vee }({\bigvee }_{{e}^{i}{\in }E({l}_{s}^{j})}{\tau }({e}^{i}))$. Since there is exactly one transition step at each ${l}_{s}^{j}$ (actually $T({e}^{j})$), $T({l}_{s}^{j})$ is true and ${\bigvee }_{{e}^{i}{\in }E({l}_{s}^{j})}{\tau }({e}^{i})$ is false. Therefore, $T({e}^{j})$ being true is equal to ${\bigwedge }_{{e}^{i}{\in }E({l}_{s}^{j})}{\lnot }{\tau }({e}^{i})$ being true because ${\lnot }({\bigvee }{\tau }({e}^{i})) = {\bigwedge }{\lnot }{\tau }({e}^{i})$.

We use an abbreviation such that ${T({e}^{j})}^{co}={\bigwedge }_{{e}^{i}{\in }E({l}_{s}^{j})}{\lnot }{\tau }({e}^{i})$ in order to represent the conjunction mentioned above. ${T({e}^{j})}^{co}$ is a transition step in the obtained counter-example path, but is represented in terms of steps that are not taken. We use ${T({e}^{j})}^{co}$ to represent ${\varphi }_{EI}$;

$$\begin{aligned} {\varphi }_{EI}= {\bigwedge }_{j=1..L}{T({e}^{j})}^{co}= {\bigwedge }_{j=1..L}{\bigwedge }_{{e}^{i}{\in }E({l}_{s}^{j})}{\lnot }{\tau }({e}^{i}). \end{aligned}$$

Furthermore, a set of delay values in the counter-example is a kind of input data value to induce a failing situation. We augment ${\varphi }_{EI}$ with ${\bigwedge }_{j=1..L}({\delta }^{j}={d}^{j})$. Therefore, the formula is that

$$\begin{aligned} {\varphi }_{EI}= ({\bigwedge }_{j=1..L}{\bigwedge }_{{e}^{i}{\in }E({l}_{s}^{j})}{\lnot }{\tau }({e}^{i}))~{\wedge }~({\bigwedge }_{j=1..L}({\delta }^{j}={d}^{j})) \end{aligned}$$

A whole formula ${\varphi }_{EI}{\wedge }{\varphi }_{TF}$ encodes the execution paths in the failing situation, which we call a sliced transition sequence. The sliced transition sequence is similar to the flow-insensitive trace formula for imperative programs [7]. The flow-insensitive trace formula is essentially constructed from $T({e}^{j})$, but we use ${T({e}^{j})}^{co}$. We will discuss the difference in Sect. 5 in regard to the second example case.

Fault Localization Steps. Below is whole fault localization steps.

• 1. Execute K-scope bounded model checking of ${\varphi }_{TF}{\wedge }{\lnot }{\varphi }_{AS}$.

• 2. Decide the minimum index L leading to the violation.

• 3. Construct ${\varphi }_{EI}$ from the counter-example.

• 4. Use pMaxSAT for ${\varphi }_{EI}{\wedge }{\varphi }_{TF}{\wedge }{\varphi }_{AS}$ to enumerate MCSes.

Recall that ${\varphi }_{EI}$ and ${\varphi }_{AS}$ are hard or non-relaxable by definition, and that some clauses in ${\varphi }_{TF}$ are soft or relaxable according to the assumed failure model.

5 Example Cases

As initial studies, we conducted experiments, under MacO/S 10.9.5 on 1.3 GHz Intel Core i5, using the Yices-1 solver [6], a pMaxSAT solver supporting LRA.

Fig. 1.

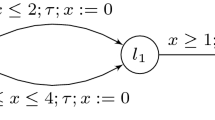
A single timed automaton (reproduced [20])

Single Timed Automaton. Figure 1 is a simple timed automaton presented in [20]. Although it is not significant, we check a safety property ${\Box }(y{\le }2)$.

• 1. We execute nine-scoped BMC of ${\varphi }_{TF}~{\wedge }~{\lnot }{\Box }(y{\le }2)$. The number of unfolding, nine, is just an initial guess. Note that ${\lnot }{\Box }(y{\le }2)={\Diamond }(y{>}{2})$. The formula is ${I}~{\wedge }~({\bigwedge }_{j=1..9}~{T}_{j})~{\wedge }~({\bigvee }_{j=1..9}~({y}_{j}~{>}~2))$.

• 2. The obtained counter-example contains a transition sequence of its length five leading to the violation. ${\ell }_{0}{\mathop {\longrightarrow }\limits ^{\delta }}{\ell }_{0}{\mathop {\longrightarrow }\limits ^{x:=0}}{\ell }_{0}$ ${\mathop {\longrightarrow }\limits ^{\delta }}{\ell }_{0}{\mathop {\longrightarrow }\limits ^{x:=0}}{\ell }_{1}$ ${\mathop {\longrightarrow }\limits ^{\delta }}{\ell }_{1}$.

• 3. The property refers to a clock variable y. The formula ${\varphi }_{EI}$ is chosen to include the encoding of delay values. Since the first, third, and fifth steps are delay transitions, a formula referring to these three ($({\delta }_{1}=1/2){\wedge }({\delta }_{3}=1/2){\wedge }({\delta }_{5}=3/2)$) is meaningful. The property ${\varphi }_{AS}$ is violated in that ${y}_{5}=5/2$, which is ${y}_{5}{>}2$.

• 4. We obtain MCSes $\{\{{\ell }_{0}{\mathop {\longrightarrow }\limits ^{x:=0}}{\ell }_{0}\},~\{{\ell }_{0}{\mathop {\longrightarrow }\limits ^{x:=0}}{\ell }_{1}\}\}$, which shows that there are two possible root causes, either ${\ell }_{0}{\mathop {\longrightarrow }\limits ^{x:=0}}{\ell }_{0}$ or ${\ell }_{0}{\mathop {\longrightarrow }\limits ^{x:=0}}{\ell }_{1}$. By using this information, we manually add, for example, a reset of clock y to the edge of the second MCS, ${\ell }_{0}{\mathop {\longrightarrow }\limits ^{x:=0;~\underline{y:=0}}}{\ell }_{1}$. The first MCS is considered as a spurious root cause. Note that the repair is not automatic, but is up to the user.

Fig. 2.

Inconsistent guards

Inconsistent Guards in Two Timed Automata. Our second example, in Fig. 2, consists of two timed automata. It is easy to see that both automata are unable to go to the state ${l}_{2}$. The system is stuck at the location pair of ${\langle }{\ell }_{1},~{\ell }_{1}{\rangle }$ ${\in }~\mathrm{Loc}^{(1)}{\times }\mathrm{Loc}^{(2)}$ because two guard conditions are not satisfiable simultaneously.

Imagine a guarantee property that ${\varphi }_{AS}={\Diamond }(({at}^{(1)}={l}_{2})~{\vee }~({at}^{(2)}={l}_{2}))$.

• 1. We execute nine-scoped BMC of ${\varphi }_{TF}{\wedge }{\lnot }{\varphi }_{AS}$. Since ${\lnot }{\varphi }_{AS}={\lnot }({\Diamond }(({at}^{(1)}={l}_{2})~{\vee }~({at}^{(2)}={l}_{2})))$ $={\Box }(({at}^{(1)}{\ne }{l}_{2})~{\wedge }~({at}^{(2)}{\ne }{l}_{2}))$, the formula is actually

      $({I}^{(1)}{\wedge }{I}^{(2)})$ ${\wedge }~{\bigwedge }_{j=1..9}~({T}_{j}^{(1)}{\wedge }{T}_{j}^{(2)})$

  ${\wedge }~({\bigwedge }_{j=1..9}~(({at}^{(1)}_{j}{\ne }{l}_{2}){\wedge }({at}^{(2)}_{j}{\ne }{l}_{2})))$ ${\wedge }~({\bigvee }_{j=0..8}~((\hat{v}^{(1)}_{9}=\hat{v}^{(1)}_{j}){\wedge }(\hat{v}^{(2)}_{9}=\hat{v}^{(2)}_{j})))$.

  where the equality $\hat{v}^{(1)}_{9}=\hat{v}^{(1)}_{j}$ stands for a conjunction of two clauses to involve the location or clock, $({at}^{(1)}_{9}={at}^{(1)}_{j}){\wedge }({x}^{(1)}_{9}={x}^{(1)}_{j})$, and $\hat{v}^{(2)}_{9}=\hat{v}^{(2)}_{j}$ is defined similarly.

• 2. The obtained counter-example contains a transition sequence of its length three leading to the violation. The loop part consists of consecutive occurrences of $\epsilon$ on ${\langle }{\ell }_{1},~{\ell }_{1}{\rangle }$.

  ${\langle }{\ell }_{0},~{\ell }_{0}{\rangle }{\mathop {\longrightarrow }\limits ^{a}}$ ${\langle }{\ell }_{1},~{\ell }_{1}{\rangle }{\mathop {\longrightarrow }\limits ^{\delta }}{\langle }{\ell }_{1},~{\ell }_{1}{\rangle }$ ${\mathop {\longrightarrow }\limits ^{\epsilon }}{\langle }{\ell }_{1},~{\ell }_{1}{\rangle }$.

• 3. The second transition step in the counter-example was delay, and its value was one. A sub-formula referring to the delay value is that ${\delta }_{2}=1$. The property to check (${\varphi }_{AS}$) is not dependent on clock variables, and thus this sub-formula (${\delta }_{2}=1$) is supposed to have no effect on the fault localization method.

• 4. We obtained MCSes consisting of one MCS element. The element consists of two transition edges, which shows that two must be repaired together. The MCSes is $\{\{{\ell }_{1}^{(1)}{\mathop {\longrightarrow }\limits ^{x>y}}~{\ell }_{2}^{(1)},~{\ell }_{1}^{(2)}{\mathop {\longrightarrow }\limits ^{y>x}}~{\ell }_{2}^{(2)}\}\}$. By using this information, we modify manually two guards, $x>y$ in the automaton ${A}^{(1)}$ and $y>x$ in the ${A}^{(2)}$. For example, we change the guard $x>y$ in the ${A}^{(1)}$ to $x{\ge }y$ and the $y>x$ in the ${A}^{(2)}$ to $y{\ge }x$, which is one possible repair.

Discussions. The first example (Fig. 1) illustrates that the fault localization problem for a timed automaton is essentially solving a set of clock constraints that are collected from a counter-example trace. Since the constraints are either invariants at locations, or guards and resets on transition edges, they are expressed in linear real arithmetic theory [1]. The property ${\varphi }_{AS}$ refers to a clock variable y, and thus ${\varphi }_{EI}$ is chosen to include a set of delay values appearing in the counter-example trace. The example indicates that the proposed repair is considered by referring to a particular counter-example involving those delay values. Therefore, it is desirable to execute the BMC again to see whether the repair works as we intend. Remember that our problem is localizing faults automatically, but is not debugging automatically.

The second example (Fig. 2) involves two timed automata that are deadlocked at particular intermediate states. The generated counter-example shows that the automata are stuck at ${\langle }{\ell }_{1},~{\ell }_{1}{\rangle }$. Although the reason for the deadlock is attributed to inconsistent guard conditions referring to clock variables, the property to check (${\varphi }_{AS}$) is ${\Diamond }(({at}^{(1)}={l}_{2}){\vee }({at}^{(2)}={l}_{2}))$ and is independent of clocks. The formula ${\varphi }_{EI}$ needs not include delay values, and thus can use only a counter-example transition sequence (${\bigwedge }_{j=1..L}{T({e}^{j})}^{co}$).

Now, we study the formula ${\varphi }_{EI}$ in detail. If we use the transitions $T({e}^{j})$ appearing directly in the counter-example such that ${\varphi }_{EI}$=${\bigwedge }_{j}T({e}^{j})$, then ${\varphi }_{EI}{\wedge }{\varphi }_{AS}$ is inconsistent regardless of ${\varphi }_{TF}$. Since the counter-example trace ends with the stuck state ${\langle }{\ell }_{1},~{\ell }_{1}{\rangle }$, the formula ${\varphi }_{EI}$ contains a sub-formula, $({at}^{(1)}_{3}={\ell }_{1}){\wedge }({at}^{(2)}_{3}={\ell }_{1})$. On the other hand ${\varphi }_{AS}$ refers to $({at}^{(1)}_{3}={\ell }_{2}){\wedge }({at}^{(2)}_{3}={\ell }_{2})$. Recall that both ${\varphi }_{EI}$ and ${\varphi }_{AS}$ are non-relaxable. The conjunction ${\varphi }_{EI}{\wedge }{\varphi }_{AS}$ is neither satisfiable nor relaxable at all. Alternatively, consider a situation where ${\varphi }_{EI}$=${\bigwedge }_{j}T({e}^{j})^{co}$= $({\bigwedge }_{j}{\bigwedge }_{{e}^{j}{\in }E({l}_{s}^{j})}{\lnot }{\tau }({e}^{j}))$. While a whole formula ${\varphi }_{EI}{\wedge }{\varphi }_{TF}{\wedge }{\varphi }_{AS}$ is unsatisfiable, some of $T({e}^{j})$ in ${\varphi }_{TF}$ can be relaxed because each $T({e}^{j})$ is itself marked soft or relaxable in our failure model. Thus, the MCSes mentioned above were obtained.

Last, enumerating MCSes is time-consuming and a scalability problem remains. We may use an efficient method implemented in [8], which adopts a technique for blocking MCSes [15].

6 Related Work

Formula-based or consistency-based fault localization methods are applied to design debugging of VLSI circuits [19, 21] or imperative programs [5, 7–9]. The method combines the model-based diagnosis [18] and Boolean satisfiability [4]. The problem is finding a diagnosis, which is MCSes when the methods use maximum satisfiability. Partial maximum satisfiability is often preferred because it allows us a way of giving a hint for the relaxation by marking clauses as either soft or hard [7–9, 21]. The precision and efficiency of finding potential root causes are dependent on the encoding of trace formulas [9]. In the application to imperative programs, the flow-insensitive trace formula [7] was proposed first. Since it is not adequate to deal with control flow bugs, in which branching conditions may be buggy, flow-sensitive trace formula is used [5]. Full flow-sensitive trace formula is equivalent to a program’s control flow graph and is the most expressive. It is shown successful in finding multiple faults in a program [8].

In the applications to VLSI circuits and imperative programs, the trace formulas are deterministic in that an execution path is unique when we determine the input values completely. Timed automata have non-deterministic transitions [1]. Especially, discrete transitions and a delay transition is taken non-deterministically. This fact makes the fault localization problem complicated. Our approach in this paper is to use a sliced transition trace formula. It is similar to the flow-insensitive trace formula [7], but is different in that we use ${T(e)}^{co}$ but not T(e) directly. ${T(e)}^{co}$ encodes a counter-example transition sequence by excluding all the transitions that are not taken. This encoding method is essential in localizing faults for deadlock cases as shown in the second example. Note that an accompanying paper [17] discusses cases for power consumption automata (PCAs) [16], in which PCAs are assumed to be deterministic weighted timed automata, and thus simplifies the fault localization problem.

7 Concluding Remarks

We reported a consitency-based fault localization method for timed automata using the partial maximum satisfiability. This work is still preliminary in that further study is needed for large example cases. It calls for an efficient algorithm to enumerate MCSes to counter the scalability problem (cf. [8, 13, 15]). There are also other important directions. First, the properties are extended from safety and bounded reachability to a wide class of LTL formulas. Second, introducing the proposed method to industrial strength tools such as UPPAAL [10] would be interesting in view of practice.