Multilateral Resistance and the Euro Effects on Trade Flows

Abstract

Recently, an investigation of unobserved and time-varying multilateral resistance and omitted trade determinants has assumed a prominent role in order to precisely measure the Euro effects on trade. We implement two methodologies: the factor-based gravity model by Serlenga and Shin (The Euro Effect on Intra-EU Trade: Evidence from the Cross Sectionally Dependent Panel Gravity Models, Mimeo, University of York, 2013) and the spatial-based techniques by Behrens et al. (J Appl Econ 27:773–794, 2012), both of which allow trade flows and error terms to be cross-sectionally correlated. Applying these approaches to the dataset over 1960–2008 for 190 country-pairs of 14 EU and six non-EU OECD countries, we find that the Euro impact estimated by the factor-based model amounts to only 4–5 %, far less than the 20 % estimated by the spatial-based model. The cross-section dependency test results also confirm that the factor-based model is more appropriate in accommodating correlation between regressors, and unobserved individual and time effects. Overall we may conclude that the trade-creating effects of the Euro should be viewed in the proper historical and multilateral perspective rather than in terms of the formation of a monetary union as an isolated event.

1 Introduction

With the formation of the Euro in 1999, the literature on the common currency effects on trade has been rapidly growing. By eliminating exchange rate volatility and reducing the costs of trade, a currency union is expected to boost trade among member countries. An important policy issue is identifying the right magnitude and the nature of the Euro’s trade impact, which is not only important for member countries but also for EU members that have not joined yet. Baldwin (2006) provides an extensive survey, establishing that the infamous Rose effect is severely (upward) biased. As an earlier evaluation of the Euro effect, Micco et al. (2003) find that the common currency increases trade among Euro zone members by 4 % in the short-run and 16 % in the long-run. See also de Nardis and Vicarelli (2003), Flam and Nordström (2006), and Berger and Nitsch (2008), from which we find that the estimated Euro effects are very wide from 2 % to over 70 %.

However, most of existing studies make an implicit assumption, which does not hold in practice, that bilateral trade flows are independent of the rest of the trading world. Anderson and van Wincoop (2003) highlight an importance of controlling for the regional interaction structure in estimating gravity equation systems. They propose including multilateral resistance terms that capture the fact that bilateral trade flows depend on bilateral barriers as well as trade barriers across all trading partners. Acknowledging such an important issue, an investigation of unobserved multilateral resistance terms together with omitted trade determinants has assumed a prominent role in measuring the Euro’s trade effects (Baldwin 2006; Baldwin and Taglioni 2006).

To address this important issue of how best to model (unobserved and time-varying) multilateral resistance and bilateral heterogeneity, simultaneously, in this paper, we implement two recently proposed methodologies: the factor-based approach proposed by Serlenga and Shin (2013, hereafter SS) and the spatial-based techniques developed by Behrens et al. (2012, hereafter BEK). The first approach extends the cross-sectionally dependent panel gravity models advanced by Serlenga and Shin (2007) and Baltagi (2010), which can control for time-varying multilateral resistance and trade costs through using both observed and unobserved factors with heterogenous loadings. The spatial model by BEK is derived from a structural gravity equation, and it allows both trade flows and error terms to be cross-sectionally correlated with the spatial weight matrix derived directly from economic theory. Chudik et al. (2011) show that the factor-based models account for strong cross section dependence while the spatial-based model addresses weak dependence. Following SS, we combine these estimators with the instrument variables estimators advanced by Hausman and Taylor (1981), Amemiya and McCurdy (1986), and Breusch et al. (1989), and develop a methodology which allows us to consistently estimate the impacts of (potentially endogenous) bilateral resistance barriers such as border and language effects.

We apply these methodologies to the dataset over 1960–2008 for 190 country-pairs. This is an extended dataset analysed by SS by enlarging the control group. Though the Euro-area economies have become more integrated with a trade boost within the region, this positive currency-union effect can be greatly mitigated by multilateral trade costs associated with the larger control group of non-Euro countries. This may help us to better disentangle the effect of the Euro on trade within and outside currency union by introducing a substitutability between intra-EU and extra-EU trade flows (Anderson and van Wincoop 2003, 2004).

Our main empirical findings are summarized as follows: First, when we control for time-varying multilateral resistance and trade costs through cross-sectionally correlated unobserved factors, we find that the Euro impact on trade amounts to 4–5 %. This magnitude is generally consistent with comprehensive evidence compiled by Baldwin (2006). We also find that the custom union effect is substantially reduced to 11 %. Next, we find that the impacts of the Euro and the custom union on trades are estimated at about 20 % and 30 %, respectively, under the spatial-based SARAR models. These magnitudes are substantially larger than those obtained under the factor-based models, but rather close to the values estimated under the basic model without controlling for cross-section dependence. Furthermore, when applying the cross-section dependency (CD) test advanced by Pesaran (2004), we find that the null of no cross-sectional dependence is strongly rejected for all of the spatial-based gravity models. Therefore, we may conclude that trade flows are likely to be better modelled by allowing for a strong form of cross section dependence rather than weak dependence.

Finally, we investigate another important issue of the Euro effect on trade integration by estimating time-varying coefficients of bilateral resistance terms, and find that border and language effects declined more sharply after the introduction of the Euro in 1999. The implication of these findings is that the Euro helps to reduce trade effects of bilateral resistance and to promote the EU integration. On the other hand, distance impacts have been rather stable, showing no pattern of downward trending. This generally supports broad empirical evidence that the notion of the death of distance is difficult to identify in current trade data (Disdier and Head 2008; Jacks 2009).

The paper is organised as follows: Sect. 12.2 provides a brief literature review on the Euro’s Trade Effects. Section 12.3 describes two alternative cross-sectionally dependent panel gravity models. Section 12.4 presents main empirical findings. Section 12.5 concludes.

2 Literature Review

Recently, there has been an intense policy debate on the effects of the Euro on trade flows. Rose (2000) was the first to introduce common currency variables in the gravity model, and documented evidence that countries in a currency union trade three times as much, using the data for 186 countries over the period, 1970–1990. It is widely acknowledged that Rose’s huge estimate of the currency union effect on trade is severely (upward) biased. In particular, his estimates are heavily inflated by the presence of very small countries (Frankel 2008). Thus, whether one can uncover similar findings for the European monetary union with the substantially large economies, is an important policy issue.

The main critiques against Rose’s (2000) original gravity approach are classified as follows: inverse causality or endogeneity, missing or omitted variables, and incorrect model specification (nonlinearity or threshold effects). Once these methodological issues have been appropriately addressed, the currency union effects appear to be far less than those estimated earlier by Rose and others. Baldwin (2006) presents an extensive survey, highlighting that recent studies report relatively smaller trade effects of the Euro. See also Micco et al. (2003), de Nardis and Vicarelli (2003), Flam and Nordström (2006) and Berger and Nitsch (2008).

Another important issue is the omitted variables bias. Omitted pro-bilateral trade variables are likely to be correlated with the currency union dummy, as the formation of currency unions is driven by factors which are omitted from the gravity specification. If so, the Euro effect may capture general economic integration among the member states, not merely the currency impact. Anderson and van Wincoop (2003) develop the micro foundation of the gravity equation by introducing the multilateral resistance terms, which are bilateral trade barriers relative to average trade barriers that both countries face with all of their trading partners. In this regard, the gravity model produces seriously misleading results, if multilateral resistance terms and trade costs are neglected. Baldwin (2006) also stresses an importance of taking into account time-varying multilateral resistance terms such as trade costs (Anderson and van Wincoop 2004), and criticises against the use of the fixed effect estimation as it may still leave a times-series trace in the residuals, which is likely to be correlated with the currency union dummy.¹

In retrospect, a large number of existing studies have already highlighted an importance of taking into account unobserved and time-varying multilateral resistance and bilateral heterogeneity, simultaneously. This raises an immediate important issue of controlling for cross section dependence or correlation among trade flows in a coherent manner. Only recently, a small number of studies have begun to explicitly address this issue, e.g., Serlenga and Shin (2007, 2013), Herwartz and Weber (2010), Behrens et al. (2012), and Camaero et al. (2012).

SS follow recent developments in panel data studies (Pesaran 2006; Bai 2009), and extend the cross-sectionally dependent panel gravity models advanced by Serlenga and Shin (2007). The desirable feature of this approach is to control for time-varying multilateral resistance, trade costs and globalisation trends explicitly through the use of both observed and unobserved factors, which are modelled as (strong) cross-sectionally correlated. Applying the proposed model to the dataset over the period 1960–2008 for 91 country-pairs amongst 14 EU member countries, SS find that the Euro’s trade effect amounts to 3–4 %, even after controlling for trade diversion effects, and conclude that these small effects of currency union provide a support for the hypothesis that the trade increase within the Euro area may reflect a continuation of a long-run historical trend of economic integrations in the EU (e.g. Berger and Nitsch 2008).

Alternatively, BEK propose the modified spatial techniques by adopting a broader definition of the spatial weight matrix, which can be derived directly from the theoretical structural gravity model. By capturing (cross-sectionally correlated) multilateral resistance through the spatial effects, they find that the measured Canada-US border effects are significantly lower than paradoxically large estimates reported by McCallum (1995). Thus, in an analysis of the trade-creation effects of a single currency, it is important to specify an estimation procedure that account for distribution of data in space. The spatial dependence may arise due to the so-called third country (neighbour) effects, which is increasingly playing a central role in examining the spatial dependence structure in the closely linked literature on foreign direct investment and multinational enterprises, e.g., Baltagi et al. (2007, 2008), Blonigen et al. (2007), and Hall and Petroulas (2008), and Camaero et al. (2012).

3 Cross Sectionally Dependent Panel Gravity Models

All of the discussions in Sect. 12.2 suggest that a Euro effect on trade flows be carefully examined under the appropriate econometric framework that is expected to deal with time-varying and cross-sectionally correlated multilateral resistance terms in a robust manner.² In what follows, we will describe two alternative approaches to the panel gravity model of the trade flows: the spatial-based techniques developed by BEK and the factor-based approach proposed by SS.

We first consider a factor-based panel data model as follows:

$$\displaystyle{ y_{it} =\boldsymbol{\beta } ^{{\prime}}\mathbf{x}_{ it} +\boldsymbol{\gamma } ^{{\prime}}\mathbf{z}_{ i} +\boldsymbol{\pi }_{ i}^{{\prime}}\mathbf{s}_{ t} +\varepsilon _{it},\;i = 1,\ldots,N,\;t = 1,\ldots,T, }$$

(12.1)

$$\displaystyle{ \varepsilon _{it} =\alpha _{i} +\boldsymbol{\varphi }_{ i}^{{\prime}}\boldsymbol{\theta }_{ t} + u_{it}, }$$

(12.2)

where $\mathbf{x}_{it} = \left (x_{1,it},\ldots,x_{k,it}\right )^{{\prime}}$ is a k × 1 vector of variables that vary across individuals and over time periods, $\mathbf{s}_{t} = \left (s_{1,t},\ldots,s_{s,t}\right )^{{\prime}}$ is an s × 1 vector of observed factors, $\mathbf{z}_{i} = \left (z_{1,i},\ldots,z_{g,i}\right )^{{\prime}}$ is a g × 1 vector of individual-specific variables, $\boldsymbol{\beta }= \left (\beta _{1},\ldots,\beta _{k}\right )^{{\prime}}$, $\boldsymbol{\gamma }= \left (\gamma _{1},\ldots,\gamma _{g}\right )^{{\prime}}$ and $\boldsymbol{\pi }_{i} = \left (\pi _{1,i},\ldots,\pi _{s,i}\right )^{{\prime}}$ are the associated column vectors of parameters, α _i is an individual effect that might be correlated with regressors, x _it and z _i , $\boldsymbol{\theta }_{t}$ is the c × 1 vector of unobserved common factors with the loading vector, $\boldsymbol{\varphi }_{i} = \left (\varphi _{1,i},\ldots,\varphi _{c,i}\right )^{{\prime}}$, and u _it is a zero mean idiosyncratic disturbance with constant variance. Notice that the cross-section dependence in (12.1) is explicitly allowed through heterogeneous loadings, $\boldsymbol{\varphi }_{i}$. Chudik et al. (2011) show that these factor models exhibit the strong form of cross section dependence (hereafter, CSD) since the maximum eigenvalue of the covariance matrix for ɛ _it tends to infinity at rate N.³ We thus expect that this factor-based panel gravity model will capture the time-varying pattern of unobserved multilateral resistance effects in a robust manner.

To avoid the potential biases associated with the cross-sectionally dependent factor structure, (12.2), SS propose using two leading approaches developed by Pesaran (2006) and Bai (2009). Hence, we consider the following cross-sectionally augmented regression of (12.1):

$$\displaystyle{ y_{it} =\boldsymbol{\beta } ^{{\prime}}\mathbf{x}_{ it} +\boldsymbol{\gamma } ^{{\prime}}\mathbf{z}_{ i} +\boldsymbol{\lambda }_{ i}^{{\prime}}\mathbf{f}_{ t} +\tilde{\alpha } _{i} +\tilde{ u}_{it}^{},\;i = 1,\ldots,N,\;t = 1,\ldots,T, }$$

(12.3)

where $\mathbf{f}_{t} = \left (\mathbf{s}_{t}^{{\prime}},\bar{y}_{t},\mathbf{\bar{x}}_{t}^{{\prime}}\right )^{{\prime}}\left \{= \left (\,f_{1,t},\ldots,f_{\ell,t}\right )^{{\prime}}\right \}$ is the ℓ × 1 vector of augmented factors with $\ell= s + 1 + k$ and $\boldsymbol{\lambda }_{i} = \left (\lambda _{1,i},\ldots,\lambda _{\ell,i}\right )^{{\prime}}$ , $\bar{y}_{t} = N^{-1}\mathop{ \sum }_{ i=1}^{N}y_{it}$, $\mathbf{\bar{x}}_{t} = N^{-1}\mathop{ \sum }_{ i=1}^{N}\mathbf{x}_{it}$, $\boldsymbol{\lambda }_{i}^{{\prime}} = \left (\boldsymbol{\pi }_{i}^{{\prime}}-\left (\varphi _{i}/\bar{\varphi }\right )\boldsymbol{\bar{\pi }}^{{\prime}}\mathbf{,}\left (\varphi _{i}/\bar{\varphi }\right ),-\left (\varphi _{i}/\bar{\varphi }\right )\boldsymbol{\beta }^{{\prime}}\right )^{{\prime}}$ with $\bar{\varphi }= N^{-1}\mathop{ \sum }_{ i=1}^{N}\varphi _{i}$ and $\boldsymbol{\bar{\pi }}= N^{-1}\mathop{ \sum }_{ i=1}^{N}\boldsymbol{\pi }_{i}$, $\tilde{\alpha }_{i} =\alpha _{i} -\left (\varphi _{i}/\bar{\varphi }\right )\bar{\alpha } -\left (\varphi _{i}/\bar{\varphi }\right )\boldsymbol{\gamma }^{{\prime}}\mathbf{\bar{z}}$ with $\bar{\alpha }= N^{-1}\mathop{ \sum }_{ i=1}^{N}\alpha _{i}$ and $\mathbf{\bar{z}} = N^{-1}\mathop{ \sum }_{ i=1}^{N}\mathbf{z}_{i}$, and $\tilde{u}_{it} = u_{it} -\left (\varphi _{i}/\bar{\varphi }\right )\bar{u}_{t}$ with $\bar{u}_{t} = N^{-1}\mathop{ \sum }_{ i=1}^{N}u_{it}$. Using (12.3), we can derive Pesaran’s Pooled Common Correlated Effects (PCCE) estimator of $\boldsymbol{\beta }$ by (12.4) below. Alternatively, we can estimate $\boldsymbol{\beta }$ consistently by Bai’s (2009) principal component (PC) estimator in which case the cross section averages are replaced by the estimated factors $\left (\boldsymbol{\hat{\theta }}_{t}\right )$ such that $\mathbf{f}_{t} = \left (\mathbf{s}_{t}^{{\prime}},\boldsymbol{\hat{\theta }}_{t}^{{\prime}}\right )^{{\prime}}$.⁴ Thus, we obtain the CSD-consistent estimator of $\boldsymbol{\beta }$ by

$$\displaystyle{ \boldsymbol{\hat{\beta }}_{CSD} = \left (\mathop{\sum }_{i=1}^{N}\mathbf{x}_{ i}^{{\prime}}\mathbf{M}_{ T}\mathbf{x}_{i}\right )^{-1}\left (\mathop{\sum }_{ i=1}^{N}\mathbf{x}_{ i}^{{\prime}}\mathbf{M}_{ T}\mathbf{y}_{i}\right ),\ \boldsymbol{\hat{\beta }}_{CSD} =\boldsymbol{\hat{\beta }} _{PCCE}\ or\ \boldsymbol{\hat{\beta }}_{PC} }$$

(12.4)

where $\mathbf{y}_{i} = \left (\,y_{i1},\ldots,y_{iT}\right )^{{\prime}}$, $\mathbf{x}_{i} = \left (\mathbf{x}_{i1},\ldots,\mathbf{x}_{iT}\right )^{{\prime}}$, $\mathbf{M}_{T} = \mathbf{I}_{T} -\mathbf{H}_{T}\left (\mathbf{H}_{T}^{{\prime}}\mathbf{H}_{T}\right )^{-1}\mathbf{H}_{T}^{{\prime}}$, $\mathbf{H}_{T} = \left (\mathbf{1}_{T},\mathbf{f}\right )$, $\mathbf{1}_{T} = \left (1,\ldots,1\right )^{{\prime}}$ and $\mathbf{f} = \left (\mathbf{f}_{1}^{{\prime}},\ldots,\mathbf{f}_{T}^{{\prime}}\right )^{{\prime}}$.

Alternatively, we will investigate the issue of CSD among trade flows by employing spatial techniques. This approach assumes that the structure of cross section correlation is related to the location and the distance among units on the basis of a pre-specified weight matrix.⁵ Hence, cross section correlation is represented mainly by means of a spatial process, which explicitly relates each unit to its neighbours. A number of approaches for modeling spatial dependence have been suggested in the spatial literature. The most popular ones are the Spatial Autoregressive (SAR), the Spatial Moving Average (SMA), and the Spatial Error Component (SEC) specifications. The spatial panel data model is estimated using the maximum likelihood (ML) or the generalized method of moments (GMM) techniques (e.g., Elhorst 2011). We follow BEK and consider a spatial panel data gravity (SARAR) model, which combines a spatial lagged variable and a spatial autoregressive error term:

$$\displaystyle{ y_{it} =\rho y_{it}^{{\ast}} +\boldsymbol{\beta } ^{{\prime}}\mathbf{x}_{ it} +\boldsymbol{\gamma } ^{{\prime}}\mathbf{z}_{ i} +\tilde{\alpha } _{i} + v_{it},\;i = 1,\ldots,N,\;t = 1,\ldots,T, }$$

(12.5)

$$\displaystyle{ v_{it} =\lambda v_{it}^{{\ast}} + u_{ it} }$$

(12.6)

where $y_{it }^{{\ast} } =\sum _{ j\not = i }^{N }w_{ij } y_{jt }$ is the spatial lagged variable, and $v_{it}^{{\ast}} =\sum _{ j\not =i}^{N}w_{ij}v_{jt}$ is the spatial autoregressive error term, w _ij ’s are the spatial weight with the row-sum normalisation, ∑ _i w _ij  = 1, and u _it is a zero mean idiosyncratic disturbance with constant variance. This approach is especially designed to deal with CSD across both variables and error terms in which ρ is the spatial lag coefficient and λ refers to the spatial error component coefficient. These coefficients capture the spatial spillover effects and measure the influence of the weighted average of neighboring observations on cross section units. Chudik et al. (2011) show that a particular form of a weak cross dependent process arises when pairwise correlations take non-zero values only across finite units that do not spread widely as the sample size rises. A similar case occurs in the spatial processes, where the local dependency exists only among adjacent observations. In particular, Pesaran and Tosetti (2011) show that spatial processes commonly used, such as the SAR or the SMA process, can be represented by a process with an infinite number of weak factors and no idiosyncratic error terms.

Both the factor- and the spatial-based models cannot estimate the coefficients, $\boldsymbol{\gamma }$ on time-invariant variables in the presence of fixed effects. In this regard, we follow SS and combine these estimators with the instrumental variables estimation proposed by Hausman and Taylor (1981, HT), Amemiya and McCurdy (1986, AM), and Breusch et al. (1989, BMS). We denote such estimators by the PCCE-HT, PCCE-AM, PCCE-BMS, PC-HT, PC-AM, PC-BMS, SARAR-HT, SARAR-AM, and SARAR-BMS estimators, respectively.

We now decompose $\mathbf{x}_{it} = \left (\mathbf{x}_{1it}^{{\prime}},\mathbf{x}_{2it}^{{\prime}}\right )^{{\prime}}$ and $\mathbf{z}_{i} = \left (\mathbf{z}_{1i}^{{\prime}},\mathbf{z}_{2i}^{{\prime}}\right )^{{\prime}}$, where x _1it , x _2it are k ₁ × 1 and k ₂ × 1 vectors, and z _1i , z _2i are g ₁ × 1 and g ₂ × 1 vectors. Then, we estimate $\boldsymbol{\gamma }$ consistently using instrumental variables in the following regression:

$$\displaystyle{ d_{it} =\boldsymbol{\gamma }_{ 1}^{{\prime}}\mathbf{z}_{ 1i} +\boldsymbol{\gamma }_{ 2}^{{\prime}}\mathbf{z}_{ 2i} +\tilde{\alpha } _{i} +\tilde{ u}_{it} =\mu +\boldsymbol{\gamma }^{{\prime}}\mathbf{z}_{ i} + e_{it},\;i = 1,\ldots,N,\;t = 1,\ldots,T.\quad }$$

(12.7)

We construct d _it as follows, for the factor models, we obtain

$$\displaystyle{ d_{it} = y_{it} -\boldsymbol{\beta }^{{\prime}}\mathbf{x}_{ it} -\boldsymbol{\lambda }_{i}^{{\prime}}\mathbf{f}_{ t}, }$$

where $\mu = E\left (\tilde{\alpha }_{i}\right )$, and $e_{it} = \left (\tilde{\alpha }_{i}-\mu \right ) +\tilde{ u}_{it}$ is a zero mean process. Next, for the spatial-based model, we have

$$\displaystyle{ d_{it} = y_{it} -\rho y_{it}^{{\ast}}-\boldsymbol{\beta }^{{\prime}}\mathbf{x}_{ it}, }$$

where $\mu = E\left (\tilde{\alpha }_{i}\right )$, and $e_{it} = \left (\tilde{\alpha }_{i}-\mu \right ) + v_{it}$ is a zero mean process. In matrix notation, we have:

$$\displaystyle{ \mathbf{d} =\mu \mathbf{1}_{NT} + \mathbf{Z}_{1}\boldsymbol{\gamma }_{1} + \mathbf{Z}_{2}\boldsymbol{\gamma }_{2} + \mathbf{e}, }$$

(12.8)

where $\mathbf{d} =\big (\mathbf{d}_{1}^{{\prime}},\ldots,\mathbf{d}_{N}^{{\prime}}\big)^{{\prime}}$, $\mathbf{d}_{i} =\big (d_{i1},\ldots,d_{iT}\big)^{{\prime}}$, $\mathbf{Z}_{j} =\big (\big(\mathbf{z}_{j1}^{{\prime}}\otimes \mathbf{1}_{T}\big)^{{\prime}},\ldots,\big(\mathbf{z}_{jN}^{{\prime}}\otimes \mathbf{1}_{T}\big)^{{\prime}}\big)^{{\prime}}$, j = 1, 2, $\mathbf{1}_{NT} =\big (\mathbf{1}_{T}^{{\prime}},\ldots,\mathbf{1}_{T}^{{\prime}}\big)^{{\prime}}$, $\mathbf{1}_{T} =\big (1,\ldots,1\big)^{{\prime}}$, and $\mathbf{e} =\big (\mathbf{e}_{1}^{^{{\prime}} },\ldots,\mathbf{e}_{N}^{^{{\prime}} }\big)^{{\prime}}$ with $\mathbf{e}_{i} =\big (e_{i1},\ldots,e_{iT}\big)^{{\prime}}$. Replacing d by its consistent estimate, $\mathbf{\hat{d}} =\big\{ \hat{d} _{it},i = 1,\ldots,N,t = 1,\ldots,T\big\}$:⁶

$$\displaystyle{ \mathbf{\hat{d} } =\mu \mathbf{1}_{NT} + \mathbf{Z}_{1}\boldsymbol{\gamma }_{1} + \mathbf{Z}_{2}\boldsymbol{\gamma }_{2} + \mathbf{e}^{\dag } = \mathbf{C}\boldsymbol{\delta } + \mathbf{e}^{\dag }\mathbf{,} }$$

(12.9)

where $\mathbf{e}^{\dag } = \mathbf{e+}\left (\mathbf{\hat{d} }-\mathbf{d}\right )$, $\mathbf{C} = \left (\mathbf{1}_{NT},\mathbf{Z}_{1},\mathbf{Z}_{2}\right )$ and $\boldsymbol{\delta }= \left (\mu,\boldsymbol{\gamma }_{1}^{{\prime}},\boldsymbol{\gamma }_{2}^{{\prime}}\right )^{{\prime}}$.

To deal with nonzero correlation between Z ₂ and $\boldsymbol{\alpha }$, we should find the $NT \times \left (1 + g_{1} + h\right )$ matrix of instrument variables:

$$\displaystyle{ \mathbf{W} = \left [\mathbf{1}_{NT},\mathbf{Z}_{1},\mathbf{W}_{2}\right ], }$$

where W ₂ is an NT × h matrix of instrument variables for Z ₂ with h ≥ g ₂ for identification. To this end, we follow SS and obtain the $NT \times \left (k_{1}+\ell\right )$ HT, the $NT \times \left (k_{1} +\ell +Tk_{1} + T\ell\right )$ AM and the $NT \times \left (k_{1} +\ell +Tk_{1} + T\ell + Tk_{2}\right )$ BMS instrument matrices as: $\mathbf{W}_{2}^{HT} = \left [\mathbf{PX}_{1},\mathbf{P\hat{\boldsymbol{\xi }}}_{1},\ldots,\mathbf{P\hat{\boldsymbol{\xi }}}_{\ell}\right ]$, $\mathbf{W}_{2}^{AM} = \left [\mathbf{W}_{2}^{HT},\left (\mathbf{QX}_{1}\right )^{\dag },\left (\mathbf{Q\hat{\boldsymbol{\xi }}}_{1}\right )^{\dag },\ldots,\right.$ $\left.\left (\mathbf{Q\hat{\boldsymbol{\xi }}}_{\ell}\right )^{\dag }\right ]$, and $\mathbf{W}_{2}^{BMS} = \left [\mathbf{W}_{2}^{AM},\left (\mathbf{QX}_{2}\right )^{\dag }\right ]$, where $\mathbf{P} = \mathbf{D}(\mathbf{D}^{{\prime}}\mathbf{D})^{-1}\mathbf{D}^{{\prime}}$ is the NT × NT idempotent matrix, D = I _N ⊗1 _T , I _N is an N × N identity matrix, $\boldsymbol{\hat{\xi }}_{j} = \left (\hat{\lambda }_{j,1}\mathbf{f}_{j}^{{\prime}},\ldots,\hat{\lambda }_{j,N}\mathbf{f}_{j}^{{\prime}}\right )^{{\prime}}$, j = 1, …, ℓ, where $\mathbf{f}_{j} = \left (\,f_{j,1},\ldots,f_{j,T}\right )^{{\prime}}$ with $\hat{\lambda }_{j,i}$ being consistent estimate of heterogenous factor loading, λ _j, i , $\mathbf{Q} = \mathbf{I}_{NT} -\mathbf{P}$, $\left (\mathbf{QX}_{1}\right )^{\dag } = \left (\mathbf{QX}_{11},\mathbf{QX}_{12},\ldots,\mathbf{QX}_{1T}\right )$ is the NT × k ₁ T matrix with $\mathbf{QX}_{1t} = \left (\mathbf{QX}_{11t},\ldots,\mathbf{QX}_{1kt}\right )^{{\prime}}$, and $\left (\mathbf{QX}_{2}\right ) = \left (\mathbf{QX}_{21},,\ldots,\mathbf{QX}_{2T}\right )$.

To derive the consistent estimator of $\boldsymbol{\delta }$, we premultiply W ^′ by (12.9)

$$\displaystyle{ \mathbf{W^{{\prime}}\hat{d} } = \mathbf{W^{{\prime}}C\boldsymbol{\delta } + W^{{\prime}}\boldsymbol{\varepsilon }}^{+}. }$$

(12.10)

Therefore, the GLS estimator of $\boldsymbol{\delta }$ is obtained by

$$\displaystyle{ \boldsymbol{\hat{\delta }}_{GLS} = \left [\mathbf{C}^{{\prime}}\mathbf{WV}^{-1}\mathbf{W}^{{\prime}}\mathbf{C}\right ]^{-1}\mathbf{C}^{{\prime}}\mathbf{WV}^{-1}\mathbf{W}^{^{{\prime}} }\mathbf{\hat{d},} }$$

(12.11)

where $\mathbf{V} = V ar\left (\mathbf{W}^{{\prime}}\mathbf{e}^{\dag }\right )$. We obtain the feasible GLS estimator by replacing V by its consistent estimator. In practice, estimates of $\boldsymbol{\delta }$ and V can be obtained iteratively until convergence. The HT-IV estimator employs only the mean of X ₁ to be uncorrelated with the effects whereas the AM-IV estimator exploits such moment conditions to be held at every time period. Hence, the AM instruments requires the stronger exogeneity assumption for X ₁, under which the AM-IV estimator is more efficient. Furthermore, the BMS instruments require uncorrelatedness of X ₂ with fixed effects separately at every point in time. The validity of AM and BMS instruments can be easily tested using the Hausman statistics testing for the difference between HT-IV and AM-IV and between AM-IV and BMS-IV, both of which follow the asymptotic χ _g ² null-distribution with the degree of freedom g, being the number of coefficients tested, see SS for details.

4 Empirical Results

We extend the dataset analysed by Serlenga and Shin (2007, 2013) to cover the longer period 1960–2008 (49 years) for 190 country-pairs amongst 14 EU member countries (Austria, Belgium-Luxemburg, Denmark, Finland, France, Germany, Greece, Ireland, Italy, Netherlands, Portugal, Spain, Sweden, the United Kingdom) plus six OECD member countries (Australia, Canada, Japan, Norway, Switzerland and the US). By considering the larger control group of countries that do not belong to the currency union, we can check for the robustness of the previous empirical results reported in SS. These additional countries constitute the meaningful control group such that we can better identify the trade effect of currency union within and outside the Euro area by introducing substitutability between them (Anderson and van Wincoop 2003, 2004). The US is still the leading trade partner of the EU, though its role has recently been challenged by China and Russia. Norway and Switzerland constitute a coherent control group since these non-member countries share with similar historical ties to the Euro-area countries and experience similar legislation and regulation. Australia, Japan and Canada also belong to the large global traders.

Our sample period consists of many important economic integrations such as the Custom Union in 1958, the European Monetary System in 1979 and the Single Market in 1993.⁷ Given that the Euro effect should be analysed as an ongoing process (Berger and Nitsch 2008), we will examine the Euro’s trading effect more carefully by applying the two alternative cross-sectionally correlated panel data gravity models described in Sect. 12.3.

We first estimate the panel data model of gravity, (12.1) and (12.2). First, we consider the basic model without unobserved time-varying factors in order to facilitate the comparison with most of existing studies. Secondly, we consider the factor-based model with both unobserved time-varying factors, φ _i θ _t , and linear time trends, $s_{t} = \left \{t\right \}$, as a single observed factor. Following Serlenga and Shin (2007), we focus on the augmented gravity model specification in which trade flows depend on (1) gravity determinants (countries’ economic mass and geographical distance); (2) time-varying covariates such as bilateral real exchange rates, free trade agreements and common currency union; and (3) time-invariant dummies that proxy common language and common border. Finally, in line with the New Trade Theory (e.g., Krugman, 1979; Helpman, 1987), we add two more variables: relative factor endowment and similarity in size. See the Data Appendix for more details with a priori expectations about the signs of their impacts on trade flows

Table 12.1 Estimation results for the panel gravity model without cross-section dependence

Table 12.1 presents the estimation results for the basic model with individual effects only, using the alternative estimation methodologies. The random effects model (REM) assumption that there is no correlation between regressors and individual effects is convincingly rejected in all cases considered. Therefore, we focus on the fixed effects model (FEM) results. The FEM estimation results are all statistically significant and consistent with our a priori expectations. The impact of GDP (the sum of home and foreign country GDPs) on trade is positive. The impact of relative difference in factor endowments between trading partners (RLF) is significant and positive whilst similarity in size (SIM) boosts trade flows significantly. A depreciation of the home currency (increase in RER) increases trade flows as the export component of the total trade is larger than the import. Importantly, we find that trade and currency union memberships (CEE and EMU) significantly boost trade flows, but their magnitudes appear to be substantial at 0.39 and 0.21. This finding confirms our main concern that upward trends in omitted trade determinants may cause them to be upward-biased.⁸ We now turn to the estimated impacts of individual-specific bilateral trade barriers. Under the maintained assumption that LAN is the only variable correlated with individual effects (as a proxy for cultural and historical proximity), we select the final set of instruments containing RER and RLF, after conducting a sequence of the Sargan tests for the validity of over-identifying restrictions. As the Hausman test does not reject the legitimacy of the AM-IV estimates, we focus on more efficient AM results, and find that impacts of DIS and LAN are significant ( − 0. 81 and 0.73) while the border impact is insignificant and negligible.

Table 12.2 Estimation results for the panel gravity model with cross section dependence and heterogeneous trends

Given that (unobserved) multilateral resistance terms and trade costs are likely to exhibit history and time dependence in a complex manner (e.g. Herwartz and Weber 2010), we turn to the factor-based panel gravity models proposed by SS. In Table 12.2, we report two consistent estimators, the PCCE and PC.⁹ The stylised findings are summarised as follows: First, the impact of RLF becomes significant and negative,¹⁰ confirming our expectations that its impact on total trade flows (the sum of inter- and intra-industry trades) may not necessarily be unambiguous (e.g. Helpman and Krugman 1985). Secondly, similarity turns out to have a larger effect. Combined together, the intra-industry trade appears to have been the main part of the total EU trade.¹¹ More importantly, the impacts of CEE and EMU are substantially smaller albeit still significant. The CEE impact falls to 0.114 and 0.117 for PCCE and PC estimators while the Euro impact drops sharply to 0.039 and 0.048 for PCCE and PC. Turing to HT-IV and AM-IV estimates of the impacts of time-invariant regressors,¹² we find that the impacts of distance dummy and language dummy are significantly negative and positive whilst the border impact is still insignificant, a finding consistent with SS. Furthermore, the Hausman test does not reject the hypothesis that the AM-IV estimates are more efficient.

Similar to the results reported in SS for a smaller EU dataset, we also confirm that both the PCCE and the PC estimation results are remarkably similar. First, the coefficient of TGDP converges at around 2.¹³ Secondly, both the Euro and the CEE impacts are significant but considerably smaller (around 0.04 and 0.11) than those reported in Table 12.2 without considering time-varying unobserved factors. This is generally consistent with the predictions of most recent studies and survey evidence (Baldwin 2006) as reviewed in Sect. 2. Finally, focussing on efficient AM-IV estimates, we find that distance and common language dummies exert significantly negative and positive impacts on trade. But, the border impact appears to be insignificant.

Table 12.3 Estimation results for the panel gravity SARAR model with W = Pop and W = Trade

Table 12.4 Estimation results for the panel gravity SARAR model with W = Border and W = Distance

Tables 12.3 and 12.4 display the estimation results for SARAR models with endogenous interaction effects among the dependent variables (spatial lag effects) and the interaction effects among the disturbance terms (spatial error component effects). To examine the robustness of the estimation results, we consider four different spatial weight matrices so as to capture potentially complex spatial interactions: namely, the population-, the trade-, the border- and the distance-based ones. Following BEK, we first construct the population-based weight matrix, which is designed to capture the concept of multilateral resistance with respect to country-pair trade flows; namely, the weight for the pair of countries i and j is given by $\frac{L_{k}} {L}$ where L _k is the third country population/trade for k ≠ i and k ≠ j, and L = ∑ _k L _k is the total population. To examine the robustness of the estimation results, we consider the trade-based weight matrix, following the global macroeconometric modelling (e.g. Greenwood-Nimmo et al. 2013). Further, as commonly used in the spatial econometric literature, we also consider the distance-based weight matrix by employing the inverse squared distance using the geographical coordinates of countries pair capitals, and the border-based one on the basis of contiguity. Hence, for the pair of countries i and j, the distance and the border matrices capture the geographical proximity between countries j and k. In all four weight matrices, our prior is a negative spatial autoregressive coefficient, ρ.¹⁴ We find that the impacts of GDP, SIM and RLF are significantly positive. A depreciation of the home currency (increase in RER) leads to an increase in trade flows for the case of W = border and W = distance, but a decrease in trade for W = trade and W = pop.¹⁵ We also find that trade and currency union memberships (CEE and EMU) boost real trade flows significantly.

We now follow LeSage and Fisher (2010), and discuss the estimation results for the spatial gravity model in terms of direct and indirect effects. To this end we rewrite (12.5) as follows:

$$\displaystyle{ \mathbf{y}_{t} =\rho \mathbf{Wy}_{t} + \mathbf{X}_{t}\boldsymbol{\beta } + \mathbf{Z\boldsymbol{\gamma }+\boldsymbol{\varepsilon }}_{t},\ t = 1,\ldots,T }$$

(12.12)

where $\mathbf{y}_{t} = \left (\,y_{1t},\ldots,y_{Nt}\right )^{{\prime}}$, $\mathbf{W} = \left \{w_{ij}\right \}_{i,j=1}^{N}$ is the N × N spatial weight matrix, $\mathbf{X}_{t} = \left (\mathbf{x}_{1t}^{{\prime}},\ldots,\mathbf{x}_{Nt}^{{\prime}}\right )$ is the N × k matrix of time-varying regressors, $\mathbf{Z} = \left (\mathbf{z}_{1}^{{\prime}},\ldots,\mathbf{z}_{N}^{{\prime}}\right )$ is the N × g matrix of time-invariant regressors,and $\boldsymbol{\varepsilon }_{t} = \left (\varepsilon _{1t},\ldots,\varepsilon _{Nt}\right )^{{\prime}}$ with $\varepsilon _{it} =\tilde{\alpha } _{i} + v_{it}$. We then rewrite (12.12) as

$$\displaystyle{ \mathbf{y}_{t} = \left (\mathbf{I}_{N} -\rho \mathbf{W}\right )^{-1}\left (\mathbf{X}_{ t}\boldsymbol{\beta } + \mathbf{Z\boldsymbol{\gamma }+\boldsymbol{\varepsilon }}_{t}\right ). }$$

(12.13)

Then, the impacts of a change in the rth time-varying regressor corresponds to the following N × N matrix of partial derivatives:

$$\displaystyle{ \frac{\partial \mathbf{y}_{t}} {\partial X_{rt}} = \left (\mathbf{I}_{N} -\rho \mathbf{W}\right )^{-1}\beta _{ r},\ r = 1,\ldots,k }$$

(12.14)

Notice that diagonal elements of (12.14) (direct impacts), are different across cross-section units; off-diagonal terms (indirect impacts) differ from zero, and the matrix is not symmetric. We now have N direct effects and N(N − 1) indirect effects. To avoid such an interactive heterogeneity issue, LeSage and Pace (2009) suggest to employ only three scalar measures to summarise information contained in the matrix (12.14): the average of the N diagonal elements as a measure of direct effects, the average of the N(N − 1) off-diagonal elements as the average of the cumulative indirect effects and the average total effect as the mean of total effects.

Table 12.5 Direct and indirect effects for the panel gravity SARAR model

From Table 12.5 we find that the direct effects are always positive while the indirect effects are mostly negative and significant.¹⁶ Thus, the estimated total effects are smaller than the main estimates reported in Tables 12.3 and 12.4. As discussed in footnote 16, we also notice that the signs of impacts of real exchange rates on trades are different across different spatial weights. Furthermore, we find that indirect spillover effects of RFL are significantly negative only for W = Pop and Distance.

Comparing the estimation results for the spatial-based panel gravity models in Tables 12.3 and 12.4 with those for the factor-based models in Table 12.2, we notice the following important differences: The impact of RLF is rather positive and significant for W = pop and W = distance. Secondly, as explained above, the effect of depreciation of home currency depends on the way we model spatial spillover effects. Thirdly, the impacts of EMU and CEE are around 0.2 and 0.3 and substantially higher than those obtained by the factor-based models. These values are rather close to the estimates obtained under the basic model specification without controlling for cross-section dependence. To investigate this issue further, we apply the cross-section dependency (CD) test advanced by Pesaran (2004) to the residuals obtained from the spatial-based gravity models, we find that the null of no cross-sectional dependence is strongly rejected for all of the models as reported in Tables 12.3 and 12.4. On the other hand, we find from Table 12.2 that the null hypothesis is only marginally rejected for the factor-based models. Overall evidence may suggest that the spatial model does not fully accommodate the potential correlation between regressors and unobserved individual and time effects.

Given that most of existing studies neglect an important issue of evaluating the currency union effects on trade through bilateral resistance channels, SS propose an alternative way to testing the Euro effect on trade integration by testing the validity of the hypothesis that the Euro might have caused a fall in trade impacts of bilateral trade barriers, if it had a positive effect on internal European trade (by reducing overall trade costs). In particular, we will examine whether the coefficients on bilateral resistance proxies (γ) tend to be more downward-sloping after the introduction of the Euro in 1999 than before. If so, this implies a (indirect) positive effect of the Euro on the European Integration. To this end, we re-estimate the model, (12.9), by the cross-section regressions for each time period. After consistently estimating $\hat{d}_{it}$ in (12.9) by the factor-based PCEE and PC estimators or the spatial-based SARAR estimators, we apply the more efficient AM-IV estimation and perform the following cross section regression for each t: 

$$\displaystyle{ d_{it} = a_{i} +\boldsymbol{\gamma }_{ t}^{{\prime}}\mathbf{z}_{ i} + e_{it},\ i = 1,\ldots,N\text{,} }$$

where z _i  includes Dis _i , Bor _i  and Lan _i .

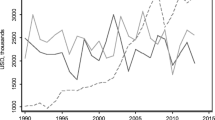
Figures 12.1 and 12.2 display the estimation results for the time-varying coefficients of $\boldsymbol{\hat{\gamma }}$. Overall, we find that the downward slopes of coefficients are steeper for both border and language effects after 1999 than before 1999.¹⁷ Also, their decreases turn out to be sharp and monotonic. The declining language impacts may reflect the progressive lessening of restrictions on labor mobility within EU (e.g. Rauch and Trindade 2002). Importantly, the monotonically declining border impacts especially after 2000 suggest that the Euro help to reduce border-linked trade costs. Finally, we find that the distance effects on trade have been more or less stable or slightly increasing over the full sample period. This evidence provides support for the studies by Disdier and Head (2008) and Jacks (2009), who document that the notion of the death of distance has been difficult to identify in the present-day trade data.¹⁸ Overall, these findings suggest that the introduction of the Euro helps to reduce trade effects of bilateral trade barriers and promote more integration among the EU countries.

Fig. 12.1

Time-varying trade impacts of bilateral trade barriers for the factor-based gravity models. Notes: We estimate the time-varying impacts of bilateral trade barriers (distance, border and language) on trade flows by applying the two-step AM-IV estimators as follows: In the first-step, we estimate the factor-based gravity model, (12.1)–(12.2), by PCCE or PC estimators as in Table 12.2. Then, in the second-step, we estimate (12.9) by the cross-section regression at each time period. See SS for details. To enhance visibility, we super-impose the fitted relative slopes

Fig. 12.2

Time-varying trade impacts of bilateral trade barriers for the spatial-based gravity models. Notes: We estimate the time-varying impacts of bilateral trade barriers (distance, border and language) on trade flows by applying the two-step AM-IV estimators as follows: In the first-step, we estimate the spatial-based gravity model, (12.11)–(12.12), by SARAR estimators with W = Pop, Trade, Border and Distance as in Tables 12.3 and 12.4. Then, in the second-step, we estimate (12.9) by the cross-section regression at each time period. See SS for details. To enhance visibility, we super-impose the fitted relative slopes

5 Conclusion

The investigation of unobserved and time-varying multilateral resistance terms in conjunction with omitted trade determinants has assumed a prominent role in the literature on the Euro’s trade effects (e.g. Baldwin 2006). To address this important issue we apply the panel gravity models to the dataset over the period 1960–2008 (49 years) for 190 country-pairs amongst 20 OECD member countries, employing two recent methodologies: the factor-based approach proposed by SS and the spatial-based techniques developed by Behrens et al. (2012).

The estimation results for the factor-based model provide the following stylised findings: First, the sum of home and foreign country GDPs significantly boosts trade while a depreciation of the home currency increases trades. Secondly, the impact of difference in relative factor endowments is significantly negative whilst the effect of similarity is positive. This suggests that similarity (in terms of countries’ GDP) helps to ease the integration process by capturing trade ties across countries and the diversity in relative factor endowments (decrease in RFL) boosts trades as suggested by Heckscher Ohlin’s theory. Thirdly, the impacts of distance and common language on trade are significantly negative and positive whereas the border impact is insignificant. Further investigation of their time-varying coefficients reveals that border and language effects started to fall more sharply after 1999. Finally and importantly, we find that both the Euro and the custom union impacts on trade amounts only to 4–5 % and 11 %. Combined together, these findings may support the idea that the potential trade-creating effects of the Euro should be viewed in terms of the proper historical and multilateral perspective rather than simply in terms of the formation of a monetary union as an isolated event.

Next, from the estimation results for the spatial-based gravity model, we find that the impacts of the Euro and the custom union on trade rises to 20 % and 30 %, respectively, which are both significantly higher than those obtained by the PCCE and the PC estimators. Furthermore, the CD test results confirm that the factor-based model is able to better accommodate correlation between regressors, unobserved individual and time effects. This evidence highlights an importance of appropriately controlling for cross-section dependence in the panel gravity models of trade flows through the use of both observed and unobserved factors in order to account for time-varying multilateral resistance, trade costs and globalisation trends.

6 The Data Appendix

Here we revise and update the data appendix of Serlenga and Shin (2007) for the sake of completeness.

All variables are converted into constant dollar prices with 2005 as the base year. The dependent variable is the logarithm of real total trade given by $Trade_{it} =\ln \left (X_{hft}^{R} + M_{hft}^{R}\right )$, where X _hft ^R is the bilateral real export from country h to country f, and M _hft ^R are bilateral real imports from country h to country f, at time t with i denoting the country-pair.

Regressors can be divided into two categories: time-varying and time-invariant variables. First, the time-varying regressors are:

TGDP is the (log of) total GDP defined as $TGDP_{it} =\ln \left (GDP_{ht}^{R} + GDP_{ft}^{R}\right )$, where GDP ^Rs are defined as gross domestic products at constant (2005) dollar prices for home and foreign countries, respectively. TGDP proxies overall economic mass of the trading pair countries, and it is expected to exert a positive effect on bilateral trade.

SIM is the measure of countries’ similarity in size constructed as

$$\displaystyle{ SIM_{it} =\ln \left [1 -\left ( \frac{GDP_{ht}^{R}} {GDP_{ht}^{R} + GDP_{ft}^{R}}\right )^{2} -\left ( \frac{GDP_{ft}^{R}} {GDP_{ft}^{R} + GDP_{ht}^{R}}\right )^{2}\right ]; }$$

This index is bounded between zero (absolute divergence) and 0.5 (equal size). The SIM effect on trade is expected to be positive.

RLF is a measure of countries’ difference in relative factor endowments, constructed as

$$\displaystyle{ RLF_{it} =\ln \left \vert PGDP_{ft}^{R} - PGDP_{ ht}^{R}\right \vert, }$$

where PGDP ^R is per capita GDP. The higher is RLF, the larger is difference between their factor endowments, resulting in the higher volume of inter-industry trade and the lower share of intra-industry trade. Therefore, the total impact of RLF on trade flows (sum of inter- and intra-industry trades) might not be unambiguous.

RER is the real exchange rate in constant (2005) dollars, defined as RER _it  = NER _it × XPI _US , where NER _it is nominal exchange rate between currencies h and f in terms of the U.S. dollars, XPI _US is the exports price index. RER is the price of the foreign currency per the home currency unit and is meant to capture the relative price effects. A depreciation of the home currency relative to the foreign currency (an increase in RER) should lead to more export and less import for home country. The effect of real exchange rates on trade flows will be positive if the export is significantly larger than the import, and vice versa, e.g., Egger and Pfaffermayr (2003).

CEE is the European Community dummy, which is equal to one when both countries belong to the European Community, and it is expected to exert a positive impact. See also De Sousa and Desdier (2005) and Cheng and Wall (2005) for an analysis of the effects of regional trading blocks.

EMU is the European Monetary Union dummy which is equal to one when both trading partners adopt the Euro. Given that an official motivation behind the EMU is that the single currency will reduce the transaction costs of trade, the impact of EMU on trade flows is expected to be positive.

Next, we consider the following time-invariant variables:

LAN is the dummy for common language, which is equal to one when both countries speak the same official language. As LAN is supposed to capture similarity in cultural and historical backgrounds of trading countries, it is expected to display a positive effect.

BOR is a dummy for common border which is equal to one when the trading partners share a border. Its effect on bilateral trade flows is expected to be positive.

DIS is the (log of) distance between countries, where the distance is measured as the (log) of great circle distance between national capitals in kilometers. The effect of geographical distance on trade flows is expected to be negative.