Keywords

1 Introduction

The tires are the only physical link between the vehicle and the road, their impact on safety is crucial. Their physical properties that affect its dynamic behavior are largely related to its pressure. A drop in pressure has a direct impact on characteristics such as damping, stiffness and rigidity of the tire. Any unsuitable inflation leads to increase fuel consumption, accentuate the risk of explosion and cause rapid wear of the tire. In addition, the chassis configuration of current vehicles, designed to provide optimum road holding, tends to mask the effects of inflation problem. For the driver, the behavior of the car seems to remain in a normal situation until it is faced with an emergency or more radically to an incident [7]. It is therefore important to inform the driver of any anomaly by displaying a message on the dashboard. It is the vocation of the tire pressure monitoring system.

The tire pressure monitoring system is intended to improve the safety of the equipped vehicle. Over the years, various statistics have shown that over 40 % of vehicles are driven with tires under inflated by an average 0.6 bars and that many accidents are due to a failure primarily caused by pressure loss [5].

These accidents have led to the development of Tire Pressure Monitoring Systems (TPMS) to supervise permanently the pressure. A European regulation which comes into force in 2012 requires the presence of such systems on all new vehicles. The constraint is that the minimum pressure loss that these systems must be able to detect, is 25 % of the hot pressure. In addition, a pressure drop on a wheel must be detected in less than 10 min and more wheels in less than 1 h [5].

Many research aims to improve the performance of existing systems and to design innovative solutions (especially without pressure sensors) corresponding to new regulations. Two techniques are proposed to measure the physical parameters of tires: The first strategy (direct approach) is to directly measure the pressure in each tire, thanks to pressure sensors installed at the inflation valve [25]. Nevertheless, the presence of the sensors may have disadvantages such as a reduction in the reliability of the system caused by the risk of damage of sensors in case of shock intervening during rolling or when the wheels are removed, furthermore, the need to add additional cabling thus a significant price increase. To overcome these disadvantages, an alternative is to favor methods without pressure sensor for reasons of economy and reliability, and also for monitoring in case of sensor failure in a direct approach.

The indirect approach can detect a fall pressure from physical measurements already used by the central computer of the vehicle (angular wheels speeds, acceleration, useful torque, steering wheel angle) without adding sensors for measuring the tire pressure. The underlying idea is to use the effect of pressure on certain physical variables to detect its variations. Indeed, the drop in tire pressure leads for example by a decreased in effective radii of wheels, an increase in their angular velocities and an increase in rolling resistance force. It would be sufficient, thanks to appropriate tools, using these physical quantities as indicators of the state of the pressure [21].

2 Motivation, Related Work, and Objectives

A variation in the pressure in the tire leads to decrease in its effective radius and increase in rolling resistance force. Thus, first key information related to the wheel is its effective radius. In fact, knowledge of effective radius has several advantages: the estimated effective radius in real time can be used to inform the driver of tire pressure level and its evolution in order to emit an alarm [19]. There is therefore a great interest in trying to estimate the effective radius. An assessment of the value of this radius may be obtained from the vehicle speed, the angular velocity of the wheel and the slip-ratio [22].

Another feature providing information about the tire pressure is the rolling resistance force. The variation of this force is in fact indicative of the general state of the vehicle in terms of load, tire pressure or road type. Moreover, the rolling resistance force acts not only on the longitudinal dynamics of the vehicle, but also, and very significantly, on the fuel consumption [26]. As it will be seen later in this chapter, the rolling resistance force is much more sensitive to pressure variation than the radius (larger relative variations) but the vehicles are not equipped with rolling resistance sensor, so there is a real interest in assessing this force. In addition to detect pressure loss, the estimation of rolling resistance force can detect a vehicle overload and improve vehicle control strategies in this type of situation.

Studies have already focused on the estimator design for vehicle wheels radii [19] and have proposed to use this estimation for the diagnosis of pressure in tires [3]. The used models consider that the rolling resistance force can be measured a priori under normal driving conditions, and then connected to the vehicle speed and the load by using empirical models. Nevertheless, according to [8], the rolling resistance force is heavily dependent on the tire parameters, e.g., pressure and temperature, type of road and the vehicle speed. Consequently, such approaches cannot be used in driving conditions and online estimation of the rolling resistance force is necessary. Note that in [27], the longitudinal stiffness and the effective radius assumed as being constant are identified from the correction terms of a sliding mode observer. An estimation of the pressure in the tire is deduced from the identified value of the radius. This observer considers the angular position, angular velocity of the wheel and the vehicle speed as state variables. It uses the measurement of the angular position of the wheel provided by the ABS encoders and the measuring speed vehicle. The unknown terms of the observation model are written as a function of the longitudinal stiffness and the effective radius in order to identify those parameters.

The work on the assessment of the rolling resistance force has been, to our knowledge, mainly based on tests using laboratory measurement benches and static models of finite elements [1]. This allows establishing the characteristic curves of the rolling resistance based on road type, vehicle load and tire temperature. The rolling resistance force is determined offline. In addition, these tests are carried out in very specific experimental conditions versus actual driving conditions. Note finally that much work has also been made on the synthesis of observers for the purpose to estimate other variables of the wheel or the vehicle (longitudinal stiffness coefficient of adhesion between tire and the soil and lateral speed of the vehicle; forces and parameters required for controlling the vehicle [27]; differential between the useful torque and braking torque applied to the wheel [24]; tire-soil friction).

The contribution of this chapter is to apply an online evaluation of effective radii of the front wheels and the rolling resistance of the whole axle, in order to analyze the unknown variations of the pressure. The originality is located in:

  • observation model using nonlinear dynamics and consideration of the effective radius and the rolling resistance force as state variables,

  • observation strategy “by sliding mode” which main features are the robustness opposite to uncertainty and disturbance and convergence in finite time.

In this chapter is proposed the synthesis of a nonlinear observer based on technical of high order sliding mode [4]: an observer, applied on the front axle, the effective radii of the wheels and the global rolling resistance force of the whole axle. As will be seen later in this chapter, these estimated values are all dependent on the pressure; their variations, thus, allows to evaluate the variation of the pressure. This observer is designed to reconstruct unmeasured variables (effective radii and the rolling resistance force) of the wheels based on available measurements of mechanical quantities (angular speeds provided by ABS encoders and useful torque).

The remaining parts of this chapter are structured as follows. Section 3 presents the notions of observability of nonlinear systems, and the canonical form of observability of such systems. Section 4 presents solutions for the observation of nonlinear systems, with particular emphasis on high order sliding mode observer. Section 5 presents the physical model of longitudinal and rotational dynamics of a vehicle coupled with the model of the vertical dynamics. From this model will be carried out, in Sect. 6, a study of the influence of the pressure drop in the front tires on three parameters: the effective radius of each wheel and the rolling resistance force of the whole axle, being based on the synthesis of a nonlinear sliding mode observer. Section 7 presents conclusions and future research directions of the work presented in this chapter.

3 Observability and Observers

The synthesis of an observer for a physical system begins by the following question: Is it the system observable, that means, is it possible to estimate the overall state of the system from the measurements performed? The corollary to this question is: which outputs measured use to make the system observable? In addition, in the case where the systems are represented by nonlinear models, analysis of observability should highlight the presence of possible singularities. Indeed, a notable difference between the observability of nonlinear and linear dynamic systems lies in the fact that the observability of nonlinear systems potentially depends of the input of the system and the state and it may therefore be losses observability according borrowed trajectories.

3.1 Observability: Concept and Criteria

Consider the nonlinear system of the form:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=f(x,u) \\ y=h(x) \\ \end{array}} \right. \end{aligned}$$
(1)

where \(x\in {\mathbb R}^{n}\) represents the state, \(u\in {\mathbb R}^{m}\) the input and \(y\in {\mathbb R}^{p}\) the output. \(f\, (:\, ; :)\) and \(h\, (:)\) are analytic functions. It is assumed that the functions \(f\, (:\, ; :)\) and \(h\, (:)\) are meromorphic functions of x and u. We also assume that u (t) is admissible, that is to say, measurable and bounded. According to [10], observability is defined from the notion of indistinguishability.

Definition 3.1.1

Two initial states \(x(t_0 )=x_1\) and \(x(t_0 )=x_2\) are indistinguishable for the system (1) if, \(\forall t\in [t_0 ,t_1 ]\) the corresponding outputs \(y_1 (t)\) and \(y_2 (t)\) are the same regardless of the allowable input u(t) of the system.

Definition 3.1.2

The nonlinear system (1) is said observable, if it does not admit indistinguishable pair. This means that the system is said observable if there is no distinct initial state that cannot be separated by review of the system output.

Definition 3.1.3

Considering the system (1), space observability H, is defined by the smallest vector space containing the outputs; \(h_1 , h_2 ,\ldots , h_p\) and closed under the operation of the derivation Lie to the vector field f(x, u), u being fixed. We denote dH the space of differential elements H.

Definition 3.1.4

The space \(dH(x_0)\) characterizes the local low observability \(x_0\) of system (1).

System (1) is said to satisfy the observability rank condition \(x_0 \text { if}: \mathrm{dim}(dH(x_0 ))=n\).

The system (1) satisfies the rank condition of observability \(\text {if }\, \forall x\in {\mathbb R}^{n}\), \(\mathrm{dim}(dH(x))=n\).

Definition 3.1.5

For system (1), the space generic observability [23] is defined by \(O=X\cap (Y+U)\), with:

$$\begin{aligned} \left\{ {\begin{array}{l} X=\textit{Span}_K \left\{ {d_x } \right\} \\ Y=\textit{Span}_K \left\{ {d_u ^{(j)}} \right\} ,j\ge 0 \\ U=\textit{Span}_K \left\{ {d_y ^{(q)}} \right\} ,q\ge 0 \\ \end{array}} \right. \end{aligned}$$
(2)

or K is the set of meromorphic functions and \(\textit{Span}_K \) is the space generated on K of meromorphic functions of x and of a finite number of derivatives of u. System (1) is said generically observable if:

$$\begin{aligned} \mathrm{dim} O=n \end{aligned}$$
(3)

A property is generically satisfied when it is locally satisfied around a point \(x_0 \in M\subset {\mathbb R}^{n}\). An equivalent algebraic definition can also be given. A system is generically observable if the whole state can be expressed as a function of y, of u and a finite number of their derivatives (with \(j\in {\mathbb N}, q\in {\mathbb N})\):

$$\begin{aligned} x=X(y,\dot{y},\ldots ,y^{(j)},u,\dot{u},\ldots ,u^{(j)}) \end{aligned}$$
(4)

In the nonlinear context, observability depends clearly of u and state x. The generic aspect is that we are not interested in any singularities.

Suppose that condition (3) is satisfied, and then we can check the equivalent condition of this definition. This ultimately amounts to analyzing the observability of a local perspective that is to say in an area defined by physical constraints.

Definition 3.1.6

System (1) is said locally observable if for any \(x\in M\subset {\mathbb R}^{n}\) and \(u\in U\subset {\mathbb R}^{p}\) (M and U being respectively open in \({\mathbb R}^{n}\) and \( {\mathbb R}^{p})\):

$$\begin{aligned} {\textit{Rang}}_K \left[ {{\begin{array}{llll} {dy}&{} {d\dot{y}}&{} {\ldots }&{} {dy^{(n-1)}} \\ \end{array} }} \right] ^{T}=n \end{aligned}$$
(5)

An equivalent criterion focuses on the analysis of vector \(\Psi \)

$$\begin{aligned} \Psi =\left[ {{\begin{array}{llll} {dy}&{} {d\dot{y}}&{} {\ldots }&{} {dy^{(n-1)}} \\ \end{array} }} \right] ^{T} \end{aligned}$$
(6)

Definition 3.1.7

System (1) is said locally observable if for \(x\in M\) and \(u\in U\):

$$\begin{aligned} \det \left( {\frac{\partial \Psi }{\partial x}} \right) \ne 0 \end{aligned}$$
(7)

The last property implies that \(\Psi \) defines a transformation of state on this consider field. In the following, the term “observable” will mean “locally observable”. If there is a singularity of observability, it obviously causes problems for the proper functioning of the observers. A first solution is to pass the observer, in estimator mode (this means to putting the observer in “open loop”: there are no correction term). Another solution is to switch to another observer structure, e.g. by using different indices of observability [17].

3.2 Canonical Forms of Observability and Observer

Based on the form of the dynamic system of the tire used in the rest of this chapter, we consider the following nonlinear system:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=f(x)+\Delta f(x,t)+\chi (y,u) \\ y=h(x) \\ \end{array}} \right. \end{aligned}$$
(8)

with \(x\in M\) and \(u\in U\) the additive uncertainty term \(\Delta f(x,t)\) sufficiently derivable and the additive terms which only depends on well-known variables (measurements and control) grouped in the vector called “input–output injection” \(\chi (y,u)\).

Consider the following assumptions:

Assumption 3.2.1

The additive uncertainty term \(\Delta f(x,t)\) does not change the observability of (8):

i.e. \(\left\| {\Delta f} \right\| \le F_H <\infty , \forall x\in M \text { and }t\ge 0\).

Like the goal is to synthesize an observer, and \(\Delta f\) is unknown and verified this assumption, therefore consider the nonlinear system (8) without any uncertainty \((\Delta f=0)\).

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=f(x)+\chi (y,u) \\ y=h(x) \\ \end{array}} \right. \end{aligned}$$
(9)

Assumption 3.2.2

The input–output injection \(\chi (y,u)\) does not change the observability of the system [2].

The main idea is simple: for the purpose to analyze the observability, then to synthesize the observer, the system (8) is transformed into a simple system and well known from which observability will be analyzed, and observer designed. Adding to the observer the input–output injection term, we obtain an observer for (9). Remains to propose an adequate solution for that this observation is sufficiently robust to provide a good estimate of the uncertain system (8). Via an input–output injection defined by \(\chi (y,u)\), the nonlinear system (9) can be transformed into:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=f(x) \\ y=h(x) \\ \end{array}} \right. \end{aligned}$$
(10)

Assumption 3.2.3

Consider the system (10) and p integers \(\left\{ {k_1 , k_2 ,\ldots , k_p } \right\} \) defined such that [14]:

\(\sum \limits _{i=1}^p {k_i =n} \text { and } k_1 \ge k_2 \ge \cdots \ge k_p\) after numbering of output components if necessary.

The function \(\Psi (x)\) defined by:

$$\begin{aligned} \Psi (x)=\left[ {\begin{array}{c} {[}y_1 (x) \cdots y_1^{(k_1 -1)} (x){]}^{T} \\ \vdots \\ {[}y_p (x) \cdots y_p^{(k_p -1)} (x){]}^{T} \\ \end{array}} \right] _{ x\in M} \end{aligned}$$
(11)

verifies:

$$\begin{aligned} \det \left( {\frac{\partial \psi (x)}{\partial x}} \right) \ne 0 \end{aligned}$$
(12)

The function \(\zeta =\Psi (x)\) is thus a state transformation. The integers \(\left\{ {k_1 , k_2 ,\ldots , k_p } \right\} \) are called observability indices.

Proposition 3.2.1

Given the Assumptions 3.2.1; 3.2.2 and 3.2.3, the system (8) is observed for \(x\in M\) and \(u\in U\).

Consider again the system (8) verifying the Assumptions 3.2.1 and 3.2.3. By asking \(\zeta =\left[ {{\begin{array}{llll} y&{} {\dot{y}}&{} \cdots &{} {y^{(n-1)}} \\ \end{array} }} \right] ^{T}\), is obtained by:

$$\begin{aligned} \begin{array}{l} \dot{\zeta } = A\zeta +\left[ {\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ \Phi (\zeta ) \\ \end{array}} \right] \\ y=C\zeta \\ \end{array} \end{aligned}$$
(13)

with:

$$\begin{aligned} A=\left[ {{\begin{array}{cccccc} 0&{} 1&{} 0&{} 0&{} \cdots &{} 0 \\ 0&{} 0&{} 1&{} 0&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0&{} 0&{} 0&{} 0&{} \cdots &{} 1 \\ 0&{} 0&{} 0&{} 0&{} \cdots &{} 0 \\ \end{array} }} \right] , C=\left[ {{\begin{array}{lllll} 1&{} 0&{} 0&{} \cdots &{} 0 \\ \end{array} }} \right] \, \mathrm{and}\, \Phi (\zeta )=y^{(n)} \end{aligned}$$
(14)

The representation (13) is called “canonical form of observability”. Given system (8), it is clear that the term \(\Phi (\zeta )\) is uncertain; is assumed to be written:

$$\begin{aligned} \Phi (\zeta )=\Phi _n +\Delta \Phi \end{aligned}$$
(15)

with \(\Phi _n\) the “nominal” part (composed of parameters and dynamics known derived from the term f(x)) and “uncertain” part \(\Delta \Phi \) (derived from \(\Delta f(x,t))\). Is thus obtained:

$$\begin{aligned} \dot{\zeta }=A\zeta +\left[ {\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ \Phi _n (\zeta ) \\ \end{array}} \right] +\left[ {\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ \Delta \Phi \\ \end{array}} \right] \end{aligned}$$
(16)

Proposition 3.2.2

An observer for the system (16) is written in the form:

$$\begin{aligned} \dot{\hat{{\zeta }}} = A\hat{{\zeta }}+\left[ {\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ \Phi _n (\zeta ) \\ \end{array}} \right] + k(y,\hat{{\zeta }}) \end{aligned}$$
(17)

The function k is the correction term which ensures convergence of the estimated state to the actual state \(\hat{{\zeta }}\rightarrow \zeta \).

The term \(k(y,\zeta )\) can be obtained by various methods (high gains, sliding mode,...) and must ensure convergence (exponentially or in finite time) of the observer to the real system, i.e., it ensures that \(\hat{{\zeta }}\rightarrow \zeta \) exponentially or in finite time despite the presence of uncertain term \(\Delta \Phi \). In addition, it depends only on the measured output y and the estimated state vector \(\hat{{\zeta }}\). To summarize, knowing that the dynamics of the estimation error is written:

$$\begin{aligned} \dot{e}=Ae+\left[ {\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ \Phi _n (\hat{{\zeta }})-\Phi _n (\zeta ) \\ \end{array}} \right] -\left[ {\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ \Delta \Phi \\ \end{array}} \right] +k(y,\hat{{\zeta }}) \end{aligned}$$
(18)

with \(e=(\zeta -\hat{{\zeta }})\rightarrow 0\)

It is necessary to choose that the correction term \(k(y,\zeta )\) such that the observer converges to the real system despite the initial error e(0) and the uncertain term \(\Delta \Phi \). From (17), two methods can be used to obtain the vector \(\hat{{x}}\), representing the estimated x.

  • When the inverse of the transformation \(\Psi \), i.e. \(\Psi ^{-1}\), can be analytically calculate, the estimated state \(\hat{{x}}\) is deduced from \(\hat{{\zeta }}\) by:

    $$\begin{aligned} \begin{array}{l} \hat{{x}}=\Psi ^{-1}(\zeta )\\ \end{array} \end{aligned}$$
    (19)

  • In many cases of applications [17], it is very difficult to calculate the inverse of \(\Psi \) (including with formal calculation software). In this case, using an approach based on the calculation of the inverse Jacobian of \(\Psi \). As \(\hat{{\zeta }}=\Psi (\hat{{x}})\), we can write:

    $$\begin{aligned} \dot{\hat{{\zeta }}}=\frac{\partial \Psi }{\partial \hat{{x}}}\dot{\hat{{x}}}\rightarrow \dot{\hat{{x}}}=\left[ {\frac{\partial \Psi }{\partial \hat{{x}}}} \right] ^{-1}\dot{\hat{{\zeta }}} \end{aligned}$$
    (20)

According to (17) and (20), is obtained

$$\begin{aligned} \dot{\hat{{x}}}=\left[ {\frac{\partial \Psi }{\partial \hat{{x}}}} \right] ^{-1}\left( {A\hat{{\zeta }}+\left[ {\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ \Phi _n (\hat{{\zeta }}) \\ \end{array}} \right] +k(y,\hat{{\zeta }})} \right) \end{aligned}$$
(21)

Then, from (17) and (21), an observer for the system (10) can be written by:

$$\begin{aligned} \dot{\hat{{x}}}=f(\hat{{x}})+\left[ {\frac{\partial \Psi }{\partial x}} \right] ^{-1}k(y,\hat{{x}}) \end{aligned}$$
(22)

Applying the inverse transform of the input–output injection \(\chi (y,u)\) allows to obtain the observer for the system (9):

$$\begin{aligned} \dot{\hat{{x}}}=f(\hat{{x}},y)+\chi (y,u)+\left[ {\frac{\partial \Psi }{\partial \hat{{x}}}} \right] ^{-1}k(y,\hat{{x}}) \end{aligned}$$
(23)

In the following section, an observer of the type (23) is proposed to estimate “sufficiently” a precise state x of the system (8) despite the uncertain term \(\Delta f\), and this thanks to a judicious choice of k. In the following, we consider:

Assumption 3.2.4

For every \(\zeta \in M_\zeta (M_\zeta \) being the area of application in the state space \(\zeta \), corresponding to M in which evolves x):

$$\begin{aligned} \left| {\Phi _n (\zeta )} \right| \le L_\Phi \end{aligned}$$
(24)

with \(L_\Phi \) being known Lipschitz positive constant. Furthermore:

$$\begin{aligned} \left| {\Delta \Phi } \right| \le L_{\Delta \Phi } \end{aligned}$$
(25)

with \(0<L_{\Delta \Phi } <\infty \).

4 Observation Technique Using Sliding Mode

Many techniques of observation of nonlinear systems exist: the observers based on linearization by input–output injection [23], high gains observers [9], continuous observer with finite time convergence [20], and sliding mode observers [4]. Each of these observation strategies is applied to a more or less broad class of nonlinear systems. In this section sliding mode observers are studied and then applied for tire pressure monitoring.

4.1 Sliding Mode Observers

One of the known classes of nonlinear robust observers is that of sliding mode observer. Among the different observation methods, sliding mode observers have been widely studied for their robust qualities [12]. The main features of observer type are:

  • finite time convergence of the estimation error,

  • robustness face to disturbances and uncertainties.

Sliding mode observer is characterized by discontinuous functions in their correction terms. The principle of sliding mode observer involves to constrain the dynamics of the estimation error, of dimension n, to evolve in finite time on a variety S, corresponding to a null estimation error. The attractiveness and the invariance of this surface are ensured by conditions called sliding conditions. If these conditions are satisfied, the observer converges to S and remains there.

In the next section, will be presented an observation solution based on sliding mode approach of first order and high order [16].

4.2 First Order Sliding Mode Observer

The first solutions were based on the approach of the first order sliding mode. In this case, the variety S is defined \(S=\left\{ {y-\hat{{y}}=0} \right\} \) with \(\hat{y}\) the estimate of the measure. The discontinuous corrective terms depend on the estimation error of y. This observer is applicable for systems with observability indices equal to 1. For observability indices 2, this observer does not allow to perfectly cancel the estimation error of \(x_2\). Another drawback is the phenomenon of “chattering”. This phenomenon is not desirable as it deteriorates the accuracy of the observation. Many studies have been work done in order to reduce or eliminate this problem. One solution is the introduction of new dynamics to act on higher order derivatives of the estimation error of y. This technique is the basic concept of higher order sliding mode which reduces the “chattering” retaining the qualities of robustness and finite time convergence of the approach first order sliding mode [11].

4.3 High Order Sliding Mode Observer

The concept of high order sliding mode was introduced in the 80s by Emelyanov [6], the principle involves acting via discontinuous corrective terms, on higher order derivatives of the measurement error y. The main advantages are:

  • improving robustness and convergence in finite time,

  • reducing the effects of chattering,

  • improving the observer performance (precision), the application to systems with indices of observability higher than 1.

4.3.1 Second Order Sliding Mode Differentiation

The problem here is to constrain the estimation error to evolve in finite time on the sliding surface:

$$\begin{aligned} S=\left\{ {\begin{array}{l} y-\hat{{y}}=0 \\ \dot{y}-\dot{\hat{{y}}}=0 \\ \end{array}} \right. \end{aligned}$$
(26)

In this way, the estimation error is now continuous and the chattering is eliminated. In this framework: The “Super Twisting algorithm” is proposed. This algorithm has been developed, to the base, for control systems (output feedback sliding mode of order 2) and is based on the technique of differentiation, hence its adequacy in observing systems written under canonical form of observability. This method is robust and does require only knowledge of it (no derivative calculation) but its use is limited to an index of observability equal to 2 [15].

4.3.2 High Order Sliding Mode Differentiation

For a given observability indices k, the objective here is to force the quantity \((y-\hat{{y}})\) and its first \((k-1)\) derivatives to zero in finite time [16]. Observers based on differentiation technique of high order sliding mode are offered in this context. This technique will be presented in detail since it was adopted in this chapter. In fact, according to its robustness and convergence in finite time it can be applied to a wide class of observable nonlinear systems. Considering system (16) with \(\zeta = \left[ {\begin{array}{llllll} {\zeta _1 }&{} {\zeta _2 }&{} {\zeta _3 }&{} {\zeta _4 }&{} {\ldots }&{} {\zeta _n } \\ \end{array} }\right] ^{T}\) in this case, a single output y is measured; the observability indices k then being equal to \(k_1\). Is obtained:

$$\begin{aligned} \begin{array}{c} \dot{\zeta }_1 =\zeta _2 \\ \dot{\zeta }_2 =\zeta _3 \\ \dot{\zeta }_3 =\zeta _4 \\ \vdots \\ \dot{\zeta }_n =\Phi (\zeta ) \\ y=\zeta _1 \\ \end{array} \end{aligned}$$
(27)

When assumptions of Sect. 3.2 are satisfied, the observer is described by form (17). The correction term k must ensure the convergence of e to 0, despite the initial error e(0) and the uncertain term \(\Delta \Phi \). A possible choice of observer based on the differentiation of higher order [16]:

$$\begin{aligned} \begin{array}{ll} &{} \dot{\hat{{\zeta }}}_1 =\hat{{\zeta }}_2 +a_1 L^{\frac{1}{n+1}}\left| {\zeta _1 -\hat{{\zeta }}_1 } \right| ^{\frac{n}{n+1}}sign(\zeta _1 -\hat{{\zeta }}_1 ) \\ &{} \dot{\hat{{\zeta }}}_2 =\hat{{\zeta }}_3 +a_2 L^{\frac{1}{n}}\left| {\gamma _1 } \right| ^{\frac{n-1}{n}}sign(\gamma _1 ) \\ &{} \dot{\hat{{\zeta }}}_3 =\hat{{\zeta }}_4 +a_3 L^{\frac{1}{n-1}}\left| {\gamma _2 } \right| ^{\frac{n-2}{n-1}}sign(\gamma _2 ) \\ &{}\quad \, \vdots \\ &{} \dot{\hat{{\zeta }}}_i =\hat{{\zeta }}_{i+1} +a_i L^{\frac{1}{n+2-i}}\left| {\gamma _{i-1} } \right| ^{\frac{n+1-i}{n+2-i}}sign(\gamma _{i-1} ) \\ &{}\quad \, \vdots \\ &{} \dot{\hat{{\zeta }}}_n =\Phi (\hat{{\zeta }})+a_n Lsign(\gamma _{n-1} ) \\ \end{array} \end{aligned}$$
(28)

with \(L>L_\Phi +L_{\Delta \Phi }\) and \(a_1 \ldots a_n\) coefficients fixed according to Table 1 [16].

Table 1 \(a_i\) coefficients \(a_{i}\) for sliding modes order 2 and 3
Full size table

Thus, from (23) a finite time convergence observer is developed for the initial system (8). It can be written:

$$\begin{aligned} \dot{\hat{{x}}}=f(\hat{{x}},y)+\chi (y,u)+\left[ {\frac{\partial \Psi }{\partial \hat{{x}}}} \right] ^{-1}\left[ {\begin{array}{c} \gamma _1 \\ \gamma _2 \\ \gamma _3 \\ \vdots \\ \gamma _n \\ \end{array}} \right] \end{aligned}$$
(29)

with:

$$\begin{aligned} \left[ {\begin{array}{c} \gamma _1 \\ \gamma _2 \\ \vdots \\ \gamma _i \\ \vdots \\ \gamma _n \\ \end{array}} \right] =\left[ {\begin{array}{c} a_1 L^{\frac{1}{n+1}}\left| {y-\hat{{x}}_1 } \right| ^{\frac{n}{n+1}}sign(y-\hat{{x}}_1 ) \\ a_2 L^{\frac{1}{n}}\left| {\gamma _1 } \right| ^{\frac{n-1}{n}}sign(\gamma _1 ) \\ \vdots \\ a_i L^{\frac{1}{n+2-i}}\left| {\gamma _{i-1} } \right| ^{\frac{n+1-i}{n+2-i}}sign(\gamma _{i-1} ) \\ \vdots \\ a_n Lsign(\gamma _{n-1} ) \\ \end{array}} \right] \end{aligned}$$
(30)

5 Vehicle Front Axle Modeling

This section presents the model of longitudinal and rotational dynamics of the vehicle front axle wheels. This model and its coupling with the vertical vehicle dynamic are the basis of wheels behavior description. With consideration of rolling resistance force and effective radii of the wheels.

5.1 Dynamics of the Front Axle

The suspension system is composed of mechanical components that connect the wheels to the main structure of the vehicle. The suspension provides an elastic connection to absorb and transmit smoothly the irregularities. There are several types of suspension, the most common are steel suspensions (called mechanical) and pneumatic suspensions. Currently the vehicles are equipped, in most cases, with pneumatic suspension that provide better dynamic stability and are less aggressive for the road [28]. This study considers a simplified air suspension mechanism described by a mass-spring-damper system. The front axle model of the vehicle is used to describe the vertical dynamics of the vehicle and those of the wheels shown in Fig. 1.

with

\(m_c :\) :

suspended mass brought on two wheels,

\(m_r :\) :

unsprung mass,

\(K_{sr} :\) :

stiff right suspension,

\(K_{sl} :\) :

stiff left suspension,

\(K_{vr} :\) :

vertical stiffness of the right tire,

\(K_{vl} :\) :

vertical stiffness of the left tire,

\(C_s :\) :

suspension damping,

\(C_v :\) :

vertical pneumatic damping,

\(R_0 :\) :

nominal radius,

R : :

tire radius,

\(C_f :\) :

viscous friction coefficient,

\(z_c :\) :

vertical position of the suspended mass,

\(z_r :\) :

vertical position of the unsprung mass,

\(z_{\textit{pro}} :\) :

profile of the wheel surface,

\(d_{\textit{pro}} :\) :

road profile.

Referring to a fixed vertical position referenced by o, \(Z_{{\textit{pro}}_{0}}\) on the initial contact (between the wheel and the ground) is located by vertical axis z shown on Fig. 1. \(Z_{c_{0}}\) is the vertical distance in the static state of the vehicle body and \(Z_{r_{0}}\) the vertical distance in the static state from the center of the wheel.

Fig. 1
figure 1

Vertical vibration model of a half vehicle

Full size image

The relative positions of wheel-ground contact \(z_{\textit{pro}}\), wheel center \(z_r\) and vehicle body \(z_c\) given by:

$$\begin{aligned}&d_{pro} =z_{pro} -Z_{pro_0 } \end{aligned}$$
(31)
$$\begin{aligned}&d_r =z_r -Z_{r_0 } \end{aligned}$$
(32)
$$\begin{aligned}&d_c =z_c -Z_{c_0 } \end{aligned}$$
(33)

The application of the second Newton’s law can write the equations of the vertical dynamics of a half vehicle and of the wheel [29] according to:

$$\begin{aligned} \left\{ {\begin{array}{l} m_c \ddot{d}_c =-K_{sl} (d_c -d_r )-C_{sl} (\dot{d}_c -\dot{d}_r ) -K_{sr} (d_c -d_r )-C_{sr} (\dot{d}_c -\dot{d}_r ) \\ m_r \ddot{d}_r =K_{sl} (d_c -d_r )+C_{sl} (\dot{d}_c -\dot{d}_r )+K_{sr} (d_c -d_r )+C_{sr} (\dot{d}_c -\dot{d}_r ) \\ \qquad \quad -K_{vl} (d_r -d_{prol} )-K_{vr} (d_r -d_{pror} )-C_v (\dot{d}_r -\dot{d}_{pro} ) \\ \end{array}} \right. \end{aligned}$$
(34)

The damping of the tires is assumed to be negligible compared to other variables \((C_v =0)\).

Thus, taking as a state vector \((x_1 , x_2 , x_3 , x_4 )^{T}=(d_c , \dot{d}_c , d_r , \dot{d}_r )^{T}\) and as input \(u=(d_{\textit{prol}} , d_{\textit{pror}})\), the state model of the pneumatic is written in the form:

$$\begin{aligned} \left[ {\begin{array}{l} \dot{d}_c \\ \ddot{d}_c \\ \dot{d}_r \\ \ddot{d}_r \\ \end{array}} \right] =\left[ {{\begin{array}{cccc} 0&{} 1&{} 0&{} 0 \\ {-a_1 }&{} {-a_2 }&{} {a_1 }&{} {a_2 } \\ 0&{} 0&{} 0&{} 1 \\ {a_3 }&{} {a_4 }&{} {-a_5 }&{} {-a_4 } \\ \end{array} }} \right] \left[ {\begin{array}{l} d_c \\ \dot{d}_c \\ d_r \\ \dot{d}_r \\ \end{array}} \right] +\left[ {{\begin{array}{cc} 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ {a_6 }&{} {a_7 } \\ \end{array} }} \right] \left[ {\begin{array}{l} d_{prol} \\ d_{pror} \\ \end{array}} \right] \end{aligned}$$
(35)
$$\begin{aligned} \text {with} \left\{ {\begin{array}{l} a_1 =\frac{K_{sl} +K_{sr} }{m_c } \\ a_2 =\frac{C_{sl} +C_{sr} }{m_c } \\ a_3 =\frac{K_{sl} +K_{sr} }{m_r } \\ a_4 =\frac{C_{sl} +C_{sr} }{m_r } \\ a_5 =\frac{K_{vl} +K_{vr} }{m_r } \\ a_6 =\frac{K_{vl} }{m_r } \\ a_7 =\frac{K_{vr} }{m_r } \\ \end{array}} \right. \end{aligned}$$
(36)

Tire/road contact forces are obtained from the tire model, which we will present in the next section. These forces are transmitted to the chassis (sprung mass) via the suspension. They depend on the characteristics of the latter and axle configuration.

5.2 Dynamics of Wheels

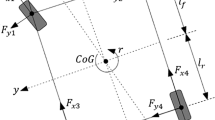
The application of the second Newton’s law to the forces acting on two wheels of front axle allows writing their rotational and longitudinal dynamics as (Fig. 2):

$$\begin{aligned} \left\{ {\begin{array}{l} J_l \dot{\Omega }_l =T_l -R_l F_{xl} -C_f \Omega _l \\ J_r \dot{\Omega }_r =T_r -R_r F_{xr} -C_f \Omega _r \\ M_{1/2} \dot{v}_x =F_{xl} +F_{xr} -F_{d1/2} -F_{rg} \\ \end{array}} \right. \end{aligned}$$
(37)

where indexes l and r respectively refer to the front left and rights wheels, \(\Omega \) is the wheel angular velocity, R is the effective radius, \(v_x\) the vehicle’s linear velocity, \(C_f\) the viscous friction coefficient of the wheel, J and \(M_{1/2}\) are respectively the inertia and the half-vehicle mass. T is the torques applied to the wheel.

Fig. 2
figure 2

Forces and torques acting on the front wheels

Full size image

The complete model of the front axle of a vehicle can be obtained from the model (37) coupled to the model of the vertical dynamics (34). The coupling is done through the normal force \(F_z\) (38).

\(\bullet \) Normal force: This force depends mainly on the half-vehicle mass and the vertical displacement of the tire-road point contact [5], it is defined by the following relationship:

$$\begin{aligned} F_{zi} =M g-K_{vi} (R_{\textit{lib}} -(d_r -d_{\textit{proi}} ))-C_v (\dot{d}_r -\dot{d}_{\textit{proi}} ) \end{aligned}$$
(38)

where \(i \, \in \{l,r\}\) and g the gravitational acceleration.

A simplifying assumption may be considered to reduce the model of normal force. This assumption is formulated by Eq. (39):

$$\begin{aligned} K_{vi} (R_{lib} -(d_r -d_{\textit{proi}} ))-C_v (\dot{d}_r -\dot{d}_{\textit{proi}} ) \langle \langle M g \end{aligned}$$
(39)

The expression of the normal force becomes:

$$\begin{aligned} F_{zi} =M g \end{aligned}$$
(40)

\(\bullet \) Aerodynamic drag force: This force is proportional to the square of the vehicle’s velocity [8].

$$\begin{aligned} F_{d1/2} =\frac{1}{2}(\rho A_{d1/2} C_{d1/2} v_x^2 ) \end{aligned}$$
(41)

with \(\rho \) the air density, \(A_{d1/2}\) the frontal area of the half-vehicle and \(C_{d1/2}\) the drag coefficient.

\(\bullet \) Tractive forces: These forces are expressed according to friction wheel-ground coefficient \(\mu (\lambda _i )\) [8] as:

$$\begin{aligned} F_x (\lambda _i )=F_{zi} \mu (\lambda _i ) \end{aligned}$$
(42)

with \(\lambda _i\) the slip ratio defined by:

$$\begin{aligned} \lambda _i =-\frac{\left( {\nu _x -R_i \Omega _i } \right) }{R_i \Omega _i }=-\frac{\nu _x }{R_i \Omega _i }+1 \end{aligned}$$
(43)

Figure 3 shows the friction coefficient evolution slip ratio for different road types.

Fig. 3
figure 3

Friction coefficient versus slip ratio

Full size image

The friction coefficient \(\mu _i\) is theoretically given by semi-empirical formulas. An acceptable approximation [13] is expressed as a function of \(\lambda _i\) by:

$$\begin{aligned} \mu _i (\lambda )=2\mu _0 \left( {\frac{\lambda _0 \lambda _i }{\lambda _0 ^{2}+\lambda _i ^{2}}} \right) \end{aligned}$$
(44)

where \(\lambda _0\) is the optimal slip ratio, leading to the maximum friction value \(\mu _0 =\mu (\lambda _0 )\). The tractive forces are then given by:

$$\begin{aligned} F_{xi} =2\mu _0 \frac{\lambda _0 \left( {1-\frac{\nu _x }{\Omega _i R_i }} \right) }{\lambda _0 ^{2}+\left( {1-\frac{\nu _x }{\Omega _i R_i }} \right) ^{2}}M_{1/2} g \end{aligned}$$
(45)

\(\bullet \) Global rolling resistance force: It is related to the normal force \(F_z\) by:

$$\begin{aligned} F_{rg} (v_x )=F_{rl} (v_x )+F_{rr} (v_x )=2F_{zi} f_r (v_x ) \end{aligned}$$
(46)

with \(f_r\) the rolling resistance coefficient. This coefficient depends mainly on the tire inflation pressure, temperature, velocity, and road surface type then this assumption can be made for heavy vehicles and is valid on light vehicles only for low speeds [8].

In the case of light vehicles with higher speeds, another equation must be considered by:

$$\begin{aligned} f_r (\nu _x )=f_0 +3.24 f_s \left( {3.6 v_x /100} \right) ^{5/2} \end{aligned}$$
(47)

This expression will be used for the model of half vehicle. The coefficients \(f_0\) and \(f_s\) of the rolling resistance force vary for a given tire, with the pressure according to the characteristic shown in Fig. 4.

Fig. 4
figure 4

\(f_0\) and \(f_s\) evolution of according to pressure

Full size image

5.3 Global Model Coupling

The complete model of the vehicle front axle is elaborated from association of the vertical axle and wheels dynamic modeling. The considered state variables are expressed as:

$$ \left[ {{\begin{array}{lllllll} {x_1 }&{} {x_2 }&{} {x_3 }&{} {x_4 }&{} {x_5 }&{} {x_6 }&{} {x_7 } \\ \end{array} }} \right] ^{T}=\left[ {{\begin{array}{lllllll} {\Omega _l }&{} {\Omega _r }&{} {v_x }&{} {d_c }&{} {\dot{d}_c }&{} {d_r }&{} {\dot{d}_r } \\ \end{array} }} \right] ^{T} $$

Then, the global model, is written as follows:

$$\begin{aligned} \dot{x}=\left[ {\begin{array}{c} \frac{1}{J_l }[T_l -R_l F_x -C_f \Omega _l ] \\ \frac{1}{J_r }[T_r -R_r F_x -C_f \Omega _r ] \\ \frac{1}{M_{1/2} }[F_{xl} +F_{xr} -F_{d1/2} -F_{rg} ] \\ x_5 \\ \frac{1}{m_c }[-K_{sl} (x_4 -x_6 )-C_{sl} (x_5 -x_7 )-K_{sr} (x_4 -x_6 )-C_{sr} (x_5 -x_7 )] \\ x_7 \\ \frac{1}{m_r }[K_{sl} (x_4 -x_6 )+C_{sl} (x_5 -x_7 )+K_{sr} (x_4 -x_6 )+ C_{sr} (x_5 -x_7 ) \\ -K_{vl} (x_6 -d_{prol} )-K_{vr} (x_6 -d_{\textit{pror}} )] \\ \end{array}} \right] \end{aligned}$$
(48)

6 Observer of Wheels’ Effective Radii and Rolling Resistance Force of the Front Axle

In this section, will first be developed the sliding mode observer for only estimation of wheel effective radii and rolling resistance force. This observer uses, in addition, measures of the angular velocity of each wheel and the wheel applied torque.

The physical area of work is defined by:

$$ M=\left\{ {0<\Omega \le 175\,\mathrm{rds}^{-1}; 0<\nu _x \le 200\,\mathrm{kmh}^{-1}; 0.29\le R\le 0.32\,\mathrm{m}; 80\le F_{rg} \le 800\,\mathrm{N}} \right\} $$

Since the aim is pressure drop detection, the knowledge of the two wheels radii gives information about pressure state in the tire of each wheel and the rolling resistance force. Therefore it seems to be judicious to develop joint estimation observers using the effective radius and the rolling resistance force.

6.1 Observation Model

In order to simplify the study, only the longitudinal dynamics of the front axle and the rotational dynamics of the two front wheels are considered. The state variables considered in this case are \(x=\left[ {{\begin{array}{lll} {\Omega _l }&{} {\Omega _r }&{} {v_x } \\ \end{array} }} \right] ^{T}\), with:

$$\begin{aligned} \dot{x}=\left[ {\begin{array}{c} \frac{1}{J_l }\left( {T_l -R_l F_{xl} (x)-C_f x_1 } \right) \\ \frac{1}{J_r }\left( {T_r -R_r F_{xr} (x)-C_f x_2 } \right) \\ \frac{1}{M_{1/2} }\left( {F_{xl} (x)+F_{xr} (x)-F_{d1/2} (x)-F_{rg} } \right) \\ \end{array}} \right] \end{aligned}$$
(49)

with \(M_{1/2}\) the mass of the two wheels, \(F_{d1/2} (x)\) the aerodynamic drag force on the train, \(T_l\) and \(T_r\) couples applied to each wheel. \(F_{rg} =F_{rl} +F_{rr}\) is the global rolling resistance force on the train. The force \(F_{xl} (x)\) and \(F_{xl} (x)\) are written:

$$\begin{aligned} F_{xl} =2\mu _0 \frac{\lambda _0 \left( {1-\frac{x_3 }{x_1 R_l }} \right) }{\lambda _0^2 +\left( {1-\frac{x_3 }{x_1 R_l }} \right) ^{2}}Mg \end{aligned}$$
(50)
$$\begin{aligned} F_{xr} =2\mu _0 \frac{\lambda _0 \left( {1-\frac{x_3 }{x_2 R_r }} \right) }{\lambda _0^2 +\left( {1-\frac{x_3 }{x_2 R_r }} \right) ^{2}}Mg \end{aligned}$$
(51)

The aerodynamic drag force for the half of vehicle is written:

$$\begin{aligned} F_{d1/2} =\frac{1}{2}(\rho A_{d1/2} C_{d1/2} x_3^2 ) \end{aligned}$$
(52)

The effective radii \(R_l\) and \(R_r\) and the global rolling resistance force \(F_{rg}\) of the front axle are unknown and may change due to loss of pressure in both wheels.

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{R}_l =\eta _l (t) \\ \dot{R}_r =\eta _r (t) \\ \dot{F}_{rg} =\eta _g (t) \\ \end{array}} \right. \end{aligned}$$
(53)

with \(\eta _l (t), \eta _r (t) \text { and } \eta _F (t) \): unknown and bounded functions,

\(u=\left[ {{\begin{array}{ll} {u_1 }&{} {u_2 } \\ \end{array} }} \right] ^{T}=\left[ {{\begin{array}{ll} {T_l }&{} {T_r } \\ \end{array} }} \right] ^{T}\quad :\) control input,

\(x=\left[ {{\begin{array}{llllll} {x_1 }&{} {x_2 }&{} {x_3 }&{} {x_4 }&{} {x_5 }&{} {x_6 } \\ \end{array} }} \right] ^{T}=\left[ {{\begin{array}{llllll} {\Omega _l }&{} {\Omega _l }&{} {v_x }&{} {F_{rg} }&{} {R_l }&{} {R_r } \\ \end{array} }} \right] ^{T}:\) state vector of the observation model.

The dynamic behavior of the whole axle is given by:

$$\begin{aligned} \dot{x}=\left[ {\begin{array}{c} - \frac{1}{J_l }\left( {x_5 F_{xl} (x)+C_f x_1 } \right) \\ - \frac{1}{J_r }\left( {x_6 F_{xr} (x)+C_f x_2 } \right) \\ \frac{1}{M_{1/2} }\left( {F_{xl} (x)+F_{xr} (x)-F_{d1/2} (x)-x_4 } \right) \\ \eta _l \\ \eta _l \\ \eta _g \\ \end{array}} \right] +\left[ {{\begin{array}{ll} {\begin{array}{l} \frac{1}{J_l } \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array}}&{} {\begin{array}{l} 0 \\ \frac{1}{J_r } \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array}} \\ \end{array} }} \right] u \end{aligned}$$
(54)

with measurements \(y=\left[ {{\begin{array}{lll} {y_1 }&{} {y_2 }&{} {y_3 } \\ \end{array} }} \right] ^{T}=\left[ {{\begin{array}{lll} {x_1 }&{} {x_2 }&{} {x_3 } \\ \end{array} }} \right] ^{T}\). The structure of the effective radii of the observer and the global force of rolling resistance, from the knowledge of the angular velocities \(\Omega _l\) and \(\Omega _r\) and torques applied to each wheels \(T_l\) and \(T_r\), is based on the observation model and the strategy of higher order sliding modes [16]. The terms \(-\frac{C_f }{J_l }x_1 +\frac{1}{J_l }u_1 , -\frac{C_f }{J_l }x_2 +\frac{1}{J_l }u_2\) depend only of known variables. Thus, system (54) can be written as:

$$\begin{aligned} \dot{x}=f(x)+\Delta f+\chi (y,u) \end{aligned}$$
(55)

where

$$\begin{aligned} f(x)=\left[ {\begin{array}{c} -\frac{1}{J_l }x_5 F_{xl} (x) \\ -\frac{1}{J_r }x_6 F_{xr} (x) \\ \frac{1}{M_{1/2} }(F_{xl} (x)+F_{xr} (x)-F_{d1/2} (x)-x_4 ) \\ 0 \\ 0 \\ 0 \\ \end{array}} \right] \end{aligned}$$
(56)
$$\begin{aligned} \Delta f=\left[ {{\begin{array}{llllll} 0&{} 0&{} 0&{} {\eta _l (t)}&{} {\eta _r (t)}&{} {\eta _F (t)} \\ \end{array} }} \right] ^{T} \end{aligned}$$
(57)
$$\begin{aligned} \chi (y,u)=\left[ {{\begin{array}{llllll} {-\frac{C_f }{J_l }x_1 +\frac{1}{J_l }u_1 }&{} {-\frac{C_f }{J_r }x_2 +\frac{1}{J_r }u_2 }&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{T} \end{aligned}$$
(58)

Assumptions 3.2.1 and 3.2.2 are satisfied for this system.

6.2 Observability Analysis

In order to analysis the observability of the studied system, the function \(\psi (x)\) is defined by:

$$\begin{aligned} \psi (x)=\left[ {\begin{array}{l} y_1 \\ \dot{y}_1 \\ y_2 \\ \dot{y}_2 \\ y_3 \\ \dot{y}_3 \\ \end{array}} \right] =\left[ {\begin{array}{c} x_1 \\ -\frac{1}{J_l }x_5 F_{xl} (x) \\ x_2 \\ -\frac{1}{J_r }x_5 F_{xr} (x) \\ x_3 \\ \frac{1}{M_{1/2} }(F_{xl} (x)+F_{xr} (x)-F_{d1/2} (x)-x_4 ) \\ \end{array}} \right] \end{aligned}$$
(59)

The measured variables are the wheels’ velocities and the vehicle’s longitudinal speed \(y=\left[ {{\begin{array}{lll} {x_1 }&{} {x_2 }&{} {x_3 } \\ \end{array} }} \right] ^{T}\). If the determinant of the Jacobian of the function \(\psi (x)\) is in all cases different from 0 on the operating trajectories, this implies that the transformation \(\psi \) is invertible and the system (54) is locally observable [5]. In this case, the observability indices vector is equal to \([2\, 2\, 2]^{ T}\).

6.3 Observer Design

According to Sect. 3, the application of the inverse input–output injection transformation \(\chi (y,u)\) allows the observer synthesis for system (54). The observer proposed as part of this problem is based on differentiation of a second order sliding mode. Thus, an observer of (54) is written as:

$$\begin{aligned} \dot{\hat{{x}}}=f(\hat{{x}},y)+\chi (y,x)+\left[ {\frac{\partial \psi }{\partial x}} \right] ^{-1}\left[ {\begin{array}{c} 1.5L_1^{1/2} \left| {y_1 -\hat{{x}}_1 } \right| ^{1/2}{} \textit{sign}(y_1 -\hat{{x}}_1 ) \\ 1.1L_1 \textit{sign}(\gamma _1 ) \\ 1.5L_2^{1/2} \left| {y_2 -\hat{{x}}_2 } \right| ^{1/2}{} \textit{sign}(y_2 -\hat{{x}}_2 ) \\ 1.1L_2 \textit{sign}(\gamma _3 ) \\ 1.5L_3^{1/2} \left| {y_3 -\hat{{x}}_3 } \right| ^{1/2}{} \textit{sign}(y_3 -\hat{{x}}_3 ) \\ 1.1L_3 \textit{sign}(\gamma _5 ) \\ \end{array}} \right] \end{aligned}$$
(60)

\(L_1 =6, L_2 =5 \text { and } L_3 =4\) are observer gains.

6.4 Simulation Results and Discussion

To verify and validate the effectiveness of the observer in more general case, simulation are carried out with full model (48) of the vehicle front axle based on the coupling between the vertical dynamic and front axle wheels modeling. The initial state of the system x(0) is given by:

$$\begin{aligned} \displaystyle \begin{array}{ll} &{} x(0)=\left[ {{\begin{array}{lllllll} {\Omega _l }&{} {\Omega _r }&{} {v_x }&{} {d_c }&{} {\dot{d}_c }&{} {d_r }&{} {\dot{d}_r } \\ \end{array} }} \right] ^{T} \\ &{} \qquad \,\,\, =\left[ {{\begin{array}{lllllll} {\frac{17}{0.3}}&{} {\frac{17}{0.3}}&{} {17}&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{T} \\ \end{array} \end{aligned}$$
(61)

From (61) it is assumed that at starting time, the vehicle vertical displacements \(d_c\) and \(d_r\) as well as wheels positions with their first derivatives are null. The parameters used for the front axle provided by Renault of the system (48) and the observer (60) are summarized in Table 2 [5].

Table 2 Wheels and vehicle model parameters for the axle model
Full size table

The Observer (60) allowing joint estimation of the two wheel effective radii the global rolling resistance forces is initialized by:

$$\begin{aligned} \begin{array}{ll} \hat{{x}}(0)&{}=\left[ {{\begin{array}{llllll} {\hat{{\Omega }}_l }&{} {\hat{{\Omega }}_r }&{} {\hat{{v}}_x }&{} {\hat{{F}}_{rg} }&{} {\hat{{R}}_l }&{} {\hat{{R}}_r } \\ \end{array} }} \right] ^{T} \\ &{} =\left[ {{\begin{array}{llllll} {\frac{17}{0.3}}&{} {\frac{17}{0.3}}&{} {17}&{} {128}&{} {0.302}&{} {0.302} \\ \end{array} }} \right] ^{T} \\ \end{array} \end{aligned}$$
(62)

A case of pneumatic pressure fall of 40 % according to nominal value of 2.3 bar between instants \(\mathrm{t}_{1} = 20\) s and \(\mathrm{t}_{2} = 30\) s is simulated. It is therefore assumed, at the initial time, that there is an error of 8 mm between actual and estimated radii and an error of 2.6 rad/s between actual and estimated angular velocities of each wheel. The control strategy imposes low variable speed.

$$\begin{aligned} v_x ^{d}=v^{d}(1+0.01sin (\omega t)) \end{aligned}$$
(63)

with: \(f=\frac{2\pi }{\omega }=0.05\,\mathrm{Hz}\) and \(v^{d}=40\,\mathrm{km/h}\)

The controller output is then:

$$\begin{aligned} z=R_i \Omega _i -\upsilon _x^d (t) \end{aligned}$$
(64)

From (49) and (64) it comes:

$$\begin{aligned} \begin{array}{ll} \dot{z} &{}=\frac{R_i }{J_i }(T_i -R_i F_x -C_f \Omega _i )+\dot{R}_i \Omega _i -\dot{\upsilon }_x^d \\ &{}=\underbrace{-\frac{R_i }{J_i }(R_i F_x +C_f \Omega _i )+\dot{R}_i \Omega _i -\dot{\upsilon }_x^d }_{\alpha (x,t)}+\underbrace{\frac{R_i }{J_i }}_{\beta (x,t)}T_i \\ &{}=-k\;z \\ \end{array} \end{aligned}$$
(65)

where \(i\in \left\{ {l,r} \right\} \).

Therefore the torque applied to each wheels can be written as follow:

$$\begin{aligned} T_i =\frac{1}{\beta _i }\left[ {-\alpha _i (x,t)-(R_i \Omega _i -\upsilon _x^d (t))} \right] \end{aligned}$$
(66)
Fig. 5
figure 5

Simulation diagram

Full size image

Figure 5 shows the schematic diagram for the simulation of the system and the observer effective radii and the rolling resistance force of the front axle.

The estimation of the left wheel radius, the right wheel radius and the rolling resistance force of the front axle are respectively shown in Figs. 6, 7 and 8. The designed observer ensures a simultaneous control of the two front wheels. It appears that when the pressure is decreased in the tire of the front left wheel, the observer gives a lower value of the left wheel radius and a very high value of rolling resistance force of the whole axle.

Fig. 6
figure 6

Estimated left wheel radius for two tire pressure

Full size image
Fig. 7
figure 7

Estimated right wheel radius for two tire pressures

Full size image
Fig. 8
figure 8

Estimated rolling resistance force of the front axle for two tire pressures

Full size image

It also presents a convergence time (around 10 s) compatible with the objectives of Automobile Manufacturers (European standard requires the pressure fall detection on a wheel in less than 10 min). The radius of the right front wheel is also estimated, this estimation is constant (Fig. 7).

The increase in the global rolling resistance force can detect a pressure drop; however, this information alone does not allow us to establish which tire presents a pressure fall. The radii of the both wheels are directly connected to their pressure. These graphical representations allow us to establish that the pressure fall comes from the left wheel.

Consequently, the joint estimation of three parameters: left effective radius, right effective radius and rolling resistance force appears to be an adequate tool for monitoring tire pressure.

7 Conclusions

In this chapter, different notions of observability have been recalled, emphasizing mainly on nonlinear systems. Then, the longitudinal and rotational dynamics of the wheels and their coupling with the vertical dynamics of the front axle of the vehicle were studied. This coupling model is used for validation of observer design. The model of longitudinal and rotational dynamics was used for nonlinear observer design which constitutes a major contribution of our work.

The synthesis of a sliding mode observer seeks on non-measurable quantities estimation (left effective radius, right effective radius and rolling resistance force of the whole axle) using only measured quantities (angular speed of each wheel, vehicle speed and useful torque) was designed. The choice of high order sliding modes observer was made for its well-known characteristics of robustness and precision. The results show a satisfactory estimation of effective radii and rolling resistance force for the vehicle front axle.

The future directions of research include:

  • Real-time implementation of the observer studied taking into account the various constraints, in particular the complexity and computation time.

  • Suggest of adequate strategy for observer gain determination or design of adaptive sliding mode observer.

  • Elaboration of a global model of the complete vehicle for the extension of the study to an observation model taking into account simultaneous operation of the 4 wheels.

  • Use of one or two pressure sensors for indirect approach elaboration [18].