1 Introduction

Many control systems in nowadays cars, contribute to achieve good driving performances together with a comfortable and safe transportation. Safety is a key factor, and it must be guaranteed in different and/or unexpected driving conditions. One of the most critical aspects of transportation safety is the car stability that is most threatened when facing critical driving situations such as extreme steering manoeuvres, sudden tyre-road friction coefficient changing or emergency braking. To this end, an active control strategy is compulsory for a vehicle to improve steerability and to maintain the vehicle stability during critical situations.

Active safety systems generally rely on a real-time knowledge of the vehicle dynamic behaviour. The state (velocities and forces) of a vehicle cannot be completely supplied in a feedback scheme unless using very advanced and expensive sensors. Such devices are not suitable for production cars, and safety-relevant state variables must be then estimated based on common available car sensors.

Vehicle state estimation has been subject of investigation for numerous research papers. Using a GPS alongside with measured acceleration and yaw rate, supplied by inertial sensors, the state of the vehicle has been estimated using kinematic Kalman filter (KKF) [1] and nonlinear observers [2]. In [3], the integration of inertial navigation system sensors with GPS measurements demonstrated more accurate estimates of the vehicle states. Nevertheless, when an estimation scheme is based on GPS, it is usually penalized by the poor accuracy of usually implemented ones and their lack of reception in some geographical areas [4].

On the other hand, vehicle velocities can be estimated using road-tyre models with an observer based on friction lateral and longitudinal forces. In addition to an accurate tyre model, a good perception of the road condition is essential for such an estimation scheme to be efficient.

Kalman filters have been widely used in the literature to estimate either the vehicle state or parameters. This algorithm is based on the use of an adaptive square-root cubature Kalman filter and on the principle of similarities. A dual extended Kalman filter (DEKF) has been appraised in [5] when estimating the longitudinal and lateral states alongside the vehicle parameters. In [6,7,8], vehicle longitudinal and lateral velocities, yaw rate and tyre parameters have been estimated using extended Kalman filter (EKF), and in [9], smooth variable structure filter (SVSF) has been used for the sideslip angle estimation to tackle modelling errors and enhance the estimation robustness. An unknown input observer was employed in [10] for estimating the lateral dynamics of the vehicle.

Unscented Kalman filters (UKF) have been introduced for the state estimation and vehicle’s lateral dynamics estimation in [11, 12] respectively. In [11], a planar two-track model has been combined with the empiric tyre Magic formula to describe the vehicle and tyre behaviour. The accuracy has been increased with advanced vertical tyre load calculation considering tyre stiffness. and increases the estimation accuracy. In [12], a qualitative comparison between EKF and UKF has been presented. More recently, authors in [13] discussed a novel method for the side-slip angle and roll angle estimation based on EKF. They included to the basic EKF algorithm a fusion algorithm integrating side-slip angle rate to compensate the side-slip angle estimate. The estimation strategy demonstrated improved accuracy. An adaptive square root cubature Kalman filter (ASCKF)-based estimator has been proposed, in [14, 15], alongside an integral correction fusion algorithm to compensate the estimation error in the presence of coloured sensor noise.

Sliding mode observers (SMO) have also been suggested to address the vehicle state and/or parameters, estimation especially in the presence of external disturbances and/or parameters uncertainties. In [16, 17], a robust \({H}_{\infty }\) SMO and a finite-frequency mixed \({H}_{-}/{H}_{\infty }\) gain scheduling observer (GSO) have been suggested, respectively. The authors targeted an electric ground vehicle, yet they converted the nonlinear vehicle model to a linear parameter varying (LPV) form. In [18], a SMO has been compared to a linear vehicle model-based linear observer, extended Luenberger observer (ELO) and EKF.

However, all these studies, have simplified the observer design assuming linear tyre models.

Nonlinear models play a fundamental role in modelling complex systems, providing a more realistic approach to describing relationships that cannot be adequately represented by linear models [19,20,21]. To accurately describe the tyre behaviour, there are nonlinear empirical and physical models. A well-known model for the automotive engineering community is the Pacejka tyre model [22]. It is widely used, and it relies on the magic formula that describes the longitudinal force and side force based on the longitudinal slip and slip angle, respectively. The model is empirical, so its parameters strongly rely on experimental tyre data and may lack of accuracy. Unlike the empirical ones, physical tyre models, typically LuGre tyre model [23] and brush tyre model [24], can accurately describe the tyre behaviour. Nevertheless, their complex structure, including too many tyre parameters, makes their use very hard especially in real-time applications. A trade-off between accuracy and simplicity may be achieved using semi-empirical nonlinear tyre model like the Dugoff one [25].

The main drawbacks of the above-mentioned observation techniques are their sensitiveness to parameters uncertainties. Furthermore, in the above-mentioned research papers, the observer/estimator stability analysis is rarely performed when nonlinear tyre models are assumed. In this paper, a sliding mode observer is proposed to estimate the longitudinal velocity, the lateral velocity, and the yaw rate for a four-wheel ground vehicle. The stability analysis is performed based on Lyapunov theory and the robustness of the observer is examined under a very challenging simulation scenario.

The rest of this paper are organized as follows. The four-wheel front steering vehicle is modelled in the next section. The dynamic equations of the rigid chassis are derived, and the tyre/road friction forces adopted model is presented. In Sect. 3, the SMO is designed. The estimation error dynamic is derived, and the stability analysis is performed using a Lyapunov quadratic function alongside with the Sylvester criterion. Simulation results and relevant discussion are presented in Sect. 4, while Sect. 5 concludes the paper.

2 Vehicle modelling

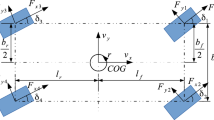
A schematic of the vehicle model used in this paper is sketched in Fig. 1. The vehicle body is assumed to be rigid, so suspension dynamics are neglected. The equations of motion are then derived using Newton’s rule.

Fig. 1
figure 1

Schematic of the 3-DOF vehicle model

Full size image

The rigid body dynamics with respect to the centre of gravity (CoG) coordinate system can be written for longitudinal, lateral and yaw motions, respectively, as follows [26, 27]:

$$m{\dot{v}}_{x}=m{v}_{y}r+\left({F}_{x1}+{F}_{x2}+{F}_{x3}+{F}_{x4}\right)$$
(1)
$$m{\dot{v}}_{y}=-m{v}_{x}r+\left({F}_{y1}+{F}_{y2}+{F}_{y3}+{F}_{y4}\right)$$
(2)
$${I}_{z}\dot{r}=\frac{{b}_{\text{f}}}{2}\left({F}_{x1}{-F}_{x2}\right)+\frac{{b}_{\text{r}}}{2}\left({F}_{x3}{-F}_{x4}\right)+{l}_{\text{f}}\left({F}_{y1}+{F}_{y2}\right)-{l}_{\text{r}}\left({F}_{y3}+{F}_{y4}\right)$$
(3)

This figure provides a detailed schematic of the 3-DOF vehicle model. Gray rectangles represent the wheels, with arrows indicating applied forces and associated distances. Vehicle velocity v and yaw rate r are depicted by arrows, and the x and y axes provide visual reference. This concise yet informative description aims to facilitate a clear understanding of the 3-DOF vehicle model.

In this paper, only front wheel steering \(\delta \) is considered, so \({\delta }_{1}={\delta }_{2}=\delta \), and \({\delta }_{3}={\delta }_{4}=0\). Tyre friction longitudinal forces \({F}_{ti}\) and friction lateral forces \({F}_{si}\) are related to the longitudinal and lateral tyre forces as follows [26, 27]:

$${F}_{x1}={F}_{t1}{\text{cos}}\left(\delta \right)- {F}_{s1}{\text{sin}}\left(\delta \right)$$
(4)
$${F}_{x2}={F}_{t2}{\text{cos}}\left(\delta \right)- {F}_{s2}{\text{sin}}\left(\delta \right)$$
(5)
$${F}_{x3}={F}_{t3}$$
(6)
$${F}_{x4}={F}_{t4}$$
(7)
$${F}_{y1}={F}_{t1}{\text{sin}}\left(\delta \right)+{F}_{s1}{\text{cos}}\left(\delta \right)$$
(8)
$${F}_{y2}={F}_{t2}{\text{sin}}\left(\delta \right)+{F}_{s2}{\text{cos}}\left(\delta \right)$$
(9)
$${F}_{y3}={F}_{s3}$$
(10)
$${F}_{y4}={F}_{s4} $$
(11)

By combining the above equations, the dynamic model of the vehicle is as follows:

$$\left[\begin{array}{c}{\dot{v}}_{x}\\ {\dot{v}}_{y}\\ \dot{r}\end{array}\right]=\left[\begin{array}{c}{v}_{y}r\\ -{v}_{x}r\\ 0\end{array}\right]+{B}_{x}\left(\delta \right){F}_{t}+{B}_{y}\left(\delta \right){F}_{s}$$
(12)

where \({F}_{t}={\left[{F}_{t1} {F}_{t2} {F}_{t3} {F}_{t4}\right]}^{T}\), \({F}_{s}={\left[{F}_{s1} {F}_{s2} {F}_{s3} {F}_{s4}\right]}^{T}\),

$${B}_{x}\left(\delta \right)=\left[\begin{array}{cccc}\frac{cos\left(\delta \right)}{m}& \frac{cos\left(\delta \right)}{m}& \frac{1}{m}& \frac{1}{m}\\ \frac{sin\left(\delta \right)}{m}& \frac{sin\left(\delta \right)}{m}& 0& 0\\ \frac{\left({l}_{\text{f}}sin\left(\delta \right)+\frac{{b}_{\text{f}}}{2}cos\left(\delta \right)\right)}{{I}_{z}}& \frac{\left({l}_{\text{f}}sin\left(\delta \right)-\frac{{b}_{\text{f}}}{2}cos\left(\delta \right)\right)}{{I}_{z}}& \frac{{b}_{\text{r}}}{2}& -\frac{{b}_{\text{r}}}{2}\end{array}\right]$$

and

$${B}_{y}\left({\delta }_{i}\right)=\left[\begin{array}{cccc}\frac{-sin\left(\delta \right)}{m}& \frac{-sin\left(\delta \right)}{m}& 0& 0\\ \frac{cos\left(\delta \right)}{m}& \frac{cos\left(\delta \right)}{m}& \frac{1}{m}& \frac{1}{m}\\ \frac{\left({l}_{\text{f}}cos\left(\delta \right)-\frac{{b}_{\text{f}}}{2}sin\left(\delta \right)\right)}{{I}_{z}}& \frac{\left({l}_{\text{f}}cos\left(\delta \right)+\frac{{b}_{\text{f}}}{2}sin\left(\delta \right)\right)}{{I}_{z}}& -\frac{{l}_{\text{r}}}{2}& -\frac{{l}_{\text{r}}}{2}\end{array}\right]$$

Friction longitudinal and lateral forces, \({F}_{ti}\) and \({F}_{si}\), respectively, are calculated based on the Pacejka tyre model [22, 28] which we assume the same for the four wheels \(\left(i=1\cdots 4\right)\) (cf. Fig. 2).

Fig. 2
figure 2

Pacejka tyre model

Full size image

Figure 2 graphically represents the Pacejka tire model by depicting the variation of the friction coefficient \(\mu \) with respect to the slip ratio \(\lambda \). \({\lambda }_{m}\) representing the slip ratio associated with the maximum friction coefficient, and \({\mu }_{s}\), the asymptotic value of \(\mu \) as \(\lambda \) approaches infinity. These points are vital in computing the parameters of the Pacejka model, including C, B, and E.

Friction forces depend on the longitudinal and lateral \({i}{\text{th}}\) wheel slip ratios \({\lambda }_{xi} {\lambda }_{yi}\) respectively, and they are given by:

$${F}_{ti}={F}_{zi} f\left({\lambda }_{xi}\right)$$
(13)
$${F}_{si}={F}_{zi} f\left({\lambda }_{yi}\right) $$
(14)

where \({F}_{zi}\) is the normal load on the \({i}^{th}\) wheel, and:

$$f\left(\lambda \right)= \mu {\text{sin}}\left(C\text{ atan}\left(B\lambda -E\left(B\lambda -{\text{atan}}\left(B\lambda \right)\right)\right)\right)$$
(15)

Pacejka tyre model parameters are defined as follows [22, 28]:

$$C=\frac{2}{\pi }{{\text{sin}}}^{-1}\left(\frac{{\mu }_{s}}{\mu }\right) $$
(16)
$$B=\frac{\mu }{{\lambda }_{m}C} $$
(17)
$$E=\frac{B{\lambda }_{m}-{\text{tan}}\left(\frac{\pi }{2C}\right)}{B{\lambda }_{m}-{{\text{tan}}}^{-1}\left(B{\lambda }_{m}\right)}$$
(18)

The normal load on a tyre is not only influenced by the vehicle weight. It also depends on the fore-aft location of the vehicle centre of gravity and longitudinal acceleration. For wheels \(1\) to \(4\), the normal loads are respectively given by [29]:

$${F}_{z1}=\frac{m}{\left({l}_{\text{f}}+{l}_{\text{r}}\right)}\left(0.5g{l}_{\text{r}}-0.5{\dot{v}}_{x}h-\frac{{l}_{\text{r}}}{{b}_{\text{f}}}{\dot{v}}_{y}h\right) $$
(19)
$${F}_{z2}=\frac{m}{\left({l}_{\text{f}}+{l}_{\text{r}}\right)}\left(0.5g{l}_{\text{r}}-0.5{\dot{v}}_{x}h+\frac{{l}_{\text{r}}}{{b}_{\text{f}}}{\dot{v}}_{y}h\right)$$
(20)
$${F}_{z3}=\frac{m}{\left({l}_{\text{f}}+{l}_{\text{r}}\right)}\left(0.5g{l}_{\text{f}}+0.5{\dot{v}}_{x}h-\frac{{l}_{\text{f}}}{{b}_{\text{r}}}{\dot{v}}_{y}h\right) $$
(21)
$${F}_{z4}=\frac{m}{\left({l}_{\text{f}}+{l}_{\text{r}}\right)}\left(0.5g{l}_{\text{f}}+0.5{\dot{v}}_{x}h+\frac{{l}_{\text{f}}}{{b}_{\text{r}}}{\dot{v}}_{y}h\right)$$
(22)

Longitudinal and lateral slip ratios are given by [2]:

$${\lambda }_{xi}=\frac{\left({\omega }_{i}{R}_{w}-{V}_{xi}\right)}{{V}_{xi}} $$
(23)
$${\lambda }_{yi}={\text{sin}}\left({\alpha }_{i}\right)$$
(24)

where \({V}_{xi}\), the velocities in x-direction of the wheel coordinate systems, and \({\alpha }_{i}\), the tyre slip angle, are respectively given by [2]:

$${V}_{xi}=\sqrt{\left({{v}_{xi}}^{2}+{{v}_{yi}}^{2}\right)}{\text{cos}}\left({\alpha }_{i}\right) \left(i=1,\ldots 4\right) $$
(25)
$${\alpha }_{i}={\delta }_{i}-{{\text{tan}}}^{-1}\left(\frac{{v}_{yi}}{{v}_{xi}}\right) \left(i=1,\ldots, 4\right)$$
(26)

The longitudinal and lateral velocities at the wheel centre relatively to the body-fixed coordinate system are given by:

$${v}_{x1}={v}_{x}-\frac{r{b}_{\text{f}}}{2}$$
(27)
$${v}_{y1}={v}_{y}-r{l}_{\text{f}}$$
(28)
$${v}_{x2}={v}_{x}+\frac{r{b}_{\text{f}}}{2}$$
(29)
$${v}_{y2}={v}_{y}+r{l}_{\text{f}}$$
(30)
$${v}_{x3}={v}_{x}-\frac{r{b}_{\text{r}}}{2}$$
(31)
$${v}_{y3}={v}_{y}-r{l}_{\text{r}} $$
(32)
$${v}_{x4}={v}_{x}+\frac{r{b}_{\text{r}}}{2}$$
(33)
$${v}_{y4}={v}_{y}-r{l}_{\text{r}} $$
(34)

Finally, the \({i}^{{\text{th}}}\) wheel rotational speed is related to the traction/braking respective torque \({T}_{i}\) as follows:

$${I}_{z}{\dot{\omega }}_{i}={T}_{i}-{F}_{xi}{R}_{w} \left(i=1,\ldots, 4\right) $$
(35)

3 Sliding mode observer design

In this section, a nonlinear sliding mode observer is proposed to give an estimation for the vehicle’s longitudinal and lateral velocities \({v}_{x}\) and \({v}_{y}\) as well as yaw rate \(r\). The observer design is based on the dynamic model derived in the previous section and lies on the following assumptions:

Assumption 1

The vehicle longitudinal acceleration \({a}_{x}\), lateral acceleration \({a}_{y}\), yaw rate \(r\), wheel speeds \({\omega }_{i}\) and front-wheel steering \(\delta \) are available outputs.

Assumption 2

The tyre-road friction coefficient for each wheel \({\mu }_{i}\left(i=1,\ldots, 4\right)\) is known.

Both assumptions are reasonable since lateral acceleration and yaw rate are available outputs via appropriate sensors in cars equipped with electronic stability program (ESP), and longitudinal acceleration is obtained with a separate inertial measurement unit (IMU) [2, 30, 31]. The tyre-road friction coefficient can be measured or estimated as discussed in [32, 33].

Let:

$${F}_{x}=\sum_{i=1}^{4}{F}_{xi}=m{a}_{x}$$
(36)
$${F}_{y}=\sum_{i=1}^{4}{F}_{yi}=m{a}_{y}$$
(37)
$${M}_{z}=\frac{{b}_{\text{f}}}{2}\left({F}_{x1}{-F}_{x2}\right)+\frac{{b}_{\text{r}}}{2}\left({F}_{x3}{-F}_{x4}\right)+{l}_{\text{f}}\left({F}_{y1}+{F}_{y2}\right)-{l}_{\text{r}}\left({F}_{y3}+{F}_{y4}\right)$$
(38)

The vehicle dynamics are then written as follows:

$${\dot{v}}_{x}={v}_{y}r+{a}_{x}$$
(39)
$${\dot{v}}_{y}=-{v}_{x}r+{a}_{y} $$
(40)
$$\dot{r}=\frac{{M}_{z}}{{I}_{z}}$$
(41)

In this paper, we propose and analyse the following observer:

$${\dot{\widehat{v}}}_{x}={\widehat{v}}_{y}r+{a}_{x}-{k}_{{v}_{x}}{\text{sign}}\left({F}_{x}-{\widehat{F}}_{x}\right)$$
(42)
$${\dot{\widehat{v}}}_{y}=-{\widehat{v}}_{x}r+{a}_{y}-{k}_{{v}_{y}}{\text{sign}}\left({F}_{y}-{\widehat{F}}_{y}\right)$$
(43)
$$\dot{\widehat{r}}=\frac{{\widehat{M}}_{z}}{{I}_{z}}+{k}_{\text{r}}{\text{sign}}\left(r-\widehat{r}\right)$$
(44)

Using the vehicle/observer dynamic Eqs. (39) to (44), the observation error dynamics are then given by:

$${\dot{\widetilde{v}}}_{x}={\widetilde{v}}_{y}r+{k}_{{v}_{x}}{\text{sign}}\left({F}_{x}-{\widehat{F}}_{x}\right)$$
(45)
$${\dot{\widetilde{v}}}_{y}=-{\widetilde{v}}_{x}r+{k}_{{v}_{y}}{\text{sign}}\left({F}_{y}-{\widehat{F}}_{y}\right)$$
(46)
$$\dot{\widetilde{r}}=\frac{1}{{I}_{z}}\left({M}_{z}-{\widehat{M}}_{z}\right)-{k}_{\text{r}}{\text{sign}}\left(\widetilde{r}\right) $$
(47)

where \({\widetilde{v}}_{x}={v}_{x}-{\widehat{v}}_{x}\), \({\widetilde{v}}_{y}={v}_{y}-{\widehat{v}}_{y}\) and \(\widetilde{r}=r-\widehat{r}\).

The observer stability is discussed using the following quadratic Lyapunov function:

$$V=\frac{1}{2}\left({{\widetilde{v}}_{x}}^{2}+{{\widetilde{v}}_{y}}^{2}+{\widetilde{r}}^{2}\right)$$
(48)

The Lyapunov function time derivative along the trajectories (45)–(47) is given by:

$$\dot{V}={k}_{{v}_{x}}{\text{sign}}\left({F}_{x}-{\widehat{F}}_{x}\right){\widetilde{v}}_{x}+{k}_{{v}_{y}}{\text{sign}}\left({F}_{y}-{\widehat{F}}_{y}\right){\widetilde{v}}_{y}+ \widetilde{r}\frac{\left({M}_{z}-{\widehat{M}}_{z}\right)}{{I}_{z}}-{k}_{\text{r}}{\text{sign}}\left(\widetilde{r}\right)\widetilde{r} $$
(49)

To demonstrate the negative definiteness of the above-mentioned Lyapunov function time derivative, we use the approximate signum function \({{\text{sign}}}_{{\text{apr}}}(x)\) defined as follows:

$${{\text{sign}}}_{{\text{apr}}}\left(x\right)=\frac{x}{\left|x\right|+\eta }$$
(50)

where \(\eta \) is a small positive scalar.

Define also:

$${k}_{x}=\frac{{k}_{{v}_{x}}}{\left|{F}_{x}-{\widehat{F}}_{x}\right|+\eta }$$
(51)
$${k}_{y}=\frac{{k}_{{v}_{y}}}{\left|{F}_{y}-{\widehat{F}}_{y}\right|+\eta }$$
(52)
$${k}_{rr}=\frac{{k}_{\text{r}}}{\left|r-\widehat{r}\right|+\eta }$$
(53)

The time derivative of the Lyapunov function is then:

$$\dot{V}={k}_{x}\left({F}_{x}-{\widehat{F}}_{x}\right){\widetilde{v}}_{x}+{k}_{y}\left({F}_{y}-{\widehat{F}}_{y}\right){\widetilde{v}}_{y}+ \widetilde{r}\frac{\left({M}_{z}-{\widehat{M}}_{z}\right)}{{I}_{z}}-{k}_{rr}{\widetilde{r}}^{2}$$
(54)

Based on the friction forces model, as discussed in [2], there exist positive constants \({c}_{i}\),\(i =1,\ldots, 9\), such that:

$$\left({F}_{x}-{\widehat{F}}_{x}\right){\widetilde{v}}_{x}\le -{c}_{1}{{\widetilde{v}}_{x}}^{2}+{c}_{2}\left|{\widetilde{v}}_{x}\right|\left|{\widetilde{v}}_{y}\right|+{c}_{3}\left|{\widetilde{v}}_{x}\right|\left|\widetilde{r}\right|$$
(55)
$$\left({F}_{y}-{\widehat{F}}_{y}\right){\widetilde{v}}_{y}\le {c}_{4}\left|{\widetilde{v}}_{y}\right|\left|{\widetilde{v}}_{x}\right|-{c}_{5}{{\widetilde{v}}_{y}}^{2}+{c}_{6}\left|{\widetilde{v}}_{y}\right|\left|\widetilde{r}\right|$$
(56)
$$\widetilde{r}\frac{\left({M}_{z}-{\widehat{M}}_{z}\right)}{{I}_{z}}\le {c}_{7}\left|{\widetilde{v}}_{x}\right|\left|\widetilde{r}\right|+{c}_{8}\left|{\widetilde{v}}_{y}\right|\left|\widetilde{r}\right|+{c}_{9}{\widetilde{r}}^{2}$$
(57)

Using (54) and (55)–(57), we have:

$$\begin{aligned}\dot{V}&\le {k}_{x}\left(-{c}_{1}{{\widetilde{v}}_{x}}^{2}+{c}_{2}\left|{\widetilde{v}}_{x}\right|\left|{\widetilde{v}}_{y}\right|+{c}_{3}\left|{\widetilde{v}}_{x}\right|\left|\widetilde{r}\right|\right)\\ & \quad +{k}_{y}\left({c}_{4}\left|{\widetilde{v}}_{y}\right|\left|{\widetilde{v}}_{x}\right|-{c}_{5}{{\widetilde{v}}_{y}}^{2}+{c}_{6}\left|{\widetilde{v}}_{y}\right|\left|\widetilde{r}\right|\right)\\&+\left({c}_{7}\left|{\widetilde{v}}_{x}\right|\left|\widetilde{r}\right|+{c}_{8}\left|{\widetilde{v}}_{y}\right|\left|\widetilde{r}\right|+{c}_{9}{\widetilde{r}}^{2}\right)-{k}_{rr}{\widetilde{r}}^{2}\le {\widetilde{x}}^{T}Q\widetilde{x}\end{aligned}$$
(58)

where \(\widetilde{x}={\left[\begin{array}{ccc}{\widetilde{v}}_{x}& {\widetilde{v}}_{y}& \widetilde{r}\end{array}\right]}^{T}\), and

$$Q=\left[\begin{array}{ccc}-{k}_{x}{c}_{1}&\quad \frac{1}{2}\left({k}_{x}{c}_{2}+{k}_{y}{c}_{4}\right)&\quad \frac{1}{2}\left({k}_{x}{c}_{3}+{c}_{7}\right)\\ \frac{1}{2}\left({k}_{x}{c}_{2}+{k}_{y}{c}_{4}\right)&\quad -{k}_{y}{c}_{5}&\quad \frac{1}{2}\left({k}_{y}{c}_{6}+{c}_{8}\right)\\ \frac{1}{2}\left({k}_{x}{c}_{3}+{c}_{7}\right)&\quad \frac{1}{2}\left({k}_{y}{c}_{6}+{c}_{8}\right)& \quad {c}_{9}-{k}_{rr}\end{array}\right]$$
(59)

According to the well-known Sylvester criterion, matrix \(Q\) is negative definite if and only if all its leading principal minors are negative.

The first principal minor of \(Q\) is \(-{k}_{x}{c}_{1}\), so \({k}_{x}\) must be positive. The second principal minor is given by:

$$\begin{aligned}&{k}_{x}{c}_{1}{k}_{y}{c}_{5}-\frac{1}{4}{\left({k}_{x}{c}_{2}+{k}_{y}{c}_{4}\right)}^{2}\\ & ={k}_{x}{c}_{1}{k}_{y}{c}_{5}-\frac{1}{4}\left({{k}_{x}}^{2}{{c}_{2}}^{2}+{{k}_{y}}^{2}{{c}_{4}}^{2}+2{k}_{x}{c}_{2}{k}_{y}{c}_{4}\right)\\ &=-\frac{1}{4}\left({{k}_{y}}^{2}{{c}_{4}}^{2}+2{k}_{y}{c}_{4}\frac{{k}_{x}\left({c}_{2}{c}_{4}-2{c}_{1}{c}_{5}\right)}{{c}_{4}}+{{k}_{x}}^{2}{{c}_{2}}^{2}\right)\\ &=-\frac{1}{4}{\left({k}_{y}{c}_{4}+\frac{{k}_{x}\left({c}_{2}{c}_{4}-2{c}_{1}{c}_{5}\right)}{{c}_{4}}\right)}^{2}\\ & -\frac{{{k}_{x}}^{2}}{4}\left({{c}_{2}}^{2}-{\left(\frac{\left({c}_{2}{c}_{4}+2{c}_{1}{c}_{5}\right)}{{c}_{4}}\right)}^{2}\right)<0 \end{aligned}$$
(60)

So:

$$\frac{1}{4}{\left({k}_{y}{c}_{4}+\frac{{k}_{x}\left({c}_{2}{c}_{4}-2{c}_{1}{c}_{5}\right)}{{c}_{4}}\right)}^{2}>\frac{{{k}_{x}}^{2}}{4}\left({\left(\frac{\left({c}_{2}{c}_{4}+2{c}_{1}{c}_{5}\right)}{{c}_{4}}\right)}^{2}-{{c}_{2}}^{2}\right) $$
(61)

And:

$${k}_{y}>\frac{{k}_{x}}{{c}_{4}}\left(\sqrt{\left({\left(\frac{\left({c}_{2}{c}_{4}+2{c}_{1}{c}_{5}\right)}{{c}_{4}}\right)}^{2}-{{c}_{2}}^{2}\right)}-\frac{\left({c}_{2}{c}_{4}-2{c}_{1}{c}_{5}\right)}{{c}_{4}}\right) $$
(62)

The third principal minor, which is the matrix determinant, is given by:

$$\begin{aligned}{\text{det}}\left(Q\right)&=-{k}_{x}{c}_{1}\left(-{k}_{y}{c}_{5}\left({c}_{9}-{k}_{rr}\right)-\frac{1}{4}{\left({k}_{y}{c}_{6}+{c}_{8}\right)}^{2}\right)\\ &-\frac{1}{2}\left({k}_{x}{c}_{2}+{k}_{y}{c}_{4}\right)\Bigg(\frac{1}{2}\left({k}_{x}{c}_{2}+{k}_{y}{c}_{4}\right)\left({c}_{9}-{k}_{rr}\right)\\ & \quad -\frac{1}{4}\left({k}_{y}{c}_{6}+{c}_{8}\right)\left({k}_{x}{c}_{3}+{c}_{7}\right)\Bigg)\\ & +\frac{1}{2}\left({k}_{x}{c}_{3}+{c}_{7}\right)\Bigg(\frac{1}{4}\left({k}_{x}{c}_{2}+{k}_{y}{c}_{4}\right)\left({k}_{y}{c}_{6}+{c}_{8}\right)\\ & \quad -\frac{1}{2}\left({k}_{x}{c}_{3}+{c}_{7}\right){k}_{y}{c}_{5}\Bigg)\end{aligned}$$
(63)

After some tedious calculation, one can notice that the determinant may be made negative by choosing \({k}_{rr}\) large enough.

4 Simulation results

4.1 General model description

In this section, we provide a detailed description of the organizational structure of the three-degrees-of-freedom (3-DOF) vehicle dynamics model and the associated sliding mode observer. The organizational chart offers a visual representation of the internal framework of the model, elucidating key components and their interconnections. This preliminary overview aims to furnish readers with a profound understanding of how the model is articulated before delving into the analysis of simulation results. The following figure illustrates the organizational chart, facilitating a visual grasp of the model's complexity.

Figure 3 provides a detailed depiction of the organizational chart for the three-degrees-of-freedom (3-DOF) vehicle dynamics model, incorporating both the Pacejka tire model and the sliding mode observer. The system's inputs are represented by the steering angle, traction or braking torque, and the friction coefficient. The observer algorithm utilizes longitudinally and laterally measured accelerations, along with wheel speed, as parameters. These variables can be easily obtained through typical sensors. The arrowed connections in the figure illustrate the interactions and information exchanges among these components, offering a comprehensive view of the model's internal structure. This visual representation is carefully crafted to enhance understanding, paving the way for a detailed analysis of simulation results.

Fig. 3
figure 3

General Model Description

Full size image

4.2 Accuracy of the observer

In this section, the performance of the proposed sliding mode observer developed in the previous section is appraised by means of numerical simulation.

The longitudinal acceleration \({a}_{x}\), lateral acceleration \({a}_{y}\), yaw rate \(r\), wheel speeds \({\omega }_{i}\) and front-wheel steering \(\delta \) are available outputs, and the observed state is:

$$\widehat{x}={\left[\begin{array}{ccc}{\widehat{v}}_{x}& {\widehat{v}}_{y}& \widehat{r}\end{array}\right]}^{T} $$
(64)

The observer algorithm has been implemented in Matlab/Simulink environment with a small step time for numerical integration to deal with the system nonlinearities. The step time has been set to \({T}_{s}=5.{10}^{-6}\text{ s}\). The nominal vehicle model used for the simulation is based on the Magic formula tyre model, and Table 1. Shows the numerical parameters that have been adopted.

Table 1 Numerical parameters adopted for simulation
Full size table

Initial states for the nominal plant and for the observer are set to:

$${x}_{0}={\left[\begin{array}{ccc}{v}_{x0}& {v}_{y0}& {r}_{0}\end{array}\right]}^{T}={\left[\begin{array}{ccc}27.78{\text{m}}.{{\text{s}}}^{-1}& 0& 0\end{array}\right]}^{T}$$
(65)
$${\widehat{x}}_{0}={\left[\begin{array}{ccc}{\widehat{v}}_{x0}& {\widehat{v}}_{y0}& {\widehat{r}}_{0}\end{array}\right]}^{T}={\left[\begin{array}{ccc}22.22{\text{m}}.{{\text{s}}}^{-1}& 0.5{\text{m}}.{{\text{s}}}^{-1}& 0.5{\text{rd}}.{{\text{s}}}^{-1}\end{array}\right]}^{T}$$
(65)

During time interval \(\left[0, 15{\text{s}}\right]\), the performance of the observer is examined. First, the vehicle is performing a lane change manoeuvre depicted in Fig. 4. Then, during time interval \(\left[4, 6{\text{s}}\right]\), the braking/accelerating torque shown in Fig. 5 is applied to the corresponding wheels. For time interval \(\left[6, 15{\text{s}}\right]\) a \(\mu -\) split scenario is introduced simultaneously with a lane change, while the vehicle is braking. Such a scenario assumes different contact surfaces for left and right vehicle tyres. For the tyres on a dry asphalt road, the tyre–road friction coefficient is assumed to be of constant value \(\left(\mu =1\right)\), and at time \(t=6{\text{s}}\), it steps to \(\left(\mu =0.5\right)\) for the right wheels (cf. Fig. 6).

Fig. 4
figure 4

The steering angle for the four wheels

Full size image
Fig. 5
figure 5

Braking/accelerating torque profiles for the four wheels

Full size image
Fig. 6
figure 6

The wheel/road friction coefficient for the four wheels

Full size image

This figure illustrates the graphical representation of the steering angle for the four wheels of the vehicle. Each wheel is associated with a specific angle, depicting the configuration of the steering system. This visualization provides a clear understanding of how the wheels respond and contribute to the overall manoeuvrability of the vehicle.

Figure 5 Detailed the graphical profiles of braking and accelerating torques for the four wheels of the vehicle. Each wheel displays its individual profile. This visualization provides a detailed understanding of how these torques act individually on each wheel, influencing the deceleration and acceleration dynamics of the vehicle

This figure presents graphical profiles of the wheel/road friction coefficients for the four wheels of the vehicle. Each wheel displays its individual profile, illustrating the variation of the friction coefficient over time or distance travelled. This visualization provides a detailed insight into how the friction coefficient evolves individually for each wheel, influencing the overall performance of traction and braking.

The upper plot of Fig. 7 depicts the vehicle longitudinal acceleration. Its sign, positive or negative, matches the piecewise braking and acceleration phases, in the driving scenario, respectively. The lateral acceleration catches the steering changing alongside with the braking carried out on the \(\mu \)-split track.

Fig. 7
figure 7

Longitudinal and lateral accelerations

Full size image

Figure 7 presents graphical profiles of the longitudinal and lateral accelerations of the vehicle. The curves depict the evolution of these accelerations over time or distance travelled. This visualization provides a detailed understanding of the vehicle's motion dynamics, highlighting changes in longitudinal and lateral accelerations during different driving phases.

Figure 8 illustrates the longitudinal velocity, lateral velocity and yaw rate estimates given by the sliding mode observer with initial state (66).

Fig. 8
figure 8

Vehicle state estimate with initial condition (66)

Full size image

While facing a notably challenging assessment scenario, our study demonstrates the observer's exceptional performance in estimating key vehicle dynamics parameters throughout the simulation intervals. The accuracy of the observer shines prominently in the estimation of longitudinal velocity, lateral velocity, and yaw rate. Additionally, the observer provides highly accurate estimates even under deliberately introduced challenging initial conditions.

This figure displays the vehicle's state estimate, considering the initial condition specified in Eq. (66). The visualization offers insights into the predicted state of the vehicle based on the given initial conditions, contributing to a comprehensive understanding of the performance of the state estimation process.

These results directly contribute to a holistic understanding of the vehicle's behaviour. The observer, by providing precise estimates of key dynamic parameters, enhances the overall comprehension of the vehicle's dynamic response.

4.3 Robustness of the observer

To examine the robustness of the proposed observer, the vehicle parameters (cf. Table 1) used in the observer algorithm are \(15{\%}\) larger compared to their nominal values used for the vehicle truth model.

Figure 9 illustrates the longitudinal velocity, lateral velocity and yaw rate estimates given by the sliding mode observer with initial state (66). The observer parameters are set to new values summarized in Table 2.

Fig. 9
figure 9

Vehicle state estimate with initial condition (66) under vehicle parameters uncertainties

Full size image
Table 2 Observer parameters for uncertain vehicle parameters
Full size table

This figure illustrates the vehicle's state estimate while considering the initial condition specified in Eq. (66) under uncertainties in vehicle parameters. The visualization provides insights into how the state estimation process performs in the presence of uncertainties, contributing to a comprehensive understanding of the robustness of the estimation algorithm.

Despite deviations in vehicle parameters from their nominal values, our sliding mode observer consistently provides highly accurate estimates of longitudinal velocity and yaw rate throughout all simulation intervals. The lateral velocity estimate remains remarkably acceptable, underscoring the robustness of the proposed sliding mode observer against uncertainties in vehicle parameters. This resilience is a testament to the effectiveness of our observer in maintaining accurate estimations even under varying and uncertain vehicle conditions.

Finally, Fig. 10 illustrates the impact of uncertain tyre/road friction coefficients on our observer's estimation. With a deliberate 20% reduction in the friction coefficient for all wheels throughout the simulation, we observe a slight influence on the lateral velocity estimate. However, it's crucial to highlight that, despite this challenge, both the longitudinal velocity and yaw rate estimates remain remarkably accurate. Importantly, the lateral velocity results, while exhibiting a marginal effect, maintain an acceptable level of reliability. This reaffirms the observer's robustness, demonstrating its ability to provide trustworthy estimations even under conditions of varying friction.

Fig. 10
figure 10

Vehicle state estimate with initial condition (66) under vehicle parameters and friction coefficient uncertainties

Full size image

This figure depicts the vehicle's state estimate considering the initial condition specified in Eq. (66) under uncertainties in both vehicle parameters and friction coefficients. The visualization provides valuable insights into the performance and robustness of the state estimation process in the face of uncertainties in these critical factors.

These results emphasize the observer's ability to maintain accuracy even in the presence of uncertainties in vehicle parameters and the friction coefficient, reinforcing its contribution to the overall control system.

5 Conclusion and perspectives

In this study, we introduced a nonlinear sliding mode observer. Our observer design assumes the availability of measurements such as longitudinal acceleration, lateral acceleration, yaw rate, wheel angular velocities, and wheel steering angle. Based on a planar double-track vehicle model, this design incorporates the Pacejka nonlinear tire model to evaluate friction forces.

The stability analysis of the observer has been thoroughly conducted using a quadratic Lyapunov function in conjunction with the Sylvester criterion. We assessed the robustness of the observer against uncertainties related to vehicle parameters and tire/road friction coefficient.

Sufficient conditions for observer gains have been established, and their numerical values have been defined for simulation, demonstrating promising results. While the driving scenario used for observer evaluation is highly challenging, the state estimation proves to be highly accurate.

The robustness of the proposed observer against uncertainties has been validated through numerical simulation. We conclude that longitudinal velocity and yaw rate are relatively insensitive to vehicle parameters and tire-road friction coefficient uncertainties. However, lateral velocity is slightly affected when the friction coefficient is not well known, although this limitation can be overcome with online estimation.

In summary, our nonlinear sliding mode observer emerges as a robust and effective solution for vehicle state estimation, providing reliable performance even in demanding driving conditions. Looking ahead, several promising research directions emerge to enhance the robustness and applicability of the proposed sliding mode observer. An intriguing avenue involves exploring the integration of additional filtering algorithms, such as the Kalman filter, to further mitigate potential noise impacting acceleration and rotation speed measurements. The utilization of these advanced filtering algorithms could contribute to refining the observer's precision, especially in challenging driving scenarios.

Furthermore, a natural extension of this research would involve investigating the practical implementation of the observer in advanced control algorithms, particularly in anti-lock braking systems (ABS) and traction control systems (ASR). By integrating this observer into these systems, we could fully leverage its precision and robustness capabilities to enhance vehicle stability and performance in diverse conditions. This synergy between the sliding mode observer and advanced control systems could open new perspectives for safer and more responsive vehicles.