Parameterisation of Multi-directional Diffusion Weighted Magnetic Resonance Images of the Heart

Abstract

This study presents a novel method for building parametric representations of myocardial microstructure of the left ventricle from multi-directional diffusion weighted magnetic resonance images (DWI). The direction of maximal diffusion is directly estimated from the DWI signal intensities using finite element field fitting. This framework avoids the need to compute diffusion tensors, which introduces errors due to least squares fitting that are generally neglected when building microstructural models of the heart from DWI. Nodal parameters describing cardiac myocyte orientations throughout a finite element model of the left ventricle were fitted to a series of raw diffusion signals using non-linear least squares optimisation to determine the direction of maximum diffusion. An ex vivo DWI data set from a Wystar-Kyoto rat was processed using the proposed method. The fitted myocyte orientations were compared against conventional diffusion tensor/eigenvector analysis and the degree of correlation was measured using a normalised dot product (nDP). Good agreement (nDP = 0.979) between the new method and the traditional tensor analysis approach was observed for regions of high fractional anisotropy (FA). In regions of low FA, the errors were much more variable, but the proposed method maintains a smoothly varying myocyte angle distribution as is generally used in tissue and organ scale heart models.

1 Introduction

Building heart models for investigating the electrical [1–3], biomechanical [4–7], and energetic function of the heart [8, 9] is crucial to fully understand the underlying effects of cardiac diseases. For such heart models, finite element (FE) interpolation is generally used to describe cardiac geometry and microstructure. These models allow for integration of structural and functional data acquired using various imaging modalities, together with other measurements, such as haemodynamic or electrophysiological recordings, to analyse the electro-mechanics of the heart on a subject-specific basis.

Shape and microstructural tissue organisation are important, well-established determinants of the biomechanical function of the heart. While in vivo measurements of cardiac geometry are readily available via computed tomography, magnetic resonance imaging (MRI), or ultrasound, in vivo microstructural measurements from the whole heart remain sparse and difficult to quantify.

One option for acquiring microstructural information throughout the whole heart is to use diffusion weighted MRI (DWI). This imaging modality exploits the Brownian motion of water molecules within myocardial tissue to determine local anisotropic diffusion in the ventricular walls [10]. Several approaches have been explored to determine myocyte orientations, using either ex vivo or in vivo imaging [11–15]. Typically, a diffusion tensor is derived at each voxel from the acquired DWI, and the direction of maximum water diffusion, as represented by the primary eigenvector of the derived local diffusion tensor, has been found to correlate well with the local histologically-measured myocyte orientation [16, 17]. The myocyte orientation is often represented as a helix angle with respect to the short-axis plane of the heart. FE models typically incorporate the spatial distribution of fibre orientations by interpolating helix angle parameters at the nodes of the FE mesh [2, 5, 6]. Representing and analysing the apparent diffusion with diffusion tensors comes with several drawbacks [18] including: (1) spatial discontinuities in helix angle distributions; and (2) misrepresentation of myocyte orientation in regions of high image noise or low fractional anisotropy (FA).

Fig. 1.

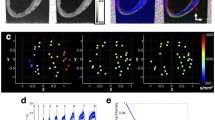
Suitability of representing DWI voxels using a diffusion tensor, as indicated by the coefficient of determination (R$^2$) of the least squares tensor fit for (a) the whole heart and (b) one mid-ventricular slice. Normalised diffusion signals are plotted as vectors at two voxels; one with a low fitting error (high R$^2$) where the vectors can be well represented by an ellipsoid (diffusion tensor), and one with a high fitting error (low R$^2$) where the signals would be poorly represented by an ellipsoid.

A third issue arises from the use of least squares fitting methods when calculating a diffusion tensor for each voxel. This leads to a generally neglected error, which expresses how well a tensor can represent the underlying diffusion behaviour. Figure 1(b) shows a slice extracted from the whole heart (Fig. 1(a)), indicating the coefficient of determination (R$^2$) of the least squares fit for each diffusion tensor¹. If the data can be well represented by a diffusion tensor, the R$^2$ would be close to 1 and therefore the error in fitting a tensor to the data would be low. In these cases, the data show a clear apparent diffusion direction. On the other hand, the diffusion tensor can be a poor representation of the DWI data for some voxels, especially if non-adjacent directions have very high normalised signal strengths. We propose that avoiding the intermediate step of least squares fitting of a diffusion tensor would therefore be useful for understanding the accuracy of the FE field and sensitivity to variation/noise in the DWI data.

In this study we have extended the modelling framework presented in [18] to avoid the least squares error issue by direct parameterisation of the myocyte orientation field from the raw diffusion signals. In contrast to the conventional method, the intermediate step of diffusion tensor calculation is not required in this process and the raw diffusion signals are carried all the way through from image acquisition to the final fibre field fitting process.

2 Methods

2.1 Experimental Procedure

The experimental study was approved by the Animal Ethics Committee of the University of Auckland and conforms to the National Institutes of Health Guide for the Care and Use of Laboratory Animals (NIH Publication No. 85-23).

A Wistar-Kyoto rat heart was excised, perfused with St Thomas cardioplegic solution for relaxation, and fixed using Bouins solution in an approximate end-diastolic state. DWI was performed using a 3D fast spin-echo pulse sequence on a Varian 4.7 T MRI scanner. The image set consisted of 12 short-axis slices with a thickness of 1.5  mm, and no gap between slices; the in-plane resolution was set to 128 voxels $\times$ 64 voxels (zero-pad interpolated to 128 voxels $\times$ 128 voxels) with an in-plane voxel dimension of 156 $\upmu$m $\times$ 156 $\upmu$m. The image data for each slice contained one non-diffusion weighted anatomical image, and 30 diffusion weighted images. The 30 diffusion gradient directions were evenly distributed across a hemisphere. Further details in [18].

2.2 Workflow for Myocyte Orientation Field Parameterisation

The following method was developed to parameterise a spatially-varying myocyte orientation field for the LV myocardium directly from the raw diffusion signals (i.e. without the calculation of diffusion tensors).

Step 1: Image Segmentation and LV FE Geometric Model Construction. The endocardial and epicardial surfaces of the LV, excluding the papillary muscles, were manually segmented from the non-diffusion images using MATLAB². Three landmark points (LV base, LV apex, and right ventricle (RV) base) defined the orientation of the orthogonal cardiac coordinate system (further details in [18]).

A prolate spheroidal-shaped 16-element (4 circumferential, 4 longitudinal and 1 transmural) hexahedral tri-cubic Hermite FE model was customised to the segmented surfaces to represent the LV geometry. The surfaces of the model were fitted using non-linear least squares minimisation.

Step 2: Field-Based Parameterisation of LV Myocyte Orientation. To parameterise the myocyte orientation field throughout the LV FE geometric model, we developed a novel method to estimate spatially-continuous myocyte angle fields (interpolated using tri-cubic Hermite basis functions) that best represent the maximal diffusion direction at all voxels within the LV. Firstly, the myocyte orientation field was initialised by setting the helix angles ($\theta _{(n)}$) to $0^\circ$ for endocardial and epicardial nodes. Initial imbrication angles ($\varphi _{(n)}$) at all nodes were also set to $0^\circ$. Secondly, the FE local coordinates within the LV geometric model were determined for each voxel (v), and an estimate of the myocyte orientation (f $_{(v)}$) at each voxel was interpolated. This was done by Euler angle rotations of vectors [19] by the interpolated angles $\theta _{(n)}$ and $\varphi _{(n)}$.

To express the amount of diffusion along the $j^{\mathrm{th}}$ gradient direction (g $_{(j)}$) we introduced a weight ($w_{(j,v)}$) for direction j in voxel v derived from the basic diffusion equation³:

$$\begin{aligned} S_{(j,v)} = S_{(0,v)} e^{- \gamma ^2 G^2 D_{(j)} \delta ^2 (\varDelta - \frac{\delta }{3})}. \end{aligned}$$

(2)

Rearranging Eq. 2 gives:

$$\begin{aligned} -\ln ({\frac{S_{(j,v)}}{S_{(0,v)}}}) = \gamma ^2 G^2 D_{(j)} \delta ^2 (\varDelta - \frac{\delta }{3}) \equiv w_{(j,v)}. \end{aligned}$$

(3)

Scaling the unit vectors g $_{(j)}$ by $w_{(j,v)}$ provided weighted direction vectors (w $_{(j,v)}$) that represented the magnitude of diffusion along each gradient direction.

Finally, an objective function ($\varPsi$) was constructed:

$$\begin{aligned} \varPsi = \sum _v \sum _j (\mathbf{w}_{(j,v)} \cdot \mathbf{f}_{(v)})^2, \end{aligned}$$

(4)

which is greatest when f $_{(v)}$ is aligned with the directions of w $_{(j,v)}$ with greatest magnitude. The objective function was maximised using non-linear optimisation⁴ by modifying the nodal parameters ($\theta _{(n)}$ and $\varphi _{(n)}$). The method was implemented using the OpenCMISS-Cmgui software package⁵ [20].

2.3 Surrogate Estimate of Fractional Anisotropy

By avoiding the calculation of a diffusion tensor the conventional estimate of FA from the eigenvalues of the diffusion tensor is not available. FA describes how much the ellipsoid associated with a diffusion tensor differs from a sphere. To provide an equivalent index, we derived an estimate of FA from the raw diffusion signals (rdsFA) in a formulation similar to the expression used to compute FA from the eigenvalues of the diffusion tensor [21]:

$$\begin{aligned} \mathrm{rdsFA} = \sqrt{\frac{d}{d-1} \frac{\sum _j (w_{(j)}-\bar{w})^2}{\sum _j w_{(j)}^2}}, \end{aligned}$$

(5)

where d is the number of directions and

$$\begin{aligned} \bar{w} = \frac{1}{d} \sum _j w_{(j)}. \end{aligned}$$

(6)

This enabled a comparison of the relative anisotropy between voxels without the need to compute diffusion tensors. As a comparison with the conventional approach, we found that there was a strong linear correlation between FA and rdsFA (correlation coefficient of R$^2 = 0.9975$).

3 Results

Having fitted the myocyte orientation field to the raw diffusion signals, the myocyte angles were then interpolated at each of the image voxel locations. The result is plotted in Fig. 2(a) using the helix angle to colour-code the myocyte orientation. The helix angle field varied smoothly throughout the LV, with positive angles at the endocardium and negative angles at the epicardial surface.

We compared the fitted myocyte orientations (f $_{(v)}$) with the primary eigenvectors (e $_{1(v)}$) calculated by conventional eigenanalysis of the diffusion tensors. We used a normalised dot product (nDP, see Eq. 7) to quantify the overall alignment of the fitted orientation and the primary eigenvector at each voxel by scaling their dot product by the FA$_{(v)}$ at the corresponding voxel. This accounts for the differing degree of confidence in the calculated eigenvectors since a voxel with a FA of 0 does not have a unique primary eigenvector. nDP ranges from 0 to 1, with 1 representing a perfect alignment of both vectors within an image voxel. The resulting nDP in this study was very close to 1, which suggests a high correlation between the primary eigenvector of the diffusion tensor and the fitted myocyte orientation across all myocardial voxels:

$$\begin{aligned} \text {nDP} = \frac{\sum _{v}(\text {FA}_{(v)} |\mathbf{f}_{(v)} \cdot \mathbf{e}_{1(v)}|)}{\sum _{v}\text {FA}_{(v)}} = 0.979. \end{aligned}$$

(7)

When building personalised models of the heart based on primary eigenvectors of diffusion tensors, it is common to parameterise myocyte orientations using a FE model by interpolating their spatial distribution (after phase-unwrapping). We processed the primary eigenvectors with this approach to provide a comparison set of myocyte orientations (h $_{(v)}$) fitted to the eigenvectors e $_{1(v)}$.

Figure 2(b) presents a map of FA (top) in a mid-ventricular slice, along with the alignment between f $_{(v)}$ and e $_{1(v)}$ (bottom-left), and between f $_{(v)}$ and h $_{(v)}$ (bottom-right). At locations where FA was high, the directions were similar, however significant differences were observed in regions of low FA (highlighted with dashed boxes in Fig. 2(b)). The alignment with spatially-interpolated eigenvectors was much closer, and remaining differences, which tended to arise near boundaries, may have been caused by those voxels containing partial-volume imaging artefacts.

Fig. 2.

(a) Fitted myocyte orientations colour-coded by the interpolated helix angles at all voxels within the LV. (b) A mid-ventricular slice showing (top) FA, and the alignment between interpolated myocyte orientations f $_{(v)}$ and (bottom-left) primary eigenvectors e $_{1(v)}$, and (bottom-right) between f $_{(v)}$ and spatially-interpolated eigenvectors h $_{(v)}$. The dotted squares indicate (top) areas of low FA and (bottom) corresponding regions of poor alignment. The FA spectrum was set to range between 0 and 0.4 to highlight the regional variability (Color figure online).

Figure 3 shows transmural gradients of raw and fitted helix angles at two locations around the LV wall, and illustrates that even in regions of low FA, such as the intersection of LV and RV, this method provided a smoothly varying myocyte angle field.

Fig. 3.

Transmural gradients of helix angle along the indicated lines at the intersection of LV and RV and at the LV free wall. Fitting to the raw diffusion signals (red lines) shows good agreement with the raw helix angles. The result for fitting to the helix angles is illustrated for comparison reasons (Color figure online).

4 Discussion

A novel method was developed to parameterise a continuous myocyte orientation field throughout a FE model of the LV by directly fitting to raw diffusion signals acquired by DWI. This method circumvents issues associated with the eigenanalysis of diffusion tensors that can potentially lead to misrepresentation of the local myocyte orientation. These disadvantages can have a significant impact on electrophysiological and mechanical modelling studies as they affect the description of the electrical, contractile, and passive mechanical constitutive properties of the tissue. In addition, this new method does not assume the diffusion to be best represented by a tensor, and thus avoids the loss of information associated with the least squares fit of the diffusion tensor. Instead of using a voxel-wise data reduction to a tensor, the new method incorporates the spatial distribution of diffusion signals. The error therefore only involves one fitting process instead of two by eliminating the intermediate step of least squares fitting of the diffusion tensor, and requires less computation. It would be possible to further extend this technique to capture microstructural features that are not well represented by a diffusion tensor. One example would be to represent crossing fibres by allowing multiple orientations within a single voxel, and another would be to allow the representation of tissue isotropy (where there is no preferred direction) as it may be found in regions of myocyte disarray. Myocyte orientations estimated using this method agree well with the conventional method of fitting a myocyte field to primary eigenvectors for regions of high FA, within which the primary eigenvector has been shown to reliably represent the local myocyte orientation. In regions of low FA, this method provides continuously varying myocyte orientations. If the main contributor to low FA is noise, then maintaining continuity in the myocyte orientation field despite low FA is an important advantage.

The results suggest that fitting to the raw diffusion signals gives a better representation of the underlying structure than fitting to the primary eigenvectors of diffusion tensors, because the objective function implicitly accounts for variations in FA.

5 Conclusions

In this study, a model-based parameterisation method was proposed to directly interpret diffusion signals provided by ex vivo DWI. Our scheme does not require the conventional calculation of diffusion tensors, but directly fits a myocyte orientation field to spatial distributions of raw diffusion signals. A comparison of the proposed framework with a conventional eigenvector fitting method showed good agreement in regions of high FA, and smooth solutions in regions with low FA. Future studies will include exploring the influence of noise and motion artefacts on the fitting results.