Time-Minimum Control of the Restricted Elliptic Three-Body Problem Applied to Space Transfer

Abstract

In this chapter, we investigate time minimal transfers in the elliptic restricted 3-body problem. We study the controllability of the problem and show that it is small-time locally controllable at the equilibrium points. We present results about the structure of the extremal trajectories, based on a previous study of the time minimum control of the circular restricted 3-body problem. We use indirect numerical methods in optimal control to simulate time-minimizing space transfers using the elliptic model from the geostationary orbit to the equilibrium points $L_1$ and $L_2$ in the Earth-Moon system, as well as a rendezvous mission with a near-Earth asteroid.

1 Introduction

The general three-body problem models the motion of three bodies under their mutual gravitational fields. This classic problem of celestial mechanics [31, 47] has aroused the curiosity of mathematicians for more than three hundred years, since its formulation at the end of the seventeenth century by Isaac Newton [43]. A standard simplification of the general problem consists of considering the motion of a massless body subjected to the gravitational attraction of two main bodies moving in a circular motion around their center of mass. This is the spatial circular restricted three-body problem [48]. When the motion of the massless body is restricted to the plane defined by the motion of the two main bodies, the problem is referred to as the planar circular restricted three-body problem. This problem has been addressed extensively from the geometrical and dynamical systems point of view. In particular, the structure of invariant manifolds in the vicinity of the colinear equilibrium points [32, 33] or complex fractal regions of unstable and chaotic motion in space [8] have been used to design space missions with low energy cost. Recently, optimal control approaches, inspired by founding studies on the Kepler problem [10, 18, 29, 30], have led to new techniques for determining low-thrust space transfers in the Earth-Moon system. In [19, 45], indirect methods of optimal control are used to compute numerical time-minimal and energy-minimal trajectories of the circular restricted three-body problem. These computations provided numerical simulations of low-thrust space transfers from the geostationary orbit to a parking orbit around the Moon [45] and rendezvous missions with near-Earth asteroids temporarily captured by the gravitational field of the Earth [19]. In a contemporary chapter of Caillau and Daoud the authors study the controllability properties of the time-minimum control of the restricted three-body problem and provide an analysis of the structure of the time-minimizing controls [17].

The goal of this chapter is to generalize the results presented in [17] from the circular to the elliptic restricted three-body problem [48]. In this context, the two main bodies are assumed to move on elliptic orbits about their center of mass and the problem is reduced to the circular one when the eccentricity of the orbit is assumed to be zero. The main difference that arises when considering the elliptic case is that the mechanical potential of the problem is non-autonomous. As a consequence, there is no first integral which increases the complexity of the problem. Numerous in-depth studies on the dynamics of the elliptic problem have been carried out to improve the understanding of this model. In the 1960s, research has been conducted on the stability of the triangular equilibrium points and the integrals of motion for orbits with small eccentricities near the two main bodies of the problem [20, 23]. In a more recent past, a canonical transformation based on the Deprit-Hori method of Lie transforms has been applied to normalize the system dynamics about the circular case and one of the triangular points [25, 26]. Resonances and Nekhoroshev stability around triangular points have been analyzed as well [27, 41]. The dynamical properties of the elliptic restricted three-body problem have been applied to space mechanics. Among the greatest examples of such applications, we can mention low-fuel spacecraft missions trajectories constructed using the Lagrangian coherent structures in the problem [28] or moderate $\varDelta v$ Earth-Mars transfers designed using ballistic capture [49]. Techniques from control theory have also been developped to derive quasi-periodic, peridodic and small-Halo orbits around the collinear equilibrium points, stabilize the motion on libration orbits [6, 35] and to investigate solar sail equilibria [7] in the elliptic restricted three-body problem.

This paper examines the structure of the time-minimal trajectories of the elliptic restricted three-body problem, defined as the solutions of a non-autonomous optimal control problem. It is organized as follows. In the first section, we derive the Hamiltonian forms of the controlled equations of both the circular and the elliptic restricted three-body problems to emphasize the intrinsic similarities and differences between these two models. In the second section, we emphasize the non-existence of a first integral as an obstacle to generalize the result of controllability previously established for the circular restricted three-body problem [17] to the elliptic restricted three-body problem. Nevertheless, we obtain a result of local controllability at the equilibrium points of the problem. In the third section, we apply the Pontryagin Maximum Principle and deduce necessary first-order optimality conditions for the time-minimum controls of the elliptic problem. We then study the structure of these time-minimum controls. In particular, we demonstrate the reason that the geometric control analysis performed in [17], based on the bi-input control affine system form of the equations, still holds in the elliptic case. In the fourth section, we introduce a shooting method which we use to compute numerical time-minimizing solutions of the elliptic problem. To overcome the challenges to initialize the algorithm, we use a continuation method [13, 15, 29, 30]. Our algorithm also verifies second-order conditions based on the notion of conjugate points [11] and allow us to generate time-minimum transfers from the geostationary orbit to the collinear equilibrium points $L_1$ and $L_2$ of the elliptic restricted three-body problem for different values of the eccentricity of the orbits of the main bodies. We also simulate a rendezvous mission with a temporarily captured near-Earth asteroid, namely $2006 \mathrm{RH}_{120}$.

2 The Controlled Planar Elliptic Restricted Three-Body Problem

The planar elliptic restricted three-body problem is the simplest generalization of the classic planar circular restricted three-body problem [48], derived from the Newton’s law of universal gravitation [43].

2.1 Controlled Equations of the Planar Circular Restricted Three-Body Problem

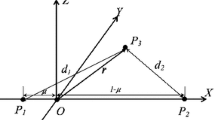
The planar circular restricted three-body problem describes the motion of a massless body M evolving in the the orbital plane of two main bodies called the primaries with constant mass $M_1$ and $M_2$ where $M_1>M_2$, and circularly orbiting at constant angular velocity 1 around their center of mass G under the influence of their mutual gravitational attraction [48]. In this problem, the distance between the two primaries is constant and can be normalized to 1. By defining the mass ratio $\mu =\frac{M_2}{M_1+M_2}$ and using a rotating frame centered at G whose axis of abscissa is set as the line joining the primaries, the location of $M_1$ and $M_2$ can respectively be fixed to $(-\mu ,0)$ and $(1-\mu ,0)$, see Fig. 1. Denoting $(q_1(t),q_2(t))$ as the coordinates of M in the rotating frame at time t, the equations of motion of M are

$$\begin{aligned} \left\{ \begin{aligned} \ddot{q_1}(t) - 2\dot{q_2}(t)&= \frac{\partial V}{\partial q_1}(q_1(t),q_2(t)) \\ \ddot{q_2}(t) + 2\dot{q_1}(t)&= \frac{\partial V}{\partial q_2}(q_1(t),q_2(t)) \end{aligned} \right. \end{aligned}$$

(1)

Fig. 1

Representation of the primaries $M_1$ and $M_2$ of the planar circular restricted three-body problem in both the synodic frame (G, X, Y) and the rotating frame (G, x, y)

where

$$\begin{aligned} V(q_1,q_2)=\frac{q_1^2+q_2^2}{2}+\frac{1-\mu }{\rho _{1}}+\frac{\mu }{\rho _{2}}+\frac{\mu (1-\mu )}{2} \end{aligned}$$

(2)

so $-V$ is the mechanical potential of the problem and

$$\begin{aligned} \rho _{1}=\sqrt{\big ((q_1+\mu )^{2}+q_2^{2}\big )}, \rho _{2}=\sqrt{\big ((q_1-1+\mu )^{2}+q_2^{2}\big )} \end{aligned}$$

are respectively the distances from M to $M_1$ and $M_2$. Using the so-called Legendre transformation $p=(p_1,p_2)=(\dot{q}_1-q_2,\dot{q}_1 + q_2)$, these equations can be written as a Hamiltonian system associated with the Hamiltonian function

$$\begin{aligned} H(q,p)=\frac{1}{2}\Vert p\Vert ^2+p_1q_2-p_2q_1-\frac{1-\mu }{\rho _{1}}-\frac{\mu }{\rho _{2}}+\frac{\mu (1-\mu )}{2}. \end{aligned}$$

The function H is a first integral of motion, called the Jacobian energy, which equals the total energy of the system. Thus we can deduce the five phase portraits for the topology of the possible region of motion, known as the Hill region [48]. The equilibrium points of the problem, defined as the critical points of the potential $-V$, divide into two categories: the collinear points $L_1$, $L_2$ and $L_3$ are located on the horizontal axis $y=0$ joining the primaries and the equilateral points $L_4$ and $L_5$ are located at the vertices of the two equilateral triangles in the plane of motion sharing the same base given by the segment linking the primaries. We can show, using Arnold’s stability theorem [5], that the collinear points are unstable whereas the equilateral points are stable when $\mu < \frac{1}{2}(1-\frac{\sqrt{69}}{9})$. In the Earth-Moon system, whose mass ratio $\mu = 0.0121536$, the colinear points are then stable. The controlled planar restricted three-body problem is simply derived from (1) and is written as

$$\begin{aligned} \left\{ \begin{aligned} \ddot{q_1}(t) - 2\dot{q_2}(t)&= \frac{\partial V}{\partial q_1}(q_1(t),q_2(t))+u_1(t) \\ \ddot{q_2}(t) + 2\dot{q_1}(t)&= \frac{\partial V}{\partial q_2}(q_1(t),q_2(t))+u_2(t) \end{aligned} \right. \end{aligned}$$

(3)

where the control $u(t)=(u_1(t),u_2(t))$ is a bounded measurable function valued in $\mathbf {R}^2$ and defined on an interval $[0,t(u)] \subset \mathbf {R}^+$. We say that u is an admissible control if there exists a solution $q(t)=(q_1(t),q_2(t))$ to (3), called a trajectory associated with u, defined on [0, t(u)]. With the change of variables

$$\begin{aligned} x_1=q_1, x_2=q_2, x_3=\dot{q}_1, x_4=\dot{q}_2, \end{aligned}$$

(4)

we can rewrite (3) as a first-order differential system

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}_1(t)&= x_3(t) \\ \dot{x}_2(t)&= x_4(t) \\ \dot{x}_3(t)&= 2x_4(t) + \frac{\partial V}{\partial x_1}(x_1(t), x_2(t)) + u_1(t) \\ \dot{x}_4(t)&= -2x_3(t) + \frac{\partial V}{\partial x_2}(x_1(t), x_2(t)) + u_2(t). \end{aligned} \right. \end{aligned}$$

(5)

Setting $x=(x_1,x_2,x_3,x_4)$, this system can be written as a so-called bi-input controlled system

$$\begin{aligned} \dot{x}(t)=F_0(x(t))+u_1(t)F_1(x(t))+u_2(t)F_2(x(t)) \end{aligned}$$

(6)

where the vector fields $F_0, F_1$ and $F_2$ are

$$ F_{0}(x)= \left( \begin{array}{c} x_3 \\ x_4\\ 2x_4 + \frac{\partial V}{\partial x_1}(x_1, x_2) \\ -2x_3 + \frac{\partial V}{\partial x_2}(x_1, x_2) \end{array} \right) , F_1(x)=\frac{\partial }{\partial x_3}, F_2(x)=\frac{\partial }{\partial x_4}. $$

Fig. 2

Representation of the primaries $M_1$ and $M_2$ of the planar elliptic restricted three-body problem in both the fixed frame $(G,\varPsi ,\zeta )$ and the rotating frame $(G,\xi ,\eta )$

2.2 Controlled Equations of the Planar Elliptic Restricted Three-Body Problem

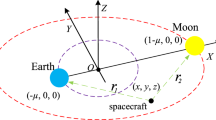
The most natural generalization of the planar circular restricted three-body problem consists of assuming that the two primaries move on elliptic orbits [25, 26, 28, 35, 48]. The smallest primary $M_2$ is orbiting the largest primary $M_1$ within an elliptic orbit with eccentricity $0<e<1$ and semimajor axis a which fits the two-body problem [31]. We denote by $\nu (t)$ the true anomaly of $M_2$, defined as the angular time-dependent parameter given by the angle that the direction of the periapsis of the ellipse makes with the position of $M_2$ along the ellipse at time t. In this context, the instantaneous distance $\rho$ between the two primaries is a function of the true anomaly (Fig. 2)

$$\begin{aligned} \rho (\nu )=\frac{a(1-e^2)}{1+e\cos (\nu )}. \end{aligned}$$

Furthermore, according to the principle of conservation of the angular momentum [43], the dynamics of true anomaly satisfies

$$\begin{aligned} \dot{\nu }=k(M_1+M_2)^{\frac{1}{2}}\frac{(1+e\cos (\nu ))^2}{(a(1-e^2))^{\frac{3}{2}}} \end{aligned}$$

(7)

where k is the universal gravitational constant. The above equation provides a relation between the true anomaly and the time. By choosing the origin of the coordinate system at the center of mass G of the two primaries and the axis of abscissa as the direction of the periapsis of the ellipse, we define an inertial, barycentric coordinate frame in which, up to appropriate normalizations of the units, the primaries $M_1$ and $M_2$ describe ellipses and have respective positions $(\varPsi _1,\zeta _1)$ and $(\varPsi _2,\zeta _2)$ parametrized by

$$\begin{aligned} (\varPsi _1(\nu ),\zeta _1(\nu ))&=\Big ( \frac{-\mu }{1+\cos (\nu )}\cos (\nu ),\frac{-\mu }{1+\cos (\nu )}\sin (\nu )\Big )\\ (\varPsi _2(\nu ),\zeta _2(\nu ))&=\Big ( \frac{1-\mu }{1+\cos (\nu )}\cos (\nu ),\frac{1-\mu }{1+\cos (\nu )}\sin (\nu )\Big ) \end{aligned}$$

where $\mu$ is the mass ratio defined in Sect. 2.1. By considering $\nu$ as the independent variable and introducing a non-uniformly rotating pulsating coordinate system, the respective positions of $M_1$ and $M_2$ can be fixed to $(-\mu ,0)$ and $(1-\mu ,0)$. In this system, the coordinates $(\xi (\nu ),\eta (\nu ))$ of the massless body M satisfy the equations of motion

$$\begin{aligned} \left\{ \begin{aligned} \frac{d^2 \xi }{d\nu ^2}(\nu ) - 2\frac{d\eta }{d\nu }(\nu )&= \frac{\partial \omega }{\partial \xi }(\xi (\nu ),\eta (\nu ),\nu )\\ \frac{d^2 \eta }{d\nu ^2}(\nu ) + 2\frac{d\xi }{d\nu }(\nu )&= \frac{\partial \omega }{\partial \eta }(\xi (\nu ),\eta (\nu ),\nu ) \end{aligned} \right. \end{aligned}$$

(8)

where

$$\begin{aligned} \omega (\xi ,\eta ,\nu ) = \frac{1}{1 + e \cos \nu }V(\xi ,\eta ) \end{aligned}$$

(9)

so $-\omega$ is the non-autonomous mechanical potential of the problem. We remark that the equations of the circular restricted problem Fig. 1 correspond the equations of the elliptic problem (8) when $e=0.$ Using a similar Legendre transformation $q=(q_1,q_2)=(\xi ,\eta ), p=(p_1,p_2)=(\dot{q}_1-q_2,\dot{q}_1 + q_2)$ as in Sect. 2.1, we can rewrite this dynamics as an Hamiltonian system through the new non-autonomous Hamiltonian function

$$\begin{aligned} H_e(q,p,\nu )=\frac{1}{2}\Vert p\Vert ^2+p_1q_2-p_2q_1-\frac{1}{1+e\cos (\nu )}\Big (\frac{1-\mu }{\rho _{1}}+\frac{\mu }{\rho _{2}}-\frac{\mu (1-\mu )}{2}\Big ) \end{aligned}$$

where $\rho _{1}$ and $\rho _{2}$ are still respectively the distances from M to $M_1$ and $M_2$. The function $\omega$ being a multiple of the function V, the elliptic restricted three-body problem has the exact same five equilibrium points as the circular restricted three-body problem. Previous studies about their stability showed that the three collinear points are unstable [48], whereas the equilateral points are linearly stable, provided that both the mass ratio $\mu$ and the eccentricity e are appropriately chosen. However, the Hamiltonian function $H_e$ being non-autonomous, it is no longer a first integral of motion. As a consequence, we can not define any possible region of motion such as the Hill region (Fig. 3).

Fig. 3

Locations of the equilibrium points of the Earth-Moon system, depicted in the rotating pulsating frame of the planar elliptic restricted 3-body problem. The locations are the same as in the planar circular restricted 3-body problem

The controlled equations of the planar elliptic restricted three-body problem is derived similarly to (3) and is written

$$\begin{aligned} \left\{ \begin{aligned} \frac{d^2 \xi }{d\nu ^2}(\nu ) - 2\frac{d\eta }{d\nu }(\nu )&= \frac{\partial \omega }{\partial \xi }(\xi (\nu ),\eta (\nu ),\nu ) +u_1(\nu )\\ \frac{d^2 \eta }{d\nu ^2}(\nu ) + 2\frac{d\xi }{d\nu }(\nu )&= \frac{\partial \omega }{\partial \eta }(\xi (\nu ),\eta (\nu ),\nu )+u_2(\nu ). \end{aligned} \right. \end{aligned}$$

(10)

where the control $u=(u_1,u_2)$ is a function of the independent variable $\nu$. Defining $x=(x_1,x_2,x_3,x_4) \in \mathbf {R}^4$, where

$$\begin{aligned} x_1=\xi , x_2=\eta , x_3=\frac{\partial \xi }{\partial \nu }, x_4=\frac{\partial \eta }{\partial \nu }, \end{aligned}$$

(11)

we get the first-order differential system

$$\begin{aligned} \left\{ \begin{aligned} \frac{d x_1}{d\nu }&= x_3 \\ \frac{d x_2}{d\nu }&= x_4 \\ \frac{d x_3}{d\nu }&= 2x_4 + \frac{\partial \omega }{\partial x_1}(x_1, x_2, \nu ) + u_1 \\ \frac{d x_3}{d\nu }&= -2x_3 + \frac{\partial \omega }{\partial x_2}(x_1, x_2, \nu ) + u_2. \end{aligned} \right. \end{aligned}$$

(12)

which we write as a non-autonomous bi-input controlled system

$$\begin{aligned} \frac{d x}{d\nu }(\nu )=F_0(\nu ,x(\nu ))+u_1(\nu )F_1(x(\nu ))+u_2(\nu )F_2(x(\nu )) \end{aligned}$$

(13)

where the non-autonomous drift vector field, $F_0$, is

$$ F_{0}(\nu ,x)= \left( \begin{array}{c} x_3 \\ x_4\\ 2x_4 + \frac{\partial \omega }{\partial x_1}(x_1, x_2, \nu ) \\ -2x_3 + \frac{\partial \omega }{\partial x_2}(x_1, x_2, \nu ) \end{array} \right) $$

and the two constant vector fields $F_1$ and $F_2$ are

$$\begin{aligned} F_1(x)=\frac{\partial }{\partial x_3}, F_2(x)=\frac{\partial }{\partial x_4}. \end{aligned}$$

We observe that this controlled equation still admits an Hamiltonian formulation. Indeed, using the Legendre transformation

$$\begin{aligned} q=(q_1,q_2)=(x_1,x_2), p=(p_1,p_2)=(\frac{d x_1}{d\nu }-x_2, \frac{d x_2}{d\nu }+x_1), \end{aligned}$$

the Eq. (12) can be written as an Hamiltonian system

$$\begin{aligned} \frac{d q}{d\nu }=\frac{\partial H^{c}_e}{\partial p}(q(\nu ),p(\nu ),u(\nu ),\nu ), \frac{d p}{d\nu }=-\frac{\partial H^{c}_e}{\partial q}(q(\nu ),p(\nu ),u(\nu ),\nu ) \end{aligned}$$

with $H^{c}_e(q,p,u,\nu )=\frac{1}{2}\Vert p\Vert ^2+p_1q_2-p_2q_1-\omega (q,\nu )-u_1q_1-u_2q_2.$ In the rest of this paper, we study the time-minimal trajectories of the elliptic restricted three-body problem between two submanifolds $M_0$ and $M_1$ of $\mathbf {R}^4$, defined as the solutions x(t) the optimal control problem

$$\begin{aligned} \left\{ \begin{array}{c} \dot{x}( \nu )=F_0(\nu ,x(\nu ))+u_1(\nu )F_1(x(\nu ))+u_2(\nu )F_2(x(\nu ))\\ {\min }_{u(.) \in B_{\mathbf {R}^2}(0,\varepsilon ))} \int _{0}^{ \nu _f} d \nu \\ x(0)=x_{0} \in M_0, x(\nu _f) \in M_1 \end{array} \right. \end{aligned}$$

(14)

where u is an admissible control on $[0,\nu _f]$ whose magnitude is bounded by a positive number $\varepsilon$. Notice that what we call time-minimal trajectories of the problem are, in fact, true anomaly-minimal trajectories. However, the true anomaly is a strictly increasing function of the time, since $\dot{\nu }$, given in (7), is strictly positive. Therefore, we can minimize the final time by minimizing the true anomaly. In Sect. 5, the value of the control bound $\varepsilon$, that we will use to simulate time-minimizing space transfers in the Earth-Moon system, corresponds to a 1 N maximum thrust capability for the spacecraft’s engine.

3 Controllability

In this section we study the controllability of the elliptic restricted three-body problem, our notations follow the ones from [17]. In that paper, the authors establish the controllability of the circular restricted three-body problem, corresponding to the case $e=0$, over a particular submanifold of $\mathbf {R}^4$ containing the collinear Lagrangian point $L_2$ located between the two primaries, independent of the bound on the control and the value of the mass ratio $\mu$. More precisely, take any $\mu \in ( 0,1)$, any positive magnitude $\varepsilon$ on the control and set $Q_{\mu }=\mathbf {R}^2\setminus \lbrace (-\mu ,0),(1-\mu ,0)\rbrace$ to be the region of motion where no collisions with the primaries occur, $X_{\mu }=TQ_{\mu }\times \mathbf {R}^2$ as the corresponding phase space, $J_{\mu }(x)$ to be the Jacobian energy evaluated at a point $x \in X_{\mu }$ and $j_1(\mu )$ as the Jacobian energy of the Lagrangian point $L_1$. With these, the authors state that the circular restricted three-body problem is controllable on the connected component of the of the subset $\lbrace x \in X_{\mu } \vert J_{\mu }(x) < j_1(\mu ) \rbrace$ containing $L_2$. Their proof is based on the classical result of geometric control theory [36] which asserts that any affine control system $\dot{x}(t)=X_0(x(t))+\sum _{i=1}^{m}u_i(t)X_i(x(t))$ on a connected manifold $M^n$ with $\ u(t) \in U \subset \mathbf {R}^m$ is controllable provided that the convex hull of U is a neighborhood of the origin, the drift $X_0$ is a recurrent vector field and the family of vector fields $\lbrace X_0,X_1,\dots ,X_m \rbrace$ satisfies the so-called Lie algebra rank condition $\text {Lie}_x\lbrace X_0,X_1,\dots ,X_m\rbrace =T_xM, x \in M^n$.

Our objective is to investigate the generalization of this result for $0<e<1$. Notice that, according to the following general Lemma, the Lie algebra rank condition still holds in this case.

Lemma 1

A non-autonomous second order controlled system on $\mathbf {R}^m$

$$\begin{aligned} \ddot{q}(t)+g(t,q(t),\dot{q}(t))=u(t) \end{aligned}$$

can be written as a control-affine system on $\mathbf {R}^{2m}$ where the distribution $\mathscr {D}$ spanned by the vector fields $X_1,\dots ,X_m$ is involutive and with a non-autonomous drift $X_0$ such that $\lbrace X_1,\dots ,X_m,[X_0,X_1],\dots ,[X_0,X_m] \rbrace$ has maximum rank.

Proof

The proof is carried out similarly to Lemma 3 in [17], which states the same result for an autonomous second order control system. Indeed, here we have

$$\begin{aligned} X_0(t,q,\dot{q})=\sum _{i=1}^{m}\dot{q_i}\frac{\partial }{\partial q_i}-g_i(t,q,\dot{q})\frac{\partial }{\partial \dot{q_i}} \end{aligned}$$

and

$$\begin{aligned} F_i(q,\dot{q})=-\frac{\partial }{\partial q_i} \end{aligned}$$

so we conclude that $[X_0,X_i]=-\frac{\partial }{\partial q_i}\,\text {mod}\,\mathscr {D}$ for all $1 \le i \le m$ which proves the result.

However, due to the explicit dependence of the drift of the elliptic restricted three-body problem on the true anomaly $\nu$, it is no longer possible to define a submanifold of finite volume containing the Lagrangian point $L_2$ on which this vector field is volume preserving, as in the circular restricted problem. As a consequence, Poincaré’s recurrence theorem can not be applied and we can no longer claim that the drift of the problem is a recurrent vector field on an adequate submanifold. Let us mention that existing results concerning controllability of nonlinear non-autonomous vector fields are derived by considering the corresponding system augmented with the independent variable and hold for control-affine systems with an autonomous drift, i.e., systems of the form $\dot{x}(t)=F_0(x(t))+\sum _{i=1}^{m}F_i(t,x(t))u_i(t)$ [9]. Since our system does not fit the hypothesis of these results, we instead examine the properties of local controllability of the problem. First, let us recall the definition of local controllability along a trajectory of a nonlinear control system [22].

Definition 1

Let $(\bar{x},\bar{u})$ be a trajectory defined on an interval $[t_0,t_1]$ of the control system $\dot{x}=f(t,x,u)$ where $x \in \mathbf {R}^n$ and $u \in \mathbf {R}^m$. This control system is said to be locally controllable along the trajectory $(\bar{x},\bar{u})$ if, for every $\varepsilon >0$, there exists $\eta >0$ such that, for every $(a,b) \in \mathbf {R}^n \times \mathbf {R}^n$ with $\vert a-\bar{x}(t_0) \vert < \eta$ and $\vert b-\bar{x}(t_1) \vert < \eta$, there exists a trajectory $(\tilde{x},\tilde{u})$ defined on $[t_0,t_1]$ such that $\tilde{x}(t_0)=a$, $\tilde{x}(t_1)=b$ and $\vert \tilde{u}(t)-\bar{u}(t) \vert \le \varepsilon$, for all $t \in [t_0,t_1]$.

Remark 1

It is well-know that any non-linear, non-autonomous control system $\dot{x}=f(t,x,u)$ is locally controllable along a trajectory $(\bar{x},\bar{u})$ defined on $[t_0,t_1]$ if the linearized control system along $(\bar{x},\bar{u})$,

$$\begin{aligned} \dot{x}=\frac{\partial f}{\partial x}(t,\bar{x}(t),\bar{u}(t))x+\frac{\partial f}{\partial u}(t,\bar{x}(t),\bar{u}(t))u, t \in [t_0,t_1], \end{aligned}$$

(15)

is controllable [22]. Notice that, in this reference, the result is given for non-linear autonomous control systems $\dot{x}=f(x,u)$. However, it is easy to verify that the same proof works for non-linear non-autonomous control systems.

Thus, we can state the following.

Theorem 1

The elliptic restricted three-body problem is locally controllable along any trajectory $(\bar{x},\bar{u})$ defined for $\nu \ge 0$ and such that $\bar{x}(.)$ is three times continuously differentiable.

Proof

Let $(\bar{x},\bar{u})$ be a trajectory of the elliptic restricted three-body problem and assume that $\bar{x}$ is 3 times continuously differentiable. We want to show the controllability of the non-autonomous linear control system $\dot{x}=A(\nu )x+B(\nu )u$, where

$$\begin{aligned} A(\nu )&= \frac{\partial }{\partial x}\big ( F_0(\nu ,\bar{x}(\nu ))+u_1(\nu )F_1(\bar{x}(\nu ))+u_2(\nu )F_2(\bar{x}(\nu ))\big ) \\ {}&= \begin{pmatrix} 0&{}0&{}1&{}0 \\ 0&{}0&{}0&{}1 \\ \frac{\partial ^2 \omega }{\partial x_1^2}(\nu ,\bar{x_1}(\nu ),\bar{x_2}(\nu ))&{}\frac{\partial ^2 \omega }{\partial x_1 \partial x_2}(\nu ,\bar{x_1}(\nu ),\bar{x_2}(\nu ))&{}0&{}2 \\ \frac{\partial ^2 \omega }{\partial x_1 \partial x_2}(\nu ,\bar{x_1}(\nu ),\bar{x_2}(\nu ))&{}\frac{\partial ^2 \omega }{\partial x_2^2}(\nu ,\bar{x_1}(\nu ),\bar{x_2}(\nu ))&{}-2&{}0 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} B(\nu )= \frac{\partial }{\partial u}\big ( F_0(\nu ,\bar{x}(\nu ))+u_1(\nu )F_1(\bar{x}(\nu ))+u_2(\nu )F_2(\bar{x}(\nu ))\big )= \begin{pmatrix} 0 &{}0 \\ 0 &{}0\\ 1 &{}0 \\ 0 &{}1 \end{pmatrix}. \end{aligned}$$

Our assumption on the regularity of $\bar{x}$ asserts that both $A(\nu )$ and $B(\nu )$ are 3 times continuously differentiable. Thus, according to the classical result about the controllability of non-autonomous linear control systems [22, 37, 40], it is sufficient to show that there exist $\nu \ge 0$ satisfying

$$\begin{aligned} \text {rank}[M_0(\nu )\vert M_1(\nu )\vert \cdots \vert M_3(\nu )]=4 \end{aligned}$$

where

$$\begin{aligned} M_0(\nu )&=B(\nu )\\ M_{k+1}(\nu )&=-A(\nu )M_k(\nu )+\dot{\widehat{M_k}}(\nu ),\,\text {for}\,k=0,\dots ,3. \end{aligned}$$

The matrix $B(\nu )$ being constant, computations give, for any $\nu \ge 0$,

$$\begin{aligned} M_1= \begin{pmatrix}-1&{}0 \\ 0&{}-1\\ 0&{}-2 \\ 2&{}0 \end{pmatrix} \end{aligned}$$

so $\det [M_0(\nu )\vert M_1(\nu )]=1$ which concludes the proof. $\square$

Then, we can deduce from Theorem 1 the property of small-time local controllability at the Lagrangian points of the problem.

Remark 2

The term “small-time” is ambiguous here, since the independent variable of the problem is the true anomaly $\nu$ and not the time. However, this terminology is so widespread in the literature that we do not break convention. In the following, we provide the definition of the notion of small-time controllability for a generic control system $\dot{x}=f(t,x,u)$ but the reader should be aware that, in the context of our study, it would be more accurate to talk about “small-true-anomaly” controllability.

Definition 2

Let $(x_e,u_e)$ be an equilibrium point of the $\dot{x}=f(t,x,u)$. This control system is said to be small-time locally controllable at $(x_e,u_e)$ if, for every $\varepsilon >0$, there exists $\eta >0$ such that, for every pair $(x_0,x_1)$ with $\vert x_0-x_e \vert < \eta$ and $\vert x_1-x_e \vert < \eta$, there exists a trajectory (x, u) of the system defined on $[0,\varepsilon ]$ satisfying

$$x(0)=x_0, \quad x(\varepsilon )=x_1, \quad \vert u(t)-u_e \vert \le \varepsilon ,\,\text {for all}\, t \in [0,\varepsilon ]$$

Corollary 1

The elliptic restricted 3-body problem is small-time locally controllable at a Lagrangian point $L_i, 1\le i \le 5$.

Proof

This is a consequence of Theorem 1, since any Lagrangian point $L_i, 1\le i \le 5$, associated with a constant control equal to 0 provide an equilibrium point for the controlled elliptic restricted three-body problem. $\square$

4 Structure of the Optimal Control

In this section, we provide an analysis of the system to investigate the structure of the time-minimizing controls and trajectories of the elliptic restricted three-body problem.

4.1 Optimality Conditions

Our analysis is based on the application of the Pontryagin maximum principle which provides first-order necessary conditions for optimality [14, 36, 39, 46]. Let an admissible control $u=(u_1,u_2)$ associated with a trajectory x(.), both defined on an interval $[\nu _0, \nu _f]$, be a solution for the time-minimum control of the elliptic restricted three-body problem

$$\begin{aligned} \left\{ \begin{array}{c} \dot{x}( \nu )=F_0(\nu ,x(\nu ))+u_1(\nu )F_1(x(\nu ))+u_2(\nu )F_2(x(\nu ))\\ {\min }_{u \in B_{\mathbf {R}^2}(0,\varepsilon ))} \int _{\nu _0}^{ \nu _f} d \nu \\ x(\nu _0)=x_{0} \in M_0, x(\nu _f) \in M_1 \end{array} \right. \end{aligned}$$

(16)

where $F_0, F_1$ and $F_2$ are the vector fields defined in Sect. 2.2 and $M_0$ and $M_1$ are 2 submanifolds of $\mathbf {R}^4$ with tangent spaces at $x_0$ and $x(\nu _f)$. According to the Pontryagin maximum principle, there exist a constant $p^0 \le 0$ and an adjoint vector function $p : [\nu _0, \nu _f] \rightarrow \mathbf {R}^4$ satisfying $(p^0, p(\nu )) \ne 0$ for all $\nu \in [\nu _0, \nu _f]$ such that, for almost every $\nu \in [\nu _0, \nu _f]$

$$\begin{aligned} \dot{x}(\nu ) = \frac{\partial H}{\partial p}(\nu ,x(\nu ),p(\nu ),u(\nu )), \dot{p}(\nu ) = - \frac{\partial H}{\partial x}(\nu ,x(\nu ),p(\nu ),u(\nu )) \end{aligned}$$

(17)

where H is the non-autonomous control Hamiltonian function

$$\begin{aligned} H(\nu ,x,p,u)= p^0+\left\langle p, F_0(\nu ,x) \right\rangle +\sum _{i=1}^{2}u_i\left\langle p, F_i(x) \right\rangle . \end{aligned}$$

Furthermore, the maximization condition

$$\begin{aligned} H(\nu ,x(\nu ),p(\nu ),u(\nu )) = \max _{v \in U}H(\nu ,x(\nu ),p(\nu ), v) \end{aligned}$$

(18)

is satisfied for almost every $\nu \in [\nu _0, \nu _f]$. Finally, at $\nu _0$ and $\nu _f$, we have the transversality conditions

$$\begin{aligned} p(\nu _0) \perp T_{x(\nu _0)}M_0, p(\nu _f) \perp T_{x(\nu _f)}M_1. \end{aligned}$$

(19)

A 3-tuple (x, u, p) which satisfies the three conditions of the maximum principle is called an extremal. It is said to be normal if $p^0 \ne 0$ and abnormal if $p^0=0$. From now on, we will denote $H_0(\nu ,x,p)=\left\langle p, F_0(\nu ,x) \right\rangle$ the non-autonomous Hamiltonian lift of the drift $F_0$ and $H_i(x,p)=\left\langle p, F_i(x) \right\rangle$ the autonomous Hamiltonian lift of the vector field $F_i$, for $i=1,2$. Thus the Hamiltonian function H is

$$\begin{aligned} H(\nu ,x,p,u)= p^0+H_0(\nu ,x,p)+\sum _{i=1}^{2}u_iH_i(x,p). \end{aligned}$$

From the maximization condition (18), we deduce that, for almost every $\nu \in [\nu _0, \nu _f]$ where $(H_1(x(\nu ),p(\nu )),H_2(x(\nu ),p(\nu ))) \ne (0,0)$, the optimal control is given by

$$\begin{aligned} u_i(\nu )=\frac{H_i(x(\nu ),p(\nu ))}{\sqrt{H_1^2(x(\nu ),p(\nu ))+H_2^2(x(\nu ),p(\nu ))}}. \end{aligned}$$

Thus, the optimal control is a feedback control and extremals are fully described by the pairs $z=(x,p)$. This observation leads to the definition of the switching function

$$\begin{aligned} \psi (\nu )=(H_1(x(\nu ),p(\nu )),H_2(x(\nu ),p(\nu ))) \end{aligned}$$

(20)

and of the switching surface

$$\begin{aligned} \varSigma =\lbrace z=(x,p) \in \mathbf {R}^4 \times \mathbf {R}^4 \vert H_1(x,p)=H_2(x,p)=0 \rbrace . \end{aligned}$$

(21)

Therefore, extremals are divided into two categories. Extremals $z=(x,p)$ that do not lie on $\varSigma$ are called bang extremal and are smooth. Extremals $z=(x,p)$ lies on $\varSigma$ are called singular extremals. Here we call switching point a point of contact between a bang arc and a singular arc along a given extremal (although generally switching points may occur in other cases, for example bang-bang, they do not occur in this study). In the following, we study the nature of such contact points to derive the structure of time-minimizing trajectories of the problem.

4.2 Singular Flow and Structure of Extremals

Definition 3

Let $z^s$ be a singular extremal, with corresponding control $u^s$. Then $z^s$ is the flow of the Hamiltonian equation $\dot{z}^s = \vec {H}{s}(z^s)$ constrained to the set $\varSigma$ (21), called the singular flow of the singular Hamiltonian.

First of all, we recall some useful results, provided in [17] and built upon in [10, 14, 18, 38], from the in-depth study of singularities of the extremal flow of time-minimizing controls of general autonomous, bi-input, control affine systems of the form

$$\begin{aligned} \dot{x}(t)=F_0(x(t))+u_1(t)F_1(x(t))+u_2(t)F_2(x(t)), u_1^2(t)+u_2^2(t) \le 1 \end{aligned}$$

(22)

defined on a manifold M of dimension four. Denote $\gamma _b$ a bang extremal arc, $\gamma _s$ a singular extremal arc and, for any $z=(x,p) \in T^*M$, $F_{ij}(x)=[F_i(x),F_j(x)]$, $H_{ij}(z)=\lbrace H_i(z),H_j(z) \rbrace$ for $1 \le i, j \le 2$. Make the assumption

• (i) $D(x)=\text {det}(F_1(x),F_2(x),F_{01}(x),F_{02}(x)) \ne 0, x \in M$

and consider the stratification $\varSigma =\varSigma _-\cup \varSigma _0\cup \varSigma _+$ where

$$\begin{aligned} \varSigma _-&=\lbrace z \in \varSigma \vert H^2_{12}(z)<H^2_{01}(z)+H^2_{02}(z) \rbrace \nonumber \\ \varSigma _0&=\lbrace z \in \varSigma \vert H^2_{12}(z)=H^2_{01}(z)+H^2_{02}(z) \rbrace \\ \varSigma _+&=\lbrace z \in \varSigma \vert H^2_{12}(z)>H^2_{01}(z)+H^2_{02}(z) \rbrace \nonumber . \end{aligned}$$

(23)

The following theorem can be stated.

Theorem 2

Let $z_0 \in \varSigma _-$; every extremal is locally of the form $\gamma _b\gamma _s\gamma _b$ (where $\gamma _s$ is empty if $H_{12}(z_0)=0$); every admissible extremal is locally the concatenation of at most two bang arcs. Let $z_0 \in \varSigma _+$; every extremal is locally bang or singular and every optimal extremal is locally bang. Optimal singular extremals are given by the flow of $H_s$ and contained in $\varSigma _0$ (saturating).

The proof of Theorem 2 is based on the connection between the flow of the specific form of Hamiltonian function H in the singular case and the singular extremals of the problem and a nilpotent approximation [10] around a point $z_0 \in \varSigma \setminus 0$. By defining, for any $x \in M$,

$$\begin{aligned} D_{1}(x)&=\text {det}(F_1(x),F_2(x),F_{12}(x),F_{02}(x)),\\ D_{2}(x)&=\text {det}(F_1(x),F_2(x),F_{01}(x),F_{12}(x)), \end{aligned}$$

replacing (i) by

• (i’) $D^2_1(x)+D^2_2(x)<D^2(x), x \in M$

and assuming

• (ii) $\mathscr {D}$ is involutive,

we get the following.

Theorem 3

The switching function is continuously differentiable and every extremal is locally bang-bang with switchings of angle $\pi$ (“$\pi$-singularities”).

Finally, assuming

• (iii) $F_0 \notin \text {Span}\lbrace F_1,F_2,F_{01} \rbrace$ is involutive,

we have the following.

Theorem 4

In the normal case $p^0 \ne 0$, there cannot be consecutive switchings in $\varSigma _1=\varSigma \cap \lbrace (x,p) \in T^*X \vert F_0(x) \in \text {Span}\lbrace F_1,F_2,F_{01} \rbrace$

Notice that this analysis does not apply when considering general bi-input control affine systems with a non-autonomous drift

$$\begin{aligned} \dot{x}(t)=F_0(t,x(t))+u_1(t)F_1(x(t))+u_2(t)F_2(x(t)), u_1^2(t)+u_2^2(t) \le 1 \end{aligned}$$

(24)

on a manifold of dimension four. Indeed, in this case, the Lie brackets (resp., Poisson brackets) $F_{01}$ and $F_{02}$ (resp., $H_{01}$ and $H_{02}$) are, a priori, non-autonomous. As a consequence, the determinants D, $D_1$ and $D_2$ may depend explicitly on t as well and the assumptions (i) and (i’) and the stratification (23) are no longer consistent, even though the switching surface $\varSigma$ can still be defined in the exact same way as in (21) since both $H_1$ and $H_2$ remain autonomous. However, in the specific context of the elliptic restricted three-body problem, straightforward computations give

$$F_{01}(\nu ,x(\nu ))=\begin{pmatrix} 1 \\ 0\\ 0 \\ -2 \end{pmatrix}, \ F_{02}(\nu ,x(\nu ))=\begin{pmatrix} 0 \\ 1\\ 2 \\ 0 \end{pmatrix}. $$

so

$$\begin{aligned} H_{01}(\nu ,x(\nu ),p(\nu ))=p_1(\nu )-2p_4(\nu ) \end{aligned}$$

and

$$\begin{aligned} H_{02}(\nu ,x(\nu ),p(\nu ))=p_2(\nu )+2p_3(\nu ). \end{aligned}$$

Thus, even though the drift $F_0$ of the elliptic restricted three-body problem is non-autonomous, the Lie brackets of length 2 (resp., Poisson brackets) $F_{01}$ and $F_{02}$ (resp. $H_{01}$ and $H_{02}$) are autonomous. In fact, they have the exact same values as in the circular restricted three-body problem, and so do the determinants $D, D_1$ and $D_2$ which do not depend explicitly on $\nu$. The first consequence is that the assumption (i), and the stronger one (i’), can be formulated in the context of our study and are satisfied, in accordance with Lemma 1. By examining the expression of the first derivative of the switching function $\psi$, which is necessarily identically zero along a singular arc, we manage to write singular extremal controls as feedback controls. Indeed, exactly as stated in [17], in the neighborhood of a point $z_0=(x_0,p_0) \in \varSigma$, an extremal control is

$$\begin{aligned} u_s(x,p)=\Big (-\frac{H_{02}(x,p)}{H_{12}(x,p)},\frac{H_{01}(x,p)}{H_{12}(x,p)} \Big ). \end{aligned}$$

(25)

Plugging in H, we derive the expression of the non-autonomous singular Hamiltonian function

$$\begin{aligned} H_s(\nu ,x,p)= p^0+H_0(\nu ,x,p)-\frac{H_{02}(x,p)}{H_{12}(x,p)}H_1(x,p)+\frac{H_{01}(x,p)}{H_{12}(x,p)} H_2(x,p). \end{aligned}$$

(26)

In addition, the stratification (23) also makes sense in the conditions of our problem, as well as assumptions (ii) and (iii) which are both clearly verified, once again in accordance with Lemma 1. The rest of the analysis carried out in [17] can then be rigorously reproduced to investigate the structure and regularity of the extremal trajectories of the elliptic restricted three-body problem. As a conclusion, we can state the following.

Theorem 5

The elliptic restricted three-body problem has bang-bang time minimizing controls with finitely many $\pi$-singularities.

5 Application to Space Transfers

In this section, we apply our analysis of the time-minimum control of the planar elliptic restricted 3-body problem to simulate time-minimum space transfers between the geostationary orbit and the equilibrium points $L_1$ and $L_2$ in the Earth-Moon system and a rendezvous mission with a near-Earth asteroid.

5.1 Numerical Methods

The numerical simulations presented in this paper are based on locally sufficient second order conditions [1, 11, 14] and indirect methods in optimal control [3, 21]. In this section, we briefly describe these principles which consist of computing solutions to optimal control problems by generating normal extremal curves solutions of the Pontryagin maximum principle whose local optimality is checked using second order conditions. Consider a generic control problem of the form

$$\begin{aligned} \left\{ \begin{array}{c} \dot{x}(t)=f(t,x(t),u(t))\\ {\min }_{u(.) \in U} \int _{0}^{ t_f} f^0(t,x(t),u(t))dt \\ x(0)=x_{0} \in M_0, x(t_f) \in M_1 \end{array} \right. \end{aligned}$$

(27)

where the time $t_f$ is not fixed, M and U are two smooth manifolds of respective dimensions n and m, $f:[0,t_f]\times M \times U \rightarrow TM$ and $f^0:[0,t_f]\times M \times U \rightarrow \mathbf {R}$ are smooth, $M_0, M_1$ are two submanifolds of M and u is an admissible control valued in U. By applying the Pontryagin maximum principle and using the maximization condition [46], we can, under some generic regularity assumptions [1, 11], write the optimal control $\bar{u}$ solution to (27) as a smooth feedback control $\bar{u}(t,\bar{x},\bar{p})$, where $(\bar{x},\bar{p})$ is an extremal trajectory solution to a smooth Hamiltonian system

$$\begin{aligned} \dot{x}(t) = \frac{\partial H_r}{\partial p}(t,x(t),p(t)), \dot{p}(t) = - \frac{\partial H_r}{\partial x}(t,x(t),p(t)). \end{aligned}$$

(28)

Define the exponential mapping $\exp _{x_0}:(t,p_0)\rightarrow x(t,x_0,p_0)$ as the function which, given a pair $(t,p_0)$, outputs the projection on M of the extremal trajectory (x, p) solution to (28) starting from the initial condition $(x_0,p_0)$ and evaluated at time t. We say that a time $t_c$ is conjugate to 0 along (x, p) if the restriction of the exponential function $p_0\rightarrow x(t_c,x_0,p_0)$ is not an immersion at $p_0$ and we say that $x(t_c,x_0,p_0)$ is a conjugate point. The notion of conjugate time is connected to the property of local optimality through the following sufficient second order condition of optimality: under generic assumptions, we can state that a trajectory $x(\cdot )$ projection of an extremal solution is locally optimal in the $L^{\infty }$-topology until the first conjugate time along the extremal [1, 11]. Hence, we can develop a process to compute locally optimal numerical solutions to the problem (27). Indeed, the boundary conditions to be satisfied by an extremal trajectory (x, p) can be written in the form

$$\begin{aligned} R(x(0),p(0),x(t_f,x_0,p_0),p(t_f,x_0,p_0))=0_{\mathbf {R}^n}. \end{aligned}$$

(29)

Furthermore, since $t_f$ is not fixed, the condition $H_r \equiv 0$ holds along any extremal [46]. Thus we can generate an extremal trajectory by solving the shooting equation, i.e., finding a zero to the shooting function

$$\begin{aligned} S: (t_f,p_0) \rightarrow \left( \begin{array}{c} R(x_0,p_0, x(x_0,p_0, t_f),p(x_0,p_0, t_f))\\ H_r(x(x_0,p_0, t_f),p(x_0,p_0, t_f))\end{array} \right) , \end{aligned}$$

(30)

and proceeding to a numerical integration of the system (28) with the corresponding initial condition $(x_0,p_0)$. The local optimality of the projection of the extremal is verified by checking that there is no conjugate time along the interval $[0,t_f]$, which amounts to checking a rank condition [11]. The shooting function being smooth, a Newton-type algorithm can be used to determine its zeroes. The most difficult aspect of this approach is to choose an accurate initial guess so that the Newton method converges. This can be achieved by means of a smooth continuation method [13, 14]. The Hamiltonian function $H_r$ is connected to another Hamiltonian function $H_0$ through a family of smooth Hamiltonian functions $(H_{\lambda })_{\lambda \in [0,1]}$, associated with a family of exponential mapping $\exp _{x_0}^{\lambda }$, such that $H_r=H_1$ and the shooting method is easy to solve for $H_0$. Assume that, for every $\lambda \in [0,1]$, the point $\exp _{x_0}^{\lambda }(t_f,p_0)$ is not conjugate to $x_0$. Then the solutions of the shooting method form a smooth curve parametrized by $\lambda$ [13]. Thus, the continuation process consists of following this curve to determine a zero of the shooting function (30). This can be managed iteratively: setting up some discretization $0=\lambda _0<\lambda _1<\dots <\lambda _N=1$ of the interval [0, 1], we can first solve the shooting method for $H_0$ and then solve the shooting method for each $H_{i+1}$ by using the solution of the shooting method for $H_{i}$ as an initial guess. As a result, the zero of the shooting function for $\lambda _N$ is a zero of the shooting function (30).

Table 1 Eccentricies of the solar system

These methods are implemented by using the software hampath [15] which allows one to integrate smooth Hamiltonian vector fields, solve shooting equations and evaluate conjugate points along extremal trajectories. Let us mention that this software also allows one to use a differential path-following method, which was not needed to obtain the results presented in this paper.

5.2 Numerical Computations

We now present results obtained using the methods above, as applied to three different missions scenarios. We choose to work in the Earth-Moon system, where the mass ratio $\mu = 0.0121536$ and the eccentricity is $e=0.0549$. This choice is justified by the fact that it is perhaps the most relevant system (arguably, besides the Sun-Earth system) in the design of actual missions, and that there is existing work for the Earth-Moon system in the circular restricted three-body problem [16, 17, 19, 45]. For some perspective on how the Earth-Moon system compares to the rest of our Solar System, Table 1 gives the eccentricities of the orbits of several of the other major bodies. As it can be observed, Mercury has the largest eccentricity of all planets orbiting around the Sun but due to its close proximity to the Sun it is not very relevant from spacecraft missions. While still small, the Moon’s orbit around the Earth presents an eccentricity that is the largest from other well-known moons orbiting their primary body. This work is centered around the analysis of the impact of a more complete model on the geometry of the transfers and we will consider unrealistic scenarios with higher eccentricities to obtain a broader understanding. For all mission scenarios we assume that the spacecraft has capabilities resembling those of an electric propulsion system, with a 1 N maximum thrust capability and a high specific impulse so that the mass variation can reasonably be ignored. This choice was made for simplicity and, again, based on prior work on low-thrust space transfers in the circular problem [16, 17, 19, 45].

We consider three different missions. For each mission, we select a starting departure point for the spacecraft $x_0 \in \mathbf {R}^4$ as well as a final arrival point $x_f \in \mathbf {R}^4$. Both points $x_0$ and $x_f$ provide the desired position and the velocity of the spacecraft at $\nu _0$ and $\nu _f$, where $\nu _0$ is the true anomaly at the mission’s start time and $\nu _f$ is at arrival time. The problem is then solved numerically to identify a time-minimal trajectory x(t) so that $x(\nu _0)=x_0$ and $x(\nu _f)=x_f$.

For a chosen eccentricity value, once the initial true anomaly is fixed to a value $\nu _0$ then the initial position and velocity of the spacecraft $x_0$ in the pulsating rotating frame corresponds to a well-defined point in the fixed frame. However, since the final time is free, the final true anomaly $\nu _f$ is free as well which creates some complexity in the problem due to the dependence of the pulsating frame position of the spacecraft with respect to the true anomaly when converting the pulsating rotating coordinates to or from the fixed coordinates. For instance, consider the eccentricity of the Moon’s orbit around the Earth, $e=0.0549$. When the true anomaly $\nu =\frac{\pi }{2}$ the position $(x_1,x_2)=(0,1)$ in the pulsating rotating frame corresponds to a point one unit from the origin in the fixed frame; however, if the true anomaly is $\nu =\pi$, the position $(x_1,x_2)=(0,1)$ in the pulsating rotating frame corresponds to a point 1.058 units from the origin in the fixed frame. To overcome this difficulty, if the destination for the spacecraft is a specific point in the dimensional frame, the true anomaly must be fixed at $\nu _f$ rather than at $\nu _0$. In this case, the shooting function integrates time backward instead. Notice however that in the pulsating rotating frame the coordinates of the equilibrium points $L_i$, $i=1,\ldots ,5$ do not depend on the true anomaly which therefore makes them convenient departing and arrival points to design a mission.

We choose to design missions with the following three scenarios:  

Mission 1::

The first scenario that we consider is a mission from the Geostationary orbit to the libration point $L_1$. Simulating such a mission is important, as it is a first step to designing optimal Earth-Moon transfers. Indeed, the vicinity of the point $L_1$ is a gateway between the Earth and the Moon gravitational fields. Therefore, Earth-$L_1$ optimal transfers provide good initializations when using a shooting method to compute Earth-Moon optimal transfers [12, 45].

Mission 2::

The second scenario is similar to the first one but the destination is a different libration point. The goal is to compute minimal transfers from the Geostationary orbit to $L_2$. This libration point has proved to play an important role as well for transfers to orbit the Moon, see for instance the Artemis mission [4].

Mission 3::

Finally, the last scenario we consider is a transfer to a temporarily captured asteroid, namely 2006RH$_{120}$. We choose the starting point to be $L_2$ because it has proved to provide the best transfers in the case of zero eccentricity [44]. Ideally the spacecraft should be considered on a Halo orbit around the $L_2$ point, but for simplicity and as a first step to the analysis of the impact of eccentricity values we assume it unrealistically at the equilibrium point.

 

5.2.1 Transfers to $L_1$ and $L_2$

Existing results from [19, 45] provided time-minimal transfers to $L_1$ and $L_2$ from a geostationary orbit GEO in the Earth-Moon circular restricted three-body problem. In this paper, we extend these results by using the elliptic model. The positions and velocities of the libration points in the non-dimensional elliptic frame do not depend on the eccentricity of the system and (the two we consider) are provided in Table 2. The other relevant location, GEO, requires more subtlety: a selected geostationary orbit in the inertial reference frame, with inertial coordinates (0.0977, 0, 0, 2.9767), corresponds to different elliptic frame coordinates depending on both the eccentricity and the initial true anomaly $\nu _0$. Table 2 also gives the corresponding elliptic frame coordinates for GEO for a few different eccentricity and $\nu _0$ ($\nu _f$ for 2006RH$_{120}$) values.

Table 2 Departure and arrival positions and velocities for the spacecraft in the non-dimensional frame

A continuation-based algorithm was used to compute transfers for 91 different eccentricity values $\{e_i\}=\{0.00,..,0.90\}$ with a step size of 0.01, e.g. $e_{1} = 0.01$, $e_{50}=0.5$, and $e_{90}=0.9$. The initial true anomaly was assumed $\nu _0=0$ for these transfers. A known solution from the CR3BP ($e_0=0$) served as the seed for the continuation algorithm, which iterates through the list of eccentricity values in both an increasing and decreasing fashion. The code can be summarized as follows, with some justification afterward:

• for $k=1,2,3,..,89,90$

  • if a solution exists for $e_{k-1}$ with transfer time $t_{k-1}$, and either no solution exists for $e_{k}$ or the best found solution for $e_{k}$ has a transfer time greater than $t_{k-1}$, initialize the shooting algorithm for $e_k$ with the solution from $e_{k-1}$.

• for $k=89,88,..,2,1,0$

  • if a solution exists for $e_{k+1}$ with transfer time $t_{k+1}$, and either no solution exists for $e_{k}$ or the best found solution for $e_{k}$ has a transfer time greater than $t_{k+1}$, initialize the shooting algorithm for $e_k$ with the solution from $e_{k+1}$.

• If any new solution was found, repeat; otherwise, the algorithm is done.

Continuation methods can be simple yet effective means to compute solutions to a family of problems related by a parameter—in our case, the eccentricity—however, there is no guarantee for convergence at each step of the algorithm. Moreover, it is possible that a locally optimal solution is computed which is far from the global minimum. These points motivate the algorithm described above; looping not only to identify solutions for each eccentricity value, but also retrying calculations that may have converged to much higher (locally optimum) transfer times. Recall that the actual eccentricity of the Earth-Moon system is $e\approx 0.05$, so all other values are strictly hypothetical.

Figure 4 shows the minimal transfer times as a function of eccentricity for GEO-to-$L_1$ and -$L_2$ transfers (blue). For comparison, the first conjugate time is also plotted (red) and we see that it is always longer than the transfer time, confirming the local optimality of our solution. For both destinations, higher eccentricity values allow shorter transfer times. Transfer and conjugate times are also given for select eccentricity values in Table 3.

Fig. 4

Minimum transfer times (blue circles) and the corresponding first conjugate times (red squares) for $e=0.0,\dots ,0.9$. a GEO-to-$L_1$, b GEO-to-$L_2$

It is interesting to notice the bifurcation that occurs around $e=0.13$ and $e=0.34$. At these points, the higher eccentricity of the system seems to enable the spacecraft to make one less revolution of the Earth before heading directly toward its destination. We can consider the spacecraft’s trajectory as a closed curve in the plane if we connect the start and end points with a line. Then we can define the winding number $w_E$ of the trajectory as the integer representing the total number of times that curve travels counterclockwise around the Earth. For example, in Fig. 5a–c, we have $w_E =$ 3, 2, and 1, respectively. For the $L_1$ transfers, for $e=0.00,\dots ,0.13$ the spacecraft makes three revolutions of the Earth; for $e=0.14,\dots ,0.34$ it makes only two revolutions; and finally, for $e=0.35,\dots ,0.9$ the craft only makes one revolution of the Earth. Similarly for the $L_2$ transfers, for $e=0.00,\dots ,0.12$ the spacecraft makes three revolutions of the Earth; for $e=0.13,\dots ,0.33$ it makes only two revolutions; and finally, for $e=0.34,\dots ,0.9$ the spacecraft only makes one revolution of the Earth. Table 3 gives $w_E$ for selected eccentricity values.

Table 3 GEO-to-$L_1$ (left) and GEO-to-$L_2$ (right) minimum transfer times $t_f^{min}$ and associated first conjugate times $t_{conj}$, in days, and winding number $w_E$, for selected eccentricity values

In Figs. 5 and 6, GEO-to-$L_1$ and -$L_2$ transfers are shown, respectively, with $e=\{0, 0.3, 0.8 \}$. The images for $e=0.05\approx 0.0549$ are indistinguishable from those of $e=0$—the transfer times and conjugate times are given in Table 3.

Fig. 5

Time-minimal transfers from GEO to $L_1$, viewed in both the dynamic and fixed frame. a e = 0, 10.38 days, dynamic frame, b e = 0, 10.38 days, fixed frame, c e = 0, 7.32 days, dynamic frame, d e = 0, 7.32 days, fixed frame, e e = 0, 1.23 days, dynamic frame, f e = 0, 1.23 days, fixed frame

Fig. 6

Time-minimal transfers from GEO to $L_2$, viewed in both the dynamic and fixed frame. a e = 0, 11.96 days, dynamic frame, b e = 0, 11.96 days, fixed frame, c e = 0.3, 9.59 days, dynamic frame, d e = 0.3, 9.59 days, fixed frame, e e = 0.8, 2.05 days, dynamic frame, f e = 0.8, 2.05 days, fixed frame

5.2.2 Transfers to a Near-Earth Asteroid

Temporarily captured orbiters (called minimoons for short) are a class of near-Earth asteroids gaining recent interest [19, 34]. Informally, minimoons are defined as near-Earth asteroids that are temporarily caught in orbit around the Earth. Although only one minimoon has ever been confirmed, the authors of [34] give rigorous calculations that demonstrate there is a steady state of minimoons in orbit around the Earth. To date, the only confirmed minimoon, known as 2006RH$_{120}$, was discovered in 2006. It is a few meters in diameter and was in orbit around the Earth for about one year. The three dimensional partial trajectory of 2006RH$_{120}$ is shown in Fig. 7 in the inertial geocentric reference frame (ephemeris retrieved from NASA’s HORIZONS database). Ongoing research is investigating methods to more regularly detect minimoons.

Fig. 7

Near-Earth asteroid 2006RH$_{120}$ (gray) viewed in the 3-dimensional fixed frame. Our choice of rendezvous location (red circle) was chosen based on low absolute z-coordinate and its vicinity to $L_2$. The moon’s orbit (black) has eccentricity of 0.0549; the major and minor axes of its orbit are plotted as the solid and dashed black lines, respectively. The true anomaly of the moon at rendezvous is $\nu _f=4.019$

We now compute a time minimal transfer to rendezvous with 2006RH$_{120}$ starting from the Earth-Moon $L_2$ point. We pre-select a rendezvous point along the trajectory of 2006RH$_{120}$ based on it’s vicinity to $L_2$ and zero z-coordinate (elliptic frame coordinates are given in Table 2). The rendezvous location is also marked on Fig. 7. It is not in the scope of this paper to optimize the chosen rendezvous location, and so this choice is admittedly arbitrary. The true anomaly of the moon at the selected rendezvous point is $\nu _f=4.019$ radians, also computed from the JPL HORIZONS database.

We use the actual eccentricity and mass ratio of the Earth-Moon system $(\mu =0.0121536$, $e=0.0549$), and compare the results to those of the circular problem ($e=0$). As mentioned, the true anomaly is fixed at rendezvous $\nu _f=4.019$ radians, and therefore the initial true anomaly $\nu _0$ is free and the shooting method integrates backward in time. Again, existing results in the circular frame are used to initialize the algorithm, and the first conjugate time is calculated to verify the local optimality of our solutions.

Figure 8 shows the time-minimal trajectories for both eccentricity values, in both the non-dimensional and dimensional frames. The trajectories are more or less indistinguishable since the eccentricity of the Earth-Moon system is so low; however, using the actual eccentricity $e=0.0549$ does provide a transfer time that is 6.4 h faster than with $e=0$ (10.53 days vs. 10.80 days). The conjugate times for $e=0$ and $e=0.0549$ were 17.22 and 16.94 days, respectively. It is likely that missions of longer duration would see larger improvements.

Fig. 8

Time-minimal transfer from $L_2$ to 2006RH$_{120}$, viewed in both the dynamic and fixed frame. a e = 0, 10.8 days, dynamic frame, b e = 0, 10.8 days, fixed frame, c e = 0.0549, 10.59 days, dynamic frame, d e = 0.0549, 10.59 days, fixed frame

6 Conclusion

In this paper, we generalize some results presented in [17] to the time-minimum control of the planar elliptic restricted three-body problem when the eccentricity e of the Keplerian orbits of the two primaries is strictly positive. The problem is written in the form of a non-autonomous control problem which is shown to be small-time locally controllable in the vicinity of the equilibrium points. We prove that the structure of the time-minimizing controls is preserved, in the sense that the time-minimizing controls are bang-bang with a finite number of $\pi$-singularities. We use this model to compute a collection of time-minimal low-thrust transfers from the geostationary orbit to the equilibrium points $L_1$ and $L_2$ of the Earth-Moon system, for a wide range of eccentricities, by means of a shooting method combined with a continuation method. The local-optimality of these transfers is verified using a second-order optimality condition related to the concept of conjugate points. We observe, numerically a decreasing relation between the minimum time transfer and the eccentricity e. Bifurcations occur for $e=0.13$ and $e=0.34$, causing the spacecraft to complete less revolutions around the Earth before it reaches its destination. We also simulate a time-minimal rendezvous mission with the near-Earth asteroid 2006RH$_{120}$ in the Earth-Moon system. The initial guesses chosen to initiate our numerical methods are time-minimal transfers in the circular restricted three-body problem computed in [19, 45]. The results show that considering the actual eccentricity of our Moon’s orbit around the Earth leads to a slightly shorter rendezvous time with the asteroid 2006RH$_{120}$ than when the eccentricity is neglected. The natural next step of this study will consist of taking into account the significant influence of the Sun on the transfers within the Earth-Moon system. One possibility to achieve this goal would be to derive the equations of a perturbed elliptic three body problem, inspired by the equations of the restricted four-body problem [42] which can be used to model a Sun-perturbed circular restricted three-body problem. The theoretical analysis of the time-minimum control of the perturbed elliptic three body problem will raise an interesting issue from the geometric control point of view. More on the practical side, the main objective will be to compare numerical computations performed with this new model with the ones that are carried out in the present chapter, in order to design even faster low-thrust transfers in the Earth-Moon system. For the sake of realism, another interesting problem would be to consider points on a small halo orbit around the equilibrium points $L_1$ and $L_2$ of the restricted 3-body problem [6] as initial conditions for a rendezvous mission to near-Earth asteroids.