Abstract
Causal trees are one of the earliest pioneering contributions of Pierpaolo Degano, in joint work with Philippe Darondeau. The idea is to record causality dependencies in processes and in their actions. As such, causal trees sit between interleaving models and truly concurrent ones and they originate an abstract, event-based bisimulation semantics for causal processes, where, intuitively, minimal causal trees represent the semantic domain. In the paper we substantiate this feeling, by first defining a nominal, compositional operational semantics based on History-Dependent automata and then we apply categorical techniques, based on named-sets, showing that causal trees form the final coalgebra semantics of a suitable coalgebraic representation of causal behaviour.
Research supported by MIUR PRIN Project CINA Prot. 2010LHT4KM and by NWO Project 612.001.113 Practical Coinduction.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Causal trees [7, 8] are one of the key pioneering contributions of Pierpaolo Degano, in joint work with Philippe Darondeau, to the field of concurrency. The idea is to enrich Milner’s synchronisation trees, the classical model for interleaving semantics, with causality information between the currently performed action and previous ones. As such, causal trees sit between interleaving models and truly concurrent ones. They differ from the non-sequential processes/event structures of Petri nets (see [2, 11] for a comparison between causal trees and event structures). In fact, the causal tree semantics does not offer an operational setting, where a concurrent computation is seen as the equivalence class of all sequential computations with concurrent events executed in any order. Rather, it suggests an abstract, event-based bisimulation semantics, where minimal causal trees represent the semantic domain. We will see in this paper that our categorical developments confirm this conclusion, since it turns out that causal trees form the final coalgebra semantics of a suitable coalgebraic representation of causal behaviour (see [16] for details about coalgebras).
At the syntax level, the basic idea is to have causal processes, i.e., processes in which each sequential agent comes with the set of its past events, called causes. When one agent performs an action, or two agents synchronise, a new event is generated and the causes of the involved agents are recorded in the label, together with the action. These causes, updated with the new event, are then assigned to the continuations of the agents. Correspondingly, the usual notion of bisimulation becomes history preserving [10], because causes must be matched.
The main issue with causal semantics is that the state-space is usually infinite, because the causes of causal processes grow after each transition. A solution was proposed in [13] by Montanari and Pistore. They introduced a class of operational models, namely causal automata, for the causal semantics of Petri netsFootnote 1. Causal automata have no direct minimal realisations, but they can be mapped (possibly provoking a state explosion) to equivalent ordinary automata, which can in turn be minimised. Later, it was observed by the same authors that event generation mechanisms of causal automata can be generalised to handle name generation in nominal calculi. This led to History Dependent (HD-)Automata [15]. They are automata featuring name allocation and deallocation, and were initially intended for the \(\pi \)-calculus. Unlike causal automata and causal trees, each state of an HD-automaton is equipped with a symmetry group, telling under which permutation of names the state is invariant. This is essential to have minimal representatives.
HD-automata admit a categorical representation as coalgebras over named sets [6], because states and transitions are indexed by sets of names. This perspective led to several results and generalisations. In [6, 12], a connection between HD-automata and the categorical operational semantics of the \(\pi \)-calculus [9] has been established. More precisely, the former can be automatically derived from the latter through a categorical equivalence. In [5] it is shown that this equivalence is much more general: if the presheaf category on which coalgebras are based has certain properties, then we have equivalent notions of named sets and coalgebras over them.
Our original contribution is two-fold, as explained next.
History-Dependent Semantics for Causal Processes. In the first part of our contribution we derive compact operational models for causal processes. In Theorem 1 we show full abstraction w.r.t. Darondeau-Degano causal semantics (DD-semantics for short). The state-space of our models is usually significantly smaller, often finite instead than infinite, than the one produced by the corresponding DD-semantics.
In order to do this, we represent events as names, and event generation as name generation. States are special causal processes, called P-processes, with the following features:
-
they include a poset, describing the causal relations among the process’ events;
-
they only keep track of immediate causes, that are the most recent events, according to the poset, for each agent;
-
they are canonical representatives of isomorphic processes.
Transitions have history maps that record the correspondence between event names along transitions. The semantics is history-dependent (HD-semantics in short), in the sense that events may have different meanings depending on past transitions.
The poset plays a crucial role in bisimilarity: two states can be compared for bisimilarity only if their posets can be related via a suitable (partial) isomorphism. This ensures that bisimilar states have the same history of events, which is essential for the correspondence with causal trees and, equivalently, with history dependent bisimilarity.
Our work is based on [4], where an analogous semantics for causal processes was first introduced. It was rather indirect and cumbersome, because it was gradually built on top of the whole (possibly infinite) DD-semantics of a causal process. Here HD-semantics is computed directly and more efficiently, via a compositional, inductive procedure that starts from transitions of individual agents in the basic, non-causal LTS.
Final Semantics. The second part of our work is concerned with representing our semantics of causal processes as coalgebras over named sets, i.e., HD-automata. This construction enables us to use results from the well-established theory of coalgebras. In particular, we have a final semantics and corresponding minimal models. This construction crucially depends on states being equipped with symmetry groups, formed by isomorphisms over the state’s poset under which the state is invariant. This way, all bisimilar states have a unique representative as a state with symmetries. A simple counterexample shows that this cannot be achieved if symmetries are not considered.
We base our technical development on [5], where a general notion of named set is introduced: symmetry groups are defined over a category \(\mathbf {C}\), and then named sets are defined as families of such groups. To instantiate \(\mathbf {C}\), we introduce a category \(\mathbf {P}\) of posets, where symmetry groups are formed by poset automorphisms. Then we define HD-automata as coalgebras for a suitable behavioural endofunctor on named sets, which captures causal information and event generation in transitions.
We provide a direct translation of causal HD-semantics into HD-automata. Behavioural equivalence is preserved by the translation, and in Theorem 2 we prove that it is indeed induced by causal trees. Thus we can conclude that causal trees, even if infinite, are the right abstract notion to represent causal semantics. The finite case, represented by a finite minimal HD automaton, corresponds to a causal tree with a finite number, up to isomorphism, of subtrees.Footnote 2
Structure of the Paper. In Sect. 2 we fix some notation on posets, recall the basic ideas around causal processes and their semantics and introduce a very simple running example, which is expressive enough to show all the key features of our approach. In Sect. 3 we introduce P-processes, our main ingredient for addressing causal semantics with nominal techniques, together with the basic operations to combine them. In Sect. 4 we define a causal semantics for P-processes, called HDC-bisimilarity and show that it agrees with the classical Darondeau and Degano’s semantics (Theorem 1). Finally, in Sect. 5, we address the issue of finding minimal models up-to HDC-bisimilarity, exploiting symmetries to the purpose (Theorem 2). Due to space limitation, the reader must have some familiarity with categories and coalgebras to appreciate the technical development in Sect. 5, although this is not needed to understand the construction of the operational model and to follow its application to the running example.
2 Background and Running Example
A poset over a set S is a pair \(O = (|O|,\preccurlyeq _O)\), where \(|O|\subseteq S\) and \(\preccurlyeq _O\) is a reflexive, transitive and antisymmetric (binary) relation on |O|. We will sometimes write posets as sets of elements and pairs, omitting reflexive and transitive pairs, for instance \(\{ e_1,e_2 \preccurlyeq _O e_3\}\) is the poset with elements \(e_1,e_2,e_3\) such that \(e_1 \preccurlyeq _O e_1\), \(e_2 \preccurlyeq _O e_2 \preccurlyeq _O e_3 \preccurlyeq _O e_3\). A morphism of posets \(O \rightarrow O'\) is a function \(\sigma :|O| \rightarrow |O'|\) that preserves order, namely \(x \preccurlyeq _O y\) implies \(\sigma (x) \preccurlyeq _{O'} \sigma (y)\). We say that \(\sigma \) reflects order whenever \(\sigma (x) \preccurlyeq _{O'} \sigma (y)\) implies \(x \preccurlyeq _O y\); \(\sigma \) is an order-embedding whenever it both preserves and reflects order. A set \(K \subseteq |O|\) is down-closed w.r.t. O whenever \(y \in K\) and \(x \preccurlyeq _O y\) implies \(x \in K\).
Throughout the paper we assume that posets are over a countable set of event names \(\mathcal {E}\). We will model event generation via the following event allocation operator, which takes a poset O and adds a new element \(e \notin |O|\) to it, with a given set of causes \(K \subseteq |O|\):
For example, \(\delta (\{ e_1,e_2 \preccurlyeq _O e_3\},\{e_1\},e) = \{ e_1 \preccurlyeq _O e,e_2 \preccurlyeq _O e_3\}\)
2.1 Abstract Posets
We assume a choice of isomorphism representatives for posets. We call such representatives abstract posets. We write \([O]\) for the canonical representative of O and we assume a choice of an abstraction map \(\alpha _O :O \rightarrow [O]\), to be exploited in the definition of synchronised product of causal processes (see Fig. 2, where we omit the subscript because it is clear from the context).
For abstract posets, the event allocation operator is simpler: we do not need to specify e, as we can add a(ny) new event, up to isomorphism. Therefore the abstract allocation operator \(\delta (O,K)\) gives \([\delta (O,K,e)]\), for any e. We assume the following operations:
-
the (injective) morphism old(O, K) embeds O into \(\delta (O,K)\);
-
\(new(O,K)\in \delta (O,K)\setminus old(O,K)(O)\) gives the unique new event in \(\delta (O,K)\).
For example, letting \(O=\{ e_1,e_2 \preccurlyeq _O e_3\}\), if \(\delta (O,\{e_1\}) = \{ e_2 \preccurlyeq _O e_1,e_3 \preccurlyeq _O e_4\}\) we can have \(new(O,\{e_1\}) = e_1\) and \(old(O,\{e_1\})(e_i) = e_{i+1}\) for \(i=1,2,3\).
These operations can be used to define the extension of \(\sigma :O \rightarrow O'\) to a morphism \({\sigma }^{\!+}_{K} :\delta (O,K) \rightarrow \delta (O',\sigma (K))\) given by
The intuition is that \({\sigma }^{\!+}_{K}\) does not mix up old and new events: it acts “as” \(\sigma \) (modulo suitable embeddings) on events that were already in O, and maps the new event in \(\delta (O,K)\) to the new one in \(\delta (O',\sigma (K))\). To ease notation, we will just write \({\sigma }^{\!+}\) when K is clear from the context.
2.2 Darondeau-Degano Causal Semantics
Let \(p,q,\dots \) denote sequential agents. Processes are generated by the following grammar
where \(\mathbf {0}\) is a distinguished inactive agent and the operator \(\parallel \) is the parallel composition of processes, which is associative and has unit \(\mathbf {0}\).
Let Act be a set of actions such that, for each \(a \in Act\), there is also \(\overline{a} \in Act\) (we let \(\overline{\overline{a}} = a\)). We assume a set of basic transitions for non-\(\epsilon \) agents
such that the subset \(\varDelta _p = \{ p \xrightarrow {a} t \in \varDelta \}\) is finite, for all p. Notice that continuations from an agent can be parallel compositions of agents.
Causal processes are process terms whose agents are decorated with finite subsets of positive natural numbers, representing their causes. They are writtenFootnote 3
where \(K_1,\dots ,K_n \subseteq \mathbb {N}^{+}\) are finite. Intuitively, the cause 1 represents a dependency with the last executed event, 2 with the one but last, and so on. The Darondeau-Degano causal semantics (DD-semantics hereafter) is a labelled transition system computed from basic transitions of agents. We illustrate it later via our running example.
Bisimilarity for the DD-semantics is the standard LTS bisimilarity. We call it DD-bisimilarity, denoted \(\sim _{dd}\). It has been shown (see, e.g., [1]) that DD-bisimilarity is fully abstract w.r.t. causal trees.
Example 1
(Running example). Consider two agents \(p_1\) and \(p_2\), with basic transitions
The DD-semantics of corresponding causal agents, for each set of causes K, is the following
The label shows the action \(a_i\) and the set K of causes of the moving agent. A new event is generated, canonically denoted 1, and is added to the causes of the continuation agent. The old causes are incremented by one, written \(\delta (K)\), to avoid a clash between the new event and the old ones.
The DD-semantics of parallel composition is computed from that of single agents. For instance
Here only the right component (\(p_2\)) moved, its label (\(a_2\) with cause \(\{1\}\)) became the overall one and its set of causes became \(\{1,2\}\). Note that despite the same symbol, the cause 1 in the source and label of the transition refer to a different event than the one associated with the cause 1 in the target of the conclusion. The left component is idle, but its event 2 needs to be incremented to avoid clashes with the continuation of the moving agent. In general, \(\delta \) needs to be applied to causes of idle agents. If we have more than one moving agent, i.e., two agents can do complementary actions \(K_1 \mathbin {\vdash }a\) and \(K_2 \mathbin {\vdash }\overline{a}\), their parallel composition can do \(K_1 \cup K_2 \mathbin {\vdash }\tau \), and causes \(\delta (K_1 \cup K_2)\) are assigned to both continuations of synchronised agents.
In Fig. 1 we show a finite part of the DD-semantics of \(\emptyset \mathbin {\vdash }p_1 \parallel \emptyset \mathbin {\vdash }p_2\): the state-space is actually infinite. States are tagged with marks (1) to (4) that will be used later to establish a correspondence with the named semantics (see Example 2 and Fig. 4): for the moment they can be ignored.
3 P-processes
Since we want to apply nominal techniques to model causal semantics, we introduce an abstraction of causal processes, where events are drawn from a set \(\mathcal {E}\) instead of \(\mathbb {N}^{+}\).
Definition 1
(Nominal causal process). A nominal causal process (n-process in short) is an expression of the form
where \(p_1,\dots ,p_n\) are agents and \(K_1,\dots ,K_n\) are finite subsets of \(\mathcal {E}\). We will use \(k,k',\dots \) to denote these processes.
We use finite posets over \(\mathcal {E}\) to keep track of causal dependencies among events in n-processes. We say that a n-process k is consistent with a poset O whenever, for all agents \(K \mathbin {\vdash }p\) in k, K is down-closed w.r.t. O. Intuitively, agents in k contain the whole history of their events, as described by O.
The history of events in a n-process can be augmented via the following closure operator.
Definition 2
(Closure operator). Given \(K \subseteq |O|\) and \(O'\) such that O is a subposet of \(O'\), the closure of K w.r.t. \(O'\) is given by
Its extension to n-processes is \({{(K \mathbin {\vdash }p)}\!\!\downarrow _{O'}} = ({{K}\!\!\downarrow _{O'}}) \mathbin {\vdash }p\) and distributes over parallel composition.
Given k consistent with O and \(O' \supseteq O\), \({{k}\!\!\downarrow _{O'}}\) is clearly consistent with \(O'\).
Definition 3
(Causes, immediate causes). The sets of causes \(\mathscr {K}(k)\) and immediate causes \(ic_O(k)\) of a n-process k w.r.t. a poset O are recursively defined by letting:
where \(max_O(K)\) is the set of maximal elements in K w.r.t. O.
The immediate causes of a n-process are events that are maximal with respect to at least one of its agents.
We assume that we have canonical representatives of n-processes. Let Aut(O) be the set of automorphisms on O, we pick a representative from \(\{ k \phi \mid \phi \in Aut(O) \}\), for any k consistent with O. We introduce an abstraction operator \([k]_O\) that, given k consistent with O, returns a canonical representative of k that is consistent with \([O]\) and a map that allows us to recover k from its representative.
Definition 4
(Process abstraction operator). Given a process k consistent with O, the process abstraction operator \([k]_O\) gives a pair \((\hat{k},\hat{\varphi })\) of a n-process \(\hat{k}\) consistent with \([O]\) and the isomorphism \(\hat{\varphi } :O \rightarrow [O]\) such that \(k\hat{\varphi } = \hat{k}\).
We now introduce the states of our causal semantics, namely P-processes.
Definition 5
(P-process). A P-process is a pair \({O}\rhd {k}\) where O is an abstract poset and k is a n-process, such that:
-
1.
\(|O| = \mathscr {K}(k)\);
-
2.
k is consistent with O;
-
3.
for all agents \(K \mathbin {\vdash }p\) in k, \(K \subseteq ic_O(k)\);
-
4.
\([k]_O = (k,\varphi )\), for some \(\varphi \);
Condition 1 says that the causes recorded in O are all and only the ones mentioned in k; condition 2 guarantees that the causes of each component in k are down-closed according to the order in O; condition 3 enforces only the most recent causes to be recorded in agents; finally, condition 4, establishes that k is a canonical representative. This makes event names local, i.e., there is no obvious relation among events in different P-processes.
3.1 Operations on P-processes
We introduce some operations on P-processes. The first one computes the “minimal” P-process that can be formed from a given poset and n-process.
Definition 6
(Immediate causes reduction operator). Given a poset O and a n-process k consistent with O, let \({O}_{\texttt {I}}\) be O restricted to \({ic_O(k)}\) and define \(norm_O(K \mathbin {\vdash }p) = K \cap |{O}_{\texttt {I}}| \mathbin {\vdash }p\), distributing over parallel composition. Then the immediate causes reduction operator is
where \([norm_O(k)]_{{O}_{\texttt {I}}} = (\hat{k},\hat{\varphi })\), and we denote by  the map \([{O}_{\texttt {I}}] \rightarrow O\) given by \(( {O}_{\texttt {I}} \hookrightarrow O ) \circ \hat{\varphi }^{-1}\).
the map \([{O}_{\texttt {I}}] \rightarrow O\) given by \(( {O}_{\texttt {I}} \hookrightarrow O ) \circ \hat{\varphi }^{-1}\).
Here the map \([{O}_{\texttt {I}}] \rightarrow O\) records the original identity of events of the reduced P-process.
We define an operation of amalgamated parallel composition, that allows us to form the parallel composition of two P-processes \({O_1}\rhd {k_1}\) and \({O_2}\rhd {k_2}\). Since events are local to P-processes, we need to specify how those in \(O_1\) and \(O_2\) are related. We do this through amalgamations, that are cospans
of order-embeddings such that \(|O|\!\!=\!\!img(\epsilon _1)\,\cup \,img(\epsilon _2)\). We denote by \(am(O_1,O_2)\) the set of all amalgamations of \(O_1\) and \(O_2\).
Definition 7
(Amalgamated parallel composition). Given two n-processes \(k_1,k_2\), consistent respectively with \(O_1\) and \(O_2\), and an amalgamation \(\epsilon = O_1 \xrightarrow {\epsilon _1} O \xleftarrow {\epsilon _2} O_2 \in am(O_1,O_2)\), we can form their amalgamated parallel composition
We extend the operator to P-processes \({O_1}\rhd {k_1}\) and \({O_2}\rhd {k_2}\) as follows:
4 HD Causal Semantics
Our causal semantics for P-processes is inductively computed from basic transitions of their agents. Transitions are of the following form

Here \(O \rhd k\) is performing an action \(\mu \in Act \cup \{ \tau \}\) with causes \(K \subseteq max(O)\). Unlike the DD-semantics, K only contains the most recent events among the causes of moving agents. This choice is sound, because down-closed sets, such as causes of agents, are fully determined by their maxima. The poset \(O'\) is \(\delta (O,K)\) reduced to immediate causes. The history map \(h :O' \rightarrow \delta (O,K)\) keeps track of the original identity of events. The presence of history maps makes the semantics history dependent, in the sense that the identity of events depend on the past transitions.
4.1 Interleaved and Synchronised Product
Our SOS rules will use two operations of left/right interleaved product and synchronised product to compute interleaving and synchronisation of two P-processes. They are defined in Fig. 2. The definitions are complicated by the need to deal with several embeddings, amalgamations, and removal of non-maximal causes, but are otherwise straightforward.
Suppose we want to compute the interleaving behaviour of a P-process that can be decomposed as an amalgamated parallel composition with amalgamation \(O_1 \xrightarrow {\epsilon _1} O \xleftarrow {\epsilon _2} O_2\). In defining the left interleaved product  , we assume that the left component has a transition to \({O_1'}\rhd {k_1}\), with causes \(K_1 \subseteq max(O_1)\) and history map \(h_1 :O'_1 \rightarrow \delta (O_1,K_1)\), while the right component is \({O_2}\rhd {k_2}\) and is idle. We want to compute action causes, history map and continuation of the interleaved transition. Action causes
, we assume that the left component has a transition to \({O_1'}\rhd {k_1}\), with causes \(K_1 \subseteq max(O_1)\) and history map \(h_1 :O'_1 \rightarrow \delta (O_1,K_1)\), while the right component is \({O_2}\rhd {k_2}\) and is idle. We want to compute action causes, history map and continuation of the interleaved transition. Action causes  are those \(K_1\) of the moving P-process, embedded in O via \(\epsilon _1\) (the superscript
are those \(K_1\) of the moving P-process, embedded in O via \(\epsilon _1\) (the superscript  is just an annotation to make clear that we are considering the left interleaved product). Some of them may become non-maximal, so they must be removed. To compute continuation and history map, we form a new amalgamation
is just an annotation to make clear that we are considering the left interleaved product). Some of them may become non-maximal, so they must be removed. To compute continuation and history map, we form a new amalgamation  . Here the vertex poset models event allocation for the overall transition. We use this amalgamation to compute parallel composition of \(k_1\) and \(k_2\). The resulting n-process may contain non-immediate causes, so we use ic to discard them and to compute a suitable history map
. Here the vertex poset models event allocation for the overall transition. We use this amalgamation to compute parallel composition of \(k_1\) and \(k_2\). The resulting n-process may contain non-immediate causes, so we use ic to discard them and to compute a suitable history map  , because we want to get a P-process. The right interleaved product
, because we want to get a P-process. The right interleaved product  is defined analogously.
is defined analogously.
The synchronised product is also similar. Now we assume that both components move, and we know their action causes, history maps and continuations. The action causes  of the synchronisation are simply the union of all action causes, embedded into O, namely \(\epsilon _1(K_1) \cup \epsilon _2(K_2)\). Again, non-maximal causes are removed. Overall continuation and history map are computed as in the interleaved product, via a new amalgamation
of the synchronisation are simply the union of all action causes, embedded into O, namely \(\epsilon _1(K_1) \cup \epsilon _2(K_2)\). Again, non-maximal causes are removed. Overall continuation and history map are computed as in the interleaved product, via a new amalgamation  .
.
4.2 HDC-semantics and Bisimulation
The History Dependent causal semantics (HDC-semantics) is the smallest LTS generated by the rules in Fig. 3.
Remark 1
Note that, given the particular nature of n-processes and P-processes, each agent p will have at most one immediate cause to expose in a transition. If a synchronisation is performed, at most two causes are recorded in the label and only one event is added to the target.
The rule (Agent) says that an agent p can become a P-process with either empty or singleton poset O. Any transition exhibits |O| as action causes, and goes to a P-process where each agent has a single cause e. The history map takes e to the maximal element of \(\delta (O,|O|)\). For instance, if \(O = \{ e \}\), \(\delta (O,\{e\}) = \{e_1 \preccurlyeq e_2\}\), and \(h(e) = e_2\).
The rules (Par-Left) ((Par-Right) is analogous, so it is omitted) and (Sync) handle the (amalgamated) parallel composition of two P-processes. The first two rules derive interleaving behaviour, and the latter derives a synchronisation between P-processes performing complementary actions. We use appropriate product operations to compute the derived transition.
We now introduce bisimilarity for P-processes, called HDC-bisimilarity. It is quite involved: when comparing two P-processes, we need to establish an explicit correspondence between their events. This correspondence can be a partial function, because some events may not be observable. Then a P-process is allowed to simulate a transition with a different transition, provided that this transition can be mapped to the original one via the partial function.
Definition 8
(HDC-bisimilarity). A HDC-bisimulation R is a ternary relation such that, whenever \(({O_1}\rhd {k_1},\sigma ,{O_2}\rhd {k_2}) \in R\):
-
\(\sigma \) is a partial isomorphism (i.e., an isomorphism between subposets) from \(O_1\) to \(O_2\);
-
if
 then \(\sigma \) is defined on K, and there are a transition
then \(\sigma \) is defined on K, and there are a transition  and \(\sigma '\) such that \(({O_1'}\rhd {k_1'},\sigma ',{O_2'}\rhd {k_2'}) \in R\) and the following diagram commutes
and \(\sigma '\) such that \(({O_1'}\rhd {k_1'},\sigma ',{O_2'}\rhd {k_2'}) \in R\) and the following diagram commutes 
-
if
 then \(\sigma \) is defined on K, and there are a transition
then \(\sigma \) is defined on K, and there are a transition  and \(\sigma '\) analogous to the previous item.
and \(\sigma '\) analogous to the previous item.
The greatest such bisimulation is denoted \(\sim _{hdc}\). We write \({O_1}\rhd {k_1} \sim _{hdc}^\sigma {O_2}\rhd {k_2}\) to mean \(({O_1}\rhd {k_1},\sigma , {O_2}\rhd {k_2}) \in \sim _{hdc}\).
The commuting diagram essentially says that \(\sigma '\) should act as \(\sigma \) on “old” events, and preserve freshness of events. The identity of new and old events is specified by the history maps.
Now we show how we can derive a HDC-semantics for (Darondeau-Degano) causal processes that is fully abstract w.r.t. DD-bisimilarity.
Theorem 1
Consider the following implementation of event names and event generation: \(\mathcal {E}= \mathbb {N}^{+}\) and \(\delta (O,K)\) is the reflexive and transitive closure of
with \(new(O,K) = 1\) and \(old(O,K)(n) = n+1\). Then \(k_1 \sim _{dd}k_2\) implies \(ic(O_1,k_1) \sim _{hdc}ic(O_2,k_2)\), for any \(O_i\) consistent with \(k_i\) (\(i=1,2\)).
Example 2
(HDC-semantics for the running example). In order to derive the HDC-semantics of \({\emptyset }\rhd {\emptyset \mathbin {\vdash }p_1 \parallel \emptyset \mathbin {\vdash }p_2}\), we start from the HDC-semantics of agents

where \(h_1 :\{1\} \rightarrow \delta (\{1\}) = \{2 \preccurlyeq 1\}\) maps 1 to itself. Then we derive other P-processes using (Par-Left) and (Par-Right). The resulting HDC-semantics is in Fig. 4, where states tagged with numbers (1) to (4) are “representations” of states in Fig. 1 with the same mark, in the sense that they are obtained from the latter by immediate causes reduction. Remarkably, this gives a finite state-space.
5 Causal History-Dependent Automata with Symmetries
We now consider minimal models for our HDC-semantics, up to HDC-bisimilarity. We do this by characterising HDC-semantics as History Dependent (HD-)automata, that are coalgebras over a suitable category of named sets. We call these coalgebras causal HD-automata (HDC-automata) because they will be defined in such a way that their transition relation matches our HDC-semantics. HDC-bisimilarity is then characterised as behavioural equivalence induced by the final HDC-automaton.
One important feature of HDC-automata is the presence of symmetries over states. Given an abstract poset O, a symmetry over O is a set \(\varPhi \subseteq Aut(O)\) (called just permutations hereafter) such that \(id \in \varPhi \) and it is closed under composition. States are of the form \({O}\rhd _{\varPhi }{s}\), where \(\varPhi \) is a symmetry over O.
Symmetries are essential for a correct notion of minimal model. In the case of ordinary labelled transition systems (LTSs), one can compute minimal versions w.r.t. bisimilarity, where all bisimilar states have been identified. Bisimilar LTSs have isomorphic minimal versions, so we may use any of them as canonical representative of the class of bisimilar LTSs. For HDC-automata, if we remove symmetries this fails: we may have minimal HDC-automata that are bisimilar but not isomorphic. We provide an example that explains this phenomenon.
Example 3
Consider the P-process \({\{1,2\}}\rhd {\{1\} \mathbin {\vdash }p_1 \parallel \{2\} \mathbin {\vdash }p_2}\) of Example 2, together with its two looping transitions. Consider the following HD-automaton

Reminding that in Example 2 we had
we can note that \(h_3' = h_3\) and \(h_4' = h_4 \circ (1 \ 2)\) (the permutation \((1 \ 2)\) swaps 1 and 2). Suppose we want to find a minimal realisation of these HDC-automata. They are not isomorphic, in the sense that there is no permutation on \(\{1,2\}\) that, applied to labels and composed with history maps, turns transitions of the former into transitions of the latter. However, we have
so these states should be identified in some way. This way is provided by symmetries: minimal behaviour, according to \(\sim _{hdc}\), is invariant under \((1 \ 2)\), so we can identify those states, provided that the resulting state is annotated with the permutation \((1 \ 2)\).
In [5] a symmetry group over a category \(\mathbf {C}\) is defined to be a collection of morphisms in \(\mathbf {C}[c,c]\), for any \(c \in |\mathbf {C}|\), which is a group w.r.t. composition of morphisms. Then generalised named sets are defined to be families of such groups. Since our symmetries are over abstract posets, we instantiate \(\mathbf {C}\) to the following category.
Definition 9
(Category P). The category \(\mathbf {P}\) has abstract posets as objects and order-embeddings as morphisms.
We give an equivalent presentation of our named sets, closer to the original one in [6]. Given a set S of morphisms and a morphism \(\sigma \) in \(\mathbf {P}\), we write \(S \circ \sigma \) for the set \(\{ \tau \circ \sigma \mid \tau \in S \}\) (analogously for \(\sigma \circ S\)).
Definition 10
(Category Sym(P)). Let \(\mathbf{Sym }(\mathbf {P})\) be the category defined as follows:
-
objects \(\varPhi \) are subsets of \(\mathbf {P}[O,O]\) that are groups w.r.t. composition in \(\mathbf {P}\);
-
morphisms \(\varPhi _1 \rightarrow \varPhi _2\) are sets of morphisms \(\sigma \circ \varPhi _1\) such that \(\sigma :dom(\varPhi _1) \rightarrow dom(\varPhi _2)\) and \(\varPhi _2 \circ \sigma \subseteq \sigma \circ \varPhi _1\).
Definition 11
(Category NSet(P)). The category \(\mathbf {NSet}(\mathbf {P})\) is defined as follows:
-
objects are \(\mathbf {P}\) -named sets, that are pairs \(N = (Q_N,\mathtt{{G}}_N)\) of a set \(Q_N\) and a function \(\mathtt{{G}}_N :Q_N \rightarrow |Sym(\mathbf {P})|\). The local poset of \(q \in Q_N\), denoted \(\Vert q \Vert \), is \(dom(\sigma )\), for any \(\sigma \in \mathtt{{G}}_N(q)\).
-
morphisms \(f :N \rightarrow M\) are \(\mathbf {P}\) -named functions, that are pairs \(( h , \varSigma )\) of a function \(h :Q_N \rightarrow Q_M\) and a function \(\varSigma \) mapping each \(q \in Q_N\) to a morphism \(\mathtt{{G}}_M(h(q)) \rightarrow \mathtt{{G}}_N(q)\) in \(Sym(\mathbf {P})\).
Then we can define the category of HDC-automata as coalgebras over a suitable endofunctor on \(\mathbf {NSet}(\mathbf {P})\). Formally, this endofunctor is yielded by a categorical equivalence between pullback-preserving presheaves on \(\mathbf {P}\) and \(\mathbf {NSet}(\mathbf {P})\) (cf. [3, 4]). We give an informal description below.
Definition 12
(Category of HDC-automata). Let \(B :\mathbf {NSet}(\mathbf {P})\rightarrow \mathbf {NSet}(\mathbf {P})\) be the following endofunctor
where:
-
\(\mathcal {P}_f:\mathbf {NSet}(\mathbf {P})\rightarrow \mathbf {NSet}(\mathbf {P})\) is the finite powerset on \(\mathbf {NSet}(\mathbf {P})\), mapping N to its finite subsets that satisfy some requirements (see [6] for the corresponding functor on named sets), equipped with a compatible symmetry group;
-
L is a \(\mathbf {P}\)-named set of labels whose elements are pairs \((K,\mu )\), where \(a \in Act \cup \{\tau \}\) and K represents the causes of a;
-
\(\varDelta :\mathbf {NSet}(\mathbf {P})\rightarrow \mathbf {NSet}(\mathbf {P})\) is the event generation functor, mapping N to a \(\mathbf {P}\)-named set made of pairs (q, e), with \(q \in Q_N\) and \(e \in \Vert q \Vert \) is an event marked as fresh; the symmetry group is the subgroup of \(\mathtt{{G}}_N(q)\) that fixes e.
5.1 HDC-automata for P-processes
We now show how we can derive HDC-automata from the HDC-semantics. The \(\mathbf {P}\)-named set of states for these automata is defined as follows.
Definition 13
( \(\mathbf {P}\) -named set of P-processes). The \(\mathbf {P}\) -named set of P-processes is \((Q_P,\mathtt{{G}}_P)\), where:
-
\(Q_P\) is the set of n-processes k such that \({O}\rhd {k}\) is a P-process and \(\Vert k \Vert = O\);
-
\(\mathtt{{G}}_P(k) = \{ \phi \subseteq Aut(\Vert k \Vert ) \mid k \phi = k\}\);
We write \({O}\rhd _{\varPhi }{k}\) for \(k \in Q_P\) such that \(\Vert k \Vert = O\) and \(\mathtt{{G}}_P(k) = \varPhi \).
Intuitively, in \({O}\rhd _{\varPhi }{k}\), \(\varPhi \) is a set of permutations that do not affect the state. Typically, when states are syntactic entities, we have \(\varPhi = \{ id \}\).
Transitions from \({O}\rhd _{\varPhi }{k}\) to \({O'}\rhd _{\varPhi '}{k'}\) are derived from those between the underlying P-processes. The idea is that we only keep one transition among the set of transitions that can be computed from each other using permutations in \(\varPhi \) and \(\varPhi '\). Formally, we say that two transitions  , \(i=1,2\), are symmetric whenever there are \(\phi \in \varPhi \) and \(\phi ' \in \varPhi '\) such that \(K_2 = \phi (K_1)\) and the following diagram commutes
, \(i=1,2\), are symmetric whenever there are \(\phi \in \varPhi \) and \(\phi ' \in \varPhi '\) such that \(K_2 = \phi (K_1)\) and the following diagram commutes

The derivation is done by taking a canonical representative among symmetric transitions. Clearly all other transitions can be reconstructed.
Bisimilarity for HDC-automata induced by the HDC-semantics can be characterised as a slight variant of Definition 8, where permutations are taken into account. It is a set of triples \(({O_1}\rhd _{\varPhi _1}{k_1},\sigma ,{O_2}\rhd _{\varPhi _2}{k_2})\) such that, for all \(\phi _1 \in \varPhi _1\) and every transition of \({O_1}\rhd _{\varPhi _1}{k_1}\), there is a transition of \({O_2}\rhd _{\varPhi _2}{k_2}\) obtained by applying \(\phi _2^{-1} \circ \sigma \circ \phi _1\) to the former transition, for some \(\phi _2 \in \varPhi _2\). The commuting diagram for the new map \(\sigma '\), relating the continuations, now involves \(\phi _2^{-1} \circ \sigma \circ \phi _1\).
It can be proved that this new notion of bisimilarity is fully abstract w.r.t HDC-bisimilarity. Under the assumptions of Theorem 1, this is equivalent to DD-bisimilarity. Therefore we have our final theorem.
Theorem 2
(Causal trees, finally). Under the assumptions of Theorem 1, the final semantics of a P-process is a HDC-automaton that represents the causal tree of the underlying causal process.
As mentioned, symmetries allow computing minimal realisations, where all bisimilar P-markings are identified. More precisely, we can identify two states \({O_1}\rhd _{\varPhi _1}{k_1}\) and \({O_2}\rhd _{\varPhi _2}{k_2}\) that are related by \(\sim _{hdc}^{\sigma }\), for some \(\sigma \). Then \(\sigma \) becomes part of the state symmetry. Actually, \(\sigma \) is a permutation between subposets of \(O_1\) and \(O_2\), but it can be shown that all HDC-bisimilar states have the same poset of observable events on which \(\sigma \) is defined. This means that \(\sigma \) is indeed a permutation on that poset.
Example 4
(HDC-automaton for the running example). The HDC-automaton for the running example can be derived by taking \({O}\rhd _{\{id\}}{k}\), for each P-process \({O}\rhd {k}\) in Example 2. Its minimal realisation has the same shape and the same transitions, but the state \({\{1,2\}}\rhd {\{1\} \mathbin {\vdash }p_1 \parallel \{2\} \mathbin {\vdash }p_2}\) is equipped with symmetry \(\{id,(1 \ 2)\}\).
6 Conclusion
In this paper we have revisited causal tree semantics under the new light offered by nominal techniques, not available when causal trees were first introduced by Pierpaolo Degano and Philippe Darondeau. While doing so, we have outlined a general methodology for providing minimal realisation up to causal semantics. The methodology is based on a nominal framework, here enriched with poset information. While the work in this paper builds on the work in [3, 4], Sect. 4 provides causal processes with a direct, compositional definition of operational semantics and of the associated bisimilarity. Moreover, the minimal realisation is shown to provide a, possibly finite, causal tree semantics.
Notes
- 1.
An analogous concept of location automata was introduced in [14] for modelling the location semantics of CCS.
- 2.
As it is common in final semantics, the final coalgebra is typically an infinite object that accounts for all possible behaviours, but the minimal representative of an HD-automaton needs to account just for the behaviours of that automaton: it decomposes uniquely the map from the HD-automaton to the final object into a surjective mapping from the HD-automaton to the representative and an embedding of the latter into the final object.
- 3.
Note that inactive agents of the form \(K \mathbin {\vdash }\mathbf {0}\) are just disregarded.
References
Basagni, S.: A note on causal trees and their applications to CCS. Int. J. Comput. Math. 71(2), 137–159 (1999)
Bodei, C.: Some concurrency models in a categorical framework. In: ICTCS (1998)
Bruni, R., Montanari, U., Sammartino, M.: A coalgebraic semantics for causality in Petri nets. J. Logic Algebr. Meth. Progr. (2015, in press). http://cs.ru.nl/M.Sammartino/publications/JLAMP15.pdf
Bruni, R., Montanari, U., Sammartino, M.: Revisiting causality, coalgebraically. Acta Inf. 52(1), 5–33 (2015). http://www.cs.ru.nl/M.Sammartino/publications/ACTA2014.pdf
Ciancia, V., Kurz, A., Montanari, U.: Families of symmetries as efficient models of resource binding. Electr. Notes Theor. Comput. Sci. 264(2), 63–81 (2010)
Ciancia, V., Montanari, U.: Symmetries, local names and dynamic (de)-allocation of names. Inf. Comput. 208(12), 1349–1367 (2010)
Darondeau, P., Degano, P.: Causal trees. In: Dezani-Ciancaglini, M., Ronchi Della Rocca, S., Ausiello, G. (eds.) ICALP 1989. LNCS, vol. 372, pp. 234–248. Springer, Heidelberg (1989)
Darondeau, P., Degano, P.: Causal trees interleaving + causality. In: Guessarian, I. (ed.) LITP 1990. LNCS, vol. 469, pp. 239–255. Springer, Heidelberg (1990)
Fiore, M.P., Turi, D.: Semantics of name and value passing. In: LICS, pp. 93–104 (2001)
Fröschle, S.B., Hildebrandt, T.T.: On plain and hereditary history-preserving bisimulation. In: Kutyłowski, M., Wierzbicki, T.M., Pacholski, L. (eds.) MFCS 1999. LNCS, vol. 1672, pp. 354–365. Springer, Heidelberg (1999)
Fröschle, S.B., Lasota, S.: Causality versus true-concurrency. Theor. Comput. Sci. 386(3), 169–187 (2007)
Gadducci, F., Miculan, M., Montanari, U.: About permutation algebras, (pre)sheaves and named sets. Higher-Order Symbolic Comput. 19(2–3), 283–304 (2006)
Montanari, U., Pistore, M.: Minimal transition systems for history-preserving bisimulation. In: Morvan, M., Reischuk, R. (eds.) STACS 1997. LNCS, vol. 1200, pp. 413–425. Springer, Heidelberg (1997)
Montanari, U., Pistore, M., Yankelevich, D.: Efficient minimization up to location equivalence. In: Riis Nielson, H. (ed.) ESOP 1996. LNCS, vol. 1058, pp. 265–279. Springer, Heidelberg (1996)
Pistore, M.: History dependent automata. Ph.D. thesis, University of Pisa (1999)
Rutten, J.J.M.M.: Universal coalgebra: a theory of systems. Theor. Comput. Sci. 249(1), 3–80 (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Bruni, R., Montanari, U., Sammartino, M. (2015). Causal Trees, Finally. In: Bodei, C., Ferrari, G., Priami, C. (eds) Programming Languages with Applications to Biology and Security. Lecture Notes in Computer Science(), vol 9465. Springer, Cham. https://doi.org/10.1007/978-3-319-25527-9_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-25527-9_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-25526-2
Online ISBN: 978-3-319-25527-9
eBook Packages: Computer ScienceComputer Science (R0)


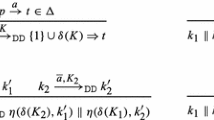





 then
then  and
and 
 then
then  and
and 