On the Impact of Forward-Facing Steps on Disturbance Amplification in Boundary-Layer Flows

Abstract

Using our DNS code NS3D boundary-layer flows over smooth walls and walls containing a forward-facing step have been simulated using a so-called disturbance formulation, i.e., by first computing a steady two-dimensional base flow and then an unsteady disturbance flow. The influence of step height and free-stream Mach number on streamwise pressure gradient and the occurrence or absence of laminar separation bubbles are shown for some base flows. A fundamental difference between subsonic and a supersonic flow over the same step height is that the flow directly after the step exhibits an adverse pressure gradient with laminar separation in the subsonic case but due to an expansion of the supersonic flow around the corner, a favourable pressure gradient without separation in the supersonic case. The unsteady disturbance flow is initialised by a wave packet in the upstream part of the integration domain that contains all frequencies which become unstable in the considered area. Amplification factors, so called N-factors, are then extracted from the frequency spectra of the disturbance flow for quantification of the impact of step parameters on disturbance amplification. Our results show that the observed differences between different cases are fully due to the local flow properties of the base flow, i.e. streamwise pressure gradient and Mach number. Three-dimensional simulation results for a supersonic case with a large step height where the N-factor approach is no longer applicable are presented towards the end. Self-excited three-dimensional disturbances appear in this case, probably due to a three-dimensional global instability.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Laminar flow is important for drag and hence fuel reduction, but laminar flow is only possible if the surface obeys certain smoothness parameters. Important generic surface roughness shapes are steps and gaps which may occur at the joint of two adjacent surface panels. Previous investigations, like [3, 12, 13, 19], tried to parameterise the detrimental influence of such surface protuberances on the growth factor of small-amplitude disturbances, so-called Tollmien-Schlichting waves. These waves are the precursors of laminar-turbulent transition in a flow with low turbulence levels in the free stream. Previous investigations measured the impact of surface imperfections by a so-called Δ N factor that quantifies the additional amplification in a flow with surface imperfection relative to the flow over the corresponding smooth surface. The present project uses Direct Numerical Simulation (DNS) on a High-Performance Computer (HPC) to investigate the effects of Mach number, pressure gradient, step position and step height on Δ N for forward-facing steps.

The paper is organized as follows. The numerical method is presented in Sect. 2 which includes discussion of implementation aspects on the HPC. This is followed by exemplary results in Sect. 3, a discussion of the limits of the present approach in Sect. 3.3 and conclusions in Sect. 4.

2 Numerical Method

A sketch of the integration domain for a flat plate with a forward-facing (i.e. against the flow direction) step is shown in Fig. 1. The x-axis is normal to the leading edge, parallel to the wall and pointing in streamwise direction. The y-axis points in the wall-normal direction, whereas the z-axis is aligned with the spanwise direction. The computational domain extends in the x-direction from x ₀ to x _E, the location of the step is given by x _S, where all x positions are measured as distances from the leading edge of the plate. The height of the step is given by H. The coordinate x _D, M denotes the position of a disturbance strip where the stability of the steady laminar base flow will be probed by small-amplitude disturbances (see further down). Most cases studied are two-dimensional and thus only an x-y plane needs to be considered. In the three-dimensional case, the flow field is assumed to be periodic in the spanwise direction with the spanwise wave length λ _z. In the following, all spatial dimensions will be given in non-dimensional form as Reynolds numbers.

Fig. 1

Sketch of computational domain with forward-facing step with step height H at x _S on a flat plate

In Fig. 2, a sketch of the domain decomposition with forward-facing step is shown. A minimum of three domains (red domains labelled 1–3) is necessary to discretise the step geometry. To increase the performance by further parallelising the simulation (see Sect. 2.2), the basic domains can be split into smaller sub-domains. An example is given by the blue sub-domains in Fig. 2.

Fig. 2

Sketch of domain decomposition with step geometry

The present DNS code NS3D was originally written by Babucke [2] and is continuously enhanced as part of the ongoing work on transition research at the IAG. In the following, the most important aspects for the present study will be explained. A more detailed insight can be found in the thesis by Babucke [2].

NS3D offers a multitude of different finite-difference schemes for spatial discretisation in x- and y- direction. These schemes can be classified in explicit, compact and sub-domain compact schemes, cf. [8, 9]. Hereby, sub-domain compact means that in every sub-domain a compact scheme is used, whereas the coupling between sub-domains is accomplished using an explicit scheme. For the present study, explicit as well as compact and sub-domain compact differences are used because of parallelisation issues (see Sect. 2.2). The numerical properties of the different schemes are chosen to be as similar as possible.

As non-linear terms generate higher harmonics, damping of under-resolved wavelengths is necessary. Thus, alternating up- and downwind-biased finite-differences are applied for convective terms. The compact finite differences used for convective terms are of 6th-order accuracy.

Time integration is performed using the classical fourth-order accurate Runge-Kutta scheme. It consists of four steps at two equidistant time levels. After each sub-step, the direction of the alternating up- and downwind-biased finite-differences changes [10]. A preferred direction is avoided by changing the alternation of the differences after each timestep, using all possible combinations in x-, y- and z-¹ direction.

2.1 Selective Frequency Damping

For stability analyses of flows, a steady baseflow solution is needed. As the code NS3D is a time-accurate high-order code with low numerical dissipation, it is impossible to reach this solution if the flow under consideration is globally unstable. Thus, selective frequency damping (SFD) was implemented in the code. With SFD, a temporal filter is used to calculate a solution which successively suppresses temporal fluctuations. The method is based on the work by Åkervik et al. [1] which again elaborates an idea by Pruett [15]. Parameters which need to be defined by the user are the filter width Δ and the control coefficient χ. Details of the method can be find in Åkervik et al. [1].

2.2 Parallelisation

Three different high performance computing systems were used for the present numerical simulations. At the beginning, two vector machines, the NEC SX-8 and SX-9 were available at the HLRS. Later on, these machines were replaced by a massive-parallel system, the Cray XE6 “Hermit”. Both vector machines have very similar requirements for parallelisation, but for the massive-parallel system some new problems arose.

For both vector and massive-parallel systems, the domain in the x-y plane is divided into sub-domains with data exchange using the Message Passing Interface (MPI) [11]. This domain decomposition in the x-y-directions not only serves for parallelisation purposes but also allows more complex geometrical configurations like the step geometry for the present study (see Fig. 2). In the z-direction, loops are parallelised utilizing a shared memory parallelisation.

A typical configuration on vector machines would be for example for a two-dimensional configuration a decomposition in eight domains using eight CPUs running on one SX-8 node or for a three-dimensional computation a decomposition in eight domains each running on one SX-8 node, using 64 CPUs in total. On the vector machines, compact finite differences are used. The resulting tridiagonal system is solved using a pipelined Thomas algorithm (see Babucke [2], pp. 48–51 and Povitsky [14]), leading to an efficient parallelisation for the typical amount of sub-domains (and thus MPI-processes) used on the vector machines.

As the new massive-parallel “Hermit” system has a much higher peak performance than the vector machines, another strategy is used to achieve highest performance. Instead of relatively few, very powerful CPUs, a great number of “standard” CPUs, similar to those used in personal computers, are built together in one big system. The large-grain sub-domain configuration used for the vector machines is no longer sufficient as the computational time for a given problem would increase severely. Therefore, for the present forward-facing step problem, the x-y-plane is typically split into up to more than 1000 sub-domains. In this scenario, the pipelined Thomas algorithm of the compact scheme performs poorly as huge dead-lock times arise when processes are waiting for other processes to calculate data they need. An illustration of this behaviour is given in Table 1 for a typical two-dimensional run which was run over 20,000 time steps using a domain that contains 448 subdomains in streamwise direction x plus 320 subdomains in wall-normal-direction y, i.e., 811,008 grid points. The performance advantage of the explicit finite differences compared to the other two alternatives is quite obvious from the data given in the table: 103 s instead of 352, i.e., a speed-up factor of 3.4. The reason for this speed-up is that data exchange is necessary only once per Runge-Kutta timestep such that each MPI-process performs the calculations for its sub-domain independent from the other processes.

Table 1 Comparison of execution times using different spatial discretisation schemes

Typical resource requirements and performance data for three-dimensional simulations are as follows: For a case with 786,432 grid points per spanwise Fourier mode, 42 Fourier modes and 129 collocation points in spanwise direction 6144 cores have been used using simultaneous OpenMP and MPI parallelisation. The execution time in this case is 0.3 s/time step.

3 Results

Many cases with different step heights, step positions and free-stream conditions (identified by the Mach number M​a _∞) have been investigated. Each case starts with the computation of a two-dimensional steady base flow. If this fails (e.g., if SFD is not applied) the according case cannot be investigated further with the present approach (see Sect. 3.3).

Baseflow results for subsonic and supersonic cases are presented in Sect. 3.1, followed by a description of the N-factor method to quantify the results in Sect. 3.2 and a discussion of a case with a large step height H in Sect. 3.3.

3.1 Base Flows

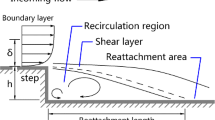
Laminar separation bubbles are the most influential flow phenomena in all base flows. Depending on flow parameters, either only one separation bubble in front of the step or two zones of separated flow, one in front and one on top of the step are found for subsonic cases.

Figure 3 shows streamlines, pressure contours, the region of reversed flow and representative velocity profiles in the area around the step for high subsonic Mach number and a small step height (M​a _∞ = 0. 8, Re _S = 2, 450, 000, Re _H = 1320), where Re _S and Re _H are the Reynolds numbers based on step position (x _S) and step height (H), respectively. Here, only one very small separation bubble is found in front of the step. Streamlines near the step are tightened but follow the contour smoothly. The pressure rises in front of the step and then decreases as the flow is accelerated around it.

Fig. 3

Baseflow near the step for M​a _∞ = 0. 8, Re _S = 2, 450, 000, Re _H = 1320. (a) Streamlines and pressure contours. Region of reversed flow visualized by dashed line. y-direction stretched by factor 2. (b) Profiles of streamwise velocity u at four streamwise positions Re _x = 2, 000, 000, Re _x = 2, 445, 000, Re _x = 2, 450, 320, and Re _x = 2, 800, 000, respectively

The profiles of the streamwise velocity component u at four streamwise positions are shown for two grid resolutions. Refined grid means a grid refinement in both the x- and y-directions by a factor of two. Results for both resolutions are found to be in very good accordance.

The boundary layer depicted in these profiles starts with a typical laminar boundary-layer profile far upstream of the step and develops an inflection point in front of the step. The third position at Re _x = 2, 450, 320 is immediately past the step. Here, a small sub-boundary-layer starting at the step corner can be seen, whereas the outer profile remains nearly unchanged. At Re _x = 2, 800, 000 the sub-boundary-layer has vanished and the flat-plate boundary layer is recovered.

Figure 4 presents a case with higher step but otherwise identical parameters (M​a _∞ = 0. 8, Re _S = 2, 450, 000, Re _H = 2640). Now, two zones of separated flow are observed. The first one is much bigger than the second, which is in particular much flatter. Compared to the first case, the first separation bubble is much longer, with the region of separated flow being roughly ten times longer, whereas the step is only twice the height in absolute values and approximately four times higher when both cases are compared using local flow properties at the step. Pressure contours show that the pressure in front of the step reaches higher values compared to the case with only one separation bubble. Additionally, a distinct low-pressure zone is observed on top of the step, after which the pressure rises again.

Fig. 4

Baseflow near the step for M​a _∞ = 0. 8, Re _S = 2, 450, 000, Re _H = 2640. (a) Streamlines and pressure contours. Region of reversed flow visualized by dashed line. y-direction stretched by factor 2. (b) Profiles of streamwise velocity u at four streamwise positions Re _x = 2, 000, 000, Re _x = 2, 445, 000, Re _x = 2, 450, 320, and Re _x = 2, 800, 000, respectively

The profiles of streamwise velocity u are shown for two grid resolutions and at the same four streamwise positions as before. Whereas profiles far upstream and downstream of the step are nearly identical to those from the case with only one separation bubble, differences around the step are visible. In front of the step, the flow separation can be seen. Only marginally negative velocities are observed. Downstream of the step, the sub-boundary-layer is now bigger than in the previous case. A very small region of separated flow is existent but barely visible.

Figure 5 compares the wall pressure along the streamwise coordinate for both cases. Upstream of the step, the pressure equals the level of the flat plate. It remains nearly unchanged until approximately Re _x = 2, 000, 000, where it rises until the step location. Here, an immediate pressure drop occurs. After the step, the wall pressure increases until the level of the flat plate solution is again asymptotically reached.

Fig. 5

Comparison of wall pressure p _w along x for M​a _∞ = 0. 8, Re _S = 2, 450, 000, Re _H = 2640 and various step heights H

When the flow at the step reaches supersonic conditions, which would be a typical situation for an airliner wing, the base-flow topology changes markedly. Figure 6 presents results for $M\!a_{\infty } = 1.06,Re_{S} = 2,300,000,Re_{H} = 2640$ in the same way as for the subsonic cases before. The relative step height in terms of boundary-layer momentum thickness is the same as for the case shown in Fig. 4 which exhibits two separation bubbles in subsonic flow. Now, only one separation zone is observed. Compared to the subsonic case, this separation bubble is approximately eight times longer. The rise of the separation streamline from the separation point at the wall towards the step is very slow and constant, such that the separation zone acts like a smooth ramp in front of the step. Thus, flow deflection around the step is much smoother than in the subsonic case, allowing the flow to follow the wall contour after the step without further separation. Due to the upward flow deflection in front of the step (because of the separation bubble) the pressure increases. Afterwards the flow expands around the step, leading to a pressure drop in the right half of the domain.

Fig. 6

Baseflow near the step for M​a _∞ = 1. 06, Re _S = 2, 300, 000, Re _H = 2640. (a) Streamlines and pressure contours. Region of reversed flow visualized by dashed line. y-direction stretched by factor 5. (b) Profiles of streamwise velocity u at four streamwise positions Re _x = 1, 800, 000, Re _x = 2, 250, 000, Re _x = 2, 300, 320, and Re _x = 2, 800, 000

The velocity profiles at four different streamwise locations show again a very good grid convergence. Far upstream of the step the nearly unaltered boundary-layer profile of the similarity solution can be seen. Inside the separation zone only marginal negative velocities are observed. The third profile is directly on top of the step. Here, like in the subsonic case, the oncoming profile is cut-off and a new sub-boundary-layer is observed. However, this sub-boundary-layer is smaller in the supersonic case because of the smoother flow deflection around the step. Far downstream, the boundary-layer profile of the flat plate is recovered as in all cases shown here.

The wall pressure distribution in streamwise direction x is illustrated in Fig. 7. Starting from the nearly constant pressure of the flat plate, the pressure rises (with inverse curvature compared to the subsonic case) until the step location. Here, a sudden pressure drop occurs, followed by a steep rise and a slow decay until a constant value is reached again. This decay stands in contrast to the progression of the wall pressure in the subsonic cases, where the wall pressure increases after the step.

Fig. 7

Wall pressure p _w along x for M​a _∞ = 1. 06, Re _S = 2, 300, 000, Re _H = 2640

For supersonic cases, three different steady flow regimes are observed when conducting two-dimensional simulations. In the first regime, one very long zone of separated flow is found in front of the step. For increasing step height, while all other parameters stay constant, secondary separation zones within the separation bubble are visible. When the step height is further increased, a second region of separated flow on top of the step is formed. However, it is found that cases within both the latter aforementioned regimes are naturally three-dimensionally unsteady, thus a purely two-dimensional analysis seems unphysical. The flow characteristics of these cases are therefore described in Sect. 3.3, where three-dimensional base flows are discussed.

3.2 Disturbance Excitation and N-factor Computations

A wave packet is introduced into the steady baseflow by blowing and suction over a finite span of time at the wall within the disturbance strip introduced in Fig. 1.

A multitude of different disturbance excitations were tested. Usually the best results are obtained when not a single Dirac-pulse is used but the amplitudes of the blowing/suction are first smoothly increased and subsequently decreased in time. By turning the disturbance strip on and off, sound waves are emitted which travel in up- and downstream direction. These sound waves interact with the step as well. A certain optimization with respect to using multiple frequencies for the blowing/suction was necessary to reduce the amplitudes of these unavoidable sound waves [4]. Nevertheless, the unsteady, instantaneous flow field is rather complex as can be seen using three snapshots of the pressure disturbances p′ in Fig. 8.

Fig. 8

Sound waves at step for M​a _∞ = 0. 8, Re _S = 2, 450, 000, Re _H = 3520. Six contour levels of p′ between $-5 \cdot 10^{-11}$ and 5 ⋅ 10⁻¹¹ shown

Two main phenomena are observed. Firstly, a part of the sound wave is reflected with the main direction pointing upstream at an angle of 45^∘. Secondly, a new wave packet emerges at the step inside the boundary layer. In the region directly after the step, a very small dominant wavelength of approximately Re _x = 6000 width and a small propagation speed of c ≈ 0. 2 is found, which leads to a frequency in the range of the dominant frequency of the sound waves. Wavelengths as well as amplitudes of the wave packet in that region very near the step increase rapidly. However, an accurate Fourier analysis is not possible as the wave packet is superposed by the sound waves. Slightly further downstream, the analysis becomes possible as the sound waves have passed.

The generation of acoustics at the disturbance strip and the thereby induced excitation of a small wave packet at the step due to receptivity is only a side effect of the chosen disturbance method. The main purpose remains the generation of a wave packet in the boundary layer where all frequencies of interest are existent with sufficient amplitude such that their amplitude development can be studied. At the beginning, the wave packet develops in the same manner as on a flat plate without step. However, as soon as the disturbance reaches the region where, caused by the step, the pressure deviates from the pressure without step, the development of the wave packet differs from the development without step.

The spatial growth of the wave packet is illustrated in Fig. 9 using contours of the streamwise velocity disturbance (u′) for three different time steps in the region around the step. At the step, the appearance of the wave packet changes as some irregular structures in the near-wall region are observed. Behind the step, the wave packet is again similar to the wave packet in front of the step but with much higher amplitude. Additionally, it can be seen that the wave packet induces sound waves at the step which are mainly directed in upstream direction.

Fig. 9

Contours of u′ for three different timesteps. Main wave packet M​a _∞ = 0. 8, Re _S = 2, 450, 000, Re _H = 3520. y-direction stretched by factor 5

For quantification of the influence of steps so-called N-factors are used. This term comes from the e ^N-method proposed by van Ingen [18] and Smith and Gamberoni [17] for prediction of laminar-turbulent transition in boundary-layer flows. The N-factor is just a measure of the maximal possible streamwise disturbance growth. Originally, it would be calculated from linear stability theory. However, here we extract it from the results of disturbance-flow calculations with our code NS3D as follows.

First, a Fourier analysis of the time signals at each grid point is performed to obtain the disturbance amplitude field Υ(x, y, f), where x and y are the spatial coordinates, and f is the frequency. Additional details like the elimination of the sound waves from the Fourier analysis are not presented here, they are discussed in [4]. A maximum search in wall-normal direction y is then performed at every streamwise station x and for all frequencies f to yield A(x, f) = max_y(Υ). Next, we define A ₀( f) as the amplitude where the growth curve A(x, f) for each frequency f enters the unstable region, i.e., starts to grow. From this we obtain normalised amplitude growth-curves $n =\ln (A(x,f)/A_{0}(\,f))$ like those which are plotted in Fig. 10. The envelope curve N(x) which is indicated by the red line in the figure is the so-called N-factor curve then.

Fig. 10

Evaluation of N-factor curve from amplitudes of simulation with optimized disturbance excitation

Quantification of the influence of surface roughness is thereafter performed by comparing the N-factor curves for the flow over the smooth wall with the results for the flow over the roughness, see Fig. 11. It turns out that the difference Δ N between the two is not a constant but rather a function of x.

Fig. 11

Definition of additional amplification Δ N

Figure 12 presents a comparison of N-factor curves for two Mach numbers, M​a = 0. 6 and M​a = 1. 06 but for the same relative step height Re _H = 2640. The first difference between the two is the stronger disturbance growth in the flat-plate boundary layer in the subsonic case that leads to generally higher N-factors there. The next difference is the different qualitative behaviour in the presence of the step. Two regions of amplification occur in the subsonic case and only one in the supersonic. Both cases show a Δ N after the step that can be quantified from the figure: Δ N ≈ 2 in the subsonic and an approximately constant Δ N ≈ 1. 6 downstream of the step in the supersonic case.

Fig. 12

Comparison of N-factor curves at different Mach number but same relative step height

Another striking qualitative difference between bot cases is that the subsonic wave packet continues to grow after the step whereas its amplitude is reduced in the supersonic case. However, in light of the above discussion of the streamwise pressure gradient, together with the occurrence (or absence) of a second separation bubble, this is not surprising but fully consistent with the observed qualitative differences in the two base flows. Adverse pressure gradients (i.e., streamwise pressure increase) and boundary-layer separation leads to increased disturbance amplification, whereas flow expansion and streamwise pressure decrease, reduce the disturbance amplitudes. Comparisons with linear stability theory have also confirmed these results in a quantitative manner. Furthermore, all N-factor results of the present research are published in [4–6]. They shall not be repeated here. Instead, we present some more DNS results that go beyond the applicability of linear stability theory and the N-factor method in the next section.

3.3 Limits of the Present Approach: High Steps in the Supersonic Regime

The influence of steps on laminar-turbulent transition has been represented by a local additional Δ N-factor in the present study. Basis for this approach is the simulation of a steady, two-dimensional baseflow (see Sect. 3.1). The time-accurate DNS-code NS3D allows simulation of steady base flows for subsequent N-factor calculations as shown above. However, when the height of the step exceeds a certain value, new phenomena arise. These steps are in the following called “high steps”. Differences are again found between sub- and supersonic cases, but we shall limit our presentation here to the supersonic case at M​a _∞ = 1. 06.

The required three-dimensional simulations are computationally extremely expensive. Thus, only relatively few cases with high steps were simulated and only a quite short description of the physical phenomena follows.

For flows at M​a _∞ = 1. 06 and the step located at Re _S = 2, 450, 000, a steady baseflow is reached for step heights up to Re _H = 7000 if a two-dimensional simulation is conducted. At Re _H = 9000, the simulation crashed after a while. A grid refinement study would be necessary to clarify the situation in this case.

The baseflow for a case with a step height of Re _H = 6000, located at Re _S = 2, 450, 000 and M​a _∞ = 1. 06 is visualized in Fig. 13. Compared to Fig. 6, used for the description of supersonic base flows in Sect. 3.1, some differences are observable. First, the separation bubble in front of the step is even bigger and has a relative length of L ₁∕H ≈ 51. Second, a very small separation bubble on top of the step emerges. However, this separation bubble is very small. The relative length of the second bubble is only $L_{2}/H \approx 1/6$ and the height of the region with negative u-velocity is approximately 1∕6H. Furthermore, a secondary separation zone is observed within the separated zone in front of the step.

Fig. 13

Baseflow around step geometry for M​a _∞ = 1. 06 with Re _S = 2, 450, 000 and Re _H = 6000. Region of reversed flow visualized by dashed line. y-direction stretched by factor 10

This flow is now used as a baseflow for a three-dimensional simulation without introduced disturbances. It is found that a spanwise (w) velocity component emerges in front of the step and grows in time. As soon as the w-component exceeds w ≈ 0. 001, the unsteady motion becomes visible in the other variables as well. Soon thereafter, the secondary separation bubble disappears. Saturation of the w-component seems to be reached at w ≈ 0. 05 which is found directly in front of the step. However, in the time simulated, neither a steady nor a truly periodic state was achieved.

A snapshot of the flow field at the last time step simulated is shown in Fig. 14. Directly in front of the step, the separation bubble is highly three-dimensional with all three velocity components being in the same order of magnitude. In the shown plane just in front of the step, two main vortices can be seen. These are of extremely short spatial extent as they are not visible after the step and the separation bubble in front of the step gets increasingly two-dimensional in the upstream direction. This fact is further illustrated by the streamline remaining two-dimensional in the upstream region and becoming chaotic, three-dimensional directly in front of the step. On top of the step, some weak streaky structures are visible. However, the maximum w-velocity in the shown plane after the step is only w ≈ 0. 001 compared to w ≈ 0. 02 in the displayed plane in front of the step. Together with a strong u-component the flow is again nearly two-dimensional after the step.

Fig. 14

Snapshot of three-dimensional flow around step geometry for M​a _∞ = 1. 06 with Re _S = 2, 450, 000 and Re _H = 6000. y- and z-directions stretched by factor 10. x-plane: w-contours with 21 contour levels between $-5 \cdot 10^{-4}$ and 5 ⋅ 10⁻⁴. λ ₂ (vortex identification criterion [7]) isolines in white. y-plane: Contours of ω _x at the walls. Twenty contour levels between $-1 \cdot 10^{-6}$ and 1 ⋅ 10⁻⁶. z-plane: u-contours with 21 contour levels between 0 and 1

The described state is only a snapshot and it is not clear whether a periodic or a steady state will be reached if the simulation is continued. A comparable behaviour is observed for a step height of Re _H = 5000. Here, the secondary separation bubble within the separated zone in front of the step is found as well, whereas the separation on top of the step is missing. However, in this case, the w-velocity grows much slower and even though the simulation is run for twice as long, the maximum w-component has only reached w ≈ 0. 015.

To check that the three-dimensional behaviour is not encountered in the earlier supersonic cases used for the N-factor calculation, an additional full three-dimensional simulation has been conducted for one of those. In that case, the w-velocity stayed within the computational error with a maximum of w ≈ 5 ⋅ 10⁻¹⁵.

4 Conclusions

The existing HPC-DNS code NS3D has been used to compute amplification factors (N-factors) for boundary-layer flows over smooth walls and walls with steps. Compressible cases with high subsonic and low supersonic Mach numbers have been investigated. Many interesting and unexpected differences between the supersonic and subsonic flow conditions have been detected. The most prominent is the occurrence of different streamwise pressure gradients and flow fields with different laminar separation bubbles. As these have a predictable influence on the growth of disturbances which are precursors of laminar-turbulent transition, it turns out that the additional amplification Δ N caused by a step relative to the smooth case can be predicted if it is possible to compute the steady base accurate enough for subsequent local linear stability analysis.

However, if the step height exceeds some critical value, new phenomena occur which need to be studied further. Here, the observed unsteady flow occurring for high steps at M​a _∞ = 1. 06 was briefly described but the flow in this case is far from being understood. The simulation was neither run long enough nor was the influence of spanwise wave length studied. Furthermore, a two-dimensional linear stability study as conducted by Robinet [16] for separation bubbles induced by shock-wave/boundary-layer interaction is recommended.