Experimental Investigation of Separated Shear Flow under Subharmonic Perturbations over a Backward-Facing Step

Abstract

Subharmonic-perturbed shear flow downstream of a two-dimensional backward-facing step was experimentally investigated. The Reynolds number was Re_h = 2.0 ×10⁴, based on free-stream velocity and step height. Planar 2D-2C particle image velocimetry was employed to measure the separating and reattaching flow in the horizontal-vertical plane in the center position. The subharmonic perturbations were generated by an oscillating flap which was implemented over the step edge and driven by periodic Ampere force. The subharmonic frequency was 55 Hz as the half of the fundamental frequency of the turbulent shear layer. As a result of the subharmonic perturbations, the size of recirculation region behind the backward-facing step is reduced and the time-averaged reattachment length is 31.0% shorter than that of the natural flow. The evolution of vortices, including vortex roll-up, growth and breakdown process, is analyzed by using phase-averaging, cross-correlation function and proper orthogonal decomposition. It is found that Reynolds shear stress is considerably increased in which the vortices roll up and then break down further downstream. In particular, rapid growth of vortices based on the “step mode” occurs at approximate half of the recirculation region, caused by in interaction between the shear layer and the recirculation region. Furthermore, the coherent structures, which are represented by a phase-correlated POD mode pair, are reconstructed in phases in order to show regular patterns of the subharmonic-perturbed coherent structures.

1 Introduction

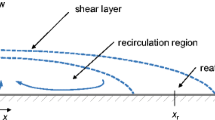
Backward-facing step (BFS) flow is a multi-scale separating and reattaching flow phenomenon which contains a separated shear layer, a recirculation flow region and a reattachment area. It is widely known that the separated free-shear layer rolls up to form spanwise vortices caused by the Kelvin-Helmholtz instability. As the vortices move downstream, they start to pair, merge or even break down, leading to rapid growth of the shear layer. The recirculation region locates right behind the step and contains a maximum backflow velocity as high as 20% of the free-stream velocity [1]. Non-dimensional reattachment length X/h is defined as the streamwise distance from the step to where the mean flow reattaches on the plate surface, as shown in Fig. 1. A two-dimensional BFS provides a typical flow separation case with a fixed separation edge, so it has been widely used as a fundamental separating/reattaching flow case in experimental and numerical research. Although a BFS model has simple geometry, the flow separation as well as reattachment is still complex. A wide scale range of shedding vortices within separated shear layers experience nonlinear growth and interact with the recirculation region. As Reynolds number increases, small- and smaller-scale vortices evolve in addition to large-scale time-varying recirculation region which makes the flow field even more complex. As the simplest and the most typical separating/reattaching flow case, backward-facing step flow has drawn continuous attention of physicist and engineers, so numerous investigations have been carried out on this topic. Eaton and Johnston [1] provided an extensive review of the experimental studies on BFS flows and discussed the effects of various parameters on flow separation and reattachment. As the most important parameter characterizing flow separation, the reattachment length varies approximately from 5 to 8 step heights, which, to varying extents, depends on initial boundary layer laminar / turbulent state, incoming turbulence level, Reynolds number, ratio of boundary layer thickness to step height and other flow conditions. Bhattacharjee et al. [2] studied a turbulent BFS flow at Re_h ≡ U₀ × h/ ν = 4.5 × 10⁴, and found a broad bandwidth of 0.2 < St_h ≡ f × h/U₀ < 0.4 other than a distinct peak in the velocity power spectrum, in which the shear layer responded well to perturbations. Hasan [3] found two distinct modes of instability in the shear layer downstream of a BFS. The one mode is the “shear layer mode” of instability at St_𝜃 ≡ f × 𝜃/U₀ ≈ 0.012, which is scaling with the momentum thickness at separation and the natural roll-up frequency of the shear layer. This optimal frequency St _𝜃 ≈ 0.012 was also used by Chun et al. [4] and Wengle et al. [5] respectively in their experiments in order to achieve the most effective flow separation control. The other mode is the “step mode” of instability at St_h ≡ f ×h/U₀ ≈ 0.185, which is scaling with the step height and the natural flapping frequency of the shear layer. The “shear layer mode” of instability is governed by the Kelvin-Helmholtz instability whereas the “step mode” of instability consists of an interaction of the shear layer with the recirculation region in the wake flow As the growth of the instability wave downstream, the “shear layer mode” of instability reduces to the “step mode” via one or more stages of vortex merging and pairing. These two different types of instability are also discussed by Smits [6] and Hudy et al. [7], respectively. In the early flow visualization study, Smits [6] observed that the initial part of a shear layer rolls up to form small vortices and then the vortices continue to pair and form large-scale coherent structures downstream, which is very similar with the scenario of a plane mixing layer. The “spatial growth” of the vortices has been referred to as the “shear layer mode” as a widely accepted view of the backward-facing step flow. However, Hudy et al. [7] discovered that a large-scale coherent structure grows in place while remaining stationary at approximately half of the reattachment length and then it sheds and accelerates in the downstream direction. This “temporal growth” of vortices is referred to as the “wake mode”, which is similar to the development of vortex structures in the wake of a bluff body. The mechanism of the “wake mode” is caused by the interaction between the shear layer and the wake flow of the step, which is governed by the absolute instability. According to the instability analysis by Huerre et al. [8], if the backflow is small, spatially growing waves are observed in mixing layer. As long as the backflow is larger than a critical velocity ratio |U₂/U₁|≥ 0.136, the mixing layer becomes absolute unstable and temporally growing disturbances occur.

Fig. 1

Schematic diagram of backward-facing step flow [11]

Sigurdson [9] classified perturbation frequency f_p into four regimes which were based on the initial Kelvin-Helmholtz frequency f_{initial KH} and the fundamental frequencies f₀ (which is also referred to as the most-amplified frequency):

• (1) f_KH ≪f_p

• (2) f₀ ≪f_p≤f_{initial KH}

• (4) f_p ≈f₀

• (4) f_p ≪f₀

In general, perturbations in the regime (1) and (4) have little effect Perturbations in the regime (2) can be amplified by the initial part of the shear layer. The regime (3) indicates a perturbation frequency in the order of the fundamental frequency of the shear layer, in which the shedding instability is primarily driven and the maximum effect in terms of an increase of Reynolds stress can be achieved Periodic perturbations which are equal or close to the fundamental frequencies f ≈ f₀ have been extensively investigated by many researchers in order to increase growth rate of shear layer or to reduce reattachment length effectively [2,3,4,5, 10,11,12,13,14, 22] Some early experimental results were compared in Table 1. On the other hand, subharmonic perturbations f ≈ f₀/2 are also able to influence the shear layer considerably. Kelly [15] carried out a theoretical research on the instability mechanism of a subharmonic perturbation which is amplified in a shear layer by weakly nonlinear theory. He predicted significant growth of a subharmonic perturbation if perturbation frequency is half of the fundamental (most-amplified) frequency. Zaman et al. [16] and Oster et al. [17] stated that subharmonic waves play in important role in causing vortex pairing and enhancing spreading rate of the shear layer in a circular jet flow and plane mixing layer, respectively. Ho and Huang [18] stated that a plane mixing layer was greatly manipulated by subharmonic forcing at f ≈ f₀/2. But if only subharmonic waves act, large vortices will form and no vortex merging occurs Chao et al. [19] investigated jet flows with excitations at f₀/2 and f₀, respectively. The flow visualization comparison showed the fundamental vortices persisted further downstream in the jet direction while the subharmonic vortices grow wider perpendicular to the jet direction. Husain et al. [20] investigated the subharmonic resonance phenomenon in a laminar plane shear layer. They used controlled forcing at fundamental frequency f, its subharmonic frequency f₀/2 and the combination of both f₀ + f ₀/2, respectively. They found that the subharmonic waves were closely related to vortex pairing in the case of the double-frequency perturbations. Benard et al. [14] found that the subharmonic perturbations by DBD plasma actuator caused the maximized wall pressure fluctuations downstream of a backward-facing step and promoted coherent flow structures over a long distance downstream as well as the reattachment point. Although much effort have been made on this flow phenomenon, a complete understanding of the physical mechanism of subharmonic wave and their influence on the development of turbulent shear layer has still not been obtained. The previous experimental results have shown that the fundamental perturbations can be amplified in the separated shear layer and lead to significant shear layer growth by vortex pairing, so the present work focuses on small subharmonic perturbations at only half of the fundamental frequency f_p ≈ f₀/2 in order to analyze behavior of subharmonic waves in the shear layer and resulting flow field.

Table 1 Comparison of the present BFS flow with the literature

This research article is organized as follows. The first section briefly reviews the research on backward-facing step flows. In the following section the wind tunnel tests and 2D-2C PIV measurement technique are presented. In the third section subharmonic waves within the perturbed shear layer are analyzed based on time-averaged and phase-averaged flow fields. The coherent structures are characterized by cross-correlation function and POD. The fourth section summarizes the characteristics of the perturbed flow structure and gives a brief outlook for future research.

2 Experimental Apparatus and Procedure

2.1 Flow facility and oscillating flap

The experiments were carried out in the 1-m low-speed wind tunnel at the German Aerospace Center (DLR) in Göttingen, Germany. The open test section was 1400 mm long with a cross-section of 1,050 × 700 mm². The freestream velocity was U₀ = 10.0 m/s with a turbulence level of 0.15%. A backward-facing step model was mounted horizontally on a flat plate with an elliptical leading edge. The BFS was 900 mm long and 1,300 mm wide with a step height of h = 30 mm. The aspect ratio of width to height was 43.3 which is larger than the two-dimensionality criterion of 10 [23] for assuming a two-dimensional mean flow in the center portion of the step. The incoming boundary layer was tripped at the leading edge by spanwise zigzag bands with a thickness of 0.4 mm to generate a turbulent boundary layer which had a thickness of δ ≈ 15 mm (δ/h ≈ 0.5), a displacement thickness of δ* ≈ 2.8 mm a momentum thickness of 𝜃 ≈ 2.0 mm and a shape factor of δ*/ 𝜃 ≈ 1.4 at the BFS. According to the previous experiments reported by Ma et al. [11, 12], the fundamental (or most-amplified) frequency of the turbulent shear layer was f ≈ 100–120 Hz, corresponding to St_h ≈ 0.3 and St _𝜃 ≈ 0.02. The Reynolds number, based on the freestream velocity and the step height, was Re_h = 2.0 ×10⁴. A two-dimensional coordinate system has its origin point at the corner on the wall, a horizontal X-axis and a vertical Y-axis.

An oscillating flap was designed to generate periodic small perturbations. A schematic diagram as well as a photo is shown in Fig. 2. The flap was l = 37 mm long, 5 mm wide and 0.2 mm thick and was mounted like a string at 5 mm high over the step and parallel with the separation edge. It was made of brass which is electroconductive and diamagnetic. A spanwise row of Neodymium magnets were implemented under the surface of the step in the same orientation in order to produce a parallel magnetic field around the oscillating flap. The oscillating flap was connected with an Agilent waveform generator, a Dynacord CL1600 power amplifier and a resistance of 5 Ω in a series circuit. The alternative current and the perpendicular magnetic field generate periodic vertical Ampere force on the flap. If the driven frequency is equal to the fundamental resonant frequency of the oscillating flap, it generates standing waves, whose frequency depends on the flap length, linear density and tension force. So the displacement of the center part of the flap can be described as:

$$ \mathrm{Y}_{\text{flap}}=\mathrm{A}\cdot\cos \left( 2\pi\mathrm{f}_{\mathrm{p}}\mathrm{t} \right)+\mathrm{Y}_{0} $$

(1)

Fig. 2

(a) Schematic diagram of the oscillating flap mounted over the backward-facing step; (b) Photo of the center portion of the oscillating flap

The neutral position was Y₀ = 5 mm (Y₀ ≈ δ/3) over the step. The oscillation amplitude was approximately A ≈ 2 mm as the maximum displacement from the neutral position. Then the oscillation velocity of the center part of the flap can be calculated by the time derivative of the displacement V_flap=dY_flap/dt which enables to estimate the oscillation velocity to be in the range of max(|V_flap|) ≈ 0.7 m/s. The ratio of the oscillation amplitude to the step height was |A/h| < 0.07 and the ratio of the oscillation velocity to the freestream velocity was |V_flap/U₀| < 0.07 so the oscillating flap can be considered as small perturbations compared with the step height and free-stream velocity. Moreover, the ratio of the peak amplitude to flap length was A/l < 0.006, so it can be considered as two dimensional perturbations in the center part of the oscillating flap. A hierarchy of the spatial scales in the present study is listed in Table 2. The phase angle in one period was defined by the position of the oscillating flap between α = 0^∘ and 360^∘. Thereby, phase angles α = 0^∘ and α = 180^∘ indicate the highest and lowest positions, respectively. Depending on the constant length, density and tension force of the oscillating flap, the perturbation frequency in the present study was fixed at f_p = 55 Hz. Because the fundamental frequency of the shear layer is f ≈ 100–120 Hz [2, 11, 12] the perturbation frequency is only the half of the fundamental frequency as f_p ≈ f₀/2. In the present study, two typical flow cases were carried out. The one flow case was the natural flow over a clean backward-facing step model without mounting an oscillating flap, which is referred to as “natural flow”. The other flow case was the incoming flow perturbed by the oscillating flap while the other flow condition was kept the same which is referred to as “perturbed flow”.

Table 2 Hierarchy of spatial scales of the present BFS flow

In order to calibrate the exact frequency of the standing waves of the oscillating flap in a quiescent flow condition, a mobile NTI microphone was placed in the vicinity of the middle of the flap without external incoming flow. The obtained frequency spectrum in Fig. 3 calibrates the perturbation frequency is equal to f_p = 55. The overtones of the fundamental standing wave show decreasing amplitudes, which have much less influence on the shear layer.

Fig. 3

Amplitude spectrum of the oscillating flap at f_p = 55 Hz by acoustic calibration in vicinity of perturbation

2.2 2D-2C PIV measurement

The present turbulent BFS flow contains multi-scale flow structures including not only the separating/reattaching flow on the order of the step height but also the rolling-up vortices on the order of the momentum thickness. Given the ratio of the perturbation amplitude to flap length A/l < 0.007, the small perturbations in the center portion of the oscillating flap can be considered as a twodimensional movement so a high-resolution 2D-2C PIV system was used to obtain the velocity vector field of the essential flow structures in the cross-sectional plane (see Fig. 4). A laser light sheet with a thickness of 1 mm was aligned in the horizontal-vertical plane from downstream illuminating a single field of view of 310 × 70 mm². Double laser pulses contained energy of 30 mJ per pulse with 150 μ s time delay. The incoming flow was homogeneously seeded by DEHS droplets with a mean diameter of 1 μ m [24, 25]. Double particle image frames were recorded from the side view by a highresolution camera PCO.4000 (4,008 × 2,672 pixel 14bit) equipped with a Nikon lens (85mm, f/4). The optical axis of the camera and lens was aligned perpendicular to the laser light sheet. Each particle image consisted of 3,900 × 910 pixels in X- and Y- directions respectively. A constant magnification factor between the image pixel and physical coordinate was obtained by a PIV calibration process before recording. The synchronization of the image recording and laser illumination was accomplished by TTL trigger signals from a programmable sequencer. In the recording process, 4,000 non-phase-locked double-frame images were recorded for the flow cases with and without perturbations. A low sampling rate of 1.7 Hz was used to make sure vector fields are statistically independent for calculating the mean flow as well as root-mean-square quantities. Then, 1,000 phase-locked double-frame images at 12 phases in one perturbation period were recorded in order to capture periodic motions in the turbulent shear layer. Image evaluation was performed by using PIVview software from PIVTEC. As a pre-process procedure a minimum background image was subtracted from the particle images in order to reduce noise and eliminate local light inhomogeneity. Then the double-frame images were evaluated by an interactive multi-grid cross-correlation method [26] with image deformation and a final interrogation window size of 16 ×16 pixel at 75% overlap, resulting in a vector spacing of 0.3 mm (= 0.01h) in the physical coordinate.

Fig. 4

Schematic diagram of 2D-2C PIV setup and close-up view of the oscillating flap

3 Results and Analysis

3.1 Time-averaged velocity fields

Statistical convergence of mean and root-mean-square velocities in the field of view was calculated by using the 4,000 non-phase-locked PIV snapshots. The convergence shows that the mean velocity vector fields achieved a norm-2 residual of 0.05% and the root-mean-square velocity converged to a norm-2 residual of 0.16%. Therefore, the time-averaged velocity vectors and contours of the natural and perturbed flows are shown in Fig. 3. The closest distance between velocity vectors to the wall is 0.30 mm (0.01h). A time-averaged zero-streamwise-velocity contour line marked by a label $\bar {u}=\mathrm {0}$ separates the reattached flow region and the backflow region. So the time-averaged reattachment length is located where the velocity contour line $\bar {u}=\mathrm {0}$ reattaches to the wall. In the natural flow, the shear layer reattaches on the wall downstream at X/h = 7.1, which locates in a reasonable range based on the present Reynolds number and turbulent flow state [1]. In the perturbed flow, the shear layer is drawn downward closer to the wall and the recirculation region is considerably reduced. As a result, the reattachment length is reduced to X/h = 4.9, with a reduction rate of 31.0%. It can be seen in Fig. 5b that the zero-streamwise-velocity contour line is detached from the step edge indicating three-dimensional mean flow lower than 0.1U₀ exists near the step. The reason for the three-dimensional mean flow is that the spanwise limited perturbations could entrain neighboring fluid from the both sides into the low-pressure low-velocity recirculation region in the center plane.

Fig. 5

Time-averaged velocity vectors and contour fields (a) the natural flow; (b) the perturbed flow. The zero-streamwise-velocity contour lines are marked by label $\bar {u}\mathrm {=0}$ and the arrows indicate the reattachment points. The vector color indicates streamwise velocity component $\bar {u} \left / \mathrm {U}_{\mathrm {0}}\right .$

The growth (or referred to as “spreading rate”) of the separated shear layer is depicted by the 0.1U₀ and 0.9U₀ streamwise velocity contours in Fig. 6a. Compared with the gradual growth of the natural shear layer, the subharmonic-perturbed shear layer becomes thicker and reattaches faster to the wall. On the other hand, a momentum thickness, which is frequently used in scaling of St_𝜃 in a shear layer [3, 16, 20], is defined as:

$$ \theta={\int}_{0}^{\infty}\frac{\bar{u}\left( \mathrm{y} \right)}{\mathrm{U}_{0}}\left[ 1-\frac{\bar{u}\left( \mathrm{y} \right)}{\mathrm{U}_{0}} \right]\text{dy} $$

(2)

Fig. 6

Comparison of growth of the natural, fundamental- and subharmonic-perturbed shear layers. (a) streamwise velocity contours of $\bar {u} \left / \mathrm {U}_{\mathrm {0}}=0.1\right .$ and $\bar {u} \left / \mathrm {U}_{\mathrm {0}}=0.9\right .$; (b) momentum thickness. The natural flow indicates the clean BFS flow without the flap. The fundamental-perturbed flow of St_h = 0.3 is from the reference article by Ma et al. [11]. The subharmonic-perturbed flow of St_h = 0.165 is the present study. The arrows indicate respective reattachment points

The comparison in Fig. 6b shows the perturbed shear layer has a slightly increased momentum thickness than that of the natural flow in the vicinity of the step within 0 < X/h < 0.5, where the initial part of the shear layer receives periodic small perturbations directly from the oscillating flap (see Fig. 12). Then it becomes nearly equal to that of the natural flow within 0.5 < X/h < 2. It is worth noting that the momentum thickness of the subharmonic-perturbed shear layer starts to grow rapidly at 2 < X/h < 3, where the maximum backflow occurs near the wall. An inferred reason of this accelerating growth of the momentum thickness from X/h ≈ 2 is that as the streamwise location X grows, the subharmonic perturbations are amplified due to the local rolling-up mechanism at X/h ≈ 2 and the subharmonic-perturbed vortices begin to grow in size, resulting in the maximum backflow region near the wall between 2 < X/h < 3. In order to compare the influences of the subharmonic and fundamental perturbations on the same shear layer, previous experimental result by Ma et al. [11] is compared in Fig. 6, in which comparable-amplitude acoustic perturbations at St_h = 0.3 was applied in the same flow condition. It is clear that the fundamental perturbations cause faster growth of the shear layer as well as the momentum thickness to a saturation level than the subharmonic perturbations do. In other words, the subharmonic-perturbed shear layer is inferred to move more like a vertical flapping motion than a pure spreading motion. The present subharmonic growth feature of the shear layer agrees well with the recent experiment of active flow control by DBD plasma actuator by Benard et al. [14], showing that fundamental perturbations reach a saturation level and then subharmonic perturbations progressively amplify further downstream. Similar scenarios of subharmonic growth in plane mixing layers have also been discussed by Oster et al. [17] and Ho et al. [18]. Further downstream at X/h > 3, the present subharmonic-perturbed shear layer has significantly growth in the reattachment area, resulting in a shorter reattachment length than the natural flow.

3.2 Length scales of coherent structures

The spatial cross-correlation function, first introduced by Taylor [27, 28], has been widely used to characterize coherent structures and vortex scales in turbulent shear flows [29, 30]. A coefficient of two-point spatial cross-correlation at a reference point $\overset {\rightharpoonup }{r_{0}} \mathrm {=}\left (\mathrm {X}_{0}\mathrm {,}\mathrm {Y}_{0} \right )$ in the same time duration is defined as:

$$\mathrm{R}_{\mathrm{v}_{\mathrm{i}}^{\prime}\mathrm{v}_{\mathrm{j}}^{\prime}}\left( {\Delta}\overset{\rightharpoonup}{r} \right)=\frac{\overline{v_{i}^{\prime}\left( \overset{\rightharpoonup}{r_{0}} \mathrm{,t} \right)\cdot v_{j}^{\prime}\left( \overset{\rightharpoonup}{r_{0}} +{\Delta}\overset{\rightharpoonup}{r} \mathrm{,t} \right)}}{\sqrt{\overline{{v_{i}^{\prime}}^{2}\left( \overset{\rightharpoonup}{r_{0}} \mathrm{,t} \right)}} \cdot\sqrt{\overline{{v_{j}^{\prime}}^{2}\left( \overset{\rightharpoonup}{r_{0}} +{\Delta}\overset{\rightharpoonup}{r} \mathrm{,t} \right)}}} $$

(3)

In the definition ${\Delta } \overset {\rightharpoonup }{r} =\left (\mathrm {\Delta x,{\Delta } y} \right )$ is the displacement vector and $\mathrm {v}_{\mathrm {i}}^{\prime }\mathrm {v}_{\mathrm {j}}^{\prime }$ indicate the fluctuating velocity components.

Figure 7 shows the spatial cross-correlation coefficients of the vertical fluctuating velocities of the natural and perturbed flows. Three reference points locate at Y/h = 1 and X/h = 1, 2 and 3, respectively. In the natural flow in Fig. 7a–c, the elliptical positivecorrelation region increases as the reference point moves downstream showing the gradual growth of the shear layer thickness. Meanwhile, the respective upstream and downstream negative correlationregions are also depicted by low-level contour of -0.05. In the perturbed flow by contrast, highly cross-correlated regions locate upstream and downstream of the reference points. As the reference point moves downstream, the horizontal distance between two adjacent negativecorrelation regions increases as well. These regular correlation patterns in Fig. 7d–f characterize large-scale vortex structures with an increasing spatial scale in the perturbed shear layer. At further downstream from the reference points, the correlated regions attenuate, mainly because of the vortex breakdown and out-of-plane motions.

Fig. 7

Spatial cross-correlation coefficients with reference points at Y/h = 1 and X/h = 1, 2, 3, respectively. (a)–(c) the natural flow; (d)–(f) the perturbed flow. The contour color indicates correlation coefficient

Furthermore, by examining a distribution of the vertical velocities v(x) along a horizontal line behind the step spatial scales of the vortex structures within the shear layer can be estimated. Based on the discrete Fourier transform (DFT) algorithm in equation (4), the vertical velocity distribution can be transformed into the wavenumber domain, as:

$$\left| \mathrm{Y}\left( \mathrm{k} \right) \right|\mathrm{=}\left| \sum\nolimits_{\mathrm{j=1}}^{\mathrm{N}_{\mathrm{x}}}{\mathrm{v}\left( \mathrm{j} \right)\mathrm{e}^{{\mathrm{-2\pi i}\left( \mathrm{j-1} \right)\left( \mathrm{k-1} \right)} \left/ \mathrm{N}_{\mathrm{x}}\right.}}\right| $$

(4)

In the present study, the vertical velocity v(x) along the horizontal line at 0 < X/h < 8 and Y/h = 1, which locates within the separated shear layer behind the step is extracted for the discrete Fourier transform. 782 spatial points (vector spacing 0.3 mm) along the horizontal line and 200 non-phase-locked snapshots are used as the dataset N_x = 782 × 200 = 156,400. The single-sided amplitude spectra are compared in Fig. 8. In the perturbed shear layer, there are four high peaks in the spectrum. The four peak wavenumbers are k₁ = 18.6, k₂ = 14.5, k₃ = 10.3 and k₄ = 4.2 [m⁻¹], which correspond to feature wavelengths of Λ₁ = 53.7, Λ₂ = 69.2, Λ₃ = 97.2 and Λ₄ = 240.0 [mm]. It should be clarified that there are identical peaks at 4.2 [m⁻¹] in both natural and perturbed flows, which correspond to the length of the measurement domain 0 < X < 240 [mm]. So the 4th peak at k₄ = 4.2 [m⁻¹] has no physical meaning and thereby it is negligible. Therefore, a broad bandwidth of k = 10.3-18.6 [m⁻¹] is characterized by the three peaks k₁, k₂ and k₃ in the spectrum, corresponding to a range of wavelengths of Λ = 1.8h-3.2h. This estimated range of wavelengths agrees well with the spatial scales of the cross-correlation contours in Fig. 7d–f. As the coherent structures increase in scale, it is also worth noting that starting from X/h > 2, the length scale of vortices (approximately equal to half of the wavelength Λ) become larger than the step height and therefore is highly influenced by the wall, resulting in a maximum backflow region in Fig. 5b and the rapid growth of the momentum thickness in Fig. 6b.

Fig. 8

Single-sided amplitude spectrum of vertical velocity v(x) along the horizontal line at 0 < X/h < 8 and Y/h = 1. (a) the natural flow; (b) the perturbed flow

3.3 Coherent and incoherent Reynolds shear stress

As an essential quantity in turbulent flows, Reynolds shear stress represents the quantity of the fluid elements fluctuating within the shear layers [31]. Based on the phase signal of the periodic perturbations, the phase-locked PIV measurements provide insight into the development of the periodic spanwise vortices in the turbulent shear layer. By applying the triple decomposition [32], a velocity vector can be decomposed as:

$$ \mathrm{\mathbf{u}}=\bar{\textbf u}\mathrm{\mathbf{+}}\tilde{\textbf u} \mathrm{\mathbf{+}}\mathrm{\mathbf{u}}^{\prime} $$

(5)

The term on the left-hand side is an instantaneous velocity vector. The terms on the right-hand side are mean, periodic and random fluctuating parts, which correspond to the time-averaged flow, periodic coherent structures and incoherent turbulence, respectively. The periodic part can be obtained by subtracting the mean flow from the phase-averaged flows as:

$$ \boldsymbol{\tilde{\textbf u}}\mathbf{=}\langle\mathbf{u}\rangle\mathbf{-}\boldsymbol{\bar{\textbf u}} $$

(6)

Because the periodic part is uncorrelated with the random fluctuations, which is described as $\mathrm {-}\overline {\tilde {u}\cdot v^{\prime }}=0,-\overline {u^{\prime }\cdot \tilde {v}}=0$, the Reynolds shear stress can be decomposed as:

$$\mathrm{\tau }_{\text{xy}}^{\prime}\mathrm{=-}\overline{\left( \tilde{u}\mathrm{+}\mathrm{u}^{\prime} \right)\cdot \left( \tilde{v}\mathrm{+}\mathrm{v}^{\prime} \right)}=\mathrm{-}\left( \overline{\tilde{u}\cdot \tilde{v}}\mathrm{+}\overline{u^{\prime}\cdot v^{\prime}} \right) $$

(7)

The terms $\mathrm {-}\overline {\tilde {u}\cdot \tilde {v}}$ and $\mathrm {-}\overline {u^{\prime }\cdot v^{\prime }}$ correspond to the contributions of the coherent motions and incoherent turbulence, respectively. Furthermore, the incoherent Reynolds shear stress $\mathrm {-}\langle \tilde {u}\cdot \tilde {v}\rangle$ at each phase is obtained by the phase-locked PIV measurements. In the incompressible flow, the constant density of air ρ is omitted.

The Reynolds shear stresses of the natural and perturbed flows are compared in Fig. 9. According to Roos et al. [10], Bhattacharjee et al. [2] and SujarGarrido et al. [12], who measured the maximum Reynolds shear stresses 0.008, 0.012 and 0.011, respectively, within the natural turbulent shear layer, the present Reynolds shear stress in the natural flow shows a close maximum value of 0.010. The comparison in Fig. 9 indicates that the total Reynolds shear stress is considerably increased by the subharmonic perturbations. It is interesting to note that there are two distinct strong shear regions “A” and “B” which locate at 0.5 < X/h < 2 as well as X/h > 3 and exhibit higher Reynolds shear stress in the perturbed shear layer. In order to reveal the cause of the increase of the Reynolds shear stress in the two regions, the coherent and incoherent parts of the Reynolds shear stress are compared in Fig. 10. It is clear that the region “A” and “B” indicate where the coherent structures and the incoherent turbulence contribute to the increase of the Reynolds shear stress, respectively. In the previous measurement fundamental-perturbed shear layer by acoustic perturbations at St_h = 0.3 [11], in which the flow condition and the measurement was identical to the present flow, the coherent, incoherent and total values of Reynolds shear stress were found to be 0.014, 0.024 and 0.017, respectively. Contrastively, the present coherent Reynolds shear stress has a lower peak value of $\mathrm {-}\overline {\tilde {u}\cdot \tilde {v}} =$ 0.011 at X/h ≈ 1.1, but that of the earlier work has a higher peak value of $\mathrm {-}\overline {\tilde {u}\cdot \tilde {v}} =$ 0.014 closer to the step at X/h ≈ 0.5. On the other hand, the incoherent Reynolds shear stress of the subharmonic perturbations becomes higher if the perturbations frequency reduced from the fundamental frequency to its 1/2 subharmonic frequency, resulting in a higher total Reynolds shear stress. The detailed comparisons are listed in Table 3. This comparison indicates that the subharmonic perturbations lead to a larger size of roll-up vortices and less interaction between consecutive coherent structures due to longer distance. It agrees well with Ho and Huang [18] who stated that if only subharmonic waves appear large vortices will form without merging in a plane mixing layer. Similarly, Chao et al. [19] also visualized that in a forced circular jet flow the subharmonic-excited coherent structures rolled up at further position from the jet exit and had a larger size than those excited by fundamental frequency.

Fig. 9

Total Reynolds shear stress ${\mathrm {-}\left (\overline {\tilde {u}\cdot \tilde {v}}\mathrm {+}\overline {u^{\prime }\cdot v^{\prime }} \right )} \left / \mathrm {U}_{\mathrm {0}}^{\mathrm {2}}\right .$. (a) the natural flow; (b) the perturbed flow. The contour color indicates total Reynolds shear stress

Fig. 10

Decomposition of Reynolds shear stress of the perturbed flow. (a) coherent contribution ${\mathrm {-}\overline {\tilde {u}\cdot \tilde {v}}} \left / \mathrm {U}_{\mathrm {0}}^{\mathrm {2}}\right .$; (b) incoherent contribution ${\mathrm {-}\overline {u^{\prime }\cdot v^{\prime }}} \left /\mathrm {U}_{\mathrm {0}}^{\mathrm {2}}\right .$. The contour color indicates Reynolds shear stress

Table 3 Comparison of the maximum Reynolds shear stress within the shear layers

As the subharmonic perturbations travel downstream, the perturbed shear layer rolls up in the near downstream at X/h ≈ 0.5 and form spanwise vortices at 0.5 < X/h < 2, which entrain neighboring fluid mass into the shear layer resulting in the increase of the Reynolds shear stress in the region “A”. The initial part of the shear layer has a small momentum thickness of 𝜃 ≈ 0.05h, so it is hardly influenced by the wall and appears to be much like a plane mixing layer. In further downstream at X/h > 3, the vortices grow to the size approximately equivalent to the step height and therefore they are strongly influenced by the wall. So the vortices start to break down into the incoherent turbulence resulting in the much more increase of the Reynolds shear stress in the region “B”. The interaction between the vortex and the wall as well as the vortex breakdown process agrees well with the reduced reattachment length in Fig. 5b the faster growth of the shear layer and the apparent increase of momentum thickness starting from X/h > 3 in Fig. 6b. Thus, the generation and breakdown process of the coherent structures plays an important role in the momentum transfer than the natural turbulent mixing process due to viscosity alone.

Interestingly, the increase of the Reynolds shear stress in Fig. 9b exhibits in the two distinct regions but not in one continuous region along the shear layer as the natural flow in Fig. 9a. It is difficult to explain such two-region distribution or the fast increase of momentum thickness at 2 < X/h < 3 by the “spatial growth” mechanism by Smits [6], who stated the small vortices have a gradual growth of size along the shear layer before reattaching to the wall. However, Hasan [3] explained that the “shear layer mode” of instability reduces to the “step mode” as the growth of the instability wave downstream. Furthermore, Hudy et al. [7] found the large-scale coherent structures actually temporally grow in size while remaining stationary in place at approximate half of the recirculation region. This vortex growth mechanism is referred to as the “wake mode” by Hudy et al. [7], which is governed by the absolute instability if a shear layer has a higher backflow velocity ratio than 0.136 [8]. Given the present maximum backflow velocity ration of approximately 0.2 the subharmonic waves excite the absolute instability between the shear layer and the recirculation region and the rolledup vortices rapidly grow in size while interacting with the maximum backflow region near the wall at 2 < X/h < 3. This rapid growth of vortices due to the “step mode” of instability (or referred to as the “wake mode”) occurs at approximately half of the reattachment length and is consistent with the upstream shift of the maximum backflow region from 3 < X/h < 5 to 2 < X/h < 3 in Fig. 5, the increase of the momentum thickness of the perturbed shear layer in Fig. 6b and the saddle-like region of lower Reynolds shear stress at 2 < X/h < 3. Such saddle-like region closer to the step under fundamental perturbations was also found in the previous experiment [11].

Figure 11 shows the phase-averaged incoherent Reynolds shear stresses based on the phase-locked PIV data. The evolution of a vortex in the phase space, including first roll-up, then growth and eventually breakdown into turbulence, is highlighted by a black dashed line. It can be seen that the passage of the large-scale spanwise vortices over the reattachment region leads to apparent upstream and downstream shifting motion of the reattachment point. This phenomenon is referred to as “the flapping motion” of the reattaching shear layer by Eaton et al. [34] and Driver et al. [35]. The suhharmonic-perturbed shear layer moves in a vertical flapping motion like a flag at 0.5 < X/h < 2 and it does not grow too much in size, which can be verified by examining the momentum thickness in Fig. 6b. The interface between the shear layer and the outer flow evolves and the high momentum fluid mass is entrained due to the Biot-Savart induction and then is engulfed into the turbulent shear layer, resulting in high momentum transfer in the vicinity (instead of the center) of the vortices, which agrees well with the cross-sectional schematic of a coherent structure depicted by Hussain [36]. The vortex roll-up process and breakdown process contribute the major part of the Reynolds shear stress in the shear layer, as above-discussed in Fig. 10. Particularly, at the phase angle of α = 60^∘, as marked by a red circle in Fig. 11b, as the oscillating flap is moving downward to the step wall it pushs the boundary layer and generates a small streamwise ejection with an approximate velocity of 0.7U₀ into the shear layer. This small ejection is the main reason of the slightly increased momentum thickness between 0 < X/h < 0.5 in the perturbed shear layer in Fig. 6b. On the other hand, at the opposite phase angle of α = 240^∘, as marked by a red circle in Fig. 11e, as the oscillating flap moves upwards away from the step wall, it pulls the separated shear layer upwards away from the step. The velocity contours at phase angles of α = 60^∘ and α = 240^∘ are shown in Fig. 12 with a black arrow indicating the small streamwise ejection. The rapid growth of the vortices occurs within 2 < X/h < 3, right between the two regions in which the vortices roll up and break down. From a time-averging point of view, it leads to a saddle-like region containing lower Reynolds shear stress, which is consistent with the distribution of the total Reynolds shear stress in Fig. 9b.

Fig. 11

Phase-averaged streamlines and incoherent Reynolds shear stress $-\langle \mathrm {u}^{\prime }\cdot \mathrm {v}^{\prime }\rangle \left / \mathrm {U}_{0}^{2}\right .$ of perturbed flow. (a)–(f) α = 0^∘, 60^∘, 120^∘, 180^∘, 240^∘, 300^∘. The contour color indicates phase-averaged incoherent Reynolds shear stress and the arrows indicate the time-averaged reattachment points

Fig. 12

Phase-averaged contours and lines of streamwise velocity $\langle \mathrm {u}\rangle \left / \mathrm {U}_{\mathrm {0}}\right .$ of perturbed flow at the phase (a) α = 60^∘ and (b) α = 240^∘. The black arrow indicates the small streamwise ejection periodically pushed by the oscillating flap. The contour color indicates phase-averaged streamwise velocity $\langle \mathrm {u}\rangle \left / \mathrm {U}_{\mathrm {0}}\right .$

3.4 POD analysis of subharmonic waves

Proper orthogonal decomposition (POD) is an effective method for identifying coherent structures in complex flows by linear decomposition and reconstruction [37]. In order to reveal the spatial structures of the vortices, the snapshot POD method [38] is applied in a rectangular region of 4h × 2h (Fig. 13), which covers the most part of the separated shear layer downstream of the step. The mathematical background is explicitly presented in Meyer et al. [39]. In the present analysis, the number of the instantaneous snapshots that are used is N = 3,000 and each snapshot contains M = 76,245 spatial points. Therefore, POD decomposes the original velocity data sequence into the mean flow and the linear combination of spatially orthogonal modes as:

$$ \mathrm{\mathbf{U}}=\boldsymbol{\overline{\textbf U}}\mathrm{+}\sum\limits_{\mathrm{\boldsymbol{i}=\boldsymbol{1}}}^{\boldsymbol{\mathrm{N}}} {\mathrm{\mathbf{a}}_{\mathrm{\mathbf{i}}}\mathrm{\mathbf{\cdot }}\mathrm{\mathbf{\boldsymbol{\phi} }}_{\mathrm{\mathbf{i}}}} $$

(8)

Φ_i is the i-th mode and a_i is the corresponding coefficient. All the modes are ranked based on the descending order of the eigenvalues, which represent the turbulent kinetic energy [39]. This energy-based hierarchy ensures that the predominant modes containing higher energy are represented in the first few modes, which may correspond to the large-scale coherent structures, whereas all further modes containing lower energy are small-scale or turbulent random fluctuations.

Fig. 13

Schematic diagram of rectangular area of 4h ×2h in which POD is applied. The vector color indicates streamwise velocity u [m/s]

The POD eigenvalue distributions of the natural and perturbed flow s are plotted in Fig. 14a. For both cases the first mode contains the most turbulent kinetic energy while the energy content of the following modes decays logarithmically. The comparison shows that the energetic fluctuating motions of the perturbed flow are greater than those of the natural flow. Additionally, the first two modes of the perturbed flow contain approximately equivalent energy content. By examining the coefficient scatter of the first few modes, the coherent interrelations can be revealed. Phase angle φ _1,2 of the scatter point (a₁, a₂) for POD₁ and POD₂ is defined as [40]:

$$ \varphi_{1,2}=\arctan\left( \frac{\sqrt{\lambda_{1}}}{\sqrt{\lambda_{2}}}\cdot\frac{\mathrm{a}_{2}}{\mathrm{a}_{1}}\right) $$

(9)

Fig. 14

(a) POD eigenvalue distributions of the first 100 modes; (b) Scatter plots of POD coefficients a₁ and a₂

The phase angle between two POD modes is determined directly from the velocity fields and thereby phase-jitter effect is reduced. The coefficients of the two pairs of POD modes are scattered in Fig. 14b. In the perturbed flow, the coefficients a₁ and a₂ are organized as a circle, indicating coherence with a fixed phase difference [11]. In the natural flow, by contrast, the coefficients a₁ and a₂ gather to the center as a disk, indicating that the two modes are independent and incoherent to each other with respect to a phase relation. The following modes, such as POD₃, POD₄ and so on, of the both cases do not show such coherent feature.

The first four single POD modes are compared in Fig. 15. Although these predominant modes contain major part of the turbulent kinetic energy, each mode has very different coherent feature. In the perturbed flow in particular the first two modes in Fig. 15e–f represent phase-correlated counter-rotating vortices, which are considered as part of the coherent structures. In contrast, the following modes in Fig. 15g–h do not show such clear coherent feature, and neither do those of the natural flow. Thus, the coherent mode pair, including the first two POD modes of the perturbed shear layer, is used in the following POD reconstructions.

Fig. 15

Comparison of the first four single POD modes. (a)–(d) POD₁, POD₂, POD₃ and POD₄ of the natural flow; (e)–(h) POD₁, POD₂, POD₃ and POD₄ of the perturbed flow. The contour color indicates spanwise vorticity $\left [\times 10^{\mathrm {3}}\mathrm {s}^{\mathrm {-1}}\right ]$

The POD reconstruction can be obtained by linearly combining modes weighted by corresponding coefficients. As shown in Fig. 16, counter-rotating vortices at 12 phases are shown in the reconstruction by POD₁ and POD₂ of the perturbed flow. This regular pattern is a sign of the coherent structures represented by POD₁ and POD₂ which are mutually orthogonal and can be written as a composite form “POD₁ + POD ₂” [41]. In other words, the reconstructions are equivalent to the interference of two oscillating modes. An estimated wavelength of the vortices is Λ_POD/h ≈ 2–3, which agrees well with the wavelengths in the spectrum in Fig. 8b and the spatial scales in phase-averaged Reynolds shear stress in Fig. 16. The POD method is used as a spatial filtering which removes the mean flow and incoherent turbulence, so it is clear to see the small streamwise ejection is generated periodically near the step at 0 < X/h < 0.5 and then the rolling up of vortices occurs between 0.5 < X/h < 2. Yet it should be noted that the linear decomposition and reconstruction of POD is limited in characterizing a nonlinear growth of the vortices in the further downstream.

Fig. 16

Phase-averaged Reconstruction by POD₁ and POD₂ of the perturbed flow. (a)–(f) φ _1,2 = 0^∘, 60^∘, 120^∘, 180^∘, 240^∘, 300^∘. The contour color indicates spanwise vorticity $\left [\times 10^{\mathrm {3}}\mathrm {s}^{\mathrm {-1}}\right ]$

4 Summary and Conclusions

The separated shear layer under the subharmonic perturbations is discussed in four consecutive regions, which are referred to as the “perturbation region”, “roll-up region”, “growth region” and “reattachment region”. The corresponding characteristics are briefly summarized as follow.

• (1) Perturbation region: The initial part of the shear layer between 0 < X/h < 0.5 is periodically perturbed by a small streamwise ejection as much as 0.7U₀ generated by the oscillating flap.

• (2) Roll-up region: In the following part of the shear layer between 0.5 < X/h < 2, the subharmonic-perturbed shear layer rolls up to form spanwise vortices. The coherent structures play an important role in this region, resulting in a high coherent Reynolds shear stress. The shear layer has a comparable momentum thickness as that of the natural flow which gradually grows according to the “shear layer mode” due to the Kelvin-Helmholtz instability.

• (3) Growth region: In the further downstream between 2 < X/h < 3, the spanwise vortices rapidly grow in size as much as the step height while interacting with the maximum backflow region near the wall at approximately half of the reattachment region, resulting in vertical flapping motion of the shear layer and a saddle-like region of low Reynolds shear stress. The rapid growth of coherent vortices is governed by the “step mode” due to the absolute instability.

• (4) Reattachment region: In further downstream after X/h > 3, the vortices start to break down into three-dimensional incoherent turbulence, resulting in another region containing high Reynolds shear stress. The perturbed shear layer significantly grows in size so the time-averaged reattachment length is considerably reduced.

The subharmonic-perturbed separated shear layer behind a two-dimensional BFS was measured by 2D-2C PIV. The phase-locked velocity fields show vortex evolution within the shear layer. Moreover, the cross-correlation function and POD method were used to analyze the coherent structures. It is found that the small-scale subharmonic perturbations are able to generate large-scale coherent structures, leading to a significant change in the shear layer. The Reynolds shear stress is considerably increased due to the vortex roll-up process and the breakdown process. In the middle of the reattachment region, the interaction between the shear layer and the recirculation region causes the rapid growth of spanwise vortices, which is governed by the absolute instability. Although the 2D-2C PIV can achieve velocity information at a high spatial resolution, spanwise velocity component and frequency information was not obtained. In future work, time-resolved measurement could be used to analyze frequency features in the perturbed shear layer.