High-Resolution Numerical Analysis of Turbulent Flow in Straight Ducts with Rectangular Cross-Section

Abstract

Turbulent secondary motion of straight open duct flows with a rectangular cross-section was studied by means of direct numerical simulations, and the unique mean flow patterns were analysed with the aid of instantaneous coherent structure analysis for their Reynolds number dependence. Similar to the closed duct counterparts, it was found that the mean streamwise vorticity pattern is the statistical footprint of the most probable locations of the quasi-streamwise vortices. Furthermore, the existence of tightly-concentrated vortices with preferable rotational directions inside the mixed corners formed by no-/free-slip boundaries was observed. Such flow structures correspond to the side-wall high-speed streaks located directly on the free-slip plane, independently of Reynolds number, as well as the following low-speed streaks reside approximately 50 wall units away from the free-slip plane for friction Reynolds number larger than 200.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fluid flow in a straight duct with rectangular cross-section exhibits turbulence-induced secondary motion of small amplitude (few percent of the bulk velocity), but with large consequences for momentum, heat and mass transport; hence the difficulties in experimental measurements and engineering significance co-exist.

Much of the previous attention was paid upon the closed duct configuration with the square cross-section at marginal to moderate Reynolds numbers (e.g. [7, 9], where high-resolution direct numerical simulations were performed up to bulk Reynolds number of 3500). As a consequence, understanding in Reynolds number dependence up to a point where the flow exhibits a clear scale separation between near-wall structures and outer-scale structures still needs to be established. Furthermore, thorough numerical investigations in aspect ratio dependence covering a range over where the flow structures start to be detached from the side-walls, to the point where the side-wall influence vanishes at the duct centre need to be achieved. Rigorous understanding in such phenomenon will, for instance, serve as a theoretical backbone of wind/water-tunnel design in fluid labs, where the side-wall effects need to be negligible at the measurement windows.

The corresponding open duct flow—featuring a free surface—is characterized by a distinct secondary flow pattern, leading to such practically important effects as the so-called “dip phenomenon”: the maximum of average streamwise velocity is not found at the surface of a river, but somewhat below. Despite such practical importance, understanding of open duct flows is less established than the closed-duct counterpart.

In the present work, we investigate the mechanism of secondary flow formation in open duct flows. Here, free-surface deformation is neglected by enforcing a free-slip boundary condition on the top boundary. In the case of negligible surface tension, this hypothesis amounts to requiring the Froude number to be sufficiently small such that gravity effectively suppresses any significant deformation of the surface. Particular emphasis in our analysis is placed upon the dynamics of coherent structures and the consequences for Reynolds number and aspect-ratio scaling.

2 Numerical Methods

2.1 Algorithm and Implementation

For the purpose of current studies, the pseudo-spectral DNS code previously used in the studies in closed square duct flows by Uhlmann et al. [9], Pinelli et al. [7] and Sekimoto et al. [8] has been extended to incorporate the free-slip boundary condition. The code integrates the Navier-Stokes equations by expanding flow variables in terms of truncated Fourier series in the streamwise direction on equidistant grid points, while Chebyshev polynomials are used in the two cross-stream directions on collocated Chebyshev–Gauss–Lobatto points. A fractional step method is employed in order to decouple the momentum equations from the continuity constraint. The temporal integration is based on the Crank–Nicolson scheme for the viscous terms and a three-step low-storage Runge–Kutta method for the nonlinear terms. The 2D Helmholtz and Poisson problems for each Fourier mode are solved by a fast diagonalisation technique. The code is MPI parallel and the parallelisation of the pseudo-spectral algorithm is achieved by a global data transpose strategy. A schematic of the data decomposition by slices is shown in Fig. 1 and a cyclic communication pattern, which avoids communication cascade and used for global data transpose, is illustrated in Fig. 2. The cost of such communication is 2 × (number of parallel process − 1) MPI send/receive calls per data transpose per MPI process. Asynchronous communications are used to minimise the communication overhead. It should be noted that this parallelisation strategy is standard in spectral methods applied to plane channel flows.

Fig. 1

“Slice” data decomposition strategy used for parallelisation of our DNS code

Fig. 2

(a) A cyclic all-to-all communication pattern used for data transpose between “X-cut” and “Z-cut” data decompositions (cf. Fig. 1), illustrated by an example of parallel execution model with 4 MPI processes. Each “P*” element represents individual MPI rank, while arrows show data flow by MPI communications. (b) Top view of the above example’s domain. Sub-domains surrounded by solid lines (coloured in light gray) are the overlapped regions between “X-cut” and “Z-cut” of each MPI process, hence no communication is required. Any other areas are required to be communicated to other MPI processes. An example of such communications for the MPI process “P0” is illustrated

2.2 Code Performance

In order to demonstrate the efficiency of our DNS code, we have carried out strong scaling tests on CRAY XC40 HORNET at HLRS (cf. Table 1, Fig. 3). The results show that for the chosen problem size (approx. 10⁸ modes), the code maintains a good parallel efficiency up to several hundred cores. With roughly 10⁶ modes per processor core we obtain the desired efficiency of ≥ 65 % over a range of system sizes, at a cost of approx. 3 s per full Runge-Kutta timestep.

Table 1 Strong scaling tests with the modal resolution of M _x = 3075, M _y = 33, M _z = 1025

Fig. 3

Parallel efficiency for two numbers of Chebyshev modes in y-direction: M _y = 33, open circle in blue; M _y = 67, plus symbol in red. The number of modes in the x-/z-direction are fixed at M _x = 3075 and M _z = 1025 respectively. The runs were performed on Cray XC40 HORNET at HLRS

2.3 Simulations

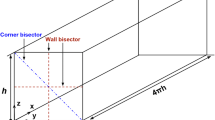
Wall-bounded turbulent flows—such as channel flow and boundary layers—suffer from severe near-wall grid resolution requirements as the Reynolds number increases. In the duct geometry, such requirement is even more demanding since the side-wall boundary layers also need to be resolved. Two kinds of Reynolds numbers need to be introduced for convenience hereafter, namely: bulk Reynolds number ($Re_{b} = U_{b}h/\nu$, formed with the bulk velocity U _b, the duct semi-(full-) height h(H) and the kinematic viscosity ν); and friction Reynolds number ($Re_{\tau } = u_{\tau }h/\nu$ or $Re_{\tau } = u_{\tau }H/\nu$, where u _τ is the friction velocity defined as $u_{\tau } = \sqrt{\tau _{w } /\rho }$ with the wall shear stress τ _w averaged in time and space on no-slip walls, and the constant density ρ). Please note that we always use h to normalise length scales in the bulk unit in the closed duct configuration, while H is used in the open duct configuration, unless stated otherwise. In the current studies, we chose the grid resolutions to satisfy $\varDelta x^{+} \leq 15.0;\ \varDelta y_{max}^{+},\varDelta z_{max}^{+} \leq 4.0$, where the superscript ‘+’ stands for wall units: $l^{+} = l/\delta _{\nu }$ with $\delta _{\nu } =\nu /u_{\tau }$ the viscous length scale. The corresponding Δ y(z)_min ⁺ values remained to be smaller than 0. 06. CFL number is maintained to be always under 0.3. Numerical box size of our simulations has a fixed streamwise length $L_{x}/h = 4\pi$ for closed ducts, and $L_{x}/H = 8\pi$ for open ducts respectively. The box size in y-direction is also fixed at $L_{y}/h = 2$ and $L_{y}/H = 1$, while the size in z-direction is varied according to the aspect ratio ($A = W/h$ for closed ducts, $A = W/H$ for open ducts) of our interests. Please refer to Fig. 4 for a schematic of the domain dimensions. It is also essential to note that the statistical data are averaged over a sufficiently long time interval which can be estimated as approximately 10,000 bulk time units (a bulk time unit is defined as h∕U _b, or H∕U _b).

Fig. 4

Coordinates system and geometry of: (a) closed; and (b) open duct

More than 30 separate simulations have been performed so far to cover a wide range of parameter space necessary for the current studies (cf. Fig. 5). The total amount of the generated data is approximately 15 TB, including several thousands instantaneous flow fields necessary for scientific visualisations as well as coherent structure analysis and its statistics discussed in the following section. Some representative simulation configurations are summarised in Table 2 including spatial resolution, number of processors and typical walltime to complete suchsimulations.

Fig. 5

Parameter map of duct DNS simulations. The red symbols represent the simulations for the current study, while the blue symbols represent the previous studies by: [1, 3, 7, 9, 10] for closed duct; [4] for open duct. Open and filled symbols represent open and closed duct configurations respectively, while the shape of the symbols shows whether those runs’ statistics are fully converged (circle), or not (triangle)

Table 2 Representative examples of simulations. In the “Type” column, “o” indicates open duct, while “c” indicates closed duct

As it is mentioned in Sect. 2.2, our DNS code maintains a good parallel efficiency up to several hundred cores. However, since queueing time for reserving such number of cores was inconveniently long, we have utilised only up to 120 CPUs in order to maximise the throughput of our simulations. In total 3.45851 million core-hours of computational time was granted for Cray XE6 HERMIT (used: 100 %); while computational time of 6.359745 million core-hours was granted for Cray XC40 HORNET (used: 53 %). The estimated percentage of usage for HORNET at the end of the current project period (31st May 2015) at the current rate of throughput is around 72 %.

3 Results and Discussions

3.1 Coherent Structure Analysis on Open Duct Flows

We have identified the centres of vortical structures by the technique proposed by Kida and Miura [5] for the open duct case at bulk Reynolds number Re _b = 2205 with the aspect ratio set at unity. It was found that the mean streamwise vorticity pattern in the turbulent open duct flows is the statistical footprint of the most probable locations of the quasi-streamwise vortices, similarly to the corresponding closed duct cases (cf. Fig. 6, also [7, 9]). There is, however, a significant difference between the open and the closed duct statistics, which is the tightly-concentrated vortices with preferable rotational directions that exist in the mixed-boundary corners. Our results show that those vortices persist in the mixed-boundary corners much more likely than anywhere else in the duct domain. By considering streaks as byproducts of those near-wall vortices, our finding is consistent with the existence of statistically highly concentrated near-free-surface low-speed streaks found experimentally by Grega et al. [2] (cf. their Fig. 12).

Fig. 6

Probability of occurrence of vortex centres for the open duct case with Re _b = 2205, detected by the technique proposed by Kida and Miura [5]. (a) vortices with positive streamwise vorticity; (b) negative streamwise vorticity; and (c) the difference between (a) and (b). The iso-contours indicate 0.1(0.1)0.9 times the maximum values (except (c) where − 0. 9(0.1)0.9 times the maximum absolute value is used instead. Negative values correspond to vortices with negative vorticity). The statistics in (a)–(c) were accumulated from 1000 instantaneous snapshots over a time interval of 721. 5H∕U _b. (d) Mean streamwise vorticity contours indicate − 0. 9(0.1)0.9 times the maximum absolute value where red and blue lines correspond to positive and negative values, respectively. The vorticity field was averaged over a time interval of 8000H∕U _b

3.2 Reynolds Number Dependence in Open Duct Flows

Gavrilakis [1] demonstrated with their direct numerical simulations of square closed duct flow (Re _b = 2205) that there is an ambiguity on the selection of the normalisation velocity scale for the near-wall dynamics. The ambiguity is caused by the fact that, unlike canonical plane channel flows, the average wall friction has a variation along the duct perimeter due to the mean secondary flow. Gavrilakis [1] highlighted this aspect of duct flows by studying the mean streamwise velocity profile along the wall bisector in logarithmic scale, and argued that the local friction velocity should be used for the quantities within the viscous sublayer, while the global friction velocity is more appropriate for the quantity near the duct centre. However, as it was pointed out by Huser and Biringen [3], Gavrilakis’ data also show a closer fit to the law of the wall ($u^{+} = \frac{1} {0.41}\log y^{+} + 5.5$) in the logarithmic region if the local friction velocity is used throughout for normalisation. Please also note that [6] experimentally determined a Reynolds number-independent logarithmic relation ($u^{+} = \frac{1} {0.412}\log y^{+} + 5.29$) from their open duct measurements.

We analysed four of our open duct simulations with Reynolds numbers Re _b = 1500,  2205,  3000,  5000 and aspect ratio A = 1 (cf. Table 3 for the configurations) and the results agree well with such observation except the lowest Reynolds number case, whose logarithmic region does not exist (cf. Fig. 7). Furthermore, it was observed that the discrepancy between the two scalings reduce as Reynolds number increases. This phenomenon can be explained by studying the distribution of the mean wall shear stress along the duct bottom wall shown in Fig. 8a. It can be seen that by increasing Reynolds number, the local variation of the bottom wall shear stress becomes smaller and develops a channel-like plateau around the bottom wall bisector. Furthermore, examining the number of extrema of the bottom wall shear stress profile shown in Fig. 8a shows that the Re _b = 1500 case exhibits a three velocity streaks state (high-, low-, and high-speed streaks arrangement, as discussed in [7]), while the Re _b = 2205 case’s profile indicates a five streaks state. The highest Reynolds case, whose bottom-wall shear profile has a plateau around the wall bisector, can theoretically host up to thirteen streaks. However, at this high Reynolds number, the middle-wall streaks travel more freely and randomly in contrast to the quasi-permanent high-speed streaks residing next to the bottom wall corners (mean distance from the closest side wall ≈ 50 wall units [7]), thus less significant signatures result in the mean wall-shear profile.

Table 3 Numerical set-up of the open duct simulations discussed in Sect. 3.2

Fig. 7

Mean streamwise velocity in logarithmic scale. Symbols indicate the bulk Reynolds numbers: triangle, Re _b = 1500; open circle in blue, Re _b = 2205; diamond symbol in red, Re _b = 3000; plus symbol in green, Re _b = 5000. Solid lines indicate the values normalised by the global friction velocity u _τ, while dotted lines indicate the values normalised by the local friction velocity (u _τ)_bisector

Fig. 8

Mean local wall shear stress normalised by the average over the whole no-slip walls, along (a) bottom wall and (b) side walls (the origin has been translated to the corner). Symbols indicate the bulk Reynolds numbers: triangle, Re _b = 1500; open circle in blue, Re _b = 2205; diamond symbol in red, Re _b = 3000; plus symbol in green, Re _b = 5000

In contrast to the bottom wall statistics behaving similarly to the closed duct counterparts, the open duct side walls host distinctive features especially near the corners formed by no-/free-slip boundaries. Such differences are apparent, for example, by examining the wall shear stress along the side walls shown in Fig. 8b. Here, we observe the signatures of existence of the nearest high-speed streak from the free-slip plane to appear directly on the plane. The positions of the following low-speed streaks appear to move away from the free-slip plane as Reynolds number increases, then settle down at approximately 50 wall units (i.e. d ⁺ ≈ 50) for Re _b ≥ 3000 with $L_{y}^{+} = L_{y}/\delta _{\nu } \geq 200$.

The time evolutions of the instantaneous low-speed streak locations, determined as the location of the minimum wall shear stress, are plotted for the three Reynolds numbers in Fig. 9. Please note that data from Re _b = 1450 had to be used here instead of Re _b = 1500, due to the availability of such large number of instantaneous data. It can be observed that the amplitude of the streaks’ lateral movement are much more restricted and therefore their paths are significantly more distinguishable than the ones from the bottom wall, which appear similar to the ones previously studied for closed ducts (cf. [7] their Fig. 6). Regarding the side-walls, the corresponding probability density function of the distance from the free-slip plane is shown in Fig. 10, illustrating that the locations of their peaks are actually at similar distances at all Reynolds numbers (d ⁺ ≈ 25), but the tails of the distribution develop away from the free-slip plane as Reynolds number is increased, which brings the averaged location of the low-speed streaks away from the plane up to ≈ 50 wall units for high enough Reynolds numbers.

Fig. 9

Time evolution of position of minimum of the wall shear stress at $z/H = 1$, $x/H = 0$. (a) Re _b = 1450; (b) Re _b = 2205; (c) Re _b = 3000

Fig. 10

Probability density function of low speed streak distance from the free-slip plane (d ⁺), computed considering the instantaneous location of the minimum value of wall skin friction. Symbols indicate the bulk Reynolds numbers: triangle, Re _b = 1450; open circle in blue, Re _b = 2205; diamond symbol in red, Re _b = 3000

4 Conclusions and Outlook

We have performed a series of direct numerical simulations both in the open and the closed duct configurations with variable Reynolds number and aspect ratio.

Our coherent structure analysis revealed that, likewise in turbulent closed duct flows, the mean streamwise vorticity pattern in turbulent open duct flows is the statistical footprint of the most probable locations of the quasi-streamwise vortices. The same analysis also revealed the existence of tightly-concentrated vortices with preferable rotational directions in the corners formed by no-/free-slip boundaries.

Those in-corner vortices and their corresponding low-speed streaks are later demonstrated to be the main players of distinctive features on the duct side walls, such as the unique wall shear stress profile whose peak laying directly on the free-slip boundary.

Results regarding other aspects of turbulent duct flows that are not reported here, including variable aspect ratio effects on open/closed duct flows, as well as closed duct flows with Reynolds numbers significantly higher than previous studies, will be discussed in details in other forms of publication in near-future elsewhere.

Overall, the outcomes of our current project at HLRS has been fruitful. However, computing high Reynolds number duct flows with high aspect ratio is still a challenge even with the aid of sophisticated HPC facilities such as Cray XC40 HORNET. Alongside the severe spatio-temporal resolution requirements mentioned earlier, the main difficulties arise from the limited flexibility of Chebyshev-Gauss-Labatto point distribution used in spatial discretisation in the cross-stream directions, which let us tweak only one parameter, namely number of grid points for each direction. As a consequence, near-wall regions are in general over-resolved in order to maintain adequate resolution around the duct core region, where Chevyshev-Gauss-Lobatto points have the coarsest distribution, which carries severe timestep size restriction thus slower computations. To cope with such challenges by obtaining better grid-design freedom while maintaining spectral accuracy, our DNS code is currently under a major upgrade with a use of spectral element spatial discretisation method in the cross-stream directions. The upgraded code would not only enable us to compute higher Reynolds number/aspect ratio duct flows efficiently, but also to incorporate wall-roughness elements as well as angled duct side walls within our simulations, which are of great interest to civil/environmental engineering applications.