The organized motion of characterized turbulent flow at low Reynolds number in a straight square duct

Abstract

We study the self-sustaining turbulent flow at minimal frictional Reynolds number in a straight square duct using direct numerical simulation. The flow in the square duct is maintained through a constant pressure gradient in the stream-wise direction. The computational investigation of the flow phenomenon for minimal, marginal and fully turbulent flow is studied using organized motion and dynamics of coherent structures. The central theme of the present work is to demonstrate the organized motion of the flow regimes below the frictional Reynolds number of the fully turbulent flow. The controlled direct numerical simulation study and vortex-detection technique unveil hairpin vortices in fully and minimal turbulent flow in the square duct for the first time. Bursting of streaks is detected with variable interval time average, and the evolution of hairpin vortices is also addressed. Turbulent intensities and energy spectra are reported and compared between the minimal, marginal and fully turbulent flow. The minimal turbulence in a square duct indicates transitional turbulent flow characteristics like lesser occurrence of ejection and sweep, intermittent bursting events, and a steeper variation of energy spectrum as compared to fully turbulent energy spectrum distribution.

1 Introduction

Flow through ducts are ubiquitous in oil and gas pipelines, heat exchangers and nuclear engineering applications. The understanding and control of turbulence in the duct are significant for both engineering needs and deep scientific perspectives. Since the pioneering dye experiment by Reynolds in 1883, the turbulent flow at low Reynolds number in ducts is still an unresolved issue. The flow characteristics and occurrence of turbulence are often comparable for square duct and pipe flow. However, unlike pipe flow, the geometry of square duct on account of four walls and corners produces turbulence-driven secondary flow. The secondary flow in the corner of a square duct is termed as secondary motion of Prandtl second kind. The eight-vortex symmetric secondary flow pattern in a fully turbulent square duct flow refers to the mean cross-flow plane orthogonal to the stream-wise direction. The secondary flow intensity is 1–2 $\%$ of the stream-wise velocity which brings the high-momentum fluid from duct core toward the corner and then transfers low-momentum fluid back to the core along the wall bisectors. It has practical use like redistribution of heat transfer or friction along the ducts perimeter and significant effect on turbulence statistics.

Nikuradse [1] first highlighted the secondary flow in the square duct through experiment. Direct Numerical Simulation (DNS) of turbulent flow in a square duct at $\hbox {Re}_\tau$ (frictional Reynolds number based on frictional velocity and duct width) = 300 was first carried out by Gavrilakis [2]. This work shows a good agreement with the published experimental results. Huser and Biringen [3] and Zhang et al. [4] illustrated turbulent flow in a square duct at higher Reynolds number. Huser and Biringen [3] numerically assessed the fully developed turbulent flow at friction Reynolds number of $\hbox {Re}_\tau$ = 600, and using the budget equation, reported the development of turbulent structures at the corner of the duct. Zhang et al. [4] performed DNS study for $\hbox {Re}_\tau$ = 300 to 1200. Pirozolli et al. [5] characterized the secondary flow motions in the square duct at $\hbox {Re}_\tau$ = 2000. Modesti et al. [6] revealed that the secondary flow in a square duct contributes 6$\%$ to the friction factor. All the above literature depict an eight-vortex flow pattern (large-scale secondary flows) at higher Reynolds number.

The occurrence of secondary flows at low Reynolds number is found to be different and has received little attention. Uhlmann et al. [7] reported marginal turbulence in a square duct at $\hbox {Re}_\tau$ = 160. They first revealed the secondary flow of marginal turbulence as two states of flow. The states of flow are short time integrated secondary flow consisting of four-vortex with pairs on opposite wall (vertical/horizontal). The conventional eight-vortex is achieved by the composition of these states of flow or through long time integration. Takeishi et al. [8] numerically reported that the aspect ratio of rectangular duct influences the localized turbulence structure. They depicted localized turbulence structure’s Reynolds number decreases monotonically with increase in the aspect ratio. Pinelli et al. [9] reported the behavior of the flow field owing to Reynolds number effect. They correlated the wall shear stress and buffer layer streaks.

In the previous literature [1,2,3,4,5,6,7,8,9] , flow characteristics from transition to turbulence in a square duct are represented by turbulence statistics. The dynamics of coherent structures and organized motion from transition to turbulence in a square duct are still lacking. The coherent structure or organized motion in wall-bounded flows is widely stated by Robinson [10]. Some of the techniques reported in the literature to study the organized motions in the wall-bounded flow are streak eduction, quadrant analysis, VITA and swirling strength. The streak eduction identifies the instabilities of low-speed streak and re-occurrence of organized motions near the wall, which are significant source of turbulence production [see 11]. The quadrant analysis proposed by Lu and Willmarth [12] explains the presence of coherent structures and their contribution to Reynolds shear stresses. Sweeps and ejections indicate the organized motion near the wall. This process helps to understand the mechanism of turbulence generation. Kline et al. [13] observed the oscillation and lift up of one of the streaky structure, resulting in the ejection and sudden interaction of the low-speed fluid with the outer flow field. This process is known as bursting, and it helps in turbulent production during the sequence. The occurrence of bursting frequency is identified with a detection method called variable-interval time average (VITA) technique proposed by Blackwelder and Kaplan [14]. The VITA events indicate powerful ejections which correspond to the emergence of hairpins. The vortex detection technique (swirling strength) visualizes the vortical coherent structures like quasi-stream-wise vortices and hairpin vortices in a wall-bounded flow (see, [15]).

To the best of authors’ knowledge, Uhlmann et al. [7] and Pinelli et al. [9] studied the square duct turbulent flow at low Reynolds number. Uhlmann et al. [7] are the first to report the marginal turbulent flow ($\hbox {Re}_\tau$ $\approx$ 160) as two states of flow; $\hbox {Re}_\tau$ is based on frictional velocity and duct width. Pinelli et al. [9] studied the range of Reynolds number from $\hbox {Re}_\tau$ $\approx$ 160 to $\hbox {Re}_\tau$ $\approx$ 450; they reported turbulent statistics and correlated the wall shear stress and buffer layer streaks. The gap from the previous literature is summarized in twofold. First, previous studies [7, 9] were not able to characterize the turbulent flow below marginal turbulence ($\hbox {Re}_\tau$ $\approx$ 160). Second, the dynamics of coherent structures/organized motion for transition and turbulence in a square duct is still unexplored.

The central theme of the present work is to study the organized motion and coherent structures' dynamics in a square duct having transitional flow coined as “minimal and marginal” flows and fully turbulent flow. The analysis and comparison of transition and turbulent flow organized motion in a square duct are studied for the first time in present work. The organized motion consisting of instantaneous flow, quadrant analysis (or sweep/ejection), bursting events, coherent structures and streak eductions are used to compare the minimal ($\hbox {Re}_\tau$ = 100), marginal ($\hbox {Re}_\tau$ = 160) and fully turbulent ($\hbox {Re}_\tau$ = 300). Through quadrant analysis and the VITA technique, this paper addresses whether the organized motion is suitable enough to initiate bursting at minimal and marginal turbulent flow. As per the authors’ knowledge, this is the first study to visualize hairpin-shaped structures in complex turbulent square duct flow (almost two decades after the first DNS study of turbulent flow in a square duct by Gavrilakis [2]). To address the question of existence of hairpin structures in a minimal turbulent flow of a square duct, the generation and evolution of hairpin-shaped structures are reported. The present study also provides a comparison of turbulent intensities in the three flow regimes. The turbulent kinetic energy spectra are used to explain the thorough statistical structural differences between flow regimes.

The paper is organized in the following five sections: The problem description is briefly introduced in Sect. 2. The description of DNS code with parameter setting and the accuracy of our code is validated in Sect. 3. In Sect. 4.1 turbulence statistics are discussed. Further, in Sect. 4 (subsection 4.2-4.7), the organized motion and coherent structures are discussed. Conclusions are presented in Sect. 5.

2 Problem description and governing equations

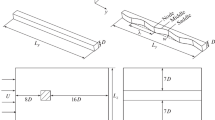
Turbulent flow at moderate Reynolds number is studied in a square duct of side h. The geometry and domain dimensions are displayed in Fig. 1. The domain is bounded by two open boundaries and four wall boundaries. The Cartesian coordinate x is the stream-wise direction, while y and z are span-wise and lateral directions, respectively. The discussion is facilitated by wall and corner bisectors as shown in Fig. 1. The dimensionless incompressible Navier–Stokes equations for a stream-wise periodic square duct (Huser et al. [3]) are shown in Eqs. (1) and (2).

$$\begin{aligned}&\nabla .\mathbf{U } = 0 \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial \mathbf{U }}{\partial t} + (\mathbf{U }.\nabla )\mathbf{U } = -\nabla P + \frac{1}{{\hbox {Re}}_\tau }(\nabla ^2 \mathbf{U } ) + 4\mathbf{i } \end{aligned}$$

(2)

The velocity and length scale used to normalize the governing equations are friction velocity ($\hbox {u}_\tau$) and width of the duct (h). The Reynolds number is defined as $\hbox {Re}_\tau$ = $\hbox {u}_\tau$h/$\nu$, where $\nu$ is kinematic viscosity. The frictional Reynolds number ($\hbox {Re}_\tau$) is based on frictional velocity and duct width. The flow is periodic in stream-wise direction, maintained with the constant pressure gradient. This pressure gradient acts effectively as a simple body force. The imposed pressure gradient is related to average wall shear stress as ${\overline{\tau }}_w = {\rho }u^{2}_\tau = -\frac{h}{4}(\frac{\mathrm{d}P}{\mathrm{d}x})$. The pressure gradient in Eq. (2) is defined as -4i, where unit vector i represents stream-wise direction. The no-slip boundary condition is imposed on four solid walls.

Fig. 1

Schematic diagram of a square duct

3 Computational setup

3.1 Description of the DNS code

The incompressible Navier–Stokes equations are discretized on the collocated grid using finite difference method. The discretized equations are fourth-order accurate in space. For second-order accuracy in time, an implicit Crank–Nicolson scheme is used for the viscous term. A two-step pressure correction type of scheme is employed to study the unsteady physics of flow [16,17,18]. The grid scale pressure oscillations on account of decoupling between the pressure and the velocity at a grid point are avoided using momentum interpolation technique of Rhie and Chow [19]. Hirsch [20] reported this scheme which is conceptually similar to the Simplified Marker and Cell (SMAC) scheme of Amsden and Harlow [21]. Cheng and Armfield [16] reported that SMAC scheme is computationally efficient for unsteady incompressible flow over other numerical methods like SIMPLE, SIMPLEC and PISO. Thus, the present numerical study utilizes scheme similar to the SMAC method. The modified SMAC scheme uses two-step predictor-corrector approach. The flow field is forward marched in time using Euler’s first-order accurate scheme, while the diffusion terms are treated implicitly second-order accurate in time by Crank-Nicolson method, to yield the guessed velocity at the new time level.

$$\begin{aligned} \mathbf{U }^{*}-\frac{\delta t}{2{\hbox {Re}}_{\tau }}\nabla ^{2}\mathbf{U }^{*} =\mathbf{U }^{n}-\delta t( \nabla P^{n}+(\mathbf{U }^{n}.\nabla )\mathbf{U }^{n}+{\tilde{f}}^{n}-\frac{1}{2{\hbox {Re}}_{\tau }}\nabla ^{2}\mathbf{U }^{n}) \end{aligned}$$

(3)

The guessed velocity at the new time level does not satisfy the continuity equation. Hence, the guessed velocity is corrected with the pressure correction field in a vorticity manner whose divergence of velocities are close to zero.

$$\begin{aligned} \mathbf{U }^{n+1}-\frac{\delta t}{2{\hbox {Re}}_{\tau }}\nabla ^{2}\mathbf{U }^{*}=\mathbf{U }^{n}-\delta t(\nabla P^{n+1}+(\mathbf{U }^{n}.\nabla )\mathbf{U }^{n}+{\tilde{f}}^{n}-\frac{1}{2{\hbox {Re}}_{\tau }}\nabla ^{2}\mathbf{U }^{n}) \end{aligned}$$

(4)

Subtracting Eq. (3) from Eq. (4) yields following expression for corrected velocity:

$$\begin{aligned} \mathbf{U }^{n+1}-\mathbf{U }^{*}=-\delta t\{\nabla (P^{n+1}-P^{n})\} \end{aligned}$$

(5)

where the corrected pressure is expressed as:

$$\begin{aligned} P^{'} = P^{n+1}-P^{n} \end{aligned}$$

(6)

The corrected pressure is such that the obtained corrected velocity from Eq. (5) must satisfy the continuity equation ($\nabla .{\mathbf{U }^{n+1}} = 0$). The divergence of Eq. (5) results in pressure correction Poisson equation (PCPE):

$$\begin{aligned} \nabla ^{2}P^{'}=\frac{\nabla .\mathbf{U }^{*}}{\delta t} \end{aligned}$$

(7)

The above Poisson equation is solved to calculate pressure correction. The discretization of Eq. (7) is handled carefully in order to avoid pressure-velocity decoupling. The non-physical behavior due to the discretization of PCPE is avoided by utilizing conservative differencing as reported by Hasan and Sanghi [17]. The divergence operator of PCPE is discretized compactly on the points midway between the grid points. The Rhie and Chow [19] momentum interpolation technique is invoked to discretize the divergence of guessed velocity. The momentum interpolation technique calculates the velocity midway between adjacent grid points which helps to maintain the pressure-velocity coupling. The discrete PCPE are solved using generalized minimal residual [22] (GMRES) solver having a residual tolerance of $10^{-5}$. Subsequently, the obtained corrected pressure ($P{'}$) is used to update new-time level pressure field ($P^{n+1}$) using Eq. (6). The new-time level velocity field is finally calculated by:

$$\begin{aligned} \mathbf{U }^{n+1}= \mathbf{U }^{*}-\delta t\{\nabla P^{'}\} \end{aligned}$$

(8)

The four solid walls are imposed with no-slip boundary conditions. The flow is periodic in stream-wise direction, maintained with the constant pressure gradient. Non-uniform grids are employed in transverse and span-wise directions to capture wall effect, whereas the stream-wise grid is uniform. The non-uniform grid distribution in transverse and span-wise directions is hyperbolic-tangent [4] function. The developed DNS code is made computationally efficient with three-dimensional domain-decomposition parallelization in Cartesian topology using MPI library. Simulations were carried out on PADUM supercomputer (Hybrid High Performance Computing Facility at IITD) consisting of 238 CPU nodes with 2x E5-2680 v3 2.5GHz/12-Core 64 GB RAM. Maximum 156480 CPU hours were required to run on 192 cores for $\hbox {Re}_\tau$ = 300 case.

3.2 Parameter settings

The physical and numerical parameters of all cases (simulations) carried out in the present study are reported in this subsection. Three frictional Reynolds numbers (based on the duct width h and frictional velocity $u_\tau$) used to study the transition to turbulence are $\hbox {Re}_\tau$ = 100, 160 and 300. The domain length considered in the stream-wise direction for all three cases is $L_x/$h = 4$\pi$. The grid points ($N_x \times N_y\times N_z$) for $\hbox {Re}_\tau$ = 100, 160 and 300 are $128 \times 78 \times 78$, $216 \times 96 \times 96$ and $384 \times 128 \times 128$, respectively, where $N_x$, $N_y$ and $N_z$ are numbers of grid points in x, y and z-direction. The resolution required for all cases in stream-wise direction is $\Delta x^{+} = 9.5$ and in the wall-normal direction is $0.20< \Delta y^{+}, \Delta z^{+} < 5.0$ similar to Gavrilakis [2] and Zhang et al. [4] work. The CFL number ($\Delta \hbox {tu}_\tau$/h) close to 0.2 corresponds to fixed time steps of 0.00033, 0.0002 and 0.0001 for $\hbox {Re}_\tau$ = 100, 160 and 300, respectively. Simulations were executed until the statistically stationary state was obtained and sampling was done at interval of every 50 time steps in the statistically stationary regime. The mean constant value of the total kinetic energy indicates that the steady state was reached. In the statistically stationary regime, the long-term time data were accumulated for 10 turnover times. The mean flow field (denoted by an overbar) was obtained through long-term statistics by averaging homogeneous (stream-wise) direction and time followed by averaging over four quadrants (similar to Gavrilakis [2]).

3.3 Validation

The present numerical procedure was verified with a reference DNS data from Gavrilakis [2]. The fully turbulent flow at $\hbox {Re}_\tau$ = 300 is compared with the previous simulation of Gavrilakis [2]. Two-point correlation checks the characteristic length of longest turbulent structures in stream-wise direction. According to Gavrilakis [2], two-point correlation suggests the domain length in the stream-wise direction as $L_x$/h = 4$\pi$. The present DNS data was first compared with the mean stream-wise velocity profile of reference results as shown in Fig. 2a, b for $\hbox {Re}_\tau$ = 300. Figure 2c, d compares the mean lateral velocity profile. Both figures show the satisfactory agreement of our mean velocity profile with the Gavrilakis [2] DNS result. Next, the stream-wise, span-wise and lateral velocity fluctuations root mean square (rms) velocity profile at wall bisector are compared with the reference data as shown in Fig. 3. The present DNS data comparison with the Gavrilakis [2] DNS data yields an excellent match.

Fig. 2

Comparison of present DNS results of mean velocity profile with DNS data of Gavrilakis [2], a stream-wise velocity at z = 0.05, b streamwsie velocity at z = 0.5, c lateral velocity at z = 0.08 and d lateral velocity at z = 0.4. Mean velocities are rescaled with centerline mean velocities

Fig. 3

Comparison of present DNS results of turbulent intensities with reference DNS data of Gavrilakis [2] a $u_{\mathrm{rms}}$, b $v_{\mathrm{rms}}$ and c $w_{\mathrm{rms}}$

4 Results and discussion

We study the flow phenomenon of minimal turbulent flow ($\hbox {Re}_\tau$ = 100), marginal turbulent flow ($\hbox {Re}_\tau$ = 160) and fully turbulent flow ($\hbox {Re}_\tau$ = 300). Figure 4 presents the mean secondary flows with stream-wise velocity isolines. The eight-vortex secondary flow location and distortion of the stream-wise isolines are $\hbox {Re}_\tau$ dependent. As observed by Pinelli et al. [9], for lower $\hbox {Re}_\tau$ the secondary flow vortices are closer to wall bisector. At higher $\hbox {Re}_\tau$ these vortices move toward the corner bisector. However, the organized motion and the dynamics of coherent structure in the three flow regimes have not been studied before. In the following subsection, the results of the three flow regimes are presented and discussed on the turbulent intensities, streak eductions, bursting events and coherent structures.

Fig. 4

Eight-vortex mean secondary flow and stream-wise flow contours, a $\hbox {Re}_\tau$ =100, b $\hbox {Re}_\tau$ =160, c $\hbox {Re}_\tau$ =300

4.1 Turbulence intensities

The wall-normal and stream-wise turbulence intensities along the wall bisector ($z=0.5$) are shown in Fig. 5. With increase in Reynolds number, the peak of stream-wise turbulent intensity ($u_{\mathrm{rms}}$) moves toward the wall. The stream-wise turbulence intensity fluctuations are lower near the wall for minimal/marginal turbulence as compared to fully turbulent flow. While the intensity is slightly higher for marginal turbulence toward the duct center. The wall-normal turbulence intensity ($w_{\mathrm{rms}}$) near the wall for $\hbox {Re}_\tau$ = 160 shows less value as compared to $\hbox {Re}_\tau$ = 300. At $\hbox {Re}_\tau$ = 100, the wall-normal turbulence intensity has a slow rate of increase across the duct center and no distinct maxima is depicted. This monotonic behavior of wall-normal turbulence intensity at $\hbox {Re}_\tau$ = 100 is elucidated farther in a discussion of secondary normal stress ($\overline{w'w'}$).

Fig. 5

Turbulence intensities, a $u_\mathrm{rms}$, b $w_\mathrm{rms}$ along the wall bisector normalized by the local friction velocity

Fig. 6

The Reynolds stress terms $\overline{u'u'}$, $\overline{v'v'}$, $\overline{w'w'}$, $\overline{u'v'}$, $\overline{u'w'}$ and $\overline{v'w'}$ (From left to right) at $\hbox {Re}_\tau$ = 100, 160 and 300 (From top to bottom). (dark and light contours shows the maximum and minimum value, respectively)

The primary normal stress ($\overline{u'u'}$), secondary normal stresses ($\overline{v'v'}$, $\overline{w'w'}$), primary shear stresses ($\overline{u'v'}$, $\overline{u'w'}$) and secondary shear stress ($\overline{v'w'}$) contour plots for different Reynolds number are displayed in Fig. 6. At lower Reynolds number ($\hbox {Re}_\tau$ = 100 and 160), the intense region of $\overline{u'u'}$ shifts toward the duct center, similar behavior is depicted in Fig. 5a. The intense region of primary normal stress ($\overline{u'u'}$) is close to the wall for fully turbulent flow and reduced $\overline{u'u'}$ are observed near the corner bisector.The secondary Reynolds stresses ($\overline{v'v'}$, $\overline{w'w'}$, $\overline{v'w'}$) play a major role in the production of secondary flow. The secondary normal stress $\overline{w'w'}$ contours are shown in Fig.  6. Low value near the horizontal wall illustrates damping effect. In marginal turbulent flow, the damping effect increases near the horizontal wall. The maximum $\overline{w'w'}$ for $\hbox {Re}_\tau$ = 300 and 160 is observed near the vertical wall and it decreases toward the duct center. For $\hbox {Re}_\tau$ = 100, $\overline{w'w'}$ remains constant toward the center and has similar behavior as shown in Fig.  5b. This elucidates that the horizontal wall damping effect is not induced toward the center of the duct at minimal turbulent flow ($\hbox {Re}_\tau$ = 100). Figure 6 presents the distribution of secondary shear stress ($\overline{v'w'}$) with significant maxima value at the corner of the duct. The horizontal and vertical wall boundary layer overlap at the corner of the duct to produce significant maxima value of $\overline{v'w'}$ at the corner of the duct. The secondary flow formation is associated with the effect of the secondary shear stress ($\overline{v'w'}$) from the corner of the ducts. The maximum magnitude of secondary shear stress is at the corner of the duct for higher $\hbox {Re}_\tau$.

4.2 Instantaneous flow

The evolution of near-wall structure is presented with the help of instantaneous vorticity. Contours of instantaneous vorticity magnitude in YZ-plane (perpendicular to the flow direction) are shown in Fig. 7. The distributions of vorticity magnitude are asymmetric and chaotic. The mushroom-shaped structures at different Reynolds number are visualized from the walls of YZ-plane (cross-flow plane) as shown in Fig. 7. The time series of the instantaneous vortices in Fig.  7 illustrate the dynamics of near-wall structures. The mushroom-shaped structure (marked with a dotted circle) is created from two counter-rotating vortices near the wall. These structures eject low-momentum fluid from the wall to the high-momentum fluid in the core. This process is called ejection. During the sweep process, the two counter-rotating vortices drift toward the corner of the duct, pulling high-momentum fluid from core to the low-momentum fluid near the wall. For fully turbulent flow ($\hbox {Re}_\tau$ = 300) the mushroom-shaped structures are close to walls (Fig. 7c), on account of counter-rotating vortices near the wall. In Fig 7a, b, the minimal ($\hbox {Re}_\tau$ = 100) and marginal ($\hbox {Re}_\tau$ = 160) turbulent flow structures elongate toward the center of the duct (in YZ-plane) or counter-rotating vortices shift toward the center. Consequently, the mean of these instantaneous secondary vortices gives eight-vortex secondary flow close to duct center which is consistent with the previous mean secondary flow results in Fig.  4. The deformation of mushroom-shaped structures is noticeable in time at minimal (Fig. 7a) and marginal (Fig. 7b) turbulence unlike the structures observed for fully turbulence (Fig.  7c) due to small structures and their chaotic nature. Thus, it is observed that the mushroom-shaped structures marked with dotted circle consist of two lobes (or counter-rotating vortices). Subsequently, with further increase in time the two-lobed mushroom-shaped structures are observed to tilt sideways, changing their shape to single-lobed mushroom structures or with disordered appearance. The dynamics of near-wall structures in a cross-flow plane are the reliable indicator of ejection and sweep occurrence and presence of hairpin vortices at minimal, marginal and fully turbulent flow. The frequency of occurrence for the ejections and sweeps at different Reynolds number is discussed in the subsequent section. The above vorticity visualization result motivates the authors to further study the dynamic evolution of three-dimensional coherent structures like hairpin vortices in the square duct.

Fig. 7

Time series of instantaneous vorticity contours on cross-flow plane (YZ-plane) represents mushroom-like structures at a $\hbox {Re}_\tau$ = 100, b $\hbox {Re}_\tau$ = 160 and c $\hbox {Re}_\tau$ = 300

4.3 Quadrant analysis

The near-wall vortices are related to the bursting process (sweep and ejection). The sweeps and ejections are depicted through time history of stream-wise and wall-normal fluctuating velocities in buffer layer and viscous sublayer using quadrant analysis. The fluctuating velocity obtained from different location above the wall are split into four quadrants of the $u'-w'$ plane. The four quadrants are Q1($u'>0, w'>0$), Q2($u'<0, w'>0$), Q3($u'<0, w'<0$) and Q4($u'>0, w'<0$). Each quadrant represents the contribution of Reynolds shear stress. The Q1 (or outward interaction) represents the movement of high-momentum fluid far from the wall and Q3 (or inward interaction) indicates the low fluid movement toward the wall. The second (Q2) and fourth (Q4) quadrant give main Reynolds stress contribution where the second quadrant represents ejection and fourth quadrant represents sweep. The ejection (Q2) occurs with the movement of low-speed fluid far from the wall. The movement of high-speed fluid toward the wall indicates sweep (Q4) events. The ejection and sweep motion contribute to rise of the instantaneous stresses more than the time-averaged Reynolds stress, whereas the interaction-type motion neutralizes the surplus stress. The sweep events dominate near the wall at $z^{+}<15$, whereas the ejections contribute more at $z^{+}>15$.

The quantitative contribution of Reynolds shear stress events is studied by the fluctuating velocity (u’ & w’) obtained from different location above the wall. The Reynolds shear stress for each event shown in Fig. 8 illustrates the change in quantitative contribution with Reynolds’s number. The contribution of sweep events near wall at different Reynolds number is illustrated in Fig. 8. $\hbox {Re}_\tau$ = 300 (fully turbulent) depicts highest sweep events near the wall. In the same figure at lower Reynolds number (160, 100), the sweep event is less near wall as compared to fully turbulent. This observation indicates less tendency to sweep events at lower Reynolds number. Similarly, Fig.  8 depicts the ejection (Q2) events. The contribution of ejection events increases far from the wall in the buffer layer at $\hbox {Re}_\tau$ = 300, 160 and 100. The fully turbulent flow ($\hbox {Re}_\tau$ = 300) contributes higher ejection indicating predominant case for turbulence production. Furthermore, the ejection is more intense as compared to interaction-type motion. The ejection contribution decreases with Reynolds number while interaction-type motion increases which counteract the contribution of ejection motion at the lowest Reynolds number ($\hbox {Re}_\tau$ = 100). The tendency of low-speed fluid movement away from wall (Q2 event) and high-speed fluid toward wall (Q4 event) are almost comparable at the lowest Reynolds number ($\hbox {Re}_\tau$ = 100) as shown in Fig.  8. The quadrant analysis indicates lesser contribution of sweep/ejection event at $\hbox {Re}_\tau$ = 100 in the square duct. Subsequently, the lowest Reynolds number ($\hbox {Re}_\tau$ = 100) flow bursting process (sweep/ejection) contribution are farther reduced because the significant amount of interaction-type motions counteracts the ejection motion.

Fig. 8

The Reynolds shear stress quadrant contribution in a turbulent square duct

4.4 Bursting events

The organized motion of streaky structures leads to the vigorous emission of low-speed streak outward from the wall causing turbulent burst. The sequence of bursting visualized in earlier studies is associated with a higher degree of fluctuating velocity. The bursting is an important aspect to investigate whether the ejection events are suitable enough to initiate bursting or turbulent production at minimal and marginal turbulent flow. The time history of fluctuating velocity is recorded at near-wall buffer layer ($z^+=20$) to investigate bursting event at minimal, marginal and fully turbulent flow. Accordingly, the Variable Interval Time Average (VITA) conditional sampling technique developed by Blackwelder and Kaplan [14] is used in present study to detect bursting in time. The variable-interval time average is defined as

$$\begin{aligned} {\widehat{Q}}(x_i,t,T)=\frac{1}{T}\int _{t-\frac{T}{2}}^{t+\frac{T}{2}} Q(x_i,\tau ) \mathrm{d}\tau \end{aligned}$$

(9)

where $Q(x_i,\tau )$ and T are fluctuating quantity and averaging time, respectively. The localized variance is measured as

$$\begin{aligned} {\hbox {var}}(x_i,t,T)=\frac{1}{T}\int _{t-\frac{T}{2}}^{t+\frac{T}{2}} u^{\prime 2}(x_i,\tau ) \mathrm{d}\tau - \bigg (\frac{1}{T}\int _{t-\frac{T}{2}}^{t+\frac{T}{2}} u^{\prime }(x_i,\tau ) \mathrm{d}\tau \bigg )^2 \end{aligned}$$

(10)

where var is the short-time variance of the signal. This VITA variance is used to detect shear-layer events. The detection criterion identifies the bursting events when the VITA variance is above the threshold level. The detection function D(t) is defined as

$$\begin{aligned} D(t)= {\left\{ \begin{array}{ll} 1,&{}\quad \text {if }\;{\hbox {var}}\ge Ku^{2}_\mathrm{rms}\\ 0, &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

The threshold level K is considered as 0.8 based on previous studies [23] of wall-bounded flows and $u_\mathrm{rms}$ is the rms of the stream-wise fluctuating velocity. The depicted VITA events at all three Reynolds number are shown in Fig. 9. Figure 9 reports more than 12 turbulent burst event for fully turbulent flow. It is clear from this investigation that burst events are also observed for minimal/marginal turbulent flow in the square duct. For $\hbox {Re}_\tau$ = 160 and 100 the burst events are 11 and 6, respectively. In spite of low VITA event in the marginal turbulent flow, it is clear that some of the turbulent production is due to bursting. Subsequently, the minimal turbulent flow ($\hbox {Re}_\tau$ = 100) considered in the present study shows the turbulent production behavior. In minimal/marginal turbulent flow, the intensity and number of turbulence burst events are less as compared to fully turbulent flow. The bursting is a powerful ejection instead of individual ejection. The obtained bursting events at low Re indicate powerful ejections which corresponds to the emergence of hairpins. The earlier subsections (Sects. 4.2, 4.3 and 4.4) illustrate the characteristics of low-momentum regions, momentum transfer (sweep/ejection) and intense bursting events (VITA); these all together lay the paradigm for the formation of hairpin vortices [10]. Hence, it becomes necessity to further investigate the presence of hairpin vortices in the square duct at minimal and fully turbulence.

Fig. 9

Comparison of bursting events at the buffer layer, a $\hbox {Re}_\tau$ =100, b $\hbox {Re}_\tau$ =160, c $\hbox {Re}_\tau$ =300

4.5 Coherent structures

The vortex-detection technique known as swirling strength ($\lambda _{ci}$) first introduced by Zhou et al. [24] is used in present study to extract the coherent structures of turbulent flow. This technique uses fluctuating velocity field to study coherent structures. The velocity-gradient tensor complex-eigenvalue pair has imaginary ($\lambda _{ci}$) and real ($\lambda _{r}$) parts. The imaginary complex-eigenvalue represents the local swirling strength inside the vortical structures, whereas the real value represents the strength of stretching or compression. The swirling strength technique has been applied to turbulent flow in square duct. The coherent structures visualized in Fig. 10b populates the more chaotic region near the wall for fully turbulent flow ($\hbox {Re}_\tau$ = 300). These near-wall structures help in turbulent production and transport processes. The coherent structures for the minimal turbulence ($\hbox {Re}_\tau$ = 100) are in the outer layer or wake region of the boundary layer as shown in Fig.  10a. According to former wall-bounded flow studies [25], the hairpin vortices in the transitional flow initially generate briefly and later show the outer layer phenomenon. The coherent structures observed have different shapes and most structures are inclined at a certain angle. The external surface of the structures shown in Fig. 10 are colored with stream-wise velocity. As expected, the structures for high Re are much smaller in size as compared to low Re. From the populated coherent structures, one single hairpin-like structure is shown in the enlarged view for both the minimal turbulence (Fig.  10a) and fully turbulent (Fig.  10b) flow. The hairpin structures shown in Fig.  10b ($\hbox {Re}_\tau$ = 300) are in the vicinity of corner, inclined at a certain angle from the wall. Interestingly, it is observed that the hairpin structure for the minimal turbulent flow shown in Fig. 10a are not close to the corner, and one of its legs is inclined to horizontal wall while the other one is inclined toward the vertical wall. This is unique to the occurrence of hairpin vortices at $\hbox {Re}_\tau$ = 100 in the square duct.

Fig. 10

The isosurface of swirling strength colored with stream-wise velocity, a $\hbox {Re}_\tau$ = 100, b $\hbox {Re}_\tau$ = 300 (the isosurface of the swirling strength are 25$\%$ of its maximum value)

The evolution of the hairpin vortex is shown in Fig.  11 to characterize these vortices for the minimal turbulence. In the process, the occurrence of the sweep and ejection with vortical structure are also noted. In Fig.  11, the first labeled figure shows the single hairpin-shaped structure consisting of head connected with two adjacent legs toward wall and upstream direction colored with stretching (red) and compression (blue) while the sweep and ejection are indicated by green and yellow isosurface, respectively. The stretching is noted on the head, while legs and the neck show compression. Figure 11a–h represents the morphological evolution process of hairpin vortices along with the sweep and ejection. The evolution is discussed in two phases, the initial phase of evolution in Fig.  11a–d while the later phase of evolution occurs from Fig. 11e–h. The ejection (yellow isosurface) is found behind the head (spherical-like part) of the hairpin always pushing the head of the hairpin upwards. The sweep (green isosurface) are found on the leg (elongated part) adjacent to hairpins necks. The structure in Fig. 11a observed with one leg larger than the other. In the evolution process from Fig.  11a–d, the ejection pushes the head of the structure upwards, and the sweep surface elongates making the left leg of hairpin adjacent to the right leg. The hairpin increases in size and legs remarkably develop from Fig.  11a–d. The lifted head which is oriented away from the wall in Fig.  11e experiences a higher velocity as compared to lower-lying parts. This higher velocity convects the head faster along downstream which results in increased lift of head and weakening of hairpin neck. In the later phase of the evolution process from Fig. 11e–h, the lift up of the head along with the weakening of the neck is shown. It is also observed that the neck breaks in Fig.  11f and the two legs try to connect with each other. The evolution of the hairpin-like structures for minimal turbulence is reminiscent to former studies [25, 26] of wall-bounded transition flow. The hairpin-like structures visualized for the first time in a square duct have been illustrated during the later phase of evolution. Figure 11e–h shows that the head (or arc) of the hairpin are slightly oriented due to the presence of nonzero span-wise velocity. Hairpin-shaped structures add the mechanism to transport vortices, low-momentum fluid and turbulent production from the wall toward the center of the duct. It is interesting to note that the minimal turbulent flow has these transport mechanism in their flow dynamics, with obvious less occurrence frequency of hairpin as compared to fully turbulence. Therefore, for minimal turbulence, the hairpin structures visualized as outer layer phenomena in Fig. 10a and the morphological evolution in Fig. 11 gives the reliable indication of transitional flow coherent structures.

Fig. 11

Evolution of hairpin-like structures, a–h at minimal ($\hbox {Re}_\tau$ = 100) turbulent flow colored with stretching (red) and compression (blue) at increasing time instant from t+$\delta \hbox {t}^+$ to t+8$\delta \hbox {t}^+$, with an time interval between frames $\delta \hbox {t}^+ \approx$ 10 (the isosurface of the swirling strength are 25$\%$ of its maximum value)

4.6 Streaks eduction

The turbulence activity in the square duct is investigated through streaks eduction procedure [11] which calculates the strength of low-velocity streaks. Low- and high-speed streaks are shown in Fig. 12 as contours of instantaneous fluctuating velocity in the XY-plane; the XY-plane is shown at a wall-normal location where maximum turbulent intensities are present (see Fig. 5a). These streaks are long and stream-wise oriented. The negative velocity fluid is presented as the low-speed streak, and the fluid is lifted away from the wall. The high-speed streak (positive velocity fluid) is pushed toward the wall. The apparent strength of low-speed streaks results in the downstream breaking of structures. Low-speed streaks play a crucial role in the buffer layer at low Reynolds number. The characteristics of low-speed streaks (shown in Fig.  12) are illustrated using Schoppa and Hussain [11] streak eduction procedure. The strength of low-speed streaks $\mid {\omega ^{+}_y}\mid _{max}$ is a vital behavior to represent the turbulent generation. Histograms of low-speed streak strength are shown in Fig.  13. The streak strength peak value is 4.5 for fully turbulent flow. Whereas, the peak value are 3.5 and 2.1 for $\hbox {Re}_\tau$ = 160 and 100, respectively. Evidently, with a decrease in Reynolds number, the average value of streak strength peak decreases on account of the reduction of unstable low-speed streaks, which is believed to be the main reason for the decrease of turbulent activity. In contrast, weakening of streak strength $\mid {\omega ^{+}_y}\mid _{max}$ means that the reproduction of the longitudinal vortices reduces which results in the decline of turbulent activity. Therefore, the occurrence of streak strength indicates that the turbulent activity is 44.4$\%$ for minimal and 77.7$\%$ for marginal turbulence as compared to the fully turbulent flow.

Fig. 12

Contour plots of stream-wise velocity fluctuations on horizontal plane close to wall, a $\hbox {Re}_\tau =100$, b $\hbox {Re}_\tau =160$, c $\hbox {Re}_\tau =300$

Fig. 13

Histograms of low-speed streak strength, a $\hbox {Re}_\tau =100$, b $\hbox {Re}_\tau =160$, c $\hbox {Re}_\tau =300$

4.7 Turbulent kinetic energy spectra

We explain the salient differences in flow characteristics of the three regimes either with turbulence intensities or organized motion. To adduce the differences in flow characteristics further, we turn to turbulent kinetic energy spectra. The turbulent kinetic energy spectra (E) is Kolmogorov’s phenomenological theory which gives a thorough description of the statistical structure of turbulent flow. Accordingly, this theory describes the distribution of turbulent kinetic energy among turbulent structures of different wave number (k). The fluctuating velocity (u’, v’ and w’) obtained from DNS data are used to compute turbulent kinetic energy spectra. Using Fourier series, the velocity fluctuation in physical space (x, y and z) are transformed in wave number space (k), where k is three-dimensional wave number. The procedure used to study turbulent kinetic energy spectra is discussed explicitly in previous studies [27]. Time-averaged spectrum of turbulent kinetic energy at different Reynolds numbers is shown in Fig.  14. At $\hbox {Re}_\tau = 300$, for low wave number, the energy spectrum exhibits $k^{-1}$ power law where most of the energy content is present. Subsequently at the end of $k^{-1}$ power law, the $k^{-5/3}$ power law (Kolmogorov law) has been noticed. The inertial range, where the energy spectrum E(k) length scale varies as $k^{-5/3}$, represents the flow is fully turbulent for that length scale. The $k^{-5/3}$ variation of E(k) is observed at $\hbox {Re}_\tau = 160$ and is less prominent as compared to $\hbox {Re}_\tau$ = 300. The variation of E(k) remains same for high wave number (small scale) at $\hbox {Re}_\tau = 160$ and 300. The minimal turbulent flow ($\hbox {Re}_\tau = 100$) does not show either of $k^{-1}$ or $k^{-5/3}$ variations. Interestingly, $k^{-2}$ variation of E(k) is observed for the minimal turbulent flow. According to Dou and Khoo [28], the energy spectrum for turbulent transition in pipe and channel flows varies as $k^{-2}$. The intermittency of flow at the lowest Reynolds number causes the steeper $k^{-2}$ variation of energy spectrum as compared to the fully turbulent $k^{-5/3}$ distribution. The conventional turbulent flow spectra are indistinguishable when compared to turbulent flow spectra at moderate Reynolds number. The turbulent flow spectra show distinguishable features when compared with turbulent flow at lowest Reynolds number. This comparison is consistent with the experimental study of the energy spectra of transition pipe flow [29]. Therefore, the $k^{-2}$ variation of energy spectrum at minimal turbulence indicates transition flow which is reminiscent to Cerbus et al. [29] and Dou and Khoo [28] pipe flow studies.

Fig. 14

Energy spectra for minimal, marginal and fully turbulent flow

5 Conclusions

A DNS study for characterizing minimal ($\hbox {Re}_\tau$ = 100) and marginal ($\hbox {Re}_\tau$ = 160) turbulent flow with detail study of turbulence structures and statistics is carried out. Connection with recent knowledge of fully turbulent flow ($\hbox {Re}_\tau$ = 300) for a square duct has been made through a systematic comparison of turbulent flow at $\hbox {Re}_\tau$ = 100, 160 and 300. Classical transitional turbulent flow characteristics like hairpin vortices and k$^{-2}$ variation of energy spectrum are shown to exist at $\hbox {Re}_\tau$ = 100. Detection of bursting events (through quadrant analysis & VITA technique) shows bursting to be present at $\hbox {Re}_\tau$ = 100 establishing the correlation between the hairpins and bursting events in the transitional instantaneous flow field. Evolution involving stretching and compression to a breakup of the hairpin is shown for the first time at $\hbox {Re}_\tau$ = 100. The patterns of instantaneous vorticity contours in the cross-plane at minimal turbulence reveal mushroom structure. The influence of structures observed on the turbulence statistics shows relevant differences in turbulence statistics of minimal turbulence when compared with marginal and fully turbulent flow. The intermittency of the flow at the minimal turbulence causes a steeper k$^{-2}$ variation of energy spectrum as compared to the fully turbulent k$^{-5/3}$ distribution.