Multi-fault Diagnosis of Roller Bearings Using Support Vector Machines with an Improved Decision Strategy

Abstract

This paper proposes an efficient fault diagnosis methodology based on an improved one-against-all multiclass support vector machine (OAA-MCSVM) for diagnosing faults inherent in rotating machinery. The methodology employs time and frequency domain techniques to extract features of diverse bearing defects. In addition, the proposed method introduces a new reliability measure (SVMReM) for individual SVMs in the multiclass framework. The SVMReM achieves optimum results irrespective of the test sample location by using a new decision strategy for the proposed OAA-MCSVM based method. Finally, each SVM is trained with optimized kernel parameters using a grid search technique to enhance the classification accuracy of the proposed method. Experimental results show that the proposed method is superior to conventional approaches, yielding an average classification accuracy of 97 % for five different rotational speed conditions, eight different fault types and two different crack sizes.

1 Introduction

Reliable fault diagnosis of rolling element bearings (REBs) is a challenging task, especially in industrial machinery. Bearing defects, if not detected in time, can eventually lead to machine failure and cause costly downtime. This has prompted research into vibration analysis [1, 2], motor current signature analysis, and oil debris analysis for fault diagnosis. Vibration analysis has been widely used because it provides essential information about diverse bearing failures [2, 3]. Recently though, the use of acoustic emissions [4] has found prominence in the detection and identification of bearing defects because of its ability to capture low-energy signals that are characteristic of low rotational speeds [4–6]. Specifically, Yoshioka et al. [6] showed that AE could be used to identify bearing defects even before they appear in the range of vibration acceleration, whereas vibration analysis can only to detect defects after they appear on the bearing’s surface [3– 7].

AE signal based fault diagnosis usually involves fault feature extraction from AE signals, feature selection and fault classification. Fault feature extraction maps the original signal to statistical parameters that reflect the diverse symptoms of bearing defects. The feature pool in this study includes 10 time-domain statistical parameters, 3 frequency-domain, and 9 complex envelope components. Once we extract features from the AE signal, our problem reduces to achieving better classification accuracy.

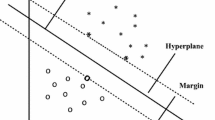
Several classification methods including support vector machines (SVM) [8, 9, 12], artificial neural networks (ANN) [4, 14], fuzzy sets theory, and expert systems have been used in bearing fault diagnosis [3, 5]. SVM is a robust classification tool [13–15] that classifies unknown data into multiple classes [9, 12] by decomposing an L-class into a number of two class problems and constructing a binary classifier for each. In this paper, an improved decision fusion based one-against-all (OAA) multi-class support vector machine is designed for improved fault diagnosis in roller bearings. OAA-MCSVM classifies an unknown feature vector based upon the binary classifier with the largest value for the classifier decision rule. This approach ignores the competence of individual classifiers and relies only on the value of the decision rule, therefore it does not always yield the best results [8–10, 14]. In Fig. 1, which shows the application of the one against all approach to a four class problem, the solid lines separate class 1 and 2 by a definite margin from the remaining classes whereas the dashed lines fail to achieve the same in case of class 3 and 4. Some regions (such as region 3) of the feature space are undecided, where a sample is accepted by more than one class or rejected by all. Individual SVMs are treated equally by the standard OAA-MCSVM method despite differences in their quality, thus compromising the overall classification accuracy. Therefore, it is advantageous to give due weight to each SVM classifier on the basis of classification competence and formulate a new decision strategy to achieve that. The contributions made in this paper are as follows:

Fig. 1.

OAA SVM. Solid lines show true boundary lines and dashed lines linear boundaries

• The OAA-MCSVM is modified to improve its classification performance, by introducing a reliability measure, SVMReM, for each SVM and formulating a new decision aggregation rule.

• The effectiveness of the proposed OAA-MCSVM is validated by accurately classify multiple bearing defects under different load conditions and at different rotational speeds.

The remaining parts of the paper is organized as follows. Section 2 explains the experimental setup. Section 3 provides analytical grounds to support our proposition under the framework of Dempster-Shafer (D-S) theory [12] and introduces a reliability measure (SVMReM) for individual SVMs that achieves optimal value irrespective of the test sample location in the feature space. Section 4 describes the proposed method with feature extraction and detailed derivation of reliability measures. Section 5 presents the experimental results, and Sect. 6 concludes this paper.

2 Experimental Setup and Data Acquisition Details

The experimental test rig used for this study is shown in Fig. 2. The AE fault signal is acquired using a general purpose, wideband AE sensor (WS α from Physical Acoustics Corporation) [3–6, 8], placed on top of the bearing housing as shown in Fig. 2. AE sensors are designed to capture high frequency acoustic emissions emanating from periodic impact events involving bearing faults.

Fig. 2.

A self-designed test rig for obtaining AE signals of bearing defects

In this study, one normal and seven different AE fault signals are obtained; (i) (DFN) the normal condition, (ii) (BCO) bearing with outer race crack, (iii) (BCR) bearing with roller crack; (iv) (BCI) bearing with inner race crack, (v) (BCIO) bearing with cracks on inner and outer raceways, (vi) bearing with inner and roller cracks (BCIR), (vii) (BCOR) bearing with roller and outer cracks, and (viii) (BCIOR) bearing with inner, outer, and roller cracks.

3 Reliable One-Against-All (OAA) Multiclass Support Vector Machine (SVM)

The OAA-MCSVM method for an L-class problem creates L binary SVM classifiers to separate each class from the remaining L-1 classes. If we consider a classification problem with P training samples $\left\{ {x_{1} ,y_{1} } \right\}, \ldots , \left\{ {x_{p} ,y_{p} } \right\}$, where $x_{j} \in R^{Dim}$ is a Dim-dimensional feature vector of the jth training sample and $y_{j} \in \left\{ {1,2,3, \ldots ,L} \right\}$ is the class to which it belongs. The jth SVM solves the optimization problem given in Eq. (1) [11–14], which provides the jth decision value function.

$$ {\text{Min L}}\left( {{\text{w, }}\mathop \delta \nolimits_{\text{j}}^{\text{k}} \, } \right) \, = \, \frac{ 1}{ 2}\left\| w \right\|^{2} +\,c\sum\limits_{j = 1}^{p} {\mathop \delta \nolimits_{\text{j}}^{\text{k}} } ,subjected,\mathop {\text{y}}\nolimits_{j}^{'} \left( {\mathop w\nolimits_{j} \cdot \phi \left( {\mathop x\nolimits_{j} } \right) + \mathop b\nolimits_{j} } \right) \ge 1 - \mathop \delta \nolimits_{\text{j}}^{\text{k}} ,\mathop \delta \nolimits_{\text{j}}^{\text{k}} \ge 0 $$

(1)

Where $y_{j}^{'} = 1~if~y_{j} = L, otherwise~y_{j}^{'} = - 1$. In the classification stage, a test sample x is classified to be in class k such that the decision function $Z_{k}$ has the highest value as given in Eq. (2).

$$ Z_{k} \left( {\text{x}} \right) = \left( {w_{k} \cdot \varphi \left( {x_{k} } \right) + b_{k} } \right), where, \mathop{k= \;}\nolimits_{k = 1, \ldots ,L}^{{argmax}} Z_{k} \left(x \right) $$

(2)

3.1 Improving the Standard OAA-MCSVM Using Dempster-Shafer Belief Theory

The proposed approach improves the standard OAA MCSVM using Dempster-Shafer (D-S) evidence theory [12, 16]. Consider a test sample x, a set of L OAA multiclass classifiers SVMk each with a decision function Zk and a set of hypotheses $\Omega = \left\{ {L_{K} } \right\}$ for 1 ≤ k ≥ L, where the kth hypothesis asserts that the sample belongs to class k. When each SVMk is applied to x, the result is a part of evidence supporting a certain proposition [8, 10, 15]. We define a basic belief assignment function (BBA) referred to as belief mass mk on hypothesis Ω [10]. It is actually based on the result of the kth classification. When sign (Zk) = 1, it is logical to enhance belief in SVMk proportional to the value of Zk, because “x fits into class k”. This piece of evidence alone does not guarantee the truth of hypothesis Lk, only part of it is committed to the belief in hypothesis Lk. The remaining part of the evidence provided by the value of Zk is assigned to the belief in hypothesis Ω as a whole which asserts that “x does not belong to class k”. The basic belief assignment (BBA) function mk is defined for an SVM with a positive response.

$$ \mathop m\nolimits_{k} \left( {\{ x\} } \right) = \left\{ {\begin{array}{*{20}l} {1 - \exp ( - \left| {\mathop Z\nolimits_{k} \left. {\left( x \right)} \right|} \right. = \mathop \lambda \nolimits_{k} ,if,x = \left\{ {\mathop L\nolimits_{k} } \right\}} \hfill \\ {\exp ( - \left| {\mathop Z\nolimits_{k} \left. {\left( x \right)} \right|} \right. = 1 - \mathop \lambda \nolimits_{k} ,if,x = \varOmega } \hfill \\ {0,else} \hfill \\ \end{array} } \right. $$

(3)

When sign (Z_k ) = −1, SVM _k classifies x as not belonging to class k. Then, the belief mass function m _k , for such SVMs with negative responses, is defined by (4).

$$ \mathop m\nolimits_{k} \left( {\{ x\} } \right) = \left\{ {\begin{array}{*{20}l} {1 - \exp ( - \left| {\mathop Z\nolimits_{k} \left. {\left( x \right)} \right|} \right. = \mathop \lambda \nolimits_{k} ,if,x = \left\{ {\overline{{\mathop L\nolimits_{k} }} } \right\}} \hfill \\ {\exp ( - \left| {\mathop Z\nolimits_{k} \left. {\left( x \right)} \right|} \right. = 1 - \mathop \lambda \nolimits_{k} ,if,x = \varOmega } \hfill \\ {0,else} \hfill \\ \end{array} } \right. $$

(4)

After finding the BBA values for all the samples and using D-S rule of combination to obtain the combined BBA, the belief function can be computed using Eq. (5) and finally a test sample x is labeled as class k* with the highest belief.

$$ \mathop k\nolimits^{*} = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {k = 1,. \ldots ,L} \\ \end{array} Bel\left( {\left\{ {\mathop L\nolimits_{k} } \right\}} \right) = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {k = 1,. \ldots ,L} \\ \end{array} \mathop \lambda \nolimits_{k} = \begin{array}{*{20}c} {\arg \hbox{min} } \\ {k = 1,. \ldots ,L} \\ \end{array} \mathop z\nolimits_{k} \left( x \right) = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {k = 1,. \ldots ,L} \\ \end{array} \left| {\mathop z\nolimits_{k} \left( x \right)} \right|, $$

(5)

Similar to Eq. (5), if at least one or more SVM_k generates a positive response, the belief function can be defined by Eq. (6)

$$ \mathop k\nolimits^{*} = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {k = 1,. \ldots ,L} \\ \end{array} Bel\left( {\left\{ {\mathop L\nolimits_{k} } \right\}} \right) = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {\mathop z\nolimits_{k} \left( x \right) \ge 0} \\ \end{array} \mathop \lambda \nolimits_{k} = \begin{array}{*{20}c} {\arg \hbox{min} } \\ {k = \mathop z\nolimits_{k} \left( x \right) \ge 0} \\ \end{array} \mathop z\nolimits_{k} \left( x \right) = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {k = 1,. \ldots ,L} \\ \end{array} \left| {\mathop z\nolimits_{k} \left( x \right)} \right| $$

(6)

However, it is not prudent to place the entire belief in decisions made by the SVMk’s. When the independent sources of evidence cannot be fully believed, the BBA should be weakened by a certain factor [16]. Thus an appropriate degree to quantify the amount of belief in every SVMk is proposed and defined in the following section.

4 Methodology

The proposed diagnosis method as shown in Fig. 3, includes feature calculation, reliability calculation of each SVMk, and a new decision strategy for the proposed OAA MCSVMs which are then used for fault classification.

Fig. 3.

The proposed fault diagnosis model

4.1 Feature Calculation

The feature pool is produced based on 10 time domain statistical features, 3 frequency domain features, and 9 envelope spectrum RMS features. Such a rich feature pool minimizes the risk of missing important aspects of the data, and it can achieve greater discrimination among various fault conditions. The time and frequency domain parameters are enumerated in the Table 1, where ‘x’ is the original time-domain signal with N data samples and “f” is a spectral component of the signal ‘x’. We divide 10 s AE signals into different samples of one time period length each. In every revolution, bearing faults give rise to impact signals depending upon their defect frequencies. Three types of defects are detected on a bearing depending on their location on the bearing surface. Bearing defect frequency could be measured on the basis of bearing parameters and rotational speed and frequency, for respective defect.

Table 1. Multi-domain feature extraction from AE signals

Figure 4 shows the typical signals produced by confined faults in rolling bearing, corresponding envelope signals are calculated using amplitude demodulation [2, 8].

Fig. 4.

Complex envelope analysis based on a unique feature extraction method

The defect region for the extraction of features can be determined using Gaussian window method [10, 14], however, it completely ignores the effects of sidebands during defect region calculation [10]. An enveloping spectrum is sensitive to very low impact related events such as sidebands. Thus, we construct a rectangular window around the defect frequency, to overcome problems with Gaussian windows and extract root mean square (RMS) features from the envelope spectrum. A distribution of the extracted features is given in Fig. 5.

Fig. 5.

3D visualization results of the discriminative fault features: all feature samples of data set #1 (3 MM_300 RPM) for 8 fault conditions (left) and training sample (right)

4.2 Reliability Calculation for Individual SVMs

The effectiveness of a classifier can be calculated using the generalization error R rate, restated as R = E[y = sign (Z(x))], where $y \in \left\{ { - 1,1} \right\}$ is the label of true class x and Z is the decision function. A classifier can be measured as more reliable if it provides a smaller value for R [10, 15, 16]. As investigated in [14], when the amount of training sets is relatively small comparing with the dimension of the feature space x, then the small value of Remp will not always ensure a small value regularization error R [11]. In this case, the upper bound of R is defined in [10, 11], and one benefit of SVM is to minimize this objective function value, also minimizes this upper bound of function. In other words, the smaller values of the objective function means smaller regularization errors, and thus it ensures a reliable classifier. So, we restate the objective function for the reliability calculation based on the SVM upper bound optimization equation in (7).

$$ ObjFunc = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\left\| {{\text{w}}\left\| {^{2} + C} \right.\sum\limits_{k = 1}^{n} {\left( {1 - \mathop y\nolimits_{k} z\left( {\mathop x\nolimits_{k} } \right)} \right)_{ + } } } \right. $$

(7)

To calculate the ObjFunc, we introduce the unconstrained optimization [9, 10] problem over ‘w’ in the training stage. Our problem is quadratic; to get a globally optimum solution for ‘w’, we utilize QP [9]. The objective function would ensure a minimum value of R with the widest margin for all samples in the training stage.

$$ \left[ {\mathop \delta \nolimits_{{SVM\text{Re} M = \exp \left( {{\raise0.7ex\hbox{${ - ObjcFunc}$} \!\mathord{\left/ {\vphantom {{ - ObjcFunc} \theta }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\theta $}}} \right) = \exp \left( { - \frac{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\left\| w \right\|^{2} + C\sum\limits_{k = 1}^{P} {\left( {1 - \mathop y\nolimits_{k} z\left( {\mathop x\nolimits_{k} } \right)} \right)_{ + } } }}{2CP}} \right)}} } \right] $$

(8)

In order to get the reliability measure for each class, and kernel function in Eq. (8), which yields an optimum value for all samples in the feature space. Furthermore, the margin of the classifier is $\frac{2}{\left\| w \right\|}$, a smaller value of $\left\| w \right\|$ ensures a larger margin, and thus more accurate generalization. The value θ = CP is used as a regulation factor to compensate the consequence of C, penalty parameter, P, number of training samples.

4.3 Derivation of Proposed Decision Strategy for Reliable OAA-MCSVM

With the reliability measure δ _SVMReM in place, we design a new decision function for our proposed one-against-all multiclass SVM (OAA-MCSVM. First, Zk values of the binary SVMs are calculated for all the given test samples using Eq. (2). Then, a decision fusion is done for all samples. After that, the L class BBA mk is generated based on Eqs. (5) and (6) for all the decisions, where all decisions are considered as information from an independent source. The evidence value that is produced by each classifier SVMk is granted more belief if SVMk is also more reliable, and our calculated competence measures are directly used as a belief factor in Eqs. (9) and (10). The final decision rules as follows:

• 1. If all the SVM_k produce negative responses,

  $$ \mathop k\nolimits^{*} = \begin{array}{*{20}c} {\arg \hbox{min} } \\ {k = 1, \ldots L} \\ \end{array} \mathop \delta \nolimits_{{SVM{\text{Re}} M\left( k \right)}} \left( {1 - \mathop {\exp }\nolimits^{{ - \left| {\mathop Z\nolimits_{k} \left( x \right)} \right|}} } \right) $$

  (9)

• 2. If one or more SVM_k produce positive responses,

  $$ \mathop k\nolimits^{*} = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {\mathop Z\nolimits_{k} \left( x \right) \ge 0} \\ \end{array} \mathop \delta \nolimits_{{SVM{\text{Re}} M\left( k \right)}} \left( {1 - \mathop {\exp }\nolimits^{{ - \left| {\mathop Z\nolimits_{k} \left( x \right)} \right|}} } \right) $$

  (10)

  δ _{SVM Re M (k)} is the reliability measure for SVM_k, and Eqs. (9) and (10) can be merged into one based on Eq. (11).

  $$ \mathop k\nolimits^{*} = \begin{array}{*{20}c} {\arg \hbox{max} } \\ {1, \ldots L} \\ \end{array} \left[ {\mathop \delta \nolimits_{{SVM{\text{Re}} M\left( k \right)}} \left\{ {sign\left( {\mathop Z\nolimits_{k} \left( x \right)} \right)\left( {1 - \mathop {\exp }\nolimits^{{ - \left| {\mathop Z\nolimits_{k} \left( x \right)} \right|}} } \right)} \right\}} \right] $$

  (11)

  The value of sign codes the hard decision rule whether “x belongs to class k or not” and the magnitude defines the strength of the decision function value.

4.4 Fault Classification

A SVM discriminates test samples into one of two categories, and subsequently we need multi-class SVMs (MCSVMs) to identify multiple bearing defects. In the OAA multiclass support vector machine approach, each SVM separates one category from the rests, and the final decision is by choosing an SVM that produces the maximum decision value for a given sample. We compare our proposed OAA-MCSVM using a new decision rule with the standard OAA-MCSVM.

5 Experimental Validation

The proposed method is tested on multi-class fault data sets obtained from the experimental setup. The proposed method delivers superior classification performance over its standard counterpart.

5.1 Configuration of the Training and Test Data

The proposed method is evaluated over ten data sets with 90 feature vectors each. Data set for each fault condition, is randomly divided into two subsets for training and testing. The training subset includes 40 randomly-selected feature vectors whereas the remaining 50 feature vectors makeup the testing subset. In the training phase of every SVM, the precision is assessed by several kernel parameters [16] (C = 2⁻⁵, 2⁻³, 2⁻¹, . . . , 2¹⁵), and (γ = 2⁻¹⁵, 2⁻¹³, . . . , 2³) and the best one is chosen using a grid search method [16] for performance comparison. Consequently, classification accuracy is computed for the standard OAA-MCSVMs and the proposed (reliable) OAA-MCSVMs on the testing datasets; the final classification performance is the average value of the accuracies achieved for each feature vector in the testing dataset.

5.2 Performance Evaluation

To ensure the effectiveness of this proposed OAA-MCSVM method, this experimental analysis compares its classification performance with the standard variant. We use confusion matrix [16] and AUC-ROC based performance analysis for the comparison.

Experiment # 1.

This analysis was carried out on ten datasets at 5 rotational speeds (300, 350, 400, 450, 500 RPM), two crack sizes (3 mm and 6 mm) and eight different fault conditions. The support vector machines use the Gaussian radial basis kernel. The results show that our proposed OAA-MCSVM is superior to the standard OAA-MCSVM. The classification accuracy for different data sets is given in Table 2. In addition, the results also validate our unique feature extraction process, which yields classification accuracy of almost 100 % at higher RPMs and larger crack sizes, because of good separation between fault features. In Fig. 6, we compare the overall performance of Standard OAA MCSVMs and Proposed OAA MCSVMs over ten data sets (in %) using three different kennel functions.

Table 2. Classification performance comparison between standard OAA MCSVMs and the proposed OAA MCSVM for eight fault conditions using radial basis kernel machine (Unit: %)

Fig. 6.

Relative comparison of the accuracy of proposed and standard methods over three different kennel machines.

Experiment # 2.

We perform the AUC-ROC based analysis of the proposed and standard approaches for all the datasets to verify the robustness of our proposed algorithm. AUC-ROC graph is actually a way of visualization, organization and selection classifiers based on their performance. An area under the receiver operating characteristics (AUC-ROC) analysis has been extended for use behavior analyzing of fault diagnostic systems [14]. In addition, AUC-ROC curves for the proposed method show that it delivers a more uniform performance in the diagnosis of all fault conditions as compared to the standard approach, as shown in Fig. 7.

Fig. 7.

AUC-ROC characteristic curve of performance comparison between the standard and proposed OAA MCSVM approach.

6 Conclusion

A reliable fault diagnosis methodology for rotating machinery was proposed and evaluated, based upon a modified form of one-against-all multi-class support vector machines, which utilizes individual reliability measures, SVMReM, of the binary SVMs and an improved decision strategy based on the Dempster-Shafer (D-S) theory of evidence. In addition to time and frequency domain analysis techniques, the acquired data from the experiments was preprocessed using envelope analysis methods to extract meaningful features from the fault signals. The experimental analysis demonstrated that the proposed approach yields better classification performance for different fault conditions, at different rotational speeds and different kernel functions for the SVMs. The proposed method yielded an average accuracy exceeding 99 %, 98 %, and 95 % for ten data sets with SVM trained using RBF kernel, polynomial kernel, and linear kernel, respectively.