Introduction

Rolling bearings are crucial machine elements present in a wide field of rotating machine applications. Bearing failures is one of the main causes of breakdowns in such machinery. There have been huge production losses and human casualties due to unexpected bearing failures. The early detection of bearing defects, therefore, is crucial to prevent the system from malfunctions that could cause damages and halt of the entire system. Hence, the fault detection and its taxonomy in rolling bearings is very important [4].

Vibration analysis is one of the most effective methods for the bearing fault diagnosis. Many vibration approaches for the fault diagnosis of rolling bearings have been developed in time, frequency, time-frequency domains with the help of artificial intelligence (AI) methods. In time domain, various statistical parameters, such as the peak, mean, root-mean-square, crest factor, standard deviation, variance, kurtosis, and skewness have been used. In frequency domain, various statistical parameters such as average, center, root-mean-square, and standard deviation of frequency spectrum have been utilized that are obtained from the fast Fourier transform (FFT). Frequency-time domain methods include the short time Fourier transform (STFT), the Wigner–Ville distribution, and the wavelet packet transform [12, 14, 15, 17].

For the automated bearing fault diagnosis, AI methods such as artificial neural network (ANN), immune genetic algorithm (GA), and fuzzy logic have been applied extensively [8, 19]. These methods are based on the empirical risk minimization (ERM) principle, and there are some common shortcomings, such as relapsing into local minimum easily and slow convergence velocity and over-fitting. Especially, the generalization ability is very low for a limited number of samples. In comparison with these methods, the support vector machine (SVM) can perform significantly well even for a limited number of samples [11].

The SVM has been introduced into rolling bearing fault diagnosis due the fact that it is difficult to obtain enough fault samples in practice and the excellent fault prediction performance of it. Meng et al. [13] introduced the comparison between the RBF neural network and the SVM for cases where only limited training samples were available for the fault diagnosis. The result showed that the SVM had better performance than the RBF neural network both in the training time and the prediction accuracy. The binary-class and multiclass classifier performances of the SVM were discussed, and the diagnosis precision was less dependent on the kernel function and its parameter. Rojas and Nandi [16] proposed the development of SVM for the detection and classification of rolling bearing faults. The training of SVM was done using sequential minimal optimization algorithm, and a mechanism for selecting adequate training parameter was also proposed. Li et al. [11] proposed rolling element bearing fault detection using the SVM with an improved ant colony optimization (IACO). It was used to select a suitable parameter for the SVM. They compared it with the cross-validation and GA methods. Experimental results indicated that the IACO was feasible to optimize parameters for the SVM, and the improved algorithm was effective with the high classification accuracy and in less time.

Sui and Zhang [22] illustrated rolling element bearings fault classification based on the feature evaluation with the SVM. The feature evaluation based on the class separability criterion was discussed in this work. Jack and Nandi [9] illustrated the fault detection of roller bearings using the SVM and the ANN. They defined and estimated statistical features based on moments and cumulants, and selected the optimal features using the GA. In the classification process, they employed the SVM using the RBF kernel with a constant kernel parameter. Zheng and Zhou [26] illustrated the rolling element bearing fault diagnosis based on the SVM. In this paper, firstly, the wavelet packet analysis was utilized to extract the features from the vibration signal and the principal component analysis was performed for features reduction. Secondly, the multiclass SVM as a classifier was employed to diagnose bearing faults. A grid search method in combination with 10-fold cross-validation was applied to find optimal parameters for the multiclass SVM model.

Sugumaran and Ramachandran [21] illustrated the effect of a number of features on the classification of roller bearing faults using the SVM and the proximal support vector machine (PSVM). A set of statistical features and histogram features were extracted from time domain signals and the order of importance was found using a decision tree. It showed the classification efficiency of features, and histogram features were found to be better as compared to statistical features. And the PSVM with the histogram performed marginal better than the SVM. Yang et al. [25] illustrated a fault diagnosis approach for roller bearing based on the intrinsic mode function (IMF) envelope spectrum and the SVM. Liu et al. [10] illustrated the multi-fault classification based on the wavelet SVM (WSVM) with the particle swarm optimization (PSO) algorithm to analyze vibration signals from rolling element bearings. And they showed that the WSVM can achieve a greater accuracy than the SVM. Zhu and Song [27] illustrated the roller bearing fault diagnosis method based on the hierarchical entropy and the SVM with the PSO algorithm.

In this paper, firstly the selection of optimum parameters such as the RBF kernel parameter (Gamma), the optimum number of datasets, and the optimum percentage of data for the training and the testing have been obtained. After selecting the optimum parameter, i.e., which is very effective for fault classification, it is further used for the multiclass classification of rolling element fault at the same speed, the interpolated speed, and the extrapolated speed as that of measurement based on time domain features by the SVM algorithm using the RBF kernel. Conclusions are drawn from the fault prediction accuracies so obtained.

Support Vector Machine Algorithm

The original SVM algorithm was developed by Vapnik in [24]. The SVM is a machine learning algorithm that analyzes data and recognizes patterns. Initially, it was used for the classification problem but recently they have been extended to the domain of regression analyses [2, 5, 7]. The basic SVM deals with the binary classification. The SVM constructs a hyperplane or a set of hyperplanes in a high or infinite dimensional space, which could be used for the classification and the regression analysis. A good separation is achieved by a hyperplane that has a largest distance to the nearest training datasets of any class. Noticeably, the larger the margin, lower the generalization error of the classifier. Now a set of training data are given to the SVM each marked as belonging to one of two classes, an SVM training algorithm builds a model that predicts whether new data falls into one class or the other.

The SVM is a relatively new machine learning technique based on the structural risk minimization (SRM) principle, which is used to solve classification problems by maximizing the margin between two different classes. It can solve the problem of over-fitting, nonlinear, model selection, the curse of dimensionality, and the local minimum in a significant way [23]. It embodies the SRM principle that has achieved higher generalization performance with a small number of samples and is shown superior to the ERM that neural networks use [4, 24]. The SRM minimizes an upper bound on the expected risk, as opposed to ERM that minimizes the error on the training data. This is the reason SVM has greater ability to generalize, which is the aim in statistical learning [13, 17, 18, 20]. The introduction of kernel function is a major advantage of the SVM. It endows with the SVM the ability to deal with nonlinear classification problems by mapping the nonlinear feature space to a high dimensional feature space to solve finally the linear problem. The training of SVM is a convex optimization problem and can always be used to find a global minimum [4].

For finding out the optimal margin classifier, the following optimization problem is defined [1]. The minimization of

$$\tau \left( {\text{w}} \right) = \frac{1}{2}||w||^{2}$$
(1)

subject to

$$y^{\left( i \right)} \left( {w^{\text{T}} x^{\left( i \right)} + b} \right) \ge 1;\quad i = 1,\,2, \ldots ,\,m;\quad w^{\text{T}} \in \,R^{N} ;\quad b \in R,$$
(2)

where the vector w T (a normal vector to the hyperplane) defines the boundary, x is the input vector of dimension, N and b are scalar thresholds. The constraint could be written as

$$g_{i} \left( w \right) = - y^{\left( i \right)} \left( {w^{\text{T}} x^{\left( i \right)} + b} \right) + 1 \le 0.$$
(3)

This optimization problem is a convex quadratic objective function problem with only linear constraints. In Fig. 1, three dark points lie on the dashed lines parallel to the decision boundary (or the hyperplane). These typical three points are called support vectors. When the Lagrangian is constructed for the optimization problem then the following expression is obtained

$$L\left( {w,\,b,\,\alpha} \right) = \frac{1}{2}||w||^{2} - \sum\limits_{i = 1}^{m} {\alpha_{i} \left[ {y^{\left( i \right)} \left( {w^{T} x^{\left( i \right)} + b} \right) - 1} \right]}.$$
(4)

Now the dual optimization problem is defined as

$$\max_{\alpha} W\left( \alpha \right) = \sum\limits_{i = 1}^{m} {\alpha_{i} } - \frac{1}{2}\sum\limits_{{i,{\kern 1pt} j = 1}}^{m} {y^{\left( i \right)} y^{\left( j \right)} \alpha_{i} \alpha_{j} \left\langle {x^{\left( i \right)} x^{\left( j \right)} } \right\rangle }$$
(5)

subject to

$$\alpha_{i} \ge 0,\quad i = 1, \ldots ,m$$
(6)

and

$$\sum\limits_{i = 1}^{m} {\alpha_{i} y^{\left( i \right)} = 0}.$$
(7)
Fig. 1
figure 1

Data classification by SVM

Full size image

For solving the nonlinear case, SVMs map the N-dimensional input vector into a higher or Q-dimensional feature space, by choosing a nonlinear mapping function ϕ(x), the SVM can construct an optimal hyperplane in new feature space. k(x, x i ) is an inner product kernel performing the nonlinear mapping into feature space and is expressed as

$$k\left( {x,\,x_{i} } \right) = k\left( {x_{i} ,x} \right) = \phi \left( x \right)\phi \left( {x_{i} } \right).$$
(8)

The radial basis function is a Gaussian kernel and is expressed as

$$k\left( {x,\,x_{i} } \right) = \exp \left( { - \gamma ||x - x_{i} ||^{2} } \right);\quad \gamma = \frac{1}{{2\sigma^{2} }} > 0,$$
(9)

where σ denotes the width of RBF kernel. After solving the optimization problem, the SVM classifier is as follows:

$$f\left( x \right) = {\text{sign}}\left\{ {\sum\limits_{i = 1}^{m} {y_{i} \alpha_{i} k\left( {x_{i} ,\,x} \right) + b} } \right\}.$$
(10)

The SVM classifiers described above are binary classifiers, and by combining it, it is possible to handle multiclass case. The multiclass SVM classifiers are described below.

Multiclass SVM Classifiers

In the binary classification only two class labels are present, i.e., +1 and −1. But in the real world machinery situation more than two class labels are found, such as the misalignment, mechanical unbalances, shaft cracks, bearing faults, and gear faults. In the bearing fault also several faults appear like the inner race fault, outer race fault, ball element fault, and a combination of these entire faults. For solving the multiclass problem, methods like one-against-all (OAA), one-against-one (OAO), and direct-acyclic-graph (DAG) are addressed [6]. The earliest used implementation for the SVM multiclass classification is OAA methods. It constructs k SVM models, where k is the number of classes. In OAO methods, if k is the number of classes then k(k − 1)/2 classifiers are constructed and each one trains data from two classes. In this method, the training process is similar to the OAO strategy by solving k(k − 1)/2 binary SVM. However, in the testing process, it uses a rooted binary DAG, which has k(k − 1)/2 internal nodes and k leaves. Hsu and Lin [6] showed a comparison of different multiclass SVM methods and concluded that ‘one-against-one’ is a competitive method for the multiclass classification. Here LIBSVM [3] software has been used for multiclass classification bearing with OAO approach.

Now in the next section, experimental setup and data acquisition are described.

Experimental Setup

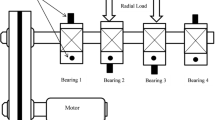
Experiments were performed on Machinery Fault Simulator (MFSTM), which was capable of simulating a range of machine faults such as in the gear box, rolling bearings, motors, shaft resonances, and shaft misalignments. The schematic diagram of MFS is shown in Fig. 2. In the MFS experimental setup, a three-phase induction motor was connected to the shaft through a flexible coupling with a healthy bearing near the motor end and a faulty (test) bearing at the other end of the shaft as shown in Fig. 3. This setup allowed the study of bearing defects by introducing faulty bearings in the machine and then studying its vibrational signature. In the study of faults in bearings, five different types of bearing fault condition were considered as shown in Fig. 4 (i) no defect bearing (ND), (ii) inner race fault bearing (IRF), (iii) outer race fault bearing (ORF), (iv) bearing element fault (BEF), and (v) combination fault bearing (CFB). Bearings were fully covered and shielded so close-view of faults could not be shown, separately.

Fig. 2
figure 2

A schematic line diagram of the MFS

Full size image
Fig. 3
figure 3

Machine fault simulator

Full size image
Fig. 4
figure 4

Rolling bearings with five individual fault conditions

Full size image

A tri-axial accelerometer (sensitivity: x-axis 100.3 mV/g, y-axis 100.7 mV/g, and z-axis 101.4 mV/g) was mounted on the top surface of the bearing housing, which could record accelerations in time domain in three orthogonal x, y, and z directions. Vibrations were monitored on a Brűel and Kjǽr FFT analyzer and vibration simulations were processed on the Pulse Lab Shop ver. 7.0.1.298. Datasets were taken for the rotational speed of 10–42.5 Hz in the interval of 2.5 Hz for each of five fault conditions. For each dataset, 320 cycles of data with 2000 samples each were taken. Total 2000 × 320 data points were collected in each of the three directions x, y, and z.

Statistical Feature Selection

In the present study, statistical moments like the standard deviation, the skewness, and the kurtosis are selected for the effective identification of the bearing fault. These statistical features are briefly explained below.

Standard Deviation (σ)

It is a measure of the energy content in the vibration signal. The standard deviation is the second standardized moment of the data and is expressed as

$$\sigma = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {x_{i} - \mu } \right)^{2} } }}{n - 1}},$$
(11)

where {x 1, x 2, …, x n } are the observed values of the sample items and μ is the mean value of these observations, while n stands for the size of the sample.

Skewness (χ)

It is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive or negative, or even undefined. It is the third standardized moment of the data and is expressed as

$$\chi = \frac{n}{{\left( {n - 1} \right)\left( {n - 2} \right)}}\sum\limits_{i = 1}^{n} {\left( {\frac{{x_{i} - \mu }}{\sigma }} \right)}^{3}.$$
(12)

Kurtosis (κ)

It is a measure of the peakedness of the probability distribution of a real-valued random variable. It is the fourth standardized moment of data and is expressed as

$$\kappa = \left\{ {\frac{{n\left( {n + 1} \right)}}{{\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)}}\sum\limits_{i = 1}^{n} {\left( {\frac{{x_{i} - \mu }}{\sigma }} \right)}^{4} } \right\} - \frac{{3\left( {n - 1} \right)^{2} }}{{\left( {n - 2} \right)\left( {n - 3} \right)}}.$$
(13)

These three statistical features were calculated from 2000 data points in a sample. Finally, 320 samples were collected in three orthogonal directions for above three features (i.e., total 9 combinations), which means 9 × 320 feature points were available for each faults. For five different faults (i.e., IRF, ORF, BEF, CFB, and ND) there were total 9 × 5 × 320 feature points available. These total feature points were divided and used for the training, testing of optimizing the parameters, and for the final testing in the simulation.

Results and Discussions

The vibration data were obtained from the machine fault simulator in time domain. After collecting the vibration data, three statistical parameters: the standard deviation, the skewness, and the kurtosis have been extracted in the x, y, and z directions using the MATLAB™. Figure 5 shows time domain features of acquired signals for the BEF at 10 Hz rotating speed. For the multiclass classification of bearing faults namely, ND, IRF, ORF, BEF, and CFB, the SVM software first needs to be trained with the data comprising these bearing faults, individually. The SVM software consists of various training functions based on different types of kernels. Here, we have used the Gaussian RBF kernel so for this kernel a parameter gamma (γ) is a very important input parameter to be chosen optimally.

Fig. 5
figure 5

Time domain features of acquired signals for BEF at 10 Hz rotating speed

Full size image

The flowchart shown in Fig. 6 summarizes the overall procedure of execution of the training and testing of the SVM algorithm. Now a study on the optimum selection of various SVM and kernel parameters would be performed.

Fig. 6
figure 6

Flow chart of multiclass fault diagnosis system

Full size image

Selection of the Optimum RBF Kernel Parameter

Firstly, we need to select the optimum RBF kernel parameter (γ) for the best prediction accuracy, so arbitrarily we choose rotational speed of 25 Hz, 260 feature datasets, and percentage of training and testing feature data as 80% and 20%, respectively. Later in this work, we will check the optimality of these two parameters also, i.e., the number of feature datasets, and the percentages of the training and testing feature data. Prediction capability performance results are summarized in Table 1 and are shown Fig. 7. The Gaussian RBF kernel parameter (gamma) value of 0.03 gives the highest prediction accuracy at the rotational speed 25 Hz as compared to the other values. For both very less and very higher values of gamma, it gives less prediction accuracy, so for further classification of bearing faults at the same speed, interpolated speed, and extrapolated speed also the value of gamma is chosen as 0.03.

Table 1 The optimum selection of the SVM (RBF kernel) parameter gamma
Full size table
Fig. 7
figure 7

The selection of the optimum gamma for best fault predictions

Full size image

Selection of the Optimum Percentage of Training and Testing Data

Here, we examine which set of the training and testing percentage is the best one for the prediction accuracy. We used the optimum gamma value of 0.03, rotational speed of 25 Hz, and 260 feature datasets. In Figs. 1, 8 represents the training dataset of 65% and the testing dataset of 35%, 2 represents the training dataset of 70% and the testing dataset of 30%, 3 represents the training dataset of 75% and the testing dataset of 25%, 4 represents the training dataset of 80% and the testing dataset of 20%, and 5 represents the training dataset of 85% and the testing dataset of 15%. Prediction performance results are summarized in Table 2 and shown in Fig. 8. It is evident that the training dataset of 80% and the testing dataset of 20%, and also the training dataset of 85% and the testing dataset of 15% give 100% fault prediction accuracy at the rotational speed 25 Hz, so for further classification of bearing fault at same speed, at interpolated speed, and at extrapolated speed, the training dataset of 80% and testing dataset of 20% have been used.

Fig. 8
figure 8

The selection of the optimum percentages of the training and testing data (1–65%, 35%; 2–70%, 30%; 3–75%, 25%; 4–80%, 20%; 5–85%, 15%)

Full size image
Table 2 The selection of optimum percentage of the training and testing data
Full size table

Selection of the Optimum Number of DataSets

Total 320 datasets were measured for all types of faulty bearing conditions from the MFS. Here the optimum number of datasets has been chosen for the fault prediction accuracy by giving optimum input gamma value of 0.03 as obtained in the above step and for 80% training data and 20% testing data, and also for 75% training data and 25% testing data at a rotational speed of 25 Hz. These prediction results are summarized in Table 3 and are shown in Figs. 9 and 10. The best prediction accuracy occurred for 260 datasets at the rotational speed of 25 Hz than any other number of datasets. Hence, for the further classification of bearing faults at the same speed, the interpolated speed and the extrapolated speed, 260 datasets have been used. The above selection of parameters is presented for a particular speed, however, similar trends are observed at other speeds also.

Table 3 The selection of optimum number of feature datasets
Full size table
Fig. 9
figure 9

The selection of the optimum number of feature datasets (for 80% and 20% of the training and testing feature data, respectively)

Full size image
Fig. 10
figure 10

The selection of the optimum number of feature datasets (for 75% and 25% of the training and testing feature data, respectively)

Full size image

Now fault prediction accuracies are obtained for the training and the testing at the same speed, interpolated speed, and extrapolated speed using the optimized parameters obtained above.

Training and Testing at the Same Rotational Speed

For obtaining the prediction accuracy, the training and testing of the SVM is done at the same rotational speed (individually), i.e., 10–40 Hz at the interval of 5 Hz. Table 4 and Fig. 11 show the fault prediction accuracy for the same speed case. It is observed that the percentage of fault prediction at 10 Hz rotational speed varies from 76.92% for BEF to 100% for ND and ORF, at 15 Hz rotational speed it varies from 65.38% for BEF to 98.08% for ND and ORF, at 20 Hz rotational speed it varies from 69.23% for CFB to 100% for ND, IRF, and ORF, at 25 Hz rotational speed it comes 100% for all, at 30 Hz rotational speed it comes 92.31% for CFB and 100% for all other faults and at 35, 40 Hz rotational speed it comes 100% for all faults.

Table 4 The percentage prediction accuracy for the same speed as measured data
Full size table
Fig. 11
figure 11

The fault prediction accuracy at same speed as measurements

Full size image

It is observed a near perfect prediction accuracy at a higher speed beyond 25 Hz since at the higher rotational speed the signal-to-noise ratio is better. This is due to better manifestation of faults at higher speeds. The prediction accuracy of BEF and CBF are lesser than other faults and the healthy bearing. For BEF, this is because it is not necessary that the BEF hit the outer race or inner race in every rotation because of spinning of rolling elements along with the rolling. And this may change the characteristics of vibration signature quite often. The prediction accuracy is very good for the ND and the ORF for higher speeds as well as lower speeds because the vibration signature that comes from no defect bearing is always good. Similarly, rolling elements are always going to hit ORF at every ball pass and it would provide better characteristics in the vibration signature and results in better prediction for the ORF. Similarly, for IRF beyond 10 Hz gives higher prediction accuracy.

Training Done at Two Different Speeds and Testing at an Intermediate Speed

For obtaining the fault prediction accuracy, the training of SVM is done at two different speeds and the testing is done at an intermediate speed for which training of SVM was not done, this is known as the frequency interpolation. Here, four different interpolation ranges are considered, i.e., 5, 10, 15, and 20 Hz which is shown in Table 5. In Table 6 and Fig. 12a–d, the fault prediction accuracy is obtained using the frequency interpolation for four different ranges. It is observed that for 5 Hz interpolated speed range, the percentage prediction accuracy varies from 23.08% to 100%, for 10 Hz it varies from 1.92% to 100%, and for 15 and 20 Hz it varies from 0% to 100%. For 5 Hz range the lowest prediction accuracy is 23.08% for the ND, for 10 Hz range the lowest prediction accuracy is 1.92% for the ND, for 15 and 20 Hz range the lowest prediction accuracy is 0% for the ND, IRF, and BEF.

Table 5 Interpolation speed ranges
Full size table
Table 6 The fault prediction accuracy for different interpolated speeds
Full size table
Fig. 12
figure 12

The fault prediction accuracy for different interpolated speeds (for 1, 2, …, in abscissa refer to Table 5)

Full size image

It is examined that the SVM capability of the fault classification decreases with increasing the range of interpolation. It results in very less prediction accuracy beyond 10 Hz interpolation speed range, so the fault prediction is not very useful for the interpolated speed range beyond 10 Hz.

Training Done at Two Different Speeds and Testing Done at an Extrapolated Speed

For obtaining the prediction accuracy, the training of SVM is done at two different speeds and the testing is done at an extrapolated speed for which training of SVM was not done, this is known as the frequency extrapolation. Here, four different extrapolation ranges are considered, i.e., 5, 10, 15, and 20 Hz, and are shown in Table 7. In Table 8 and Fig. 13e–h, the fault prediction accuracy is obtained using the frequency extrapolation for four different frequency ranges. For the extrapolation, the fault prediction accuracy varies from 0% to 100% for all speed ranges. The lowest prediction accuracy comes 0% for ND and IRF for 5 Hz as well as 10 Hz speed range. The lowest prediction accuracy comes 0% for all other faults except CFB for 15 Hz speed range. The lowest prediction accuracy comes 0% for ND, IRF, and ORF for 20 Hz speed range. It is observed that the SVM capability of fault classification decreases with increasing the range of extrapolation frequency. It results in very less prediction accuracy beyond 10 Hz extrapolation speed range and the fault prediction is not very useful for extrapolated speed beyond 10 Hz.

Table 7 Extrapolation speed ranges
Full size table
Table 8 The fault prediction accuracy for different extrapolated speeds
Full size table
Fig. 13
figure 13

The fault prediction accuracy for different extrapolated speeds (for 1, 2, …, in abscissa refer to Table 7)

Full size image

The prediction accuracy increases with the rotational speed, i.e., at a higher speed beyond 25 Hz the classification of faults are better at the same speed, the interpolated speed, and the extrapolated speed. The worst prediction accuracy 65.38% for the BEF at 15 Hz and 69.23% for the CFB at 20 Hz comes for the same speed case. The interpolation and extrapolation techniques for the multiclass classification of bearing fault are very useful when vibration data are not available for particular speeds but beyond the 10 Hz range interpolation as well as extrapolation techniques are not useful for fault predictions. By this exercise, it is concluded that nearly 100% classification of fault can be achieved by the same speed prediction case, somewhat good for the interpolated speed case and marginal for extrapolated speed case. It is observed that fault classifications by the interpolation technique are better than the extrapolation technique for the same range of speed and at a higher speed as well as lower speed of operation.

Conclusions

In this paper, the fault diagnosis of rolling bearings using the SVM is presented. First, we extracted features from the vibration signal in time domain and then applied one-versus-one technique for the multiclass fault classification of rolling bearings. The selection of optimum SVM parameters, such as gamma value (RBF kernel parameter), the percentage of training and testing data, and the number of datasets for further fault classification of bearing faults have been illustrated. Finally, the capability of SVM to classify bearing faults at the same rotational speed, at the interpolated speed, and at the extrapolated speed has been presented. In the present paper, it has been observed that the SVM prediction performance when the training and testing is done at a higher rotational speed a near perfect prediction accuracy is found. This is because at the higher rotational speed the noise does not affect so much due to better signal-to-noise ratio in the measurement data. And it shows that a better prediction accuracy for the same rotational speed as compared to the frequency interpolation and the frequency extrapolation. Also the SVM capability of fault classification decreases with increase in the range of interpolation and extrapolation frequencies. The interpolation and extrapolation techniques could be applied to measurement data in the frequency and time-frequency (wavelet) domains.