Micromechanical-Based Models for Describing Damage of Ferritic Steels

Abstract

Usually the safety margin against failure for precracked components is calculated with fracture mechanics approaches. Due to several severe limitations of these approaches, it was searched for alternative calculation models. Starting with McClintock and Berg in the sixties, so-called damage models have been developed for describing ductile fracture on the basis of micromechanical processes. The development of such kind of models is in progress now for nearly 50 years, but until today no model is generally accepted and incorporated into the international standards. In an extended introduction, the micromechanical phases of ductile rupture of metal and alloys are presented. Against this background, a summary of the evolution and the different kinds of micromechanical-based model approaches is given. The theoretical background, the advantages/ disadvantages and the limitations of the models are discussed critically. Finally non-local formulations of damage models are presented. Combinations of ductile damage models and models for cleavage to describe fracture in the brittle-ductile transition region are discussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

To guarantee safe operation of technical components and systems, the safety margins against failure must be quantified. One possible approach to predict these safety margins is the use of numerical simulation methods with advanced material models. For the prediction of crack initiation, crack growth and fracture of ductile metals so-called micromechanical-based damage models based on the early work of McClintock [169] and Berg [33] have been established. In this context micromechanical-based means that the models try to simulate the processes on the microscopic level with continuum mechanical approaches.

For the development and application of damage models it is fundamental to understand the micromechanical processes in the material leading to fracture. In ductile fracture, these micromechanical processes can be divided into three phases: void formation, void growth and void coalescence [74, 207, 261, 276]. A detailed summary of this failure development is given in Sect. 2.

The classical micromechanical-based damage models known from literature try to describe the three fracture phases with continuum mechanical approaches. Generally for each phase, a separate model is needed: void initiation [6, 34, 72, 115], void growth [115, 154, 169, 211, 224, 277] and void coalescence [26, 61, 272].

The classic micromechanical-based damage models are derived for high stress multiaxialities and a pronounced void growth. Such models are described in Sect. 3. Mechanisms observed in pure shear mode are not or insufficiently described by these models. Micromechanical-based models to describe the failure at such low stress multiaxialities are not in the focus of interest here. Models which describe both high and low stress multiaxialities are usually empirical in nature.

Nearly all models discussed so far are of local nature. This means that the material behaviour depends only on the local state variables. Neighboring points have no influence on the local material behaviour. If material softening occurs, this can lead to so-called bifurcation problems. This means that a homogeneous strain or damage field will get unstable against a strongly localized one [209]. In finite element calculations, this means that strains and damage locate in one element layer [244]. The so-called pathological mesh dependence of results is observed.

In practice, this problem can be overcome by keeping the mesh size constant. Often the mesh size is directly coupled to the microstructure [45, 62, 86, 182, 216, 240, 241, 262]. To eliminate the pathological mesh dependence different concepts have been published, for example [21, 55, 92, 205]. Together, all these concepts and the derived models introduce a material-specific characteristic length. A summary of the most common approaches is given in Sect. 4.

Following the concept of the Local Approach [201], fracture toughness values can be predicted by numerical calculations only. Different possibilities for the description of competing brittle and ductile damage in the entire toughness region are discussed in Sect. 5.

2 Failure by Void Initiation, Growth and Coalescence [244]

Materials and components can be deformed up to a characteristic extent. Fracture limits the deformation and often leads to a catastrophic failure of vehicles, machines and plants with consequences for safe operation. Therefore it is essential to investigate the causes and the mechanism of fracture to find adequate simulation approaches for being able to predict the failure behaviour.

There is no uniform classification of fractures in literature. Classifications which are based on load type or macroscopic phenomena can be helpful, however, they are not suitable to be used in a damage mechanical calculation model [244] which describes the local material behaviour.

The microscopic description of the failure behaviour by means of micromechanical processes only requires the local state and the local kinematic laws. Therefore, this description is more suitable to be used in a damage model. With such damage models the macroscopic definition of fracture which is necessary for practical application can be calculated by means of the finite-element-method. Damage models belong to the group of the so-called advanced material models.

To understand the local failure process, it is indispensable to know the micromechanical processes which occur on the micro level. They determine the microscopical and macroscopical processes in the material as well as the future appearance of the fracture (cleavage fracture or dimple/shear fracture). Hereinafter it is referred only to the dimple fracture.

The dimple fracture [240] is characterized by locally very high plastic deformations on the fracture surface. The dissipated energy is much higher than in cleavage fracture. This reflects the rough dimpled fracture surface [83, 113] which is characteristic for all technical metals and metal alloys, see Figs. 1 and 2.

Fig. 1

Dimple fracture, copper, REM image

Fig. 2

Dimple fracture, Al-Cu-alloy, REM image

It depends on the surface energy, on the stress state as well as the elastic energy released during the crack growth whether dimple fracture is stable or not.

Investigations done in the 1940s and 1950s [74, 207, 276] have already shown that for almost all metal alloys, the micro-mechancial processes which lead to dimple fracture can be divided into 3 phases, see Fig. 3:

• I. void initiation,

• II. void growth,

• III. void coalescence.

Fig. 3

Phases of dimple fracture [240, 261]

Not only ferritic [113, 240] and austenitic [17, 242] steels show this behaviour but also for example aluminium [60, 241], nickel [11], magnesium [68], cobalt [119] and titanium [166] alloys. This kind of failure behaviour affects many technically pure metals [113, 207] too.

In the following sections, the three phases of failure are described in detail.

2.1 Formation of Voids

The first phase of dimple fracture, i.e. the formation of voids, can occur [240] at:

• particles of a secondary phase [113, 119, 146, 207],

• grain boundaries [120, 166],

• perlite cracks [118, 202, 218] and

• dislocation cell boundaries [108, 290].

In the majority of technical metals, inclusions and precipitations are relevant for the primary formation of voids. A distinction is often made between primary and secondary voids [267]. Primary voids occur at the beginning of the deformation process at relatively small plastic strains. Generally, they show a significant void growth [65] and are relevant for initiating the failure process [268]. Secondary voids often initiate very late within the load history [44]. Compared to primary voids, they are small and play an important role [60, 228] during the coalescence of the voids.

The procedures during the formation of voids at particles are determined by a variety of possible factors, see for example as well [93, 94, 251, 274]:

• atomic structure, micro- und macroscopic defect and homogeneity of the particles

• size and form of the particles

• arrangement of the particles, clustering

• distance of the particles to each other

• different populations of particles

• position of the particles in the microstructure (i.e. on grain boundaries)

• the orientation of the slip or cleavage planes in the matrix and in the particles

• plastic deformation at and in the particle

• cohesive strength between particle and matrix

• deformation behaviour (elastic/ plastic) of particles and matrix

• stresses and stress multiaxiality in particle and matrix

• grain size of the matrix

• hardening behaviour of the matrix

• free surface energy

• manufacturing process and damage of particles and/ or matrix which may be caused

In principle voids can be initiated by the following two mechanisms:

• debonding between matrix (see Figs. 4 and 5) and particle and

  Fig. 4

  

  Void initiation by debonding between matrix and particle

  Fig. 5

  

  Manganese sulfid with total debonding between matrix and particle, 20 MnMoNi5-5, REM image

• particle fracture (see Figs. 6 and 7).

  Fig. 6

  

  Void initiation by particle fracture

  Fig. 7

  

  Cracked iron carbide, steel, TEM foil

It depends on various factors whether voids are initiated by particle fracture or by debonding. An essential factor is the particle shape.

In loading direction, elongated particles often fail by particle fracture [14, 93, 111, 119, 146, 149, 213]. It seems as it is not so important whether the particles behave ductile, like i. e. certain manganese sulphides [119, 123] or more brittle, like i. e. carbides [93, 146, 149]. The extent to which the fragments of an inclusion remain attached to the matrix [29, 146] or whether they debond with increasing plastic deformation from the matrix [27, 122] mainly depends on the cohesive strength between the matrix and particle as well as the multiaxiality of the stress state [29].

At more spherical particles debonding is often observed between particle and matrix [14, 111, 119, 240]. But also at elongated or sheet-like particles, which are arranged perpendicular to the major principal stress, voids can be caused by decohesion beween particle and matrix [77, 123]. Whether the debonding is only partially [93] or completely depends among other things on the applied stress condition. At high multiaxiality a complete debonding is observed frequently, while low stress multiaxiality (σ^m/σ^vM < 2/3) only leads to partial separation [29].

However, the link between particle shape and failure mechanism described before is not mandatory. Initiation by particle cracking can be found as well at perfectly spherical particles [122, 125] and debonding at elongated ones.

Experimental studies and simulations on the microstructure level show that not only the cohesive strength between particle and matrix, toughness and shape of the particles have an influence on the initiation mechanism (fracture or debonding). Soppa et al. [250, 251] show that both the arrangement and the volume fraction of the particles as well as the hardening behaviour of the matrix influence the mechanism leading to void initiation.

2.1.1 Which Deformations Lead to Voids?

The presence of plastic deformations [213] is considered as a prerequisite for void initiation. During plastic deformation, dislocations accumulate at particles which can be deformed worse than the matrix [120, 171, 261] and slip bands are blocked [113]. These processes lead to stress peaks at and in the particles. Void initiation will take place if these stress peaks are higher than the cohesive strength between particle and matrix or the tensile strength of the particle. If the yield strength of the particle is lower than the one of the surrounding matrix, slip bands in the inclusion are blocked at the interface between particles and matrix, thus leading to a stress peak [75, 291].

Void formation by particle fracture or debonding from the matrix can either be observed soon after exceeding the yield strength [147, 190] or only after large plastic deformation [149, 274]. At which deformation void initiation at particles will be observed depends primarily on

• cohesive strength between particle and matrix,

• deformation behaviour of the particles

• deformation behaviour of the matrix and

• the degree of stress multiaxiality.

Many materials already contain voids initiated during the production process [8, 27, 63, 70, 236, 291].

A very early void initiation is often observed at particles that can deform plastically. As examples, manganese sulfides in steels, [8, 27, 63, 70, 236, 291], or spherical graphite cast iron [258] have to be mentioned. Numerous authors observe void initiation at zero or very low plastic deformations in steels containing manganese sulphides [8, 30, 77, 146, 213, 293]. Likewise sometimes, a very early void initiation can be observed at brittle particles [27, 93, 113, 250].

In other particles with a high cohesive strength between particle and matrix, very large deformations are needed to initiate voids. For iron carbides in steel, strains of over 50 % were measured until the void initiation started [7, 93, 149]. Even at very small manganese sulfides (ϕ < 0.22 μm)¹ in a high-strength steel, voids are initiated at strains of about 50 %.

The onset of void formation is also affected by the yield strength of the matrix material. For example, Huber et al. [125] observed at a near eutectic Al-Si casting alloy that for a low-strength version voids initiation occurs by particle fracture at much higher strains than for a high-strength version of the alloy.

In addition the multiaxial stress state affects the amount of plastic deformation which is necessary for void initiation.

2.1.2 At Which Particles Void Initiation Takes Place?

At which particles in a given alloy void initiation is observed is mainly determined by the chemical composition, the origin and the size distribution of the particles. The strength of the interface between particles and matrix depends not only on the material characteristics of the particle, but also on the chemical composition and the micro-structure of the matrix. In [93] for example, it is observed in a steel with globular cementite that void formation by debonding primarily occurs at particles on grain boundaries.

Depending on the material void initiation can often be observed simultaneously at very different precipitations and inclusions. For steels, these are often impurity-related inclusions, such as manganese sulfides and oxides as well as precipitations in combination with carbon and nitrogen. For example in the inclusions of a 22MnMoNi3 7 steel aluminum, calcium, magnesium, titanium and zirconium [44, 212, 215, 267,] are often detected, see Fig. 8.

Fig. 8

Void initiation at different particles, material 22NiMoCr3-7, REM image, [215]

Most metallographic studies show that void initiation takes place first at above-average-sized particles [60, 65, 75, 93, 113, 114, 228, 268, 289]. “Above-average” does not necessarily reflect the absolute size, but the size in relation to the present distribution. After voids occurred at the above-average-sized particles, voids at smaller particles initiate as well with increasing deformation. With decreasing particle size, larger plastic strains are required for the void initiation [75]. From these observations it can be deduced directly that there is a more or less large initiation interval depending on the size distribution of the particles. This statement contradicts with experimental studies on a copper-chromium alloy in which no size-dependent initiation time point was found [7].

It is also observed that particles below a certain size neither have voids [27, 28, 119, 217] nor existing voids grow any more [27]. It is also reported of niobium carbides (> 1μm) in a steel (X52) that no damage occurs because of the strong binding with the matrix [27].

2.2 Void Growth

A more or less pronounced void growth follows void initiation, see Figs. 9, 10 and 11. The void volume can grow by a multiple compared to the initial volume [14]. For example, Benzerga et al. [27] observed in the low alloy steel X52 a void growth up to a factor of 50.

Fig. 9

Void size at a strain of 0.59, material 20MnMoNi5-5, REM image [78]

Fig. 10

Void size at a strain of 0.69, material 20MnMoNi5-5, REM image [78]

Fig. 11

Void size at a strain of 1.19, material 20MnMoNi5-5, REM image [78]

2.2.1 Dependence of Void Growth on Stress Multiaxiality

Whether and how strongly voids grow largely depends on the multiaxiality of the stress state. With the help of tomographic studies, this can be directly observed [165]. Many authors state that the void growth increases with increasing plastic deformation and increasing stress multiaxiality [27, 46, 75, 165, 168, 282].

Under uniaxial loading a void, initiated at a particle, deforms in the direction of the external force. A growth perpendicular to the main direction of loading is hardly observed [75]. Thus the volume growth is low. This behaviour can be demonstrated very well with Finite Element calculations. In Fig. 12, one-eighth of a spherical void is shown. While under uniaxial loading the void is only streched in the loading direction, see Fig. 13, an increased volume void growth can be observed [75] under multiaxial loading, see Fig. 14.

Fig. 12

Initial void shape, FE model, quarter model

Fig. 13

Elongated void caused by uniaxial loading, FE model, quarter model

Fig. 14

Spherical void caused by multiaxial loading, FE model, quarter model

It is also assumed that voids loaded with negative stress multiaxiality, i. e. within the pressure range, can become smaller again. Experimental studies showing such a decrease in void volume, however, cannot be found in the relevant literature.

2.2.2 Dependence of Void Growth on Particle Form and Size

The void growth is highly dependent on the absolute size of the void [75]. Large voids grow much faster than small ones. For flat particles with a loading perpendicular to the major particle axes, bigger voids can be formed [27, 213] by planar delamination of inclusions and matrix.

2.2.3 Void Locking

At low stress multiaxiality, elongated voids can be formed as described above. In pure shear (e.g. torsion) even a decrease of the void diameter, perpendicular to the main loading direction, i.e. a closure, is predicted by cell model calculations. The particles leading to void initiation can hinder such a void closure. Due to their finite dimensions, they block the transverse contraction of a void [29]. Benzerga [29] indicates that this type of ‘void locking’ especially occurs in a multiaxiality range of $\upsigma^{\text{m}}/\upsigma^{\text{vM}} \le 2/ 3.$

Even at higher stress multiaxialities where a strong growth in void volume can be observed, the remaining particles can influence the growth behaviour. For example the void volume growth can be hindered by particle fragments with a good adhesion between particle and matrix [149], see Figs. 15 and 16.

Fig. 15

Void growth at the fracture sites of a niobium carbide, material X10CrNiNb18-10

Fig. 16

Void growth at the fracture sites of a niobium carbide, material X10CrNiNb18-10

2.2.4 Dependence of Void Growth on the Yield Strength and the Hardening of the Matrix Material

The void growth is of course also affected by the yield behaviour of the matrix material. Van Stone et al. [282] show in their literature review that the void growth is more pronounced in high strength materials with low hardening than in comparable low strength materials with high hardening.

2.3 Coalescence of Voids

Void growth is limited. Depending on the material and the stress multiaxiality, the materials bridges between the voids are teared apart. This merging of voids is called void coalescence.

By breaking of the materials bridges between the voids, a dimpled structure is being formed on the fracture surface. Within the individual dimples the complete or broken particles which led to void initiation can often still be found, see Figs. 17 and 18.

Fig. 17

Dimple with inclusion, material 20MnMoNi5-5, [MPA-archive]

Fig. 18

Fracture surface with voids containing fractured niobium carbids, material X10CrNiNb18-10

Dimpled fracture surfaces can be observed in almost all technical metals and alloys, see Figs. 19, 20, 21, 22, 23 and 24. Size and shape of dimples vary strongly depending on the materials and load conditions.

Fig. 19

Fracture surface copper

Fig. 20

Fracture surface NiCr70Nb

Fig. 21

Fracture surface aluminium

Fig. 22

Fracture surface austenite

Fig. 23

Fracture surface 20MnMoNi5 5

Fig. 24

Fracture surface Ti–Al alloy

In most cases coalescence of voids is initiated by a strain localization between the large primary voids. Two fundamentally different mechanisms of void coalescence can be observed in experiments and are predicted in simulations:

• Formation of shear bands between neighbouring primary voids [36, 148, 190], see Fig. 25.

  Fig. 25

  

  Shear band between two primary voids

• Plastic collapse of the material bridge between two neighboring primary voids [27, 76, 119, 213, 274], see Fig. 26.

  Fig. 26

  

  Plastic collapse of the material bridge between two primary voids

Often secondary voids initiated at much smaller particles are involved in the void coalescence process [117, 171, 228]. The model for this is that due to the strain localisation very large local plastic strains occur, which lead to the initiation of the small secondary voids [75, 274]. For example these secondary voids can be seen on shear bands between the larger voids [28, 75, 76, 148, 268], see Fig. 27. Small secondary voids can play a role, too, when the materials bridges fail by plastic collapse, see Fig. 28. In this failure mode secondary voids have the effect that the large voids do not fully grow together and the residual ligament is not stretched to a tip, but being connected via the secondary voids [119, 274]. Usually not only one of the described mechanisms leads to void coalescence, but several mechanisms are observed simultaneously.

Fig. 27

Shear band with secondary voids between two primary voids

Fig. 28

Plastic collapse of the material bridge through secondary voids between two primary voids

2.3.1 Influence of the Stress Multiaxiality on Void Coalescence

Numerous studies show that void growth and void coalescence depend on the multiaxial stress state [119]. Since the coalescence process occurs in a quite small time interval (sometimes unstable) and material volume, it is difficult to examine it experimentally. However, the coalescence process can often be concluded from the shape of the dimples on the fracture surface. For high multiaxial stress states, as they are observed for example inside a necked round tensile bar, spherical or ellipsoide voids develop. On fracture surface, almost equiaxed dimples are found, see Fig. 29. At loads which are almost uniaxial, with fracture parallel to the greatest shear stress, the dimples are strongly defomed in the direction of shear, see Fig. 30. Finally pure shear stress leads to extremely distorted, squashed and elongated dimples [283], see Fig. 31. Baechem [24] even describes 14 possible honeycomb shapes.

Fig. 29

equiaxed dimples, material copper [MPA archive]

Fig. 30

dimples from tension-shear, material austenite [MPA archive]

Fig. 31

dimples from pure shear, material HDT1200M [MPA archive]

Metallographic examinations show that the stress multiaxiality has a direct influence on the mechanism of void coalescence and the formation of secondary voids. Bandstra et al. [16] examine the ductile failure behaviour of a HY-100 steel with elongated manganese sulphides perpendicular to the loading direction. At higher multiaxiality $\upsigma^{\text{m}}/\upsigma^{\text{vM}} > 1$ the authors mainly find void coalescence perpendicular to the main direction of loading with the formation of small secondary voids, whereas they observed a shear failure with secondary voids between the large primary voids at lower multiaxiality. These results are confirmed by Bron & Besson [58] for an aluminium alloy AL2024. The influence of stress multiaxiality on the formation of secondary voids/ dimples is described by Besson et al. and Tanguy et al. [44, 267]. The authors show for steel X100 that the number of small secondary dimples on the fracture surface increases with decreasing stress multiaxiality.

2.3.2 Effect of Void Formation on the Void Coalescence

In general, if the void distance (perpendicular to the loading direction) is small, a failure by plastic collapse of the material bridges occurs [25]. If the voids are oriented rather under 45° with larger distances in between, the probability of shear band formation increases [25]. In elongated voids it seems as if orientation and rotation of the voids during deforming affect the coalescence mechanism [28]. Systematic studies on the influence of the void arrangement on the failure mechanism are hardly feasible because due to the manufacturing process the voids have a random position. Samples with artificially laser-drilled voids in the form of holes [284–287] offer a possibility to study the impacts more systematically. To analyze the void arrangement, Weck investigates two different types of tensile specimens a) two holes arranged perpendicular (90°) to the loading direction and b) two holes shifted under 45°. For the 90° arrangement Weck shows that coalescence takes place by a failure of the material bridge perpendicular to the loading direction, seeFig. 32. The specimen with the 45° shifted holes fails by shear band formation, see Fig. 33. On both fracture surfaces ‘secondary’ dimples were found.

Fig. 32

Void coalescence of two voids arranged under 90° to loading direction, material Al 5052 [285]

Fig. 33

Void coalescence of two voids arranged under 45° to loading direction, material Al 5052 [285]

2.3.3 Influence of the Materials on the Coalescence

The microstructure of the materials as well as size and composition of the particles affect the coalescence mechanism. Cox and Low [75] examine the failure behaviour of four different high-strength steels:

• 1. A commercial steel type AISI 4340 with large manganese sulphides (∅ ≈ 7.5 μm) and much smaller iron carbides. The volume fraction of manganese sulfides is 0.14 %.

• 2. A high purity version of the steel type AISI 4340 with slightly smaller manganese sulfides (∅ ≈ 4.2 μm) and also smaller iron carbides. The volume fraction of manganese sulfides here is only 0.06 %.

• 3. A commercial maraging steel (18Ni, 200 grade) with titanium carbonitrides (∅ ≈ 8.6 μm) and much smaller particles of an intermetallic phase. The volume fraction of titanium carbonitrides is 0.21 %.

• 4. A high purity version of maraging steel 18Ni, 200 grade with smaller titanium carbonitrides (∅ ≈ 3.0 μm) and much smaller particles of an intermetallic phase. The volume fraction of titanium carbonitrides is 0.09 %.

All four steels have a comparable yield strength of about 1400 MPa. While the void coalescence in the maraging steel mainly takes place by direct merging of the voids, in the AISI 4340 versions shear bands with secondary voids are observed. In the AISI 4340 steels, the small iron carbides are involved in void coalescence, while the small intermetallic phases have no direct influence on the convergence of the maraging steel.

3 Continuum Mechanical Models for Failure by Void Initiation, Growth and Coalescence [244]

To predict the macroscopic deformation and failure behaviour (crack initiation, crack growth and instability) of components and assembly groups, macroscopic continuum mechanical approaches are needed. Calculations on the level of microstructure or even on the atomic level which simulate single voids and/ or details from microstructure [13, 203, 206, 214, 225, 245, 251, 252], see Figs. 34 and 35, are not applicable to real components because of the huge computation time and time consuming modelling.

Fig. 34

Blocked dislocation by a copper precipitation (∅ = 1 nm) in cbc iron, atomistic simulation [172]

Fig. 35

Strain distribution in a dual phase Al-Al₂O₃ alloy; plane simulation [251]

Based on the derivation of the macroscopic materials models it can be distinguished between empirical and micromechanical-based models:

• Empirical models approximate the experimentally observed macroscopic behaviour. These approaches are also called phenomenological or heuristic models. Due to the number of introduced material-dependent variables a more or less complex material behaviour can be approximated. Drawback of these models is that the used material parameters have no direct reference to material-physical parameters. The transferability of the empirical parameters to other load cases and materials is not given a priori. For example the following models are referred to:

  • Cockcroft and Latham [73]

  • Oyane [185]

  • Gao et al. [106],

  • Chaouadi et al. [71]

  • Bai and Wierzbicki [15].

  A discussion of this kind of models is found in [233].

• Another approach to describe the mechanical behaviour of materials is the use of so-called micromechanical-based models. These models try to describe the discontinuous micromechanical processes on a macroscopic level with mechanical and/ or thermo-mechanical approaches. For this purpose, the discontinuous stress and strain field is homogenized and described with continuum mechanical approaches. The advantage of this class of models is that a transferability of the material law and the used parameters to other loading situations is more likely. [86, 181, 182, 204]. Severe disadvantages are the simplifications needed for the derivation, for example ideal plastic material behaviour, axially symmetric voids and so on. As a result the transferability is limited.

In the following the focus of interest will be on the micromechanical-based material models. In case of dimple failure these models have to describe the microscopic processes

• 1. void initiation

• 2. void growth

• 3. void coalescence which leads to the formation of a micro crack

by means of continuum mechanical approaches. In general, each phase is described by a separate model. However, there are models which describe two or all three phases simultaneously. In this chapter, the classic models from the late 1960s, 1970s and 1980s are presented. Later published damage models are based almost exclusively on these classic formulations. Recent systematic reviews of Chaboche et al. [69] and Besson [46] confirm this.

3.1 Models Describing Void Initiation

The void initiation models described below simulate the formation of a void by decohesion (detachment) of a particle from the surrounding matrix. Micromechanical models that explicitly describe the fracture of a particle are not very common. An exception is for example the model of Huber et al. [125]. As being described later the decohesion models can often similarly be used to describe particle fracture. In principle, the decohesion models can be divided into three groups [6, 240], such as:

• stress criteria

• strain criteria

• energy criteria

If assuming void initiation by decohesion the normalized void volume ${\text{f}}_{ 0}$ is usually set equal to the normalized particle volume ${}^{\text{inc}}{\text{f}}$:

$${\text{f}}_{0} = {}^{\text{inc}}{\text{f}} = \frac{{{}^{\text{inc}}{\text{V}}}}{{{\text{V}}_{0} }}$$

(1)

In the following, the normalized void volume ${\text{f}}_{0}$ and the normalized particle volume ${}^{\text{inc}}{\text{f}}$ will be called void and particle volume.

In void formation by particle fracture the formed void volume ${\text{f}}_{0}$ is much smaller than the corresponding particle volume ${}^{\text{inc}}{\text{f}}$.

$${\text{f}}_{0} \ll {}^{\text{inc}}{\text{f}} = \frac{{{}^{\text{inc}}{\text{V}}}}{{{\text{V}}_{0} }}$$

(2)

3.1.1 Void Initiation Model of Tanaka et al.

Tanaka et al. [269] derived an energy based void initiation criterion. They assumed an elastic particle with radius R (in cm) in a plastic matrix. They derived a critical strain $\upvarepsilon^{\text{c}}$ above which a void will initiate. Due to simplification they assumed that plastic strain in loading direction is higher than 1 % and that the macroscopically applied stress ${\tilde{\sigma }}$ is less than E/1000. If the elastic modulus of the particle is smaller than that of the matrix $\upvarepsilon^{\text{c}}$ can be calculated as:

$$\upvarepsilon^{\text{c}} \ge\upbeta\sqrt {\frac{1}{\text{R}}}$$

(3)

The advantage of the Tanaka et al. approach is that a solution can also be found for particles with a higher elastic modulus than the matrix:

$$\upvarepsilon^{\text{c}} \ge\upbeta\sqrt {\frac{1}{{\upalpha{\text{R}}}}} \quad {\text{mit}}\quad\upalpha = \frac{{{}^{\text{inc}}{\text{E}}}}{{{}^{\text{mat}}{\text{E}}}}$$

(4)

R describes the radius of an inclusion and α the ratio between the elastic modulus of the inclusion and the matrix. β is a material dependent constant which can be calculated as follows:

$$\begin{aligned}\upbeta & = \sqrt 2 \sqrt {\frac{{48 \times 10^{ - 9} \left\{ {(7 - 5{}^{\text{mat}}\upnu)(1 + {}^{\text{inc}}\upnu) + \alpha (1 + {}^{\text{mat}}\upnu)(8 - 10{}^{\text{mat}}\upnu)} \right\}}}{{(7 - 5{}^{\text{mat}}\upnu)^{2} \left\{ {2(1 - 2{}^{\text{inc}}\upnu) + \alpha (1 + {}^{\text{mat}}\upnu)} \right\}}}} \\ & \quad * \sqrt {(7 - 5{}^{\text{mat}}\upnu)(1 - {}^{\text{inc}}\upnu) + 5\alpha (1 - {}^{\text{mat}}\upnu^{2} )} \\ \end{aligned}$$

(5)

3.1.2 Void Initiation Model of Argon, Im and Safoglu

Argon, Im and Safoglu [6, 8] derived a stress-based criterion to predict void initiation by particle-matrix decohesion. For the initiation of voids by decohesion, sufficient energy for the creation of new surfaces must be available and the critical stress ${}^{\text{deb}}\upsigma^{\text{c}}$ necessary for the debonding must be reached. The derived debonding stress ${}^{\text{deb}}\upsigma$ can be calculated with the following equation:

$${}^{\text{deb}}\upsigma \approx {\text{k}}{\tilde{\sigma }}^{\text{vM}} + {\tilde{\sigma }}^{\text{m}} \ge {}^{\text{deb}}\upsigma^{\text{c}}$$

(6)

In this equation ${\tilde{\sigma }}^{\text{vM}}$ describes the macroscopic equivalent stress and ${\tilde{\sigma }}^{\text{m}}$ the macroscopic hydrostatic stress. The constant k characterises the particle shape. For spherical particles k became 1.

3.1.3 Void Initiation Model of Gurson

The derivation of Gurson’s void initiation model [115] is mainly based on the experimental work of Gurland [114] and the theoretical work of Argon et al. [6]. Gurland [114] observed in an uniaxially deformed steel with 1.05 % carbon content and coagulated cementite that the number of initiated voids depends approximately linear on the plastic equivalent strain. From this observation Gurson derives his strain based void initiation criterion in which the void initiation rate ${\dot{f}}^{\text{nuc}}$ is proportional to the plastic equivalent strain rate ${\dot{\varepsilon }}^{{{\text{p}}^{\text{v}} }}$. In addition, Gurson slightly modified the stress based void initiation criterion by Argon et al. [6]. Finally he defined a criterion that takes into account both strain and stress induced void formation:

$${\dot{f}}^{\text{nuc}} = {\text{M}}_{1} {\dot{\varepsilon }}^{{{\text{p}}^{\text{v}} }} + {\text{M}}_{2} \frac{{{\dot{\tilde{\sigma }}}^{\text{m}} }}{{(1 - {\text{f}})}}$$

(7)

M ₁ and M ₂ are material dependent functions which should describe the interaction of particles. This model suggested by Gurson is of pure empirical nature.

3.1.4 Void Initiation Model of Goods and Brown

Goods and Brown derived a strain based micromechanical model to describe the void initiation [111]. By superposition of tension and a hydrostatic stress field as well as further simplification, the following equation for the local plastic limit strain $\upvarepsilon^{{\text{p}^{\text{c}}}}$ was found in dependence on the particle radius R:

$${}\upvarepsilon^{{\text{p}^{\text{c}} }} \ge {\text{KR}}\left( {{}^{\text{deb}}\upsigma^{\text{c}} - \frac{{3{\tilde{\sigma }}^{\text{m}} - \tilde{\sigma }_{\text{I}} }}{3}} \right)^{2}$$

(8)

Factor K can be calculated from the void volume ${}^{\text{inc}}{\text{f}}$ und Burgers vector b_i. Due to their dislocation based approach the authors assumed that the criterion is valid for particles up to a diameter of 2 μm.

3.1.5 Void Initiation Model Acc. to Chu and Needleman

The model suggested by Chu and Needleman [72] is based on the theories of Gurson [115] and Argon et al. [6]. They defined an empirical strain based and a stress based initiation model.

For the definition of their strain based initiation criteria Chu & Needleman started with Eq. 9 published by Gurson [115]. While Gurson assumed a proportional relationship between void initiation rate ${\dot{f}}^{\text{nuc}}$ and plastic equivalent strain rate ${\dot{\varepsilon }}^{{\text{p}^{\text{v}} }}$, Chu and Needleman proposed a dependency in the form of a normal distribution. For the void initiation volume rate they obtained their often cited relationship [3, 12, 39, 66, 72]:

$${\dot{f}}^{\text{nuc}} = {C\dot{\varepsilon }}^{{\text{p}^{\text{v}} }}$$

(9)

$$\text{C} = \frac{\uppsi}{{\text{s}^{\upvarepsilon} \sqrt {2\uppi} }}{\text{e}}^{{ - \frac{1}{2}\left( {\frac{{\upvarepsilon^{{\text{p}^{\text{v}} }} -\upvarepsilon^{\text{N}} }}{{\text{s}^{\upvarepsilon} }}} \right)^{2} }}$$

(10)

$\upvarepsilon^{\text{N}}$ is the expected value of the equivalent strain at void initiation and $\text{s}^{\upvarepsilon}$ the standard deviation of the function. $\uppsi$ is determined in a manner that the resulting void initiation volume associates with the consistent materials specific value. The reason why they assume a Gaussian distribution is not discussed by the authors. At high stress multiaxiality the void initiation predicted with Eq. 10 approaches zero.

For the derivation of their stress based criterion Chu and Needleman used the Argon et al. [6] criterion. Based on the work of Gurson [115] the authors derived the following equation with the assumption of a normally distributed void initiation volume rate ${\dot{f}}^{{\text{nuc}}}$:

$${\dot{f}}^{{\text{nuc}}} = \text{K}({\dot{\tilde{\sigma }}}^{\text{v}} + {\dot{\tilde{\sigma }}}^{\text{m}} )\quad {\text{with}}\quad {\text{K}} = \frac{\upkappa}{{\text{s}^{\upsigma} \text{R}_{\text{e}} \sqrt {2\uppi} }}{\text{e}}^{{ - \frac{1}{2}\left( {\frac{{{\tilde{\sigma }}^{\text{v}} + {\tilde{\sigma }}^{\text{h}} -\upsigma^{\text{N}} }}{{{\text{s}}^{\upsigma} \;{\text{R}}_{\text{e}} }}} \right)^{2} }}$$

(11)

s^σ represents the standard deviation and R_e the the yield stress. $\upsigma^{\text{N}}$ is the expected value of the normal distribution. $\upkappa$ is again determined in a way that the resulting void initiation volume is consistent with the experimental value.

It is possible to describe the decohesion process with cell models calculations. In a later work Needleman [178] showed that it was not possible to describe this micromechanical process (simulated with cell model calculations) correctly with both criteria proposed by Chu and Needleman [72]. To take better account of the stress multiaxiality he introduced another material dependent constant c to consider the influence of stress multiaxiality [178]:

$$\upsigma^{\text{N}} = {\tilde{\sigma }}^{{\text{v}{\text{M}}}} + {c\, \tilde{ \sigma }}^{\text{m}}$$

(12)

3.1.6 Void Initiation Model of Beremin

In the derivation of their void initiation criterion, the research group Beremin assumed an elastic particle in an elastic-plastically deformable infinite matrix [34]. They used a self-consistent approach [121, 138], in which the matrix material has the properties of the entire material. In their definition the entire material is the matrix material with particles.

$${}^{\text{deb}}\upsigma = {\tilde{\sigma }}_{\text{I}} +\upchi\left( {{\tilde{\sigma }}^{{\text{v}{\text{M}}}} - \text{R}_{\text{e}} } \right) \ge {}^{\text{deb}}\upsigma^{\text{c}}$$

(13)

If the debonding stress ${}^{\text{deb}}\upsigma$ reaches the critical value ${}^{\text{deb}}\upsigma^{\text{c}}$, a void initiates. The stress ${\tilde{\sigma }}_{\text{I}}$ refers to the macroscopic largest principal stress, ${\tilde{\sigma }}^{{\text{v}{\text{M}}}}$ to the macroscopic equivalent stress and the parameter $\upchi$ to the shape of the particle.

3.1.7 Void Initiation Model of Huber et al.

In contrast to the authors discussed so far, Huber et al. [125] defined a model for predicting particle fracture. Their void initiation criterion combines the micromechanical-based void initiation criterion of Beremin [34] with the simple empirical strain criterion of Gurson [115]. They assumed that the maximum principal stress triggers particle fracture and that there is a dependence of the fracture stress on the particle size. They justified this size dependence with an increasing number of defects in larger particles due to the larger volume. Their model is defined as follows:

• Void initiation starts if the criterion of the Beremin model (Eq. 13) is fulfilled for the largest particles:

  $${}^{\text{disb}}\upsigma^{\text{c}} \le {}^{\text{disb}}\upsigma = {\tilde{\sigma }}_{\text{I}} +\upchi\left( {{\tilde{\sigma }}^{{\text{v}{\text{M}}}} - {\text{R}}_{\text{e}} } \right)$$

  (14)

  For initiation the corresponding value of equivalent plastic strain is denoted by ${}^{\text{start}}\upvarepsilon^{{\text{p}^{\text{v}} }}$.

• For $\upvarepsilon^{{\text{p}^{\text{v}} }} > {}^{\text{start}}\upvarepsilon^{{\text{p}^{\text{v}} }}$ a phase of continuous void formation follows. To describe this phase they modified the void initiation criterion of Gurson [115]:

  $${\dot{f}}^{\text{nuc}} = \text{C}(\upvarepsilon^{{\text{p}^{\text{v}} }} ){\dot{\varepsilon }}^{{\text{p}^{\text{v}} }}$$

  (15)

  The constant C from the Gurson equation is defined by Huber et al. as a polynomial function of the equivalent plastic strain:

  $$\text{C}(\upvarepsilon^{{\text{p}^{\text{v}} }} ) = \text{a}_{1} (\upvarepsilon^{{\text{p}^{\text{v}} }} )^{6} + \text{a}_{2} (\upvarepsilon^{{\text{p}^{\text{v}} }} )^{4} + \text{a}_{3} (\upvarepsilon^{{\text{p}^{\text{v}} }} )^{2} + \text{a}_{4}$$

  (16)

• Void initiation is finished if the material dependent equivalent plastic strain ${}^{\text{end}}\upvarepsilon^{{\text{p}^{\text{v}} }}$ is reached.

The factors a_i are defined in such a way that $\text{C}({}^{\text{start}}\upvarepsilon^{{\text{p}^{\text{v}} }} ) = \text{C}({}^{\text{end}}\upvarepsilon^{{\text{p}^{\text{v}} }} ) = 0$ is valid. Simultaneously the derivatives at these points should be zero. These requirements does not have a micromechanical background, but are justified by numerical advantages.

3.1.7.1 Void Initiation Model of Morgeneyer et al.

Starting point for the derivation of the void initiation model by Morgeneyer et al. [173] are experimental investigations on the failure behaviour of thin metal sheets. Several studies [44, 57, 58] showed that for shear fracture the number of secondary voids increases sharply. Morgeneyer et al. postulated that the formation of the secondary voids depends on the multiaxiality of the strain state. They assumed that the tendency for shear fracture can be described with the Lode angle $\upmu_{{{\dot{\varepsilon }}}}$ [162]:

$$\upmu_{{{\dot{\varepsilon }}}} = \frac{{{\dot{\varepsilon }}_{{\text{II}}} }}{{{\dot{\varepsilon }}_{\text{I}} - {\dot{\varepsilon }}_{\text{III}} }},$$

(17)

where ${\dot{\varepsilon }}_{\text{I}}$, ${\dot{\varepsilon }}_{\text{II}}$ and ${\dot{\varepsilon }}_{\text{III}}$ describe the principal strain rates.

The authors assumed that the initiation rate of secondary voids is particularly high for a Lode angle close to 0 (pure shear). As Gurson and Chu & Needleman they accepted, that void initiation further depends on the equivalent plastic strain rate. Starting from the initiation equation proposed by Gurson, the authors proposed the following empirical formula to describe the initiation of secondary voids:

$${\dot{f}}^{\text{nuc}} = {\text{A}}_{0} {\text{e}}^{{ - \left( {\frac{{\upmu_{{{\dot{\varepsilon }}}} }}{{\upmu_{{{\dot{\varepsilon }}}}^{0} }}} \right)^{2} }} {\dot{\varepsilon }}^{{\text{p}^{\text{v}} }} \quad {\text{for}}\;\upvarepsilon^{{\text{p}^{\text{v}} }} > {}^{\text{start}}\upvarepsilon^{{\text{p}^{\text{v}} }} ,$$

(18)

where A₀ is a material dependent constant. $\upmu_{{{\dot{\varepsilon }}}}^{0}$ describes the shape of the normal distribution of the void initiation. Void initiation is predicted only for equivalent plastic strains $\upvarepsilon^{{\text{p}^{\text{v}} }} > {}^{\text{start}}\upvarepsilon^{{\text{p}^{\text{v}} }}$.

3.1.8 Void Initiation Caused by Particle Fracture

Especially in materials with pronounced elongated and branched particles void formation is often caused by particle fracture. The previously presented void initiation models, with the exception of the Huber criterion, are all based on the assumption that the voids are formed by a separation of matrix and second phase particles. If non plastically deformable particles are assumed, then the results that have been achieved for failure by matrix detachment can be transmitted very easily to the failure mechanism of particle fracture.

Relevant for the fracture of a brittle particle is the major principal stress perpendicular to the respective cross section. If the particles are linear-elastic it can be assumed approximately that stresses and strains are constant in the particle, for example [88]. In this case, the first principal stress in the particle ${}^{\text{inc}}\upsigma_{\text{I}}$ is equal to the debonding stress ${}^{\text{deb}}\upsigma$, see for example [8, 195].

3.2 Models Describing Void Growth

Due to their derivation micromechanical-based models for describing void growth can be divided into two groups [200, 240]:

• 1. The growth of a cylindrical, spherical or ellipsoidal void in a finite or infinite matrix is explicitly described with continuum mechanics based formulations.

• 2. The behaviour of porous materials is described with thermodynamic and continuum mechanics laws. Within these approaches no single voids are examined and due to this the derivation of the model is not so clear but nevertheless the basic laws of mechanics and thermodynamics are fulfilled.

Another classification of void growth models, as it is used in this study, is whether the void growth has an influence on the macroscopic deformation behaviour or not:

• 1. uncoupled models: The void growth is determined by a constitutive relation as a function of stress, strain and internal state variables. However, there is no coupling between void volume growth with the macroscopic material behaviour. The mechanical behaviour of the material is still described with the von Mises yield criterion. The void growth does not affect the hardening and deformation behaviour of the material. The material softening caused by void initiation and growth cannot be described with this class of models. Consequently, strain localisation which is important for the failure process cannot be simulated.

• 2. coupled models: Here, the calculated void volume has a direct influence on the yield behaviour of the material. A high degree of damage leads to a reduced load bearing capacity of the material. Damage becomes an internal state variable in the constitutive equations and thus influences directly the strength and yield behaviour of the material. Strain localisation can be described with this class of models.

In the following some of the well-established uncoupled and coupled void growth models are presented:

3.2.1 Uncoupled Models

3.2.1.1 McClintock Model

McClintock’s void growth model [169] is the first known void growth model. For the derivation of his model McClintock made the following assumptions:

• a cylindrical void with circular cross section in an infinite matrix

• the matrix material is rigid and perfectly plastic

• the material behaviour is described with the von Mises yield criteria

• the material is fully plastic in the unit cell

• ‘generalized plane strain’ conditions are assumed

• The infinite unit cell is loaded with an axisymmetric radial stress $\upsigma_{\text{r}}$ and with an uniaxial strain $\upvarepsilon_{\text{z}}$ in axial direction.

McClintock derived the following void growth law:

$$\frac{{{\dot{R}}}}{\text{R}} = \frac{\sqrt 3 }{2}{\dot{\tilde{\varepsilon }}}_{\text{z}} \sinh \left[ {\sqrt 3 \frac{{{\tilde{\sigma }}_{\text{r}} }}{{{\text{R}}_{\text{e}} }}} \right] - \frac{{{\dot{\tilde{\varepsilon }}}_{\text{z}} }}{2}$$

(19)

Following Gross and Seelig [112], Eq. 19 can be transformed into an evolution law which describes void volume growth:

$$\frac{{{\dot{f}}}}{\text{f}} = \sqrt 3 {\dot{\tilde{\varepsilon }}}^{\text{v}} \sinh \left[ {\sqrt 3 (\frac{{{\tilde{\sigma }}^{\text{m}} }}{{{\text{R}}_{\text{e}} }} - \frac{1}{3})} \right]$$

(20)

3.2.1.2 Rice and Tracey Model

The basis for the development of the void growth model acc. to Rice and Tracey [211] is a spherically shaped void in an infinite matrix. Similar to McClintock, the matrix material is assumed to be rigid and perfectly plastic.

Using these approximations, they obtained their well-known void growth model:

$$\frac{{{\dot{R}}}}{\text{R}} = {\alpha \dot{\tilde{\varepsilon }}}^{\text{v}} {\text{e}}^{{\frac{{3\,{\tilde{\sigma }}^{\text{m}} }}{{2\,{\text{R}}_{\text{e}} }}}} \quad {\text{with}}\;\upalpha = 0.283$$

(21)

To be able to compare the different void growth models, the radial growth ${\dot{R}}$ is converted into void volume growth ${\dot{f}}$:

$$\frac{{{\dot{f}}}}{\text{f}} =\upalpha^{*}{\dot{\tilde{\varepsilon }}}^{\text{v}} {\text{e}}^{{\frac{{3\,{\tilde{\sigma }}^{\text{m}} }}{{2\,{\text{R}}_{\text{e}} }}}} \quad {\text{with}}\;\upalpha^{*} = 0.849$$

(22)

The original Rice and Tracey model is not able to describe a strain hardening material behaviour. Perfect plastic material behaviour is assumed in the derivation of their model. In practice, the yield strength ${\text{R}}_{\text{e}}$ is often replaced by the current yield stress σ₀ or by the equivalent stress σ^v respectively to take material hardening into account. However, the micromechanical background does not cover this assumption. Only for visco-plastic material behaviour a solution of the problem is known [64].

Several other authors which applied the model to experimental data achieved different results for the factor α: The research group Beremin [35] found α = 0.5, Shi [246] α = 0.6 − 0.7, Pardoen et al. [190] α = 0.4 and α = 0.34, Maire et al. [165] confirmed the original factor of Rice and Tracey α = 0.283, Marini et al. [168] recognized a dependence of α on the volume fraction f₀ and Bandstra et al. [16] recognized a dependence of α on stress multiaxiality.

In the following, the extension by Huang [124] of the Rice and Tracey will be discussed.

Huang also solved the mechanical problem of a spherical void in an infinite matrix. However, compared to Rice and Tracey, he assumed much more complex shape functions for describing the stress field in the matrix. Due to the complexity he solved the problem only numerically. For stress multiaxiality σ^m/σ^vM ≥ 1 he received a value of α = 0.427. This value is close to the experimentally determined Beremin value.

For smaller multiaxiality $\frac{1}{3} \le \frac{{{\tilde{\sigma }}^{\text{m}} }}{{{\text{R}}_{\text{e}} }} < 1$ Huang suggested the following equation:

$$\frac{{{\dot{R}}}}{\text{R}} = 0.427\, {\dot{\tilde{\varepsilon }}}^{\text{v}} \left( {\frac{{{\tilde{\sigma }}^{\text{m}} }}{{{\text{R}}_{\text{e}} }}} \right)^{\frac{1}{4}} {\text{e}}^{{\frac{{3\,{\tilde{\sigma }}^{\text{m}} }}{{2\,{\text{R}}_{\text{e}} }}}}$$

(23)

3.2.2 Coupled Models

3.2.2.1 Lemaitre Type Models

The basis of Lemaitre’s models [153–159] are the works of Kachanov [134] and Rabotnov [208]. When calculating the macroscopic stresses ${\tilde{\sigma }}_{\text{ij}}$ these authors took into account the decrease of the loaded cross section caused by voids, see Fig. 36. This results in an increase of the averaged stresses acting in the matrix, the so called effective stress:

$${}^{\text{mat}}\upsigma_{\text{ij}} = \frac{{{\tilde{\sigma }}_{\text{ij}} }}{{1 - {\text{D}}}}$$

(24)

Fig. 36

Volume element with voids, acc. to [159]

For the derivation of his model Lemaitre made the following assumptions and simplifications:

• The increase in volume caused by void growth is neglected.

• In the elastic range there is a linear relationship between stresses and strains for the matrix material.

• Damage D is coupled with the elastic strains.

• The elastic and plastic strains do not depend directly on each other.

• The damage D and the plastic strains do not depend directly on each other.

For the derivation of his damage law Lemaitre followed thermo-mechanical approaches. For the description of the material state he selected the internal variable r to describe the plastic equivalent strain and D to describe the material damage. The associated state variable R is related to the internal variable r. R describes the material hardening in dependence of r. The state variable associated with D is called Y which is defined in such a way that the product ${\text{Y}}{\dot{D}}$ is equal to the dissipated energy caused by fracture.

To describe the yield limit Lemaitre used the von Mises yield criterion. Derogating from the original model he replaced the equivalent stress in the total material by the equivalent stress in the matrix, where the function R(r) described the hardening of the matrix material:

$${\varphi } = \frac{{{\tilde{\sigma }}^{{\text{v}{\text{M}}}} }}{{1 - {\text{D}}}} - {\text{R}}_{\text{e}} - {\text{R}}({\text{r}}) = 0$$

(25)

To deduce the damage evolution via the normality rule Lemaitre selected a non-associated flow rule. With this, the damage evolution is calculated as:

$${\dot{D}} = - \frac{\text{Y}}{\text{A}}{\dot{\tilde{\varepsilon }}}^{{{\text{p}}^{\text{v}} }} {\text{H}}({\tilde{\varepsilon }}^{{{\text{p}}^{\text{v}} }} - {}^{\text{c}}\upvarepsilon^{{{\text{p}}^{\text{v}} }} ),$$

(26)

where A is a material dependent scalar. By means of the Heaviside step function H the damage evolution starts when reaching the critical strain ${}^{\text{c}}\upvarepsilon^{{{\text{p}}^{\text{v}} }}$. The associated state variable Y can be calculated with:

$$\text{Y} = - \frac{{\left( {{\tilde{\sigma }}^{\text{vM}} } \right)^{2} }}{{2{\text{E}}(1 - {\text{D}})^{2} }}\left[ {\frac{2}{3}(1 +\upnu) + 3(1 - 2\upnu)\left( {\frac{{{\tilde{\sigma }}^{\text{m}} }}{{{\tilde{\sigma }}^{{\text{v}{\text{M}}}} }}} \right)^{2} } \right]$$

(27)

In addition, Lemaitre often indicated the following extended evolution equation for damage [153, 156, 157]:

$${\dot{D}} = \left( {\frac{{ - \text{Y}}}{\text{A}}} \right)^{{{\text{s}}0}} {\dot{\tilde{\varepsilon }}}^{{{\text{p}}^{\text{v}} }} {\text{H}}({\tilde{\varepsilon }}^{{{\text{p}}^{\text{v}} }} - {}^{\text{c}}\upvarepsilon^{{{\text{p}}^{\text{v}} }} ),$$

(28)

where s0 is an additional material dependent parameter.

In the following two modifications of the Lemaitre approach will be discussed.

Bonora [50] modified the evolution equation proposed by Lemaitre in the following way:

$$\begin{aligned} & {\dot{D}} =\upalpha\frac{{\left( {\text{D}_{\text{c}} - \text{D}_{0} } \right)^{{\frac{1}{\upalpha}}} }}{{\ln \left( {\frac{{{}^{\text{end}}\upvarepsilon}}{{{}^{\text{start}}\upvarepsilon}}} \right)}}\text{f}\left( {\frac{{{\tilde{\sigma }}^{\text{m}} }}{{{\tilde{\sigma }}^{{\text{v}{\text{M}}}} }}} \right)\left( {\text{D}_{\text{c}} - \text{D}} \right)^{{\frac{{\upalpha - 1}}{\upalpha}}} \frac{{{\dot{\tilde{\varepsilon }}}^{{\text{pv}}} }}{{{\tilde{\varepsilon }}^{{\text{pv}}} }}\quad {\text{with}}\\ &\quad {\text{f}}\left( {\frac{{{\tilde{\sigma }}^{\text{m}} }}{{{\tilde{\sigma }}^{\text{vM}} }}} \right) = \frac{2}{3}(1 +\upnu) + 3(1 - 2\upnu)\left( {\frac{{{\tilde{\sigma }}^{\text{m}} }}{{{\tilde{\sigma }}^{\text{vM}} }}} \right)^{2}\\ \end{aligned}$$

(29)

The damage evolution starts with the value ${\text{D}}_{0}$ and grows up to the critical value ${\text{D}}^{\text{c}}$ at which failure is predicted. ${}^{\text{start}}\upvarepsilon$ denotes the strain at the beginning of damage and ${}^{\text{end}}\upvarepsilon$ the fracture strain (both under the assumption of uniaxial loading).

In contrast to most of the other models Bonora et al. [48, 50, 51] describe explicitly how to determine the material dependent parameters.

Chaboche et al. [69] modified the Lemaitre approach to take into account the volume growth induced by void growth. Lemaitre neglected this volume change in his model. In the new formulation acc. to Chaboche et al. hydrostatic stresses can induce plastic hydrostatic strains which induce a change in volume.

3.2.2.2 Gurson Model

The aim of Gurson was to derive a yield criterion and a flow rule for a ductile material containing voids [115, 116]. His model takes into account the influence of the hydrostatic stress on void growth and on the plastic deformation behaviour. The new defined yield criterion represents an upper limit for yielding.

For the derivation of his yield criterion Gurson made the following assumptions for simplicity:

• Gurson defined a unit cell which contains a single void and derived a yield criterion for a spherical void in a spherical matrix.

• The assumed material behaviour of the matrix is rigid/perfectly plastic and is described by the von Mises yield criterion.

With a brilliant derivation Gurson obtained the following upper bound approximation for the yield function:

$${\varphi } = \left( {\frac{{{\tilde{\sigma }}^{\text{vM}} }}{{{\text{R}}_{\text{e}} }}} \right)^{2} + 2{\text{f}}\cosh \left( {\frac{{3{\tilde{\sigma }}^{\text{m}} }}{{2{\text{R}}_{\text{e}} }}} \right) - 1 - {\text{f}}^{2} = 0,$$

(30)

where R_e is the yield strength of the matrix material and not that of the whole unit cell.

With a similar derivation strategy Gurson [115] succeeded to transform approximately the Rice and Tracey model [211], see Eq. 21, into a yield function, that means, into a coupled model:

$${\varphi } = {\tilde{\sigma }}^{\text{vM}} + 2\, \upalpha\, {\text{f}}\, {\text{R}}_{\text{e}} {\text{e}}^{{\frac{{3{\tilde{\sigma }}^{\text{m}} }}{{2{\text{R}}_{\text{e}} }}}} - {\text{R}}_{\text{e}} = 0\quad {\text{mit}}\quad\upalpha = 0.283$$

(31)

The number of published modifications and extensions of the Gurson model is quite high. This depends among other things on the fact, that the original, unmodified Gurson model cannot describe correctly void growth in strain hardening materials [199, 270, 277, 279].

Good, but not exhaustive overviews can be found for example in [29, 32, 46, 232, 235]. Some of the major extensions of the Gurson model will be discussed in the following:

• Modification of the Gurson yield function for strain hardening materials

To take strain hardening into account Gurson [115] suggested to replace the yield strength ${\text{R}}_{\text{e}}$ of the perfectly plastic matrix material by the averaged current yield stress σ₀ in the unit cell. To calculate this averaged yield stress σ₀, which is dependent on the material hardening, he suggested the following relationship:

$$\upsigma_{0} {\dot{\varepsilon }}^{{{\text{p}}^{\text{v}} }} = \frac{{{\tilde{\sigma }}_{\text{ij}} {\dot{\tilde{\varepsilon }}}_{\text{ij}}^{\text{p}} }}{{1 - {\text{f}}}}$$

(32)

With this assumption, the Gurson model loses much of his micromechanical background. Pardoen and Besson [32] indicated that this simplification is only approximately permitted if the hardening exponent is less than 0.2.

A much broader suggestion to describe the material hardening is made by Leblond, Perrin and Devaux [152] with her LPD model. They developed an analytical model for the behaviour of a spherical void in a spherical hardening matrix material.

• Modification of the Gurson model of Tvergaard

Starting point for the development of the so-called Gurson Tvergaard model (GT model) [277] was the experimental work of Weinrich and French on shear band mechanisms [96, 97, 288]. Tvergaard attempted to simulate the shear band formation mechanisms with plane cell model calculations. For his cell model simulations with finite elements he assumed regularly arranged voids in a hardening elastic-plastic matrix. Due to the assumption of plane strain condition, he simulated the voids as infinitely long cylinders with circular cross sections. To simulate the behaviour of this cell model with a continuum mechanical macroscopic model, Tvergaard used the Gurson model which was actually derived for spherical voids. His results showed that the Gurson model overestimates the results from the cell model calculations. To get a better match with his cell model calculations, Tvergaard introduces three empirical constants q₁, q₂ and q₃:

$${\varphi } = \left( {\frac{{{\tilde{\sigma }}^{\text{vM}} }}{{\upsigma_{0} }}} \right)^{2} + \,2{\text{fq}}_{1} \cosh \left( {{\text{q}}_{2} \frac{{3{\kern 1pt} {\tilde{\sigma }}^{\text{m}} }}{{2\upsigma_{0} }}} \right) - 1 - \text{q}_{3} {\text{f}}^{2} = 0$$

(33)

Due to the introduction of the ‘adjusting parameters’ [277] the micromechanical background of the original Gurson model becomes questionable.

For the best parameter combination to describe the behaviour of cylindrical voids in copper and brass he found the following values:

$${\text{q}}_{ 1} = 1, 5,{\text{ q}}_{ 2} = 1,0\quad {\text{and}}\quad {\text{q}}_{3} = {\text{q}}_{1}^{2}$$

(34)

In the same paper [277] Tvergaard mentions that the q-parameters are dependent on the hardening exponent of the material. Numerous studies show that the q-parameters can be influenced by:

• stress multiaxiality

• material hardening

• void shape

• void arrangement

• void volume

• kinematic hardening

• plastic strains

A more detailed discussion of the factors can be found in [244].  

• Additional modifications of the Gurson model

In literature, numerous modifications of the original Gurson or GT model can be found. Some examples are mentioned in the following:

• Pan et al. [186] extended the Gurson Tvergaard (GT) model for the description of viscous material behaviour.

• Gologanu et al. [110, 264] derived a void growth model for ellipsoidal voids in an ellipsoidal unit cell.

• Feucht et al. [91] and Ockewitz and Sun [183] tried to improve the model for low stress multiaxiality by coupling the GT model with the Johnson-Cook model [132, 133].

• An alternative suggestion to improve the failure prediction in the shear range is given by Nahshon et al. [177]. Nahshon et al. took the yield function of the GT model without modifications. To improve the results in the shear range, they expanded the evolution law for the calculation of the void volume growth with an additional term:

  $${\dot{f}} = (1 - \text{f}){\dot{\tilde{\varepsilon }}}_{\text{ii}}^{\text{p}} + \text{k}_{\upomega}{\text{f}}\upomega({\tilde{\sigma }}_{\text{kl}} )\frac{{{\tilde{s}}_{\text{ij}} {\dot{\tilde{\varepsilon }}}_{\text{ij}}^{\text{p}} }}{{\upsigma^{\text{vM}} }}$$

  (35)

In Eq. 36 the function $\upomega({\tilde{\sigma }}_{\text{kl}} )$ depends on the third invariant of the stress deviator.

The kinematic and mixed isotropic kinematic approaches referred to in literature rely almost exclusively on the work of Gurson, Tvergaard, and Gologanu. An overview of these models can be found in Besson and Guillemer-Neel [42].

3.2.2.3 Rousselier Model

Based on the thermo-mechanical approaches by Lemaitre and Chaboche [154] and own early works [223], Rousselier derived a model for simulating ductile damage. His model [220, 224] describes the elastic-plastic deformation and failure behaviour of a porous material, i.e. a material with voids. Rousselier defined a continuum mechanical yield condition with an associated flow rule:

$${\varphi } = \frac{{{\tilde{\sigma }}^{\text{vM}} }}{\uprho} + {{D\,} \sigma }^{\text{k}}{\text{f}}\exp \left( {\frac{{{\tilde{\sigma }}^{\text{m}} }}{{\uprho \, \upsigma ^{\text{k}} }}} \right) -\upsigma_{0} \left( {{\tilde{\varepsilon }}^{{{\text{p}}^{\text{v}} }} } \right)$$

(36)

Here $\upsigma_{0}$ describes the hardening behaviour of the overall material. D and σ^k are two integration constants resulting from the derivation. The original Rousselier yield criterion was derived for isothermal behaviour and small strains. In [220] Rousselier discusses these two points. He indicates that mainly the yield curve and the material-dependent constant $\upsigma^{\text{k}}$ depend on the temperature. The second integration constant D is assumed to be material independent D = 2. In the form presented here, it is assumed that $\uprho \approx 1 - {\text{f}}$:

$${\varphi } = \frac{{{\tilde{\sigma }}^{\text{vM}} }}{{1 - {\text{f}}}} +\upsigma^{\text{k}} ({\text{T}}){\text{f}}\,{\text{D e}}^{{\tfrac{{{\tilde{\sigma }}^{\text{m}} }}{{(1 - {\text{f}})\, \upsigma^{\text{k}} ({\text{T}})}}}} -\upsigma_{0} ({\tilde{\varepsilon }}^{{{\text{p}}^{\text{v}} }} ,\;{\text{T}})$$

(37)

The assumption $\upsigma^{\text{k}} =\upsigma^{\text{k}} ({\text{T}})$ is not in contrast to the derivation of the original model. Whether D is temperature dependent or not is still an open point in literature.

Sainte Catherine et al. [229] and Poussard et al. [204] extended the Rousselier model for strain-rate dependent material behaviour. They selected a strain rate-dependent flow curve and extended the Rousselier model by defining $\upsigma^{\text{k}}$ as a function of strain rate:

$${\varphi } = \frac{{{\tilde{\sigma }}^{\text{vM}} }}{{1 - {\text{f}}}} +\upsigma^{\text{k}} ({\dot{\varepsilon}}){\text{f}}\,{\text{D e}}^{{\tfrac{{{\tilde{\sigma }}^{\text{m}} }}{{(1 - {\text{f}})\upsigma^{\text{k}} ({\dot{\varepsilon }})}}}} -\upsigma_{0} ({\tilde{\varepsilon }}^{{\text{p}}^{\text{v}} } ,{\dot{\varepsilon }})$$

(38)

These authors do not violate any assumptions made in the derivation. The theoretical nature of Rousselier the yield function is not affected by their modification.

In contrast to the extensions shown before Tanguy and Besson [265, 266] modified the yield condition more extensively. For the definition of their visco-plastic material law the authors introduced the effective equivalent stress $\upsigma^{\text{eff}}$. In their formulation $\upsigma^{\text{eff}}$ describes the behaviour of the matrix material and not of the overall material.

Lorentz et al. [163] showed that the constitutive equations of the Rousselier model are not convex with regard to all variables and therefore the solutions obtained do not have to be unique. To ensure a robust solution they proposed, among other things, to calculate the void growth not only from the plastic hydrostatic strains, but also to take into account the elastic parts. In addition they defined the yield condition and the constitutive equations with Cauchy stresses. Future applications will demonstrate whether and in which cases the new yield criterion provides comparable or better results compared to experiments.

Rousselier et al. [221, 222] formulated a polycrystalline damage model. Such a polycrystalline model allows the simulation of the orientation of crystal lattice and the resulting slip systems. This should improve the description of anisotropic and cyclic material behaviour. Rousselier et al. indicated that the needed computing time is not significantly higher than for other advanced material models and thus macroscopic structures can be simulated.

3.2.3 Discussion of the Void Growth Models

The micromechanical-based void growth models can be compared on the basis of the predicted void growth [2]. Only the empirical Lemaitre model, which uses a damage parameter, cannot be compared directly to the other models. For the comparison of the models the parameters and equations given in the original publications, see Table 1, are used.

Table 1 Comparison of void growth models

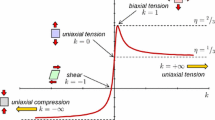
As postulated in the derivations perfectly plastic behaviour of the matrix material is assumed. For the comparison of the models, it is postulated that failure occurs when a critical void volume f_c is reached. If the plastic equivalent failure strain is plotted as a function of the stress multiaxiality [10, 237] so called limit strain curves result. With the assumption of a critical void volume fraction of ${\text{f}}_{c} = 0.05$ the limit strain curves calculated with the models are shown in Fig. 37.

Fig. 37

Limit strain curves determined with different void growth laws, f_c = 0.05

It can be seen that all the predicted curves are in a relatively narrow scatter band. This is not surprising, since all models are based on very similar basics.

At high multiaxialities the models of Rousselier, Gurson and Rice and Tracey (in the formulation of Gurson) produce comparable results. Lower fracture strains are only predicted by the original Rice and Tracey and McClintock model.

For low multiaxialities the Rousselier and the Rice and Tracey model (both formulations) give similar results. In comparison to this, the Gurson and McClintock model predicts much higher fracture strains.

3.3 Models to Describe Void Coalescence

The mechanism of void coalescence depends on the one hand on the microstructure of the materials, on the other hand on the external loads, see Sect. 2.3. However, which mechanism occurs and how to model it numerically has been investigated so far least of the three failure stages (initiation, growth, coalescence) [36, 187, 190].

Most authors assumed [137, 294] for their derivation that void coalescence can microscopically be described by plastic collapse of the material bridges between the single voids. Only the model proposed by Brown and Embury [61] describes the formation of shear bands. None of the models can predict which one of the two mechanisms is activated. Several approaches to model void coalescence are discussed in the following.

3.3.1 Coalescence When Reaching a Critical Void Volume, a Critical Void Growth or a Critical Damage Condition

The simplest and most often used approach is to assume the occurrence of void coalescence when a critical void volume ${\text{f}}_{\text{c}}$ [240, 281, 292] or a critical void growth $\left( {{\text{R}}/{\text{R}}_{0} } \right)_{\text{c}}$ [35, 36, 167, 246, 247] is reached.

$${\text{f}} \ge {\text{f}}_{c}$$

(39)

Based on experiments, Lemaitre also suggested that a critical damage [155] describes the final fracture. All these approaches are based on fractographic observations finding a void growth nearly independent of the multiaxiality of the stress state, e.g. [246].

The law defined by Tvergaard and Needleman [281], enabling the calculation of an accelerated void growth during coalescence, can be assigned to this model category as well. Since the original Gurson model predicts a, compared to experiments, too small void growth when considering the state of advanced void growth, Tvergaard and Needleman replaced the void volume fraction f by an empirical function ${\text{f}}^{*} ({\text{f}})$:

$${\varphi } = \left( {\frac{{{\tilde{\sigma }}^{\text{vM}} }}{{\upsigma_{0} }}} \right)^{2} +\,2{\text{f}}^{*} {\text{q}}_{1} \cosh \left( {\frac{{3{\kern 1pt} {\tilde{\sigma }}^{\text{m}} }}{{2\upsigma_{0} }}} \right) - 1 - ({\text{q}}_{1} {\text{f}}^{*} )^{2} = 0$$

(40)

For ${\text{f}}^{*} ({\text{f}})$, the following growth function is assumed:

$$\begin{aligned} & {\text{f}}^{*} = \left\{ {\begin{array}{*{20}l} {\text{f}} \hfill & {\text{for}} \hfill & {{\text{f}} \le {\text{f}}_{\text{c}} } \hfill \\ {{\text{f}}_{\text{c}} +\upkappa({\text{f}} - {\text{f}}_{\text{c}} )} \hfill & {\text{for}} \hfill & {{\text{f}} > {\text{f}}_{\text{c}} } \hfill \\ \end{array} } \right.\\ &{\text{with the acceleration coefficient}}\;\upkappa = \frac{{{\text{f}}_{\text{u}}^{*} - {\text{f}}_{\text{c}} }}{{{\text{f}}_{\text{f}} - {\text{f}}_{\text{c}} }}\\ \end{aligned}$$

(41)

${\text{f}}_{\text{c}}$ is the void volume at which void coalescence is starting. ${\text{f}}_{\text{f}}$ is the void volume at final fracture of the material. ${\text{f}}_{\text{u}}^{*}$ can be calculated with the relation ${\text{f}}_{\text{u}}^{*} = 1/{\text{q}}_{1}$. This approach simulates a continuous failing of the material. The empirical assumption of continuous formation has the advantage of resulting in less convergence problems in a finite element computation than a discontinuous formulation of the damage evolution.

In their studies, many authors find a more or less large dependence of the critical void volumes on the multiaxiality of the stress state [9, 35, 36, 136, 247, 257, 275], on the Lode angle [105, 235] and on the void shape [9]. This is contrary to experimental works of Shi et al. [247] finding a rather minor dependence on muliaxiality. These contradictions can possibly be solved by the volume portion of the voids. With cell model calculations, Kim et al. [136] showed that the influence of stress multiaxiality on the critical void volume is only minor when considering small initial void volumes (f₀ < 0.001). This observation is also described by Scheyvaerts and Pardoen [234].

When using any model of this category it has to be taken care that metallographic meaningful values are used for the critical void volumes and void growth rates.

3.3.2 Coalescence Triggered by Formation of Shear Bands Between Voids

Brown and Embury [61] assume that the voids coalesce due to the formation of shear bands between the single voids. As criterion for the critical strain $\tilde{\upvarepsilon }^{{\text{c}}}$ between void initiation and void coalescence, they found the following relation:

$$\tilde{\upvarepsilon }^{{\text{c}}} = \ln \left( {\sqrt {\frac{\pi }{{6{\text{f}}}}} - \sqrt {\frac{2}{3}} } \right)$$

(42)

This theory is supported by several experimental and numerical studies [149, 213, 245].

3.3.3 Plastic Limit Load-Model by Thomason for the Calculation of Void Coalescence

The best-known models describing the plastic collapse of material bridges between voids are the coalescence criteria by Thomason [271, 272, 275]. Thomason derived stress-based criteria for the description of void coalescence for different loading conditions and void geometries. In his derivations, he assumed cubic primitive arranged unit cells having one void at the center each, see Fig. 38. The material deformation behaviour of the matrix between the voids is assumed to be rigid/ perfectly-plastic.

Fig. 38

Cubic primitive arrangement of unit cells

For the derivation of a three-dimensional coalescence criterion [272, 273] he assumed periodically arranged cuboidal voids with quadratic cross sections. The principal load direction is perpendicular to the quadratic base. The distance of the voids perpendicular to the principal load direction is 2d, the void height is 2a and the side length of the quadratic voids is 2b, see Fig. 39. For the localisation zone between the single voids, Thomason assumed simple displacement rate fields. Doing so, he obtained an upper limit for the load [47]. Thomason approximated his complex solutions for the upper limit of the ultimate load with the empirically found relation:

$${\tilde{\sigma }}_{\text{I}}^{\text{c}} = {}^{\text{mat}}{\text{R}}_{\text{e}} \left( {1 -\upxi^{2} } \right)\left( {0.1\left( {\frac{{\upxi^{ - 1} - 1}}{\upkappa}} \right)^{2} + 1.2\, \upxi^{{ - \frac{1}{2}}} } \right) \quad {\text{with}}\,\upxi = \frac{\text{b}}{\text{d}}\;{\text{and}}\;\upkappa = \frac{\text{a}}{\text{b}}$$

(43)

Fig. 39

Sizes and distances of cuboidal voids with cubic primitive arrangement [272]

Here ${}^{\text{mat}}{\text{R}}_{\text{e}}$ is the yield strength of the matrix material. In order to be able to apply Eq. 43 to ellipsoidal voids as well, Thomason assumed that he can set the semi-axes of the ellipsoid (R_a und R_b) equal to the length of the sides of the cuboidal voids (a, b) [272, 273], see Fig. 40. He claimed this approximation to be valid as long as the void volume is smaller than 0.2. Analogous to Eq. 43 he obtained an upper limit for the ultimate stress acting macroscopically at the unit cell:

$${\tilde{\sigma }}_{\text{I}}^{\text{c}} = {}^{\text{mat}}{\text{R}}_{\text{e}} \left( {1 -\upxi^{2} } \right)\left( {0.1\left( {\frac{{\upxi^{ - 1} - 1}}{\upkappa}} \right)^{2} + 1.2\upxi^{{ - \frac{1}{2}}} } \right) \quad {\text{with}}\;\upxi = \frac{{{\text{R}}_{\text{b}} }}{\text{d}}\;{\text{and}}\;\upkappa = \frac{{{\text{R}}_{\text{a}} }}{{{\text{R}}_{\text{b}} }}$$

(44)

Fig. 40

Sizes and distances of ellipsoidal voids [272]

The Thomason-criterion is also used to compute a critical void volume ${\text{f}}_{\text{c}}$ that depends on the state of strain or stress. In this case, ${\text{f}}_{\text{c}}$ is not a material constant any more but a variable [293].

In order to incorporate material hardening, Pardoen et al. [187] enhanced the coalescence criterion derived by Thomason, Eq. 44. For the matrix surrounding the void, they assumed the following material law:

$${}^{\text{mat}}\upsigma_{0} = \left( {1 + \frac{{{E\varepsilon }^{\text{p}} }}{{{\text{R}}_{\text{e}} }}} \right)^{\text{n}} {\text{R}}_{\text{e}} \quad {\text{for}}\;{}^{\text{mat}}\upsigma_{0} > {\text{R}}_{\text{e}}$$

(45)

Equation 44 is replaced by the empirical formulation:

$$\upsigma_{\text{I}}^{\text{c}} = {}^{\text{mat}}\upsigma_{0} \left( {1 -\upxi^{2} } \right)\left( {\upalpha({\text{n}})\left( {\frac{{\upxi^{ - 1} - 1}}{\upkappa}} \right)^{2} +\upbeta({\text{n}})\upxi^{{ - \frac{1}{2}}} } \right) \quad {\text{with}}\;\upxi = \frac{{{\text{R}}_{\text{b}} }}{\text{d}}\;{\text{and}}\;\upkappa = \frac{{{\text{R}}_{\text{a}} }}{{{\text{R}}_{\text{b}} }}$$

(46)

The values of α and β depend on the hardening exponent n. In the range of $0 \le n \le 0.3$ the authors found $\upalpha({\text{n}}) = 0.1 + 0.217{\text{n}} + 4.83{\text{n}}^{2} \quad {\text{and}}\quad\upbeta({\text{n}}) = 1.24.$

3.3.4 Yield Criterion to Describe Material Behaviour in the Case of Plastic Collapse

To describe the material behaviour during void coalescence for arbitrary stress states, Benzerga [26] introduced an empirical yield condition based on the works by Pardoen and Hutchinson [187]:

$${\varphi } = {\tilde{\sigma }}^{\text{vM}} + \frac{3}{2}\left| {{\tilde{\sigma }}^{\text{m}} } \right| - \frac{3}{2}{\tilde{\sigma }}_{\text{I}}^{\text{c}} = 0$$

(47)

Seen in the principal stress space, his yield surface has the form of a double cone with the symmetry axis being on the hydrostatic stress axis, see Fig. 41.

Fig. 41

Benzerga yield surface in the principal stress space

The fact that the stress state around a void changes drastically during coalescence, as known from cell model calculations, is accounted for by the transition to the new yield surface. This approach models void coalescence as a continuous process.

3.3.5 Simulation of Void Coalescence Using Void Growth Models

Void growth models like the Rousselier- or the Gurson model also implicitly predict void coalescence. When the void volume fraction is about to reach 1 in the Rousselier- and Gurson model, respectively ${\text{q}}_{1}^{ - 1}$ in the GT model, the calculated stresses go to zero. Values of about one for the void volume however are unrealistically high seen from a metallographic point of view. Likewise the predicted stress decreasing for high void volumes is too slow. The stresses in the Rousselier model approach zero only asymptotically. Due to these deficiencies, these void growth laws are in practice almost exclusively used in combination with an additional coalescence criterion.

3.3.6 Discussion of the Models Describing Void Coalescence

The models describing coalescence processes differ in their mechanisms. It is therefore difficult to compare them directly. Pardoen et al. [190] studied the growth and coalescence processes of voids in technical pure copper with different material hardening for different stress multiaxialities. They compared the following coalescence criteria:

• critical void growth

• shearing of material bridges (Brown & Embury criterion)

• plastic collapse of material bridges (Thomason-criterion)

They concluded that none of the models can reproduce the whole spectrum of investigated multiaxial stress states independently.

3.4 Common Combinations of Damage Models and a Comparison

To describe the whole process of dimple fracture, model combinations describing all three phases (void initiation, void growth and void coalescence) are needed. In principle it is possible to combine any models depending on the used material behaviour. However, in practice certain model combinations have become established and are successfully applied by a variety of users in research and industry.

3.4.1 Gurson, Tvergaard and Needleman (GTN) Model Combinations

The certainly most common combination of models describing void initiation, void growth and coalescence is the so-called Gurson-Tveergaard-Needleman model combination (GTN model) [39, 56, 90, 164, 176, 182, 238, 258, 259, 262, 263]. Although it is a combination of three independent damage mechanics models, the GTN combination is very often just called GTN model. Following models are combined in the GTN model combination:

• Void initiation by Chu and Needleman [72]

• Model of void growth by Gurson und Tvergaard [277]

• Void coalescence criterion by Tvergaard and Needleman [281]

Besides the initial void volume ${\text{f}}_{0}$, the characteristic length ${\text{l}}_{c}$ (see Sect. 3.5) and the flow curve of the whole material, up to 10 additional material-depending parameters are needed for the GTN model:

$${\text{s}}^{\upvarepsilon} ,\;\upvarepsilon^{\text{N}} ,\;\uppsi,\;\upkappa,\;\upsigma^{\text{N}} ,\;\text{s}^{\upsigma} ,\;{\text{q}}_{1} ,\;{\text{q}}_{2} ,\;{\text{f}}_{\text{c}} \;{\text{and}}\;\upkappa$$

(48)

The large number of parameters that are in addition usually hard to determine presents a disadvantage [49, 51, 275] of the GTN model. From literature research it is known that different parameter sets can yield the same global response [1]. Especially the empirical parameters, having no actual physical meaning, cannot be identified independently. This problem will be discussed in Sect. 3.6.

3.4.2 Rousselier Seidenfuss (RS) Model Combination

Since the Rousselier model is not able to model the steep stress decrease occurring in void coalescence with sufficient accuracy, Seidenfuss proposed [146, 241] to combine the Rousselier model with a critical void volume for modelling void coalescence. This so-called RS model combination is often used in literature to describe the failure behaviour of different materials [67, 79, 81, 142–145, 191, 205].

• Modelling of void initiation. The above mentioned model combination assumes that an initial void volume ${\text{f}}_{0}$ exists, respectively, that the volume is created right after the yield stress is exceeded. These assumptions have been confirmed by a variety of authors, [8, 23, 59, 87, 89, 113, 125, 146, 190, 213, 243, 266, 274, 293].

• Void growth model of Rousselier [224]

• Void coalescence when reaching a critical void volume [240]

Besides the initial void volume ${\text{f}}_{0}$, the characteristic length ${\text{l}}_{\text{c}}$ and the flow curve of the material mix, only 3 more model dependent material parameters are needed when using the RS model combination.

Many practical applications show that the GTN and RS model combinations yield similar results [20, 31, 175, 191, 241].

3.4.3 Gologanu, Leblond and Devaux (GLD) Model with Thomason-Criterion

The GLD model for the simulation of material behaviour with void growth of nonspherical voids has been combined very often with the Thomason coalescence criterion in form of a yield function [26, 188, 189]. Additionally, different model combinations in connection with the GLD model have been used, e.g. [105].

• Modelling of void initiation. In a first approximation, it is also assumed that the whole initial void volume ${\text{f}}_{0}$ exists from the beginning on.

• Model of void growth by Gologanu et al. [110, 264]:

• Model of void coalescence by Thomason [272] and Benzerga [26]

3.5 Mesh Dependency of Results and Definition of a Characteristic Length

Caused by increasing material damage resulting from the initiation and growth of voids, the material sooner or later starts to soften. If the material softens in a certain limited volume, strain localisation resulting in a shear band can occur. Therefor material models being able to capture material softening must be capable of predicting the finite dimension of strain and damage localization.

All so far presented material models are local models. Local means here that e.g. the stresses at a material point A are only dependent on the local state variables at that point. Neighbouring material points do not influence the stresses at point A. However, such a behaviour would only be valid for a perfectly isotropic and homogeneous material. Macroscopically seen, real metals and metal alloys fulfill these requirements only in a coarse approximation since they have a discrete microstructure resulting in inhomogeneity on microscopic scale. Material constituents have a finite size and influence each other. A void growing at point A can influence the growth of a neighbouring void at point B. This reciprocal influence is not considered with local material models.

Real mechanical problems can usually not be solved analytically, numerical approximations like e.g. the method of finite elements are used. If material softening is simulated with a local material model in combination with finite elements, the ellipticity of the initial-boundary value problem is lost and a bifurcation problem results. This means that a homogeneous strain respectively damage field will get unstable against a strongly localized one [209]. Since the method of finite elements approximates the displacement field volume by volume, the strains respectively damages cannot localize in an infinitely thin band due to the mathematical definition. The width of the localization zone is coupled with the size of the elements. This effect leads to the very often in literature discussed pathologic mesh dependency of results. The localization problem can only be solved by introducing an additional parameter, the characteristic length ${\text{l}}_{\text{c}}$.

Using finite element computations, the localisation problem is solved in practice very often by introducing a constant material-specific element size in areas where material softening can occur [18, 19, 39, 46, 90, 182, 224, 240]. Very often authors assume that the width of localization zones is directly related with the distance of the primary, failure causing voids [18, 62, 100, 107, 128, 150, 188, 199, 224, 240, 262, 292].

Numerous practical applications [45, 62, 86, 182, 216, 240, 241, 262] show that the problem can be solved satisfactorily (seen engineering-wise) this way. For steel materials, element sizes in the range of a few tenth of a millimeter result [20, 62, 100, 107, 135, 146, 199, 224, 240, 266].

A more general approach to solve the localisation problem and to avoid the mesh dependency of results is provided by the so-called nonlocal damage models as discussed in detail in Sect. 4.

3.6 Determination of the Material Dependent Parameters

When using damage models for simulating specimen and component behaviour it is not only necessary to select appropriate models but also crucial to determine the needed parameters reliably and uniquely. Although the majority of the presented models is in use for over 20 years now, no verified standardised procedures for the determination of the used parameters are available.

Determination procedures described in literature and/ or used in practice:

• Metallographical and fractographic determination of the parameters out of the microstructure of the material,

• direct or iterative determination out of macroscopically measured values from simple specimen or

• adaption to results of cell model computations are described shortly in the following sections.

3.6.1 Determination of the Parameters Out of the Microstructure of the Material

Since the models have been derived from micromechanical theories, some of the needed material dependent parameters have a direct relation to the microstructure. Examples are the initial void volume fraction ${\text{f}}_{0}$, the characteristic length ${\text{l}}_{\text{c}}$ as well as the critical void volume fraction ${\text{f}}_{\text{c}}$. The determination can be done with metallographical cuts and/or with tomographic methods. The advantage of this method is that parameters can be determined isolated and conclusively without other parameters interfering. Drawbacks are an often occurring strong scattering of measured material constituents values as well as a relatively large fuzziness in the determination of the parameters [240].

3.6.2 Direct or Iterative Determination Out of Macroscopically Measured Values from Simple Specimens

Various parameters resulting from the derivations of the models or having been introduced as adjusting parameters do not have a direct relation to the microstructure and can therefore not be determined with metallographic methods. These parameters can partly be determined directly out of the load-deflection behaviour of a specimen or indirectly through a numerical adaption to experimental results.

The indirect determination is also called numerical calibration. Hereto, the deformation behaviour of a selected specimen is being simulated with finite elements. The parameter to be determined is varied in the simulation until a satisfying accordance between simulation and experiment is found.

The geometry of the specimen has to be chosen in a way that allows a preferably independent identification of the single parameters. The variation of a parameter should have a preferably large influence on the calculated macroscopic specimen behaviour. The numerical calibration has been tested in an European round robin test with only little success [31]. Values determined by the different participators turned out to have significant differences.

Springmann and Kuna [253, 255] present a method allowing an automatized determination of damage-mechanical parameters. Their approach is based on a nonlinear optimisation algorithm. With their method they tried to determine the material-dependent parameters out of the load-deformation behaviour of a simple specimen (notched flat tensile specimen, notched round tensile specimen, C(T)-specimen). However, it turned out that basically only one parameter can be determined with certainty. The other parameters have to be known. If more than one parameter is optimised with only one experiment, the parameters cannot be determined conclusively.

An advanced approach for a numerical parameter identification is presented by Springmann in [254]. Within this approach not only the macroscopic specimen length change is measured but additionally the displacement field on the surface with an optical measurement method [5]. Using a nonlinear optimisation algorithm several parameters can be adapted simultaneously. The authors claims that a maximum of 4 parameters can be identified with the adaption to the displacement field at the same time. The method could certainly be improved by using not only the result of one experiment but several specimen with different multiaxial stress states simultaneously.

3.6.3 Adaption to Results of Cell Model Computations

Often, damage-mechanical parameters are identified by adapting them to results of cell model calculations [136, 137, 141]. The results of cell model computations are strongly influenced by the chosen boundary conditions [141, 244]. The quantitative identification of parameters for real materials is therefore not or only with strong restrictions possible, additionally, the validity has to be scrutinized very critically.

3.7 Concluding Remarks Considering Damage-Mechanical Models

The different damage models have often been compared among each other with respect to their ability to predict the failure behaviour in comparison to experiments. Especially the GTN model and the Rousselier model—in its original as well as in the RS formulation—have been investigated quite often. However, it is in the nature of such comparisons that different authors come to different conclusions:

• For fracture mechanics, some authors conclude that the models yield similar results [175, 241], while others see an advantage in the Rousselier model, e.g. [20].

• Pineau [200] calculates the behaviour of notched round tensile specimen with the models of Rice & Tracey, Rousselier and GTN. Compared to experiments, all three models deliver similar results, however, the Rousselier model has a slight advantage.

• An European ring round robin test also showed that the RS model delivers better results than the GTN model when compared to experiments [31] although less material-dependent parameters are needed.

• When considering cyclic loading in both tension and compression, the GTN model surely will deliver better predictions since the Rousselier model cannot describe a decrease of void volume when loading in compression occurs. Research done by e.g. Steglich et al. [256] shows that the LPD model which is based on the Gurson model can basically describe the processes occurring in cyclic plasticization.

• However, when considering loading with low multiaxiality, the original Rousselier model seems to have an advantage compared to the GTN model as Besson et al. [41, 43] shoed using the example of fractures with shear lips. Due to the basic assumptions in the derivation of the discussed models none of the models will give satisfactory results for very low multiaxialities like pure shear.

• Perrin and Leblond [194] on the other hand see advantages in the GTN model. In a theoretical study connected with a self-consistent unit cell they find disadvantages in the mathematical formulation of the Rousselier model. A restriction of this study is the used ‘Rousselier’ yield condition in a modified form. It is not stated how or from where it was derived.

A disadvantage of the micromechanical-based damage models based on the employed approach is the disability to correctly model a sharp crack tip occurring in a structure. The damage-mechanical approaches model the growth of the crack by a decrease of stress in the damaged elements. Since an element has a finite volume, the crack thus always has the width of this volume. In practice this circumstance is explained with a damage area growing in the vicinity of the crack tip. Since the damaged elements are usually not deleted from the structure stiffness matrix, such elements can lead to numerical problems. Suggestions on how to transform the volume damage to a crack path can for example be found in [80, 170, 249].

4 Nonlocal Damage Models

In experiments that are carried out until specimen’s failure, i.e. the complete loss of integrity of the material, technical steels typically show the formation of a process zone: while large parts of the specimen are deformed purely elastically, micromechanical processes such as plasticity or damage take place locally limited. The size of the process zone is determined by the micromechanical structure of the material and thus represents a material property.

4.1 Localization

The increase of strain or stress caused by the nucleation of microcracks or voids in the vicinity of microstructural defects or inclusions can lead to the localization of strain [226] in the process zone. This results in an increased evolution of damage [278, 279] and therefore to a further narrowing of the micromechanical active region. With increasing damage the load bearing capacity of the material reduces; with increasing strain a local decrease of stress is observed as local softening [109]. The force-displacement-curves of tensile tests with porous materials with hardening matrix materials show a maximum, which is followed by a region with a negative slope. This is caused by geometrical and material softening.

As shown in Sect. 3, in the framework of continuum mechanics, material softening can be reproduced by the consideration of damage in a plasticity model. With increasing damage lower stresses lead to plastic flow, the yield surface and thus the elastic region decrease.

The static equilibrium of a simple softening plastic continuum is unstable [180] and leads to strain localization. Mathematically, this means the loss of ellipticity [55] of the underlying system of differential equations, which is now of hyperbolic type.

The strain localization at the loss of ellipticity theoretically takes place in an infinite small zone. If a discretization of the continuum under investigation is carried out prior to the solution of the boundary value problem, the size of the localization zone is determined by the discretization size [55, 197]. When using the finite element method this effect is called mesh sensitivity: for meshes of smaller element sizes, the size of the localization zone reduces. As a result, the energy dissipated by damage converges to zero for infinitesimally small elements. This contradicts the experimental observation that both the size of the localization zone as well as the energy dissipated by the failure of the material are material properties [109].

4.2 Regularization Methods, Non-local Formulations

As shown in the previous section, the modeling of ductile damage within the framework of continuum mechanics of simple materials in combination with the numerical solution of the corresponding system of partial differential equations results in two fundamental properties of the considered problem: First, the material softening leads to instability of the material behavior. Second, material instability and strain localization are directly connected due to the strong interactions between increase of strain and evolution of damage for simple continua. For the numerical treatment of the boundary value problem this results in a size of the localization zone that depends on the discretization.

One possibility for setting a fixed size of the localization zone when using the FEM is to define a characteristic element size [38, 39, 184, 239]. In this method strain localization and material softening will take place within a certain element, element row or element layer, depending on the dimension of the problem. The element edge length becomes a model parameter. Thus, the accuracy of the solution cannot be judged by conventional convergence criteria. Furthermore, considerable numerical disadvantages arise in the treatment of problems with different length scales.

With the help of regularization approaches material softening and strain localization can occur independently. The use of so-called non-local formulations thus differs fundamentally from the pragmatic method above: the loss of ellipticity and the influence of discretization are eliminated [53, 196, 198, 259, 260].

The reduction of the mesh dependence which occurs when continuum damage models are used numerically was the subject of numerous physically motivated and phenomenological approaches. Reviewing articles can be found in [21, 85, 130, 193].

The fundamental approach of non-local formulations to reduce localization effects caused by discretization is to consider a finite region of surrounding material in the underlying equations

$$f(\omega ) \Rightarrow f(\omega ,\bar{\omega }),$$

(49)

where $\omega$ and $\bar{\omega }$ are local and non-local variables, respectively. This can be done efficiently by averaging a variable within an area characterized by a certain length parameter.

Depending on how averaging is done non-local formulations can be divided into non-local integral types [22, 196], explicit [54] and implicit gradient methods [84, 192]. Other classification may distinguish whether internal variables of a constitutive model or stresses and strains are averaged. Finally non-local formulations may be divided into weakly non-local and strongly non-local formulations [21, 130].

4.2.1 Nonlocal Integral Types

When using non-local integral type approaches a local variable $\omega$ is replaced by its non-local average $\bar{\omega }$ which is calculated by integrating the weighted local variable

$${\bar{\omega }}({\text{x}}) = \frac{1}{\text{B}}\int\limits_{\text{B}} {{\text{G}}(\upxi)}\upomega({\text{x}} +\upxi){\text{dB}}.$$

(50)

The influence of the surrounding material characterized by the distance vector $\upxi$ on the considered material point is given by the definition of the weight function ${\text{G}}(\xi )$. Here, typically GAUSSIAN or similar bell-shaped functions are used, which must at least satisfy the condition

$$\frac{1}{\text{B}}\int\limits_{\text{B}} {{\text{G}}(\upxi)} {\text{dB}} = 1.$$

(51)

Integral type approaches are strongly non-local methods, as the integration is carried out over the entire body under consideration. They are numerically robust methods and can in principle be applied to every type of constitutive models. In the treatment of complex geometries, the weight functions ${\text{G}}(\xi )$ must meet high standards, which requires the use of numerically robust algorithms in three dimensions.

4.2.2 Explicit Gradient Formulations

A formulation of Eq. 50 using gradients can be derived using Taylor series at the material point under consideration

$$\omega (x+\xi) = \omega (x) + \nabla\omega (x)\cdot\xi +\frac{1}{2!}\nabla(\nabla\omega (x)):\xi\otimes\xi +\frac{1}{3!}\nabla^{(3)}\omega (x)\dots\xi\otimes\xi\otimes\xi + \cdots$$

(52)

Assuming isotropy and substituting back in Eq. 50, Eq. 52 gives

$$\bar{\omega }(x) = \omega (x) + c\nabla^{2} \omega (x) + d\nabla^{4} \omega (x) + \cdots$$

(53)

and after neglecting gradients of higher order an explicit gradient formulation of Eq. 50 can be written in reduced form as

$$\bar{\omega }(x) = \omega (x) + c\nabla^{2} \omega (x).$$

(54)

Explicit gradient methods are weakly non-local methods, since only the infinitesimal neighborhood of a material point is taken into account. Compared with nonlocal integral type approaches explicit gradient formulations possess significant numerical disadvantages [131, 193]. The constant $\sqrt c$ is introduced as an length parameter that controls the influence of the surrounding material.

4.2.3 Implicit Gradient Formulations

Differentiating Eq. 53 twice and reordering gives

$$\nabla^{2} \omega (x) = \nabla^{2} \bar{\omega }(x) - c\nabla^{4} \omega (x) - d\nabla^{6} \omega (x) - \cdots ,$$

(55)

and after substituting Eq. 55 back into Eq. 53

$$\bar{\omega }(x) - c\nabla^{2} \bar{\omega }(x) = \omega (x) + (d - c^{2} )\nabla^{4} \omega (x) + \cdots$$

(56)

Thus, after neglecting higher gradients as done in Eq. 54 one finds an implicit gradient method to carry out the non-local averaging as

$$\bar{\omega }(x) - c\nabla^{2} \bar{\omega }(x) = \omega (x).$$

(57)

As well as non-local integral type approaches, implicit gradient formulations are strongly non-local formulations and are much easier to implement numerically compared to explicit methods. However, the partial differential equation of the HELMHOLTZ type Eq. 57 represents an additional field equation which necessitates the formulation of additional, possibly non-physical boundary conditions. A critical discussion of possible boundary conditions can be found in [193].

4.2.4 Non-local Formulations of Ductile Damage Models

The development of non-local formulations of ductile damage models has been the subject of numerous publications. Non-Local modifications of the GTN-model (Sect. 3.4.1) can be found in [82, 129, 151, 160, 210, 280]. Samal and coworkers [231] developed an implicit gradient formulation of the ROUSSELIER model (Sect. 3.4.2, [224]. From the above-mentioned modifications, the implicit gradient formulations used in [209, 230] spatially average the rate of the (modified) void volume fraction in a non-local sense

$$\dot{d} - c\nabla^{2} \dot{d} = \dot{f}.$$

(58)

The non-local modification of the GTN-model by Linse et al. [126, 160] is based on the micro-dilatational approach [95] and replaces the dilatational part of the plastic strain $\varepsilon_{p}$ by its non-local spatial average

$$\bar{\varepsilon }_{p} - c\nabla^{2} \bar{\varepsilon }_{p} = \varepsilon_{p} ,$$

(59)

where the rate of the non-local plastic strain enters the evolution equation for the growth of existing voids.

5 Combination of Damage Models in the Brittle-Ductile Transition Region

In the brittle and brittle-ductile transition region of ferritic steels cleavage fracture initiates at microcracks, while microvoids nucleate as a result of plastic deformation in the upper shelf. A consistent and independent description of these micromechanical processes is needed if the entire toughness region of ferritic steels is to be analyzed.

5.1 Beremin Model—Uncoupled Probabilistic Model for Cleavage Fracture

For ferritic steels, the brittle and transition region is characterized by a large scatter of fracture toughness values that results from the statistical distribution of microcracks. Using the WEIBULL theory, the BEREMIN-model was developed to describe cleavage of ferritic steels [37, 174]. Here, three fundamental assumptions are made:

• microcracks are created during plastic deformation; the probability density function for the size of the microcracks follows a constant power law

• the critical stress of each microcrack is determined by the GRIFFITH criterion

• weakest-link: the propagation of one single crack leads to the failure of the whole structure.

Under these assumptions, the probability of failure for a specific load level L is derived by

$$P_{f} (L) = 1 - { \exp }\left\{ { - \left( {\frac{{\sigma_{W} (L)}}{{\sigma_{u} }}} \right)^{m} } \right\}.$$

(60)

The WEIBULL-stress $\sigma_{W}$ is calculated as

$$\sigma_{W} (L) = \sqrt[m]{{\frac{1}{{V_{0} }}\int\limits_{{V_{pl} }} {(\sigma_{I} (L))^{m} dV} }},$$

(61)

where $\sigma_{I}$ is the maximum principal stress and $V_{pl}$ the plastic volume of the structure. The reference volume $V_{0}$ must be large enough to represent the microstructure of the material as well as small enough to fulfill the requirements of the Griffith criterion. If the reference volume is chosen constant, the BEREMIN model uses two model parameters: the WEIBULL reference stress $\sigma_{u}$ and the WEIBULL-modulus $m$.

Bordet et al. [52] showed that most of the problems that arise in engineering applications of the model are a result of a oversimplified description of local cleavage in the BEREMIN-model. Most modifications of the BEREMIN-model [37, 100–104, 139] change the calculation of the WEIBULL-stress. Bernauer et al. [40] proposed a modification that takes into account that the nucleation of voids is promoted by the presence of carbide particles. Consequently, the number of cleavage initiation points is reduced with the increase of the nucleated void volume fraction.

Note that in the sense of the classification of damage models given in Sect. 3.2 the BEREMIN-model and its modifications must be termed uncoupled, since cleavage is not modeled for each individual microcrack but rather by quantifying the cleavage fracture probability of many microcracks.

In principle, the BEREMIN-model for the calculation of the probability of cleavage fracture can be used together with a ductile damage model to account for ductile crack growth preceding cleavage in the transition region [4, 227]. In conjunction with the Griffith criterion the stress fields must be resolved very accurate which requires the use non-local ductile damage models in the presence of high stress gradients. However, following the weakest-link assumption, the model cannot predict cleavage crack arrest and thus most likely underestimates the fracture toughness values in the case of such effects as pop-in or crack arrest, see e.g. [127, 161]. In [161] fracture toughness values were predicted by numerical simulation of fracture mechanics tests using a combination of a non-local GTN-model together with the BEREMIN model. The calculated values agree well with experimental results in the brittle region and in the ductile region. However, in the brittle-ductile transition region, the predicted fracture toughness values are much smaller than the experimental values.

5.2 Coupled Models for Cleavage Softening

Among simplified strip yield models, e.g. [98], softening of metals by cleavage is mostly modeled in a coupled way by means of cohesive zone elements, see e.g. [140]. Here, softening initiates when the maximum principal stress exceeds the cohesive strength and the work of cohesive separation can be correlated to the fracture toughness.

The combination of cleavage softening with ductile damage models was realized numerically using computational cell simulations, see e.g. [99, 179, 248]. Here, discrete volumes of material (cells) are removed on a the basis of a stress criterion for cleavage, ductile damage is modelled in a continuous way. The results strongly depend on the discretization, since not only the accuracy of the computed stress and strain fields depend on the chosen mesh size, but the properties of the microstructure are directly correlated to the chosen cell size.

In [127] a consistent continuum formulation covering both cleavage softening and ductile damage is formulated using a non-local modification of the GTN model [126, 160] together with a cohesive zone model [219] for cleavage. The developed formulation captures many effects known from experiments such as the constraints sensitivity, cleavage initiation, cleavage crack propagation and crack arrest (pop-ins), a size independent lower-bound toughness and the possibility of stable cleavage crack propagation. The simulations were performed with homogeneous material properties and a high sensitivity with respect to small deviations of the material parameters was obtained in the transition region. However, in contrast to the application of probabilistic models, statistical predictions on the failure of structures cannot be obtained with this type of model.

6 Conclusions

Within this article the micromechanical processes leading to dimple fracture are discussed in detail. It is shown that for this kind of fracture mode the processes leading to material failure are similar for very different metals and metal alloys. Especially the processes leading to void initiation and void coalescence are complex and depend to a great extent on the microstructure of the selected materials. To describe the three phases of dimple fracture at high stress multiaxialities a large number of different mathematical approaches are available. The special focus of this paper is on so-called micromechanical-based models.

For the micromechanical derivation of the void initiation models, many simplifications must be made concerning the microstructure, the material behaviour and the initiation mechanisms. Hence, to select an adequate model for the considered material metallographic examinations are essential. It is also recommended to calibrate the material specific parameters on the basis of metallographic observations when using such micromechanical-based models. To take all the parameters only from literature or to use only numerical calibration procedures is not recommended at all.

Since the basics for the derivation of the void growth models are similar, the received results are comparable when taking into account the assumptions made in the derivations of the models. However, when these assumptions are not valid for a given material, e.g. when observing strain hardening, this can lead to different results of the models. In conclusion it can be said that none of the discussed void growth models is able to describe exactly the micromechanical processes in a strain hardening material in a wide range of stress multiaxiality. The Gurson model in the GT, LDP and GLD formulation has probably the largest potential in describing void growth.

The particular void coalescence models describe different kinds of merging mechanisms. Therefore a direct comparison is difficult. Pardoen et al. [190] compared different coalescence criteria. They came to the conclusion that none of the models is able to describe independently the whole area of the examined multiaxiality range. To simulate the different micromechanical processes during void coalescence, probably several models must be coupled.

In summary it can be said that the all models should be selected with respect to material and microstructure. If possible, the material-dependent parameters needed for the models should be determined metallographically or the numerically adjusted parameters should be verified with metallographic values. It is surely not recomended to regard the parameter determination as pure adaptation procedure to experimental values. Thus, there is a risk that the micromechanical background of the models is lost and the models are reduced to pure ‘fitting models’ [275].

The greater the number of material-dependent parameters is, the more difficult a unique determination is. Especially for the GTN-model, the large number of parameters partly difficult to access is often felt as a disadvantage [49, 51].In particular, the empirical parameters which have no physical background, cannot be determined independently. The following quote summarises the problem in determining the material-dependent constants:

The limited success that has been achieved with the dilational-plastic models of ductile fracture is mainly the result of the large number of adjustable parameters that have been incorporated in the models. These models can now act in an analogous manner to a polynomial curvefitting technique, and the parameters (q₁, q₂, f_c, f_F, f_u) can be suitably adjusted to give a reasonable fit to any particular set of experimental results [275].

While basically applicable for the prediction of cleavage failure probabilities, uncoupled BEREMIN-type models most likely overestimate cleavage fracture in the presence of ductile damage. For the case of using coupled cleavage softening models, it remains open to perform (numerically expensive) Monte-Carlo-simulations for statistical failure predictions. In both cases, non-local formulations of ductile damage models are advantageous.