Keywords

1 Introduction

Learning of a new motor behaviour is one of the key skills that a humanoid robot should have. Programming by demonstration is a popular way to acquire new motor behaviour [1], which can be done by using different sensory systems, i.e. visual [2] or kinaesthetic guidance [3]. The main advantage is that the robot kinematics is adapted and the posture is preserved even for redundant robots. A common way of learning kinematic trajectories is by using the Dynamic Movement Primitives (DMPs) [4]. To execute the desired DMP trajectory on a robot the underlying controller, usually based on high gain feedback loop, is employed to guarantee that the trajectory is accurately executed. However, using high gains in a feedback loop makes robots inherently unsafe for interaction with the environment or humans, due to the high interaction forces that may occur during unforeseen contacts.

Different approaches can be used to minimize the interaction forces during contacts: e.g., by actively detecting them using proximity sensors or artificial skin [5]; by using passively compliant mechanical structures like artificial pneumatic muscles [6] or by using control algorithms for active compliance [7]. The latter is achieved using the control approaches based on the inverse dynamic models. Obtaining a dynamical model is a challenging and time consuming task even for experts. But it only needs to be done once. On the other hand, it is impossible to obtain the generic dynamic model, even for simple task like table wiping, due to the unknown friction between the sponge and the table. Therefore, instead of modelling the task, we propose a novel method for learning yet unknown and undefined task-specific torque primitives. The proposed method would replace the need for modelling the task dynamics and if the dynamic model is already in use, it will compensate for additional uncertainties. By learning the exact dynamic model of the task, one can achieve both the compliant robot behaviour and the accurate tracking of the desired motion. While accurate tracking is required for proper task execution, the compliant behaviour is an essential feature for safe interaction with the environment or with a human [8].

While the DMPs and their possible modulations during contact with the environment have been thoroughly analysed [9–12], their extension towards torque controlled robots was not sufficiently explored yet. Inspired by the human sensory motor ability [13–16] we propose a novel method based on Compliant Movement Primitives (CMPs), which represent a new model-free approach, while keeping simple and smooth modulation properties of the position based DMPs. Similar to what can be observed in humans [14], the proposed approach independently learns the kinematic trajectory in Cartesian space (DMPs) and the task dynamics in the joint space (TPs). The proposed approach exploits the motion pattern encoded by the DMPs to acquire the task-specific torques and encodes them as TPs.

The first step in gaining the CMPs is learning the desired motion trajectory in DMP. Next, the DMP trajectory is executed on a robot using low-feedback gains with the proposed method for learning the task-specific TPs. In each subsequent step the TPs are then used as a feedforward term, which essentially represents new learned task-specific dynamics. The stability of the proposed controller is assured by keeping the low-gain feedback loop, which ensures that the desired task is performed safely even in unstructured environment or with humans. While the proposed approach eliminates the need for dynamical modelling, the CMPs still have to learn TPs for each task variation. Once several CMPs for different task variations are learned, they can be added to a database and statistical generalization can be used as in [17]. This allows learning and performing different variations of the same task in a compliant manner without the need of any analytical models of the task or programming experts.

2 Compliant Movement Primitives

Compliant Movement Primitives (CMPs) h(t) are defined as a combination of kinematic trajectories encoded in Dynamic Movement Primitives (DMPs) and corresponding task-specific dynamics encoded in Torque Primitives (TPs)

$$ \varvec{h}\left( t \right) = [\ddot{\varvec{y}}_{d} \left( t \right), \dot{\varvec{y}}_{d} \left( t \right),\varvec{y}_{d} \left( t \right),\varvec{\tau}_{f} (t)] $$
(1)

Here \( {\ddot{\varvec{y}}}_{d} (t),\dot{\varvec{y}}_{d} (t),\varvec{y}_{d} (t) \) are vectors of the desired task-space accelerations, velocities and positions respectively encoded in the DMPs, and \( \varvec{\tau}_{f} (t) \) is the vector of corresponding task-specific feedforward joint torques encoded in TPs.

First the kinematic part is obtained using the learning by demonstration approach. A short overview of the periodic version of the DMPs [4, 12] with the recursive learning algorithm is given first. The following equations are valid for one DOF; for multiple DOF the equations are used in parallel. A nonlinear system of differential equations defines DMP for periodic movements

$$ \dot{z} =\Omega \left( { \alpha_{z} \left( { \beta_{z} \left( {g - y} \right) - z } \right) + f\left( \phi \right)} \right), \quad \dot{y} =\Omega z, \quad \dot{\phi } =\Omega , $$
(2)

where Ω is the frequency of motion, ϕ is the phase, α z and β z are the positive constants set to 8 and 2 respectively. They ensure critical damping so that the system monotonically converges to the trajectory oscillating around anchor point g. The nonlinear part f(ϕ) is given by

$$ f\left( \phi \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \psi_{i} w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} \psi_{i} }},\quad \psi_{i} = \exp (h(\cos (\phi - c_{i} ) - 1)), $$
(3)

where w i are the weights that define the shape of the trajectory, ψ i are the Gaussian like kernel functions where parameter h defines their width, and c i is equally spaced between 0 and 2π. To acquire the target signal for recursive learning the Eq. (2) is rewritten in the form

$$ f_{t} (t) = \frac{{\ddot{{y}}_{d} }}{{\Omega ^{2} }} - \alpha_{z} (\beta \_z(g - y_{d} ) - \frac{{\dot{y}_{d} }}{{\Omega }}) , $$
(4)

where \( {\ddot{y}}_{d} ,\,\dot{y}_{d} ,\,y_{d} \) are respectively the desired acceleration, velocity and position of the desired trajectory. To update the weights w i , an incremental regression is used:

$$ w_{i} \left( {t + 1} \right) = w_{i} \left( t \right) + \psi_{i} P_{i} (t + 1)e(t), $$
(5)
$$ P_{i} \left( {t + 1} \right) = \frac{1}{\lambda }\left( {P_{i} \left( t \right) - \frac{{P_{i}^{2} \left( t \right)}}{{\frac{\lambda }{{\psi_{i} }}P_{i} \left( t \right)}}} \right), $$
(6)
$$ e(t) = f_{t} (t) - w_{i} (t), $$
(7)

where P i is the covariance. The initial parameters are set to P i  = 1, w i  = 0 and λ = 0.995 (see [10] for details).

To obtain the dynamical part of the CMP, i.e. the corresponding TP, the motion is executed on a robot using a low gain feedback loop and a learning algorithm for acquiring the task specific torque primitive (TP). The desired motion \( {\ddot{y}}_{d} ,\,\dot{y}_{d} ,\,y_{d} \) encoded in DMPs is executed using the following control law

$$ \varvec{\tau}_{u} = {\mathbf{J}}^{\# } \left( {\mathbf{K}}_{p} \left( {\varvec{y}_{d} - \varvec{y}} \right) + {\mathbf{K}}_{d} \left( {\dot{\varvec{y}}_{d} - \dot{\varvec{y}}} \right) + {\mathbf{K}}_{i} \left( {{\ddot{\varvec{y}}}_{d} - {\ddot{\varvec{y}}}} \right) \right) + {\mathbf{NK}}_{n} \dot{\varvec{q}} +\varvec{\tau}_{f} (\phi ), $$
(8)

where, \( {\mathbf{J}}^{\# } \) is the pseudo inverse, N is the null-space matrix and K p , K d , K i and K n are the constant gain matrices selected such that the robot behaves compliantly, i.e. set to match the low feedback gain requirements.

Here \( \varvec{\tau}_{f} (\phi ) \) is the feedforward term encoded in TPs. For one DOF it is given by

$$ \tau_{f} (\phi ) = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \psi_{i} w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} \psi_{i} }}, $$
(9)

where the kernel functions ψ i are defined as in Eq. (3) and the weights are updated by inserting the error given by

$$ \varvec{e}\left( t \right) = {\mathbf{J}}^{\# } \left( {\alpha_{t} \left( { y_{d} \left( t \right) - y\left( t \right)} \right) + \beta_{t} \left( {\dot{y}_{d} \left( t \right) - \dot{y}\left( t \right)} \right)} \right) $$
(10)

into Eqs. (5)–(6). The rate of learning is defined by setting parameters \( \alpha_{t} \) and \( \beta_{t} \).

3 Experimental Evaluation

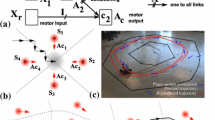
The proposed method was evaluated on a 3-DOF planar robot simulated in Matlab using a Planar Manipulator Toolbox [18]. The simulation step was set to 0.01 s and the link lengths of the robot were set to 1 m. The initial task space position of the robot was y 0 = [1, 1.5] m. The initial robot configuration (green line) is shown in Fig. 1.

Fig. 1
figure 1

Left hand side plot shows eight examples of the initial (blue) and the learned (red) robot behaviour in Cartesian space. Right hand side plots show one detailed example of the initial (top) and the learned (bottom) robot behaviour in Cartesian space

Full size image

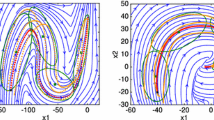
The task was to reach towards certain points in space and return back to the initial position. A proposed controlled given by Eq. (8) with low feedback gains was used. Note that inverse dynamical model for compensating the robot dynamics was not used. This task is also similar to the task used in a study of human sensory motor learning ability reported in [14]. To compare the results we chose eight different positions equally spaced on a circle with a radius of 1 m from the initial position. The desired Cartesian kinematic trajectories y d were encoded in DMPs as a part of the CMPs. They are shown with black dotted lines on the left plot in Fig. 1.

Note that the desired kinematic trajectory is encoded in the task-space, i.e. Cartesian space, and the corresponding task-specific torques are encoded in the joint space, see Eq. (8). The mapping of the task-space error e(t) to the joint space is done by using a pseudo-inverse of the Jacobean. The learning of the TPs was performed after each iteration of the executed motion. Note that each executed motion started from the same initial position. The left hand side plot in Fig. 1 shows comparatively eight different examples between initial movement execution (blue lines) and the last iteration of learning (red line). One can see in all eight examples that the proposed approach was able to learn proper TPs in order to execute the task accurately. Note that in this example the proposed system was learning the unknown robot dynamics.

The successful learning of the torque primitives can be seen on the right hand side plots in Fig. 1 where we compare the behaviour of one representative example, i.e. moving to the right. For clarity we only show the first half of the movement. The top right plot shows the robot’s behaviour for initial movement execution, i.e. feedforward torques were zero. Here we can clearly see that the low gain feedback loop is not able to track the desired trajectory accurately. However, by applying the proposed learning algorithm to obtain the TPs, the tracking performance was improved significantly. The robot’s behaviour after learning, i.e. after 25th iterations, is shown in the bottom plot, where perfect matching between the desired (black dotted line) and actual (blue line) Cartesian position can be observed.

The evolution of the TPs for all 25 iterations and for all three joints is shown in Fig. 2, were the red line shows the initial TPs, the thick blue line shows the final TPs and the black dotted line shows the ideal task-specific torques computed by using the exact inverse dynamic model.

Fig. 2
figure 2

Comparison with an ideal inverse dynamic model and evolution of the TPs during 25 learning iterations for all three joints. The initial TPs are in red, the final TPs are in blue and the ideal joint torques using exact dynamic models are shown with black dotted line

Full size image

Note that the initial torque primitives are zero. By comparing the TPs with the ideal dynamical model, we can see that they are similar in shape and amplitude. This shows that the proposed algorithm can successfully learn the required task-specific dynamics autonomously.

The proposed learning algorithm essentially minimises the error function given by Eq. (10). Thus, when e(t) in Eq. (10) is converging towards 0, \( \varvec{\tau}_{f} (\phi ) \) in Eq. (9) is converging toward the exact inverse dynamic model. Ideally, if e(t) in Eq. (10) is zero then \( \varvec{\tau}_{f} (\phi ) \) in Eq. (9) is the perfect inverse dynamic model.

The convergence of the proposed algorithm and the ability to re-learn the task-specific torques is also illustrated on the left hand side plot in Fig. 3, where the mean value and the standard deviation of the tracking error for all eight examples are shown. In studies about humans it has been demonstrated that they can quickly adapt to the changes in the task dynamics [14]. To show that the proposed approach can also cope with changes of task dynamics, the parameters of robot dynamics were changed after the 25th iteration. In the 26th iteration the inertia parameter of the robot was increased by a factor five and remained afterwards at that new value.

Fig. 3
figure 3

Left plot shows the average error and the standard deviation (shaded area) for all eight examples. Right plot shows the interaction force in case of collision using the proposed control approach (CMP) and standard feedback (FB) control approach with high gains

Full size image

In general the learning rate of the proposed algorithm is defined with the gains α t and β t . If the gains are set too high, the system may potentially be destabilized, or vice versa, if the gains are too low, the learning rate would be slow and impractical. We set them empirically to α t  = 20 and β t  = 10, which results in similar learning rate as observed in human sensory motor learning ability reported in [14]. The results are shown on the right hand side plot in Fig. 3, where we can see that only 10 iterations were needed in order to obtain perfect tracking performance even after the dynamics was significantly altered, i.e. inertia parameters were increased by factor five. This also shows that the proposed approach can cope with sudden changes in the task dynamics and re-adapt online if necessary.

Since low feedback gains are used in combination with the CMPs we also assume that the interaction force in case of a collision with an unforeseen object will be significantly smaller compared to the general feedback approach with similar tracking performance. To investigate and compare the performance in case of unforeseen collisions, a solid wall was placed on the desired end-effector path. The results are shown on the right hand side plot in Fig. 3, where the normalized interaction force at the end effector is given. The blue line shows the results of the proposed approach and the red line shows the results of the high gain feedback control.

On the right hand side plot in Fig. 3 we can see that, at the beginning of the impact, resulting forces are similar in both cases. This was expected since the initial force is mainly a result of the robot inertia, i.e. the robot is suddenly forced to stop in both cases. This also explains why the forces are almost identical at the beginning of the impact. However, one can see that by using the proposed approach (CMPs), the impact force only appears initially and then goes towards zero. In this particulate example the normalized force impulse was only 0.035 Ns. On the contrary, in the case of the high gain feedback control, the force after impact remains rather large, i.e. it keeps almost the same value as it was at the beginning of the impact, resulting in a large force impulse of 0.33 Ns. In the latter case the force impulse was almost 10 times larger compared to the CMPs approach.

4 Conclusion

It was shown that the proposed approach (CMPs) can successfully learn both the kinematic trajectories in Cartesian space encoded with the DMPs and the corresponding torque primitives in the joint space encoded in TPs. The main contribution of the proposed approach is learning of the previously unknown task specific dynamics. With the proposed learning method, the control system was able to significantly improve the tracking accuracy in each of the subsequent iterations. Once the TPs are fully learned, the CMPs ensure accurate task execution and, at the same time, compliant robot behaviour. As such, the proposed learning framework enables simple and computationally inexpensive control of dynamically challenging tasks. Moreover, the results were also similar to human studies of sensorimotor learning abilities. Since learning of the task-specific dynamic is done autonomously by using a low gain feedback loop, the compliant behaviour is maintained during learning of task-specific torque primitives. This makes the robot safe for working in unstructured environments or with humans even during learning.