Finding Optimal Discretization Orders for Molecular Distance Geometry by Answer Set Programming

Abstract

The Molecular Distance Geometry Problem (MDGP) is the problem of finding the possible conformations of a molecule by exploiting available information about distances between some atom pairs. When particular assumptions are satisfied, the MDGP can be discretized, so that the search domain of the problem becomes a tree. This tree can be explored by using an interval Branch & Prune (iBP) algorithm. In this context, the order given to the atoms of the molecules plays an important role. In fact, the discretization assumptions are strongly dependent on the atomic ordering, which can also impact the computational cost of the iBP algorithm. In this work, we propose a new partial discretization order for protein backbones. This new atomic order optimizes a set of objectives, that aim at improving the iBP performances. The optimization of the objectives is performed by Answer Set Programming (ASP), a declarative programming language that allows to express our problem by a set of logical constraints. The comparison with previously proposed orders for protein backbones shows that this new discretization order makes iBP perform more efficiently.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Experiences of Nuclear Magnetic Resonance (NMR) are able to estimate distances between some pairs of atoms of a given molecule [12]. The problem of finding the possible conformations of the molecule that are compatible with this distance information is known in the scientific literature as the Molecular Distance Geometry Problem (MDGP) [6, 12, 18]. Generally, the distance information is given through a list of lower and upper bounds on the distances, i.e. by a list of real-valued intervals [19]. The MDGP, by its nature, is a constraint satisfaction problem, which is NP-hard [24].

Let $G=(V,E,d)$ be a simple weighted undirected graph where the vertices in V represent the atoms of the molecule and $d : E \rightarrow \mathbb {R}_+$ assigns positive weights d(i, j) to edges which are in E if the distance between the atoms i and j is available. The MDGP asks therefore to find an embedding $x : V \rightarrow \mathbb {R}^3$ satisfying the distance information, i.e. a conformation in the three-dimensional space such that:

$$\begin{aligned} \underline{d}(i,j) \le \Vert x_i - x_j \Vert \le \overline{d}(i,j) , \quad \forall (i,j) \in E, \end{aligned}$$

(1)

where $\underline{d}(i,j)$ and $\overline{d}(i,j)$ denote, respectively, the lower and upper bounds for the distance d(i, j) (notice that $\underline{d}(i,j) = \overline{d}(i,j)$ if d(i, j) is exact). In this paper, we suppose that the given set of distances is actually embeddable in $\mathbb R^3$; in other words, it is supposed that no distance is affected by errors.

Over the years, the solution of MDGPs has been attempted by formulating global optimization problems in a continuous space, where a penalty objective function is generally employed in order to measure the violation of the distance constraints for given molecular conformations. More recently, a new class of MDGPs has been introduced, for which the search domain of the optimization problem can be reduced to a discrete space having the structure of a tree. Instances belonging to this class can be solved by employing an interval Branch & Prune (iBP) algorithm [15, 17].

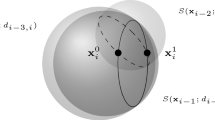
In order to perform the discretization, MDGP instances need to satisfy some particular assumptions. In practice, the atoms of the molecule must be sorted in a way that there are at least three reference atoms for each of them. We say that an atom z is a reference for another atom y when z precedes y in the given atomic order, and the distance d(z, y) is known. In such a case, indeed, candidate positions for y belong to the sphere centered in z and having radius d(z, y). When the reference distance d(z, y) is given through a real-valued interval, a spherical shell centered in z can be instead defined. If three reference atoms are available for y, then candidate positions (for y) belong to the intersection of three Euclidean objects. The easiest situation is the one where the three available distances are exact, and the intersection gives, in general, two possible positions for y [14]. However, if only one of the three distances is allowed to take values into a certain interval, then the intersection gives two curves, generally disjoint, where sample points can be chosen [15]. In both situations, the discretization can be performed. More details about the discretization process are given in Sect. 2.

Necessary preprocessing step for solving MDGPs by this discrete approach is therefore the one of finding suitable atomic orders that allow each atom y to have at least three reference atoms. We refer to such orders as discretization orders. In previous works, discretization orders have been either handcrafted [5, 15], or designed by using a pseudo de Bruijn graph representation of the cliques in G [21], or even automatically obtained by a greedy algorithm [13, 20]. In the present paper, we propose an approach for selecting, among all discretization orders that might exist for a given MDGP instance, the ones that are able to improve iBP performances. To this aim, we define some objectives (with a given priority) to be optimized during the search for the discretization orders. These objectives, together with the discretization assumptions, define a multi-level optimization problem for finding optimal discretization orders. Although this optimization problem can be cast as a mathematical programming problem (see for example [4]), we consider instead in this work an Answer Set Programming (ASP) approach [7, 9]. ASP provides in fact more flexible tools for managing the constraints we need to deal with.

The rest of the paper is organized as follows. The basic idea behind the discretization and the sketch of the iBP algorithm are presented in Sect. 2. In Sect. 3, we present our ASP model for the generation of partial orders for the MDGP. Given one unique partial order provided as a result by the ASP solver, several total orders for the protein backbones can be extracted. By considering one of such total orders, we present in Sect. 4 some computational experiments where we compare the properties of this new order to those of previously proposed orders for protein backbones. Finally, Sect. 5 concludes the paper.

2 Discretization Orders and the iBP Algorithm

Let $G=(V,E,d)$ be a simple weighted undirected graph representing an instance of the MDGP. In order to perform the discretization, G needs to satisfy the following assumptions. Let $E' \subset E$ be the subset of edges for which the associated weight is an exact distance.

Definition 2.1

(The interval Discretizable DGP in dimension 3 (iDDGP $_3$)) Given a simple weighted undirected graph $G=(V,E,d)$, we say that G represents an instance of the iDDGP$_3$ if and only if there exists an order relationship “$<$” on the vertices of V verifying the following assumptions:

• (a) $\{1,2,3 \}$ is a clique and $\{ (1,2),(2,3),(1,3) \} \subset E'$;

• (b) $\forall i \in \{ 4,\dots ,|V| \}$, there exists a subset $ref(i) = \left\{ i',i'',i'''\right\}$ such that

  • 1. $i'''< i$, $i'' < i$, $i'< i$;

  • 2. $\left\{ (i'',i),(i',i)\right\} \subset E'$ and $(i''',i) \in E$;

  • 3. $d(i',i''') < d(i',i'') + d(i'',i''')$.

We refer to orders satisfying (a) and (b) as “discretization orders”. These orders can be either partial or total.

Assumption (a) allows us to fix the positions of the first three atoms, avoiding to consider congruent solutions that can be obtained by rotations and translations. Assumption (b.1) ensures the existence of the three reference atoms for every atom $i > 3$, and assumptions (b.2) ensures that at most one of the three reference distances is represented by an interval. We say that the reference distances are the ones used in the discretization process; additional distances that might be available can be used in the pruning process (see below). Finally, assumption (b.3) avoids the reference atoms to be co-linear. Note that assumption (b.3) cannot always be verified a priori, because some of the necessary distances may not be available (the corresponding edges may not be in E). However, this assumption can fail to be satisfied with probability 0 when considering either molecular instances or even generic graphs, and therefore we do not really need to verify it in advance [13, 22].

Under the assumptions (a) and (b), the MDGP can be discretized. The search domain becomes a tree containing, layer by layer, the possible positions for a given atom. In this tree, the number of branches increases exponentially layer by layer. After the discretization, the MDGP can be seen as a combinatorial problem.

The discretization assumptions strongly depend on the existence of an order for the vertices of G, i.e. for the atoms of the considered molecule. When working on molecules with known chemical structure such as proteins, some distance information is always available, because related to this chemical structure. In this case, orders, that are valid for an entire class of instances, can be obtained, where only “guaranteed” distance information is exploited. This kind of information includes bond lengths and angles, and also structural information, such as peptide plane induced distances [19]. In this work, we focus our attention on protein backbones, which consist of the set of atoms that, in proteins, are common to all amino acids (the side chains are not considered).

In previous works, discretization orders were identified by employing different approaches. In [5, 15], handcrafted orders were presented for the protein backbone and the side chains belonging to the 20 amino acids that can take part to the protein synthesis. More recently, in [21], orders were identified by searching for total paths on pseudo de Bruijn graphs containing cliques of the original MDGP graph G. In both cases, these orders were conceived for satisfying an additional assumption on the reference atoms: $i'''$, $i''$, $i'$ and i have to be consecutive (consecutivity assumption). Because of this additional assumption, the calculation of the atomic coordinates was possible by using the method described in [14], which is more stable than the general approach based on the solution of a sequence of quadratic systems (each for one sphere intersection). Successively, however, it was proved that the same efficiency and the same accuracy can be obtained by employing another method for which the consecutivity assumption does not have to be satisfied [10].

Another way to construct discretization orders is given by the greedy algorithm firstly proposed in [13] and subsequently extended for interval distances in [20]. This algorithm is able to find orders where the consecutivity assumption is not ensured. In fact, requiring the consecutivity assumption be satisfied makes the problem of finding a discretization order NP-hard [4]. A heuristic has also been proposed for finding discretization orders without consecutivity assumption, which outperformed the greedy algorithm on large instances, but for which there are no guarantees of convergence [11].

This work finds its place in the context of this last approach for the identification of discretization orders without the consecutivity assumption. Our aim is not only to find orders that allow for the discretization, but also to optimize these orders in a way that the corresponding search domain (the tree) is easier to explore by the iBP algorithm. Section 3 provides details about the objectives that we optimize for improving the search on the tree.

Algorithm 1 is a sketch of the iBP algorithm [15]. The algorithm recursively calls itself for exploring the search tree. The if structure in line 6 discriminates between the two situations: there are three exact reference distances/only two of these distances are exact. In the first case, two atomic positions are generated by the sphere intersection, and two new branches are added to the tree at the current layer (see Introduction). In the second case, instead, the intersection gives 2 disjoint curves, from which sample points need to be taken for discretizing. The parameter of the algorithm named $\textit{discr}\_\textit{factor}$ gives in fact the (fixed) number of samples that are taken from each curve. The other parameters of the algorithm are: j, the current atom; n, the total number of atoms; $\textit{order}$, the available discretization order; d, the set of weights on the edges of G. The discretization order allows to define, for each j, the set $ref(j) = \{ j',j'',j''' \}$ of reference atoms for j.

After the computation of possible positions for the current atom j, the feasibility of these atomic positions are verified by applying what we call pruning devices (see lines 13 and 16 of Algorithm 1). Even if tree branches grow exponentially layer by layer, the pruning devices allow iBP to focus the search on the feasible parts of the tree. The easiest and probably most efficient pruning device is the Direct Distance Feasibility (DDF) criterion [14], which consists in verifying the ${\upvarepsilon }$-feasibility of the constraints:

$$\begin{aligned} \underline{d}(k,j) - \upvarepsilon \le || x_k - x_j || \le \overline{d}(k,j) + \upvarepsilon , \quad \forall (k,j) \in E, \quad \mathrm{with} \,\, k < j . \end{aligned}$$

(2)

All distances related to edges (k, j), with $k < j$ and that are not used in the discretization, are named pruning distances, because they can be used by DDF for discovering infeasibilities. Several pruning devices can be integrated in iBP, that can be based on either pure geometric features of molecules, or rather on chemical and biological properties [3]. In this work, in order to focus the attention on the discretization orders, only the pruning device DDF will be considered in our computational experiments.

3 Looking for Optimal Orders for the Protein Backbone

Besides satisfying the assumptions in Definition 2.1, discretization orders can be optimized with the aim of improving the performances of the iBP algorithm. We propose in this work some objectives to be optimized during our search for discretization orders for protein backbones. These objectives are sorted with their priority levels: higher priority objectives are optimized first.

The protein backbone is defined by the sequence of atomic subgroups common to all amino acids, which are bonded together to form the protein chain [19]. Side chains are omitted in this work, and we consider proteins formed by only one chain. Only four different atoms compose protein backbones: carbons (C), nitrogens (N), hydrogens (H) and oxygens (O). We will use the symbol $C_\alpha$ for the “central” carbon of the amino acid, and we will use the symbol $H_\alpha$ for the hydrogen bonded to this $C_\alpha$. Other atom types appear only once per amino acid, so that it is not necessary to use special characters when referring to them. Superscripts associated to atom’s labels will denote the position of the amino acid to which the atom belongs in the protein chain. For example, $H_\alpha ^i$ denotes the hydrogen bonded to $C_\alpha ^i$, in the amino acid at position i. The superscript “0” is associated to the second hydrogen $H^0$ belonging to the first amino acid; the superscript “$n+1$” is instead associated to the second oxygen belonging to the last amino acid, where n is the total number of amino acids.

Recall that, when three exact reference distances are available for the discretization, there are two possible positions for the current atom. Otherwise, when one of such distances is instead represented by an interval, $2 \times \textit{discr}\_\textit{factor}$ possible candidate positions for the atom can be computed (see Sect. 2).

Our list of objectives is given below, together with their priority levels. Together with the assumptions (a) and (b) in Definition 2.1, these objectives define a multi-level optimization problem.

• 4. Maximize the number of exact distances used in the discretization.

  In order to keep the tree width as small as possible, the situation where all three reference distances used in the discretization are exact is preferable. This way, the number of branches on each layer can be at most the double of the number of branches on the previous one.

• 3. Maximize the number of distances $(H_{\alpha }^i,H^{i+1})$ and $(H^i,H_\alpha ^i)$ used in the discretization.

  The interval distances $(H_{\alpha }^i,H^{i+1})$ and $(H^i,H_\alpha ^i)$ can always be estimated by studying the structure of protein backbones. Even if represented by real-valued intervals, these distances can be employed for the discretization. Moreover, it is likely NMR experiments can provide a better estimate for them, i.e. sharper intervals [16].

• 2. Postpone the interval distances used in the discretization.

  When an interval distance is used in the discretization process, potentially $2 \times discr\_factor$ new branches are added to the tree at the current layer, while, at most, only two branches need to be added when all distances are exact. Therefore, if an interval distance is used for discretization at deeper layers of the tree, this phenomenon can be delayed, so that fewer internal nodes in the search tree are generated, and this may favor early pruning.

• 1. Anticipate the pruning distances.

  Pruning distances are employed for verifying the feasibility of generated candidate positions. The sooner they appear, the earlier infeasible positions can be discovered and branches of the tree can be pruned. Since the set of pruning distances is instance-dependent, it is not possible to find orders where this objective is optimal for an entire class of instances. Therefore, we only consider NMR distances that are likely to be available in every protein instance: the distance between pairs of hydrogens $(H^i,H^{i+1})$ and $(H_{\alpha }^i,H_{\alpha }^{i+1})$ belonging to consecutive amino acids [16]. Note that, since there are two hydrogens bonded to $N^1$ in the first amino acid, the distances related to both hydrogens are supposed to be known.

In order to consider the above objectives, we discriminate among: (i) exact distances; (ii) generic interval distances; (iii) interval distances between hydrogen pairs $(H_{\alpha }^i,H^{i+1})$ and $(H^i,H_\alpha ^i)$; (iv) pruning distances. While looking for optimal orders, we will fix the length of the protein backbone to three. In fact, the regular structure of the protein backbone will allow us to easily extend the obtained orders to protein backbones of any length.

4 Computational Experiments and Discussion

We present and discuss in this section two sets of computational experiments. First of all, by using ASP, we generate an optimal partial order for which the objectives detailed in Sect. 3 are optimized (see Sect. 4.1). Secondly, we extract one total order from the optimal partial one, and we compare the performances of the iBP algorithm while using this new order and some previously proposed ones (see Sect. 4.2). Both experiments will be commented in details.

4.1 Finding an Optimal Partial Order by ASP

We use the ASP framework to find solutions to the multi-level optimization problem described in Sect. 3. ASP is a form of declarative programming adapted to combinatorial and optimization problems [2], which offers a language of clauses to express constraints on given variables. Once all constraints are expressed as logical formulas, a grounder transforms such constraints into a (large) set of Boolean equations, while a solver looks for possible models (possible answers) for this set. From the set of obtained answers, solutions to the initial problem can be derived.

To the four objectives given in Sect. 3, we also added the one of minimizing the number of ranks in the partial order. This actually makes the searched order a partial order, where the same rank can be associated to more than one atom. We point out that the expressiveness and efficiency of ASP modeling allowed us to test multiple objective functions and to converge towards a single solution with a few simple objectives. In other words, the list of objectives presented above was tested by ASP and refined several times before defining the current list (given in Sect. 3) for which only one partial order is given as optimal by ASP. In our experiments, we employ the grounder Gringo and the solver Clasp developed in Potsdam University [8].

We focus our attention on the protein backbone of a short polypeptide consisting of three amino acids (without side chains). The regular structure of protein backbones allows to extend any solution found for three amino acids to protein backbones of any length. There is only one slight variation on the backbone in presence of one single amino acid: the proline. This amino acid has no hydrogen H bonded to its nitrogen N.

Before presenting the results obtained by ASP, we briefly present two previously proposed orders for protein backbones. In [15], the following handcrafted order was introduced:

$$\begin{aligned} \begin{array}{c} | N^1, H^1, H^0, C_{\alpha }^1, N^1, H_{\alpha }^1, C_{\alpha }^1, C^1 | N^2, C_{\alpha }^2, H^2, N^2, C_{\alpha }^2, H_{\alpha }^2, C^2, C_{\alpha }^2 | \\ | N^3, C^{2}, C_{\alpha }^3, H^3, N^3, C_{\alpha }^3, H^3_{\alpha }, C^3, C_{\alpha }^3, O^3, C^3, O^4 | . \\ \end{array} \end{aligned}$$

(3)

Recall that superscripts are used for referring to the amino acid the atom belongs to. Recall also that $H^0$ refers to second hydrogen belonging to the first amino acid and bonded to $N^1$, and that $O^4$ is one of the oxygens belonging to the last amino acid. Repetitions are allowed in this order, because of the consecutivity assumption (see Sect. 2). Repetitions increase MDGP instances in length because atoms can appear in the order more than once; this, however, does not imply any increase in complexity, because there is no branching in iBP when copies of already placed atoms are considered. The symbol “|” is used for separating the amino acids. Since there are repetitions, however, some atoms belonging to one amino acid can be repeated in the next one.

In [20], another order was generated by using a greedy algorithm:

$$\begin{aligned} | N^1, H^1, H^0, C_{\alpha }^1, H_{\alpha }^1, C^1 | N^2, H^2, C_{\alpha }^2, H_{\alpha }^2, C^2 | N^3, H^3, C_{\alpha }^3, H_{\alpha }^3, C^3, O^3, O^4 | . \end{aligned}$$

(4)

Repetitions are not necessary in this order and the consecutivity assumption is not satisfied (see Sect. 2). The employed greedy algorithm iteratively constructs the order by placing at the current position the atom that has at least three reference atoms and for which the total number of references is maximized. When it exists, the greedy algorithm is able to find a discretization order for a given instance.

Our ASP execution provided us with one unique solution: the partial order is depicted in Fig. 1. For the 18 atoms of our 3-amino acid protein backbone, the greatest rank is 13 in this partial order. There are in fact clusters of atoms where the relative positioning of the atoms is irrelevant. In the initial amino acid, there is a cluster with 4 atoms; in the other amino acids, the positions in the order for the atoms $N^i$ and $C_{\alpha }^i$ can be exchanged. When considering three amino acids, there are therefore 96 (4! $\cdot$ 2! $\cdot$ 2!) total orders corresponding to the partial order in Fig. 1.

Fig. 1

A partial order, for the discretization of protein backbones, found by our ASP model

In order to verify whether these 96 total orders have similar properties, we generated 96 iDDGP$_3$ instances related to the 3-amino acid backbone used in the ASP simulation. For all of them, we ran the iBP algorithm and monitored the total number of iBP recursive calls necessary to explore the entire tree. This analysis showed that all generated total orders are equivalent (same number of solutions, same number of iBP calls). Note that, even if the theoretical number of solutions should be order-independent, the branching over intervals currently implemented in iBP (see Algorithm 1) could lead to different numbers of found solutions when using different orders. Nevertheless, we did not have any variation for any instance of our set.

In order to perform computational experiments on realistic protein instances (see Sect. 4.2), we selected, among the 96 total orders that can be extracted from the partial order in Fig. 1, one total order:

$$\begin{aligned} | N^1, C_{\alpha }^1, H_{\alpha }^1, C^1 | H^2, N^2, C_{\alpha }^2, H_{\alpha }^2, C^2 | H^3, N^3, C_{\alpha }^3, H_{\alpha }^3, C^3 | H^0, H^1, O^3, O^4 | . \end{aligned}$$

(5)

In this order, the two hydrogens $H^0$ and $H^1$ bonded to $N^1$, as well as the two oxygens $O^3$ and $O^4$ beloging to the last amino acid, are placed at the end of the order. As it is easy to remark, the specific orders for the second and the third amino acids are identical. For backbones composed by a longer list of amino acids, it is necessary to repeat this generic order as many times as the total number of amino acids in the molecule. In the special case of proline, where the hydrogen bonded to $N^i$, with $i > 1$, does not appear, we can just omit $H^i$ in the order. This change does not make the order non-discretizable.

4.2 Comparison to Other Orders

We present some experiments on a subset of realistic protein instances where, for each instance, we consider the three orders (3), (4), and (5), and we compare the performances of iBP. The iBP algorithm was implemented in C programming language (GNU C compiler v.4.0.1 with -O3 flag), and the executions were carried out on an Intel Core 2 Duo @ 2.4 GHz with 2GB RAM, running Mac OS X.

The instances that we consider in our experiments have been generated as follows. We consider a subset of proteins from the Protein Data Bank (PDB) [1] related to human immunodeficiency. Together with the PDB coordinates of the atoms, we consider the chemical structure of the protein, i.e. information about its bond lengths and angles. All distances between atom pairs are computed, and a distance is included in our instances if it is between

• 1. two bonded atoms (considered as exact);

• 2. two atoms that are bonded to a common atom (considered as exact);

• 3. two atoms belonging to a quadruplet of bonded atoms forming a torsion angle (considered as an interval);

• 4. two hydrogen atoms (considered as an interval, if the distance lies in the interval [2.5, 5] Å).

The first three items are related to the chemical structure of the molecule; only the last item concerns distances that simulate NMR data. The distances that are related to item 3 are generally intervals; however, one of the possible torsion angles is related to the peptide bond between two amino acids: in such a case, the distance is considered as exact, because the peptide bond forces all atoms to lie on the same plane. Interval distances coming from torsion angles are computed so that all corresponding values for the torsion angle are allowed. The interval distances related to item 4 have instead width equal to 2 Å, and their bounds were generated so that the true distance is randomly placed inside the interval. After the calculation of the distance information, the atoms in every instance have been reordered by considering three total orders: the handcrafted order (3), the greedy order (4), and our new order (5). Table 1 contains some information about the generated instances.

Table 1 Some properties of the instances that we generated from PDB files related to human immunodeficiency

Table 2 presents a comparative analysis of the three orders. The table provides the minimum value for $discr\_factor$ ($d\_f$ in the table) necessary to obtain at least one solution with the iBP algorithm, the total number of iBP calls, and the CPU time, in seconds. In order to obtain the minimum value for the discretization factor, we gradually increased $discr\_factor$ from 3 to 9, until one solution was found in less than 30 s. In these experiments, we considered $\upvarepsilon = 0.1$ in the feasibility test (see Eq. (2)) given by DDF. All found solutions are “good-quality” solutions: we considered as index for measuring the solution quality the LDE, which ranges between $10^{-5}$ and $10^{-4}$ in our solutions. The reader can refer to [10] for the definition of the LDE index.

Table 2 Comparison among three total discretization orders

As the table shows, the total order that we found in this work is generally the optimal one (in terms of both iBP calls and CPU time, while the quality of the solutions remains unchanged). There are a few examples, however, where the performances of iBP are better when using the other orders. This can be due to the fact that sample points are chosen during the discretization from the curves that are generated in presence of interval data (see Sect. 2). Not considering entire curves, but some sample points only, makes iBP a heuristic, whose performances can drastically vary on the basis of the sample points that are chosen. Nevertheless, the experiments in Table 2 show that the order (5) is almost always the best one.

In order to validate this result, we performed all experiments for a second time, and we replaced the deterministic choice on line 11 of Algorithm 1 for the selection of the sample distances with a random choice of ($discr\_factor =)$ 5 uniformly distributed samples on the two obtained curves. Table 3 shows the average performances of iBP over 10 runs. Only the runs taking less than 10 s are considered in the average: S denotes the number of considered runs. This table shows a more regular pattern for the greedy order (4) and our new order.

Table 3 Experiments with iBP and the random selection of the samples from the intervals

5 Conclusions

We proposed a new discretization order for distance geometry with interval data that allows for the discretization of protein backbones. This order comes from a complete search of the space of possible discretization orders, implemented through an ASP model. This model ensures that the assumptions for the discretization are satisfied, and that some additional objectives (aimed at improving iBP performances) are optimized. Priorities were assigned to the considered objectives. We compared the proposed discretization order to two orders that were previously proposed in the literature [15, 20]. Our computational experiments on protein instances showed that iBP performances actually improve when using the new proposed order.

Future works will be devoted to strategies for reducing the degrees of freedom of our protein backbones. In general, there are two (continuous) degrees of freedom per amino acid (on the protein backbone), which can be modeled by using two torsion angles $\phi$ and $\psi$ [19]. One possibility for an improvement is to explore the favorable regions of the so-called Ramachandran map to reduce the discretization intervals in length [23]. Moreover, an interesting property of the new proposed order is that it allows to easily set the reference atoms so that the planarity of the peptide plane and the chirality around the carbons $C_{\alpha }$ can be exploited [3]. As a consequence, this new order could be used for branching only over interval distances (the planarity and the chirality properties allow to uniquely position an atom when three reference distances are exact). We point out that this feature of the new order was not considered in the experiments presented in this paper because the two older orders (3) and (4) do not allow for an easy implementation of a method based on this feature.

Finally, notice that this work can be extended to protein side chains. Side chains generally have constrained structures and preferred configurations, for which optimal discretization orders might be identified. Subject of future research is also the problem of finding the optimal discretization orders that consider the chemical structure of the whole molecule at once, as well as the entire set of pruning distances that might be available (obtained by NMR).