Development of Unstructured Curved Meshes with G ¹ Surface Continuity for High-Order Finite Element Simulations

Abstract

This paper presents a curved meshing technique for unstructured tetrahedral meshes where G ¹ surface continuity is maintained for the triangular element faces representing the curved domain surfaces. A bottom-up curving approach is used to support geometric models with multiple surface patches where either C ⁰ or G ¹ geometry continuity between patches is desired. Specific parametrization approaches based on Bézier forms and blending functions are used to define the mapping for curved element faces and volumes between parametric and physical coordinate systems. A preliminary result demonstrates that using G ¹-continuity meshes can improve the solution results obtained.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

It is well known that high-order finite element methods are among the most powerful methods for simulating complex engineering problems [2]. In order to fully realize the benefits of the high-order methods, the mesh entities representing curved portions of the domain geometry must be curved and provide an high-enough order of geometry approximation [11, 12]. The ability to provide such a higher order of geometric approximation is facilitated by the use of greater than C ⁰ geometric shape continuity between elements [8, 14–16]. Although such higher order geometric continuity is being increasingly used with tensor product representations over quadrilaterals (see [6, 10]), there is also the desire to have higher than C ⁰ geometry continuity between elements on unstructured meshes where curved triangular finite element faces are used. The current work is intended to investigate and address the technical difficulties with developing curved meshing techniques for unstructured meshes where G ¹ surface geometry continuity is maintained for the triangular element faces representing the curved domain surfaces. A preliminary result is also included that shows improved solution results when G ¹ surface triangulations are used.

2 Procedure to Create G ¹ Curved Meshes

Many triangular patches have been developed in the CAGD community to construct G ¹ continuous surface interpolations [8, 9, 14–16]. The techniques can in general be categorized into one of the two sets—polynomial based patches or rational blend based patches. The schemes using polynomials address the problem by either using single patch with relatively high polynomial degree or creating piecewise parametrization using sub-patches [13], both of which lead to more control points to be determined for the patch. The schemes using rationals are able to keep a patch complete by using blending functions [3]. Rational patches achieve G ¹ with relatively low degree and require fewer control points. For the study in this paper, the rational blend based scheme is chosen because of its relatively straight-forward to construct and the data structure is similar to a regular Bézier triangle. The procedure to create G ¹ curved meshes from C ⁰ straight-sided meshes using rational triangular patches is introduced in the following subsections. It is assumed that a straight-sided mesh is given with the set of boundary mesh entities correctly classified on a CAD model. Each mesh vertex on the model boundary is able to obtain its position and surface normal data by interacting with the CAD model.

2.1 Rational Triangular G ¹ Patch

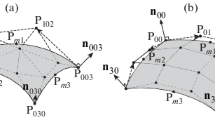
The essential part of the procedure to create G ¹ curved meshes is the scheme to construct triangular G ¹ patches for mesh faces that interpolate the position $x_{i}(\xi )$ and normal data n _j at their bounding vertices. The scheme used in this work to represent the curved geometry is based on an extension of the Gregory patch proposed by Walton et al. [16]. For each individual mesh face, each of the three bounding edges is assigned with a geometric representation of a cubic Bézier curve $B^{(3)}(\xi )$. Tangent vectors are obtained along the curve direction by taking the derivatives of the Bézier curve parametrization $t^{(2)} = \frac{\partial B} {\partial \xi }$. Cross-boundary tangent vectors are calculated by taking cross product with the surface normal given at mesh vertices g ⁽²⁾ = n _j × t ⁽²⁾. In order to obtain the required G ¹ continuity, the cross-boundary tangent fields associated with the three mesh edges have to be satisfied simultaneously, thus requiring more degrees of freedom than a typical triangular Bézier patch. As a result, the order of the polynomials representing the surface patch is increased from cubic to at least quartic $B^{(4)}(\xi )$, which leads to a set of three surface control points. Each of the three surface control point is subsequently split into two and related together using linear blending functions. The rational blend degree-4 triangular Bézier patch is defined by

$$\displaystyle{ B^{(4)}(\xi ) = P_{ ijk}b_{ijk}^{4}(\xi ) }$$

(1)

where P _{i j k} are the control points and $b_{ijk}^{4}(\xi )$ are 4t h order Bernstein basis functions. The surface control points P ₁₁₂, P ₁₂₁, P ₂₁₁ are affine combinations of the split surface control points G _i, j and are calculated using $P_{1,1,2} = \frac{1} {\xi _{1}+\xi _{2}} (\xi _{1}G_{2,2} +\xi _{2}G_{0,1}),P_{1,2,1} = \frac{1} {\xi _{3}+\xi _{1}} (\xi _{3}G_{0,2} +\xi _{1}G_{1,1}),P_{2,1,1} = \frac{1} {\xi _{2}+\xi _{3}} (\xi _{2}G_{1,2} +\xi _{3}G_{2,1})$.

Figure 1 shows an example patch and its control point set.

Fig. 1

Triangular Gregory patch and its control points

2.2 Surface Mesh with Mixed C ⁰ and G ¹ Continuity

The procedure introduced in Sect. 2.1 serves the purpose of creating G ¹ surface meshes for models with a single model face. In the mean time, most 3D models with challenging geometric features consist of more than one model face. Any procedure aiming to create proper surface meshes for such multi-patch models has to account for the mixture of C ⁰ and G ¹ continuity. In this work, a bottom-up approach is adopted based on the different topological types of model entities on which a mesh entity is classified. Specifically, the mesh edges that represent the model edges where model faces join with C ⁰-continuity are curved first to be G ¹ along the model edge direction while maintaining C ⁰ in the cross-edge direction. After that, the remaining surface mesh entities that represent the rest of the model boundary are curved using the procedure discussed in Sect. 2.1. As a result, a piecewise G ¹ surface mesh is created where it is G ¹ within each model face as well as along the bounding model edges and C ⁰ in the cross-boundary direction at the model edges where model faces join together. Note that in the case where two model faces join with G ¹ continuity in the first place, G ¹ continuity is maintained by curving the mesh edges representing the model edge in the same way as those representing model faces. The pseudo code for the overall procedure is given in Algorithm 1. Figure 2 shows an example mesh created using the algorithm.

Fig. 2

Curved G ¹ mesh of a linear accelerator model

Algorithm 1 Algorithm for creating G ¹ meshes for multi-patch CAD models

3 Integration with Finite Element Analysis Solver

With the conventional isoparametric approach with C ⁰ meshes, the volumetric mapping between a standard parametric space and the physical space is constructed based on the same polynomial basis functions used for the finite element space. However, the basis functions used to represent the rational G ¹ curved mesh are generally not the same as the finite element shape functions used for analysis. Therefore, a more general approach is adopted to construct the volumetric mapping in order to account for the G ¹ surface geometry. The approach taken in this work is based on blending [7]. More specifically, the shapes of lower dimensional mesh entities bounding the element volume are multiplied with linear blending functions, and the contributions are summed together to get the complete volume mapping. The equation to calculate the mapping is given in Eq. (2).

$$\displaystyle\begin{array}{rcl} & & x_{i}(\xi _{j}) = (1 -\xi _{1})E_{1}(\xi ') + (1 -\xi _{2})E_{2}(\xi ') + (1 -\xi _{3})E_{3}(\xi ') + (1 -\xi _{4})E_{4}(\xi ') \\ & & \qquad \ \ \ \ \ \ \ - (1 -\xi _{1} -\xi _{2})F_{1}(\xi ') - (1 -\xi _{1} -\xi _{3})F_{2}(\xi ') - (1 -\xi _{1} -\xi _{4})F_{3}(\xi ') \\ & & \qquad \ \ \ \ \ \ \ - (1 -\xi _{2} -\xi _{3})F_{4}(\xi ') - (1 -\xi _{2} -\xi _{4})F_{5}(\xi ') - (1 -\xi _{3} -\xi _{4})F_{6}(\xi ') \\ & & \quad \ +\xi _{1}V _{1}(1,0,0,0) +\xi _{2}V _{2}(0,1,0,0) + +\xi _{3}V _{3}(0,0,1,0) +\xi _{4}V _{4}(0,0,0,1){}\end{array}$$

(2)

Here, E _j , j = 1, 2, 3, 4 represent the four edge parametrization. Similarly, F _j , j = 1, 2, 3, 4, 5, 6 represent face parametrization. V _j are the vertices. It is worth noting that the blending approach is independent of the chosen face and edge parametrization, therefore can be used with other types of parametric representations of mesh faces.

With the blending based volume parametrization, coordinate mapping can be easily evaluated. Derivatives quantities $\frac{\partial x_{i}} {\partial \xi _{j}}$ can also be evaluated by applying chain rule to Eq. (2) to obtain the analytic express of the derivatives of the blending mapping. With calculated derivatives, Jacobian of the mapping and its determinant can be easily evaluated.

4 Geometric Interpolation Accuracy

To study and quantify the geometric interpolation properties of the quartic G ¹ patch discussed in Sect. 2.1, a set of numerical experiments have been conducted. A series of uniformly refined meshes are generated on a CAD model representing a cylinder. The distance between the mesh faces and CAD model faces is measured for each of the uniformly refined meshes. The distance is measured in terms of the Hausdorff norm which is commonly used to measure the distance between two parametric faces [1]. The definition of Hausdorff distance is given by Eq. (3).

$$\displaystyle{ d(S,S') =\max _{p\in S}\min _{p'\in S'}\left \|p - p'\right \|_{2} }$$

(3)

As a comparison, the measurement is done for both the G ¹ meshes and a set of C ⁰ meshes using quartic Lagrange basis functions with optimal point distribution scheme proposed by Chen and Babuska [5]. Figure 3 shows the convergence plot generated from the distance data. For the quartic G ¹ meshes, 4t h order interpolation accuracy is observed, and for quartic C ⁰ meshes, it shows 5t h order interpolation accuracy. It is a well known result in 1D that the order of accuracy for polynomial interpolation is p + 1, where p is the highest complete polynomial order [8]. The one order difference in interpolation accuracy between the G ¹ and C ⁰ is due to the fact that certain portion of the control points of the G ¹ patch have to be constrained to ensure the higher surface continuity.

Fig. 3

Convergence of geometric approximation error

5 Impact on Finite Element Solution Accuracy

The primary interest for using G ¹ meshes is to see if they produce better finite element simulation results. The test problem chosen is the Poiseuille flow, which models viscous flow inside a pipe of constant circular cross-section. Governing Equation for the Poiseuille flow is defined as:

$$\displaystyle{ \frac{1} {r} \frac{\partial } {\partial r}(r\frac{\partial u_{z}} {\partial r} ) = \frac{1} {\mu } \frac{\partial p} {\partial z} }$$

(4)

The fully developed flow is assumed to be incompressible, steady, laminar and has a closed form exact solution which indicates a velocity profile of a parabola. The analytic expression is given as:

$$\displaystyle{ u_{z} = -\frac{1} {4\mu } \frac{\partial p} {\partial z}(R^{2} - r^{2}) }$$

(5)

In the numerical test, it is of interest to solve for the fully developed velocity profile and compare it with the exact solution. A CAD model is constructed to represent the flow domain of a cylinder with radius r = 0. 5. No-slip condition is set for the wall. At inlet, the velocity profile is set to be fully developed: $u_{z} = 0.25 - r^{2}$. The pressure at the outlet is set to be constant.

The finite element solver package being used to perform the analysis is Nektar++ [4], which is a spectral/hp element framework being developed by research groups at the University of Utah and Imperial College London. It has a set of flow solvers that use high-order finite element methods. Specific modifications are made to Nektar++ to account for the G ¹ mesh construction including elemental mapping evaluation, derivatives and Jacobian calculation procedures. Two types of meshes with the same number of elements, the same order of polynomial degree, but different order of geometric continuity are used, namely, quartic C ⁰ curved and quartic G ¹ curved meshes (See Fig. 4). A series of simulations are performed with each type of the meshes using 4th and 5th order Legendre polynomial shape functions. The error of finite element solution of the velocity field against the exact analytic solution is measured in terms of the L ₂ norm and is shown in Table 1. It is observed in this test case that meshes with G ¹ surface continuity achieve better solution accuracy compared with C ⁰ meshes for the same order of shape functions.

Table 1 Finite element solution error for different types of curved meshes

Fig. 4

CAD model and quartic G ¹ mesh

6 Closing Remarks

This paper presented a procedure to create G ¹ curved surface meshes for high-order finite element simulations. A method to create G ¹-continuous surface patches is introduced and an approach to integrate a G ¹ mesh with existing finite element solver is presented. A preliminary test result shows the advantage of using G ¹ continuous meshes, compared with conventional C ⁰ meshes, in terms of finite element solution accuracy of a standard integral norm. Additional studies to examine the influence of G ¹ continuity on more problems and for other solution norms must be carried out. There is particular interest to examine solution parameters more local to the surface. For future developments, it is of interest to study other types of high-order surface patches. Furthermore, the capability of using the CAD model surface parametrization to define exact geometric mapping is to be developed. In order to support adaptive simulations, extensions of existing mesh modification operations and mesh adaptation procedure [11] will be needed to account for high-order curved meshes.