Keywords

1 Introduction

Now it has become necessary to simulate multiphysics coastal ocean flow phenomena at distinct scales, especially those at small scales, in many emerging problems such as hydrodynamic impact on coastal bridges during Hurricane Katrina in 2005 and oil spill at the Deepwater Horizon in the Gulf of Mexico in 2010 (e.g., [2, 4]). Efforts using numerical simulations to predict coastal ocean flows have been greatly successful but strictly speaking, until now, are limited to large spatial scales in range O(10)–O(10,000) km and individual phenomena such as circulation currents and surface waves.

A natural and actually the most effective and feasible approach to simulate multiphysics coastal ocean flows at an affordable computational expense will be an integration of a fully three dimensional fluid dynamics (F3DFD) model, which is commonly referred as to a computational fluid dynamics (CFD) model in the coastal ocean community, and a geophysical fluid dynamics (GFD) model into a single modeling system using a domain decomposition method (DDM). In this approach, a flow field is divided into many subdomains dominated with different physical phenomena, and each subdomain will be assigned either with a F3DFD or a GFD model, whichever appropriate. With this idea, the authors proposed to couple the Solver for Incompressible Flow on Overset Meshes (SIFOM) developed by ourselves, which is a F3DFD model, and the unstructured grid Finite Volume Coastal Ocean Model (FVCOM), which is a GFD model, and demonstrated its capabilities and performance in capturing multiple physical phenomena [6, 9]. The SIFOM–FVCOM system is the first-of-its-kind system for coastal ocean flows, and it is able to simulate many flows that are beyond the reach of any other existing models.

This paper makes a numerical experiment to evaluate the performance of the SIFOM–FVCOM system, illustrating its promise in simulation of complicated flows as well as difficulties to be overcome. A comprehensive study on the SIFOM–FVCOM system has been presented in [8].

2 Governing Equations and Discretization

The governing equations of the F3DFD model are the continuity and the Reynolds-averaged Navier–Stokes equations that read as

$$\displaystyle{ \begin{array}{l} \nabla \cdot \mathbf{u} = 0,\end{array} }$$
(1)
$$\displaystyle{ \begin{array}{l} \mathbf{u}_{t} + \nabla \cdot \mathbf{uu} = -\dfrac{1} {\rho } \nabla p + \nabla \cdot \left ((\nu +\nu _{t})\nabla \mathbf{u}\right ),\end{array} }$$
(2)

where u is the velocity, with component u, v, and w in x, y, and z direction respectively. Here x and y are in the horizontal direction, respectively, and z is in the vertical direction. p is the pressure, ρ the density, ν the viscosity, and ν t the turbulence viscosity. Different turbulence closures are available to evaluate the turbulence viscosity, such as the mixing length model, k −ε model, and detached eddy simulation.

SIFOM has been developed by the first author and co-workers to solve the above governing equations (e.g., [3, 7]). In SIFOM, the governing equations are discretized using a second-order accurate, implicit, finite difference method in curvilinear coordinates, and they are solved using a dual time-stepping artificial compressibility method. The time derivative is approximated using a three-point backward difference, the convective terms are discretized using the QUICK scheme, and the other terms are treated using central difference. A DDM approach in conjunction with Chimera grids is implemented to deal with complex geometry. An effective mass conservation algorithm, which is a mass-flux based interpolation (MFBI), is proposed to achieve seamless transition of solutions between subdomains. For details about the technical aspects of the model, the reader is referred to [3, 5, 7].

FVCOM is a popular GFD model, and it has an external and an internal mode. The governing equations for the external mode in the hydrostatic version of the model are the two dimensional continuity and momentum equations [1]:

$$\displaystyle{ \begin{array}{l} \eta _{t} + \nabla _{H} \cdot (\mathbf{V}D) = 0,\end{array} }$$
(3)
$$\displaystyle{ \begin{array}{l} (\mathbf{V}D)_{t} + \nabla _{H} \cdot (\mathbf{VV}D) = -gD\nabla _{H}\eta + \dfrac{\boldsymbol{\tau }_{\mathbf{s}} -\boldsymbol{\tau }_{\mathbf{b}}} {\rho } + \mathbf{G}.\end{array} }$$
(4)

For the internal mode in that version, the governing equations are the three dimensional continuity and momentum equations:

$$\displaystyle{ \begin{array}{l} \eta _{t} + \nabla _{H} \cdot (\mathbf{v}D) + \omega _{\sigma } = 0,\\ \end{array} }$$
(5)
$$\displaystyle{ \begin{array}{l} (\mathbf{v}D)_{t} + \nabla _{H} \cdot (\mathbf{vv}D) + (\mathbf{v}\omega )_{\sigma } = -gD\nabla _{H}\eta \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ + \nabla _{H} \cdot (\alpha \mathbf{e}) + \dfrac{1} {D}(\beta \mathbf{v}_{\sigma })_{\sigma } + \mathbf{H}.\\ \end{array} }$$
(6)

In the external mode, V is the depth-averaged horizontal velocity, D is the water depth, \(\boldsymbol{\tau }_{\mathbf{s}}\) and \(\boldsymbol{\tau }_{\mathbf{b}}\) are the shear stress on water surface and seabed, respectively, g is the gravity, and G includes the rest terms such as the Coriolis force. ∇ H is the gradient operator in the horizontal plane. In the internal mode, \(\sigma\) is the vertical coordinate, η is water surface elevation, v is the horizontal velocity, e is the strain rate, ω is the vertical velocity in \(\sigma\)-coordinate, and H represents the other terms. Subscript \(\sigma\) stands for the derivative in \(\sigma\)-direction. α and β are diffusion coefficients, which are evaluated by the Mellor and Yamada level-2.5 turbulent closure [1].

3 Methodology

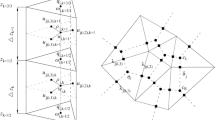
A schematic representation of the hybrid SIFOM–FVCOM system is depicted in Fig. 1a, in which SIFOM is employed within a subdomain that covers the local flow around a seamount and FVCOM is used for the large-scale background flow. An overlapping zone is arranged between the regions of SIFOM and FVCOM, and it is assumed that the overlapping zone is located at a place where the hydrostatic assumption holds. Since variable u in the governing equations of SIFOM and variables v and ω in the internal mode of FVCOM are essentially the same, or, they are the three components of velocity, the two models will exchange solutions for them (Fig. 1b). In addition, pressure p at the boundary of SIFOM can be determined by the value of η obtained with FVCOM using the hydrostatic assumption, which states that pressure is proportional to water depth. Chimera grids, or overset grids, will be used to couple SIFOM and FVCOM, and grid connectivity and solutions exchange at interfaces of them will be implemented using interpolation. The Schwarz alternative iteration method is employed for the iteration between the solutions of the two models, and, in advancing solution of the hybrid system at time step n to that at n + 1, it reads as

Step I.:

Assign solution at time step n to all grid nodes/elements.

Step II.:

Exchange solution at model interfaces by interpolation.

Step III.:

Solve SIFOM and FVCOM.

Step IV.:

If SIFOM and FVCOM solutions converge, go to Step V. If not, return to Step II.

Step V.:

Assign the convergent solution as the solution at time step n + 1.

Fig. 1
figure 1

A schematic representation of the hybrid SIFOM–FVCOM system. (a) Domain decomposition. (b) Solution exchange

Full size image

SIFOM and FVCOM will exchange solution at each time step. It is noted that the two models may use different time steps. In addition, the external and internal mode in FVCOM also permit different time steps. For details of the modeling system, the reader is referred to [6, 8, 9].

4 Numerical Experiment

Sill is a typical form of topography at bottom of oceans, and flows over it are rich in physical phenomena. Previous investigation indicates that it is necessary to include non-hydrostatic effects to adequately reproduce mixing and other processes involved in the flows (e.g., [10]). The hybrid SIFOM–FVCOM system is applied to simulate a transient flow over sill with configuration

$$\displaystyle{ \left \{\begin{array}{ll} - 1500 < x < 2000, \\ y = \pm 200(1 - 0.8e^{-4\times 10^{-6}x^{2} }),\quad x < 0;\ \ y = \pm 40,\ x > 0, \\ z = -150 + \dfrac{140} {1 + (x/500)^{4}},\ x < 0;\ \ z = -120 + \dfrac{110} {1 + (x/500)^{4}},\ x > 0, \\ \end{array} \right. }$$
(7)

and initial and boundary condition

$$\displaystyle{ \left \{\begin{array}{ll} u,v,w = 0,\ t = 0, \\ \eta u = 0.9175(1 - e^{-0.01t}),\ x = -1500;\ \eta = 0,\ x = 2000. \end{array} \right. }$$
(8)

In above expressions, length is in m, time in s, and velocity in m/s.

The grid of FVCOM covers the whole flow field, and that of SIFOM is located over the sill (Fig. 2). The grid of FVCOM has 10,400 triangle elements in the horizontal plane and 41 \(\sigma\)-layers in the vertical direction, and the number of grid nodes of SIFOM is 161 × 33 × 49 in the longitudinal, lateral, and vertical direction, respectively. The time step of the SIFOM–FVCOM system is 0.5.

Fig. 2
figure 2

Meshes for the sill flow

Full size image

As indicated in the initial condition in Eq. (8), the water body is initially stationary. Because of the imposition of an inflow at the entrance, a current occurs and moves to the right. Instantaneous solutions for the current at different moments are shown in Fig. 3. Figure 3a–f illustrate the current roughly when its front approaches, arrives at, and passes the top of the sill. Figure 3g and h present solutions for the flow after the front exits the computational domain, and it seems that it is at its equilibrium state at this moment. The solutions presented in the figures are reasonable in large scales in aspect of streamlines and velocity distribution.

Fig. 3
figure 3

Simulation of the sill flow at different moments. The solid lines around the sill indicate the boundary of SIFOM

Full size image

Nevertheless, a detailed examination of the solutions in Fig. 3 finds problems with them. Figure 4a, e indicate that, near the front of the current, where water bodies in motion and at rest are adjacent to each other, the solutions of the SIFOM model cannot react simultaneously to those obtained with the FVCOM model, and there is a delay in them. In addition, there is a pronounced difference, in both magnitude and direction, between the velocity solutions provided by the two models in their overlapping regions (Fig. 4a, c, e). In Fig. 4c, near the top of the sill, FVCOM provides a forward flow in the upper layer, while SIFOM produces a reverse flow in the lower layer. It is expected that there is no physical mechanism to generate such reverse flow, and apparently it is an artifact. It is not clear what causes the delay and difference in solutions and the reverse flow. All of these indicate that the hybrid system in its current form has difficulties to correctly resolve the flow at the current front, which is complicated and involves strong unsteadiness and non-hydrostatic effect. After the front passes, the solution becomes normal and above mentioned problems disappear, see Fig. 4b, d, f.

Fig. 4
figure 4

Zoom of the simulated sill flow at y=0

Full size image

5 Concluding Remarks

Hybrid of F3DFD and GFD models based on domain decomposition is a feasible approach to simulate multiscale and multiphysics coastal processes. However, this approach is challenging in view it involves coupling of different governing equations, distinct numerical methods, and dissimilar computational meshes. This paper indicates that, while its performance is promising, such approach faces difficulties to correctly resolve a current front associated with strong transient effect and it needs discretion in implementation.

Recently, a method has been proposed to overcome the difficulties reported in this paper. In this method, pressure is decomposed into hydrostatic pressure and dynamic pressure in the governing equations of SIFOM. As a result of the pressure decomposition, a term for gradient of surface elevation appears in the momentum equations, and it serves as a driving force in the horizontal direction. Details of this method and a comprehensive evaluation of the SIFOM–FVCOM system in aspects of theoretical analysis, numerical experiment, and laboratory measurement are presented in [8].