Reliability-Based Shape Design Optimization of Structures Subjected to Fatigue

Abstract

Fatigue has been played a key role into the design process of structures, since many failures of them are attributed to repeated loading and unloading conditions. Crack growth due to fatigue, represents a critical issue for the integrity and resistance of structures and several numerical methods mainly based on fracture mechanics have been proposed in order to address this issue. Apart from loading, the shape of the structures is directly attributed to their service life. In this study, the extended finite element is integrated into a shape design optimization framework aiming to improve the service life of structural components subject to fatigue. The relation between the geometry of the structural component with the service life is also examined. This investigation is extended into a probabilistic design framework considering both material properties and crack tip initialization as random variables. The applicability and potential of the formulations presented are demonstrated with a characteristic numerical example. It is shown that with proper shape changes, the service life of structural component can be enhanced significantly. Comparisons with optimized shapes found for targeted service life are also addressed, while the choice of initial imperfection position and orientation was found to have a significant effect on the optimal shapes.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The failure process of structural systems is considered among the most challenging phenomena in solid and structural mechanics. Despite of the advances achieved over the past decades in developing numerical simulation methods for modeling such phenomena, there are issues still open to be addressed for accurately describing failure mechanisms at the macro as well as at the micro level. Reliability and accuracy of the numerical description of failure process, plays an important role for the design of new materials as well as for understanding their durability and resistance to various loading conditions.

In case of structural components subjected to cycling loading, fatigue plays an important role to their residual service life. When loading exceeds certain threshold value, microscopic cracks begin to form that propagate and possibly lead to fracture. Additionally, the shape of these components is a key parameter that significantly affects their residual service life and designers can control. Square holes or sharp corners lead to increased local stresses where fatigue cracks can initiate whereas round holes and smooth transitions or fillets will increase fatigue strength of the component. Hence, it is required not only a reliable simulation tool for crack growth analysis able to predict the crack paths and accurately describe the stiffness degradation due to damage, but also there is a need for an optimization procedure capable to identify improved designs of the structural components with regard to a targeted service life.

Limitations of the analytical methods in handling arbitrary complex geometries and crack propagation phenomena led to the development of numerical techniques for solving fracture mechanics problems. In recent years, finite elements with enrichments have gained increasing interest in modeling material failure, with the extended finite element method (XFEM) being the most popular of them. XFEM [50] is capable of modeling discontinuities within the standard finite element framework and its efficiency increases when coupled with the level set method (LSM) [52]. In this framework, Edke and Chang [13] presented a shape sensitivity analysis method for calculating gradients of crack growth rate and crack growth direction for 2D structural components under mixed-mode loading, by overcoming the issues of calculating accurate derivatives of both crack growth rate and direction. This work was further extended [14] to a shape optimization framework to support design of 2D structural components again under mixed-mode fracture for maximizing the service life and minimizing their weight. Furthermore, Li et al.  [46] proposed elegant XFEM schemes for LSM based structural optimization, aiming to improve the computational accuracy and efficiency of XFEM, while Wang et al. [64] considered a reanalysis algorithm based on incremental Cholesky factorization which is implemented into an optimization algorithm to predict the angle of crack initiation from a hole in a plate with inclusion.

Many numerical methods have been developed over the last four decades in order to meet the demands of design optimization. These methods can be classified in two categories, gradient-based and derivative-free ones. Mathematical programming methods are the most popular methods of the first category, which make use of local curvature information, derived from linearization of objective and constraint functions and by using their derivatives with respect to the design variables at points obtained in the process of optimization. Heuristic and metaheuristic algorithms are nature-inspired or bio-inspired procedures that belong to the derivative-free category of methods. Metaheuristic algorithms for engineering optimization include genetic algorithms (GA) [34], simulated annealing (SA) [38], particle swarm optimization (PSO) [37], ant colony algorithm (ACO) [12], artificial bee colony algorithm (ABC) [27], harmony search (HS) [23], cuckoo search algorithm [67], firefly algorithm (FA) [66], bat algorithm [68], krill herd [20], and many others. Evolutionary algorithms (EA) are among the most widely used class of metaheuristic algorithms and in particular evolutionary programming (EP) [19], genetic algorithms [26, 34], evolution strategies (ES) [55, 59] and genetic programming (GP) [39].

The advancements in reliability theory of the past 30 years and the development of more accurate quantification of uncertainties associated with system loads, material properties and resistances have stimulated the interest in probabilistic treatment of systems [58]. The reliability of a system or its probability of failure constitute important factors to be considered during the design procedure, since they characterize the system’s capability to successfully accomplish its design requirements. First and second order reliability methods, however, that have been developed to assess reliability, they require prior knowledge of the means and variances of component random variables and the definition of a differentiable limit-state function. On the other hand, simulation based methods are not restricted by form and knowledge of the limit-state function but many of them are characterized by high computational cost.

In this study, XFEM and LSM are integrated into a shape design optimization framework, aiming to investigate the relation between geometry and fatigue life in the design of 2D structural components. Specifically, shape design optimization problems are formulated within the context of XFEM, where the volume of the structural component is to be minimized subjected to constraint functions related to targeted service life (minimum number of fatigue cycles allowed) when material properties and crack tip initialization are considered as random variables. XFEM is adopted to solve the crack propagation problem as originally proposed by Moës et al. [50] and Stolarska et al. [61], with the introduction of adaptive enrichment technique and the consideration of asymptotic crack tip fields and Heaviside functions. XFEM formulation is particularly suitable for this type of problem since mesh difficulties encountered into a CAD-FEM shape optimization problem are avoided by working with a fixed mesh approach. In association to XFEM, the level set description is used to describe the geometry providing also the ability to modify the CAD model topology during the optimization process. Nature inspired optimization techniques have been proven to be computationally appealing, since they have been found to be robust and efficient even for complex problems and for this purpose are applied in this study. An illustrative example of a structural component is presented, and the results show that, with proper shape changes, the service life of structural systems subjected to fatigue loads can be enhanced. Comparisons between optimized shapes obtained for various targeted fatigue life values are also addressed, while the location of the initial imperfection along with its orientation were found to have a significant effect on the optimal shapes for the components examined [24].

2 Handling Fatigue Using XFEM

Fatigue growth occurs because of inelastic behavior at the crack tip. The present study is focused on 2D mixed-mode linear elastic fracture mechanics (LEFM) formulation, where the size of plastic zone is sufficiently small and it is embedded within an elastic singularity zone around the crack tip.

2.1 Fatigue Crack Growth Analysis at Mixed-Mode Loading

In order to quantify crack growth around the crack tip in the presence of constant amplitude cyclic stress intensity, the basic assumptions of LEFM are employed. The conditions at the crack tip are uniquely defined by the current value of the stress intensity factors (SIFs) $K$. For extractiing mixed-mode SIFs, the domain form of the interaction energy integral [70] is used, based on the path independent J-integral [56], providing mesh independency and easy integration within the finite element code. When both stress intensity factors ($K_{I}, K_\textit{II}$) are known, the critical direction of crack growth $\theta _{c}$ as well as the number of fatigue cycles $N$ can easily be computed.

2.1.1 Computation of the Crack Growth Direction

The accuracy and reliability of the analysis of a cracked body depends primarily on continuity and accurate determination of the crack path. It is therefore important to select the crack growth criteria very carefully. Among the existing criteria, the maximum hoop stress criterion [17], is used in this study. The crack growth criterion states that (i) crack initiation will occur when the maximum hoop stress reaches a critical value and (ii) crack will grow along direction $\theta _{cr}$ in which circumferential stress $\sigma _{\theta \theta }$ is maximum.

Fig. 1

Polar coordinates in the crack tip coordinate system

Then the circumferential stress $\sigma _{r \theta }$ (see Fig. 1) along the direction of crack propagation is a principal stress, hence the crack propagation direction $\theta _{cr}$ is determined by setting the shear stress equal to zero, i.e.:

$$\begin{aligned} \sigma _{r\theta } = \frac{1}{2\pi r}cos\frac{\theta }{2} \Big ( \frac{1}{2}K_{I}sin\theta + \frac{1}{2}K_\textit{II}(3cos\theta - 1\Big ) = 0 \end{aligned}$$

(1)

This leads to the expression for defining the critical crack propagation direction $\theta _{cr}$ in terms of local crack tip coordinate system as:

$$\begin{aligned} \theta _{cr} = 2 atan\frac{1}{4} \Big ( \frac{K_{I}}{K_\textit{II}} \pm \sqrt{\frac{K_{I}^2}{K_\textit{II}} + 8} \Big ) \end{aligned}$$

(2)

It is worth mentioning that according to this criteria, the maximum propagation angle $\theta _{cr}$ is limited to 70.5$^{\circ }$ for pure Mode II crack propagation problems.

2.1.2 Computation of Fatigue Cycles

Fatigue crack growth is estimated using Paris law [53], which is originally proposed for single mode deformation cases, relating the crack propagation rate under fatigue loading to SIFs. For the case of mixed-mode loading, a modified Paris law can be expressed using the effective stress intensity factor range $\varDelta K_{\text {eff}}=K_\textit{max}-K_\textit{min}$. For a certain fatigue loading level, where the crack grows by length $\varDelta a$ in $\varDelta N$ cycles, Paris law reads:

$$\begin{aligned} \frac{\varDelta a}{\varDelta N} \approx \frac{da}{dN} = C (\varDelta K_{\text {eff}})^{m} \end{aligned}$$

(3)

where $C$ and $m$ are empirical material constants. $m$ is often called as the Paris exponent and is typically defined in the range of 3–4 for common steel and aluminium alloys. Equation 3 represents a linear relationship between $log(\varDelta K_{\text {eff}})$ and $log(\frac{da}{dN})$ which is used to describe the fatigue crack propagation behavior in region II (see Fig. 2). For calculating the effective mixed-mode stress intensity factor $\varDelta K_{\text {eff}}$, various criteria have been proposed in the literature. In this study, the energy release rate model has been adopted, leading to:

$$\begin{aligned} \varDelta K_{\text {eff}} = \sqrt{\varDelta K_{I}^{2} + \varDelta K_\textit{II}^{2}} \end{aligned}$$

(4)

and consequently, the number of the corresponding cycles is computed according to [2]:

$$\begin{aligned} \varDelta N = \frac{\varDelta a}{C (\varDelta K_{\text {eff}})^{m}} \end{aligned}$$

(5)

Fig. 2

Logarithmic crack growth rate and effective region of Paris law

2.1.3 Fracture Toughness

Similar to the strength of materials theory where the computed stress is compared with an allowable stress defining the material strength, LEFM assumes that unstable fracture occurs when SIF $K$ reaches a critical value $K_{c}$, called fracture toughness, which represents the potential ability of a material to withstand a given stress field at the crack tip and to resist progressive tensile crack extension. In other words, $K_{c}$ is a material constant and is used as a threshold value for SIFs in each pure fracture.

In XFEM, special functions are added to the finite element approximation based on the partition of unity (PU) [3]. Finite element mesh is generated and then additional degrees of freedom are introduced to selected nodes of the finite element model near to the discontinuities in order to provide a higher level of accuracy. Hence quasi-static crack propagation simulations can be carried out without remeshing, by modeling the domain with standard finite elements without explicitly meshing the crack surfaces.

2.2 Modeling the Crack Using XFEM

For crack modeling in XFEM, two types of enrichment functions are used: (i) The Heaviside (step) function and (ii) the asymptotic crack-tip enrichment functions taken from LEFM [2]. The displacement field can be expressed as a superposition of the standard $u^{\text {std}}$, crack-split $u^{\text {H}}$ and crack-tip $u^{\text {tip}}$ fields as:

$$\begin{aligned} \mathbf {u}(\mathbf {x}) = \mathbf {u}^{\text {std}} + \mathbf {u}^{\text {enr}} = \mathbf {u}^{\text {std}} + \mathbf {u}^{\text {H}} + \mathbf {u}^{\text {tip}} \end{aligned}$$

(6)

or more explicitly:

$$\begin{aligned} \mathbf {u}(\mathbf {x}) = \sum _{j=1}^{n} N_{j}(\mathbf {x}) \mathbf {u}_{j} + \sum _{h=1}^{n_{h}} N_{h}(\mathbf {x}) H(\mathbf {x}) \mathbf {a}_{h} + \sum _{k=1}^{n_{t}} N_{k}(\mathbf {x}) \Big (\sum _{l=1}^{n_{f}} F_{l}(\mathbf {x})\mathbf {b}_{k}^{l} \Big ) \end{aligned}$$

(7)

where $n$ is the number of nodes in each finite element with standard degrees of freedom $\mathbf {u}_{j}$ and shape functions $N_{j}(\mathbf {x})$, $n_{h}$ is the number of nodes in the elements containing the crack face (but not crack tip), $\mathbf {a}_{h}$ is the vector of additional degrees of freedom for modeling crack faces by the Heaviside function $H(\mathbf {x})$, $n_{t}$ is the number of nodes associated with the crack tip in its influence domain, $\mathbf {b}_{k}^{l}$ is the vector of additional degrees of freedom for modeling crack tips. Finally, $F_{l}(\mathbf {x})$ are the crack-tip enrichment functions, given by:

$$\begin{aligned} \left\{ F_{l}(r, \theta )\right\} _{l=1}^{4} =\left\{ \sqrt{r}\sin (\frac{\theta }{2}); \sqrt{r}\cos (\frac{\theta }{2}); \sqrt{r}\sin (\frac{\theta }{2})\sin (\theta ); \sqrt{r}\cos (\frac{\theta }{2})\sin (\theta ) \right\} \end{aligned}$$

(8)

The elements which are completely cut by the crack, are enriched with the Heaviside (step) function $H$. The Heaviside function is a discontinuous function across the crack surface and is constant on each side of the crack. Splitting the domain by the crack causes a displacement jump and Heaviside function gives the desired behavior to approximate the true displacement field.

The first contributing part ($u^{\text {std}}$) on the right-hand side of Eq. (7) corresponds to the classical finite element approximation to determine the displacement field, while the second part ($u^{\text {enr}}$) refers to the enrichment approximation which takes into account the existence of any discontinuities. This second contributing part utilizes additional degrees of freedom to facilitate modeling of the discontinuous field, such as cracks, without modeling it explicitly.

3 The Structural Optimization Problem

Structural optimization problems are characterized by objective and constraint functions that are generally non-linear functions of the design variables. These functions are usually implicit, discontinuous and non-convex. In general there are three classes of structural optimization problems: sizing, shape and topology problems. Structural optimization was focused at the beginning on sizing optimization, such as optimizing cross sectional areas of truss and frame structures, or the thickness of plates and shells and subsequently later, the problem of finding optimum boundaries of a structure and optimizing its shape was also considered. In the former case the structural domain is fixed, while in the latter case it is not fixed but it has a predefined topology.

The mathematical formulation of structural optimization problems can be expressed in standard mathematical terms as a non-linear programming problem, which in general form can be stated as follows:

$$\begin{aligned} \begin{aligned} \text {opt:} \quad&F(\varvec{s}) \\ \text {subject to:} \quad&g_{j}(\varvec{s})\le 0, \quad j = 1,\ldots , k \\&s_{i}^\textit{low} \le s_{i} \le s_{i}^{up}, \quad i = 1,\ldots , n \end{aligned} \end{aligned}$$

(9)

where $\varvec{s}$ is the vector of design variables, $F(\varvec{s})$ is the objective function to be optimized (minimized or maximized), $g_{j}(\varvec{s})$ are the behavioral constraint functions, while $s_{i}^\textit{low}$ and $s_{i}^{up}$ are the lower and upper bounds of the $i$th design variable. Due to fabrication limitations the design variables are not always continuous but discrete since cross-sections or dimensions belong to a certain design set. A discrete structural optimization problem can be formulated in the form of Eq. (9) where $s_{i} \in \mathfrak {R}_{d}, \; i = 1, 2, \ldots , n$ where $\mathfrak {R}_{d}^{n}$ is a given set of discrete values representing for example the available structural member cross-sections or dimensions and design variables $\varvec{s}$ can take values only from this set.

3.1 Shape Optimization

In structural shape optimization problems the aim is to improve the performance of the structural component by modifying its boundaries [4, 6, 28, 60]. All functions are related to the design variables, which are coordinates of key points in the boundary of the structure. The shape optimization methodology proceeds with the following steps:

• (i) At the outset of the optimization, the geometry of the structure under investigation has to be defined. The boundaries of the structure are modeled using cubic B-splines that, are defined by a set of key points. Some of the coordinates of these key points will be considered as design variables.

• (ii) An automatic mesh generator is used to create the finite element model. A finite element analysis is carried out and displacements, stresses are calculated.

• (iii) The optimization problem is solved; the design variables are improved and the new shape of the structure is defined. If the convergence criteria for the search algorithm are satisfied, then the optized solution has been found and the process is terminated, else a new geometry is defined and the whole process is repeated from step (ii).

3.2 XFEM Shape Optimization Considering Uncertainties

In this study, two problem formulations are considered, a deterministic and a probabilistic one. According to the deterministic formulation, the goal is to minimize the material volume expressed by optimized geometry of the structural component subject to constraints related to the minimum service life allowed (calculated using fatigue cycles as described in Sect. 2.1.2).

3.2.1 Deterministic Formulation (DET)

The design problem for the deterministic formulation (DET) is defined as:

$$\begin{aligned} \begin{aligned} \text {min:} \quad&V(\varvec{s}) \\ \text {subject to:} \quad&N(\varvec{s})\ge N_\textit{min} \\&s_{i}^\textit{low} \le s_{i} \le s_{i}^{up}, \quad i = 1, 2, \dots , n \end{aligned} \end{aligned}$$

(10)

$V$ is the volume of the structural component, $s_{i}$ are the shape design variables with lower and upper limits $s_{i}^\textit{low}$ and $s_{i}^{up}$, respectively, and $N$ is the service life in terms of number of fatigue cycles with the lower limit of $N_\textit{min}$.

3.2.2 Probabilistic Formulation (PROB)

The probabilistic design problem (PROB) is defined as:

$$\begin{aligned} \begin{aligned} \text {min:} \quad&V(\varvec{s}) \\ \text {subject to:} \quad&\bar{N}(\varvec{s},\varvec{x})\ge N_\textit{min} \\&s_{i}^\textit{low} \le s_{i} \le s_{i}^{up}, \quad i = 1, 2,\dots , n \\&x_{j} \sim f_{x}(\mu _{x},\sigma _{x}^{2}) \quad j = 1, 2, \dots , nr \end{aligned} \end{aligned}$$

(11)

where $\varvec{s}$ and $\varvec{x}$ are the vectors of the design and random variables, respectively, $\bar{N}$ is the mean number of fatigue cycles.

The probabilistic quantity $\bar{N}$ of Eq. (11) is calculated by means of the Latin hypercube sampling (LHS) method. LHS was introduced by McKay et al. [49] in an effort to reduce the required computational cost of purely random sampling methodologies. LHS can generate variable number of samples well distributed over the entire range of interest. A Latin hypercube sample is constructed by dividing the range of each of the $nr$ uncertain variables into $M$ non-overlapping segments of equal marginal probability. Thus, the whole parameter space, consisted of $M$ parameters, is partitioned into $M^{nr}$ cells. A single value is selected randomly from each interval, producing $M$ sample values for each input variable. The values are randomly matched to create $M$ sets from the $M^{nr}$ space with respect to the density of each interval for the $M$ simulations.

4 Metaheuristic Search Algorithms

Heuristic algorithms are based on trial-and-error, learning and adaptation procedures in order to solve problems. Metaheuristic algorithms achieve efficient performance for a wide range of combinatorial optimization problems. Four metaheuristic algorithms that are based on the evolution process are used in the framework of this study. In particular evolution strategies (ES), covariance matrix adaptation (CMA), elitist covariance matrix adaptation (ECMA) and differential evolution (DE) are employed. Details on ES, CMA and ECMA can be found in the work by Lagaros [42], while the version of DE implemented in this study is briefly outlined below.

4.1 Evolution Strategies (ES)

Evolutionary strategies are population-based probabilistic direct search optimization algorithm gleaned from principles of Darwinian evolution. Starting with an initial population of $\mu$ candidate designs, an offspring population of $\lambda$ designs is created from the parents using variation operators. Depending on the manner in which the variation and selection operators are designed and the spaces in which they act, different classes of ES have been proposed. In ES algorithm employed in this study [55, 59], each member of the population is equipped with a set of parameters:

$$\begin{aligned} \varvec{a}= & {} [(\varvec{s}_{d},\varvec{\gamma }), (\varvec{s}_{c},\varvec{\sigma },\varvec{\alpha })] \in (I_{d},I_{c}) \nonumber \\ I_{d}= & {} D^{n_{d}} \times R_{+}^{n_{\gamma }} \\ I_{c}= & {} D^{n_{c}} \times R_{+}^{n_{\sigma }} \times [-\pi , \pi ]^{n_{\alpha }} \nonumber \end{aligned}$$

(12)

where $\varvec{s}_{d}$ and $\varvec{s}_{c}$, are the vectors of discrete and continuous design variables defined in the discrete and continuous design sets $D^{n_{d}}$ and $R^{n_{c}}$, respectively. Vectors $\varvec{\gamma , \sigma }$ and $\varvec{\alpha }$, are the distribution parameter vectors taking values in $R_{+}^{n_{\gamma }}$, $R_{+}^{n_{\sigma }}$ and $[-\pi , \pi ]^{n_{\alpha }}$, respectively. Vector $\varvec{\gamma }$ corresponds to the variances of the Poisson distribution. Vector $\varvec{\sigma } \in R_{+}^{n_{\sigma }}$ corresponds to the standard deviations $(1 \leqslant n_{\sigma } \leqslant n_{c})$ of the normal distribution. Vector $\varvec{\alpha } \in [-\pi , \pi ]^{n_{\alpha }}$ is related to the inclination angles $(n_{\alpha }=(n_{c}-n_{\sigma }/2)(n_{\sigma }-1))$ defining linearly correlated mutations of the continuous design variables $\varvec{s}_{d}$, where $n=n_{d}+n_{c}$ is the total number of design variables.

Let $P(t)=\{a_{1},\dots ,a_{\mu }\}$ denotes a population of individuals at the $t$-th generation. The genetic operators used in the ES method are denoted by the following mappings:

$$\begin{aligned} {rec}{:}&(I_{d},I_{c})^{\mu } \longrightarrow (I_{d},I_{c})^{\lambda } \quad (recombination)\nonumber \\ {mut}{:}&(I_{d},I_{c})^{\lambda } \longrightarrow (I_{d},I_{c})^{\lambda } \quad (mutation) \\ {sel_{\mu }^{k}}{:}&(I_{d},I_{c})^{k} \longrightarrow (I_{d},I_{c})^{\mu } \quad (selection, k \in \{\lambda , \mu + \lambda \}) \nonumber \end{aligned}$$

(13)

A single iteration of the ES, which is a step from the population $P_{p}^{t}$ to the next parent population $P_{p}^{t+1}$ is modeled by the mapping:

$$\begin{aligned} {opt_{EA}}{:} \;(I_{d},I_{c})_{t}^{\mu } \longrightarrow (I_{d},I_{c})_{t+1}^{\mu } \end{aligned}$$

(14)

4.2 Covariance Matrix Adaptation (CMA)

The covariance matrix adaptation, proposed by Hansen and Ostermeier [30] is a completely de-randomized self-adaptation scheme. First, the covariance matrix of the mutation distribution is changed in order to increase the probability of producing the selected mutation step again. Second, the rate of change is adjusted according to the number of strategy parameters to be adapted. Third, under random selection the expectation of the covariance matrix is stationary. Further, the adaptation mechanism is inherently independent of the given coordinate system. The transition from generation $g$ to $g+1$, given in the following steps, completely defines the Algorithm 2.

Generation of offsprings. Creation of $\lambda$ new offsprings as follows:

$$\begin{aligned} s_{k}^{g+1} \sim N (\mathbf {m}^{(g)}, \sigma ^{(g)^{2}}{\mathsf {C}}^{({\text {g}})}) \sim \mathbf {m}^{(g)} + \sigma ^{(g)}N(\mathbf {0},{\mathsf {C}}^{(g)}) \end{aligned}$$

(15)

where $s_{k}^{g+1} \in \mathfrak {R}^{n}$ is the design vector of the $k$th offspring in generation $g+1, (k = 1,..., \lambda )$, $N (\mathbf {m}^{(g)}, {\mathsf {C}}^{({\text {g}})})$ are normally distributed random numbers where $\mathbf {m}^{(g)} \in \mathfrak {R}^{n}$ is the mean value vector and ${\mathsf {C}}^{(g)}$ is the covariance matrix while $\sigma ^{(g)}\in \mathfrak {R}_{+}$ is the global step size. To define a generation step, the new mean value vector $\mathbf {m}^{(g+1)}$, global step size $\sigma ^{(g+1)}$, and covariance matrix ${\mathsf {C}}^{(g+1)}$ have to be defined.

New mean value vector. After selection scheme $(\mu , \lambda )$ operates over the $\lambda$ offsprings, the new mean value vector $\mathbf {m}^{(g+1)}$ is calculated according to the following expression:

$$\begin{aligned} \mathbf {m}^{(g+1)} = \sum _{i=1}^{\mu } w_{i} \mathbf {s}_{i: \lambda }^{(g+1)} \end{aligned}$$

(16)

where $\mathbf {s}_{i: \lambda }^{(g+1)}$ is the $i$th best offspring and $w_{i}$ are the weight coefficients.

Global step size. The new global step size is calculated according to the following expression:

$$\begin{aligned} \sigma ^{(g+1)} = \sigma ^{(g)} exp\left( \frac{c_{\sigma }}{d_{\sigma }} \left( \frac{\Vert \mathbf {p}_{\sigma }^{(g+1)}\Vert }{E \Vert N({\mathsf {0}}, {\mathsf {I}}) \Vert } - 1 \right) \right) \end{aligned}$$

(17)

while the matrix ${\mathsf {C}}^{(g)^{-\frac{1}{2}}}$ is given by:

$$\begin{aligned} {\mathsf {C}}^{(g)^{-\frac{1}{2}}} = {\mathsf {B}}^{(g)} {\mathsf {D}}^{(g)^{-1}} {\mathsf {B}}^{(g)^{T}} \end{aligned}$$

(18)

where the columns of ${\mathsf {B}}^{(g)}$ are an orthogonal basis of the eigenvectors of ${\mathsf {C}}^{(g)}$ and the diagonal elements of ${\mathsf {D}}^{(g)}$ are the square roots of the corresponding positive eigenvalues.

Covariance matrix update. The new covariance matrix ${\mathsf {C}}^{(g+1)}$ is calculated from the following equation:

$$\begin{aligned} {\mathsf {C}}^{(g+1)}&= (1-c_{\text {cov}}){\mathsf {C}}^{(g)} + \frac{c_{\text {cov}}}{\mu _{\text {cov}}} \mathbf {p}_{c}^{(g+1)} \mathbf {p}_{c}^{(g+1)^{T}} \nonumber \\&+ c_{\text {cov}} \left( 1 - \frac{1}{\mu _{\text {cov}}}\right) \sum _{i=1}^{\mu } w_{i} OP \left( \frac{s_{i:\lambda }^{(g+1)} - \mathbf {m}^{(g)}}{\sigma ^{(g)}} \right) \end{aligned}$$

(19)

$\textit{OP}$ denotes the outer product of a vector with itself and $\mathbf {p}_{c}^{(g)} \in \mathfrak {R}^{n}$ is the evolution path $(\mathbf {p}_{c}^{(0)}=0)$.

4.3 Elitist Covariance Matrix Adaptation (ECMA)

Elitist CMA evolution strategies algorithm is a combination of the well-known $(1+\lambda )$-selection scheme of evolution strategies [55], with covariance matrix adaptation [35]. The original update rule of the covariance matrix is applied to the $(1+\lambda )$-selection while the cumulative step size adaptation (path length control) of the CMA$(\mu /\mu , \lambda )$ is replaced by a success rule based step size control. Every individual $a$ of the ECMA algorithm is comprised of five components:

$$\begin{aligned} a = \{s, \overline{p}_{succ}, \sigma , \mathbf {p}_{c}, {\mathsf {C}}\} \end{aligned}$$

(20)

where $s$ is the design vector, $\overline{p}_{succ}$ is a parameter that controls the success rate during the evolution process, $\sigma$ is the step size, $\mathbf {p}_{c}$ is the evolution path and ${\mathsf {C}}$ is the covariance matrix. Contrary to CMA, each individual has its own step size $\sigma$, evolution path $\mathbf {p}_{c}$ and covariance matrix ${\mathsf {C}}$. A pseudo code of the ECMA algorithm

is shown in Algorithm 3. In line #1 a new parent $a_{parent}^{(g)}$ is generated. In lines #4–6, $\lambda$ new offsprings are generated from the parent vector $a_{parent}^{(g)}$. The new offsprings are sampled according to Eq. (8), with variable $\mathbf {m}^{(g)}$ being replaced by the design vector $s_{parent}^{(g)}$ of the parent individual. After the $\lambda$ new offsprings are sampled, the parent’s step size is updated by means of $UpdateStepSize$ subroutine (see Procedure 4). The arguments of the subroutine are the parent $a_{parent}^{(g)}$ and the success rate $\lambda _{succ}^{(g+1)}/\lambda$, where $\lambda _{succ}^{(g+1)}$ is the number of offsprings having better fitness function than the parent. The step size update is based upon the $1/5$ success rule, thus when the ratio $\lambda _{succ}^{(g+1)}/\lambda$ is larger than $1/5$ step size increases, otherwise step size decreases. If the best offspring has a better fitness value than the parent, it becomes the parent of the next generation (see lines #8–9), and the covariance matrix of the new parent is updated by means of $UpdateCovariance$ subroutine (see Procedure 5). The arguments of the subroutine are the current parent and the step change:

$$\begin{aligned} \frac{s_{parent}^{(g+1)}-{s_{parent}^{(g)}}}{\sigma _{parent}^{(g)}} \end{aligned}$$

(21)

The update of the evolution path and the covariance matrix depends on the success rate:

$$\begin{aligned} \overline{p}_{succ} = \frac{\lambda _{succ}}{\lambda } \end{aligned}$$

(22)

If the success rate is below a given threshold value $p_{thresh}$ then the step size is taken into account and the evolution path and the covariance matrix is updated (see lines #2–3 of Procedure 5). If the success rate is above the given threshold $p_{thresh}$ the step change is not taken into account and evolution path and covariance matrix happens are updated (see lines #5–6).

4.4 Differential Evolution (DE)

Storn and Price [62] proposed a floating point evolutionary algorithm for global optimization and named it differential evolution (DE), by implementing a special kind operator in order to create offsprings from parent vectors. Several variants of DE have been proposed so far [9]. According to the variant implemented in the current study, a donor vector $\mathbf {v}_{i,g+1}$ is generated first:

$$\begin{aligned} \mathbf {v}_{i,g+1} = \mathbf {s}_{r_{1},g} + F \cdot (\mathbf {s}_{r_{2},g} - \mathbf {s}_{r_{3},g}) \end{aligned}$$

(23)

Integers $r_{1}$, $r_{2}$ and $r_{3}$ are chosen randomly from the interval $[1,NP]$ while $i \ne r_{1}, r_{2}$ and $r_{3}$. $NP$ is the population size and $F$ is a real constant value, called the mutation factor. In the next step the crossover operator is applied by generating the trial vector $\mathbf {u}_{i,g+1}$ which is defined from the elements of $\mathbf {s}_{i,g}$ or $\mathbf {v}_{i,g+1}$ with probability $CR$:

$$\begin{aligned} \begin{aligned} u_{j,i,g+1}&= \left\{ \begin{array}{ll} v_{j,i,g+1} \text{, } &{} \text {if} \;\; \text {rand}_{i,j} \le CR \;\; \text {or} \;\; j = I_{\text {rand}} \\ s_{j,i,g} \text{, } &{} \text {if} \;\; \text {rand}_{i,j} \ge CR \;\; \text {or} \;\; j \ne I_{\text {rand}} \end{array} \right. \\ i&= 1, 2, \ldots , NP \; \text {and} \; j = 1, 2, \ldots , n \end{aligned} \end{aligned}$$

(24)

where $\text {rand}_{j,i} \sim U[0,1],I_{rand}$ is a random integer from $[1,2,\dots ,n]$ which ensures that $\mathbf {v}_{i,g+1} \ne \mathbf {s}_{i,g}$. The last step of the generation procedure is the implementation of the selection operator where the vector $\mathbf {s}_{i,g}$ is compared to the trial vector $\mathbf {u}_{i,g+1}$:

$$\begin{aligned} \begin{aligned} \mathbf {s}_{i,g+1}&= \left\{ \begin{array}{ll} \mathbf {u}_{i,g+1} \text{, } &{} \text {if} \;\; F(\mathbf {u}_{i,g+1}) \le F(\mathbf {s}_{i,g}) \\ \mathbf {s}_{i,g} \text{, } &{} \text {otherwise} \end{array} \right. \\ i&= 1, 2, \ldots , NP \end{aligned} \end{aligned}$$

(25)

where $F(\mathbf {s})$ is the objective function to be optimized, while without loss of generality the implementation described in Eq. (25) corresponds to minimization.

5 Towards the Selection of the Optimization Algorithm

In the past a number of studies have been published where structural optimization with single and multiple objectives are solved implementing metaheuristics. A sensitivity analysis is performed for four metaheuristic algorithms in benchmark multimodal constrained functions highlighting the proper search algorithm for solving the structural optimization problem.

5.1 Literature Survey on Metaheuristic Based Structural Optimization

Perez and Behdinan [54] presented the background and implementation of a particle swarm optimization algorithm suitable for constraint structural optimization problems, while improvements that effect of the setting parameters and functionality of the algorithm were shown. Hasançebi [31] investigated the computational performance of adaptive evolution strategies in large-scale structural optimization. Bureerat and Limtragool [5] presented the application of simulated annealing for solving structural topology optimization, while a numerical technique termed as multiresolution design variables was proposed as a numerical tool to enhance the searching performance. Hansen et al. [29] introduced an optimization approach based on an evolution strategy that incorporates multiple criteria by using nonlinear finite-element analyses for stability and a set of linear analyses for damage-tolerance evaluation, the applicability of the approach was presented for the window area of a generic aircraft fuselage. Kaveh and Shahrouzi [36] proposed a hybrid strategy combining indirect information share in ant systems with direct constructive genetic search, for this purpose some proper coding techniques were employed to enable testing the method with various sets of control parameters. Farhat et al. [18] proposed a systematic methodology for determining the optimal cross-sectional areas of buckling restrained braces used for the seismic upgrading of structures against severe earthquakes, for this purpose single-objective and multi-objective optimization problems were formulated. Chen and Chen [7] proposed modified evolution strategies for solving mixed-discrete optimization problems, in particular three approaches were proposed for handling discrete variables.

Gholizadeh and Salajegheh [25] proposed a new metamodeling framework that reduces the computational burden of the structural optimization against the time history loading, for this purpose a metamodel consisting of adaptive neuro-fuzzy inference system, subtractive algorithm, self-organizing map and a set of radial basis function networks were used to accurately predict the time history responses of structures. Wang et al. [65] studied an optimal cost base isolation design or retrofit design method for bridges subject to transient earthquake loads. Hasançebi et al. [32] utilized metaheuristic techniques like genetic algorithms, simulated annealing, evolution strategies, particle swarm optimizer, tabu search, ant colony optimization and harmony search in order to develop seven optimum design algorithms for real size rigidly connected steel frames. Manan et al. [47] employed four different biologically inspired optimization algorithms (binary genetic algorithm, continuous genetic algorithm, particle swarm optimization, and ant colony optimization) and a simple meta-modeling approach on the same problem set. Gandomi and Yang [21] provide an overview of structural optimization problems of both truss and non-truss cases. Martínez et al. [48] described a methodology for the analysis and design of reinforced concrete tall bridge piers with hollow rectangular sections, which are typically used in deep valley bridge viaducts. Kripakaran et al. [40] presented computational approaches that can be implemented in a decision support system for the design of moment-resisting steel frames, while trade-off studies were performed using genetic algorithms to evaluate the savings due to the inclusion of the cost of connections in the optimization model. Gandomi et al. [22] used the cuckoo search (CS) method for solving structural optimization problems, furthermore, for the validation against structural engineering optimization problems the CS method was applied to 13 design problems taken from the literature.

Kunakote and Bureerat [41] dealt with the comparative performance of some established multi-objective evolutionary algorithms for structural topology optimization, four multi-objective problems, having design objectives like structural compliance, natural frequency and mass, and subjected to constraints on stress, were used for performance testing. Su et al. [63] used genetic algorithm to handle topology and sizing optimization of truss structures, in which a sparse node matrix encoding approach is used and individual identification technique is employed to avoid duplicate structural analysis to save computation time. Gandomi and Yang [21] used firefly algorithm for solving mixed continuous/discrete structural optimization problems, the results of a trade study carried out on six classical structural optimization problems taken from literature confirm the validity of the proposed algorithm. Degertekin [11] proposed two improved harmony search algorithms for sizing optimization of truss structures, while four truss structure weight minimization problems were presented to demonstrate the robustness of the proposed algorithms. The main part of the work by Muc and Muc-Wierzgoń [51] was devoted to the definition of design variables and the forms of objective functions for multi-layered plated and shell structures, while the evolution strategy method was used as the optimization algorithm. Comparative studies of metaheuristics on engineering problems can be found in two recent studies by the authors Lagaros and Karlaftis [43], Lagaros and Papadrakakis [44] and in the edited book by Yang and Koziel [69].

5.2 Sensitivity Analysis of Metaheuristic Algorithms

Choosing the proper search algorithm for solving an optimization problem is not a straightforward procedure. In this section a sensitivity analysis of four search algorithms is performed for five constrained multimodal benchmark test functions in order to identify the best algorithm and to be used for solving the structural shape optimization problem studied in the next section. This sensitivity analysis is carried out to examine the efficiency of the four metaheuristic algorithms and thus proving their robustness. In particular, for the solution of the five problems ES, CMA, ECMA and DE methods are implemented, since they were found robust and efficient in previous numerical tests [43, 44]. This should not been considered as an implication related to the efficiency of other algorithms, since any algorithm available can be considered for the solution of the optimization problem based on user’s experience.

The control parameters for DE are the population size ($NP$), probability ($CR$) and constant ($F$), while for ES, CMA and ECMA the control parameters are the number of parents ($\mu$) and offsprings ($\lambda$). The characteristic parameters adopted for the implementation are as follows: (i) for DE method, population size $NP$ = 15, probability $CR$ = 0.90 and constant $F$ = 0.60, while (ii) for all three ES, CMA and ECMA methods, number of parents $\mu$ = 1 and offsprings $\lambda$ = 14 for the case of ES and ECMA and number of parents $\mu$ = 5 and offsprings $\lambda$ = 15 for the case of CMA.

For all four algorithms the initial population is generated randomly using LHS in the range of design space for each test example examined, while for the implementation of all algorithms, the real valued representation of the design vectors is adopted. For the purposes of the sensitivity analysis 50 independent optimization runs were performed, for the combination of the algorithmic parameters given above. The 50 independent optimization runs, represents a necessary step since non deterministic optimization algorithms do not yield the same results when restarted with the same parameters [57]. Using the optimum objective function values achieved for the 50 independent optimization runs, mean and coefficient of variation of the optimum objective function value are calculated.

For comparative reasons the method adopted for handling the constraints and the termination criterion is the same for all metaheuristic optimization algorithms. In particular, the simple yet effective, multiple linear segment penalty function [44] is used in this study for handling the constraints. According to this technique if no violation is detected, then no penalty is imposed on the objective function. If any of the constraints is violated, a penalty, relative to the maximum degree of constraints’ violation, is applied to the objective function, otherwise the optimization procedure is terminated after 10,000 function evaluations. For the results found in the literature and used for our comparative study different constraint handling techniques and termination criteria were implemented.

5.2.1 Test Case S-6ACT

The first test case considered in this sensitivity analysis study is the so called S-6ACT [33] problem that is defined as follows:

$$\begin{aligned} \text {min:} \quad F(x)&= x_{1}^{2} + x_{2}^{2} + x_{1}x_{2} - 14x_{1} -16x_{2} + (x_{3} - 10)^{2} + 4(x_{4} - 5)^{2} \\&+ (x_{5} - 3)^{2} + 2(x_{6} - 1)^{2} + 5x_{7}^{2} + 7(x_{8} - 11)^{2} + 2(x_{9} - 10)^{2} \\&+ (x_{10} - 7)^{2} + 45 \\ \text {subject to:} \quad g_{1}(\mathbf {x})&= 105 - 4x_{1} - 5x_{2} + 3x_{7} - 9x_{8} \ge 0 \\ g_{2}(\mathbf {x})&= -10x_{1} + 8x_{2} + 17x_{7} - 2x_{8} \ge 0 \\ g_{3}(\mathbf {x})&= 8x_{1} - 2x_{2} + 17x_{7} - 2x_{8} \ge 0 \\ g_{4}(\mathbf {x})&= -3(x_{1} - 2)^{2} - 4(x_{2} -3)^{2} - 2x_{3}^{2} + 7x_{4} + 120 \ge 0 \\ g_{5}(\mathbf {x})&= -5x_{2} - 8x_{2} - (x_{3} - 6)^{2} + 2x_{4} + 40 \ge 0 \\ g_{6}(\mathbf {x})&= -x_{1}^{2} - 2(x_{2} - 2)^{2} + 2x_{1}x_{2} - 14x_{5} + 6x_{6} \ge 0 \\ g_{7}(\mathbf {x})&= -0.5(x_{1} - 8)^{2} - 2(x_{2} - 4)^{2} + 3x_{5}^{2} + x_{6} + 30 \ge 0 \\ g_{8}(\mathbf {x})&= 3x_{1} - 6x_{2} - 12 (x_{9} - 8)^{2} \ge 0 \\ -10&\le x_{i} \le 10, \; i = 1,\dots ,10 \end{aligned}$$

It is a 10 design variables problem with 8 inequality constraints. As it can be observed in Table 1 the better COV value is achieved by CMA and the worst one by ES algorithm, while the best mean value is obtained by DE algorithm and the worst by ES.

Table 1 Results comparison for test case S-6ACT

The best optimized designs achieved by the four metaheuristics among the 50 independent optimization runs is given in Table 2. Although, the best optimized design is achieved by CMA and DE algorithm, DE algorithm had slightly better performance with reference to the statistical data of Table 1. It should be noted also that for all 50 independent optimization runs performed for each algorithm, feasible optimized designs were obtained.

Table 2 Results comparison for test case S-6ACT

5.2.2 Test Case S-CRES

This test case problem was proposed by Deb [10] and is formulated with 2 design variables and 2 inequality constraints:

$$\begin{aligned} \text {min:} \quad F(x)&= (x_{1}^{2} + x_{2} - 11)^{2} + (x_{1} + x_{2}^{2} - 7)^{2} \\ \text {subject to:} \quad g_{1}(\mathbf {x})&= 4.84 - (x_{1} - 0.05)^{2} - (x_{2} - 2.5)^{2} \ge 0 \\ g_{2}(\mathbf {x})&= x_{1}^{2} + (x_{2} - 2.5)^{2} - 4.84 \ge 0 \\ 0&\le x_{1} \le 6 \\ 0&\le x_{2} \le 6 \end{aligned}$$

In Fig. 3 the feasible and infeasible domain of the problem is shown. The feasible domain is approximately 0.7 % of the total search space. The two constraint functions $g_{1}, g_{2}$ create a crescent shape for the feasible domain, as it is shown in Fig. 4 with the zoomed area around the optimal point.

Fig. 3

Feasible and infeasible domain for S-CRES problem

Fig. 4

Enlarged space around the optimal point

Similar to the previous test case, statistical results (mean value and COV) are given in Table 3. Furthermore, in Table 4, the results are compared with the best result found in literature [10]. It should be noted also that for all 50 independent optimization runs performed for each algorithm, feasible optimized designs were obtained.

Table 3 Results comparison for test case S-CRES

The CMA and DE algorithms had better performance, since COV values of the optimized objective function value obtained at the end of the evolution process was orders of magnitude smaller than the one obtained by the other two algorithms.

Table 4 Results comparison for test case S-CRES

5.2.3 Test Case S-0.5F

The optimization problem S-0.5F [8] is formulated with 7 design variables and 4 inequality constraints:

$$\begin{aligned} \text {min:} \quad F(x)&= (x_{1} - 10)^{2} + 5(x_{2} - 12)^{2} + x_{3}^{4} + 3(x_{4} - 11)^{2} \\&+ 10x_{5}^{6} + 7x_{6}^{2} + x_{7}^{4} - 4x_{6}x_{7} \\ \text {subject to:} \quad g_{1}(\mathbf {x})&= 127 - 2x_{1}^{2} - 3x_{2}^{2} - x_{3} - 4x_{4}^{2} - 5_x{5}^{2} \ge 0 \\ g_{2}(\mathbf {x})&= 282 - 7x_{1} - 3x_{2} - 10x_{3}^{2} - x_{4} - x_{5} \ge 0 \\ g_{3}(\mathbf {x})&= 196 - 23x_{1} - x_{2}^{2} - 6x_{6}^{2} + 8x_{7} \ge 0 \\ g_{4}(\mathbf {x})&= -4x_{1}^{2} - x_{2}^{2} + 3x_{1}x_{2} - 2x_{3}^{2} - 5x_{6} + 11x_{7} \ge 0 \\ -10&\le x_{i} \le 10, \; i = 1,\dots ,7 \end{aligned}$$

In this problem, only 0.5 % of the space is feasible. Similar to the previous test functions for all 50 independent optimization runs performed for each algorithm, feasible optimized designs were obtained. Statistical results (mean value and COV) are given in Table 5. Table 6 shows that even thought all algorithms managed to locate the optimal design domain, only CMA and DE algorithms found the global optimum design. CMA algorithm had the best performance, since COV value of the optimized objective function is almost zero.

Table 5 Results for test case S-0.5F

Table 6 Results comparison for test case S-0.5F

5.2.4 Test Case S-HIM

The optimization problem S-HIM [8] is formulated with 5 design variables and 6 inequality constraints:

$$\begin{aligned} \text {min:} \quad F(x)&= 5.3578547x_{3}^{2} + 0.8356891x_{1}x_{5} + 37.293239x_{1} - 40792.141 \\ \text {subject to:} \quad g_{1}(\mathbf {x})&= 85.334407 + 0.0056858x_{2}x_{5} + 0.0006262x_{1}x_{4} \\&- 0.0022053x_{3}x_{5} \ge 0 \\ g_{2}(\mathbf {x})&= 92 - g_{1}(\mathbf {x}) \ge 0 \\ g_{3}(\mathbf {x})&= 80.51249 + 0.0071317x_{2}x_{5} + 0.0029955x_{1}x_{2} \\&+ 0.0021813x_{3}^{2} - 90 \ge 0 \\ g_{4}(\mathbf {x})&= 20 - g_{3}(\mathbf {x}) \ge 0 \\ g_{5}(\mathbf {x})&= 9.300961 + 0.0047026x_{3}x_{5} + 0.0012547x_{1}x_{3} \\&+ 0.0019085x_{3}x_{4} - 20 \ge 0 \\ g_{6}(\mathbf {x})&= 5 - g_{4}(\mathbf {x}) \ge 0 \\ 78&\le x_{1} \le 102 \\ 33&\le x_{2} \le 45 \\ -27&\le x_{i} \le 45, \; i = 3,4,5 \end{aligned}$$

Statistical results (mean value and COV) are given in Table 7. The optimal value of the objective function value is equal to $-$31005.7966 [1], which was achieved after 350,000 function evaluations. From Table 8 is shown that for all 50 independent optimization runs performed only for ES, CMA and DE algorithms, feasible optimized designs were obtained. In contrast to the previous test functions, CMA algorithm failed to identify the area of the optimal solution.

Table 7 Results for test case S-HIM

Table 8 Results comparison for test case S-HIM

5.2.5 Test Case S-G08

The optimization problem S-G08 [1] is formulated with 2 design variables and 2 inequality constraints:

$$\begin{aligned} \text {min:} \quad F(x)&= \frac{sin(2\pi x_{1})^{3} sin(2\pi x_{2})}{x_{1}^{3}(x_{1} + x_{2})} \\ \text {subject to:} \quad g_{1}(\mathbf {x})&= x_{1}^{2} - x_{2} + 1 \ge 0 \\ g_{2}(\mathbf {x})&= 1 - x_{1} + (x_{2} - 4)^{2} \ge 0\\&=1\le x_{1}\le 3\\&=1\le x_{2}\le 5\\ \end{aligned}$$

Figure 5 depicts the search space, while Fig. 6 depicts the area around the optimal solution found in the literature. Similar to the previous test case, statistical results (mean value and standard deviation) are given in Table 9. The DE algorithm had better performance, since COV value of the optimized objective function value obtained at the end of the evolution process was orders of magnitude smaller than that obtained for the other three algorithms. The optimal value of the objective function found in the literature is equal to $-$0.09582 [1], achieved after 350,000 function evaluations. Similar to the previous test functions, in Table 10 is shown that for all algorithms feasible optimized designs were obtained.

Table 9 Results for test case S-G08

Fig. 5

Design variables domain for test case S-G08

5.3 Selection of the Appropriate Search Algorithm

The sensitivity of the four algorithms with respect to different optimization runs characterized by the mean and coefficient of variation of the optimized objective function values for each metaheuristic algorithm was identified in the corresponding tables of Sect. 5.2. The lower mean and COV values are, the better the algorithm is. This is due to the fact that low COV values mean that the algorithm is not influenced by the independent runs. Overall, the algorithm resulting to the lower mean value (in case of minimization problem) and COV is used for performing the optimization run with the specific algorithm, i.e. the DE algorithm.

Fig. 6

Domain around global minimum for test case S-G08

Table 10 Results comparison for test case S-G08

6 Numerical Examples

A fillet from a steel structural member [61] is analyzed in this section to illustrate the capabilities of the proposed methodology described in the previous sections of this study. The geometry, loading conditions, and design variables of the structural component are shown in Fig. 7. Four-node linear quadrilateral elements under plane stress conditions with constant thickness equal to 5 mm and isotropic material properties are assumed. For the purposes of this study two boundary conditions are considered; in the first one, designated as fillet rigid, all nodes of the bottom edge are fixed while in the second one, denoted as fillet flexible, only the two end nodes of the bottom edge of the component are fixed.

For both test examples deterministic and probabilistic shape optimization problems are solved. The objective function to be minimized, corresponds to the material volume while two sets of constraints are enforced, i.e. deterministic and probabilistic constraints on the fatigue cycles. Furthermore, due to manufacturing limitations the design variables are treated as discrete in the same way as in a single objective design optimization problems with the discrete version of Evolution Strategies [45]. The design variables correspond to the dimensions of the structural component taken from Table 11. The design load $P$ (see Fig. 7), is applied as a concentrated tensile load at the midpoint of the top edge and is equal to 20 KN.

Fig. 7

Fillet geometry, loading and design variables of the problem

Table 11 Upper and lower bounds of design variables and corresponding steps (in mm)

It is common in probabilistic analysis to distinguish between uncertainty that reflects the variability of the outcome of a repeatable experiment and uncertainty due to ignorance. The last one is sometimes referred as “randomness”, commonly known as “aleatoric uncertainty”, which cannot be reduced. However, both deterministic and probabilistic approaches rely on various model assumptions and model parameters that are based on the current state of knowledge on the behavior of structural systems under given conditions. There is uncertainty associated with these conditions, which depends upon the state of knowledge that is referred as “epistemic uncertainty”.

In this study various sources of uncertainty are considered: on crack tip initialization (aleatoric randomness) which influences the shape of the crack propagation path and on modeling (epistemic uncertainty) which affects the structural capacity. The structural stiffness is directly connected to the Young modulus $E$, of structural steel, while the number of fatigue cycles is influenced by the material properties $C$ and $m$. The crack length increment $\varDelta a$ and the poison ratio are taken equal to 5.0 mm and 0.3, respectively, both implemented as deterministic. Thus, for the structural component five random variables are used, i.e. the ordinate $y_{0}$ of the crack tip initialization and the corresponding angle $\theta$ along with the Young modulus $E$ and parameters $C$, $m$. The material properties for the structural steel of the component are implemented as independent random variables whose characteristics were selected according to Ellingwood et al. [16], Ellingwood and Galambos [15] and are given in Table 12.

Table 12 Random variables with the type of distribution and each statistical parameters: mean value ($\mu$) and standard deviation ($\sigma$)

The numerical study that follows comprises of two parts: in the first part a parametric investigation is performed in order to find the number of simulations required for computational efficiency and robustness regarding the calculation of the statistical quantities required and the identification of the most appropriate one that can be used in order to characterize the influence of randomness on the fatigue cycles. In the second part, the performance of structural components under fatigue is investigated within a probabilistic shape design optimization framework.

6.1 Parametric Investigation

For the purpose of this parametric investigation the fillet rigid case is examined and three designs, corresponding to the upper (Design 1), lower (Design 3) bounds of the designs variables and an intermediate one (Design 2) are chosen. The scope of this investigation is to find the lower number of simulations for a reliable calculation of certain statistical quantities that are related to the number of fatigue cycles. To this end, Monte Carlo (MC) simulations based on LHS are performed for the three designs described above and the mean, median and standard deviation of the number of fatigue cycles are calculated (see Table 13).

Table 13 Statistical quantities of the parametric investigation for the three designs of the rigid fillet case

The performance of the different number of MC simulations is depicted in the histograms of Fig. 8. For the needs of this investigation, the three designs are subjected to the ensemble of different number of simulations (100 + 200 + 500 + 1000). Thus, 5400 XFEM analyses have been postprocessed for the three designs in order to create a response databank with the quantities of interest. The propagation of uncertainties is performed by means of the MC simulation method in connection to the LHS technique which has been incorporated into the XFEM framework as described above. According to LHS a given design is run repeatedly, for each MC simulation using different values for the uncertain parameters, drawn from their probability distributions as provided in Table 12. It is worth mentioning that the characteristic mesh size generated for the nested XFEM analysis in both probabilistic analysis and optimization cases, is kept constant in the region of the crack path.

Fig. 8

Histograms of each design

In the group of histograms of Fig. 8 the variability of the number of fatigue cycles with respect to the number of simulations is depicted. These histograms show the probabilistic distribution of the fatigue cycles value for different number of simulations implemented into XFEM and for the three designs, respectively. The frequency on the occurrence of the number of fatigue cycles is defined as the ratio of the number of simulations, corresponding to limit state values in a specific range, over the total number of simulations ($N_{tot}$). $N_{tot}$ is equal to 100, 200, 500 or 1000 depending on the number of simulations used.

Comparing the histograms of Fig. 8, it can be noticed that the width of the confidence bounds corresponding to the intermediate design is narrower compared to the other two, while for the case corresponding to the upper bounds of the design variables there are two zones of concentration for the frequency values. Furthermore, comparing the mean versus median values of the number of fatigue cycles, the median value is considered more reliable since it is not influenced by the extreme lower and upper values obtained. Specifically, in the framework of an optimization problem, search procedure might lead to designs where such extreme lower and upper values might be often encountered. In addition, 200 LH simulations were considered as an acceptable compromise between computational efficiency and robustness. To this extend an equal number of simulations are applied for the solution of the probabilistic formulation of the shape optimization problem which is investigated in the second part of this study.

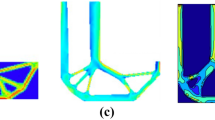
The influence of the uncertain variables on the shape of the crack propagation paths is presented in Figs. 9, 10 and 11, where the cloud of the typical crack paths obtained for 200 simulations is depicted. A crack path is defined as typical, if its shape is similar to deterministic one. Especially, for Design 1, due to its geometric characteristics, many not typical crack paths were obtained, however only the typical ones are shown in Fig. 9. This is an additional reason for choosing the median versus mean value as the statistical quantity to be incorporated into the probabilistic formulations of the problems studied in the second part of this work.

Fig. 9

Design 1

Fig. 10

Design 2

Fig. 11

Design 3

From the results obtained, it can be concluded that the crack paths obtained by means of XFEM is highly influenced by the random parameters considered in this study, thus the importance of incorporating them into the design procedure is examined in the following second part.

6.2 Optimization Results

In the second part of this study four optimization problems are solved with the differential evolution (DE) metaheuristic optimization algorithm. The abbreviations DET$*$K and PROB$*$K correspond to the optimum designs obtained through a deterministic (DET) and probabilistic (PROB) formulation where the lower number of fatigue cycles allowed is equal to $*$ thousands.

6.2.1 Design Optimization Process

The optimization process that is based on the integration of XFEM into a deterministic and a probabilistic formulation of structural shape optimization is shown in Fig. 12. Within each design iteration of the search process there is a nested crack growth analysis loop performed for each candidate optimum design. Thus, a complete crack growth analysis is conducted until the failure criterion is met, i.e. $K_{eq}<K_{c}$ and the corresponding service life is evaluated in order to assess the candidate optimum design.

Fig. 12

XFEM shape optimization process for deterministic and probabilistic formulation

The parameters used for the DE algorithm are as follows: population size $NP$ = 30, the probability $CR$ = 0.90 and the mutation factor $F$ = 0.60. For comparative reasons the method adopted for handling the constraints and the termination criterion is the same for all test cases. On the other hand, the optimization procedure is terminated when the best value of the objective function in the last 30 generations remains unchanged.

6.2.2 Fillet Rigid Test Case

The fillet rigid structural component examined in the previous section is the test example of this study. For this case two groups of formulations were considered, deterministic and probabilistic ones (defined in Eqs. (10)–(11), respectively), where $N_\textit{min}$ was taken equal to 100, 200 and 500 thousands of fatigue cycles. The objective function to be minimized in this problem formulation, is the material volume. DE managed to reach optimum designs as shown in Figs. 13 and 14 together with the optimization history for the deterministic and probabilistic formulation respectively. The optimized designs achieved are presented in Table 14 along with the material volume, while the shapes of deterministic optimized designs are shown in Figs. 15, 16 and 17.

Fig. 13

Objective function versus generation for DET case (rigid fillet)

Fig. 14

Objective function versus generation for PROB case (rigid fillet)

Table 14 Optimum design for each problem formulation and corresponding statistical parameters for fillet rigid (MCS $=$ 200)

Fig. 15

Optimum design for deterministic formulation DET100 for rigid fillet

From Table 14, comparing the three designs achieved by means of the deterministic formulation it can be said that the material volume of DET500K is increased by 33 and 28 % compared to DET100K and DET200K respectively, while that of DET200K is increased by almost 3.5 % compared to DET100K. Furthermore, it can be seen that there are differences to almost all design variables considered to formulate the optimization problem. The results obtained for the probabilistic formulation revealed that the material volume of PROB500K is increased by 68 and 43 % compared to PROB100K and PROB200K respectively, while that of PROB200K is increased by almost 17.5 % compared to PROB100K. In addition, it can be seen that the material volume of designs PROB100K, PROB200K and PROB500K is increased by 26, 43 and 60 % compared to DET100K, DET200K and DET500K, respectively.

In order to justify the formulation of the shape optimization problem considering uncertainties, probabilistic analyses are performed for all six optimized designs obtained through the corresponding problem formulations and the statistical quantities related to the number of fatigue cycles are calculated. These quantities are provided in Table 14 and as it can be seen there are cases where deterministic formulation overestimates the number of fatigue cycles compared to the median value when considering uncertainty. Furthermore, it can be seen that the mean value of the fatigue cycles is not a reliable statistical quantity since it is highly influenced by the crack paths due to high COV values (see Table 14 and Fig. 18). The high COV values which found from the reliability analysis proposed in emerges the necessity of a robust design formulation for the optimization problem, by minimizing these COV values and find the “real” optimum.

Fig. 16

Optimum design for deterministic formulation DET200 for rigid fillet

Fig. 17

Optimum design for deterministic formulation DET500 for rigid fillet

Fig. 18

Crack patterns for DET100, DET200, DET500 case respectively (rigid fillet)

7 Conclusions

In this study structural shape optimization problems are formulated for designing structural components under fatigue. For this reason the extended finite element and level set methods are integrated into a shape design optimization framework, solving the nested crack propagation problem and avoiding the mesh difficulties encountered into a CAD-FEM shape optimization problem by working with a fixed mesh approach.

Based on observations of the numerical test presented the deterministic optimized design is not always a “safe” design with reference to the design guidelines, since there are many random factors that affect the design. In order to find a realistic optimized design the designer has to take into account all important random parameters. In the present work a reliability analysis combined with a structural shape design optimization formulation is proposed where probabilistic constraints are incorporated into the formulation of the design optimization problem. In particular, structural shape optimized designs are obtained, considering the influence of various sources of uncertainty. Randomness on the crack initialization along with the uncertainty on the material properties are considered. Shape design optimization problems were formulated for a benchmark structure, where the volume of the structural component is minimized subjected to constraint functions related to targeted service life (minimum number of fatigue cycles allowed) when material properties and crack tip initialization are considered as random variables.

A sensitivity analysis of four optimization algorithms based on evolution process was conducted in order to identify the best algorithm for the particular problem at hand to be used for solving the structural shape optimization problem. This sensitivity analysis is carried out in order to examine the efficiency and robustness of four metaheuristic algorithms. Comparing the four algorithms it can be said that evolutionary based algorithms can be considered as efficient tools for single-objective multi-modal constrained optimization problems. In all test cases examined, a large number of solutions need to be found and evaluated in search of the optimum one. The metaheuristics employed in this study have been found efficient in finding an optimized solution.

The aim of this work in addressing a structural optimization problem considering uncertainties was twofold. First the influence of the uncertain parameters and the number of Latin hypercube samples was examined and in particular those related to the statistical quantities and consequently to the number of fatigue cycles. In the second part of this study the two formulations of the optimization problem were considered feasible for realistic structures. The analysis of the benchmark structure has shown that with proper shape changes, the service life of structural systems subjected to fatigue loads can be enhanced significantly. Comparisons with optimized shapes found for targeted fatigue life are also performed, while the choice of the position and orientation of initial imperfection was found to have a significant effect on the optimal shapes for the structural components examined.