Disorder and critical phenomena: the $\alpha =0$ copolymer model

Abstract

The copolymer model is a disordered system built on a discrete renewal process with inter-arrival distribution that decays in a regularly varying fashion with exponent $1+ \alpha \;\geqslant \;1$. It exhibits a localization transition which can be characterized in terms of the free energy of the model: the free energy is zero in the delocalized phase and it is positive in the localized phase. This transition, which is observed when tuning the mean h of the disorder variable, has been tackled in the physics literature notably via a renormalization group procedure that goes under the name of strong disorder renormalization. We focus on the case $\alpha =0$—the critical value $h_c(\beta )$ of the parameter h is exactly known (for every strength $\beta$ of the disorder) in this case—and we provide precise estimates on the critical behavior. Our results confirm the strong disorder renormalization group prediction that the transition is of infinite order, namely that when $h\searrow h_c(\beta )$ the free energy vanishes faster than any power of $h-h_c(\beta )$. But we show that the free energy vanishes much faster than the physicists’ prediction.

1 Introduction

The effect of disorder on phase transitions and critical phenomena is a key issue to which a considerable attention has been paid in the physical literature and, more recently, also in the mathematical one. We refer to [11, 22] for a (necessarily partial) overview of this vast subject from mathematicians’ perspective. One of the basic questions—do phase transitions withstand the introduction of impurities, i.e. disorder, and, if it is so, is the critical behavior the same as the one of the pure model or not?—has been repeatedly at the center of the attention. On the other hand there are also cases in which the disorder induces a phase transition that is absent in the pure model (this is for example the case for the Directed Polymers in Random Environment in dimension three or larger, see e.g. [16]).

In spite of a number of remarkable results—let us cite for instance the works [1, 12] on the Ising model with random external field—the issue of understanding the critical behavior in presence of disorder is very delicate and certainly little understood (at times even the issue of whether there is any transition at all is out of reach or far from obvious: [1, 12] are good examples of this). The renormalization group (RG) approach proposed by Harris [25] turned out to be quite successful from a physics standpoint for a considerable number of disordered systems. It is helpful for us to take the Harris’ viewpoint at least for exposition purposes. Harris’ approach demands a model in which: (i) the disorder can be made small and switched off by tuning a parameter; (ii) the non-disordered (or pure) model displays a phase transition. Then we can consider tackling the issue in a perturbative way and ask what is the effect of a small amount of disorder. Following [25], it is customary to say that the disorder is irrelevant if the action of the RG makes the disorder weaker and we say that it is relevant if the disorder is enhanced by the transformation. Making a long story short, in the first case the phase transition persists and disorder essentially does not alter the critical behavior (for example: unchanged critical exponent(s)), while in the second case it is reasonable to expect a different critical behavior and possibly even that the transition is washed out. Of course this scenario is not the most general and is far from being mathematically understood. But the notion of relevant disorder clearly identifies cases in which the nature of the critical behavior is determined by the disorder. In this sense, possibly going beyond the scope of [25], it is natural to consider that disorder is relevant also in cases like the one in [1] where the transition is smoothed out, possibly to the level of washing it out completely (even if this issue is open).

Our work is about a relevant disorder case and aims at determining in a precise way the nature of the critical phenomenon. In this direction, results have been obtained recently in the context of localization transitions for random polymers and interfaces, notably copolymer near selective interface models (copolymer for short) and pinning models. These models depend on two parameters: $\beta \ge 0$ that controls the strength of the disorder (if $\beta =0$, the model is pure) and $h\in {{\mathbb {R}}}$ which plays in favor, respectively against, localization if it is larger, respectively smaller than zero. In the limit of infinitely large systems, there is a critical value $h_c(\beta )$ such that the model is in a localized state if $h>h_c(\beta )$ and it is in a delocalized state if $h < h_c(\beta )$: in these models the transition can be characterized in a very simple way in terms of the free energy, namely the free energy is non negative and localization is equivalent to the positivity of the free energy. This class of models is particularly interesting because of the numerous applications, but also because several (not always compatible) predictions have been set forth by physicists. But it seems now that a certain agreement has grown about the fact that these models fall into the realm of the (real space) strong disorder RG approach (see [26] for an overview), also known as Ma–Dasgupta RG [17, 28]. The novelty of the Ma–Dasgupta RG is that it focuses on the inhomogeneous nature of the disorder instead of resorting to the homogeneous RG procedures such as block averaging, sub-lattice decimation, etc$\ldots$, often performed by taking advantage of transforms (for example, the Fourier transform). The alternative they proposed is to perform a coarse graining starting with sites on which the disorder is larger. These ideas were substantially developed by Fisher [20] who realized that this procedure can yield exact results, and who set forth the idea that, iterating the strong disorder RG, one may end up on an infinite disorder fixed point or on a finite disorder fixed point: exact results are expected in the first case. We retain of this approach that it predicts for copolymer and pinning models that the transition becomes of infinite order in the sense that the free energy for $h \searrow h_c(\beta )$ vanishes faster than any power of $(h-h_c(\beta ))$ [26, 30, 31]. A result of this type has been established in [27], for a pinning model based on the two dimensional free field, hence a $2+1$-dimensional model: it is not clear whether or not this model can be understood via strong disorder RG approach (this approach has been almost always applied in cases in which the disorder is one dimensional), but we point out that the disorder makes the transition of infinite order. For the pinning model based on higher dimensional free fields [23]—d $+$ 1 dimensions with $d \ge 3$—the result is different, with a milder smoothing phenomenon. The articles [23, 27] are up to now the only cases in which the critical exponents in presence of relevant disorder have been determined.

Here we present a third case: a special case of the copolymer model. The copolymer model has been tackled via the strong disorder RG approach with precise claims [26, 30]. Our results are in agreement with the fact that the transition is of infinite order, but as we will explain, from a finer perspective our results disprove, in some precise sense, the existing conjectures.

1.1 The $\alpha =0$ copolymer model and the localization transition

We work with IID disorder $\{\omega _n\}_{n=1,2, \ldots }$ of law ${{\mathbb {P}}}$ and we use the notation

$$\begin{aligned} \lambda (\beta ):= \log {{\mathbb {E}}} \exp (\beta \omega _1). \end{aligned}$$

(1.1)

We assume that $\overline{\beta }:= \sup \{\beta \in {{\mathbb {R}}} :\, \lambda (\beta )< \infty \}\in (0, \infty ]$, and for the sake of normalization

$$\begin{aligned} {{\mathbb {E}}} [\omega _1^2]\,=\,1 \ \ \text { and } \ \ {{\mathbb {E}}} [\omega _1]=0. \end{aligned}$$

(1.2)

We consider the discrete probability density $K(n)=L(n)/n, n\in {{\mathbb {N}}} :=\{1,2, \ldots \}$, with $L(\cdot )$ slowly varying at $+\infty$ and such that $\sum _{n=1}^\infty K(n)=1$. $L: (0, \infty ) \rightarrow (0, \infty )$ is slowly varying [6] if it is measurable and if $\lim _{x \rightarrow \infty } L(cx)/L(x)=1$ for every $c>0$: examples are presented in Definition 1.1 and, without loss of generality for us, we can assume $L(\cdot )$ to be smooth [6, Th. 1.3.3]. ${{\mathbf {P}}}$ is the law of the two random sequences $\tau = \{\tau _j\}_{j=0,1, \ldots }$ and $\iota =\{\iota _{j=1,2, \ldots }\}$ with $\tau$ and $\iota$ independent and

• $\tau$ is a renewal sequence with $\tau _0=0$ and inter-arrival distribution $K(\cdot )$;

• $\iota$ is a sequence of independent Bernoulli variables of parameter 1 / 2.

Given $(\tau , \iota )$ we say, for $j=1, 2, \ldots$, that $\{\tau _{j-1}+1, \ldots , \tau _{j}\}$ is the jth excursion and this excursion is below the interface (respectively, above the interface) if $\iota _j=1$ (respectively, $\iota _j=0$)—this is not a standard convention but it simplifies notations, see Sect. 1.2 for the relation with standard notations. Given $n=0,1, \ldots$ there exists a unique $j=j(n)$ such that $n \in \{\tau _{j-1}+1, \ldots , \tau _{j}\}$: we then define $\Delta _n=\iota _{j(n)}$, so we have also that $\Delta _{\tau _j+1}=\Delta _{\tau _{j+1}}= \iota _{j+1}$. Note that, once $\Delta =\{\Delta _n\}_{n=1,2, \ldots }$ is introduced, the process $(\tau , \iota )$ is equivalent to the process $(\tau , \Delta )$, and we will mostly prefer to use this second representation.

The partition function and central expression for our analysis is for $N\in {{\mathbb {N}}}$

$$\begin{aligned} Z_{N, \omega }\,:=\, {{\mathbf {E}}} \bigg [ \exp \bigg ( \sum _{n=1}^N \left( \beta \omega _n - \lambda (\beta )+h\right) \Delta _n \bigg );\, N \in \tau \bigg ], \end{aligned}$$

(1.3)

and of course this defines a statistical mechanics model. We set also $Z_{0, \omega }:=1$. A way of thinking of it is to consider a directed $1+1$ dimensional polymer which touches (and possibly, but not necessarily, crosses) a flat interface—the horizontal axis—that separates the two half planes that are full of two different solvents. Each monomer carries a charge $\beta \omega _n - \lambda (\beta )+h$ which can be positive or negative and, while the solvent above the interface does not interact with the monomers, the solvent below the interface favors the positively charged monomers and penalizes the negatively charged ones. This can be read out of (1.3) once we stipulate that excursions with $\Delta =0$, respectively $\Delta =1$, are above, respectively below, the interface.

Consider now the free energy (density)

$$\begin{aligned} \textsc {f}(\beta , h):= \lim _{N \rightarrow \infty } \frac{1}{N} {{\mathbb {E}}} \log Z_{N, \omega }. \end{aligned}$$

(1.4)

The existence of the limit follows from the super-additivity of $\{ {{\mathbb {E}}} \log Z_{N, \omega }\}_{N=1, 2, \ldots }$, see [21, Chapter 4, § 4.4]. Moreover since $Z_{N, \omega }\ge Z_{N, \omega }( \tau _1=N, \Delta _1=0)=K(N)/2$ one directly infers that $\textsc {f}(\beta , h)\ge 0$. On the other hand, for $\beta <{\bar{\beta }}$,

$$\begin{aligned}&\frac{1}{N}{{\mathbb {E}}} \log Z_{N, \omega } \, \le \, \frac{1}{N} \log {{\mathbb {E}}} Z_{N, \omega } \nonumber \\&\quad =\, \frac{1}{N} \log {{\mathbf {E}}} \Big [ \exp \Big ( h\sum _{n=1}^N \Delta _n \Big );\, N \in \tau \Big ] {\mathop {\longrightarrow }\limits ^{N \rightarrow \infty }}h \mathbf {1}_{(0, \infty )}(h), \end{aligned}$$

(1.5)

where the upper bound corresponding to the limit is obvious and for the lower bound it suffices to restrict to the events $\tau _1=N$ and $\iota _1=0$ (for $h\le 0$) or 1 (for $h>0$). Therefore (1.5) implies $\textsc {f}(\beta , h)=0$ if $h\le 0$. It is easy to see that $\textsc {f}(\beta , h)>0$ for h large, for instance by restricting the partition function to $\tau _1=N$ and $\iota _1=1$ (we get $\textsc {f}(\beta , h)\ge h-\lambda (\beta )$). This is already enough to claim that there exists a critical point $h_c(\beta )$, in the sense that $\textsc {f}(\beta , \cdot )$ cannot be real analytic at $h_c(\beta )$, with $h_c(\beta ):= \max \{h: \, \textsc {f}(\beta , h)=0\}$ (note that the monotonicity of $\textsc {f}(\beta , \cdot )$ is obvious, as well as the convexity). In fact $\textsc {f}(\beta , h)>0$ as soon as $h>0$ (this follows from the so called rare stretch strategy, see [21, Chapter 6], and it is also a byproduct of the proof in Sect. 2) and therefore $h_c(\beta )=0$. As it is explained at length for example in [14], the transition from zero to positive free energy is, in a precise sense, a delocalization to localization transition, in particular in terms of path properties of the system. Here we just focus on the free energy and we note that the two rightmost terms in (1.5) are the annealed free energy of the model for finite N and for $N=\infty$. This is the pure model associated to the (quenched) disordered model we are analyzing, and it is therefore important to remark that the annealed model has a first order transition, i.e. the first derivative of the free energy is discontinuous.

1.2 The general copolymer and the pinning model

For the sake of better understanding and motivating our results, it is important to consider a larger class of models. First of all, the notation we use in this work is not customary: the copolymer model in the literature is typically introduced via the partition function

$$\begin{aligned} Z^{\text {cop}}_{N, \omega }\,:=\, {{\mathbf {E}}} \bigg [ \exp \bigg ( \varrho \sum _{n=1}^N ( \omega _n + h ) s_n \bigg );\, N \in \tau \bigg ], \end{aligned}$$

(1.6)

where $s_n= 1-2 \Delta _n \in \{-1, +1\}, \varrho \ge 0$ and $h\in {{\mathbb {R}}}$ (but $h \ge 0$ without loss of generality). So the signs $s_n$ determine whether the excursions are above or below the interface. The expression of the partition function in (1.6) is the most natural for the interpretation of the model [21], but from the technical viewpoint it is very useful to observe that

$$\begin{aligned} Z^{\text {cop}}_{N, \omega } \exp \bigg ( -\varrho \sum _{n=1}^N \left( \omega _n + h \right) \bigg ) \,:=\, {{\mathbf {E}}} \bigg [ \exp \bigg ( -2 \varrho \sum _{n=1}^N \left( \omega _n + h \right) \Delta _n \bigg );\, N \in \tau \bigg ], \end{aligned}$$

(1.7)

and the right-hand side is a partition function that defines the same model because it differs from $Z^{\text {cop}}_{N, \omega }$ only by a factor that does not depend on the process $(\tau , \iota )$. Moreover it is evident that the right-hand side of (1.7) and $Z_{N, \omega }$ are directly related by a change of variables. The variables we use, i.e. $\beta$ and h, separate better the role of the parameter that measures the strength of the disorder ($\varrho$ or $\beta$) and the other parameter, h, with which one changes the average value of the charges. Another reason to use (1.7) is for the formal similarity with

$$\begin{aligned} Z^{\text {pin}}_{N, \omega }\,:=\, {{\mathbf {E}}} \bigg [ \exp \bigg ( \sum _{n=1}^N ( \beta \omega _n - \lambda (\beta )+h) \delta _n \bigg );\, N \in \tau \bigg ], \end{aligned}$$

(1.8)

where $\delta _n$ is the indicator function that $n\in \tau$, that is that there exists j such that $n=\tau _j$. $Z^{\text {pin}}_{N, \omega }$ is the partition function of the pinning model that displays a similar localization transition, with the analogous critical point $h^{\text {pin}}_c(\beta )$. We refer to [22] for a complete introduction to the model and to the questions related to it.

For both the copolymer and the pinning models it is natural to consider the general context of an inter-arrival distribution $K(n)=L(n)/n^{1+ \alpha }$, with $\alpha \ge 0$. The pinning model exhibits a richer phenomenology than the copolymer model, in the sense that for the pinning model, disorder is irrelevant for $\alpha < 1/2$, and it is relevant for $\alpha >1/2$. A first illustration of this fact is that when $\alpha < 1/2$ we have $h^{\text {pin}}_c(\beta )=0$ (at least for $\beta$ small enough, and for all $\beta <{\bar{\beta }}$ in the case $\alpha =0$, considered in [3]), while for $\alpha >1/2$ we have $h^{\text {pin}}_c(\beta )<0$. But a more important point is that the critical behavior of the pure and disordered models coincide for $\alpha <1/2$ and differ for $\alpha >1/2$ (we refer to [5] for the state of the art in the marginal case $\alpha =1/2$). We stress that neither the exact value of $h^{\text {pin}}_c(\beta )$ (see however [15]) nor the critical behavior is known for $\alpha >1/2$, and the relevant character of the transition is established via a smoothing inequality [24] (see [13] for a generalization) that implies that the critical behaviors of disordered and pure systems differ.

On the other hand, for the copolymer model, it is known that disorder is relevant for every $\alpha \ge 0$: the free energy $\textsc {f}(0, h)$ of the pure model (which coincides with the annealed model) is simply equal to $h\mathbf {1}_{(0, \infty )}(h)$ (first order phase transition), see (1.5), whereas the free energy of the disordered model verifies $\textsc {f}(\beta , h)=O\left( (h-h_c(\beta ))^2\right)$ by the smoothing inequality [13, 24]. Moreover, we have $h_c(\beta )< 0$—bounds and even sharp bounds for $\beta \searrow 0$ are known [4, 7,8,9,10, 34] but the exact value is unknown—except (as we have already mentioned) for $\alpha =0$ where $h_c(\beta )= 0$.

We have reported only the mathematically rigorous results. About non rigorous approaches we refer to [22, § 6.4] for an overview of some claims made on criticality for copolymer models. Here we focus on the fact that both pinning and copolymer models are expected to fall into the universality classes of the strong disorder RG [20, 26, 35] that predicts that the transition becomes of infinite order if disorder is relevant. Precise claims in this direction are contained in [26, 30, 31] where a critical behavior of the type $\exp (-c/(h-h_c(\beta )), c>0$, is predicted both for the copolymer [30] and pinning models [31]. For pinning models however, we find also the prediction $\exp (-c/\sqrt{h-h_c(\beta )})$ in [33] and this latter claim reappears in [19], with arguments that are still non rigorous but with a much richer and more convincing analysis developed for a simplified version of the pinning model on hierarchical (diamond) lattices.

We present in the next sections results proving that for the $\alpha =0$ copolymer the transition is of infinite order, and in particular we show that the free energy close to criticality is much smaller than $\exp (-c/(h-h_c(\beta )))$, in the sense that c should be replaced by a function that diverges as $h\searrow h_c(\beta )$.

1.3 Main results

We introduce ${\widetilde{L}}(x):=\int _x^\infty (L(y)/y) \,\mathrm{d}y$: by [6, Prop. 1.5.9a] ${\widetilde{L}}(\cdot )$ is slowly varying and $\lim _{x \rightarrow \infty } {\widetilde{L}}(x) /L(x)=\infty$. The following definition identifies a useful framework of models:

Definition 1.1

We say that the decay at infinity of the slowly varying function L:

• (i) is sub-logarithmic if L satisfies

  $$\begin{aligned} L(x)=(1+o(1))\ c_L/(\log x ( \log \log x)^\upsilon ), \end{aligned}$$

  (1.9)

• (ii) is logarithmic if L satisfies

  $$\begin{aligned} L(x)= (1+o(1))\ c_L/(\log x) ^\upsilon , \end{aligned}$$

  (1.10)

• (iii) is super-logarithmic if L satisfies

  $$\begin{aligned} L(x) = (1+o(1)) \ c_L \exp (-( \log x)^{1/\upsilon }), \end{aligned}$$

  (1.11)

where in (1.9)–(1.11) $x \rightarrow \infty$ and the parameters $\upsilon >1$ and $c_L>0$ can be chosen arbitrarily. These assumptions correspond to asymptotic estimates on the decay of ${\widetilde{L}}$:

$$\begin{aligned} {\widetilde{L}}(x)= (1+o(1)) \times {\left\{ \begin{array}{ll} (c_L/(\upsilon -1)) (\log \log x)^{-\upsilon +1} \quad &{}\text {for sub-logarithmic decay},\\ (c_L/(\upsilon -1)) (\log x)^{-\upsilon +1}\quad &{}\text {for logarithmic decay},\\ c_L \upsilon (\log x)^{1-1/\upsilon }\exp (-( \log x)^{1/\upsilon }) \quad &{}\text {for super-logarithmic decay}. \end{array}\right. } \end{aligned}$$

(1.12)

To state the results we introduce for $\beta < \overline{\beta }$

$$\begin{aligned} q_1(\beta )\, =\, \beta \lambda '(\beta )-\lambda (\beta ) \ \ \text { and } \ \ q_2(\beta )\,:=\,\lambda (2\beta )- 2 \lambda (\beta ). \end{aligned}$$

(1.13)

Note that both quantities are positive if $\beta >0$ and that $q_1(\beta )< \infty$ for $\beta \in [0, \overline{\beta })$ while $q_2(\beta )< \infty$ for $\beta \in [0, \overline{\beta }/2)$. On the other hand, $q_1(\beta )= \beta ^2/2+ O( \beta ^3)$ and $q_2(\beta )= \beta ^2+ O( \beta ^3)$ for $\beta \searrow 0$. We start with a general result—i.e. not restricted to the context of Definition 1.1—that says in particular that the transition is of infinite order.

Theorem 1.2

Consider a general slowly varying function L satisfying $\sum _n L(n)/n=1$. For every $\beta \in (0, \overline{\beta })$ and every $b \in (0,1)$ there exists $h_0>0$ such that for every $h \in (0, h_0)$

$$\begin{aligned} \textsc {f}(\beta , h) \, \le \, \exp \bigg ( - b \, q_1(\beta ) \frac{1}{h} \log \bigg ( \frac{{\widetilde{L}}(1/h)}{L(1/h)} \bigg ) \bigg ). \end{aligned}$$

(1.14)

Note that

$$\begin{aligned}&\log \left( \frac{{\widetilde{L}}(x)}{L(x)}\right) \, =\, (1+o(1)) \nonumber \\&\quad \times {\left\{ \begin{array}{ll} \log \log x &{}\text {for sub-logarithmic and logarithmic decay}, \\ \left( \frac{\upsilon -1}{ \upsilon }\right) \log \log x &{} \text {for super-logarithmic decay}. \end{array}\right. } \end{aligned}$$

(1.15)

Therefore, in the framework of Definition 1.1, (1.14) can be stated as

$$\begin{aligned} \textsc {f}(\beta , h) \, \le \, \exp \bigg ( - {\bar{c}}_L q_1(\beta ) \frac{1}{h} \log \log (1/h) \bigg ), \end{aligned}$$

(1.16)

with ${\bar{c}}_L$ a positive constant that depends only on $L(\cdot )$.

Remark 1.3

The upper bound (1.16) holds in much greater (but not in full) generality. In fact, consider the case in which ${\widetilde{L}}(x)= C \exp \left( -\int _1^x \eta (u) \,\mathrm{d}u /u\right)$, with $C>0$ and $\eta (\cdot )$ a positive continuous function vanishing at infinity – it is straightforward to see that the right-hand side defines a slowly varying function. Since $\lim _{x \rightarrow \infty } {\widetilde{L}}(x)=0$, we have also that $\int _1^\infty \eta (u) \,\mathrm{d}u /u =\infty$. We then have $L(x)= -x {\widetilde{L}}'(x)$ so we compute

$$\begin{aligned} \log \frac{{\widetilde{L}}(x)}{L(x)}\, =\, - \log \eta (x). \end{aligned}$$

(1.17)

Therefore, for (1.16) to hold, it suffices that there exists $c>0$ such that $\log \eta (x) \ge -c \log \log x$ for x large (and necessarily $c\le 1$ otherwise $\int _1^\infty \eta (u) \,\mathrm{d}u /u <\infty$). On the other hand, by choosing $\eta (x)= 1/ \log \log (x+x_0), x_0>e$, we have an example to which we can apply (1.2), but for which (1.16) fails. For this example, like for many others that we can write by straightforward generalization, $L(\cdot )$ decays even faster than super-logarithmically.

If we restrict to the context of Definition 1.1 we have much sharper results:

Theorem 1.4

Choose $L(\cdot )$ as in Definition 1.1 and fix $\beta \in (0, \overline{\beta })$.

• (i) In the sub-logarithmic case we can choose two positive constants $c_+$ and $c_-$ depending only on $\upsilon$ so that there exists $h_0$ such that for $h \in (0, h_0)$

  $$\begin{aligned}&\exp \bigg (- c_- \ q_2(\beta ) \frac{1}{h} \log \log (1/h) \bigg ) \, \le \, \textsc {f}(\beta , h) \nonumber \\&\quad \le \exp \bigg (- c_+ \ q_1(\beta ) \frac{1}{h} \log \log (1/h) \bigg ). \end{aligned}$$

  (1.18)

• (ii) In the logarithmic case we can choose two positive constants $c_+$ and $c_-$ depending only on $\upsilon$ so that there exists $h_0$ such that for $h \in (0, h_0)$

  $$\begin{aligned}&\exp \bigg (- c_-\ q_1(\beta )\frac{1}{h} \log (1/h) \bigg ) \, \le \, \textsc {f}(\beta , h) \nonumber \\&\quad \le \, \exp \bigg (- c_+\ q_1(\beta ) \frac{1}{h} \log (1/h) \bigg ). \end{aligned}$$

  (1.19)

• (iii) In the super-logarithmic case, for $h \searrow 0$ we have

  $$\begin{aligned} \textsc {f}(\beta , h) \, = \, \exp \bigg (- (1+o(1))\left( \frac{h}{q_1(\beta )} \right) ^{-\upsilon /(\upsilon -1)} \bigg ). \end{aligned}$$

  (1.20)

We have not made $c_\pm$ explicit in order to keep the statement lighter, but they are very explicit (even if probably none is optimal): in (1.18) it suffices to choose $c_->\upsilon +1$ and $c_+< \upsilon$, in (1.19) it suffices to choose $c_->5/2 + \upsilon$ and $c_+ < \upsilon -1$. Note that the lower bound in (1.18) becomes empty if $\beta > \overline{\beta }/2$, and possibly also for $\beta = \overline{\beta }/2$.

Let us also stress that we work here in the framework of Definition 1.1 for simplicity: some of the expressions simplify thanks to this assumption, but our results can be adapted to a much wider class of slowly varying function $L(\cdot )$. We can already point out the only places where Definition 1.1 is used: to obtain (2.15)–(2.19) in Sect. 2; in Sect. 3; to obtain (5.36)–(5.38) in Sect. 5.

1.4 About our methods, about perspectives and overview of the work

Some important remarks are in order:

(1) We stress once again the partial agreement with respect to the physical literature. Theorem 1.2 establishes that the transition is of infinite order, but it is not in agreement with the works that predict a behavior of the type $\exp (-c/h)$, with c a constant. Note that c is rather a diverging function, and Theorem 1.4 gives more information: the divergence is only slowly varying for the sub-logarithmic and logarithmic cases, but it behaves as a power law in the super-logarithmic case.

(2) We note that the result we find go in the opposite direction with respect to the $\exp (-c/\sqrt{h})$ behavior of [19, 33]: there is no disagreement between our results and the claim in [19, 33] because [19, 33] are about pinning models. Nevertheless this is very intriguing and calls for deeper understanding. With respect to this, we recall that the strong disorder RG analysis in [20] is inspired and built on the results of McCoy and Wu [29] on the two dimensional Ising model with columnar disorder. McCoy and Wu predict an infinite order transition, with a precise form of the singularity that is different from the exponential type of essential singularity found or predicted for copolymer and pinning.

(3) Our results definitely exploit the fact that the critical point of the quenched system is explicitly known and, considering also [23, 27], this appears to be for the moment an unavoidable ingredient. Also in the case of [19] the critical value is exactly known and this is exploited in the analysis of the model. It would be of course a major progress if methods could be developed to deal with cases in which the critical point is known only implicitly. And this appears as a necessary step if one wants to understand the criticality of the copolymer model for $\alpha >0$ or if one wants to really apprehend the strong disorder universality class.

The rest of the paper is devoted to the proofs.

• In Sect. 2, we prove a general lower bound based on revisiting the rare stretch strategy in the direction of making it sharper. Essentially, we exploit local limit results instead of rougher integral limit results like in previous works [7] and [21, Sec. 6.2 and Sec. 5.4]. This covers the lower bounds in (1.19) and (1.20).

• In Sect. 3 we provide the lower bound in (1.18): this requires a new, more entropic strategy with respect to the rare stretch strategy and it is based on applying the second moment method on a suitably trimmed partition function. Of course here the difficulty is in finding a suitable subset of the renewal trajectories that yield a contribution to the partition function that is sufficient to match the upper bound and that is not too wide so that the second moment can be compared with the square of the first moment on sufficiently large volumes.

• In Sect. 4 we provide the proof of Theorem 1.2. This is achieved via a penalization argument inspired by the analogous bound used for the two dimensional free field in [27]. The strategy is sketched at the beginning of Sect. 4.

• In Sect. 5 we provide the proof of the upper bounds in Theorem 1.4. The key idea here is to pass from a global to a targeted penalization: we avoid penalizing the charges in regions that are not visited. In practice this requires setting up an appropriate coarse graining procedure that builds on the basic structure of the argument in [18]. Therefore, with respect to the case of the two dimensional free field [27], we are able to upgrade the upper bound penalization procedure to get to results that are optimal (in a sense that can be read out of Theorem 1.4).

We complete this introduction with a last comment about our arguments of proof in relation to the Ma–Dasgupta RG and Fisher’s infinite disorder fixed point approach. We always proceed, for the upper and lower bounds, to a coarse graining step, that is a one step block averaging. After this first step, for the lower bound, we do exploit the inhomogeneous character of the realizations of the disorder in a way that is close in spirit to the RG procedures.

We use the notation $\llbracket n,m \rrbracket := [n,m]\cap {{\mathbb {Z}}}$, for $n, m \in {{\mathbb {Z}}}$ and $n\le m$.

2 The lower bound: rare stretch strategy

We develop in this section a more quantitative version of the rare stretch strategy argument in [21, Sec. 6.2 and Sec. 5.4]. This relatively simple argument yields optimal bounds in the logarithmic and super-logarithmic cases.

Recall the definition of $q_1(\beta )$ in (1.13).

Theorem 2.1

For $\beta \in (0, \overline{\beta })$ we have:

• (i) For every $b>7/2$ in the sub-logarithmic case and for every $b>5/2+\upsilon$ in the logarithmic case there exists $h_0>0$ such that for every $h\in (0, h_0)$

  $$\begin{aligned} \textsc {f}(\beta ,h) \, \ge \, \exp \bigg ( -b\, q_1(\beta ) \frac{\log (1/h)}{h} \bigg ); \end{aligned}$$

  (2.1)

• (ii) In the super-logarithmic case, for every $b>1$ there exists $h_0>0$ such that for every $h\in (0, h_0)$

  $$\begin{aligned} \textsc {f}(\beta ,h) \, \ge \, \exp \bigg ( -b \left( \frac{q_1(\beta )}{h} \right) ^{- \frac{\upsilon }{\upsilon -1}} \bigg ). \end{aligned}$$

  (2.2)

The argument is not optimal in the sub-logarithmic case, in particular because in that setup the entropic cost for having renewal points only at multiples of $\ell$ becomes non-negligible.

Proof

Recall the assumptions on $\omega$, cf. (1.1)–(1.2). A sharp version of the Cramér’s Large Deviation principle says that for every $x \in (0, C), C:= \lim _{\beta \nearrow {\bar{\beta }}} \lambda '(\beta )\in (0,\infty ]$, there exists $c(x)>0$ such that for

$$\begin{aligned} {{\mathbb {P}}} \bigg ( \sum _{j=1}^n \omega _j \,\ge \, n x \bigg ) {\mathop {\sim }\limits ^{n \rightarrow \infty }}\frac{c(x)}{n^{1/2}} \exp \big ( -n I(x) \big ), \end{aligned}$$

(2.3)

where $I(x):= \sup _y [ xy - \lambda (y)]$. The value of c(x) is irrelevant for us, but it can be found in [32, Th. 1 and Th. 6] along with a proof of (2.3).

Now we fix $\beta \in (0, \overline{\beta })$ and we define $q:= \lambda '(\beta )$: note that q is the maximizer of the variational problem $\lambda (\beta )= \sup _x (\beta x - I(x))$, that is $\lambda (\beta )= \beta q - I(q)$. Note that $q_1(\beta )=I(\lambda '(\beta ))$. We choose a (sufficiently large) integer $\ell$ and for $j=1,2, \ldots$ we set

$$\begin{aligned} E_j\,:=\, \bigg \{\omega : \, \sum _{n=1}^\ell \omega _{(j-1) \ell +n}\, \ge \, q \ell \bigg \}, \end{aligned}$$

(2.4)

so that $\{\mathbf {1}_{E_j}\}_{j=1,2, \ldots }$ is an IID sequence of Bernoulli random variables of parameter $p(\ell )$, where

$$\begin{aligned} p(\ell )\,:=\,{{\mathbb {P}}} \left( E_1\right) \, \in \, \left( \frac{c(q)}{2\ell ^{1/2}} \exp \left( -\ell I(q)\right) , \frac{2c(q)}{\ell ^{1/2}} \exp \left( -\ell I(q)\right) \right) . \end{aligned}$$

(2.5)

and the inclusion statement follows from (2.3) for $\ell$ greater than a suitably chosen value that depends on q. Associated with such a sequence we introduce the sequence of IID geometric random variables $\{G_j\}_{j=1,2, \ldots }$, $G_j\in \{0,1, \ldots \}$, that count the number of failures between the $(j-1)$th and the jth success in the Bernoulli sequence $\{\mathbf {1}_{E_i}\}_{i= 1,2, \ldots }$, defined recursively as follows

$$\begin{aligned} G_j:= \min \bigg \{ k = 1,2, \ldots \,:\,\sum _{i=1}^k \mathbf {1}_{E_i}(\omega )= j \bigg \} - \bigg (\sum _{m=1}^{j-1} G_m \bigg ) - j, \end{aligned}$$

(2.6)

where the sum from $m=1$ to $j-1$ should be read as zero for $j=1$. We call ${{\mathcal {N}}} _N(\omega )$ the number of successes up to epoch N, that is ${{\mathcal {N}}} _N(\omega ) = \sum _{j\le N/\ell } \mathbf {1}_{E_j}(\omega )$. Alternatively, ${{\mathcal {N}}} _N(\omega ) = \sup \{k:\, \sum _{i=1}^k(G_k+1)\ell \le N\}$. By the law of large numbers, ${{\mathbb {P}}} (\,\mathrm{d}\omega )$ almost surely we have

$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{{{\mathcal {N}}} _N(\omega )}{N} \,= \,\frac{p(\ell )}{\ell }. \end{aligned}$$

(2.7)

The rare stretch lower bound strategy is based on selecting, once the disorder $\omega$ is known, only the renewal and excursion trajectories $(\tau , \Delta ) \in \Omega _{N, q}(\omega )$ for which the process stays above the interface except in the ${{\mathcal {N}}} _N(\omega )$ successful $\ell$-blocks

$$\begin{aligned} \Omega _{N, q}(\omega ):= & {} \bigg \{(\tau , \Delta ):\, \{ n\in \llbracket 1,N \rrbracket : \, \Delta _n=1\} = \mathop {{{\mathrm{\bigcup }}}}\limits _{i \le \frac{N}{\ell }-1:\, \mathbf {1}_{E_i}(\omega )=1} \llbracket i\ell +1, (i+1)\ell \rrbracket \bigg \}.\nonumber \\ \end{aligned}$$

(2.8)

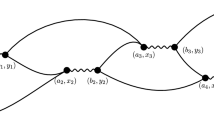
In order to find a lower bound for ${{\mathbf {P}}} \left( \Omega _{N, q}(\omega ) \right)$ it is sufficient to consider the strategy where the renewal only targets the extremities of the intervals $\llbracket i\ell +1, (i+1)\ell \rrbracket$ for which $\mathbf {1}_{E_i}(\omega )=1$ plus the last point N, and chooses the sign of each excursion adequately. We invite the reader to look at Fig. 1. We obtain thus

$$\begin{aligned} \log {{\mathbf {P}}} \left( \Omega _{N, q}(\omega ) \right) \,\ge & {} \, \sum _{j=1}^{{{\mathcal {N}}} _N(\omega )} \log \left( \frac{1}{2}K\left( G_j \ell \right) \right) \mathbf {1}_{\{G_i\ge 1\}} \nonumber \\&+\, {{\mathcal {N}}} _N(\omega ) \log \left( \frac{1}{2} K(\ell ) \right) - 2 \log N, \end{aligned}$$

(2.9)

where the term $- 2 \log N$ comes from a rough estimate of the last excursion, which could be empty and in any case it is not longer than N, hence for large N its contribution is bounded from below by $\log (K(N)/3)$, and 1 / 3 is used instead of the probability 1 / 2 of being above the interface because $K(\cdot )$ is asymptotically equivalent to a decreasing function but it is not necessarily decreasing (or non increasing), see [6, Th. 1.5.3].

Fig. 1

The system is partitioned into blocks of length $\ell$ and the jth block is successful if the average of the $\omega _j$’s in the block is at least $q>0$: these blocks are marked by a thick line and we see 5 of them in the example we consider. The variables $G_j$’s recursively count the unsuccessful blocks before a successful one. So for this illustration case, $G_1=3, G_2=4, G_3=0, G_4=2, G_5=1$ and $G_6>1$. The excursions we choose are indicated by the arrows: they begin and terminate at the extremity of a block, except possibly the last one which ends in N which is not necessarily a multiple of $\ell$. The excusions below the interface are always of length $\ell$ and they correspond to the $\ell$-blocks that are subset of [0, N]. All the other excursions are above

Therefore using the convention $K(0):=1$, we obtain that ${{\mathbb {P}}} (\,\mathrm{d}\omega )$ almost surely

$$\begin{aligned}&\liminf _{N \rightarrow \infty } \frac{1}{N} \log {{\mathbf {P}}} \left( \Omega _{N, q}(\omega ) \right) \nonumber \\&\quad \ge \, \frac{p(\ell )}{\ell }\Big ( {{\mathbb {E}}} \left[ \log K\left( G_1 \ell \right) \right] + \log K(\ell ) -2 \log 2 \Big ). \end{aligned}$$

(2.10)

In order to estimate the term ${{\mathbb {E}}} \left[ \log K\left( G_1 \ell \right) \right]$, we consider the variable $g_1:= p(\ell )G_1$. By the Potter bound [6, Th. 1.5.6] for every $a>0$ there exists $b>0$ such that $L(y)/L(x)\le e^b \max ((y/x)^a,(x/y)^a)$ for every $x,y\ge 1$, so we see that

$$\begin{aligned} \begin{aligned} \left| \log K\left( G_1 \ell \right) - \log K\left( \ell /p(\ell )\right) \right| \,&=\, \left| \log K\left( g_1 \ell /p(\ell )\right) - \log K\left( \ell /p(\ell )\right) \right| \\&\le \, \left( b+(1+a) \vert \log g_1\vert \right) \mathbf {1}_{\{g_1>0\}} \\&\quad +\, 2\log (\ell /p(\ell )) \mathbf {1}_{\{g_1=0\}}, \end{aligned} \end{aligned}$$

(2.11)

and one directly checks that the expectation of the right-hand side in (2.11) is uniformly bounded in $\ell$.

In what follows $\varepsilon >0$ is an arbitrarily small constant that may change from line to line. For $\ell$ sufficiently large

$$\begin{aligned} \begin{aligned} \liminf _{N \rightarrow \infty } \frac{1}{N} \log {{\mathbf {P}}} \left( \Omega _{N, q}(\omega ) \right) \,&\ge \, \frac{p(\ell )}{\ell } \left( \log \frac{p(\ell )}{\ell }+ \log L\left( \frac{\ell }{p(\ell )}\right) \right. \\&\quad \left. +\, \log L(\ell )- \log \ell - 2 \log 2 \right) \\&\ge \, \frac{p(\ell )}{\ell } \left( -\ell I(q) +\log L\left( \frac{1}{p(\ell )}\right) -(5/2+\varepsilon ) \log \ell \right) , \end{aligned} \end{aligned}$$

(2.12)

where the first inequality is obtained by replacing $G_1$ with $p(\ell )^{-1}$ (by using (2.11)) and by replacing $K(\ell )$ by $L(\ell )/\ell$. The second inequality is obtained by using (2.3) and by using again the Potter bound to replace $L(\ell /p(\ell ))$ with $L(1/p(\ell ))$ and to neglect $\log L(\ell )$. From this estimate we readily obtain that $\textsc {f}(\beta , h)$ is bounded below by

$$\begin{aligned} \liminf _{N \rightarrow \infty } \frac{1}{N}&\log Z_{N, h} \big ( \Omega _{N, q}(\omega ) \big )\, \ge \, \ell ( \beta q-\lambda (\beta )+h) \lim _{N \rightarrow \infty } \frac{{{\mathcal {N}}} (\omega )}{N} \nonumber \\&\quad +\,\liminf _{N \rightarrow \infty } \frac{1}{N} \log {{\mathbf {P}}} \big (\Omega _{N, q}(\omega ) \big ) \nonumber \\&\ge \, \frac{p(\ell )}{\ell } \Big ( \left( \beta q -\lambda (\beta ) - I(q)+h\right) \ell + \log L(p(\ell )^{-1})- (5/2+\varepsilon ) \log \ell \Big ) \nonumber \\&\ge \, \frac{p(\ell )}{\ell } \Big ( h \ell - (5/2+\varepsilon )\log \ell +\log L(p(\ell )^{-1}) \Big )\, =: \, \frac{p(\ell )}{\ell } g(h,\ell ), \end{aligned}$$

(2.13)

where in the last line we have used that q verifies $\lambda (\beta ) = \beta q - I(q)$, and the very last step defines $g(h,\ell )$.

It is now a matter of going through the three classes of slowly varying functions that we consider and see how large $\ell =\ell (h)$ has to be chosen in order to guarantee a positive $g(h, \ell (h))$ gain. In what follows h is chosen small, possibly smaller than a constant that depends also on $\varepsilon$. Moreover $C>0$ is a constant that in all cases can be easily identified:

• In the super-logarithmic case we have

  $$\begin{aligned} \log L\left( p(\ell )^{-1}\right) \,\ge \, - \left( \ell I(q)+ (\log \ell )/2 + C\right) ^{1/\upsilon } \, \ge \, -(1+ \varepsilon ) \ell ^{1/\upsilon } I(q) ^{1/\upsilon },\nonumber \\ \end{aligned}$$

  (2.14)

  and we readily see that if $\ell \ge (1+ \varepsilon )h^{-\upsilon /(\upsilon -1)} I(q) ^{1/(\upsilon -1)}$ then there exists $c(\varepsilon , \upsilon )>0$ such that $g(h, \ell )\ge c(\varepsilon , \upsilon ) h\ell$. Therefore (2.13) yields

  $$\begin{aligned} \textsc {f}(\beta , h) \, \ge \, c(\varepsilon , \upsilon ) h p(\ell ) \, \ge \, \exp \left( - (1+\varepsilon ) h^{-\upsilon /(\upsilon -1)} I(\lambda '(\beta ))^{\upsilon /(\upsilon -1)}\right) , \end{aligned}$$

  (2.15)

  where in the last step we have used the explicit expression for q.

• In the logarithmic case

  $$\begin{aligned} \log L\left( p(\ell )^{-1}\right) \ge - \upsilon \log \big ( \ell I(q) \big ) -\frac{1}{2}\upsilon \log \log \ell -C \, \ge \, -(1+ \varepsilon ) \upsilon \log \ell ,\quad \end{aligned}$$

  (2.16)

  so that

  $$\begin{aligned} g(h, u) \, \ge \, h\ell -\left( 5/2+v+\varepsilon \right) \log \ell , \end{aligned}$$

  (2.17)

  and it suffices to choose $\ell \ge (5/2+\upsilon +2\varepsilon ) \log (1/h) /h$ to have $g(h, u)\ge c(\varepsilon , \upsilon ) h \ell$. Therefore

  $$\begin{aligned} \textsc {f}(\beta , h) \, \ge \, c(\varepsilon , \upsilon ) h p(\ell ) \, \ge \, \exp \left( -(5/2+\upsilon +\varepsilon ) I(\lambda '(\beta )) \frac{\log (1/h)}{h} \right) .\nonumber \\ \end{aligned}$$

  (2.18)

• Last, in the sub-logarithmic case the computation is the same as in the logarithmic case because the iterated logarithm in the asymptotic of L(x) is irrelevant for the purpose of this computation and L(x) can be replaced, with an error that can be hidden by $\varepsilon$, by $1/\log (x)$, that is the logarithmic case with $\upsilon =1$. Hence the net result is

  $$\begin{aligned} \textsc {f}(\beta , h) \, \ge \, c(\varepsilon , \upsilon ) h p(\ell ) \, \ge \, \exp \left( - \left( 7/2+\varepsilon \right) I(\lambda '(\beta )) \frac{\log (1/h)}{h} \right) . \end{aligned}$$

  (2.19)

The proof is complete once we recall that $I(\lambda '(\beta ))= \beta \lambda '(\beta )-\lambda (\beta )=q_1(\beta )$. $\square$

3 Improved lower bound in the sub-logarithmic case

Recall the definition (1.13) of $q_2(\beta )\,:=\,\lambda (2\beta )- 2 \lambda (\beta )$, which is positive for $\beta >0$ and finite for $\beta < \overline{\beta }/2$.

Theorem 3.1

Assume that $L(\cdot )$ satisfies (1.9) and that $q_2(\beta ) < \infty$. Then for every $c> \upsilon +1$ there exists $h_0>0$ such that for every $h \in (0, h_0)$

$$\begin{aligned} \textsc {f}(\beta , h) \, \ge \, \exp \left( -c\, q_2(\beta ) \frac{\log \log (1/h)}{h}\right) . \end{aligned}$$

(3.1)

Proof

We introduce

$$\begin{aligned} k= & {} k(h) := c_1 \frac{\log \log (1/h)}{h}, \ \ M := \exp \left( c_2 k\right) , \nonumber \\ N= & {} M^{\mu } (\log M)^2\ \text { and } m= \frac{N}{M^{\mu }\log M}, \end{aligned}$$

(3.2)

with $c_1,c_2$ positive constants and $\mu \in (1,2)$: all these constants are made explicit in the course of the proof. At times we will also do as if k, M and m were integers. We introduce the event

$$\begin{aligned} H_m:= & {} \Big \{(\tau , \Delta ):\, \tau _{2i+1}-\tau _{2i} \in [M, M^\mu ] \text { and } \tau _{2i+2}-\tau _{2i+1} \in [1,k] \text { for } i \in \llbracket 0, m-1\rrbracket , \nonumber \\&\Delta _{\tau _{j}+1}= \frac{1-(-1)^j}{2}\text { for } j\in \llbracket 0, 2m\rrbracket \text { and } \tau _{2m+1}=N \Big \}. \end{aligned}$$

(3.3)

In words, we focus on the trajectories that make alternatively a long and a short excursion, and this is repeated a fixed number of times (m) before reaching the point N: long jumps do not collect any energy ($\Delta$ in the excursion is zero), while the short ones do ($\Delta$ in the excursion is one). The last excursion is long, hence it does not collect any energy, but we stress that it is very long: in fact the 2m excursions that precede the last excursion add up at most to $m(M^\mu +k)= (1+o(1)) N/ \log M$, and therefore the length of the last excursion is asymptotically equivalent to the size of the system as $h \searrow 0$. We then consider the partition function restricted to these trajectories:

$$\begin{aligned} {\widetilde{Z}}_{N, \omega }\,:=\,Z_{N, \omega }\left( H_m \right) . \end{aligned}$$

(3.4)

We have

$$\begin{aligned} {{\mathbb {E}}} \log Z_{N, \omega } \,&=\, {{\mathbb {E}}} \Big [ \log Z_{N, \omega }; \, {\widetilde{Z}}_{N, \omega } \ge \tfrac{1}{2} {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega } \Big ] + {{\mathbb {E}}} \Big [ \log Z_{N, \omega }; \, {\widetilde{Z}}_{N, \omega }< \tfrac{1}{2} {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega } \Big ] \nonumber \\&\ge {{\mathbb {P}}} \Big ({\widetilde{Z}}_{N, \omega } \ge \tfrac{1}{2} {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega } \Big ) \log \Big ( \tfrac{1}{2} {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega } \Big )+ {{\mathbb {P}}} \Big ({\widetilde{Z}}_{N, \omega } < \tfrac{1}{2} {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega } \Big ) \log \big ( K(N)/2 \big ) \nonumber \\&\ge \frac{{{\mathbb {E}}} \big [{\widetilde{Z}}_{N, \omega }\big ]^2}{4{{\mathbb {E}}} \big [ ({\widetilde{Z}}_{N, \omega })^2 \big ]} \log \Big ( \tfrac{1}{2} {{\mathbb {E}}} \widetilde{Z}_{N, \omega } \Big ) - 2 \log N. \end{aligned}$$

(3.5)

where in the first inequality we used $Z_{N, \omega }\ge K(N)/2$ (that holds in full generality) and in the second one we have applied the Paley–Zygmund inequality and we have assumed that $\log ( (1/2) {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega } )\ge 0$ (we indeed have ${{\mathbb {E}}} \widetilde{Z}_{N, \omega }\ge 2$, see (3.9) below).

To conclude we need to estimate the first two moments of ${\widetilde{Z}}_{N, \omega }$. $\square$

First moment estimate

We have

$$\begin{aligned} \begin{aligned} {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega }\,&=\, {{\mathbf {E}}} \bigg [ \exp \Big ( h \sum _{i=1}^m (\tau _{2i+2}-\tau _{2i+1}) \Big ); \, H_m \bigg ] \\&\ge \, \bigg (\frac{1}{2} \sum _{n=M}^{M^\mu } K(n) \bigg )^m \bigg ( \frac{1}{2} \sum _{n=1}^k e^{hn}K(n)\bigg )^m \frac{K(N)}{3}, \end{aligned} \end{aligned}$$

(3.6)

where the inequality comes from the last excursion which is shorter than N (3 is present instead of 2 because K is monotonic only in an asymptotic sense). It follows from our sub-logarithmic decay assumption (recall (1.12)) and our choice of parameters (3.2) that when h tends to zero

$$\begin{aligned} \sum _{n=M}^{M^\mu } K(n)\, =\, {\widetilde{L}}(M)-{\widetilde{L}}(M^\mu )= \frac{c_L\log \mu }{\left| \log h\right| ^\upsilon }(1+o(1)). \end{aligned}$$

(3.7)

For the second term instead we split $\sum _{n=1}^k e^{hn}K(n)$ according to whether n is smaller or larger than 1 / h and we see that the first sum is bounded by e. For the second sum, we remark that we have for h sufficiently small

$$\begin{aligned}&\sum _{n= \lfloor 1/h\rfloor }^{ k} e^{hn}K(n)\, =\, e^{hk} \sum _{j=0}^{k- \lfloor 1/h\rfloor } e^{-hj} \frac{L(k-j)}{k-j} \nonumber \\&\quad \ge e^{hk} \frac{L(k)}{hk}(1-\varepsilon ) \ge \frac{c_L \vert \log h \vert ^{c_1-1}}{c_1 (\log \log (1/h))^{\upsilon +1}}(1-2\varepsilon ). \end{aligned}$$

(3.8)

The first inequality can be achieved by considering the sum restricted to $j\le \sqrt{k/h}$ (or anything that tends to infinity faster than 1 / h but much slower than k) and observe that, uniformly for these values of j, we have $\frac{L(k-j)}{k-j}=(1+o(1)) \frac{L(k)}{k}$. The last step is a consequence of the sub-logarithmic decay assumption and of (3.2). The interested reader can check that both inequalities correspond to asymptotic equivalences.

It is now sufficient to observe that (3.6)–(3.8) readily imply that for every $\varepsilon >0$ we can find $h_0>0$ so that we have

$$\begin{aligned} {{\mathbb {E}}} {\widetilde{Z}}_{N, \omega }\,\ge \, \Big ( \vert \log h \vert ^{c_1-\upsilon -1-\varepsilon } \Big )^m, \end{aligned}$$

(3.9)

for every $h\in (0, h_0)$. We also used that $m=\log M \;\geqslant \;- \frac{1}{2} \log K(N)$ (recall $\mu <2$), so that $K(N)\ge e^{-2 m}$, for h small enough. Therefore if

$$\begin{aligned} c_1\, >\, \upsilon +1, \end{aligned}$$

(3.10)

we have in particular, possibly redefining $h_0$, that ${{\mathbb {E}}} {\widetilde{Z}}_{N, \omega }\ge 2$ (recall that the last step in (3.5) was made under this assumption).

Second moment estimate

We aim at showing that for $h \searrow 0$

$$\begin{aligned} \frac{{{\mathbb {E}}} \big [ ({\widetilde{Z}}_{N, \omega } )^2 \big ]}{{{\mathbb {E}}} \big [ {\widetilde{Z}}_{N, \omega } \big ]^2}\, =\, 1 +o(1), \end{aligned}$$

(3.11)

and we start by observing that

$$\begin{aligned} \frac{{{\mathbb {E}}} \big [ ({\widetilde{Z}}_{N, \omega } )^2 \big ]}{{{\mathbb {E}}} \big [ {\widetilde{Z}}_{N, \omega } \big ]^2}\, =\, \widetilde{{{\mathbf {E}}} }^{\otimes 2}_h \bigg [ \exp \bigg ( q_2(\beta ) \sum _{n=1}^N \Delta ^{(1)}_n \Delta ^{(2)}_n \bigg ) \bigg ], \end{aligned}$$

(3.12)

where $q_2(\beta )$ is given in (1.13) and the measure ${\widetilde{{{\mathbf {P}}} }}_h$ is defined by

$$\begin{aligned} \frac{\,\mathrm{d}{\widetilde{{{\mathbf {P}}} }}_h}{\,\mathrm{d}{{\mathbf {P}}} }(\tau , \Delta ):= \frac{1}{{{\mathbb {E}}} \big [ {\widetilde{Z}}_{N, \omega } \big ]} \exp \bigg ( h \sum _{i=1}^m |\tau _{2i}-\tau _{2i-1}| \bigg ) \mathbf {1}_{H_m}(\tau , \Delta ). \end{aligned}$$

(3.13)

In order to obtain an upper bound for the right hand side of (3.12), we are going to prove a bound for the expectation with respect to $\Delta ^{(1)}$ which is uniform for every realization of $\Delta ^{(2)}$ in $H_m$. Let A denote an arbitrary set of the form

$$\begin{aligned} A:= \bigcup _{i=1}^\infty \llbracket a_i,b_i\rrbracket , \end{aligned}$$

(3.14)

where $a_1\ge M$ and for all $i= 1,2, \ldots$

$$\begin{aligned} (b_i-a_i)\le k \quad \text { and } \quad b_{i+1}-a_{i}\ge M. \end{aligned}$$

(3.15)

Note that it would be more natural to consider the union to stop at m but it is more practical for us to consider here an infinite set. To conclude it is sufficient to show that, uniformly over all possible sets A of the form (3.14)

$$\begin{aligned} {\widetilde{{{\mathbf {E}}} }}_h \bigg [ \exp \bigg ( q_2(\beta )\sum _{i=1} ^{m} \big \vert \llbracket \tau _{2i-1}+1, \tau _{2i} \rrbracket \cap A \big \vert \bigg ) \bigg ] {\mathop {=}\limits ^{h \searrow 0}} 1+ o(1). \end{aligned}$$

(3.16)

Our first step is to replace ${\widetilde{{{\mathbf {P}}} }}_h$ by a nicer measure under which jumps are independent. For $m\in {{\mathbb {N}}}$ let $\widehat{{{\mathbf {P}}} }^m_h$ be a measure on a finite sequence $\{\tau _i\}_{i\in \llbracket 0, 2m\rrbracket }$ for which $\tau _0=0$, the increments are independent and for which for every $i\in \llbracket 0,m-1\rrbracket$

$$\begin{aligned} \begin{aligned} {\widehat{{{\mathbf {P}}} }}^m_h \left( \tau _{2i+1}-\tau _{2i}= n\right)&= \frac{K(n)\mathbf {1}_{n\in [M,M^\mu ]}}{\sum _{n=M}^{M^\mu } K(n)},\\ {\widehat{{{\mathbf {P}}} }}^m_h\left( \tau _{2i+2}-\tau _{2i+1}= n\right)&= \frac{e^{hn} K(n)\mathbf {1}_{n\in [1,k]}}{\sum _{n=1}^k e^{kn} K(n)}. \end{aligned} \end{aligned}$$

(3.17)

Analogously we define also the infinite random sequence $\{\tau _i\}_{i=0,1, \ldots }$ and its law is denoted by ${\widehat{{{\mathbf {P}}} }}_h$. We set

$$\begin{aligned}&{\widetilde{H}}_m\,:=\,\left\{ \tau :\, \tau _{2i+1}-\tau _{2i} \in [M, M^\mu ] \text { and } \tau _{2i+2}-\tau _{2i+1} \in [1,k] \text { for } i \in \llbracket 0, m-1\rrbracket \right\} . \end{aligned}$$

(3.18)

We will commit abuse of notation in using the same notations for random variables and standard, i.e. non-random, variables.

Lemma 3.2

Let ${\widetilde{{{\mathbf {P}}} }}^m_h$ be the distribution of $\{\tau _i\}_{i\in \llbracket 0, 2m\rrbracket }$ under ${\widetilde{{{\mathbf {P}}} }}_h$. Then we have

$$\begin{aligned} \sup _{\{\tau _i\}_{i\in \llbracket 0, 2m\rrbracket }\in {\widetilde{H}}_m} \frac{\,\mathrm{d}{\widetilde{{{\mathbf {P}}} }}^m_h}{\,\mathrm{d}{\widehat{{{\mathbf {P}}} }}^m_h} \left( \tau _0, \tau _1, \ldots , \tau _{2m}\right) {\mathop {=}\limits ^{h \searrow 0}}1+o(1). \end{aligned}$$

(3.19)

Proof

${\widehat{{{\mathbf {P}}} }}^m_h(\tau _0, \tau _1, \ldots , \tau _{2m})$ can be directly expressed from (3.17), but it is helpful to write it in the more implicit fashion:

$$\begin{aligned} \frac{ {\mathbf {1}_{\{\tau \in {\widetilde{H}}_m\}}} \prod _{i=1}^m K(\tau _{2i-1}-\tau _{2i-2})K(\tau _{2i}-\tau _{2i-1})e^{h(\tau _{2i}-\tau _{2i-1}) } }{ \sum _{\tau '\in {\widetilde{H}}_m}\prod _{i=1}^m K(\tau '_{2i-1}-\tau '_{2i-2})K(\tau '_{2i}-\tau '_{2i-1})e^{h(\tau '_{2i}-\tau '_{2i-1}) } }. \end{aligned}$$

(3.20)

On the other hand ${\widetilde{{{\mathbf {P}}} }}^m_h(\tau _0, \tau _1, \ldots , \tau _{2m})$ instead is

$$\begin{aligned} \frac{ {\mathbf {1}_{\{\tau \in {\widetilde{H}}_m\}}} \prod _{i=1}^m K(\tau _{2i-1}-\tau _{2i-2})K(\tau _{2i}-\tau _{2i-1})e^{h(\tau _{2i}-\tau _{2i-1}) } K(N- \tau _{2i}) }{ \sum _{\tau '\in {\widetilde{H}}_m}\prod _{i=1}^m K(\tau '_{2i-1}-\tau '_{2i-2})K(\tau '_{2i}-\tau '_{2i-1})e^{h(\tau '_{2i}-\tau '_{2i-1}) } K(N- \tau '_{2i})}, \end{aligned}$$

(3.21)

and the denominator of this expression cannot be easily simplified. But for every $\tau \in {\widetilde{H}}_m$ we have that $N-\tau _{2m}\ge N-m(M^\mu +k)\ge N(1-2/ \log M)$. Therefore we have that the ratio

$$\begin{aligned} \frac{K(N- \tau _{2i})}{K(N- \tau '_{2i})} \,=\, 1+o(1), \end{aligned}$$

(3.22)

for $h \searrow 0$, uniformly in $\tau$ and $\tau '$ in ${\widetilde{H}}_m$. But the ratio of (3.21) and (3.20) can be bounded precisely by this ratio and therefore Lemma 3.2 is proven.

To conclude we are going to show that for A satisfying (3.14) and any j

$$\begin{aligned} {\widehat{{{\mathbf {E}}} }}_h \bigg [ \exp \bigg ( q_2(\beta )\sum _{i=1} ^{j} \big | \llbracket \tau _{2i-1}+1, \tau _{2i} \rrbracket \cap A \big | \bigg ) \bigg ] \le \left( 1 +e^{kq_2(\beta )}\frac{ C k \log k \log M}{M}\right) ^j, \end{aligned}$$

(3.23)

for a $C>0$ depending only on $L(\cdot )$. It is in fact straightforward to check that with the choices made in (3.2) the right-hand side is equal to $1+o(1)$ for $j=m$ (so (3.16) and therefore (3.11) hold true) if

$$\begin{aligned} c_2\,>\, q_2(\beta )\,. \end{aligned}$$

(3.24)

We prove (3.23) by induction. Let us start with the simpler case $j=1$. We have

$$\begin{aligned}&{\widehat{{{\mathbf {E}}} }}_h \Big [ \exp \Big ( q_2(\beta ) \big | \llbracket \tau _{1}+1, \tau _{2} \rrbracket \cap A \big | \Big ) \Big ] \nonumber \\&\quad \le 1+ e^{kq_2(\beta )} \widehat{{{\mathbf {P}}} }_h \big ( \llbracket \tau _{1}+1,\tau _1+k \rrbracket \cap A \ne \emptyset \big ). \end{aligned}$$

(3.25)

Provided $k/M\le 1/2$ we have

$$\begin{aligned}&\sum _{i=1}^{\infty } \sum _{n=a_i-k}^{b_i} K(n)\mathbf {1}_{\{n\in [M,M^\mu ]\}} \le \sum _{i=1}^{M} \sum _{n=a_i-k}^{b_i} \frac{c}{n}\le c \sum _{i=1}^{M} \sum _{n= iM-k}^{iM+k} \frac{1}{n} \nonumber \\&\quad \le \frac{ 3c k \log M}{M}. \end{aligned}$$

(3.26)

where in the first inequality we used that $K(n)\le c n^{-1}$ and that $a_i\ge iM$ to show that all terms beyond the M first ones do not participate in the sum. In the second inequality we used again the fact that $a_i\ge iM$ and $b_i-a_i\le k$ to bound each sum $\sum _{n=a_i-k}^{b_i} (1/n)$. Now we observe that

$$\begin{aligned} \begin{aligned} {\widehat{{{\mathbf {P}}} }}_h \big ( \llbracket \tau _{1}+1,\tau _1+k \rrbracket \cap A \ne \emptyset \big )\,&=\, \frac{ \sum _{i=1}^{\infty } \sum _{n=a_i-k}^{b_i} K(n)\mathbf {1}_{\{n\in [M,M^\mu ]\}} }{\sum _{n=M}^{M^\mu }K(n)} \\&\le \, \frac{ 4c\, k \log k \log M}{c_L (\log \mu ) M}\,=: \frac{ C k \log k \log M}{ M}, \end{aligned} \end{aligned}$$

(3.27)

where we have used (3.7)—recall that $\log k = (1+o(1)) \vert \log h \vert$—and the last step defines  C.

To prove the induction step, we condition with respect to $\tau _{2j}$. Let us consider

$$\begin{aligned} A'\,:=\,(A-\tau _{2j})\cap [M,\infty ). \end{aligned}$$

(3.28)

Using independence of the jumps and the fact that $\tau _{2j+1}-\tau _{2j}\ge M$,

$$\begin{aligned}&{\widehat{{{\mathbf {E}}} }}_h \bigg [ \exp \bigg ( q_2(\beta ) \, \big |\llbracket \tau _{2j+1}+1, \tau _{2j+2} \rrbracket \cap A \big | \bigg )\ \Big \vert \ \{\tau _{i}\}_{i\in \llbracket 0,2j\rrbracket } \bigg ] \nonumber \\&\quad = {\widehat{{{\mathbf {E}}} }}_h \Big [ \exp \Big ( q_2(\beta ) \big |\llbracket \tau _{1}+1, \tau _{2} \rrbracket \cap A' \big | \Big ) \Big ]. \end{aligned}$$

(3.29)

Noting that $A'$ is of the type described in (3.14)–(3.15) we can conclude that

$$\begin{aligned}&{\widehat{{{\mathbf {E}}} }}_h \bigg [ \exp \bigg ( q_2(\beta ) \, \big \vert \llbracket \tau _{2j+1}+1, \tau _{2j+2} \rrbracket \cap A \big \vert \bigg )\ \Big \vert \ \{\tau _{i}\}_{i\in \llbracket 0,2j\rrbracket } \bigg ] \nonumber \\&\quad \le \left( 1 +e^{kq_2(\beta )}\frac{ C k \log k\log M}{M}\right) , \end{aligned}$$

(3.30)

which concludes the induction step. $\square$

Completion of the proof Going back to (3.5) and using (3.9) and (3.11), which require $c_1$ and $c_2$ to be chosen according to (3.10) and (3.24), for h sufficiently small we obtain

$$\begin{aligned} \frac{1}{N} {{\mathbb {E}}} \log Z_{N, \omega } \,&\ge \, \frac{m}{N} \frac{(c_1- \upsilon -1 -\varepsilon )}{5} \log \log (1/h) - 2 \frac{\log N}{N}\, \nonumber \\&\ge \frac{1}{M^\mu \log M}\, = \, \frac{h}{c_1 c_2 \log \log (1/h) } \exp \left( - \mu c_1 c_2 \frac{\log \log (1/h)}{h}\right) \,, \end{aligned}$$

(3.31)

and, since we can choose $\mu$ close to one, the proof of Theorem 3.1 is complete. $\square$

4 Upper bound based on a global change of measure: proof of Theorem 1.2

Instead of applying Jensen’s inequality directly for ${{\mathbb {E}}} \log Z_{N,\omega }$ (which yields the usual annealed bound), we can first split $\log Z_{N,\omega }$ in two terms and obtain

$$\begin{aligned} {{\mathbb {E}}} \log Z_{N,\omega }= & {} {{\mathbb {E}}} \log \left( f(\omega ) Z_{N,\omega } \right) - {{\mathbb {E}}} \log f (\omega ) \, \le \, \log {{\mathbb {E}}} \left[ f(\omega ) Z_{N,\omega }\right] \nonumber \\&-\,{{\mathbb {E}}} \log \left[ f(\omega ) \right] , \end{aligned}$$

(4.1)

where f is an arbitrary positive measurable function. We choose to apply the above inequality for a function f which has the effect of penalizing environments $\omega$ which have small probability but contribute for most of the expectation ${{\mathbb {E}}} [Z_{N,\omega }]$: we select a collection of events whose probability is small under ${{\mathbb {P}}}$, but large under the size-biased measure ${\widetilde{{{\mathbb {P}}} }}_N(\,\mathrm{d}\omega ):= \frac{Z_{N,\omega }}{{{\mathbb {E}}} [Z_{N,\omega }]} \, {{\mathbb {P}}} (\,\mathrm{d}\omega )$. What helps us in our choice of f is that the size biased measure has a rather explicit description: it can be obtained starting with ${{\mathbb {P}}}$ and tilting the law of the $\omega _n$ along a randomly chosen renewal trajectory.

We choose to penalize stretches of environment where $\omega$ assumes unusually large values. Let k(h) be a large positive integer. The exact value of k is to be fixed at the end of the proof as the result of an optimization procedure, but let us mention already that we choose it of the form $k(h)= h^{-1}\varphi (h)$, where $\varphi (h)\ge 1$ is a slowly varying function which tends to infinity when h goes to zero. For $n,m\in \llbracket 0, N\rrbracket$, with $m>n$, and $b\in (0,1)$ we introduce the event

$$\begin{aligned} {{\mathcal {E}}} (n,m)= {{\mathcal {E}}} _\beta (n,m) \,:=\,\bigg \{ \omega :\, \sum _{j=n+1}^m \omega _j \,\ge \, b \lambda '(\beta ) (m-n) \bigg \}. \end{aligned}$$

(4.2)

We define the penalizing density

$$\begin{aligned} f(\omega )\,:=\,\exp \left( - 4h \sum _{\begin{array}{c} n, m \in \llbracket 0, N\rrbracket \\ n<m, \, m-n >k \end{array}} (m-n)\mathbf {1}_{{{\mathcal {E}}} (n,m)} (\omega )\right) . \end{aligned}$$

(4.3)

To control the second term on the right in (4.1), it is sufficient to notice that by the standard Chernoff bound, there exists a constant $c_1(\beta )$ (which can be taken as large as the Large Deviation function $I(b \lambda '(\beta ))$) such that for every $m\ge n, {{\mathbb {P}}} \left( {{\mathcal {E}}} (n,m)\right) \le e^{-c_1(\beta ) (m-n)}.$ Hence

$$\begin{aligned} {{\mathbb {E}}} \log \left( 1/ f(\omega ) \right) \,&=\, 4h \sum _{\begin{array}{c} n, m \in \llbracket 0, N\rrbracket \\ n<m, \, m-n>k \end{array}} (m-n) {{\mathbb {P}}} \left( {{\mathcal {E}}} (n,m)\right) \le \, 4h \sum _{n=0}^{N-1}\sum _{l>k} e^{-c_1(\beta )l} \end{aligned}$$

(4.4)

$$\begin{aligned}&\le \, \frac{4hN}{c_1(\beta )} \exp (-c_1(\beta ) k) \, \le \, N \exp (-c_1(\beta ) k)\,, \end{aligned}$$

(4.5)

where the last inequality requires $h\le c_1(\beta )/4$. Therefore

$$\begin{aligned} \limsup _{N \rightarrow \infty }\frac{1}{N} {{\mathbb {E}}} \left[ \log \left( 1/ f(\omega ) \right) \right] \,\le \, \exp (-c_1(\beta ) k). \end{aligned}$$

(4.6)

We now turn to the first term in the right-hand side of (4.1). We prove that, that h is sufficiently small, ${{\mathbb {E}}} \left[ f(\omega ) Z_{N,\omega }\right] \le 1$ for N large, where the choice for k appearing in f is given by $k = h^{-1} \varphi (h)$ with $\varphi (\cdot )$ given by

$$\begin{aligned} \varphi (h)\, =\, b\, \log \left( \frac{ {\widetilde{L}}(1/h) }{ L(1/h)}\right) . \end{aligned}$$

(4.7)

where b is the paremeter introduced in (4.2). Then dividing (4.1) by N and sending N to infinity, we obtain that an upper bound on the free energy is given by (4.6). We have

$$\begin{aligned} {{\mathbb {E}}} \left[ f(\omega ) Z_{N,\omega }\right] \, = \, {{\mathbf {E}}} \bigg [ {{\mathbb {E}}} \bigg [ f(\omega ) \exp \bigg ( \sum _{n\in A} \left( \beta \omega _n - \lambda (\beta )\right) \bigg ) \bigg ] \exp \left( h \vert A \vert \right) ; N \in \tau \bigg ], \end{aligned}$$

(4.8)

where

$$\begin{aligned} A= A(N)\,:=\,\bigcup _{j\in \llbracket 1,{{\mathcal {M}}} _N\rrbracket : \, \iota _j=1} \llbracket \tau _{j-1}+1,\tau _j\rrbracket , \end{aligned}$$

(4.9)

and ${{\mathcal {M}}} _N$ is the integer such that $\tau _{{{\mathcal {M}}} _N}=N$. We have

$$\begin{aligned}&{{\mathbb {E}}} \bigg [ f(\omega ) \exp \bigg (\sum _{n\in A} \left( \beta \omega _n - \lambda (\beta )\right) \bigg ) \bigg ] \nonumber \\&\quad \le \, {{\mathbb {E}}} \bigg [ \bigg ( \prod _{\begin{array}{c} j\in \llbracket 1,{{\mathcal {M}}} _N\rrbracket \\ \iota _j=1, \tau _j-\tau _{j-1}\ge k \end{array}} e^{-4h(\tau _j-\tau _{j-1}) \mathbf {1}_{{{\mathcal {E}}} (\tau _j,\tau _{j-1})}} \bigg ) \exp \bigg (\sum _{n\in A} \left( \beta \omega _n - \lambda (\beta ) \right) \bigg ) \bigg ] \nonumber \\&\quad = \, {{\mathbb {E}}} \bigg [ \prod _{\begin{array}{c} j\in \llbracket 1,{{\mathcal {M}}} _N\rrbracket \\ \iota _j=1, \tau _j-\tau _{j-1}\ge k \end{array}} e^{ -4h (\tau _j-\tau _{j-1}) \mathbf {1}_{{{\mathcal {E}}} (\tau _j,\tau _{j-1})}+\sum _{n\in \llbracket \tau _{j-1}+1,\tau _j \rrbracket } \left( \beta \omega _n - \lambda (\beta )\right) } \bigg ] \nonumber \\&\quad = \, \prod _{\begin{array}{c} j\in \llbracket 1,{{\mathcal {M}}} _N\rrbracket \\ \iota _j=1, \tau _j-\tau _{j-1}\ge k \end{array}} {{\mathbb {E}}} _{\beta }\left[ e^{ -4h (\tau _j-\tau _{j-1}) \mathbf {1}_{{{\mathcal {E}}} (\tau _j,\tau _{j-1})}} \right] , \end{aligned}$$

(4.10)

where in the last line the expectation is taken with respect to the probability measure ${{\mathbb {P}}} _{\beta }$ under which all the variables $\omega _n$ are still IID, but with tilted marginal density

$$\begin{aligned} {{\mathbb {P}}} _{\beta }(\omega _1\in \,\mathrm{d}u)\, =\, e^{\beta u-\lambda (\beta )}{{\mathbb {P}}} (\omega _1\in \,\mathrm{d}u). \end{aligned}$$

(4.11)

Note that the term $\exp \left( \sum _{n\in \llbracket \tau _{j-1}+1,\tau _j \rrbracket } \left( \beta \omega _n - \lambda (\beta )\right) \right)$ is a probability density. In particular ${{\mathbb {E}}} _\beta [\omega _n]=\lambda '(\beta ) >0$, and Chernoff bounds yields again for every $m\ge n$,

$$\begin{aligned} {{\mathbb {P}}} _\beta \left( {{\mathcal {E}}} (n,m)^{\complement }\right) \, \le \, e^{-c_2(\beta )(m-n)}, \end{aligned}$$

(4.12)

for an adequate choice of $c_2(\beta )>0$ that depends also on b. Hence, for h sufficiently small (depending on $c_2(\beta )$), for all $m-n>k$ we obtain

$$\begin{aligned} \begin{aligned} {{\mathbb {E}}} _{\beta }\left[ e^{- 4h(m-n) \mathbf {1}_{{{\mathcal {E}}} (n,m)}}\right] \,&=\, e^{- 4h(m-n)} + {{\mathbb {P}}} _\beta \big ( {{\mathcal {E}}} (n,m)^{\complement } \big )(1-e^{- 4h(m-n)}) \\&\le e^{- 4h(m-n)} + e^{-c_2(\beta )(m-n)}\, \le \, e^{-2h(m-n)}. \end{aligned} \end{aligned}$$

(4.13)

Therefore, going back to (4.10), we see that

$$\begin{aligned}&{{\mathbb {E}}} \bigg [ f(\omega ) \exp \bigg (\sum _{n\in A} \left( \beta \omega _n - \lambda (\beta )\right) \bigg ) \bigg ] \nonumber \\&\quad \le \, \prod _{\begin{array}{c} j\in \llbracket 1,{{\mathcal {M}}} _N\rrbracket \\ \iota _j=1, \tau _j-\tau _{j-1}\ge k \end{array}} \exp \big ( -2 h (\tau _j-\tau _{j-1}) \big ), \end{aligned}$$

(4.14)

and this estimate, inserted into (4.8), is sufficient to transform the reward $(+h)$ into a penalty $(-h)$ for excursions of length larger than k. We thus obtain

$$\begin{aligned} \begin{aligned} {{\mathbb {E}}} \left[ f(\omega ) Z_{N,\omega }\right] \,&\le \, \sum _{n=1}^N \sum _{\ell \in {{\mathbb {N}}} ^n: \vert \ell \vert =N} \prod _{j=1}^n K(\ell _j) \left( \frac{1}{2} + \frac{1}{2} e^{h \ell _j (\mathbf {1}_{\{\ell _j\le k\}}-\mathbf {1}_{\{\ell _j>k\}})}\right) \\&=: \, \sum _{n=1}^N \sum _{\ell \in {{\mathbb {N}}} ^n: \vert \ell \vert =N} \prod _{j=1}^n K_k(\ell _j), \end{aligned} \end{aligned}$$

(4.15)

To conclude we need to show that $K_k(\cdot )$ can be interpreted as the inter-arrival law for a renewal process—this simply means that $\sum _{\ell =1}^\infty K_k(\ell ) \le 1$—so that the last term in (4.15) is bounded by one because it is the probability that N belongs to the renewal with inter-arrival law $K_k(\cdot )$. We have therefore to establish the non positivity of

$$\begin{aligned} 2 \Big (\sum _{\ell =1}^{\infty } K_k(\ell )-1 \Big ) \, =\,\sum _{\ell \le k } K(\ell ) \left( e^{h\ell } -1\right) - \sum _{\ell > k } K(\ell ) \left( 1-e^{-h\ell } \right) . \end{aligned}$$

(4.16)

To estimate the second term we recall that we have chosen $kh\ge 1$ so that when k is sufficiently large we have

$$\begin{aligned} \sum _{\ell> k } K(\ell ) \left( 1-e^{-h\ell } \right) \ge (1-e^{-1})\sum _{\ell >k} K(\ell )\ge \frac{1}{2}{\widetilde{L}}(k). \end{aligned}$$

(4.17)

For the first term, using that $e^x-1\le e^X x$ for $x\in [0,X]$, we remark that

$$\begin{aligned} \sum _{\ell \le k } K(\ell ) \left( e^{h\ell } -1\right) \, \le \, e^{hk}h \sum _{\ell \le k} L(\ell )\,\le \, 2e^{hk}hk L(k), \end{aligned}$$

(4.18)

where the last step holds (for h sufficiently small) because $\sum _{\ell \le k} L(\ell )= (1+o(1))k L(k)$ for $k \rightarrow \infty$, see [6, Prop. 1.5.8]. Choosing $k = h^{-1} \varphi (h)$ with $\varphi (h) \ge 1$, we can conclude that the right hand side of (4.16) is negative if

$$\begin{aligned} e^{\varphi (h)}\varphi (h)\frac{4 L(h^{-1}\varphi (h))}{ {\widetilde{L}}(h^{-1}\varphi (h))}\le 1. \end{aligned}$$

(4.19)

Using the Potter bound [6, Th. 1.5.6], we obtain that for h sufficiently small

$$\begin{aligned} \frac{4 L(h^{-1}\varphi (h))}{ {\widetilde{L}}(h^{-1}\varphi (h))}\le \varphi (h) \frac{L(h^{-1})}{{\widetilde{L}}(h^{-1})}, \end{aligned}$$

(4.20)

and thus, recalling (4.7), (4.19) is satisfied for all h sufficiently small. The estimate on the free energy is therefore determined by (4.6). the next result is that for $h>0$ sufficiently small

$$\begin{aligned} \textsc {f}(\beta , h)\, \le \, \exp \left( - I\left( b\lambda '(\beta )\right) \frac{\varphi (h)}{h}\right) . \end{aligned}$$

(4.21)

Since b can be chosen arbitrarily close to one, the proof of Theorem 1.2 is complete. $\square$

5 Improved upper bound: proof of the upper bounds in Theorem 1.4

Choose $\varepsilon \in (0,1)$ and, with reference to Definition 1.1, define

$$\begin{aligned} M_h \,:=\,{\left\{ \begin{array}{ll} e^{ (1-\varepsilon ) v h^{-1} \log |\log h|} &{} \text { sub-logarithmic case}\\ e^{(1-\varepsilon )(\upsilon -1) h^{-1} |\log h| } &{} \text { logarithmic case}\\ e^{(1-\varepsilon ) h^{-v/v-1}} &{} \text { super-logarithmic case} \end{array}\right. } \end{aligned}$$

(5.1)

The heart of the proof is the next proposition: we prove it after having shown that it implies the upper bounds we are after. Recall the definition (1.13) of $q_1(\beta )$.

Proposition 5.1

Choose $L(\cdot )$ in the framework of Definition 1.1, and $M_{\cdot }$ as in (5.1). Then, for every $\beta \in (0,{\bar{\beta }})$, and for every $c_3<q_1(\beta )$, there exists $h_0>0$ such that for all $h\in (0,h_0)$

$$\begin{aligned} {{\mathbb {E}}} \big [ \log Z_{M_{h/c_3}, \omega } \big ] \, \le \, 4. \end{aligned}$$

(5.2)

Proof of Theorem 1.4 (Upper bounds)

Proposition 5.1 would directly imply the result if the sequence $\{{{\mathbb {E}}} [\log Z_{N,\omega }]\}_{N=1,2, \ldots }$ were a sub-additive sequence. But this is not the case: rather, it is super-additive. However, given any $b>0$ and $L(\cdot )$, one can choose two positive constants $c_3$ and $c_4$ such that the sequence formed by

$$\begin{aligned} \textsc {g}_N \,:=\,{{\mathbb {E}}} \left[ \log Z_{N,\omega }\right] +c_4 \log N + c_5, \end{aligned}$$

(5.3)

is sub-additive for every choice of $\beta \in [0, b]$ and $\vert h \vert \le b$. Therefore $\textsc {f}(\beta , h)=\lim _N \textsc {g}_N /N = \inf _N \textsc {g}_N /N\le \textsc {g}_M/M$ for any choice of M. Therefore, using (5.2), we have

$$\begin{aligned} \textsc {f}(\beta , h) \, \;\leqslant \;\, \frac{4+c_4 \log M_{h/c_3} +c_5 }{M_{h/c_3}}, \end{aligned}$$

(5.4)

which yields the upper bounds in Theorem 1.4.

The proof that (5.3) forms a sub-additive sequence can be found for example in [21, Ch. 4, § 4.2], but we recall the argument for completeness. We start from the estimate that for every $N, M\in {{\mathbb {N}}}$

$$\begin{aligned} {{\mathbb {E}}} \left[ \log Z_{N+M,\omega }\right] \, \le \, {{\mathbb {E}}} \left[ \log Z_{N, \omega }\right] + {{\mathbb {E}}} \left[ \log Z_{M, \omega }\right] + C \log \left( \min (N, M)\right) +C, \end{aligned}$$

(5.5)

with $C=C(b, L(\cdot ))>0$ which can easily be made explicit. A proof of (5.5) can be found for example in [21, proof of (4.16), p. 93]. Without loss of generality we can assume $N\ge M$ and we rewrite (5.5) as

$$\begin{aligned} \textsc {g}_{N+M}- \textsc {g}_N - \textsc {g}_M\le & {} C \log M +C + c_4 \log (N+M) \nonumber \\&-c_4 \log N -c_4 \log M -c_5, \end{aligned}$$

(5.6)

and we are left with showing that the right-hand side is smaller or equal to zero, with suitable choices of $c_4$ and $c_5$. For this we can use $\log (N+M)\le \log 2 + \log N$ and the fact that the resulting expression vanishes if we choose $c_4=C$ and $c_5= (1+ \log 2)C$. $\square$

We now move to the proof of Proposition 5.1 and as a first important step, we prove the following lemma.

Lemma 5.2

For any constant $c_3<q_1(\beta )$, there exist $\eta \in (0,1)$ and $h_1>0$ such that for all $h\in (0,h_1)$, setting $N= e^{c_{3}/h}$, and $\theta =1- h/c_3$, we have that for every $j\in \llbracket 1, N \rrbracket$

$$\begin{aligned} {{\mathbb {E}}} [Z_{j, \omega }^{\theta }] \le e^{3} \, \check{{\mathbf {P}}} _h(j\in \tau ) , \end{aligned}$$

(5.7)

where $\check{{\mathbf {P}}} _h = \check{{\mathbf {P}}} _h^{(\eta )}$ is the renewal process whose inter-arrival law is defined by

$$\begin{aligned} \check{{\mathbf {P}}} _h (\tau _1= \ell )=\check{K}_h(\ell ):= K(\ell )\Big ( \frac{1}{2}+ \frac{1}{2} e^{h \ell \big ( \mathbf {1}_{\{\ell \le 1/(\eta ^2 h) \} }- \eta \, \mathbf {1}_{\{\ell > 1/(\eta ^2 h) \}} \big )}\Big ), \end{aligned}$$

(5.8)

and satisfies (also for h sufficiently small, how small depends on $\eta$)

$$\begin{aligned} \sum _{\ell =1}^\infty \check{K}_h(\ell ) \le 1 - \frac{1}{6} {\widetilde{L}}(1/h). \end{aligned}$$

(5.9)

Note that this already proves that

$$\begin{aligned} {{\mathbb {E}}} [\log Z_{N,\omega }] \le \theta ^{-1} \log {{\mathbb {E}}} [ Z_{N,\omega }^{\theta }]\le 3\theta ^{-1}\le 4 \end{aligned}$$

(5.10)

for $N= N_h:= e^{c_{3} /h}$, which in turn implies the upper bound, analogous to (5.4)

$$\begin{aligned} \textsc {f}(\beta ,h) \le \frac{4 +c_4 \log N_{h} +c_5 }{ N_h} \le e^{ - c'_{3} /h}. \end{aligned}$$

(5.11)

However, this bound alone is worse than the one achieved in Theorem 1.2.

Proof

The method we use to prove this statement presents some similarity with the proof of Theorem 1.2 (Sect. 4): in particular it relies on the same notion of penalizing density. However, we need a different choice for $f(\omega )$ in order to run computation of non-integer moments.

We fix $\eta >0$, we choose $k:= (\eta h)^{-1}$ (so that $N=e^{-c_3 \eta k}$), and we work as if $1/\eta$ and k were integers in the following. We define for $u \in {{\mathbb {N}}}$ (compare with (4.2))

$$\begin{aligned} {{\mathcal {E}}} _k(u) := \bigg \{ \sum _{i=k(u-1)+1}^{k u} \omega _i \ge (1-\eta ) \lambda '(\beta ) k \bigg \} \end{aligned}$$

(5.12)

(we simply write ${{\mathcal {E}}} _k$ for ${{\mathcal {E}}} _k(1)$), and also

$$\begin{aligned} f(\omega ) = \prod _{u=1}^{ \lfloor N/k \rfloor } e^{- \frac{1+4\eta }{\eta }\, \mathbf {1}_{{{\mathcal {E}}} _k(u)}(\omega )}. \end{aligned}$$

(5.13)

By using Hölder inequality, we get that for $\theta \in (0,1)$

$$\begin{aligned} {{\mathbb {E}}} [(Z_{j,\omega })^{\theta }] = {{\mathbb {E}}} \big [ f(\omega )^{-\theta } (f(\omega ) Z_{j,\omega })^{\theta } \big ] \le {{\mathbb {E}}} \big [ f(\omega )^{- \frac{\theta }{1-\theta }}\big ]^{1-\theta } {{\mathbb {E}}} \big [ f(\omega ) Z_{j,\omega }\big ]^{\theta }.\quad \end{aligned}$$

(5.14)

For the first term, a simple computation gives

$$\begin{aligned} {{\mathbb {E}}} \big [ f(\omega )^{-\theta /(1-\theta )}\big ]^{1-\theta } = {{\mathbb {E}}} \Big [e^{ \frac{1+4\eta }{\eta } \, \frac{\theta }{1-\theta }\mathbf {1}_{{{\mathcal {E}}} _k}} \Big ]^{(1-\theta )\lfloor N/k \rfloor } \le \Big ( 1+ e^{\frac{1+4\eta }{\eta (1-\theta )}} {{\mathbb {P}}} \big ( {{\mathcal {E}}} _k\big ) \Big )^N. \end{aligned}$$

(5.15)

From the standard Chernoff bound, for any $c_3<q_1(\beta )$, we can fix $\eta$ small, so that for all k large enough, we have ${{\mathbb {P}}} ({{\mathcal {E}}} _k) \le e^{- (1+5\eta ) c_3 k }$. Here we use $1-\theta = h/c_3$ and $k=(\eta h)^{-1}$, to obtain that

$$\begin{aligned} e^{\frac{1+4\eta }{\eta (1-\theta )}} {{\mathbb {P}}} \big ( {{\mathcal {E}}} _k\big ) \,\le \, e^{- c_{3} \eta k} \, =\, N^{-1}, \end{aligned}$$

(5.16)

and hence that

$$\begin{aligned} {{\mathbb {E}}} \big [ f(\omega )^{-\theta /(1-\theta )}\big ]^{1-\theta } \le \big (1+ N^{-1} \big )^N \le e. \end{aligned}$$

(5.17)

To estimate the second term in (5.14), we observe that

$$\begin{aligned} {{\mathbb {E}}} \big [ f(\omega ) Z_{j,\omega }\big ] = {{\mathbf {E}}} \bigg [ e^{h |A|} \mathbf {1}_{\{j\in \tau \}} {{\mathbb {E}}} \Big [ f(\omega ) \exp \Big (\sum _{n\in A} \beta \omega _n -\lambda (\beta ) \Big ) \Big ] \bigg ], \end{aligned}$$

(5.18)

where $A=A(j)$ is defined by (4.9). If we set

$$\begin{aligned} \mathcal {I}_A = \big \{ v \in \llbracket 1, \lfloor N/k \rfloor \rrbracket \,:\,\ \llbracket k(v-1)+1,kv \rrbracket \subset A \big \}, \end{aligned}$$

(5.19)

by proceeding like in (4.10) we obtain that

$$\begin{aligned} {{\mathbb {E}}} \Big [ f(\omega ) \exp \Big (\sum _{n\in A} \beta \omega _n -\lambda (\beta ) \Big ) \Big ]\le & {} {{\mathbb {E}}} \Big [ \prod _{u\in \mathcal {I}_A} e^{-\frac{1+4\eta }{\eta }\, \mathbf {1}_{{{\mathcal {E}}} _k(u)}} e^{\sum _{n\in A}\beta \omega _n -\lambda (\beta ) }\Big ] \nonumber \\\le & {} \Big ( e^{-\frac{1+4\eta }{\eta }}+ {{\mathbb {P}}} _{\beta }\big ( ({{\mathcal {E}}} _k)^{\complement } \big ) \Big )^{|\mathcal {I}_A|}, \end{aligned}$$

(5.20)

where ${{\mathbb {P}}} _{\beta }$ is the tilted probability defined in (4.11). As we have ${{\mathbb {E}}} _{\beta }[\omega _n]=\lambda '(\beta )$, by the law of large number, ${{\mathbb {P}}} _{\beta }(({{\mathcal {E}}} _k)^{\complement })$ gets arbitrarily small if k is chosen large (that is if h is small). Hence for h sufficiently small we obtain that

$$\begin{aligned}&{{\mathbb {E}}} \Big [ f(\omega ) \exp \Big (\sum _{n\in A} \beta \omega _n -\lambda (\beta ) \Big ) \Big ] \le e^{- \frac{1+3\eta }{\eta } |\mathcal {I}_A| } \nonumber \\&\quad \le \, \exp \left( - \left( \frac{1+3\eta }{\eta }\right) \left( \frac{(1/\eta ) -1}{1/\eta } \right) \frac{ W_k}{k} \right) , \end{aligned}$$

(5.21)

where (recall that ${{\mathcal {M}}} _j$ is defined by $\tau _{{{\mathcal {M}}} _j}=j$ if $j\in \tau$)

$$\begin{aligned} W_k \,=\, W_k(\tau , \iota )\,:=\, \sum _{i\le {{\mathcal {M}}} _j:\, \iota _i=1} (\tau _i-\tau _{i-1})\mathbf {1}_{\{\tau _i-\tau _{i-1}\ge k/\eta \}}, \end{aligned}$$

(5.22)

is the sum of the lengths of the excursions below the interface that are of length $k/\eta$ or more. Note that in (5.21), for the last inequality, we have used that an excursion of length $k/\eta$ or more covers at least $(1/\eta )-1$ consecutive blocks $\llbracket k(v-1)+1,kv \rrbracket$ in ${{\mathcal {I}}} _A$. We therefore get from (5.18) and our choice $k= (\eta h)^{-1}$ that provided that $\eta$ is small,

$$\begin{aligned} {{\mathbb {E}}} \big [ f(\omega ) Z_{j,\omega }\big ]\le & {} {{\mathbf {E}}} \Big [ e^{ h \big ( |A| - (1+\eta ) W_k \big )} \mathbf {1}_{\{j\in \tau \}} \Big ] \nonumber \\= & {} \sum _{q=1}^j \sum _{\begin{array}{c} (\ell _1, \ldots , \ell _q) \in {{\mathbb {N}}} ^q: \\ \sum _{i=1}^q \ell _i =j \end{array}} \prod _{i=1}^q K(\ell _i) \Big ( \frac{1}{2} + \frac{1}{2} e^{h \ell _i(\mathbf {1}_{\{ \ell _i<k/\eta \}} - \eta \, \mathbf {1}_{\{\ell _i \ge k/\eta \}}) } \Big ) \nonumber \\= & {} \check{{\mathbf {P}}} _h \big ( j\in \tau \big ), \end{aligned}$$

(5.23)

with $\check{{\mathbf {P}}} _h$ defined by (5.8). Going back to (5.14), and collecting (5.17)–(5.23), we end up with

$$\begin{aligned} {{\mathbb {E}}} [(Z_{j,\omega })^{\theta }] \,\le \, e\, \check{{\mathbf {P}}} _h(j\in \tau )^{\theta } \, \le \, e\, \check{{\mathbf {P}}} _h(j\in \tau )^{\theta -1} \check{{\mathbf {P}}} _h(j\in \tau ). \end{aligned}$$

(5.24)

Then, we simply notice that $\check{{\mathbf {P}}} _h (j\in \tau ) \ge \frac{1}{2} K(j) \ge N^{-2}$ for all $j \le N$ (provided that N is large), so that $\check{{\mathbf {P}}} _h (j\in \tau )^{\theta -1} \le N^{ 2 (\log N)^{-1} } = e^{2}$. This concludes the proof of (5.7).

It remains only to prove (5.9). We have

$$\begin{aligned} \begin{aligned} 2 \left( \sum _{\ell = 1}^\infty \check{K}_h(\ell )-1 \right)&= \sum _{\ell \le k/\eta } (e^{h \ell } -1 ) K(\ell ) - \sum _{\ell> k/\eta } (1-e^{ - \eta h\ell }) K(\ell ) \\&\le e^{1/\eta ^2} h \sum _{\ell \le k/\eta } \ell K(\ell ) - \frac{1}{2}\sum _{\ell > k /\eta } K(\ell )\\&\le 2 e^{1/\eta ^2} h k L(k) - \frac{2}{5} {\widetilde{L}}(k) \le - \frac{1}{3} {\widetilde{L}}(k). \end{aligned} \end{aligned}$$

(5.25)

For the first inequality, we used that that $e^{x}-1\le e^{1/\eta ^2} x$ for all $0\le x \le 1/\eta ^2$ (recall $hk=1/\eta$), and that $e^{ - \eta h\ell }\le e^{-1/\eta }\le 1/2$ in the second term. The second inequality holds provided that k is large enough, and the last one because $hk=1/\eta$ and ${\widetilde{L}}(k) / L(k)$ diverges to infinity as $k\rightarrow \infty$. This completes the proof of Lemma 5.2. $\square$

Proof of Proposition 5.1

Let $N= e^{ c_{3} / h}$ and $\theta = 1 - h/c_3$, as in Lemma 5.2.

We prove that for all $1\le m\le M:=M_{h/c_3}$ we have ${{\mathbb {E}}} [ (Z_m)^{\theta }] \le e^{3}$, which gives the conclusion like in (5.10). To that end as in [18] we write for any $m\ge N$

$$\begin{aligned} Z_{m,\omega } = \sum _{n=N}^m \sum _{j=1}^{N-1} Z_{m-n,\omega } K(n-j) Z_{j,T^{m-j} \omega }, \end{aligned}$$

(5.26)

so that, using translation invariance, we have

$$\begin{aligned} {{\mathbb {E}}} \big [ (Z_{m,\omega } \big )^\theta \big ] \le \sum _{n=N}^m \sum _{j=0}^{N-1} {{\mathbb {E}}} \big [ ( Z_{m-n,\omega })^{\theta } \big ] K(n-j)^\theta {{\mathbb {E}}} \big [ ( Z_{j, \omega } )^{\theta } \big ]. \end{aligned}$$

(5.27)

We prove below that, for $M= M_{h/c_{3}}$ with $M_h$ defined as in (5.1), we have

$$\begin{aligned} \rho := \sum _{n=N}^{M} \sum _{j=0}^{N-1} K(n-j)^\theta {{\mathbb {E}}} \big [ ( Z_{j, \omega } )^{\theta } \big ] \le 1. \end{aligned}$$

(5.28)

Then, since from (5.27) we have

$$\begin{aligned} {{\mathbb {E}}} \big [ (Z_{m,\omega } \big )^\theta \big ] \le \rho \max _{i\in \llbracket 0, m-N\rrbracket } {{\mathbb {E}}} \big [ ( Z_{i,\omega })^{\theta } \big ], \end{aligned}$$

(5.29)

an easy induction gives that for any $N\le m\le M_{h/c_{3}}$ we have

$$\begin{aligned} {{\mathbb {E}}} [ (Z_{m,\omega } \big )^\theta ] \le \max _{i\in \llbracket 0, N\rrbracket } {{\mathbb {E}}} \big [ ( Z_{i, \omega } )^{\theta } \big ] \le e^{3}, \end{aligned}$$

(5.30)

the last inequality coming from Lemma 5.2. $\square$

Remark 5.3

Let us stress that the method used above corresponds to the simplified coarse-graining strategy developed in [18]. The idea is that visited blocks are coarse-grained one by one rather than all at the same time: (5.26) performs a decomposition of the trajectories only over the second to last visited block, and then this procedure is iterated. A finer coarse-graining procedure such as the one performed e.g. in [5] would not substantially improve the result, in the sense that it may yield a better value for the constant $c_+$ in Theorem 1.4, parts (i) and (ii), but not enough to match the lower bound.

To prove (5.28) we also use Lemma 5.2: we assume that N is even for simplicity and we write

$$\begin{aligned} \frac{\rho }{e^{3}}\le & {} \sum _{n=N}^{M} \sum _{j=0}^{N/2-1} K(n-j)^\theta \check{{\mathbf {P}}} _h (j\in \tau ) \nonumber \\&\quad + \sum _{n=N}^{M} \sum _{j=N/2}^{N-1} K(n-j)^\theta \check{{\mathbf {P}}} _h (j\in \tau )\, =: A+B, \end{aligned}$$

(5.31)

and we estimate separately the two terms. We will show that, with our choice for $M_h$ in (5.1), both terms can be made arbitrarily small for $h\searrow 0$.

As far as A is concerned, we observe that, since we have $\check{{\mathbf {P}}} _h (\tau _1=\infty )\ge {\widetilde{L}}(1/h)/6$, as noted in (5.9), we obtain $\sum _{j=1}^\infty \check{{\mathbf {P}}} _h (j\in \tau )\le 7/ {\widetilde{L}}(1/h)$ for h sufficiently small. Hence, since $K(\cdot )$ is regularly varying with exponent $-1$, for N large enough we have

$$\begin{aligned} A\, \le \, 3\, \frac{ 7}{ {\widetilde{L}}(1/h)} \sum _{n=N}^{M} K(n)^\theta \, =\, \frac{21}{ {\widetilde{L}}(1/h)} \sum _{n=N}^{M} \frac{L(n)^{1- h/c_3}}{n^{1- h/c_3}}. \end{aligned}$$

(5.32)

Using the fact that L(n) / n is regularly varying (or the explicit value of L in the framework of Definition 1.1), we have for all N and M sufficiently large

$$\begin{aligned} \sum _{n=N}^{M} \frac{L(n)^{1-h/c_3 }}{n^{1- h/c_3}} \, \le \, 2 \int _{N}^{M} \frac{L(x)^{1- h/c_3}}{x^{1- h/c_3}}\,\mathrm{d}x. \end{aligned}$$

(5.33)

Then, we define $\psi (\cdot )$ by:

$$\begin{aligned} \psi (u)\, = \, (1-\varepsilon ) \times {\left\{ \begin{array}{ll} \upsilon \log \log u &{} \text { in the }sub{\text {-}}logarithmic \text { case,} \\ (\upsilon -1) \log u &{} \text { in the }logarithmic \text { case,} \\ u^{1/(\upsilon -1)} &{} \text { in the }super{\text {-}}logarithmic\text { case,} \end{array}\right. } \end{aligned}$$

(5.34)

so that $M= \exp (c_3 \psi (c_3/h)/h)$. Using the change of variable $x=e^{\frac{ c_{3} }{h} y}$, we have

$$\begin{aligned} \int _{N}^{M} \frac{L(x)^{1- h/c_3 }}{x^{1- h/c_3}}\,\mathrm{d}x \, = \, \frac{ c_3}{h} \int _{1}^{ \psi (h/c_3)} L\left( e^{\frac{ c_3}{h}y}\right) ^{1- h/c_3} \exp (y) \,\mathrm{d}y. \end{aligned}$$

(5.35)

It is now a matter of direct evaluation of this last expression, with the help of Definition 1.1.

(i) In the sub-logarithmic case, replacing L in the integral by its asymptotic equivalent, we obtain the following upper bound for the the r.h.s. of (5.35), valid for h sufficiently small

$$\begin{aligned} \frac{2 c_L c_3}{h} \int _1^{(1-\varepsilon ) \upsilon \log \log (c_3/h)} \frac{h}{ c_3 y} \big ( \log (c_3/h) \big )^{-\upsilon } e^{y } \,\mathrm{d}y \, \le \, 4 c_L \frac{ \left( \log (c_3/h)\right) ^{-\varepsilon \upsilon }}{ \log \log (c_3/h)}.\nonumber \\ \end{aligned}$$

(5.36)

We have used, for $a=1$, the inequality $\int _1^x e^z z^{-a}\,\mathrm{d}z \le 2e^x x^{-a}$ valid for x sufficiently large. We conclude that A is small by comparing the last term with ${\widetilde{L}}(1/h)$ (cf. (1.12)).

(ii) The same computation yields a similar upper-bound in the logarithmic case:

$$\begin{aligned}&\frac{2c_L c_3}{h} \int _1^{(1-\varepsilon )(\upsilon -1) \log (c_3/h)} \left( \frac{c_3 y}{h}\right) ^{-\upsilon } e^y \,\mathrm{d}y \nonumber \\&\quad \le 4 c_L c_3^{1-\upsilon } h^{\upsilon -1} \left( \frac{h}{c_3}\right) ^{-(1-\varepsilon )(\upsilon -1)} \frac{c_{\varepsilon ,\upsilon }}{ \log (c_3/h)}\le c'_{L,\varepsilon }\frac{h^{\varepsilon (\upsilon -1)}}{\log (1/h)} \end{aligned}$$

(5.37)

where $c_{\varepsilon ,\upsilon },c'_{L,\varepsilon }>0$, and one can check again that the last term is much smaller than ${\widetilde{L}}(1/h)$ for small values of h.

(iii) We are left with the super-logarithmic case. Using that $1- h/c_3 \ge 1/2$ for h sufficiently small, we obtain the following upper bound

$$\begin{aligned}&\frac{2c_L c_3}{h} \int _1^{(1-\varepsilon ) (c_3/h)^{1/(\upsilon -1)}} \exp \Big (- \frac{1}{2} \left( \frac{c_3 y}{h}\right) ^{1/\upsilon } +y \Big ) \,\mathrm{d}y \nonumber \\&\quad \le \, \frac{2c_L c_3}{h} \left( \frac{c_3}{h}\right) ^{1/(\upsilon -1)} \exp \Big (- c_{\upsilon } \left( \frac{c_3 }{h}\right) ^{ 1/(\upsilon -1)} \Big ) \nonumber \\&\quad \le \, \exp \Big (- \frac{c_{\upsilon }}{2} \left( \frac{c_3 }{h}\right) ^{1/(\upsilon -1)} \Big ). \end{aligned}$$

(5.38)

In the first step we set $c_{\upsilon }:=(2\upsilon )^{\upsilon /(1-\upsilon )}(\upsilon -1)$, and used the fact that the argument of the exponential, for y in the integration range, is maximal at $y=(2\upsilon )^{\upsilon /(1-\upsilon )} (c_3/h)^{1/(\upsilon -1)}$. The second inequality is valid for h sufficiently small. We conclude by observing that the last term is again of a smaller order than ${\widetilde{L}}(1/h)$ in that case.

Therefore, in view of (5.32), (5.33) and (5.36)–(5.38), A can made arbitrarily small, in particular smaller smaller than $e^{-3}/2$, in all cases. Let us show that the same holds true also for B. We will make use of the following Green function estimate.

Lemma 5.4

There exists $C=C(\eta )>0$ such that

$$\begin{aligned} \check{{\mathbf {P}}} _h ( n \in \tau ) \, \le \, C \frac{K(n)}{\big ({\widetilde{L}}(1/h)\big )^2}, \end{aligned}$$

(5.39)

for every n (in particular for $n\ge \exp (c_3/h)$).

Proof

The proof is derived from the following inequality: there is a constant $c>0$ (independent of h), such that for all $n\ge k \ge 1$

$$\begin{aligned} \check{{\mathbf {P}}} _h ( \tau _k =n ) \le c k \check{{\mathbf {P}}} _h \big ( \tau _1<\infty \big )^k K(n). \end{aligned}$$

(5.40)

Then, summing over k gives the identity, since we have $\check{{\mathbf {P}}} _h \big ( \tau _1<\infty \big ) \le 1- c / {\widetilde{L}}(1/h)$, and $\sum _{k=0}^{\infty }k (1-x)^k = 1/x^2$.

The proof of (5.40) follows from that of [2, Theorem 1.1-Equation (1.11)]: one simply has to notice that Lemma 2.1 in [2] is valid under the assumption that ${{\mathbf {P}}} (\tau _1 =j ) \le c L(j)/j$ (the constant here depends on $\eta$ but not on h), and then all the computations of Section 2.2 in [2] can be applied and yield (5.40). This completes the proof of Lemma 5.4. $\square$

Thanks to Lemma 5.4, and by using that $L(\cdot )$ is a slowly varying function, we obtain that for N large enough we have $\check{{\mathbf {P}}} _h ( j \in \tau )\le 3C N^{-1}L(N)/ {\widetilde{L}}(1/h)^2$ uniformly for $N/2\le j\le N-1$. By considering the definition (5.31) of B, we obtain

$$\begin{aligned} B \, \le \frac{3C L(N) }{N {\widetilde{L}}(1/h)^2 } \sum _{n=N}^{M} \sum _{j= N/2}^{N-1} K(n-j)^\theta . \end{aligned}$$

(5.41)

Then we control

$$\begin{aligned} \sum _{n=N}^{M} \sum _{j= N/2}^{N-1} K(n-j)^\theta \, \le \, \sum _{t=1}^{N/2} t K(t)^{\theta } + \frac{N}{2} \sum _{t=N/2}^{M} K(t)^\theta \le N \sum _{t=N/2}^{M} K(t)^\theta , \end{aligned}$$

(5.42)

where in the last inequality we used the fact that from slowly varying properties

$$\begin{aligned} \sum _{t=1}^{N/2} tK(t)^{\theta }\le C N^{2-\theta } L(N)^{\theta } \, =\, C e N L(N)^{\theta }, \end{aligned}$$

(5.43)

which is negligible with respect to the second sum (we used the definition of $\theta$ to get that $N^{(1-\theta )} = e$). We end up with

$$\begin{aligned} B \le \frac{3C L(N) }{{\widetilde{L}}(1/h) } \times \frac{1}{\widetilde{L}(1/h) } \sum _{n=N/2}^{M} K(n)^\theta . \end{aligned}$$

(5.44)

Since we have already proven that the right-hand side in (5.32) vanishes as h becomes small, to prove that also B vanishes in the same limit it suffices to show that ${L(N)}/{\widetilde{L}}(1/h)$ is bounded for h small. By recalling that $N=\exp (c_3/h)$, it is straightforward to see that in the cases we consider, cf. Definition 1.1, such a ratio vanishes as h goes to zero. Therefore also B is under control and $\rho \le 1$ when h is smaller than a well chosen constant. This completes the proof of Proposition 5.1. $\square$