Keywords

1 Introduction

Control charts are commonly used tools in process signal detection to improve the quality of manufacturing processes and service processes. In the past few years, more and more statistical process control techniques are applied to the service industry, and control charts are also becoming an effective tool in improving service quality. There have been a few studies in this area, like those of Tsung et al. (2008) and Ning et al. (2009). Much service process data comes from processes with variables having non-normal or unknown distributions so the commonly used Shewhart variables control charts, which depend on the normality assumption, are not suitable. Hence the question arises: “How to monitor a process with non-normal or unknown distribution data?” Some research has been done to deal with such a situation; see, for example, Ferrell (1953), Amin et al. (1995), Chakraborti et al. (2001), Altukife (2003), Bakir (2004, 2006), Li et al. (2010), Zou and Tsung (2010), and Graham et al. (2011). Little research has been done to deal with process variability monitoring; see, for example, Das and Bhattacharya (2008) and Jones-Farmer and Champ (2010).

A major drawback of the previous nonparametric approaches is that they are not easy for practitioners to apply because they are not statisticians and do not quite understand the proper way to implement the schemes. Yang et al. (2011) proposed a new Sign Chart for variables data to monitor the deviation of the process measurement from the target without the assumption of a normal process distribution or a distribution of known form. Yang and Cheng (2011) proposed a CUSUM Mean Chart to monitor small shifts in the process mean. Yang et al. (2012) addressed a new Mean Chart based on a simple statistic to monitor the shifts of the process mean. Their approaches are quite easy to use, and even easier than some of the above published nonparametric approaches. However, Yang and Cheng (2011), and Yang et al. (2011, 2012) did not consider a variance chart.

In this paper, we propose using both an EWMA-V Chart and an EWMA-M Chart for variables data to monitor the process variance and mean, extending Yang et al.’s approach (2012). The approach is still quite easy to use, and has better detection ability than the existing standard deviation and mean charts. The paper is organized as follows: In Sect. 2, we describe the EWMA-M Chart, and illustrate its detection performance. In Sect. 3, we discuss the construction of a newly proposed EWMA-V Chart, and measure its detection performance. In Sect. 4, we measure the detection performance of using both the new EWMA-V and EWMA-M Charts simultaneously. In Sect. 5, we describe the estimates for unknown population parameters. In Sect. 6, a numerical example of a service system in a bank branch was used to construct the proposed new EWMA-V and EWMA-M Charts to monitor the quality of service time, and their performance compared with those of some existing charts. Section 7 summarizes the findings and provides a recommendation.

2 The Proposed EWMA-M Chart

Assume that a critical quality characteristic, X, has a mean μ and variance σ 2. Following Yang and Cheng (2011), let \(Y = X-\mu\) and p = P(Y > 0) = the “Process Proportion.” If the process were in-control, then p = p m0, and if the process were out-of-control, that is if μ had shifted, then p = p m1 ≠ p m0. If p m0 is not given, it will be estimated using a preliminary data set.

To monitor the process mean, a random sample of size n 1, \(X_{1},X_{2},\ldots,X_{n_{1}}\), is taken from X. Define

$$\displaystyle{ Y _{j} = X_{j}-\mu \quad \text{ and }\quad I_{j} = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\,,\quad &\mbox{ if $Y _{j} > 0$,} \\ 0\,,\quad &\text{otherwise}, \end{array} \right.\quad,\;j = 1,2,\ldots,n_{1}\,. }$$
(1)

Let M t be the total number of Y j  > 0 at time t, then \(M_{t} =\sum _{ j=1}^{n_{1}}I_{j}\) would follow a binomial distribution with parameters (n 1, p m0) for an in-control process.

2.1 The Control Limits of EWMA-M Chart

Monitoring the process mean shifts is equivalent to monitoring the changes in process proportion. However, the binomial distribution is discrete and is asymmetric for p m0 ≠ 0.5. In addition the values of out-of-control average run length (ARL) (ARL M1) of the M t Chart do not change inversely with sample size as they normally should (see Yang et al. 2012). To rectify this problem, they propose an “arcsine transformed EWMA-M chart.” Each of these EWMA charts has the usual value of 370 for in-control ARL, and they are sensitive for monitoring small shifts in the process mean quickly and effectively.

Let \(T_{M} =\sin ^{-1}\big(\sqrt{M/n_{1}}\big)\), then the distribution of T M is approximately normal with a mean \(\sin ^{-1}\big(\sqrt{p_{M}}\big)\) and variance 1∕(4n 1) (see Mosteller and Youtz 1961). The EWMA-M statistic is

$$\displaystyle{ \mathrm{EWMA}_{T_{M_{ t}}} =\lambda _{1}T_{M_{t}} + (1 -\lambda _{1})\mathrm{EWMA}_{T_{M_{ t-1}}},\;0 <\lambda _{1} \leq 1,\;t = 1,2,\ldots. }$$
(2)

The New EWMA-M chart is constructed as follows. Define

$$\displaystyle{ \mathrm{UCL}_{1} =\sin ^{-1}\big(\sqrt{p_{ m0}}\big) + L_{1}\sqrt{ \frac{\lambda _{1 } } {4n_{1}(2 -\lambda _{1})}}\,, }$$
(3)
$$\displaystyle{ \mathrm{CL}_{1} =\sin ^{-1}\big(\sqrt{p_{ m0}}\big)\,, }$$
(4)
$$\displaystyle{ \mathrm{LCL}_{1} =\sin ^{-1}\big(\sqrt{p_{ m0}}\big) - L_{1}\sqrt{ \frac{\lambda _{1 } } {4n_{1}(2 -\lambda _{1})}}\,, }$$
(5)

and plot \(\mathrm{EWMA}_{T_{M_{ t}}}\). If any \(\mathrm{EWMA}_{T_{M_{ t}}} \leq \mathrm{ LCL}_{1}\) or \(\mathrm{EWMA}_{T_{M_{ t}}} \geq \mathrm{ UCL}_{1}\), an out-of-control signal is issued. The two parameters, L 1 and λ 1, are chosen to yield an in-control ARL, \(\mathrm{ARL}_{T_{M0}} = 370\), using the Markov chain approach proposed by Lucas and Saccucci (1990).

2.2 The In-Control and Out-of-Control Average Run Lengths of the EWMA-M Chart

The \(\mathrm{ARL}_{T_{M0}}\) of the new EWMA-M chart is a function of (n 1, L 1, λ 1). Adopting the in-control process proportion p m0 = 0. 5, \(\mathrm{ARL}_{T_{M0}} \approx 370\) with λ 1 = 0. 2 and L 1 = 2. 86, the out-of-control ARL, \(\mathrm{ARL}_{T_{M1}}\), of the EWMA-M chart is listed for n 1 = 8(1)20 and p m1 = 0. 30(0. 05)0. 50 in Table 1. From Table 1, we found that \(\mathrm{ARL}_{T_{M1}}\) decreases when the out-of-control value of p m1 is far away from the in-control value of p m0, and when n 1 increases.

Table 1 The \(\mathrm{ARL}_{T_{M1}}\) of the EWMA-M chart when p m0 = 0. 5
Full size table

3 The Proposed EWMA-V Chart

To monitor the process variance, another random sample of size n 2, \(X_{1},X_{2},\ldots,X_{n_{2}}\), is taken from the process, X. Assume that the sample size n 2 is even for convenience (if not, delete one observation). Define

$$\displaystyle{ Y _{1}^{{\ast}} = (X_{ 2} - X_{1})^{2}/2\,,\;Y _{ 2}^{{\ast}} = (X_{ 4} - X_{3})^{2}/2\,,\;\ldots \,,\;Y _{\frac{n_{ 2}} {2} }^{{\ast}} = (X_{ n_{2}} - X_{n_{2}-1})^{2}/2\,, }$$
(6)
$$\displaystyle{ E(Y _{j^{{\prime}}}^{{\ast}}) =\sigma ^{2}\quad,\;j^{{\prime}} = 1,2,\ldots,n_{ 2}/2\,,\text{ and} }$$
(7)
$$\displaystyle{ I_{j^{{\prime}}} = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\,,\quad &\mbox{ if $Y _{j^{{\prime}}}^{{\ast}} >\sigma ^{2}$} \\ 0\,,\quad &\text{otherwise} \end{array} \right.,\quad j^{{\prime}} = 1,2,\ldots,n_{ 2}/2\,. }$$
(8)

Let V be the total number of \(Y _{j^{{\prime}}}^{{\ast}} >\sigma ^{2}\), then \(V =\sum _{ j^{{\prime}}=1}^{0.5n_{2}}I_{j^{{\prime} }}\) will have a binomial distribution with parameters (0. 5n 2, p v0) for an in-control process, where \(p_{v0} = P(Y _{j^{{\prime}}}^{{\ast}} >\sigma ^{2})\). The value of p v0 will depend on the distribution of the X i ’s. For example, if the X i ’s are normally distributed, then \(p_{v0} = P(Y _{j^{{\prime}}}^{{\ast}} >\sigma ^{2}) = P(Z^{2} > 1)\) where Z ∼ N(0, 1). Thus in this case p v0 = 0. 3147. If the distribution of \(X_{n_{2}} - X_{n_{2}-1}\) is unimodal, as it frequently is, the version of the Chebychev inequality for unimodal variables implies that the quantity p v0 is bounded above by 4/9. The value of p v0 can be arbitrarily small but it usually will be in the range 0.25–0.50.

Similar to the M t Chart, the V t Chart is a new chart in that the binomial variable is not the count of nonconforming units in the sample but rather the number of pairs of X values in a sample that are in-control with respect to the process variance. Monitoring process variance shifts is equivalent to monitoring the changes in process proportion, p v0. The V t Chart is also asymmetric for p v0 ≠ 0. 5, and the values of out-of-control ARL (ARLV1) of the V t Chart do not change inversely with sample size as they normally should. Hence, we propose an “arcsine transformed EWMA-V chart.” Each of these EWMA charts has the usual value of 370 for in-control ARL, and they are sensitive for monitoring small shifts in the process variance quickly and effectively.

3.1 The Control Limits of EWMA-V Chart

Let \(T_{V } =\sin ^{-1}\big(\sqrt{V/0.5n_{2}}\big)\), then the distribution of T V is approximately normal with a mean \(\sin ^{-1}\big(\sqrt{p_{V}}\big)\) and variance 1∕(2n 2) (see Mosteller and Youtz 1961). We define the New EWMA-V statistic as:

$$\displaystyle{ \mathrm{EWMA}_{T_{V_{ t}}} =\lambda _{2}T_{V _{t}} + (1 -\lambda _{2})\mathrm{EWMA}_{T_{V_{ t-1}}},\quad 0 <\lambda _{2} \leq 1\,. }$$
(9)

Analogous to the derivation of the arcsine transformed EWMA-M chart, we can construct the new EWMA-V chart as follows. Define

$$\displaystyle{ \mathrm{UCL}_{2} =\sin ^{-1}\big(\sqrt{p_{ v0}}\big) + L_{2}\sqrt{ \frac{\lambda _{2 } } {2n_{2}(2 -\lambda _{2})}}\,, }$$
(10)
$$\displaystyle{ \mathrm{CL}_{2} =\sin ^{-1}\big(\sqrt{p_{ v0}}\big)\,, }$$
(11)
$$\displaystyle{ \mathrm{LCL}_{2} =\sin ^{-1}\big(\sqrt{p_{ v0}}\big) - L_{2}\sqrt{ \frac{\lambda _{2 } } {2n_{2}(2 -\lambda _{2})}}\,, }$$
(12)

and plot \(\mathrm{EWMA}_{T_{V_{ t}}}\). If any \(\mathrm{EWMA}_{T_{V_{ t}}} \geq \mathrm{ UCL}_{2}\) or \(\mathrm{EWMA}_{T_{V_{ t}}} \leq \mathrm{ LCL}_{2}\), an out-of-control signal is issued. Here again, the two parameters, L 2 and λ 2, are chosen to yield the desired in-control ARL (\(\mathrm{ARL}_{T_{V 0}} \approx 370\)) using the Markov chain approach.

3.2 The In-Control and Out-of-Control Average Run Lengths of the EWMA-V Chart

The \(\mathrm{ARL}_{T_{V 0}}\) of the new EWMA-V chart is a function of (n 2, L 2, λ 2). Adopting the in-control process proportion p v0 = 0. 3, \(\mathrm{ARL}_{T_{V 0}} \approx 370\) with λ 2 = 0. 2 and L 2 = 2. 86, the out-of-control ARL, \(\mathrm{ARL}_{T_{V 1}}\), of the EWMA-V chart is listed for 0. 5n 2 = 4(1)15 and p v1 = 0. 2(0. 2)0. 8 in Table 2. From Table 2, we found that \(\mathrm{ARL}_{T_{V 1}}\) decreases when the out-of-control value of p v1 is far away from the in-control value of p v0, and when n 2 increases.

Table 2 The \(\mathrm{ARL}_{T_{V 1}}\) of the EWMA-V chart when p v0 = 0. 3
Full size table

4 Performance Measurement of Using the EWMA-V Chart and the EWMA-M Chart Simultaneously

Use of both the EWMA-V Chart and EWMA-M Chart permits monitoring of the process variance and mean simultaneously. We will use the ARL to measure the out-of-control detection performance of using both the EWMA-V Chart and EWMA-M Chart.

4.1 The In-Control Average Run Lengths of the EWMA-V Chart and the EWMA-M Chart

In a production process, we take a sample of size n 1 + n 2, the first n 1 observations are used to calculate the statistic \(\mathrm{EWMA}_{T_{M}}\), then the remaining n 2 observations are taken to calculate the statistic \(\mathrm{EWMA}_{T_{V }}\). The statistics \(\mathrm{EWMA}_{T_{M}}\) and \(\mathrm{EWMA}_{T_{V }}\) are independent since the two groups of observations are independent. The in-control overall ARL, ARL0, of the newly proposed charts is well approximated as follows (see Hawkins 1992),

$$\displaystyle\begin{array}{rcl} \mathrm{ARL}_{0}& =& \frac{1} { \frac{1} {\mathrm{ARL}_{T_{M0}}} + \frac{1} {\mathrm{ARL}_{T_{V 0}}} -\left ( \frac{1} {\mathrm{ARL}_{T_{M0}}} \frac{1} {\mathrm{ARL}_{T_{V 0}}} \right )} \\ & \approx & \frac{1} { \frac{1} {\mathrm{ARL}_{T_{M0}}} + \frac{1} {\mathrm{ARL}_{T_{V 0}}} } \,. {}\end{array}$$
(13)

The ARL0 of using both the EWMA-M Chart and EWMA-V Chart with any combinations of (n 1, n 2) and (p m0, p v0) are all approximately 185 because of

$$\displaystyle{ \mathrm{ARL}_{0} \approx \frac{1} { \frac{1} {\mathrm{ARL}_{T_{M0}}} + \frac{1} {\mathrm{ARL}_{T_{V 0}}} } = \frac{1} { \frac{1} {370} + \frac{1} {370}}\,. }$$

Usually, the most efficient way of using a combined charting procedure is to use all the observations for both the mean and variance charts but this was not considered in our scheme. The reason is that the two monitoring statistics EWMA-V and EWMA-M are dependent if all the observations are used, and this will complicate the calculation of the overall ARLs of the two proposed control charts. Of course, we may use simulation to estimate the overall ARLs.

4.2 The Out-of-Control Average Run Lengths of the EWMA-V Chart and the EWMA-M Chart

When the process is out of control due to a shift in the process mean, μ, the process proportion becomes p m1 ( ≠ p m0). For an out-of-control process whose variance σ 2 has changed, the process proportion becomes p v1 ( ≠ p v0). The out-of-control overall ARL, ARL1, of using the EWMA-V Chart and EWMA-M Chart simultaneously could be calculated approximately using

$$\displaystyle{ \mathrm{ARL}_{1} \approx \frac{1} { \frac{1} {\mathrm{ARL}_{T_{M1}}} + \frac{1} {\mathrm{ARL}_{T_{V 1}}} } \,. }$$
(14)

The ARL1s of using both the EWMA-M Chart and EWMA-V Chart with the combinations of n 1 = 8(2)24, 0. 5n 2 = 4(1)12, p v0 = 0. 1, p m0 = 0. 5, p v1 = 0. 2, and p m1 = 0. 25(0. 05)0. 45 are listed in Table 3. In Table 3, we observe that the ARL1 changes inversely with n 1 and n 2, and the ARL1 decreases when p m1 is far away from p m0 and/or p v1 is far away from p v0. The results are much more reasonable than those corresponding to use of both the V Chart and M Chart.

Table 3 The ARL1 of the EWMA-V and EWMA-M charts when p v0 = 0. 1, p m0 = 0. 5, and p v1 = 0. 2
Full size table

5 When the Population Mean and Variance Are Unknown

When the in-control process mean, μ, and the process variance, σ 2, are unknown, and hence the in-control process proportions, p m0 and p v0, are unknown, we can use the following two preliminary independent sample data sets

$$\displaystyle\begin{array}{rcl} X_{t,1}& &,X_{t,2},\ldots,X_{t,n_{1}}\;,\;\;t = 1,2,\ldots,k\,. {}\\ X_{t,n_{1}+1}& &,X_{t,n_{1}+2},\ldots,X_{t,n_{1}+n_{2}}\;,\;\;t = 1,2,\ldots,k\,. {}\\ \end{array}$$

from k sampling periods, each with an even number of observations, n 1 and n 2, to estimate them (see, e.g., Montgomery 2009), i.e.

$$\displaystyle{ \hat{\mu }=\bar{\bar{ x}} = \frac{\sum _{t=1}^{k}\sum _{j=1}^{n_{1}}x_{t,j}} {\mathit{kn}_{1}} \;,\;\;\hat{\sigma }= \frac{\bar{S}} {c_{4}} = \frac{\sum _{t=1}^{k}S_{t}} {c_{4}k} \,, }$$

where

$$\displaystyle\begin{array}{rcl} \hat{p}_{m0}& =& \frac{\sum _{t=1}^{k}\frac{M_{t}} {n_{1}} } {k} \;,\;\;\hat{p}_{v0} = \frac{\sum _{t=1}^{k} \frac{V _{t}} {0.5n_{2}} } {k} \;,\;\;S_{t} = \sqrt{\frac{\sum _{j=n_{1 } +1 }^{n_{1 } +n_{2 } }\big(X_{t,j } -\bar{ X}_{t } \big)^{2 } } {n_{2} - 1}} \;,\;\;t = 1,\ldots,k\,, {}\\ c_{4}& =& \left ( \frac{2} {n_{2} - 1}\right )^{0.5} \frac{\varGamma (0.5n_{2})} {\varGamma \big(0.5(n_{2} - 1)\big)}\;,\;\;\text{ and }\quad \bar{S} = \frac{\sum _{t=1}^{k}S_{t}} {k} \,. {}\\ \end{array}$$

The EWMA-V and EWMA-M Charts are thus constructed using these estimated values of p m0 and p v0. The statistics \(\mathrm{EWMA}_{T_{M}}\) and \(\mathrm{EWMA}_{T_{V }}\) corresponding to the samples of sizes n 1 and n 2 are plotted on the resulting EWMA-V and EWMA-M Charts simultaneously. If no points fall outside their control limits, then we would deem the process to be in-control.

6 Example

We will use an example of service time from Yang et al. (2012) to illustrate the use of the new EWMA-V and EWMA-M Charts. Service time is an important quality characteristic in the banking industry. To measure the efficiency in the service system of a bank branch, the in-control sampling service times (unit: minutes) is measured from twenty counters every day for 15 days. That is, fifteen samples of size \(n_{1} + n_{2} = 20\), where \(n_{1} = n_{2} = 10\) are available. This in-control data has been analyzed assuming a non-normal distribution. For each sample, the first ten observations illustrated in Table 4 are used to calculate the \(\mathrm{EWMA}_{T_{M}}\) statistic and the last ten observations illustrated in Table 5 are used to calculate the \(\mathrm{EWMA}_{T_{V }}\) statistic.

Table 4 The service times from the first ten counters in a bank branch
Full size table
Table 5 The service times from the last ten counters in a bank branch
Full size table

To construct the EWMA-V and EWMA-M charts, the variance and mean of the service time are estimated by \((\bar{S}/c_{4})^{2}\) and \(\bar{\bar{x}}\) using the fifteen samples in Tables 5 and 4, respectively. The estimate of the variance is \(\hat{\sigma }^{2} = (\bar{S}/c_{4})^{2} = 30.159\) and the estimate of the mean is \(\hat{\mu }=\bar{\bar{ x}} = 5.77\). For each sample in Table 5, the monitoring statistic \(\mathrm{EWMA}_{T_{V }}\) is calculated. For each sample in Table 4, the monitoring statistic \(\mathrm{EWMA}_{T_{M}}\) is calculated. Hence, the estimates of proportions (p m0, p v0) are (\(\hat{p}_{m0} = \frac{\sum _{t=1}^{15}M_{ t}/10} {15} = 0.39\), \(\hat{p}_{v0} = \frac{\sum _{t=1}^{15}V _{ t}/5} {15} = 0.24\)), where M t  = Total number of (Y j  > 5. 77) and j = 1, 2, …, 10, V t  = Total number of (Y j ∗ > 30. 159) and j = 11, 12, …, 20. The EWMA-V and EWMA-M Charts with \(\lambda _{1} =\lambda _{2} = 0.2\) are constructed as follows based on the fifteen in-control samples, respectively.

The EWMA-V Chart:

$$\displaystyle{ \mathrm{UCL}_{2} = 0.725\;,\;\;\mathrm{LCL}_{2} = 0.299\,. }$$

The EWMA-M Chart:

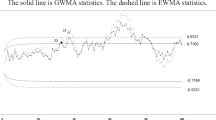
$$\displaystyle{ \mathrm{UCL}_{1} = 0.85\;,\;\;\mathrm{LCL}_{1} = 0.47\,. }$$

The monitoring statistics EWMA-V and EWMA-M are calculated (see Tables  4 and 5). The EWMA-V and EWMA-M Charts show no signals (see Fig. 1a, b).

Fig. 1
figure 1

First 15 control chart points. (a) The EWMA-V chart. (b) The EWMA-M chart. (c) Shewhart S chart. (d) Shewhart \(\bar{X}\) chart. (e) The EWMA-S chart. (f) The EWMA-\(\bar{X}\) chart. (g) The transformed Shewhart S chart. (h) The transformed Shewhart \(\bar{X}\) chart

Full size image

For comparison, we constructed the corresponding Shewhart standard deviation and mean (S-\(\bar{X}\)) charts, EWMA-S and EWMA-\(\bar{X}\) charts, and transformed S and \(\bar{X}\) charts by applying X 0. 278 transformation (see Montgomery 2009), respectively. The Shewhart S-\(\bar{X}\) charts are constructed with bounds as follows:

$$\displaystyle{ \mathrm{UCL}_{S} = 9.66\,,\;\mathrm{LCL}_{S} = 1.597\;,\;\;\mathrm{UCL}_{\bar{X}} = 10.98\,,\;\mathrm{LCL}_{\bar{X}} = 0.55\,. }$$

The Shewhart S-\(\bar{X}\) charts also show no signals (see Fig. 1c, d). The EWMA-S and EWMA-\(\bar{X}\) charts are constructed with bounds as follows:

$$\displaystyle\begin{array}{rcl} \mathrm{UCL}_{\mbox{ EWMA-$S$}}& =& 7.495\,,\;\mathrm{LCL}_{\mbox{ EWMA-$S$}} = 2.485\;, {}\\ \mathrm{UCL}_{\mbox{ EWMA-$\bar{X}$}}& =& 11.02\,,\;\mathrm{LCL}_{\mbox{ EWMA-$\bar{X}$}} = 0.53\,. {}\\ \end{array}$$

The EWMA-S and EWMA-\(\bar{X}\) charts also show no signals (see Fig. 1e, f). The transformed S and \(\bar{X}\) charts are constructed with bounds as follows:

$$\displaystyle{ \mathrm{UCL}_{TS} = 0.732\,,\;\mathrm{LCL}_{TS} = 0.121\;,\;\;\mathrm{UCL}_{T\bar{X}} = 1.77\,,\;\mathrm{LCL}_{T\bar{X}} = 1.08\,. }$$

The transformed S chart shows no signal but the transformed \(\bar{X}\) chart shows a false signal (see Fig. 1g, h).

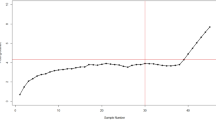
A data set consisting of ten samples of ten service times from an improved new automatic service system of the bank branch was collected and shown in Fig. 2. The service times should be reduced because of the improved new automatic service system. The new service times are regarded as out-of-control data set. The new proposed EWMA-V and EWMA-M Charts are used to monitor the new service times to illustrate their out-of-control detection ability

Fig. 2
figure 2

Next 10 control chart points. (a) The EWMA-V chart. (b) The EWMA-M chart. (c) Shewhart S chart. (d) Shewhart \(\bar{X}\) chart. (e) The EWMA-S chart. (f) The EWMA-\(\bar{X}\) chart. (g) The transformed Shewhart S chart. (h) The transformed Shewhart \(\bar{X}\) chart

Full size image

The EWMA-V and EWMA-M Charts detected out-of-control signals from the third sample and the second sample onward, respectively (samples 3–10 on EWMA-V Chart and samples 2–10 on EWMA-M Chart) (see Fig. 2a, b). That is, the variance and mean of the new service times are significantly reduced because of the improved new automatic service system. However, the corresponding Shewhart S-\(\bar{X}\) charts produced only one true out-of-control signal (sample 9 on S chart) (see Fig. 2c, d). The EWMA-S and EWMA-\(\bar{X}\) charts produced six true out-of-control signals (samples 4–10 on EWMA-\(\bar{X}\) chart) (see Fig. 2e, f), and transformed S and \(\bar{X}\) charts produced two true out-of-control signals (samples 2–3 on transformed \(\bar{X}\) chart) (see Fig. 2g, h).

To construct the Shewhart S-\(\bar{X}\) charts, EWMA-S and EWMA-\(\bar{X}\) charts and transformed S and \(\bar{X}\) charts one requires the normality assumption but this is not the case for the EWMA-V and EWMA-M Charts. In this example, the EWMA-V and EWMA-M charts detected most of the out-of-control signals. The New EWMA-V and EWMA-M Charts showed better detection ability than the existing charts in monitoring and detecting process variance and mean shifts. The new EWMA-V and EWMA-M Charts are thus recommended.

7 Conclusions

In this paper, we propose using both the EWMA-M and EWMA-V Charts, based on two simple independent statistics to monitor the mean and variance shifts in the process simultaneously when the distribution of a quality characteristic is not known or is not believed to be normal. A numerical example of service times from a bank branch with a right skewed distribution illustrated the application of the new EWMA-M and EWMA-V Charts which were compared with some existing charts. The proposed new EWMA-M and EWMA-V Charts showed better detection ability than the existing charts in monitoring and detecting both the process mean and variance shifts. The new EWMA-M and EWMA-V Charts are thus recommended. The M-V charts have the advantage of simplicity, but this is counter weighed by some anomalies in their performance due to the discrete nature of the monitoring variables. In an analysis based on two data sets, the EWMA-M and EWMA-V charts appear to have good performance. Knoth and Morais (2013) deal with what they termed an ARL-unbiased chart. We may consider ARL-unbiased EWMA charts based on non-transformed statistics in a future study.