Input-to-State Stability of Large-Scale Stochastic Impulsive Systems with Time Delay and Application to Control Systems

Abstract

This chapter deals with large-scale nonlinear delay stochastic systems where the system states are subject to impulsive effects and perturbed by some disturbance input having bounded energy. The interest is to develop a comparison principle and establish input-to-state stability (ISS) in the mean square (m.s.) using vector Lyapunov function and Razumikhin technique. Impulses are being viewed as perturbation to stable systems, and they have a stabilizing role to unstable systems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Technology has been producing a new generation of high-dimensional, structurally sophisticated dynamical systems, known as large-scale systems. Typically, a large-scale system is described by a large number of variables, nonlinearities, and uncertainties. Nowadays, large-scale systems, as a tool, have been used to model numerous processes in many fields in science and engineering, such as large electric power network systems, control systems, aerospace systems, solar systems, nuclear reactors, chemistry, biology, and ecology systems. Readers may consult [5,8].

A large class of systems in natural science and engineering are subjected to state changes over short time periods. The durations of these changes are often negligible when compared to the duration of the system process, so that these changes can be approximated as instantaneous changes of states or impulses. The resulting systems are called impulsive systems [4].

If time delay and random noise are considered in the later systems, we are led to stochastic impulsive systems with time delay [1,2].

Input-to-state stability (ISS) is essential in modern nonlinear feedback and control system design. Generally, ISS studies the response of the forced system to a disturbance input where the underlying unforced system is asymptotically stable [3,6,7].

2 Problem formulation

Denote by $\mathbb{N}$ the set of natural numbers, $\mathbb{R}_+$ the set of nonnegative real numbers, $\mathbb{R}^n$ the n-dimensional real space with the Euclidean norm $\|\cdot\|$, and $\mathbb{R}^{n\times m}$ the set of $n\times m$ matrices. If $g\in \mathbb{R}^{n\times m}$, its induced norm is $\|g\|=\sqrt{\mbox{trace}(g^Tg)}$. Let $r>0$ be the time delay, $\mathbb{C}([-r,0],\mathbb{R}^n)$ ($\mathbb{PC}([-r,0],\mathbb{R}^n)$) be space of continuous (piecewise continuous) functions φ mapping $[-r,0]$ into $\mathbb{R}^n$. If x is a function from $[t-r,\infty)$ to $\mathbb{R}^n$, then $x_t=x(t+s)$ for $s\in [-r,0]$ mapping $[-r,0]$ into $\mathbb{R}^n$, and $\|x_t\|_r=\sup_{t-r\leq \theta\leq t}\|x(\theta)\|$. Define $x_{t^-}\in \mathbb{PC}([-r,0],\mathbb{R}^n)$ by $x_{t^-}(s)=x(t+s)$ for $s\in [-r,0]$ and $x_{t^-}(s)=x(t^-)$ for s = 0. Let $W(t,\omega)$ denote an m-dimensional Wiener process.

Typically, an interconnected system with decomposition $\mathbb{D}_i$ may have the form

$$\mathbb{D}_i:\left\{\begin{array}{ll} dw^i(t)=f_i(t,w_t^i)dt+g_i(t,w_t^1,w_t^2,\cdots,w_t^l)dt+\sum_{j=1}^l\sigma_{ij}(t,w_t^j)dW_j(t),&t\not=\tau_k,\\\Updelta w^i(t)=\mathcal{I}_i(t,w_{t^-}^i),&t=\tau_k,\\w^i_{t_0}=\phi_i(s),\quad\quad\quad\qquad s\in [-r,0],\end{array} \right.$$

(1)

where $k\in \mathbb{N}$ and $i=1,2,\cdots l$ for some $l\in\mathbb{N}$. w ⁱ (or $w_t^i)\in \mathbb{R}^{n_i}$ is an n _i -dimensional vector state (or deviated state) and $n=\sum_i^l n_i$ for some $n_i\in \mathbb{N}$. $f_i:\mathbb{R}_+\times \mathbb{R}^{n_i}\to \mathbb{R}^{n_i}$, $g_i:\mathbb{R}_+\times \mathbb{R}^n\to \mathbb{R}^{n_i}$, $\sigma_{ij}:\mathbb{R}_+\times \mathbb{R}^{n_j}\to \mathbb{R}^{n_i\times m_j}$, $m=\sum_i^l m_i$ for some $m_i\in \mathbb{N}$, $\mathcal{I}_i:\mathbb{T}\times \mathbb{R}^{n_i}\to \mathbb{R}^{n_i}$ with $\mathbb{T}=\{\tau_k \big| \, k=1,2,\cdots\}$ with impulsive moments $0<\tau_1<\tau_2< \cdots$, and $\lim_{k\to \infty}\tau_k=\infty$, and $\phi_i: [-r,0]\to \mathbb{R}^{n_i}$. Define the isolated subsystems $\mathbb{S}_i$ by

$$\mathbb{S}_i:\left\{\begin{array}{ll} dw^i(t)=f_i(t,w_t^i)dt+\sigma_{ii}(t,w_t^i)dW_i(t),&t\not=\tau_k,\\\Updelta w^i(t)=\mathcal{I}_i(t,w_{t^-}^i),&t=\tau_k,\\w^i_{t_0}=\phi_i(s), s\in [-r,0].\end{array} \right.$$

(2)

For $x\in \mathbb{R}^n$, let $x^T=[(w^1)^T,(w^2)^T,\cdots,(w^l)^T]$, and define $f:\mathbb{R}_+\times \mathbb{R}^n\to \mathbb{R}^n$ by $f^T(t,x_t)=[f_1^T(t,w_t^1),f_2^T(t,w_t^2),\cdots,f_l^T(t,w_t^l)]$, $g:\mathbb{R}_+\times \mathbb{R}^n\to \mathbb{R}^n$ by $g^T(t,x_t)=[g_1^T(t,x_t),g_2^T(t,x_t),\cdots,g_l^T(t,x_t)]$, $\sigma:\mathbb{R}_+\times \mathbb{R}^n\to \mathbb{R}^{n\times m}$ by $\sigma(t,x_t)=[\sigma_{ij}(t,w_t^j)]$, $W:\mathbb{R}_+\to \mathbb{R}^m$ by $W^T=[W^T_1,W^T_2,\cdots,W^T_l]$, where $W_i:\mathbb{R}_+\to \mathbb{R}^{m_i}$, and impulsive functional $\mathcal{I}:\mathbb{T}\times \mathbb{R}^n\to \mathbb{R}^n$ by $\mathcal{I}^T(t,x_{t^-})=[\mathcal{I}_1^T(t,w^1_{t^-}), \mathcal{I}_2^T(t,w^2_{t^-}), \cdots,\mathcal{I}_l^T(t,w^l_{t^-})].$

Then, the composite (or interconnected) system can be written in the form $\mathbb{S}$

$$\mathbb{S}:\left\{\begin{array}{ll} dx(t)=F(t,x_t)dt+\sigma(t,x_t)dW(t),&\qquad t\not=\tau_k,\\\Updelta x(t)=\mathcal{I}(t,x_{t^-}),&\qquad t=\tau_k,\\x_{t_0}=\Upphi(s),\qquad\qquad s\in [-r,0],\end{array} \right.$$

(3)

where $F(t,x_t)=f(t,x_t)+g(t,x_t)$, and $\Upphi^T=[\phi_1^T, \phi_2^T,\cdots, \phi_l^T]$ with $\mathbb{E}[\|\Upphi\|^2]<\infty$.

Definition 1

A function $\alpha\in \mathbb{C}(\mathbb{R}_+; \mathbb{R}_+)$ is said to belong to $\mathcal{K}$ (briefly, $\alpha\in \mathcal{K}$) if $\alpha(0)=0$ and it is strictly increasing; it is said to belong to $\mathcal{K}_1$ (or $\mathcal{K}_2$) if $\alpha\in \mathcal{K}$ and it is convex (or concave). A function $\beta\in \mathbb{C}([0,a)\times \mathbb{R}_+;\mathbb{R}_+)$ is said to belong to class $\mathcal{KL}$ if, for each fixed s, the mapping $\beta(\cdot,s)\in \mathcal{K}$, and, for each fixed r, the mapping $\beta(r,\cdot)$ is decreasing and $\beta(r,s)\to 0$ as $s\to \infty$.

Definition 2

System (3) is said to be ISS in mean square (m.s.) if there exist functions $\beta\in \mathcal{KL}$ and $\gamma\in \mathcal{K}$ such that, for any $x_{t_0}$ and bounded input u, the solution x satisfies

$$\begin{aligned} \mathbb{E}[\|x(t)\|^2]\leq \beta\big(\mathbb{E}[\|x_{t_0}\|_r^2],t-t_0\big)+\gamma\Big(\sup_{t_0\leq \theta\leq t}\|u(\theta)\|\Big).\end{aligned}$$

If, moreover, $\beta\big(\mathbb{E}[\|x_{t_0}\|_r^2],t-t_0\big)=K\mathbb{E}[\|x_{t_0}\|_r^2]e^{-\lambda (t-t_0)}$, for some positive constants K and λ, then system (3) is said to be exponential ISS in the m.s.

Definition 3

The isolated subsystem $\mathbb{S}_i$ in (2) is said to possess Property A if there exist functions $c_i\in \mathcal{K}_1$ and $a_i\in \mathbb{C}\big([\tau_{k-1},\tau_k)\times \mathbb{R}_+\times \mathbb{R}^q; \mathbb{R}\big)$, where $a_i(t,v,u)$ is concave in v for all $t\in \mathbb{R}_+$ and $u\in \mathbb{PC}(\mathbb{R}_+;\mathbb{R}^q)$, and $\lim_{(t,y,v)\to (\tau^-_k,x,u)}a_i(t,y,v)=a_i(\tau^-_k,x,u)$, and $V^i\in \mathbb{C}^{1,2}\big([-r,\infty)\times \mathbb{R}^n; \mathbb{R}_+\big)$, which is decrescent and satisfies

(i):

$\forall (t,\psi^i(0)) \in [-r,\infty)\times \mathbb{R}^n$, $c_i(\|\psi^i(0)\|^2)\le V^i(t,\psi^i(0)), \mbox{(a.s.)},$ and, $\forall t\not=\tau_k$, $\psi^i\in \mathbb{PC}\big([-r,0]; \mathbb{R}^n\big)$, and $u\in \mathbb{PC}(\mathbb{R}_+;\mathbb{R}^q)$,

$$\mathcal{L}_iV^i(t,\psi^i,u)\le a_i(t, V^i(t,\psi^i(0)),u(t)), \mbox{(a.s.)},$$

provided that $V^i(t+s,\psi^i(s))\le \bar{q}V(t,\psi^i(0))$ for some $\bar{q}>1$ and $s\in [-r,0]$;

(ii):

for any $\tau_k\in \mathbb{T}$ and $\psi^i\in \mathbb{PC}\big([-r,0]; \mathbb{R}^n\big)$,

$$V^i\big(\tau_k,\psi^i(0)+\mathcal{I}_i(\tau_k,\psi^i(\tau_k^-))\big) \le \alpha(d_k)V^i(\tau_k^-,\psi^i(0)), \mbox{(a.s.)},$$

where $\psi^i(0^-)=\psi^i(0)$ and $\prod_{k=1}^{\infty}\alpha(d_k)<\infty$ with $\alpha(d_k)>1$ for all k.

3 Main results

Theorem 1

Comparison principle. Assume that the following assumptions hold:

(i):

Every isolated subsystem $\mathbb{S}_i$ has Property A;

(ii):

For any $i=1,2,\cdots,l$ , there exist a function $\bar{b}_i\in \mathbb{C}\big([\tau_{k-1},\tau_k)\times \mathbb{R}_+\times \mathbb{R}^q; \mathbb{R}\big)$ and $\bar{b}_i$ is quasi monotone nondecreasing such that

$$\begin{aligned} & g^T_i(t, \psi,u)V_{\psi^i(0)}^i(t,\psi^i(0))+\frac{1}{2}\sum_{j=1,i\not=j}^l\mbox{tr}\big[\sigma^T_{ij}(t,\psi^j,u)\\ &\qquad \times V_{\psi^i(0)\psi^i(0)}^i(t,\psi^i(0))\sigma_{ij}(t,\psi^j,u)\big]<\bar{b}_i(t,V(t,\psi(0)),u),\end{aligned}$$

where $V^T(t,x)=\big(V^1(t,w^1),\cdots,V^l(t,w^l)\big)$ ;

(iii):

Let $a^T(\cdot)=\big(a_1(\cdot), a_2(\cdot),\cdots, a_l(\cdot)\big)$ and $\bar{b}^T(\cdot)=\big(\bar{b}_1(\cdot), \bar{b}_2(\cdot),\cdots, \bar{b}_l(\cdot)\big)$ , where $a_i(\cdot)$ and $\bar{b}_i(\cdot)$ are defined in (i) and (ii), respectively, and assume that

$$\begin{aligned} & |a(t,v',u')+\bar{b}(t,v',u')|^2\le h_1(t)+h_2(t)\kappa(\|v'\|^2),\\ & |a(t,v',u')+\bar{b}(t,v',u')-a(t,v'',u'')-b(t,v'',u'')| \le K\big(\|v'-v''\|+\|u'-u''\|\big),\end{aligned}$$

where $t\in \mathbb{R}_+$ , h ₁ and h ₂ are $\mathbb{PC}(\mathbb{R}_+, \mathbb{R}_+)$ functions, $\kappa:\mathbb{R}_+\to \mathbb{R}_+$ is continuous, increasing, concave function, $v'$ and $v''\in \mathbb{R}_+^{l}$ , $u'$ and $u''\in \mathbb{R}^{q}$ , and $K>0$ ;

(iv):

There exists a function $p:\mathbb{R}_+\times \mathbb{R}^l\times \mathbb{R}^q\to \mathbb{R}$ such that

$$\sup_{V(t,x)\le v} \sum _{i,j=1}^l \|\sigma^T_{ij}(t,\psi^j,u)V_{\psi^i(0)^i(t,\psi^i(0))}(t,\psi^i(0))\|^2\le p(t,v,u)\le h_2(t)\kappa(\|v\|^2)+ \gamma(\|u\|).$$

Then, $V(t_0,x_0)< v_0$ implies that $V(t,x(t))< v(t)=(v^1,\cdots,v^l)^T$ , where

$$\left\{\begin{array}{ll} dv=[a(t,v,u)+\bar{b}(t,v,u)]{d}t+ \mathcal{V}{d}W(t), & \forall\, t\geq t_0, t\not=\tau_k,\\\Updelta v(t)=\alpha_M(d_k)v(t^-),& t=\tau_k,\end{array} \right.$$

(4)

with $\mathcal{V}=[v_{ij}]_{l\times l}$ , $\|\mathcal{V}\|^2\le p(t,v,u)$ , and $\alpha_M(\cdot)=\max_i\{\alpha_i(\cdot)\}$ .

Proof

Define $V^T(t,x(t))=\big(V^1(t,w^1),\cdots,V^l(t,w^l)\big)$, where V ⁱ is the Lyapunov function of ith subsystem. Then, ${d}V^T(t,x(t))= \big({d}V^1(t,w^1),\cdots,{d}V^l(t,w^l)\big)$, where

$$dV^i(t,w^i)<[a_i(t,V^i(t,w^i),u)+b_i(t,V^i(t,w^i),u)]dt+\sum_{ij}^ly_{ij}{d}W_i(t),$$

with $y_{ij}=V_{w^i}^{i^T}(t,w^i)\sigma_{ij}(t,w_t^j,u)$. It follows that, for all $t\in [\tau_{k-1},\tau_k)$, $k=1,2,\cdots$,

$$\begin{aligned} dV(t,x(t)) < \big[a(t,V(t,x(t)),u(t))+b(t,V(t,x(t)),u(t))\big] dt+Y{d}W(t).\end{aligned}$$

At $t=\tau_k$, one can get $V^T(t,x(t)) \le \alpha_M(d_k)V^T(t^-,x(t^-))$. Particularly, for $t\in [\tau_0,\tau_1)$, we have $V^i(t_0,w^i(t_0))<y_0$ and

$$dV^i(t,w^i)-dy_i<\Big\{[a_i(t,V^i(t,w^i),u)-a_i(t,y_i,u)]+[b_i(t,V^i(t,w^i),u)-b_i(t,y_i,u)]\Big\}{d}t.$$

By Theorem 4.5.2 in [5], $V^i(t,w^i(t))<y_i(t)$ $\forall t\in [\tau_0,\tau_1)$, and, at $t=\tau_1$, we have

$$V^i\big(\tau_1,w^i(\tau_1)\big)-y_i(\tau_1)<\alpha_M(d_k)\Big[V^i(\tau_1^-,w^i(\tau_1^-))-y_i(\tau_1^-)\Big]<0,$$

i.e., $V^i(\tau_1,w^i(\tau_1))<y_i(\tau_1)$. Similarly, for $k=1,2,\cdots$ and $t\in [\tau_{k-1},\tau_k)$, $V^i(t,w^i(t))<y_i(t)$ and, at $t=\tau_k$, $V^i(\tau_k,w^i(\tau_k))<y_i(\tau_k)$. Therefore, for all $t\geq t_0$, and $i=1,2,\cdots,l$, $V_i(t,w^i(t))<y_i(t)$, which implies that $V(t,x(t))<y(t)$, $\forall\, t\geq t_0$, as required.

Theorem 2

Stability results. Suppose that the assumptions of Theorem 1 hold, and there exist $\alpha\in \mathcal{K}_2$ , $c\in \mathcal{K}_1$ , a function $\bar{h}\in \mathbb{C}\big([\tau_k,\tau_{k-1})\times \mathbb{R}^l;\mathbb{R}_+\big)$ , $z\in \mathbb{R}^l$ , and $U\in \mathbb{C}^{1,2}\big([\tau_k,\tau_{k-1})\times \mathbb{R}^l:\mathbb{R}_+\big)$ which is decrescent, $U(t,0)=0$ , and satisfies

(i):

For all $t\in \mathbb{R}_+$ and $y\in \mathbb{PC}(\mathbb{R}_+;\mathbb{R}^l)$ , $\alpha(\|y\|^2)\le U(t,y)$ , $z^TU_{yy}(t,y)z\le \bar{h}(t,y) \|z\|^2$ , and

$$U_t(t,y)+U_y(t,y)\big[a(t,y,u)+b(t,y,u)\big]+\frac{1}{2}h(t,y)p(t,y,u)\le -c(\|y\|)$$

whenever $\|y\|> V^i(t,w^i)\geq \rho(\|u\|)$ for some $\rho\in \mathcal{K}$ and i ;

(ii):

For any $\tau_k\in\mathbb{T}$ and $y\in \mathbb{PC}(\mathbb{R}_+;\mathbb{R}^l)$ , $U(\tau_k, y(\tau_k))=\alpha(d_k) U(\tau_k^-, y(\tau_k^-)).$

Then, comparison system $(</i> <InternalRef RefID="Equ4">4</InternalRef> <Emphasis Type="Italic">)$ , and hence composite system $(</Emphasis> <InternalRef RefID="Equ3">3</InternalRef> <i>)$ are ISS in m.s.

Proof

Let $y\geq 0$ be the solution of $(<InternalRef RefID="Equ4">4</InternalRef>)$. Applying the Itô formula to U gives

$$\begin{aligned} \mathcal{L}U(t,y,u)\le -c(\|y\|), \mbox{whenever} \|y\|\geq \rho(\|u\|).\end{aligned}$$

By the previous analysis, $(<InternalRef RefID="Equ4">4</InternalRef>)$ has the desired stability property. As for the composite system $(<InternalRef RefID="Equ3">3</InternalRef>)$, we have shown in Theorem 1 that $V(t,x(t))< y(t)$ holds for all $t\geq t_0$, and, from (i), we obtain $\|y\|> \|V(t,x)\|\geq V^i(t,w^i)\geq \rho(\|u\|)$. It follows that

$$\begin{aligned} c(\|x(t)\|^2)\le \Big[\sum_{i=1}^lc_i^2(\|w^i\|^2)\Big]^{1/2}\le \|V(t,x(t))\|< \|y(t)\|, \qquad c\in \mathcal{K}_1.\end{aligned}$$

Taking the mathematical expectation and applying c ^-1 implies the desired result.

3.1 Application. Control system

Example 1

Consider the control system, which describes the longitudinal motion of an aircraft. This example is a modification of Example 4.6.1 in [5].

$$\left\{\begin{array}{ll} dx=Axdt+bf(y){d}t+\sigma_{11}(x(t-1)){d}W_1+\sigma_{12}(y){d}W_2,\qquad t\not=\tau_k,\\dy=\big(-\zeta y-\xi f(y)+u\big){d}t+a^Tx{d}t+\sigma_{21}(x){d}W_1 +\sigma_{22}(y(t-1)){d}W_2,t\not=\tau_k,\end{array} \right.$$

(5)

where $x^T=(x_1,x_2,x_3,x_4)$ is the system state, $y\in \mathbb{R}$ is the controller (i.e., $n_1=4,\, n_2=1$), $A\in \mathbb{R}^{4\times 4}$, $b\in \mathbb{R}^4$, $\zeta, \xi\in\mathbb{R}$, $f\in \mathbb{R}$ is continuous for all $y\in \mathbb{R}$, $f(y)=0$ if and only if y = 0, and $0<yf(y)< k|y|^2$ for all $y\not=0$ and $k>0$, $u\in \mathbb{R}$, $a\in \mathbb{R}^4$, $\sigma_{11}\in \mathbb{R}^{4\times 4}$, $\sigma_{12}\in \mathbb{R}^{1\times 1}$, $\sigma_{21}\in \mathbb{R}^{4\times 1}$, $\sigma_{22}\in \mathbb{R}^{1\times 1}$, $W_1\in \mathbb{R}^4$, and $W_2\in\mathbb{R}$. Let

$$\begin{aligned} A= \left(\begin{array}{cccc} -5 & 0 & 0 & 0\\ 0 & -6 & 0 &0\\ 0 &0 &-8 &0\\ 0&0 &0 &-10\end{array}\right), \sigma_{11}=0.01 \left(\begin{array}{cccc} \sin x_1(t-1) & 0 & \frac{x_2(t-1)}{1+x^2_4} & 0\\ 0 & \frac{x_2(t-1)}{1+x_1^2} & 0 &-x^2_3(t-1)\\ 0 &0 &x_3(t-1) &0\\ 0&0 &0 &-x_4(t-1)\end{array} \right),\end{aligned}$$

$b^T=(1,1,1,1)$, $a^T=(1,1,1,1)$, $\zeta=5$, $\xi=2$, $\sigma_{12}=\frac{0.01y}{1+y^2}$, $\sigma^T_{21}=0.01(x_2,x_1,x_4,x_3)$, $\sigma_{22}=0.01\sin y(t-1)$, and $u(t)=\sin(t)$. The impulses are given by

$$\left\{\begin{array}{ll} \Updelta x(\tau_k)= \mathcal{I}_1(\tau_k, x(\tau_k^-))= \frac{1}{k^2}\big(-2x_1(\tau^-_k),-2x_2(\tau^-_k),2x_3(\tau^-_k),0\big)^T,&\\\Updelta y(\tau_k)=\mathcal{I}_2 (\tau_k,y(\tau_k^-))=-\frac{1}{1+k^2}y(\tau^-_k).&\end{array} \right.$$

(6)

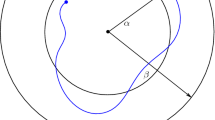
Let $V^1(x)=\|x\|^2$ and $V^2(y)=y^2$. One can show the conditions are satisfied with $\tau_{k+1}-\tau_k\ge 0.6$ [2], i.e., ${(x^{T},y)^T}\equiv(0^T,0)$ is exponentially stable in the m.s. Applying the disturbance $u(t)=\sin(t)$, the composite system is ISS in m.s. See Fig. 1 (left).

Fig. 1

Mean square input-to-state stability (left) and stabilization (right) of $(x^(T),y)^T$ where $u(t)=\sin(t)$.

Example 2

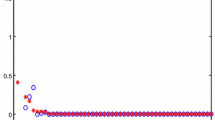
Reconsider the control composite continuous system (5) with unstable state subsystem in which the entry a ₁₁ of matrix A is changed to 5, and the impulsive difference equations are defined by $\Updelta x(\tau_k)=-\frac{5}{4}x(\tau_k^-), \Updelta y(\tau_k)=-\frac{5}{4}y(\tau_k^-)$. Then, one gets $\tau_k-\tau_{k-1}< 0.33$ for all k. That is, the solution has been stabilized by the impulsive effects. See Fig. 1 (right).