Sliding Mode Control Scheme of Variable Speed Wind Energy Conversion System Based on the PMSG for Utility Network Connection

Abstract

The study of a Variable Speed Wind Energy Conversion System (VS-WECS) based on Permanent Magnet Synchronous Generator (PMSG) and interconnected to the electric network is presented. The system includes a wind turbine, a PMSG, two converters and an intermediate DC link capacitor. The effectiveness of the WECS can be greatly improved by using an appropriate control. Furthermore, the system has strong nonlinear multivariable with many uncertain factors and disturbances. Accordingly, the proposed control law combines Sliding Mode Variable Structure Control (SM-VSC) and Maximum Power Point Tracking (MPPT) control strategy to maximize the generated power from Wind Turbine Generator (WTG). Considering the variation of wind speed, the grid-side converter injects the generated power into the AC network, regulates DC-link voltage and it is used to achieve unity power factor, whereas the PMSG side converter is used to achieve Maximum Power Point Tracking (MPPT). Both converters used the sliding mode control scheme considering the variation of wind speed. The employed control strategy can regulate both the reactive and active power independently by quadrature and direct current components, respectively. With fluctuating wind, the controller is capable to maximize wind energy capturing. This work explores a sliding mode control approach to achieve power efficiency maximization of a WECS and to enhance system robustness to parameter variations. The performance of the system has been demonstrated under varying wind conditions. A comparison of simulation results based on SMC and PI controller is provided. The system is built using Matlab/Simulink environment. Simulation results show the effectiveness of the proposed control scheme.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

During the last few decades, the progress in the use of renewable green energy resources is becoming the key solution to the environment contamination caused by the traditional energy sources and to the serious energy crisis (Tseng et al. 2014; Chou et al. 2014). Thus, power generation systems based on renewable energy are making more and more contributions to the total energy production all over the world (He et al. 2014; Guo et al. 2014). On the other hand, among available renewable energy technologies, wind energy source is the most promising options, as it is omnipresent, environmentally friendly, and freely available (Chen et al. 2013a). Compared to other types, wind energy system is regarded as an important renewable green energy resource, mainly as a consequence of its high reliability and cost effectiveness. So, wind energy conversion, has become a fast increasing energy source in the global market (Ma et al. 2014; She et al. 2013). In addition, it is predicted that the wind power system could be supplying 29.1 % of the world energy by 2030 and higher later on (Meng et al. 2013). Consequently, this increasing trend must be accompanied by continuous technological advance and optimization, leading to better options concerning integration to the electric network, reductions in expenses, and improvements concerning turbine performance and dependability in the electricity deliverance (Che et al. 2014; Wang et al. 2014; Nguyen et al. 2014).

In addition, wind energy source could be utilized by mechanically converting it to electrical energy using wind turbine (WT). During the last two decades, various WT concepts have been developed into wind power technologies and led to significant augmentation of wind power capacity. Wind turbine systems can be classified into two main types: fixed speed and variable speed. The fixed velocity system operates almost at constant speed even in variable wind speed which allows direct connection of the generator to the electric network. Recently, fixed speed wind energy conversion systems, due to poor power quality, poor energy capture and stress in mechanical parts have given way to variable velocity systems (Meng et al. 2013). Furthermore, variable speed wind generation system has distinct advantages over fixed-speed generation system, such as lower mechanical stress, operation at maximum power point, less power fluctuation and increased energy capture (Chen et al. 2013a; Li et al. 2012). So, to design reliable and effective systems to utilize this energy, variable speed wind generation systems are better then fixed velocity systems. This is due to the fact that variable velocity systems can accomplish reliability at all wind speeds and the maximum efficiency, improved electric network disturbance rejection characteristics, and the reduction of the flicker problem (Patil and Bhosle 2013; Melo et al. 2014; Li et al. 2013).

Fig. 1

Evolutions of wind turbine dimension and the corresponding capacity coverage by power electronics converters seen from 1980 to 2018 (estimated)

In the field of wind energy generation technology, Permanent Magnet Synchronous Generator (PMSG) and Doubly Fed Induction Generators (DFIG) are emerging as the preferred equipment which is used to transform the wind power into electrical energy (Nian et al. 2014; Zhang et al. 2013; She et al. 2013; Tong et al. 2013; Chen et al. 2013b). At present, one of the troubles associated with VS-WECS is the existence of gearbox coupling the generator to the wind turbine and which causes problems. So, the gearbox suffers from faults and requires regular maintenance (Cheng et al. 2009; Najafi et al. 2013). In contrast, PMSG with higher numbers of poles has been used to eliminate the need for gearbox which can be translated into higher generation efficiency (Orlando et al. 2013). Besides, wind power generation based on the PMSG has gained increasing popularity due to several advantages, including its higher power density and better controllability, the elimination of a dc excitation system, low maintenance requirements, higher efficiency compared to other kinds of generators and low energy loss (Alizadeh et al. 2013; Xia et al. 2013; Alshibani et al. 2014; Zhang et al. 2014). Besides, the performance of PMSG equipment has been improving and the price has been decreasing recently (Yaramasu et al. 2013). Therefore, it has been considered a promising candidate for new designs in Wind Energy Conversion Systems (WECS). With those advantages, PMSGs are attracting great attention and interests all over the world. So, some of them have become commercially accessible, for example, Enercon E70 (2.5 MW), Vestas V112 (3.0 MW) and Goldwind 1.5 MW series products (Cárdenas et al. 2013; Yaramasu et al. 2013).

To control the PMSG based WECS, power electronic converter systems are commonly adopted as the interface between the WECS and the power grid (Blaabjerg et al. 2013; Ma et al. 2013). They give the ease for integrating the WECS units to achieve high performance and efficiency when connected to the electric network (Cespedes et al. 2014). Thus, the wind power converters have various power rating coverages of the WECS (Blaabjerg et al. 2013), as shown in Fig. 1. Then, under variable speed operation, the power converters are used to transfer the PMSG output power in the form of variable frequency and variable voltage to the fixed frequency also fixed voltage electric network (Vazquez et al. 2014; Ma et al. 2014). Several power converter configurations were presented in the literature for PMSG based WECS (Nuno et al. 2014; Li et al. 2013; Xia et al. 2013).

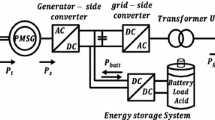
Figure 2 shows the schematic diagram of a typical WECS connected to an electric network. The power electronic conversion system consists of a back-to-back PWM power converter which is composed of a PMSG side converter, a grid-side converter and a dc link. The capacitor decoupling, offers the opportunity of separate control for each power converter. The generator side converter works as a rectifier and it is used to control the torque, the speed or power for PMSG (Chen et al. 2013b; Giraldo et al. 2013; Xin et al. 2013). The grid side converter works as an inverter. The main role of the inverter is to remain the dc-link voltage constant and to synchronize the ac power generated by the WECS with the electric network (Alizadeh et al. 2013; Zhang et al. 2014). Besides, the inverter should have the capability of adjusting active and reactive power that the WECS exchange with the power grid and achieve unity power factor of the system (Nguyen et al. 2013).

On the other hand, to increase the annual energy yield of wind energy conversion system (WECS), Maximum Power Point Tracking (MPPT) control is necessary at below the rated wind velocity. The MPPT technique enables operation of the turbine system at its maximum wind power coefficient over a wide range of wind velocities. Consequently, maximum power can be extracted from available wind power by adjusting the rotational velocity of the PMSG according to the varying in wind speed (Chen et al. 2013c; He et al. 2013; Elkhatib et al. 2014). In addition, it is vital to control and limit the converted mechanical power during higher wind velocities and when the turbine output is above the nominal power (Alizadeh et al. 2013; Melo et al. 2014). The power limitation may be done either by pitch control, stall control, or active stall (Polinder et al. 2007; Spruce et al. 2013). Figure 2 shows the general control structure for modern WECS.

Fig. 2

Control of active and reactive power in a WECS based PMSG

With high penetration of wind power resources in the modern electric network, the power quality from WECS is attracting great attention and interests all over the world (Nguyen et al. 2013). The recent development has been focused mainly on control methodologies for maximum electrical power production (Karthikeya et al. 2014). Accordingly, various control methods have been proposed. Conventional design of WECS control systems is based on Vector Control with d–q decoupling (Xin et al. 2013; Alepuz et al. 2013; Shariatpanah et al. 2013). The control strategy involves relatively complex transformation of currents, voltages and control outputs. Also, the standard design methods consist of properly tuned proportional integral (PI) controllers. Thus, the performance highly relies on the modification of the PI parameters (Chen et al. 2013a; Giraldo et al. 2013; Corradini et al. 2013). So, this technique requires accurate information of WECS parameters. Consequently, the performance is degraded when the actual system parameters differ from those values used in the control system. In addition, VC requires complex reference transformation. Due to the advantages of simple structure and low dependency on the parameters, direct control techniques such as Direct Power Control (DPC) and Direct Torque Control (DTC) were widely used into the WECS (Rajaei et al. 2013; Zhang et al. 2013; Harrouz et al. 2013). They are an alternative to the VC control for WECS because they reduce the complexity of the VC strategy and minimize the employ of generator parameters. The voltage vectors are selected directly according to the differences between the reference and actual value of torque and stator flux or between active and reactive power. Consequently, the converter switching states were selected from an optimal switching table. Besides, DPC and DTC do not necessitate coordinate transformations, specific modulations and current regulators. But, there are high ripples in flux/torque or reactive/active powers at stable state and the switching frequency is variable with operating point due to the employ of predefined switching table and hysteresis regulator (Rajaei et al. 2013). Also, its performance deteriorates during very low speed operation.

For WECS integration into power network and, because the VC and direct control techniques show a limited performances, especially against uncertainties and cannot follow the changes in WECS parameters (Leonhard 1990), Sliding Mode Control approach (SMC) can be used. It has low sensitivity with respect to uncertainty, dynamic performance and good robustness (Slotine and Li 1991; Utkin 1993; Utkin et al. 1999; Sabanovic et al. 2002; Evangelista et al. 2013a). It is one of the powerful control approaches for systems with unknown trouble and uncertainties (Li et al. 2013a, b). Besides, SMC is insensitive to parameter variations of systems. Thus, SMC is suitable for wind power applications (Evangelista et al. 2013a, b; Huang et al. 2013; Susperregui et al. 2013) propose sliding mode control to maximize the energy production of a WECS. Subudhi et al. (2012), Xiao et al. (2013) propose a pitch control based siding mode approach to control the extracted power above the rated wind speed. Xiao et al. (2011), Martinez et al. (2013) introduce sliding mode regulator to control the WECS for fault conditions. Chen et al. (2013), Bouaziz and Bacha (2013), Guzman et al. (2013) present a sliding mode control methodology of power converters.

Among the main research subjects in the WECS field, there is the study of novel control methodologies which can maintain MPPT despite the effects of the parameter variations of system, uncertainties in both the electrical and the aerodynamic models and variations of wind speed. In this context, this chapter presents proposes a nonlinear power control strategy for a grid connected VS-WECS topology based on Permanent Magnet Synchronous Generator (PMSG). The schematic diagram of proposed system is shown in Fig. 3. The system under consideration employs WECS based PMSG with a back-to-back voltage source converter (VSC). The generator side converter is employed to control the speed of the PMSG with MPPT. The grid-side converter is used in order to control the DC link voltage and to regulate the power factor during wind variations. This work explores a sliding mode control approach to achieve power efficiency maximization of a WECS and to enhance system robustness to parameter variations. Also, a pitch control scheme for WECS is proposed so as to prevent wind turbine damage from excessive wind velocity.

The rest part of the study is organized as follows. In Sect. 2, the models of the wind turbine system and the PMSG are developed. SMC strategy for WECS is proposed, designed, and analyzed in Sect. 3. Section 4 presents the simulation results to demonstrate the performance of the proposed SMC strategy. Finally, the conclusion is made in Sect. 5.

Fig. 3

Schematic of control strategy for WECS

2 Modelling Description of WECS

The block diagram of proposed WECS is shown in Fig. 3. So, it is seen that the system consists of different components including: wind turbine, PMSG, voltage source converter, and controllers. The wind turbine is used to capture the wind energy that is converted to the electricity by PMSG with variable frequency. Consequently, the generated voltages are rectified by a rectifier and an inverter. The extracted power will be transferred to the grid through a filter.

2.1 Wind Turbine

Wind turbine is used to convert the wind power to a mechanical power. The power generated by a wind turbine can be written as Chen et al. (2013a):

$$\begin{aligned} P_{Turbine} =\frac{1}{2}\rho AC_P (\lambda ,\beta )\nu ^{3} \end{aligned}$$

(1)

where, $P_{Turbine}$ is the mechanical power of the turbine in watts, $\rho$is the air density (typically 1.225 kg/m$^{3 })$, $A$ is the area swept by the rotor blades (in m$^{2})$, $C_P$ is the power performance coefficient of the turbine, $v$ is the wind velocity (in m/s), $\beta$ is the turbine blade pitch angle, and $\lambda$ is the Tip Speed Ratio (TSR). Thus, if the air density, swept area and wind speed are constants, the output aerodynamic power is determined by the power performance coefficient of wind turbine system.

The wind turbine mechanical torque output $T_m$ given as:

$$\begin{aligned} T_m =\frac{1}{2}\rho AC_P (\lambda ,\beta )\nu ^{3}\frac{1}{\omega _m } \end{aligned}$$

(2)

In addition, $C_P$ is influenced by the tip-speed ratio $\lambda$ which is defined as the ratio between the rotor blade tip and the speed of the wind, and is given by Errami et al. (2013):

$$\begin{aligned} \lambda =\frac{\omega _m R}{v} \end{aligned}$$

(3)

where $\omega _m$ and $R$ are the rotor angular speed (in rad/sec) and the radius of the swept area by turbine blades (in m), respectively. The computation of the power performance coefficient $C_P$ requires the use of the information of blade geometry and blade element theory. Consequently, these complex issues are usually empirical considered and a generic equation is used so as to model the power performance coefficient $C_P (\lambda ,\beta )$ based on the modeling turbine system characteristics described in Errami et al. (2013) as:

$$\begin{aligned} C_P&=\frac{1}{2}(\frac{116}{\lambda _i }-0.4\beta -5)e^{-(\frac{21}{\lambda _i })} \nonumber \\ \frac{1}{\lambda _i}&= \frac{1}{\lambda +0.08\beta }-\frac{0.035}{\beta ^{3}+1} \end{aligned}$$

(4)

where $\beta$ is the blade pitch angle (in degrees). $C_P$ is a nonlinear function of both blade pitch angle ($\beta )$ and the tip speed ratio ($\lambda )$.

The $C_P (\lambda ,\beta )$ characteristics, for various values of the pitch angle $\beta$ , are illustrated in Fig. 4. The maximum value of $C_P$, that is $C_{P\max } =0.41$, is achieved for $\lambda _{opt} =8.1$ and for $\beta =0$. According to Fig. 4, there is one specific $\lambda$ at which the turbine is most efficient. This optimal value of $C_P$ occurs in different values of $\lambda$. Consequently, if $\beta$ is fixed, there is an optimal value $\lambda _{opt}$ at which the turbine system follows the $C_{P\max }$ to capture the maximum power up to the rated velocity by adjusting rotor speed. Besides, if wind speed is supposed constant, $C_P$ value will be dependent on rotor velocity of the wind turbine. Accordingly, for a given wind velocity, there is an optimal value for rotor velocity which maximizes the power supplied by the wind. If the PMSG velocity can always be controlled to make the turbine operate under optimum tip-speed-ratio $\lambda _{opt}$ during wind velocity variations, then the power coefficient reaches its maximum value $C_{P\max }$. That is equally saying, the turbine system realizes Maximum Power Point Tracking (MPPT) function (Chen et al. 2013c).

Fig. 4

Characteristics $C_p$ versus $\lambda$; for various values of the pitch angle $\beta$

Then, for a given wind velocity the system can operate at the peak of the $P(\omega _m )$ curve and the maximum power is extracted continuously from the wind. Consequently, the curve connecting the peaks of these curves will generate the maximum output power and will follow the path for maximum power operation. That is illustrated in Fig. 5.

When the rotor velocity is adjusted to maintain its optimal value, the maximum power can be gained as:

$$\begin{aligned} {P_{Turbine}} =\frac{1}{2}\rho _{{AC}_{\text {Pmax}}}\nu ^{3} \end{aligned}$$

(5)

Fig. 5

Wind generator power curves at various wind speed

2.2 Mathematical Model of the PMSG

The PMSG dynamic model is given in a rotative frame (dq) where the d axis is aligned with the rotor flux. So, the generator model in the d-q frame can be described by the following equations. The electrical equations of the PMSG are shown in (6), (7)and (8), the torque equation in (9) and the mechanical equation in (10) (Shariatpanah et al. 2013).

$$\begin{aligned} v_{gq} =R_g i_q +\omega _e \phi _d +\frac{d}{dt}\phi _q \end{aligned}$$

(6)

$$\begin{aligned} v_{gd} =R_g i_d -\omega _e \phi _q +\frac{d}{dt}\phi _d \end{aligned}$$

(7)

The quadratic and direct magnetic flux are given by:

$$\begin{aligned} \phi _q&= L_q i_q \nonumber \\ \phi _d&= L_d i_d +\psi _f \end{aligned}$$

(8)

$$\begin{aligned} T_e =\frac{3}{2}p_n \left[ {\psi _f i_q +\left( {L_d -L_q } \right) i_d i_q } \right] \end{aligned}$$

(9)

$$\begin{aligned} J\frac{d\omega _m }{dt}=T_e -T_m -F\omega _m \end{aligned}$$

(10)

The electrical rotating speed of the PMSG, $\omega _e$ is defined as:

$$\begin{aligned} \omega _e =p_n \omega _m \end{aligned}$$

(11)

where

$v_{gq}, v_{gd}$ stator voltage in the dq frame;

$i_q, i_d \quad \;\,\,$stator current in the dq frame;

$L_q , L_d\;\,\,$inductances of the generator on the q and d axis;

$R_g\quad \quad \;\,\,$stator resistance;

$\psi _f\quad \quad \;\,$ permanent magnetic flux;

$\omega _e\quad \quad \quad$electrical rotating speed of the PMSG;

$p_n\quad \quad \quad$machine pole pairs;

$J\quad \quad \quad \;$ total moment of inertia of the system (turbine-generator);

$F\quad \quad \quad$ viscous friction coefficient;

$T_m\quad \quad \quad$mechanical torque developed by the turbine.

Thus,

$$\begin{aligned} \frac{di_q }{dt}=\frac{1}{L_q }(v_{gq} -R_g i_q -\omega _e L_d i_d -\omega _e \psi _f ) \end{aligned}$$

(12)

$$\begin{aligned} \frac{di_d }{dt}=\frac{1}{L_d }(v_{gd} -R_g i_d +\omega _e L_q i_q ) \end{aligned}$$

(13)

If the PMSG is assumed to have equal d-axis, q-axis in inductances ($L_q =L_d =L_s)$, the expression for the electromagnetic torque can be described as:

$$\begin{aligned} T_e =\frac{3}{2}p_n \left[ {\psi _f i_q } \right] \end{aligned}$$

(14)

3 Control Strategy of the WECS

3.1 Adopted MPPT Control Algorithm

The reference velocity of the PMSG corresponding to the maximum power extractable from the wind turbine system at a given wind speed is retrieved by the MPPT technique. This algorithm is operated when the wind speed is below the threshold. Then, for each instantaneous wind velocity, the PMSG optimal rotational speed $\omega _{m-opt}$ can be computed on the basis of the following expression (Zhang et al. 2014):

$$\begin{aligned} \omega _{m-opt} =\frac{v\lambda _{opt} }{R} \end{aligned}$$

(15)

Each wind turbine can produce maximum power by (5). Therefore, the maximum mechanical output power of the turbine system is given as follows:

$$\begin{aligned} P_{Turbine\_\max } =\frac{1}{2}\rho AC_{P\max } \left( {\frac{R\omega _{m-opt} }{\lambda _{opt} }} \right) ^{3} \end{aligned}$$

(16)

Accordingly, we can get the maximum power $P_{Turbine\_\max }$ by regulating the turbine velocity in different wind speed under rated power of the WECS. In addition, if the speed of generator can always be controlled in order to make turbine system work under optimum tip speed ratio $\lambda _{opt}$, regardless of the wind velocity, then the power coefficient reaches its maximum value $C_{P\max }$ (Kuschke et al. 2014). The $P_{{ MPPT}}$ curve is defined as function of $\omega _{m-opt}$, the speed referred to the generator side:

$$\begin{aligned} P_{{ MPPT}} =K\omega _{m-opt}^3 \end{aligned}$$

(17)

$$\begin{aligned} K=\frac{1}{2}\rho AC_{P\max } \left( {\frac{R}{\lambda _{opt} }} \right) ^{3} \end{aligned}$$

(18)

$K$ depends on the blade aerodynamics and wind turbine parameters. The MPPT controller system computes this optimal speed $\omega _{m-opt}$ and an optimum value of tip speed ratio $\lambda _{opt}$ can be maintained. Thus, maximum wind power of the turbine can be captured. Depending on the wind velocity, the MPPT algorithm regulates the electric output power, bringing the turbine system operating points onto the “maximum power point,” like in Fig. 5 (Errami et al. 2013).

3.2 Pitch Angle Control System

At wind velocities below the rated power area, the wind turbine system regulator maintains the power performance coefficient $C_P$ of the turbine at its maximum. But, at higher wind velocities, the power coefficient decreases to limit the turbine speed. So, most high power wind turbine systems are equipped with pitch control to achieve power limitation, and where wind speed is low or medium, the pitch angle is controlled to allow turbine system to operate at its optimum condition. On the contrary for high wind speeds, the pitch control is active and it is designed to prevent wind turbine system damage from excessive wind speed (Polinder et al. 2007). This means that, when the wind speed reaches the rated value, the pitch angle controller enters in operation to decrease the performance coefficient of power. The angle of blades $\beta$, will increase until the wind turbine system is at the rated velocity. Figure 6 illustrates the schematic diagram of the implemented turbine blade pitch angle controller. $P_g$ is the generated power.

Fig. 6

WECS Pitch angle controller

3.3 Sliding Mode Control (SMC) and MPPT Algorithm for Generator Side converter

The generator side converter controls the PMSG rotational speed to produce the maximum power extractable from the wind turbine system. Thus, the generator side three phase converter is used as a rectifier and it is used to keep the PMSG velocity at an optimal value obtained from the MPPT algorithm. This controller makes the WECS working at highest efficiency. The proposed control strategy for the generator side converter is based on SMC methodology. The adopted MPPT algorithm generates $\omega _{m\_opt}$, the reference speed. On the other hand, it is deduced from equations (10) and (14) that the generator velocity can be controlled by regulating the q-axis stator current component ($i_{qr} )$.

According to the theory of SMC, the error of PMSG speed is selected as sliding surface:

$$\begin{aligned} S_\omega =\omega _{m\_opt} -\omega _m \end{aligned}$$

(19)

$\omega _{m\_opt}$is generated by a MPPT controller.

Consequently:

$$\begin{aligned} \frac{dS_\omega }{dt}=\frac{d\omega _{m\_opt} }{dt}-\frac{d\omega _m }{dt} \end{aligned}$$

(20)

Using (10), the time derivative of $S_\omega$ can be calculated as:

$$\begin{aligned} \frac{dS_\omega }{dt}=\frac{d\omega _{m\_opt} }{dt}-\frac{1}{J}(T_e -T_m -F\omega _m ) \end{aligned}$$

(21)

When the trajectory of PMSG speed coincides with the sliding surface (Evangelista et al. 2013a),

$$\begin{aligned} S_\omega =\frac{dS_\omega }{dt}=0 \end{aligned}$$

(22)

In order to obtain commutation around the sliding surface, each component of the control algorithm is proposed to be calculated as the addition of two terms (Evangelista et al. 2013b):

$$\begin{aligned} u_c =u_{eq} +u_n \end{aligned}$$

(23)

where $u_{eq}$ is the equivalent control concept of a sliding surface. It is the continuous control that allows the continuance of the state trajectory on the sliding surface. The expression for the equivalent control term is obtained from the equation formed by equalling to zero the first time derivative of $S_\omega$. As a result, during the sliding mode and in permanent regime, $u_{eq}$ is calculated from the expression:

$$\begin{aligned} \frac{dS_\omega }{dt}=0 \end{aligned}$$

(24)

Although, $u_n$ is used so as to guarantee the attractiveness of the variable to be controlled towards the commutation sliding mode surface. So, it maintains the state on the sliding surface in the presence of the parametric variations and external disturbances for all subsequent time. Also, the system state slides on the sliding surface until it reaches the equilibrium point. Then it is restricted to the surface

$$\begin{aligned} u_n =k_\omega \mathrm{sgn}(S_\omega ) \end{aligned}$$

(25)

where $k_\omega$ is a positive constant, which is the gain of the sliding mode regulator. $u_n$ keeps the system dynamic on the sliding surface $S_\omega =0$ for all the time.

Moreover, SMC is a discontinuous control. So as to reduce the chattering, the continuous function as exposed in (26) where $\mathrm{sgn}(S_\omega )$ is a sign function defined as (Xiao et al. 2011):

$$\begin{aligned} \mathrm{sgn}(S_\omega )=\left\{ {\begin{array}{ll} 1 &{}\quad S_\omega \succ \varepsilon \\ \frac{S_\omega }{\varepsilon } &{}\quad \varepsilon \ge \left| {S_\omega } \right| \\ -1 &{}\quad -\varepsilon \succ S_\omega \\ \end{array}} \right. \end{aligned}$$

(26)

where $\varepsilon$ the width of the boundary layer. It is a small positive number and it should be chosen attentively, otherwise the dynamic quality of the system will be reduced.

On the other hand, to ensure the PMSG speed convergence to the optimal velocity and to reduce the copper loss by setting the d axis current to be zero, current references are derived. Based on equations (10), (14), (19), (22), (23), (24) and (25), the following equation for the system of speed can be obtained:

$$\begin{aligned} i_{qr} =\frac{2}{3p_n \psi _f }(T_m + J\frac{d\omega _{m\_opt} }{dt} + F \omega _m + Jk_\omega \mathrm{sgn}(S_\omega )) \end{aligned}$$

(27)

where $k_\omega \succ 0$.

$$\begin{aligned} i_{dr} =0 \end{aligned}$$

(28)

In addition, from (21) the following equation can be deduced:

$$\begin{aligned} S_\omega \frac{dS_\omega }{dt}&= S_\omega \frac{d\omega _{m\_opt} }{dt}-\frac{S_\omega }{J}(T_e -T_m -F\omega _m ) \nonumber \\&= -k_\omega S_\omega \mathrm{sgn}(S_\omega )+\frac{S_\omega }{J}(T_m -\frac{3}{2}p_n \psi _f i_q +F\omega _m +Jk_\omega \mathrm{sgn}(S_\omega )+J\frac{d\omega _{m\_opt} }{dt}) \end{aligned}$$

(29)

Then, to regulate the currents components $i_d$ and $i_q$ to their references, it is necessary to define the sliding surfaces, as follows:

$$\begin{aligned} S_d =i_{dr} -i_d \end{aligned}$$

(30)

$$\begin{aligned} S_q =i_{qr} -i_q \end{aligned}$$

(31)

Substituting (12) and (13) into above equations gives:

$$\begin{aligned} \frac{dS_d }{dt}=\frac{di_{dr} }{dt}-\frac{di_d }{dt}=-\frac{1}{L_s }(v_{gd} -R_g i_d +L_s \omega _e i_q ) \end{aligned}$$

(32)

$$\begin{aligned} \frac{dS_q }{dt}&= \frac{di_{qr} }{dt}-\frac{di_q }{dt} \nonumber \\&= \frac{di_{qr} }{dt} - \frac{1}{L_s }(v_{gq} -R_g i_q -L_s \omega _e i_d -\omega _e \psi _f) \end{aligned}$$

(33)

when the sliding mode occurs on the sliding mode surfaces:

$$\begin{aligned} S_q =\frac{dS_q }{dt}=0 \end{aligned}$$

(34)

$$\begin{aligned} S_d =\frac{dS_d }{dt}=0 \end{aligned}$$

(35)

Consequently, the control voltages of q axis and d axis are defined by:

$$\begin{aligned} v_{qr} =R_g i_q +L_s \omega _e i_d +\omega _e \psi _f + L_s \frac{di_{qr} }{dt} + L_s k_q \mathrm{sgn}(S_q) \end{aligned}$$

(36)

$$\begin{aligned} v_{dr} =R_g i_d -L_s \omega _e i_q +L_s k_d \mathrm{sgn}(S_d ) \end{aligned}$$

(37)

where $k_q \succ 0$ and $k_d \succ 0$.

In addition:

$$\begin{aligned} S_d \frac{dS_d }{dt}&= S_d \left[ {-\frac{1}{L_s }(v_{gd} -R_g i_d +L_s \omega _e i_q )} \right] \nonumber \\&= -k_d S_d \mathrm{sgn}(S_d ) + \frac{S_d }{L_s }\left[ {-v_{gd} +R_g i_d -L_s \omega _e i_q +L_s k_d \mathrm{sgn}(S_d )} \right] \end{aligned}$$

(38)

$$\begin{aligned} S_q \frac{dS_q }{dt}&= S_q \left[ {\frac{di_{qr} }{dt}-\frac{di_q}{dt}}\right] \nonumber \\&=-k_q S_q \mathrm{sgn}(S_q ) + \frac{S_q }{L_s} \left[ L_s \frac{di_{qr}}{dt}-v_{gq} +R_g i_q +L_s \omega _e i_d +\omega _e \psi _f + L_s k_q \mathrm{sgn}(S_q)\right] \end{aligned}$$

(39)

Theorem 1

If the dynamic sliding mode control laws are designed as (27), (28), (36) and (37), therefore the global asymptotical stability is ensured.

Proof

The proof of the theorem 1 will be carried out using the Lyapunov theory of stability. To determine the required condition for the existence of the sliding mode, it is fundamental to design the Lyapunov function. So, the Lyapunov function can be chosen as (Evangelista et al. 2013b):

$$\begin{aligned} \Upsilon _1 =\frac{1}{2}S_\omega ^2 +\frac{1}{2}S_q^2 +\frac{1}{2}S_d^2 \end{aligned}$$

(40)

From Lyapunov theory of stability, to ensure controller stability and convergence of the state trajectory to the sliding mode, $\Upsilon _1$ can be derived that (Huang et al. 2013),

$$\begin{aligned} \frac{d\Upsilon _1 }{dt}\prec 0 \end{aligned}$$

(41)

According to the definition of $\Upsilon _1$, the time derivative of $\Upsilon _1$ can be calculated as:

$$\begin{aligned} \frac{d\Upsilon _1 }{dt}=S_\omega \frac{dS_\omega }{dt}+S_d \frac{dS_d }{dt}+S_q \frac{dS_q }{dt} \end{aligned}$$

(42)

Using Equations (29), (38) and (39), we can rewrite (42) as:

$$\begin{aligned} \frac{d\Upsilon _1 }{dt}&= -k_\omega S_\omega \mathrm{sgn}(S_\omega )+\frac{S_\omega }{J}(T_m -\frac{3}{2}p_n \psi _f i_q +F\omega _m +Jk_\omega \mathrm{sgn}(S_\omega )+J\frac{d\omega _{m\_opt} }{dt}) \nonumber \\&\quad -k_d S_d \mathrm{sgn}(S_d ) + \frac{S_d }{L_s }\left[ {-v_{gd} +R_g i_d -L_s \omega _e i_q +L_s k_d \mathrm{sgn}(S_d )} \right] \nonumber \\&\quad -k_q S_q \mathrm{sgn}(S_q ) + \frac{S_q }{L_s }\left[ {L_s \frac{di_{qr} }{dt}-v_{gq} +R_g i_q +L_s \omega _e i_d +\omega _e \psi _f + L_s k_q \mathrm{sgn}(S_q) } \right] \end{aligned}$$

(43)

Substituting (27), (36) and (37) into above equation gives:

$$\begin{aligned} \frac{d\Upsilon _1 }{dt}=-k_\omega S_\omega \mathrm{sgn}(S_\omega )-k_d S_d \mathrm{sgn}(S_d )-k_q S_q \mathrm{sgn}(S_q ) \end{aligned}$$

(44)

As a result:

$$\begin{aligned} \frac{d\Upsilon _1 }{dt}=-k_\omega \left| {S_\omega } \right| -k_d \left| {S_d } \right| -k_q \left| {S_q } \right| \prec 0 \end{aligned}$$

(45)

Accordingly, the global asymptotical stability is ensured and the velocity control tracking is achieved.

Finally, PWM is used to generate the control signal to implement the SMC for the PMSG. The double closed-loop control diagram for generator side converter is shown as Fig. 7.

3.4 Grid Side Controller Methodology with SMC

The grid side converter (GSC) works as an inverter. The main function of the GSC is to keep constant dc bus voltage, regulates the reactive and active power flowing into the grid and to provide grid synchronization. So, it can regulate the grid side power factor during wind variation. Besides, there are many strategies used to control GSC (Yaramasu et al. 2013; Blaabjerg et al. 2013; Ma et al. 2013). In this study, Pulse Width Modulation (PWM) associated with SMC is used in order to control the converter. Double-loop structure is used: the inner control loops regulates q-axis current and d-axis current, but outer voltage loop regulates the dc-link voltage via controlling the output power. The schematic diagram of the GSC based on the proposed control strategy is shown by Fig. 7.

Fig. 7

Schematic of SMC strategy for WECS

The voltage balance across the inductor $L_f$ and $R_f$is given by:

$$\begin{aligned} \left[ {\begin{array}{l} e_a \\ e_b \\ e_c \\ \end{array}} \right] =R_f \left[ {\begin{array}{l} i_a \\ i_b \\ i_c \\ \end{array}} \right] +L_f \frac{d}{dt}\left[ {\begin{array}{l} i_a \\ i_b \\ i_c \\ \end{array}} \right] +\left[ {\begin{array}{l} v_a \\ v_b \\ v_c \\ \end{array}} \right] \end{aligned}$$

(46)

where

$e_a,e_b,e_c\quad$ voltages at the inverter system output;

$v_a,v_b,v_c\quad$ grid voltage components;

$i_a,i_b,i_c\quad \;\;$ line currents;

$L_f\quad \quad \quad \quad$ filter inductance;

$R_f\quad \quad \quad \quad$ filter resistance.

Transferring equation (46) in the rotating dq reference frame gives:

$$\begin{aligned} \frac{di_{d-f} }{dt}=\frac{1}{L_f }(e_d -R_f i_{d-f} +\omega L_f i_{q-f} -v_d ) \end{aligned}$$

(47)

$$\begin{aligned} \frac{di_{q-f} }{dt}=\frac{1}{L_f }(e_q -R_f i_{q-f} -\omega L_f i_{d-f} -v_q ) \end{aligned}$$

(48)

where

$e_d,e_q \quad \;\;\quad$ inverter d-axis and q-axis voltage components;

$v_d,v_q \quad \quad \;$ grid voltage components in the d-axis and q-axis;

$i_{d-f},i_{q-f}$ d-axis current and q-axis current of grid.

$\omega \quad \quad \quad \quad \;\;$ network angular frequency

The network angular frequency is computed by a Phase Locked Loop (PLL).

The instantaneous powers are given by:

$$\begin{aligned} P=\frac{3}{2}(v_d i_{d-f} +v_q i_{q-f} ) \end{aligned}$$

(49)

$$\begin{aligned} Q=\frac{3}{2}(v_d i_{q-f} -v_q i_{d-f} ) \end{aligned}$$

(50)

Thus, the DC-link system equation can be given by:

$$\begin{aligned} C\frac{dU_{dc} }{dt}=\frac{3}{2}(\frac{v_d }{U_{dc} }i_{d-f} +\frac{v_q }{U_{dc} }i_{q-f} )-i_{dc} \end{aligned}$$

(51)

where

$U_{dc}\quad \;$ dc-link voltage;

$i_{dc}\quad \;\;$ grid side transmission line current;

$C\quad \;\;\,\;$ dc-link capacitor.

If the grid voltage space vector $\mathop u\limits ^\rightarrow$ is oriented on d-axis, then:

$$\begin{aligned} v_d =V \, \text {and} \, v_q = 0 \end{aligned}$$

(52)

Therefore, using Eq. (52), we can rewrite Eqs. (47–48) as:

$$\begin{aligned} L_f \frac{{di_{d-f}}}{dt} = {{e}_{d}} -{R_{f}} {{i}_{d-f}} +\omega {L_{f}} {{i}_{q-f}} -V \end{aligned}$$

(53)

$$\begin{aligned} L_f \frac{{di_{q-f}}}{dt} = {e_q} -{R_f} {i_{q-f}} -\omega {L_f} {i_{d-f}} \end{aligned}$$

(54)

Also, the active power and reactive power can be expressed as:

$$\begin{aligned} P=\frac{3}{2}Vi_{d-f} \end{aligned}$$

(55)

$$\begin{aligned} Q=\frac{3}{2}Vi_{q-f} \end{aligned}$$

(56)

As a result, reactive and active power control can be achieved by controlling quadrature and direct grid current components, respectively. So, the q-axis current reference is set to zero for unity power factor, but the d-axis current is determined by dc-bus voltage controller to control the converter output active power. The GSC controller is implemented based on the electric network current d-q components, as it is depicted in Fig. 7. The control method consists of a two closed loop controls to regulate the reactive power and the dc link voltage independently. Then, the fast dynamic is associated with the line current control, in the inner loop, where the SMC is adopted to track the line current control. Moreover, in the outer loop, slow dynamic is associated with the dc-bus control. The outer control loop uses the Proportional Integral (PI) controller to generate the reference source current $i_{dr-f}$ and regulate the DC voltage, although the reference signal of the q-axis current $i_{qr-f}$ is produced by the reactive power $Q_r$according to (56).

We adopt the following surfaces for $i_{d-f}$ and $i_{q-f}$:

$$\begin{aligned} S_{d-f} =i_{dr-f} -i_{d-f} \end{aligned}$$

(57)

$$\begin{aligned} S_{q-f} =i_{qr-f} -i_{q-f} \end{aligned}$$

(58)

where $i_{dr-f}$ and $i_{qr-f}$ are the desired value of d-axis current and q-axis current, respectively. Also, $i_{dr-f}$ is produced by the loop of DC-bus control and the reference signal of the q-axis current $i_{qr-f}$, is directly given from the second loop outside of the controller and it sets to zero to reach unity power factor control.

Using equations (53) and (54), the time derivatives of $S_{d-f}$and $S_{q-f}$can be

calculated as:

$$\begin{aligned} \frac{{dS_{d-f}}}{dt} = \frac{{di_{dr-f}}}{dt} - \frac{{di_{d-f}}}{dt} = \frac{{di_{dr-f}}}{dt} - \frac{1}{L_f}({e_d}-{R_f} {i_{d-f}} +\omega {L_f}{i_{q-f}} -V) \end{aligned}$$

(59)

$$\begin{aligned} \frac{{dS_{q-f}}}{dt} = \frac{{di_{qr-f}}}{dt}-\frac{{di_{q-f}}}{dt}=\frac{{di_{qr-f}}}{dt}-\frac{1}{L_f}({e_q}-{R_f}{i_{q-f}} - \omega {L_f}{i_{d-f}}) \end{aligned}$$

(60)

when the sliding mode takes place on the sliding mode surface, then:

$$\begin{aligned} {S_{d-f}} =\frac{{dS_{d-f}}}{dt}=0 \end{aligned}$$

(61)

$$\begin{aligned} {S_{q-f}} =\frac{{dS_{q-f}}}{dt}=0 \end{aligned}$$

(62)

Combining (53), (54) and (57)–(62) the controls voltage of d axis and q axis are defined by:

$$\begin{aligned} {v_{dr-f}} ={L_f}\frac{{di_{dr-f}}}{dt}+{R_f}{i_{d-f}} -{L_f} \omega {i_{q-f}} +{V}+{L_f}{k_{d-f}} \mathrm{sgn}({S_{d-f}}) \end{aligned}$$

(63)

$$\begin{aligned} {v_{qr-f}} ={R_f}{i_{q-f}} +{L_f}\omega {i_{d-f}}+{L_f}{k_{q-f}} \text {sgn}({S_{q-f}}) \end{aligned}$$

(64)

where $k_{d-f} \succ 0$ and $k_{q-f} \succ 0$.

Besides, from (59) and (60), the following equations can be deduced:

$$\begin{aligned} {S_{d-f}} \frac{{dS_{d-f}}}{dt}&= {S_{d-f}} \left[ {\frac{{di_{dr-f}}}{dt}-\frac{1}{L_f }({e_d} -{R_f}{i_{d-f}} +{L_f}\omega {i_{q-f}} -V)} \right] \nonumber \\&=-{k_{d-f}} {S_{d-f}} \text {sgn}({S_{d-f}}) \nonumber \\&\quad + \frac{{S_{d-f}}}{L_f }\left[ {L_f} \frac{{di_{dr-f}}}{dt}-{e_d} +{R_f}{i_{d-f}} -{L_f}\omega {i_{q-f}} +V+{k_{d-f}} {L_f} \text {sgn}({S_{d-f}}) \right] \end{aligned}$$

(65)

$$\begin{aligned} {S_{q-f}} \frac{{dS_{q-f}}}{dt}&= {S_{q-f}} \left[ {-\frac{{di_{q-f}}}{dt}} \right] \nonumber \\&= -{k_{q-f}} {S_{q-f}} \text {sgn}({S_{q-f}}) \nonumber \\&\quad +\frac{{S_{q-f}}}{L_f}\left[ -{e_q} +{R_f}{i_{q-f}} +{L_f}\omega {i_{d-f}} + {k_{q-f}} {L_f} \text {sgn}({S_{q-f}}) \right] \end{aligned}$$

(66)

Theorem 2

If the Dynamic sliding mode control laws are designed as (63) and (64) therefore the global asymptotical stability is ensured.

Proof

The proof of the Theorem 2 will be carried out using the Lyapunov theory of stability. To determine the required condition for the existence of the sliding mode, it is fundamental to design the Lyapunov function. So, the Lyapunov function can be chosen as:

$$\begin{aligned} \Upsilon _2 =\frac{1}{2}S_{d-f}^2 +\frac{1}{2}S_{q-f}^2 \end{aligned}$$

(67)

From Lyapunov theory of stability, to ensure controller stability and convergence of the state trajectory to the sliding mode,$\Upsilon _2$ can be derived that,

$$\begin{aligned} \frac{d\Upsilon _2 }{dt}\prec 0 \end{aligned}$$

(68)

By differentiating the Lyapunov function (67), we obtain:

$$\begin{aligned} \frac{d\Upsilon _2 }{dt}=S_{d-f} \frac{dS_{d-f} }{dt}+S_{q-f} \frac{dS_{q-f} }{dt} \end{aligned}$$

(69)

Based on equations (65) and (66), it can be obtained:

$$\begin{aligned} \frac{d\Upsilon _2 }{dt}&= -k_{d-f} S_{d-f} \mathrm{sgn}(S_{d-f} ) \nonumber \\&\quad + \frac{S_{d-f} }{L_f }\left[ {L_f \frac{di_{dr-f} }{dt}-e_d +R_f i_{d-f} -L_f \omega i_{q-f} +V+k_{d-f} L_f \mathrm{sgn}(S_{d-f} )} \right] \nonumber \\&\quad -k_{q-f} S_{q-f} \mathrm{sgn}(S_{q-f} )+\frac{S_{q-f} }{L_f }\left[ {-e_q +R_f i_{q-f} +L_f \omega i_{d-f} + k_{q-f} L_f \mathrm{sgn}(S_{q-f} )} \right] \end{aligned}$$

(70)

Substituting (63) and (64) into above equation gives:

$$\begin{aligned} \frac{d\Upsilon _2 }{dt}=-k_{d-f} S_{d-f} \mathrm{sgn}(S_{d-f} ) -k_{q-f} S_{q-f} \mathrm{sgn}(S_{q-f} ) \end{aligned}$$

(71)

Therefore:

$$\begin{aligned} \frac{d\Upsilon _2 }{dt}=-k_{d-f} \left| {S_{d-f} } \right| -k_{q-f} \left| {S_{q-f} } \right| \prec 0 \end{aligned}$$

(72)

As a result, the asymptotic stability in the current loop is guaranteed and the dc-bus voltage control tracking is achieved. Finally, PWM is used to produce the control signal. The structure of the dc-link voltage and current controllers for grid-side converter, for the WECS, is illustrated in Fig. 7.

4 Simulation Result Analysis

This paragraph presents the simulated responses of the WECS under varying wind conditions. In this example simulation, Matlab/Simulink simulations were carried out for a 2 MW PMSG variable speed wind energy conversion system to verify the feasibility of the proposed method. The parameters of the system are given in the Tables 1 and 2. Besides, during the simulation, for the PMSG side converter control, the d axis command current component, $i_{dr}$, is set to zero; while, for the grid side inverter system, $Q_{ref}$, is set to zero. On the other hand, the DC link voltage reference and the grid frequency value are $U_{dc-r} =$ 1500 V and 50 Hz, respectively. The topology of the studied WECS based on PMSG connected electric network is depicted in Fig. 7. The grid voltage phase lock loop (PLL) system is implemented to track the fundamental phase and frequency. On the other hand, this paragraph is divided into two parts, that is, Sect. 4.1 demonstrates the satisfactory performance of the WECS under varying wind conditions, while Sect. 4.2 reflects the robustness of both the rectifier and inverter control systems against electrical and mechanical parameter deviations.

4.1 WECS Characteristics with SMC Approach

The WECS response under SMC strategy is illustrated by Figs. 8, 9, 10 and 11. Figures 8 and 9 show, respectively, the wind speed profile, the simulation results of pitch angle, coefficients of power conversion $C_p$, tip speed ratio, rotor angular velocity of the PMSG and total power generated of WECS. The rated wind speed considered in the simulation is $v_n =$12.4 m/s. Then, it can be seen, that when the wind velocity increases, the rotor angular speed increases proportionally too with a limitation, the power coefficient will drop to maintain the rated output power. Then, at the wind velocities less than the rated rotor velocity, the pitch angle is fixed at $0^{\circ }$ and the power performance coefficient of the turbine is fixed at its maximum value, around 0.41. The speed of PMSG is controlled in order to make the turbine system operates under its optimum tip speed ratio $\lambda _{opt} =8.1$, regardless of the wind speed. So, the PMSG velocity is regulated at an optimal value obtained from the MPPT algorithm. Thus, this control makes the wind turbine working at highest efficiency. On the contrary, for high wind speeds and if $\nu$ is greater than the rated velocity $\nu _n$, the operation of the pitch angle control is actuated and the pitch angle $\beta$ is increased. Then, the pitch control is used to maintain the PMSG power at rated power and it is designed to prevent damage from excessive wind velocity. So, the power performance coefficient of the turbine decreases to limit the rotor speed. Consequently, extracted power is optimized with MPPT algorithm and keeps at his nominal value when the wind speed exceeds the nominal value. Figure 9c shows the power extracted. As can be seen, if the wind velocity is up the rated wind speed, the power extracted reaches its maximum level. Figure 9b illustrates the waveforms of the mechanical velocity of the PMSG tracks the optimum velocity obtained from MPPT algorithm so as to guarantee the maximum power conversion at the optimal tip speed ratio. Then, it is clearly shown that the PMSG speed tracks the reference velocity closely. As the WECS successfully operates with MPPT ($\lambda =\lambda _{opt})$, the primary control objective is adequately attained, and the PMSG power finely follows the maximum value. Figure 10a depicts the simulation result of reactive power. As can be seen, the WECS supplies grid system with a purely active power. The fulfilment of the second control objective can be appreciated in Fig. 10b, where the WECS dc link voltage and the external reference $U_{dc-r}$ are depicted together. The dc link voltage is regulated toward its reference of 1,500 V. This proves the effectiveness of the established controller systems. Figure 11 illustrates the variation and a closer observation of three phase current and voltage of grid. Besides, the frequency is controlled and maintained at 50 Hz through a Phase Lock Loop (PLL) process. It is obvious that the grid voltage is in phase with the current since the reference of reactive current is set to zero. So, unity power factor of wind energy conversion system is achieved approximatively and is independent of the variation of the wind velocity but only on the reactive power reference ($Q_{ref} )$. Consequently, the simulation results demonstrate that the SMC strategy shows very good dynamic and steady state performance and works very well.

Fig. 8

Waveforms of WECS characteristics with SMC(Part 1). a Instantaneous wind speeds (m/s). b Pitch angles $\beta$ (in degree). c Coefficients of power conversion $C_p$

Fig. 9

Waveforms of WECS characteristics with SMC(Part 2). a Tip speed ratio. b Speed of PMSG (rd/s). c Power generated (W)

Fig. 10

Waveforms of WECS characteristics with SMC(part 3). a Total reactive power (VAR). b DC link voltage (V)

Fig. 11

The waveforms of three phase current and voltage of GRID

4.2 Robustness of the SMC Controller Under Electric and Mechanic Parameter Variations of WECS

In order to prove the robustness of the proposed controllers, model uncertainties were included considering the parametric uncertainties. Besides, these variations were also used in a percentage scale that takes the respective nominal values as references. An increase was considered in the stator resistor, the magnetising inductance and the total moment of inertia of the system values. So, the robustness in face of parameter variations was tested for the cases when the parameter that used in Sect. 4.1 is perturbed 50 % from its nominal value. Moreover, in order to establish a basis for performance comparisons, we also implemented a traditional linear control scheme based on Proportional Integral (PI) control scheme. The results are compared in Figs. 12, 13, 14 and 15. With the similar control parameter values and grid voltage condition as used in Sect. 4.1, superscripts ‘A’ and ‘B’ in Figs. 12 and 13 refer to present section (affected by parameter variations) and to waveforms corresponding to Sect. 4.1 (with nominal parameters), respectively. Figure 12 shows the comparison of the generator speed between the SMC method and PI strategy. In Fig. 13, the curves describe the test of sensitivity in face of parameter deviations for the coefficient of power. The responses of both control strategies shown in Figs. 14 and 15 verify the parametric robustness of the proposed scheme for the dc link voltage. As it is shown in the simulation result, the SMC strategy gives lower overshoot and faster response. The result indicates that the SMC control has faster velocity response and shorter settling time. Furthermore, it can be concluded that the proposed nonlinear sliding mode control is rather robust against parameter variations than its PI counterpart. Consequently, the robustness of proposed SMC to the parameter deviations is convincingly verified.

Fig. 12

Generator speed (rd/s). a Sliding mode. b PI controller

Fig. 13

Coefficient of power. a Sliding mode. b PI controller

Fig. 14

DC link voltage (V) (with nominal values). a Sliding mode. b PI controller

Fig. 15

DC link voltage (V) (with parameter variations). a Sliding mode. b PI controller

5 Conclusion

This chapter deals with a control strategy of the variable speed wind energy conversion system based on the PMSG and connected to the power network. A structure of back to back PWM is presented. The Sliding Mode Control approach (SMC) is used to implement the Maximum Power Point Tracking, DC link voltage regulation and unity power factor control under varying wind conditions. The employed control strategy can regulate both the total reactive and active power independently. The detailed derivation for the control laws has been provided and the conditions for the existence of the sliding mode are found by applying Lyapunov stability theory. The WECS robustness and performances under the studied control strategy are discussed. The robustness in the presence of parametric uncertainties was tested for the cases when the parameters are perturbed 50 % from its nominal value. A comparison of simulation results based on SMC and PI controller is provided, where the proposed nonlinear sliding mode control is rather robust against parameter variations than its PI counterpart. Besides the SMC strategy gives lower overshoot and faster response. The simulation results show the effectiveness of the proposed sliding mode control.

Appendix

Table 1 Parameters of the power synchronous generator

Table 2 Parameters of the turbine