Dynamic Modelling of a Four Legged Robot

Abstract

In this paper we present the kinematic model of a mechanism, which represent the legs of a four legged robot. The anterior legs and posterior are realized as plane mechanisms, with articulated bars. Each anterior leg has a complex structure, with four closed loops, mean while each posterior leg has only three closed loops. Each mechanism is actuated by an electric motor. The geometric and kinematic modelling of the anterior leg mechanism is achieved by means of some vectorial and scalar equations. Also, the dynamic simulation is achieved during walking, by means of ADAMS software.

1 Introduction

In case of four legged mammals, the structure of anterior and posterior legs is very similarly with the structure of most majorities of actual four legs quadrupeds [1–3]. To some quadrupeds, the anterior legs are short that those posterior. To remark, that at quadrupeds, the anterior legs have the degree of mobility larger than the posterior. Legged walking robots such as biped robots, quadrupeds, hexapods and eight-legged robots have attracted great interests in the past decades. Legged locomotion has a lot of advantages as compared with wheeled locomotion. It is versatile and flexible when it operates in rough terrain or in unstructured environments [1, 4].

Leg mechanisms with a limited number of degrees of freedom (DOF) are widely used in legged walking robots for the purpose of reducing the number of motors and simplifying the control algorithms [4, 5]. At LARM: Laboratory of Robotics and Mechatronics in Cassino, reduced DOF leg mechanisms have been implemented in several prototypes like one-DOF biped robot [4, 5], and a rickshaw walking robot [6]. A one-DOF biped robot has been able to perform a biped walking gait in a lab test [7].

In this paper is presented the design problem for a new quadruped walking robot by looking at solutions in dog’s locomotors system. Thus, a mechanism design is proposed as to be implemented for a novel quadruped—like walking robot.

2 Mechanism Structural and Kinematics Analysis

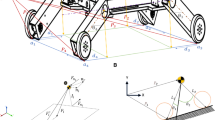
The kinematics scheme of the quadruped biomechanism is achieved in vertical longitudinal plane (Fig. 1), in which are represented the plane articulated mechanisms of those two legs, from rear (Fig. 1a) and front (Fig. 1b). The booth mechanisms are articulated in the upper side to a horizontal link, which represent the body of the physically modeled robot. The joints D and F of each mechanism to the upper mobile platform (Fig. 1) are considered as basis joints, by this reason this platform has been noted with 0. Each of those two mechanisms (rear and front), has a first kinematic chain, the four bar mechanism ABCD, which is composed by the links 0, 1, 2 and 3. The others kinematical chains of each mechanism are the four bar articulated mechanisms DEFG, HIGJ, with the links 0, 3, 4, 5, and 4, 5, 6, 7, as can be seen in Fig. 1.

Fig. 1

Kinematical scheme of the mechanism from posterior legs (a) and anterior (b)

The mechanism of the front leg contain in his structure another kinematic chain KJLM, composed by the links 5, 7, 8 and 9.

The mobility of each from those two plane mechanisms is calculated with the Dobrovolski formula:

$$ M_{bf} = (6 - f)n - \sum\limits_{k = f + 1}^{5} {(k - f)C_{k} } $$

(1)

This for $f = 3$ (plane mechanisms) becomes the Grübler-Cebâşev relation:

$$ M_{b3} = 3n - \sum\limits_{k = f + 1}^{5} {(k - 3)C_{k} } = 3n - 2C_{5} - C_{4} $$

(2)

where the class of the kinematic joint reveals the imposed restrictions (k = 5, k = 4).

Also, the mechanism degree of mobility, can be calculated with the general formula, of Păun Antonescu [8, 9]:

$$ M_{b} = \sum\limits_{m = 1}^{5} {mC_{m} - } \sum\limits_{r = 2}^{6} {rN_{r} } $$

(3)

where is emphasized the kinematics joints mobility: $m = 6 - k$ and the class of each independent closed loop: $r = 6 - f$. For plane mechanism the relation (3), can be writhed as:

$$ M_{b} = \sum\limits_{m = 1}^{2} {mC_{m} } - 3N_{3} = C_{1} + 2C_{2} - 3N_{3} $$

(4)

To calculate the mobility of those two mechanisms (Fig. 1a, b) we use the relations 2 or 4:

• a)
  $$ M_{b3} = 3n - 2C_{5} - C_{4} = 3 \times 7 - 2 \times 10 - 0 = 1;\quad M_{b} = C_{1} + 2C_{2} - 3N_{3} = 10 + 2 \cdot 0 - 3 \cdot 3 = 1. $$
• b)
  $$ M_{b3} = 3n - 2C_{5} - C_{4} = 3 \times 9 - 2 \times 13 - 0 = 1;\quad M_{b} = C_{1} + 2C_{2} - 3N_{3} = 13 + 2 \times 0 - 3 \times 4 = 1. $$

The characteristics dimensions of those two mechanisms are (Fig. 1 a, b):

• a)
  $$ \begin{aligned} & l_{AB} = 5;\quad \, l_{BC} = 17;\quad l_{DC} = 12;\quad l_{CE} = 18;\quad l_{FH'} = 11;\quad l_{HH'} = 4;\quad l_{H'G} = 15;\quad l_{EG} = 13;\quad l_{GH} = 15.52;\quad l_{HI} = 19; \\ & l_{GJ} = 27.29;\quad \, l_{IJ} = 17.5;\quad l_{JM} = 54; \\ \end{aligned} $$
• b)
  $$ \begin{aligned} & l_{AB} = 5;\quad l_{BC} = 17;\quad l_{DC} = 12;\quad l_{CE} = 18;\quad l_{FH'} = 11;\quad l_{HH'} = 4;\quad l_{H'G} = 15;\quad l_{EG} = 13;\quad l_{GH} = 15.52;\quad l_{HI} = 19; \\ & \, l_{GJ} = 27.29;\quad l_{IJ} = 17.5;\quad l_{JM} = 47.5;\quad l_{KL} = 56;\quad l_{LM} = 10; \\ \end{aligned} $$

In the topological structure of each mechanism we identify the link 1, as motor, and three or four dyadic kinematics chains.

The mechanism has four independent contours (Fig. 2) first is the four bar mechanism ABCD, which is composed by the links 0, 1, 2, 3. The second kinematical chain of each mechanism is the four bar articulated mechanism DEFG, with the links 0, 3, 4 and 5 as can be seen in Fig. 2.

Fig. 2

Kinematical scheme of the anterior leg mechanism

The third and four kinematics chain are HIGJ and KJLM, composed by the links 4, 5, 6, 7 and 5, 7, 8, 9. The assumption made for the kinematic modelling is that the leg mechanism operates on a supporting stand.

We choose a coordinate system with the origin in the fixed joint A, having the axis Ax and Ay orientated from right to left, respectively from upper to bottom. For each side of those four closed independent contours we choose conveniently senses, for that the positioning angles (measured in trigonometric sense) to be most small (Fig. 2).

We write the closing vectorial equation for the contours, the purpose being to establish the variations of angles $\varphi_{i}$, considering an uniform angular speed of the motor element: $\omega_{1} = d\varphi_{1} /dt = 1.2 \, \text{rad}/s$. The variation of angles $\varphi_{i}$, $i = 1 \ldots 9$, are determined by solving some equations under the form:

$$ \varphi_{i} = 2arctg\left( {\frac{{A_{i} \pm \sqrt {A_{i}^{2} + B_{i}^{2} - C_{i}^{2} } }}{{B_{i} - C_{i} }}} \right), $$

(5)

The expression of variable coefficients is calculated with relations under the form:

$$ \begin{aligned} & A_{2} \left( {\varphi_{2} ,\varphi_{3} } \right) = 2b_{1} l_{BC} ;\quad B_{2} \left( {\varphi_{2} ,\varphi_{3} } \right) = 2a_{1} l_{BC} ;\quad A_{3} \left( {\varphi_{2} ,\varphi_{3} } \right) = - 2b_{1} l_{DC} ;\quad B_{3} \left( {\varphi_{2} ,\varphi_{3} } \right) = - 2a_{1} l_{DC} ; \\ \,C_{2} \left( {\varphi_{2} ,\varphi_{3} } \right) = l_{DC}^{2} - a_{1}^{2} - b_{1}^{2} - l_{BC}^{2} ;\quad C_{3} \left( {\varphi_{2} ,\varphi_{3} } \right) = l_{BC}^{2} - a_{1}^{2} - b_{1}^{2} - l_{DC}^{2} ; \\ & a_{1} = \left( {x_{D} - x_{B} } \right),\quad b_{1} = \left( {y_{D} - y_{B} } \right) \\ \end{aligned} $$

(6)

$$ \begin{aligned} & A_{4} \left( {\varphi_{3} ,\varphi_{4} ,\varphi_{5} } \right) = 2b_{2} l_{FG} ;\quad B_{4} \left( {\varphi_{3} ,\varphi_{4} ,\varphi_{5} } \right) = 2a_{2} l_{FG} ; \, \\ & A_{5} \left( {\varphi_{3} ,\varphi_{4} ,\varphi_{5} } \right) = 2b_{2} l_{GE} ;\quad B_{5} \left( {\varphi_{3} ,\varphi_{4} ,\varphi_{6} } \right) = 2a_{2} l_{GE} ; \\ & C_{4} \left( {\varphi_{3} ,\varphi_{4} ,\varphi_{6} } \right) = l_{GE}^{2} - a_{2}^{2} - b_{2}^{2} - l_{FG}^{2} ;\quad C_{5} \left( {\varphi_{3} ,\varphi_{4} ,\varphi_{6} } \right) = l_{FG}^{2} - a_{2}^{2} - b_{2}^{2} - l_{GE}^{2} ; \\ & a_{2} \left( {\varphi_{3} } \right) = \left( {x_{F} - x_{D} } \right) + l_{DE} cos\varphi_{3} ;\quad \, b_{2} \left( {\varphi_{3} } \right) = \left( {y_{F} - y_{D} } \right) + l_{DE} \sin \varphi_{3} \\ \end{aligned} $$

(7)

$$ \begin{aligned} & A_{6} \left( {\varphi_{6} ,\varphi_{7} } \right) = 2b_{3} l_{IH} ;\quad B_{6} \left( {\varphi_{6} ,\varphi_{7} } \right) = 2a_{3} l_{IH} ;\quad C_{6} \left( {\varphi_{6} ,\varphi_{7} } \right) = l_{IJ}^{2} - a_{3}^{2} - b_{3}^{2} - l_{IH}^{2} ; \\ & A_{7} \left( {\varphi_{6} ,\varphi_{7} } \right) = - 2b_{3} l_{IJ} ;\quad B_{7} \left( {\varphi_{6} ,\varphi_{7} } \right) = 2a_{2} l_{IJ} ;\quad C_{7} \left( {\varphi_{6} ,\varphi_{7} } \right) = l_{IH}^{2} - a_{3}^{2} - b_{3}^{2} - l_{IJ}^{2} ; \\ & a_{3} \left( {\varphi_{4} ,\varphi_{5} } \right) = l_{JG} \cdot \cos \varphi_{5} - l_{HG} \cos \varphi '_{4} ;\quad {\text{b}}_{3} \left( {\varphi_{4} ,\varphi_{5} } \right) = l_{JG} \cdot \sin \varphi_{5} - l_{HG} \sin \varphi '_{4} ; \\ \end{aligned} $$

(8)

$$ \begin{aligned} & A_{8} \left( {\varphi_{8} ,\varphi_{9} } \right) = 2b_{4} l_{KL} ;\quad B_{8} \left( {\varphi_{8} ,\varphi_{9} } \right) = 2a_{4} l_{KL} ;\quad C_{8} \left( {\varphi_{8} ,\varphi_{9} } \right) = l_{ML}^{2} - a_{4}^{2} - b_{4}^{2} - l_{KL}^{2} ; \\ & A_{9} \left( {\varphi_{8} ,\varphi_{9} } \right) = - 2b_{4} l_{ML} ;\quad B_{9} \left( {\varphi_{8} ,\varphi_{9} } \right) = - 2a_{4} l_{ML} ;\quad C_{9} \left( {\varphi_{8} ,\varphi_{9} } \right) = l_{KL}^{2} - a_{4}^{2} - b_{4}^{2} - l_{ML}^{2} ; \\ & a_{4} \left( {\varphi_{5} ,\varphi_{7} } \right) = l_{JM} \cdot \cos \varphi_{7} - l_{JK} \cos \varphi_{5} ;\quad b_{3} \left( {\varphi_{5} ,\varphi_{7} } \right) = l_{JM} \cdot \sin \varphi_{7} - l_{JK} \sin \varphi_{5} ; \\ \end{aligned} $$

(9)

Solving the equations which describe the kinematic model, in Maple software package, we represent the law of variation of mechanism angles of motion, in Fig. 3.

Fig. 3

Computed plot of the angle φ ₆ variation and φ ₉ variation

3 Dynamic Modelling of the Robot

Dynamic simulation has been computed trough a suitable Adams modelling, during the walking activity, on the ground, taking into account the ground contact, and the joints friction. To achieve this purpose it is developed an assembly model with the four legs of the walking robot, each leg being positioned in a suitable position, corresponding to the walking phases.

To simulate the mechanism in Adams environment, there is modelled as a 3D structure, on which the kinematics links are defined as shape, geometry and material property. They are defined the kinematical joints of the mechanism with corresponding constraints and mobility’s, we define the local and global coordinates systems upon we calculate the mechanism kinematical parameters. We define the motor element and eventually loads (forces or moments which act upon the kinematical links) upon we process the kinematical analysis. For this step the mechanism is considered fixed to basis joints on an operating stand. The motion of motor is considered uniform, by 1.2 rad/s, (Fig. 2). In Fig. 4, is presented the trajectory described by the leg, when she operates on a supporting stand. From figure is also observed the initial position of the mechanism and the final position of the mechanism, corresponding to one step of the dog robot. The trajectory was obtained with MSC.Adams software, by tracking the motion of point L. The CAD model of the robot is imported into Adams data basis, and trough a suitable modelling in achieved the dynamic modelling, when the robot is walking on ground. For the rotation joints are defined the friction from the pin hole joint, the ground contact model. Simulation parameters of the leg mechanisms considered for dynamic analysis are indicated in Table 1.

Fig. 4

Computed path of the front legs ankle trajectory, standing and walking

Table 1 Simulation parameters for dynamic analysis

For each crank of those four leg mechanism is defined the motor motion. It is observed that the cranks are positioned at 180° for the opposite legs, for a suitable walking phase.

Considering the body weight of the robot by 20 kg and the angular speed of actuation motor by 1.2 rad/s, there are computed in Adams dynamic simulation the motion trajectories of ankle joints, when the model walks on ground. In Fig. 4 is presented the Adams computed path described by ankle joints.

Sequences from the walking activity of the robot model, obtained in Adams are presented in Fig. 5. Stepping sequences during walking on ground, demonstrate the viability of the solution implemented for legs mechanism.

Fig. 5

Sequences from the walking activity

From dynamic simulation is obtained the resistant torque at the shaft which actuates those four legs cranks. From the variation of resistant motor, presented in Fig. 6, it’s depicted the conclusion that the maximum value is by 4 Nm, that being useful for the choice of an actuation electric motor for the experimental prototype (Fig. 7).

Fig. 6

Computed torque motor variation for the right, and left posterior leg, during walking

Fig. 7

Computed contact force upon x and y axis, for the posterior right leg

4 Conclusions

In this paper a kinematics and dynamic simulation of a one DOF robot leg mechanism is carried out, in order to characterize the mechanism performance. They are two different structures, for the legs, one for the anterior leg, and another one for the posterior legs. Each leg is actuated by a single motor element. Kinematics equations of the proposed leg mechanism are formulated for a situation when the leg operates on a supporting stand and solved in Maple computational algorithm. In Adams software is simulated the walking activity taking into account the ground contact with the leg. There are obtained the paths for trajectories when leg operates on a supporting stand and walking on ground. Simulation results show suitable performance of the proposed leg mechanism structure. The novelty of the design structure represents the fact that for each mechanism is needed only one motor, which has a constant angular rotation, so is no needed a complex command and control algorithm.