1 Introduction

One of the notable discussions in the analysis of wheel-leg robots is their stability, which is a significant factor for system dynamics and control due to the considerable change during movement. Wheel-leg robots, also called hybrid robots, can be explored from speed and motion efficiency perspectives. The hybrid design combines the compatibility of stepping robots with the efficiency of wheeled robots and offers a powerful hybrid system. However, it complicates the stability study of these robots due to the simultaneous use of two different propulsion mechanisms. This paper thus investigates and implements one of the stability analysis methods on an actual prototype.

1.1 Background on Manufactured Robots

The rover Sherpa can be classified as one of the hybrid robots. Cordes and Babu studied the hardware and stability of this robot, wherein the stability study, ground contact forces, roll angles, and pitch are considered [1]. Thomson et al. developed another wheel-leg robot with 12 actuators, eight hydraulic motors for moving the legs, and four electric motors to move the wheels [2].

Shen et al. introduced a wheel-leg hybrid robot with a different operating mechanism. The robot had two motion modes, including wheel motion and stepping motion. This change was a hardware alteration and was performed by the robot's moving half-rings [3]. Reid et al. designed and built a wheel-leg robot with a linear leg mechanism. The robot used Robotis Dynamixel actuators to move all joints. They studied the robot stability using inverse kinematics and the help of surface processing using a camera. Nevertheless, no assumption was considered in kinematics or motion due to slow motion [4].

Niu et al. designed a robot with a wheel and leg, having 6 degrees of freedom on each of its leg This robot was optimized by imitating human motions and also including the sliding joint [5].

Soresh et al. presented a four-wheeled robot designed for uneven grounds. They used feedback control to compensate for all the rolls and pitches and to give the appropriate input signal to the leg rotation joint. The robot consisted of a chassis and four legs that had servo motors, as well as four wheels with DC motors [6].

Momaro robot [7] had a unique motion design with four legs attached to a pair of guided wheels. The robot used Robotis Dynamixel Pro actuators to move all joints. The legs had three joints in the hip, knee, and ankle that allowed adjusting the position of the pair of wheels relative to the plate.

MuJoCo was a wheel-leg robot which Bellegarda and Katie provided a trajectory optimization framework for a skating system on passive wheels, arguing that no means of movement is possible without using tangential frictional forces [8]. ANYmal robot, a wheeled-legged robot, was examined with a walking robot and a wheeled-legged robot [9].

The BIT-6NAZA robot is mainly composed of an environment perception system, sensor system, power system, control system, and wheel-based motion units. Thirty-six electric cylinders and six motors are in the control system. This robot has six combined legs with a wheel at the end, but due to the mechanical mechanism of the robot, its maneuverability for height changes is less than the wheeled-legged robot [10].

1.2 Research Background on Stability Analysis

In mobile robots, the loss of positional stability can result in potentially serious consequences, requiring a thorough analysis to predict better and eliminate this possibility. Attempts to propose dynamic stability criteria have provided successful results [11].

In wheeled mobile robots, the Zero Moment Point (ZMP) approach was suggested as a ground reference point, exploited for the first time by Sugano and Huang et al. Meanwhile, if (ZMP) is calculated in a presented way by Sugano et al., the mass moment of inertia of different rigid bodies would be ignored [12, 13].

Foot Rotation indicator (FRI) point extends the concept of (ZMP) and quantifies the severity of foot rotation acceleration in the single-phase[14]. Additionally, the (ZMP) and (FRI) methods, another ground reference point, have been introduced recently as the Centroidal Moment Point [15] or the zero rate of change in angular momentum (ZRAM) point [16].

Papadopoulos and Rey have reported another measure called Force-Angle (FA) margin [17]. Its geometric stabilization is investigated, which has been conducted based on the stability polygon, linear velocities, angular accelerations, and locating the point of the center of mass in the stability polygon 18]. The assessment of Moment-Height Stability (MHS) is a novel criterion for positional stability that Mousavian and Alipour have suggested [19]. This measure is based on stabilizing and destabilizing moments applied to the moving base, which provides system mobility and has been used to evaluate the positional stability of moving manipulators with rigid elements. The (MHS) has recently been examined with several other sustainability measures [20]. It has been indicated experimentally that the three algorithms studied above can be used to evaluate robot stability, with (FA) and (MHS) being more effective methods than (ZMP), due to the effects of height displacement in the robot. The basic robot platform, in which the robot's center of mass remained stationary with respect to the robot itself, presumably explains the lack of significant differences between the (FA) and (MHS) measures.

Grand et al. studied the Hylos robot by developing an algorithm based on the robot's position and path parameters. Next, they presented a control algorithm that guided the robot's position and path separately. To analyze the motion of the Hylos robot, they divided stability into three parts:

  1. 1.

    Distance Stability Limit: Stability Margin was first developed by McGee and Frank. They proposed the algorithm so that it is the minimum distance between the image of the robot's center of mass and the edges of the supporting polygon.

  2. 2.

    Stability limit of the Force-Angle: Papadopoulos and Ray presented it as the lowest angle between the gravitational force vector from the center of mass and the vertical vector from the center of mass to the edge of the supporting polygon.

  3. 3.

    Energy Stability Limit: Adopted by Missouri and Klein, and is the minimum amount of energy required to align the plate on the edge of the support polygon [21, 22].

In the motion of wheel-leg robots, the main contribution is a motion control framework designed for the entire robot system. It takes into account the greater degrees of freedom provided by the torque-controlled wheels. The online motion planning algorithm based on ZMP is updated along with path tracking [23]. Roan has examined all three stability algorithms (ZMP, FA, and MHS) and compared each. Three stability indices of FA, zero moment point and MHS are compared, and the numerical average of these indices for instability is calculated. To prevent robot instability, FA and MHS outperform the ZMP because the calculations are not accurate and reliable in the moment point method, and also, the study is 2D [20]. ZMP method considers the inertial moment effect of each link, in addition to their mass, which is a significant factor in robot dynamics [24].

Chen et al., a novel adaptive hierarchical walking control framework based on FGP and GFR with behavioral rules is proposed to achieve high maneuverability and flexibility in unstructured terrain for the developed six-legged wheelbase robot (BIT-6NAZA). Because this robot has six legs in contact with the ground, it can perform better in maintaining stability than a four-legged robot with moving wheels [25].

Mousavian et al. studied a four-wheeled robot with two moving manipulators that move a heavy object. Robot stability is studied based on the assumption that the initial and final spatial conditions of the load are known, and the manipulator's path is first traversed without considering positional stability. However, the robot's body path is traversed with consideration of positional control and all initial conditions such as speeds as well as initial and final locations are accounted [19, 26].

Chen et al. have presented some advantages for the BIT-NAZA-II robot: first, this type of walking is better with the dominant foot, and the walking speed is also faster. Second, the support surface (stability) of the robot legs [27]—BIT-NAZA-II is larger, therefore, it is more stable and has a higher load capacity [35]. However, the problem of collision and slippage must be solved in foot walking for the heavy-footed robots. Therefore, they have proposed a control strategy for stable walking based on multi-sensor information feedback for heavy foot robots. This strategy combines the advantages of both BC-based ACC and SLR, which can solve not only the foot end contact collision problem but also the foot slip problem [28].

The study also deals with other methods of leg rotation, zero moment point, instantaneous central point, and zero rate angular motion indices. In other works [29, 30], authors investigated six involving factors in stability, including the height of the center of mass of the whole system, acceleration rate of the body and links, body mass inertia, body velocity, external forces, and Torques of endpoints with the environment, and the loads transmitted by the links. Mousavian et al. have studied a four-wheeled robot with two moving manipulators that move an object [31]. Grand et al. presented a kinetostatic model, where the Hylos robot is used, and the standing position of the robot in different conditions with four internal variables (related to the bodies) and three general variables is displayed. The aim was to optimize the kinematic state of the robot in relative to parameters such as stability, energy consumption and navigation [32]. In this paper, a wheel-leg robot is studied, and its stability is investigated. This robot adjusts its stability with active systems on the legs, but as the two links have a motor and exciter, the symmetrical movement is a significant limitation. The next assumption is to place the center of mass in the middle of the robot [33]. Although the forces acting on the center of mass and their moments are used, only the base of the robot is wheeled, and no height change through the base is considered in modeling and stability analysis [34]. However, due to the 2D force assumption (projection on the surface) in this paper, as well as the force assumptions, its implementation on the robot is incomplete because the wheeled robot has a height change which is why the MHS method is investigated.

Due to the presence of various devices on the robot and their location in a limited space, the robot's center of mass cannot be precisely considered at the center. In many of them, the manipulator is situated on the body owing to the many uses of robots and their ability to move objects. Therefore, considering a fixed location for the center of mass that has been assumed in previous works is not an accurate assumption in the stability study, and it could be considered with a variable distance from the robot's center of mass. The stability is analyzed through this accurate modeling for the robot, and the stability area is determined using the Force-Angle method. Then designing and زonstructing the robot by placing different masses in different locations on the body, the robot was tested, and the simulation results were compared with the experimental tests.

2 Stability and Robot Stability Criterion

Checking the stability is one of the most important cases of mobile robots, which can be used for DLCC calculations of a moving robot in an environment with obstacles [36, 37]. Due to the height changes of the robot, the stability criterion is highly important. Relevant theories have been used to investigate the robot's condition as well as to adjust the torque on the wheels and joints. Regarding the fact that the sufficient number of wheels and legs of the robot leads to maintaining the complete stability of the robot and makes dynamic analysis independent of the control system, a four-wheeled and four-legged robot should be considered to maintain stability and better control. The stability of the four-wheeled and four-legged robots may be guaranteed even offline with the assistance of the motors connected to the legs. The proposed robot is affected by a total of eight inputs since it has eight servo motors, four of which are on the joints of the legs and the other four on the wheels. The combination of legs and wheels allows the robot platform to have all six spatial degrees of freedom.

2.1 Stability Criteria Study

One of the most critical problems of mobile robots is maintaining stability. The effective components should be identified, controlled and analyzed to maintain stability. To do this, at least one of the appropriate stability analysis methods should be selected and implemented on the robot. In this section, two stability analysis methods are reviewed, and the advantages and disadvantages of each are discussed. According to past studies, the force-angle approach in the first casse is the most stable and effective strategy. Alternatively, this method has been used to study the robot in this paper.

2.1.1 Zero Moment Point Method

In this method, an area is initially determined by connecting the outermost points of the wheels that are in contact with the ground. This area is called the stability polygon. The point where the combined torques of inertial, gravitational, and external forces are zero is then established, and if it lies inside the polygon area, the robot will be stable. However, it is not a suitable method for dynamic analysis since it does not take into account all of the robot's components, particularly for hybrid robots with variable heights.

2.1.2 Force-Angle Margin Method

In this method, the same stability polygon is determined. For this purpose, the outermost points of the wheels, in contact with the ground, are connected to each other to determine an area. The center of mass, or base or body of the robot, must obviously be taken into consideration while calculating the stability margin of a system over-turn. In this work, it is assumed that the robot's wheels are generally in contact with the ground. Instability or overturning occurs when the body of the robot is generally standing and undergoes a rotation, reducing the number of points of contact with the ground so that all remaining points are on a line. Once the stability control is compromised, the robot will eventually topple over if the condition is not changed. A low center of gravity (c.g.) is always preferred from a stability perspective, whereas weightiness preserves stability at low speeds and leads to instability at high speeds. Low-speed systems that are expected to have a significant impact on the environment are taken into account in this approach. As a result, gravity is thought to have a stabilizing impact.

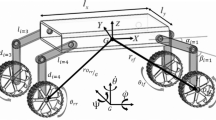
Figure 1 demonstrates the state in which two points are in contact with the ground; a planar system whose center of mass is under a net force, including the sum of all forces acting on the robot body except the support reaction forces (which do not contribute to reverse motion instability). This force vector forms two angles of \({\uptheta }_{1}\) and \({\uptheta }_{2}\) with two torsional axis normals \({\mathrm{L}}_{1}\) and \({\mathrm{L}}_{2}\). The force-angle stability measure α, is given the minimum angle among the measured angles. The critical tip-over stability occurs when \(\uptheta \) approaches zero. If a negative angle is obtained by examining \({\mathrm{L}}_{1}\) or \({\mathrm{L}}_{2}\), the tip-over is happening. According to the variable length of the contact points, the length of the legs (D) is obtained from the following equation.

$$ \begin{aligned} D_{i} & = \sqrt {{\text{WHEEL}} + {\text{Leg}}*{\text{abs}}\left( {\sin \left( {Q\left( i \right)} \right)} \right))^{ \wedge } 2 + \left( {{\text{Leg}}*{\text{cos}}\left( {Q\left( i \right)} \right)} \right)^{ \wedge } 2} \\ i :{\text{Number}} {\text{of}} {\text{Legs}}\;{\text{WHEEL}}: \\ {\text{Wheel radius}} & = \, 0.035m\,Leg:{\text{ leg length }} = \, 0.135m \\ \end{aligned} $$
(1)
Fig. 1
figure 1

Three-dimensional schematics of the Force-Angle stability method on the robot

Full size image

For a mobile robot capable of adjusting its center of mass height or for a robot carrying a variable load, the tip-over stability margin should be topheavy sensitive[18].

Figure (1) indicates the Force-Angle stability measurement in which the increase in the height of center of mass results in a smaller minimum angle and reduction in the tip-over stability margin measures, as shown by \({\mathrm{f}}_{\mathrm{r}}\) in Part C of Fig. 1, according to what was described before. By linking the points where the wheels make contact with the ground, the supporting polygon is first identified. The unit vector for each side of the polygon that is between two points of contact with the ground is then identified. Equations (2) and (3) are used for this purpose.

$$ \hat{l}_{i} = \frac{{P_{{i + 1}} - P_{i} }}{{\left\| {P_{{i + 1}} } \right.\left. { - P_{i} } \right\|}}\,\quad i = \left\{ {\begin{array}{*{20}c} 2 \\ \end{array} } \right., \ldots ,n - 1\} $$
(2)
$$ \hat{l}_{1} = \frac{{P_{1} - P_{n} }}{{\left\| {P_{1} } \right.\left. { - P_{n} } \right\|}}\,\quad n = {\text{Total\;Number\;of\;Legs}} $$
(3)
$$ r_{c} = P_{c} + x $$
(4)

According to the coordinates and variables that have been considered, the unit vectors should be calculated from Eqs. (6) and (7) and supporting polygon points:

$$ \begin{aligned} & d_{i} = \sqrt {D_{i}^{ \wedge } 2 - \left( {WHEEL + Leg*abs\left( {\sin \left( {Q\left( i \right)} \right)} \right)} \right)^{ \wedge } 2}\\ &\quad i: Number\, of\, Legs \end{aligned}$$
(5)
$$ \begin{aligned} & H_{i} = abs\left( {\left( {WHEEL + Leg*abs\left( {\sin \left( {Q\left( i \right)} \right)} \right)} \right)} \right) \\ &\quad i:Number\, of\, Legs \end{aligned} $$
(6)
$$ \begin{aligned} & l_{1} = \left[ {\begin{array}{*{20}c} {\cos \left( {U_{1} } \right)} \\ {\sin \left( {U_{1} } \right)} \\ 0 \\ \end{array} } \right] ; l_{2} = - \left[ {\begin{array}{*{20}c} {\cos \left( {U_{2} } \right)} \\ {\sin \left( {U_{2} } \right)} \\ 0 \\ \end{array} } \right]; \\ & l_{3} = \left[ {\begin{array}{*{20}c} {\cos \left( {U_{3} } \right)} \\ {\sin \left( {U_{3} } \right)} \\ 0 \\ \end{array} } \right] ; l_{4} = \left[ {\begin{array}{*{20}c} {\cos \left( {U_{4} } \right)} \\ {\sin \left( {U_{4} } \right)} \\ 0 \\ \end{array} } \right]\end{aligned} $$
(7)

U1 = 0.

U2 = Arccos((d3-d2)/\(\sqrt {W^{ \wedge } 2 + \left( {d3 - d2} \right)^{ \wedge } 2}\).

U3 = 180.

U4 = Arccos((d1-d4)/\(\sqrt {W^{ \wedge } 2 + \left( {d1 - d4} \right)^{ \wedge } 2}\).

W: Robot width = 0.3575 m.

Now, according to Part B of Fig. 1, vectors are drawn from the center of mass to the contact points of the supporting polygon with the ground, and the points are obtained.

$$ {\text{P}}_{{{\text{ii}}}} = {\text{P}}_{{\text{i}}} - {\text{P}}_{{\text{c}}}\quad \;{\text{i}} = 1:4 $$
(8)

Assuming that the vector \({P}_{c}\) is zero, i.e., external coordinate center is placed on the center of mass. These vectors are obtained for the points of contact of the robot wheels with the ground:

$$ d_{{{\text{ii}}}} = d_{{\text{i}}} \pm {\text{B}}\;\quad {\text{i}} = 1:4 $$
(9)

B: projection of a robot on the ground

$$ P_{11} = \left[ {\begin{array}{*{20}c} {d_{11} + x} \\ \frac{W}{2} \\ { - H_{1} } \\ \end{array} } \right] ; P_{22} = \left[ {\begin{array}{*{20}c} {d_{22} + x} \\ \frac{W}{2} \\ { - H_{2} } \\ \end{array} } \right] $$
(10)
$$ P_{33} = \left[ {\begin{array}{*{20}c} {d_{33} + x} \\ { - \frac{W}{2}} \\ { - H_{3} } \\ \end{array} } \right] ; P_{44} = \left[ {\begin{array}{*{20}c} {d_{44} + x} \\ { - \frac{W}{2}} \\ { - H_{4} } \\ \end{array} } \right] $$
(11)

In the next step, Eqs. (10) and (11) must be used to calculate the vector perpendicular to the midpoint of the vertices of the supporting polygon passing through the center of mass. In fact, this vector is used to determine the angle of force with the support polygon lines, while writing it, the height is also included:

$$ L_{i} = \left( {L_{3 \times 3} - \hat{l}_{i} \hat{l}_{i}^{T} } \right)\left( {P_{i + 1} - P_{c} } \right) $$
(12)
  1. (1)

    Now for all sides, these measures are taken:

    $$ L_{1} = \left( {\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]} \right) P_{22} $$
    (13)
    $$ L_{2} = \left( {\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]} \right)P_{33} $$
    (14)
    $$ L_{3} = \left( {\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]} \right)P_{44} $$
    (15)
    $$ L_{4} = \left( {\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]} \right)P_{11} $$
    (16)

All forces and Torques related to the movement of the manipulators, including gravitational forces, and inertial forces, as well as the generated torque due to the forces, which are transmitted to the body, are calculated. After determining the forces, it is necessary to compute the torques that are generated as a result of the manipulator's movement, the forces applied to the body's center of mass, and the forces applied to the vertices of the supporting polygon.

$$ f_{r} \, _{ = }^{\Delta } \sum \left( {f_{grav} + f_{inertial} } \right) $$
(17)
$$ \tau_{r} \;_{ = }^{\Delta } \sum \left( {\tau_{grav} + \tau_{inertial} } \right) $$
(18)
$$ f_{i} = \left( {1 - \hat{l}_{i} \hat{l}_{i}^{T} } \right)f_{r} $$
(19)
$$ \tau_{i} = \left( {\hat{l}_{i} .\hat{l}_{i}^{T} } \right)\tau_{r} $$
(20)

After determining \({\widehat{l}}_{i}\), it is possible to compute the force and torque vectors around the sides of the component as well as the torque vectors around the axis by taking into account the determined vectors and vector computations, according to Part B of Fig. 1. As a result, the prior computations are applied in light of the calculated Torques to produce the Torque vectors.:

$$ \tau_{1} = \left( {\hat{l}_{1} .\hat{l}_{1}^{T} } \right) \left[ {\begin{array}{*{20}c} {\frac{w}{2}{\text{Mg}}} \\ { - {\text{Mg}}\left( {d_{11} + x} \right)} \\ { 0} \\ \end{array} } \right] $$
(21)
$$ \tau_{2} = \left( {\hat{l}_{2} .\hat{l}_{2}^{T} } \right) \left[ {\begin{array}{*{20}c} {\frac{w}{2}{\text{Mg}}} \\ { - {\text{Mg}} \left( {d_{22} + x} \right)} \\ { 0} \\ \end{array} } \right] $$
(22)
$$ \tau_{3} = \left( {\hat{l}_{3} \widehat{.l}_{3}^{T} } \right)\left[ {\begin{array}{*{20}c} {\frac{{\text{w}}}{2}{\text{Mg}}} \\ { - M{\text{g }}\left( {d_{33} + x} \right)} \\ {{ }0} \\ \end{array} } \right] $$
(23)
$$ \tau_{4} = \left( {\hat{l}_{4} .\hat{l}_{4}^{T} } \right)\left[ {\begin{array}{*{20}c} {\frac{w}{2}{\text{Mg}}} \\ { - {\text{Mg}} \left( {d_{44} + x} \right) } \\ { 0} \\ \end{array} } \right] $$
(24)
$$ f_{{n_{i} }} = \frac{{{\hat{L}}_{i} \times \tau _{i} }}{{\parallel L_{i} \parallel }} $$
(25)
$$ f_{i}^{*} = f_{i} + \frac{{\hat{L}_{i} \times \tau _{i} }}{{\parallel L_{i} \parallel }} $$
(26)

Now to calculate the angle of each \({f}_{i}\) with \({I}_{i}\), Eqs. (26) to (28) must be applied.

$$ \theta _{i} = \sigma _{i} {\text{cos}}\left( {f_{i}^{*} .} \right.\hat{L}_{i} )\quad \;i = \left\{ {\begin{array}{*{20}c} {1,2} \\ \end{array} } \right., \ldots ,n\} $$
(27)
$$ \sigma_{i} = \left\{ {\begin{array}{*{20}c} { + 1} & {if \left( {\hat{L}_{i} \times f_{i}^{*} } \right) \cdot \hat{l}_{i} < 0} \\ {} & {} \\ {\begin{array}{*{20}c} {} \\ { - 1} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ {{\text{otherwise}}} \\ \end{array} } \\ \end{array} i = \left\{ {\begin{array}{*{20}c} {1,2} \\ \end{array} } \right., \ldots ,n\} } \right. $$
(28)
$$ \alpha_{i} = {\text{min}}\left( {\theta_{i} } \right)f_{r} $$
(29)

The minimum angle or the stability limit can be determined by placing Eqs. (26) to (28) in the simulations and determining the angles in the MATLAB software. The stability area for the whole robot has been defined after performing this simulation for several centers of mass.

3 3. Case Study

The robot design is generally divided into two parts of mechanical and electrical design. To build the robot, first, a preliminary design was carried out and based on the existing conditions and selected motors, as well as the reliability coefficient for motors, the design was completed, and the related materials were selected. (weight of the robot: 2.4 kg).

3.1 Wheel-leg Robot Mechanics

In addition to having no intersection between pieces, related software has been utilized to design and assemble parts in the best possible way Fig. 2. The mechanical parts of the robot include the parts listed in Table 1.

Fig. 2
figure 2

Wheel-legged robot designed in Catia software

Full size image
Table 1 Mechanical parts
Full size table

The weight of the robot body is 1000 g, and also the geometric dimensions of the body finally reached to 6 mm body thickness, 240 mm in 380 mm dimensions Fig. 3. The body is made of 6061 aluminum alloy.

Fig. 3
figure 3

All mechanical parts of the robot. a Motors of legs, b Motors of wheels, c wheels, d Schematic of mechanical parts, e Robot body, f Legs

Full size image

3.2 Electrical Robot

This robot uses a U2D2 converter and USB communication wire to transmit and receive orders from the motors. The Atmega board was also used to collect data from the gyroscope module. The electrical part generally includes motors, relay module, motor communication board, Hub-USB, SMPS2Dynamixel power supply circuit, U2D2 converter, 12 to 5-V converter, gyroscope module (mpu6050), and Atmega control board Fig. 4.

Fig. 4
figure 4

WLRIUST / wheel-leg robot

Full size image

3.2.1 Motors

The use of Dynamixel servo motors was thought to be advantageous since, in addition to being lighter and having a torque control mode, the models selected had starting voltages of 12 to 14 V DC. The XM540-W150-R series dynamixel motors have been chosen for the legs' joints in order to provide the necessary torque, while the XL430-W250-T motors have been employed for the wheels.

3.2.2 Electronic Connections of Robot

A U2D2 converter is used to link the motors to the laptop, and an interface board that was created and made is utilized for communication between the motors.

4 Results

The center of mass variable is an important factor in this paper. Now we have to accurately determine the location of center of mass for the different angles at which the robot stands, so that the robot does not become unstable. Figures 5 and 6 show possible positions for the robot's center of mass at various angles. In these pictures, the robot is supposed to be in a stable condition while the number 1 is present and to be unstable when the number -1 is present. The below pictures are illustrated from different angles of the robot's legs. The robot's legs are at a 170-degree angle to the horizon in Part B of Fig. 5, and it is obvious from the Figure that if the robot's center of mass moves more than 4.61 cm away from its center, it will enter an unstable zone. Part A of the Figure shows that at a 150-degree angle, this value is about 7.16 cm (5).

Fig. 5
figure 5

Stability investigation of the moving body of the robot at two different angles

Full size image
Fig. 6
figure 6

Simulation Of Stability test at 90 °The torque asymmetry is connected to the parallelogram condition of the robot's legs

Full size image

However, the findings of the theory show that the closer the angles between the legs are to the vertical position, the wider the robot's stability range would be, as is seen in Fig. 6. When the angle between the legs is 90 degrees, the robot is completely stable and does depend on the location of the robot's center of mass.

Because the quadrilateral represents the stability range with dimensions, the value given in Fig. 6 at an angle of 90 degrees (L: 34.60, W: 35.75 cm). After the center of mass has departed from the stability range, instability occurs at this angle.

Because there is no instantaneous change in engine torque, Fig. 7 displays the torque at which the robot has not experienced instability. They display almost the same value. Its oscillations, however, are brought on by mistakes in practical testing, including friction, step system uncertainties, and environmental disturbances.

Fig. 7
figure 7

Experimental test

Full size image

5 Comparison of theoretical and experimental results

Considering that the robot's center of mass may change due to external factors or the displacement of its internal mechanisms, the robot's stability has been investigated by considering the change of the center of mass. Therefore, by considering the displacement term of the center of mass on wheeled robots and implementing the generalized force-angle method, the stability range of the robot was determined at different points of the center of mass and with possible angles for the robot's legs, and scientific and theoretical comparisons were made. According to that moment, entering the instability range was accompanied by a torque jump. The related test was carried out in accordance with the Force-Angle method and the robot testing procedure shown in Fig. 8 at an angle of 170 degrees for the front joints and 170 degrees for the rear joints, as well as taking into account the relevant center of mass of the robot and its supporting polygon. The robot became unstable by 4.61 cm of center of mass displacement when the torque around each side of the supporting polygon was estimated based on theoretical assumptions and the test results. The two front joints bore higher torque, which is the consequence of weight and other external forces, while the rear joints bore just the weight of the links, due to the displacement of the robot's center of mass in the corresponding joints' motors. These Figures therefore precisely demonstrate that the Torques have reached a particular value where the robot has entered the instability region, both theoretically and practically. This is completely consistent with what was discussed in the earlier section. The robot reaches the region of instability at a certain position in Fig. 5 part B by shifting its center of mass. In Figs. 8 and 9, the robot has reached the zone of instability at a certain point in time, and the two joints have borne different torques. This is the same problem that we are looking at with regard to the output torque of the motors of the front and rear joints. These abrupt changes in Fig. 9 Torque reveal the robot's propensity for shifting its center of mass.

Fig. 8
figure 8

Comparison of results of experimental test and stability theory estimation

Full size image
Fig. 9
figure 9

Entering the instability area in the theory of a wheel-leg robot – torque 2 : torque rear, torque 4 : torque front

Full size image

6 Conclusion

In this paper, considering that the robot's center of mass may change due to external factors or the displacement of its internal mechanisms, the robot stability was examined by considering another variable. Hence, regarding the displacement term of the center of mass on wheel-leg robots and the implementation of the Force-Angle (FA) method, the robot stability range was determined in different locations of the center of mass, with possible angles for the legs of the robot. Also, in parallel with determining these ranges, stability tests have been performed by changing conditions, especially changing the center of mass at different angles using a wheel-leg robot. In these cases, the Torques are compared together. The accuracy of the results is assessed by contrasting theoretical and practical results linked to the torque of the front and rear wheels. Any sudden change in the torques of the motors indicates that forces have disturbed the robot system, which can cause instability in the robot system. This disorder causes an increase in torque in a part of the robot and a decrease in a part. The maximum force (torque) is investigated according to the force parameter. As a result, it is possible to create better performance in stability by considering this factor, which is thought to be an inevitable variable, especially in robots containing the manipulator, and also needs to be taken into account in unfamiliar environments. This is because the stability range could be estimated with greater accuracy and by taking other environmental factors into consideration.