Abstract
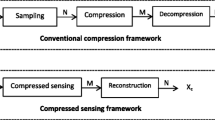
Compressed sensing (CS) has drawn quite an amount of attentions as a joint sampling and compression approach. Its theory shows that if a signal is sparse or compressible in a certain transform domain, it can be decoded from much fewer measurements than suggested by the Nyquist sampling theory. In this paper, we propose an unequal-compressed sensing algorithm which combines the compressed sensing theory with the characteristics of the wavelet coefficients. First, the original signal is decomposed by the multi-scale discrete wavelet transform (DWT) to make it sparse. Secondly, we retain the low frequency coefficients; meanwhile, one of the high frequency sub-band coefficients is measured by random Gaussian matrix. Thirdly, the sparse Bayesian learning (SBL) algorithm is used to reconstruct the high frequency sub-band coefficients. What’s more, other high frequency sub-band coefficients can be recovered according to the high frequency sub-band coefficients and the characteristics of wavelet coefficients. Finally, we use the inverse discrete wavelet transform (IDWT) to reconstruct the original signal. Compared with the original CS algorithms, the proposed algorithm has better reconstructed image quality in the same compression ratio. More importantly, the proposed method has better stability for low compression ratio.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Discrete wavelet transform
- Random Gaussian matrix
- Unequal-compressed sensing
- Image compression
- SBL algorithm
1 Introdution
With the recent advances in computer technologies and Internet applications, the number of multimedia files increase dramatically. Thus, despite extraordinary advances in computational power, the acquisition and processing of signals in application areas such as imaging, video and medical imaging continues to pose a tremendous challenge. The recently proposed sampling method, Compressed Sensing (CS) introduced in [1–3], can collect compressed data at the sampling rate much lower than that needed in Shannon’s sampling theorem by exploring the compressibility of the signal. Suppose that x ∈ ℝN × 1 is a length-N signal. It is said to be K-sparse (or compressible) if x can be well approximated using only K ≪ N coefficients under some linear transform
where Ψ is the sparse transform basis, and ω is the sparse coefficient vector that has at most K (significant) nonzero entries.
According to the CS theory, such a signal can be acquired through the random linear projection:
where, y ∈ ℝ M × 1 is the sampled vector with M ≪ N data points. Φ represents a M × N random matrix, which must satisfy the Restricted Isometry Property (RIP) [4], and n ∈ ℝ M × 1 is the measurement noise vector. Solving the sparsest vector ω consistent with the Eq. (73.2) is generally an NP-hard problem [4]. For the problem of sparse signal recovery with ω, lots of efficient algorithms have been proposed. Typical algorithms include basis pursuit (BP) or l 1-minimization approach [5], orthogonal matching pursuit (OMP) [6], and Bayesian algorithm [7].
CS theory provides us a new promising way to achieve higher efficient data compression than the existing ones [8–10]. The reference [9] proposed a new kind of sampling methods, it sampled the edge of the high frequency part of the image densely and the non-edge part randomly in the encoder, instead of using the measurement matrix to obtain the lower-dimensional observation directly in the traditional compressed sensing theory. The reference [10] proposed an improved compressed sensing algorithm based on the single layer wavelet transform according to the properties of wavelet transform sub-bands. But this article doesn’t consider the characteristic of high sub-band frequency coefficients. In this paper, the proposed unequal-compressed sensing algorithm combines the compressed sensing theory with the characteristics of the wavelet coefficients. The proposed algorithm has better reconstructed image quality in the same compression ratio. Usually, the coefficients are not zero but compressible (most of them are negligible) after sparse transform (e.g., DWT). Therefore, the sparse Bayesian learning (SBL) algorithm is used to resolve the reconstructed problem, which can recover the image correctly and effectively.
The remainder of this paper is organized as follows. Section 73.2 introduces the characteristics of wavelet coefficients. In Sect. 73.3, the proposed algorithm for image compression is presented. In Sect. 73.4, experiment results are given. Conclusions of this paper and some future work are given in Sect. 73.5.
2 Characteristics of Wavelet Coefficients
2.1 Characteristic One
Wavelet transform as the sparse decomposition has been widely used in compressed sensing. In this paper, we choose the discrete wavelet transform (DWT) as the sparsifying basis. As we know, the low frequency coefficients are much more important than the high frequency coefficients. Table 73.1 gives an idea about the PSNR (in dB) achieved that the image restoration only used low frequency coefficients or high frequency coefficients when the images are decomposed by four-scale DWT. In the Table 73.1, we can see that the low frequency coefficients make far greater contribution to the PSNR than the high frequency coefficients. Therefore, we retain the low frequency to ensure the quality of image restoration, and the high frequency coefficients are measured by the random Gaussian matrix to achieve compression.
Table 73.2 shows that the PSNR is achieved by the Lena images using multi-scale DWT. We can see that the scale of the decomposition S is smaller, the contribution to the PSNR which is made by low frequency coefficients is greater, and the length of the low frequency coefficients (N/2S) is longer. Therefore, we can choose the proper the scale of the decomposition S according to the compression ratio.
2.2 Characteristic Two
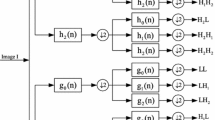
In order to reduce the computational complexity and storage space, we make each column of image x as a N × 1 signal to be coded alone. It is compressible in the discrete wavelet basis Ψ. The coefficients of the two-scale decomposition structure are shown in Fig. 73.1.
We can see that wavelet coefficient c consists of three parts, which are cA 2 (low frequency coefficients), cD 2 (one of the high frequency sub-band coefficients) and cD 1 (the other high frequency sub-band coefficients). We choose one column of image 256 × 256 Lena as a 256 × 1 signal to be decomposed alone. The decomposed high frequency sub-band coefficients are shown in Fig. 73.2.
We can see that, the locations of the larger coefficients in cD 1 are almost two times than the locations of the larger coefficients in cD 2. Then, we extend cD 2 using the zero insertion method, the comparison of the extended cD 2 and cD 1 are shown in Fig. 73.3. As can be seen from the Fig. 73.3, if the high frequency coefficient is lager (or smaller) at a certain location in cD 1, the high frequency coefficient is also larger (or smaller) with a great probability at the same location in the extended cD 2(ex _ cD 2). Let s _ cD 1 _ cD 2 represents the sum of ex _ cD 2 and cD 1, it has only a few of larger coefficients c d , other coefficients are almost close to zero. More importantly, the locations of the larger coefficients in s _ cD 1 _ cD 2 are almost the same as the locations of the larger coefficients in cD 1 and ex _ cD 2. Let
Then
Let c d represents the only a few of the largest coefficients in s _ cD 1 _ cD 2. According to ex _ cD 2 and c d , we can recover cD 1 approximately.
3 The Proposed Algorithm for Image Compression
In the original CS algorithm for image compression, the N × N image is firstly decomposed by a certain sparse transform (e.g. wavelet transform). And then, random Gaussian matrix Φ is employed to measure the wavelet coefficients. At the decoder, the original image is recovered by SBL algorithm and inverse wavelet transform. However, we study that the high frequency sub-band coefficients have a strong relevance. The algorithm which combines compressed sensing theory with the characteristics of the wavelet coefficients is proposed. The specific steps are as follows:
-
Step 1: in order to reduce the computational complexity and storage space, we make each column of image X as a N × 1 signal x to be decomposed alone. It is compressible in the DWT Ψ. We decompose the signal x by S-scale DWT. Retain the low frequency coefficients cA s . The scale of the decomposition S is decided by the compression ratio.
-
Step 2: let s _ cD S _ cD i represent the sum of ex _ cD S and cD i , i = 1, … S–1. Restore the only a few of the larger coefficients c i , i = 1, … S–1. Let m represents the number of the largest coefficients c i .
-
Step 3: the random Gaussian matrix \( M\times \frac{N}{2^s}\left(M<N/{2}^s\right) \) Φ is employed to measurement sampling the cD S to yield a sampled vector y = Φ ⋅ cD S .
-
Step 4: we can use the SBL algorithm to recover the vector \( \boldsymbol{c}{\widehat{\boldsymbol{D}}}_S \) and then, according to \( \boldsymbol{c}{\widehat{\boldsymbol{D}}}_S \) and c i to recover \( \boldsymbol{c}{\widehat{\boldsymbol{D}}}_i \), i = 1, … S–1. Finally, we use the inverse discrete wavelet transform to reconstruct the original signal.
The compression ratio of the proposed CS method is
Where, N/2S is the number of the low frequency coefficients, m × i represents the total number of the largest coefficients c i , i = 1, … S–1. M is the dimension of measurement matrix Φ, and, M < N/2S.
4 Experimental Results
The performance of the proposed algorithm has been evaluated by simulation. We choose the 256 × 256 Lena, Fruits, Baboon and Boat image as the original signals. We set the compression ratio α from 0.1 to 0.9. First, we determine the scale of the wavelet transform S according to the compression ratio α, and then get the length of the low frequency coefficients N/2S. Secondly, we choose the proper the dimension M of measurement matrix to guarantee the high frequency coefficients cD S transmits reliably. When the result is decimal, we choose the integer ⌊M⌋. Thirdly, we get the number of the largest coefficients m according to the formula (73.3). When the result is decimal, we choose the integer ⌊m⌋. In conclusion, the principle of distribution of these parameters is to ensure the reliable transmission of more important information in the fixed compression ratio α.
Similarly, we conduct the simulation using two types of original CS algorithm. One method is that the signal is decomposed by four-scale DWT (In general, the decomposition level of 256 × 256 image should be more than four to satisfy the sparsity), and then, all of the wavelet coefficients are measured by random Gaussian matrix. (In this paper, we named the general CS method). The compression ratio is calculated by the formula α 1 = M/N. The other method is that the signal is decomposed by single layer DWT, and then, the low frequency coefficients are retained, the high frequency coefficients are measured [10]. (In this paper, we named the single layer CS method). The compression ratio is calculated by the formula \( {\alpha}_2=\frac{N/2+M}{N} \), α 2 ≥ 0.5. Both of the two methods have not considered the characteristics of high frequency coefficients.
The PSNR of Lena, Fruits, Baboon and Boat images at different compression ratio using unequal-CS, general CS and single layer CS algorithms are shown in Fig. 73.4.
These figure shows that the proposed unequal-CS method achieves much higher PSNR than the other two CS methods. Especially, the gap is much larger in low compression ratio. What’s more, with the decrease of compression ratio, the PSNR of the rate of decline is much lower than the other two CS methods. And, the PSNRs which are achieved by the proposed unequal-CS method are not less than 18 dB. It indicates that the proposed method has a better stability for various compression ratios.
However, from the Fig. 73.4, we can see that the PSNR of Baboon image are lower than that of Lena, Fruits and Boat image at the same situations, because there are more high frequency coefficients in Baboon. After measurement, the loss is much. As this type of sources, the high frequency coefficients are larger relatively; the proposed method is not suitable for them.
Conclusion
An unequal-compressed sensing algorithm is proposed in this paper. According to the characteristics of the wavelet coefficients, we propose an unequal-compressed sensing algorithm which combines the compressed sensing theory with the characteristics of the wavelet coefficients and the PSNR of the proposed algorithm is greatly improved than the original CS algorithms. What’s more, it indicates that the proposed method has a better stability for various compression ratios.
References
Donoho DL (2006) Compressed sensing. IEEE Trans Inform Theory 52(4):1289–1306
Tsaig Y, Donoho DL (2006) Extensions of compressed sensing. IEEE Trans Signal Process 86(3):549–571
Candès EJ, Romberg J, Tao T (2006) Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inform Theory 5:489–509
Candès EJ (2008) The restricted isometry property and its implications for compressed sensing. CR Math 346(9):589–592
Chen SS, Donoho DL, Saunders MA (1998) Atomic decomposition by Basis Pursuit. SIAM J Sci Comput 20(1):33–61
Pati YC, Rezaiifar R, Krishnaprasad PS (1993) Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. In: IEEE 1993 conference record of the twenty-seventh Asilomar conference on signals, systems and computers, 1–3 Nov 1993, Pacific Grove. IEEE, pp 40–44
Wipf D, Rao BD (2004) Sparse Bayesian learning for basis selection. IEEE Trans Signal Process 52(8):2153–2164
Zhang Y, Mei S, Chen Q, Chen Z (2008) A novel image/video coding method based on compressive sensing theory. In: Proceedings of the international conference on acoustics, speech and signal processing (ICASSP), pp 1361–1364
Sun J, Lian QS (2013) An image compression algorithm combined nonuniform sample and compressed sensing. J Signal Process 29(1):31–37
Cen YG, Chen XF, Cen LH, Chen SM (2010) Compressed sensing based on the single layer wavelet transform for image processing. J Commun 31(8A):52–55
Acknowledgement
This work was supported by National Science Foundation of China (61171176).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Li, W., Jiang, T., Wang, N. (2015). Unequal-Compressed Sensing Based on the Characteristics of Wavelet Coefficients. In: Mu, J., Liang, Q., Wang, W., Zhang, B., Pi, Y. (eds) The Proceedings of the Third International Conference on Communications, Signal Processing, and Systems. Lecture Notes in Electrical Engineering, vol 322. Springer, Cham. https://doi.org/10.1007/978-3-319-08991-1_73
Download citation
DOI: https://doi.org/10.1007/978-3-319-08991-1_73
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-08990-4
Online ISBN: 978-3-319-08991-1
eBook Packages: EngineeringEngineering (R0)