1 Introduction

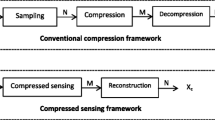
Traditional signal processing methods need to sample the original signals according to the Nyquist Theorem for facilitating subsequent signal sample processing. When majority of the information is unnecessary, such traditional sampling method would waste much time and storage space. Therefore, it is particularly necessary to develop a new methodology for signal acquisition as widely used in various image analysis applications [1,2,3,4,5]. Recently, compressed sensing (CS) [6, 7] has received more and more attention for that CS can achieve sampling and compression simultaneously while greatly reducing the sampling rate and storage space of digital signal acquisitions.

In CS research field, the precise reconstruction plays a critical role in the practical applications. Generally, the reconstruction of CS can be formulated as a non-convex \(l_0\) norm problem, which is an NP-hard problem. Thus, the most common solution is to convert it into a \(l_1\) norm problem [8] that could be solved by using some convex optimization algorithms. As for image reconstruction, prior knowledge of the image is exploited as the constraints for solving the \(l_1\) norm problem, which could be solved with some optimization algorithms, such as the interior points method [9], alternate projections onto convex sets (POCS) [10], the iterative shrinkage thresholding algorithm [11], iteratively reweighted algorithms [12]. Among the optimization methods, the constraint condition is a key factor that affects the reconstruction precision. Thus far, the sparse representation of image has been commonly used as constraint, because a suitable sparse base could fully represent the image and ensure a high-quality reconstruction.

Currently, although the orthogonal wavelet base is popular for the image reconstruction of CS, it has obvious shortcomings. It lacks significant directional selectivity and the shift invariance which renders it unable to fully represent the image textures, profiles, and some geometrical features. Therefore, the orthogonal wavelet base is not the best choice. Rauhut et al. [13] has proved that redundant dictionaries could be utilized for image reconstruction. The main distinction is that Rauhut used an over-complete dictionary for the selection of atoms which results in the chosen atoms matching the image contents more accurately. Meanwhile, Mun et al. [15] employed the framework of block compressed sensing (BCS) [14] to reconstruct the images and also used different directional wavelets to characterize the image. In addition, the bivariate shrinkage algorithm [16, 17] was utilized in the multi-scale decomposition structure fashion to provide the sparsity constraints. In the work of [18], the Bandlet dictionary was treated as the sparse base.

Inspired by Mun’s work, the major contributions of our paper can be summarized as follows: (1) Taking advantage of two transforms, the 2-D discrete cosine transform (DCT) and the 2-D double-density dual-tree complex discrete wavelet transform (DDDTCWT) [19], to represent the image alternately, which could better characterize the image compared with only single sparse transformation. (2) In order to achieve a high precision reconstruction, the adaptive sampling was integrated into the measurement for acquiring the specific information of different parts of image.

The remainder of this paper is organized as follows. In Sect. 2, a brief description is presented for the selected sparse bases. Then, the specific reconstruction is described in Sect. 3. The experimental results are shown and discussed in Sect. 4, and the conclusion is then presented in Sect. 5.

2 Sparse bases selection

As is known, different sparse bases could be used to represent different content of the image. In this paper, to better characterize the image, two bases were adopted to represent the texture and the edges in the image, respectively. Thus, the sparse representation with two sparse bases could be the constraint conditions in the image reconstruction.

Firstly, for the representation of image containing abundant texture information, the commonly used reversible transforms have mainly included DCT and wavelet atoms [20]. However, the spatial locality of wavelet atoms is very limited and its basis function has obvious wake phenomenon, which results in the artifact in reconstruction [21]. Consequently, the 2-D DCT was exploited to represent the texture of image in this paper. On the other hand, the DDDTCWT was adopted as the sparse base for the image edges representation. In particular, the DDDTCWT is a kind of DWT that combines the dual-tree DWT and the double-density DWT, and it apparently holds the characteristics and advantages of these two types of wavelets [22]. The principle of DDDTCWT is described briefly below.

Fig. 1
figure 1

Decomposition of an image based on the 2-D double-density dual-tree real DWT

Full size image
Fig. 2
figure 2

Images used in the experiments

Full size image
Fig. 3
figure 3figure 3

Image Lenna, Barbara, and Curtain reconstruction with a fixed sampling rate. a DCT, b DWT, c DDWT, d CT, e DDDTCWT, f DCT-DDDTCWT

Full size image
Table 1 PSNR performance of gray images based on different sparse bases
Full size table

The DDDTCWT presented in this paper is based on two scaling functions \(\phi _h (t)\), \(\phi _g (t)\), four distinct wavelets \(\psi _{h,i} (t)\), \(\psi _{g,i} (t)(i=1,2)\), and the wavelets satisfy the following rules:

$$\begin{aligned} \psi _{h,1} (t)\approx & {} \psi _{h,2} (t-0.5) \end{aligned}$$
(1)
$$\begin{aligned} \psi _{g,1} (t)\approx & {} \psi _{g,2} (t-0.5) \end{aligned}$$
(2)
$$\begin{aligned} \psi _{g,1} (t)\approx & {} H\left\{ {\psi _{h,1} (t)} \right\} \end{aligned}$$
(3)
$$\begin{aligned} \psi _{g,2} (t)\approx & {} H\left\{ {\psi _{h,2} (t)} \right\} \end{aligned}$$
(4)

where H represents the Hilbert transform. It can be seen that the two wavelets \(\psi _{h,i} (t)\) are offset from one to another by half, and the wavelets \(\psi _{g,i} (t)\) and \(\psi _{h,i} (t)\) form an approximate Hilbert transform pair. As the specific filter design procedure for the DDDTCWT described in [19], the emphasis would be put on the description of the process using the DDDTCWT for image decomposition and reconstruction. Figure 1 shows the decomposition of an image based on the 2-D double-density dual-tree real DWT.

In Fig. 1, \(h_0 (g_0 )\), \(h_1 (g_1 )\) and \(h_2 (g_2 )\) indicate a low-pass filter, a first-order high-pass filter and a second-order high-pass filter, respectively. The 2-D double-density dual-tree real DWT of an image is implemented by using two oversampled 2-D double-density DWTs in parallel. Similarly, the DDDTCWT of the input image is implemented by four 2-D double-density DWTs in parallel. Thus, it can produce 32 oriented wavelets and lead to a more precise representation for the image than traditional transforms. The primary properties of the DDDTCWT include: approximate shift invariance, directional selectivity, a redundancy of 4:1 along with invariance to different scales of the transform, and a similarity to a continuous wavelet transform. Obviously, all these properties are instrumental to the image reconstruction of CS.

3 Image reconstruction

In the CS reconstruction, the model under the constraint condition of a signal’s sparsity can be described as follows:

$$\begin{aligned} \min ||\Psi ^{\mathrm{H}}x||_{l_1 }\ s.t\ {\Phi }x=y \end{aligned}$$
(5)

where \(x\in R^{N\times 1}\) represents a discrete-time signal, \(\Psi \in R^{N\times N}\) indicates the selected sparse base, y denotes the measured signal with a dimension of \(M\times 1\), \(\Phi \in R^{M\times N}\) is the measurement matrix which satisfies the RIP and can be obtained by random generation method [23]. In addition, the value of M / N is the sampling rate of CS. Herein, two sparse bases have been exploited to represent the image alternately, and the model can be described as:

$$\begin{aligned} \min ||\Psi _i ^{\mathrm{H}}x||_{l_1 }\ s.t\ {\Phi }x=y \end{aligned}$$
(6)

where \(i=1,2\), \(\Psi _1\) and \(\Psi _2\) indicate DCT and DDDTCWT, respectively. In order to use the framework of BCS and the smoothed projected Landweber reconstruction (SPL) algorithm for solving this question, \(\Phi \) is constructed by \(\Phi _B \), and \(\Phi _B\) is the measurement matrix for each image block after the segmentation. Concretely, the core of this paper’s reconstruction method will be presented in the next two parts: the reconstruction algorithm based on DCT and DDDTCWT, the entire reconstruction process integrated with the adaptive sampling.

Fig. 4
figure 4

Image Rose, Plant reconstruction with a fixed sampling rate. a DCT, b DWT, c DDWT, d CT, e DDDTCWT, f DCT-DDDTCWT

Full size image

3.1 The reconstruction algorithm based on DCT and DDDTCWT

To solve Eq. (5), Gan [14] and Mun [15] proposed the SPL algorithm which has been used widely. The algorithm starts from an approximative image, which is obtained from the measured vectors and corrupted by noises initially; then, the corrupted image is optimized by the iterative projecting and the thresholding to get the optimal image. In particular, the optimization process can be summarized: Initially project the vectors gained from the last iteration onto a convex set to obtain the new vectors; then, arrange the new vectors to form a new image; finally, apply the thresholding based on a sparse base to get the optimal results. Obviously, it can be seen that the projection and the thresholding are very important for the reconstruction. However, the thresholding has a close relationship with the used sparse base. Thus, the used sparse base is a key factor for the reconstruction of CS. The work of [15] has proved that the SPL algorithm can solve Eq. (5) with single sparse base. Considering the complexity of images, an effort was made to embed DCT and DDDTCWT into the SPL algorithm synchronously for solving Eq. (6). Thus, the thresholding will be performed in both DCT domain and DDDTCWT domain alternately to get the optimal results.

In addition, it is needed to segment the entire image into many image blocks before the sampling for fast processing and memory saving. Thus, the dimension of measurement matrix \(\Phi _B\) which satisfies the RIP similarly should match the dimension of each image block. The algorithm is described below.

Input The \(M\times B^{2}\) measurement matrix for each image block whose dimension is \(B\times B\) is designated as \(\Phi _B \), it satisfies \(\Phi _B^T \cdot \Phi _B =\mathbf{I}\) and can be obtained by the random generation method as described in [15]. The vector obtained from a image measurement by arranging all of its elements into a column is designated as \(y_{i}\), \(i=1,2,\ldots ,L^{2}/(B\times B)\), \(L\times L\) is the original image’s dimension. The convergence threshold to stop the iterations is designated as \(\varepsilon \). The number of maximum iterations allowed is designated as \(j_{\mathrm{max}}\).

Initialization Compute \(\tilde{x}_i =\Phi _B ^{+}\cdot y_i\) for each image block, then, convert and combine each vector \(\tilde{x}_i\) to construct an initial image \(x_0\). Additionally, set the iteration time \(j=0\);

Table 2 PSNR performance of color images based on different sparse bases
Full size table

Repetitions Iterate on the jth time.

  1. (1)

    Divide the image \(x_1\) obtained from the latest iteration into a set of non-overlapping image blocks \(x_i\). Convert each \(x_i\) into a 1-dimensional vector \(x_i ^{\prime }\), and calculate the optimized vector \(x_i ^{\prime \prime }\) as \(x_i ^{\prime \prime }=x_i ^{\prime }+\Phi _B ^{T}(y_i -\Phi _B x_i ^{\prime })\). Then, generate the image \(x_2\) by combining all the optimized vectors.

  2. (2)

    Use DCT to transform image \(x_2\), yielding f and processing it with a hard threshold. After that, the inverse DCT is applied to generate image \(x_3\) for the next step.

  3. (3)

    Optimize the image \(x_3 \) to obtain a new image \(x_4\). Note that the detailed optimization procedure is same as Step (1).

  4. (4)

    Use DDDTCWT to decompose image \(x_4\) and yield coefficient \(f_1\). Then, implement the thresholding, and obtain image \(x_5\) through the inverse DDDTCWT. This process seems very similar to Step (2) at first glance, nevertheless, there existing differences in terms of the thresholding. The bivariate shrinkage is adopted in the thresholding for \(f_1\) as it can exploit the statistical dependency between the transform coefficients and their corresponding parents’ coefficients (the upper level coefficients) and is more appropriate for the directional transforms. Specifically, the bivariate shrinkage is performed in the DDDTCWT domain, which is almost identical to the application in the dual-tree DWT (DDWT) domain, except that more sub-bands are needed to be handled.

  5. (5)

    Remove the blocking artifacts of image \(x_5\) by using the Wiener filter. The image \(x_6\) is the result after filtering.

  6. (6)

    Calculate \(E_j =\frac{1}{\sqrt{N}}\left\| {x_6 -x_1 } \right\| _2 \) and determine whether \(\left| {E_j -E_{j-1} } \right| <\varepsilon \) or \(j>j_{\max }\) is satisfied. Here, \(E_{j-1}\) represents the MSE between \(x_6\) and \(x_1 \), which is calculated in the (\(j-1\))th iteration. If the condition is met, the optimization will stop, otherwise, designate \(j=j+1\) and enter the next iteration.

Output The reconstructed image \(x_\mathrm{rec} =x_6\).

Obviously, the improvement in the SPL algorithm of this paper just change the sparse bases and does not change the essence of the algorithm (the projection method); thus, the algorithm of this paper can realize the image reconstruction at the preliminary analysis. The specific experimental validation is displayed in the next section.

Fig. 5
figure 5

Image Lena, Zebra, Temple, and Bookcase reconstruction utilizing different methods. a DCT-DDDTCWT, b adaptive-TV, c this paper’s methodology

Full size image

3.2 The entire reconstruction process integrated with the adaptive sampling

It is known that the smoother the image block is, the greater its sparsity is. Generally, only a small amount of measurement information is required to achieve a precise reconstruction. On the contrary, a larger amount of measurement information would be needed for the reconstruction of an image block with rich detail information. Thus, it can give a revelation whether the image can be reconstructed in the different sampling rates. For the smooth part of the image, a low dimension matrix can be used to measure it, while a high dimension matrix can be used to measure the non-smooth part of the image. If there is just one measurement matrix is used in the reconstruction, the sampling rate is difficult to set. The low sampling rate will lower the overall reconstruction precision, while the higher sampling rate will be not very necessary for the reconstruction of the smooth part in image. Thus, in this way, it is easy to balance the reconstruction precision and can make both the smooth part and the non-smooth part of the image achieve a higher reconstruction precision theoretically.

Table 3 PSNR performance of gray image utilizing different methods
Full size table

However, there exists one question: how to distinguish the image’s smooth and non-smooth part? It is known the image is needed to be segmented in the reconstruction as mentioned before, thus considering these factors comprehensively the block-based sampling approach can be adopted. That means, the image can be divided into many blocks firstly; then, classify all the blocks into two types according to their smoothness; lastly, use different matrixes to measure and reconstruct the blocks.

In particular, the classification principle is based on the variance of image blocks [24]. The threshold T is designated as \(T=p\cdot (\sigma _{\max }^2 -\sigma _{\min }^2 )+\sigma _{\min }^2 \), where \(\sigma _{\max }\) and \(\sigma _{\min }\) indicate the maximum and minimum value of all blocks’ variance, respectively, and p is an adjustable parameter. The two measurement matrices designed for the smooth blocks and the non-smooth blocks are \(\Phi _{Bl}\) and \(\Phi _{Bh}\), respectively. The method of generating \(\Phi _{Bl}\) and \(\Phi _{Bh}\) is same as that of generating \(\Phi _{B}\), and the process to make sure the dimension of \(\Phi _{Bl} \) and \(\Phi _{Bh}\) is described below.

Firstly, the sampling rate for smooth blocks is defined as \(s_1\), and the other sampling rate for non-smooth blocks is \(s_2\). If s is the average sampling rate for the entire image, it will satisfy \(n_0 s=n_1 s_1 +n_2 s_2 \), \(n_0\) is the total number of all blocks, \(n_1\) is the number of smooth blocks, \(n_2\) is the number of non-smooth blocks. Then, make sure \(n_1\) and \(n_2\) by adjusting the parameter p. Obviously, if \(s,n_0 ,n_1 , n_2\) are known, it is easy to find the range of \(s_1\) and \(s_2\). (In this paper, make \(s_2 =2s_1\) and \(n_1 =n_2\) for determining \(s_1\) and \(s_2\) easily.) If \(s_1\) and \(s_2\) are known, the dimension of \(\Phi _{Bl}\) and \(\Phi _{Bh}\) will be made sure.

After obtaining \(\Phi _{Bl}\) and \(\Phi _{Bh} \), the specific information of the original image can be acquired. Then, the algorithm described in Sect. 3 is employed to reconstruct the image. However, it should be noted that the optimization process is not identical to that mentioned above. The difference is primarily in the initialization, in both Steps (1) and (3), where \(\Phi _{B}\) is replaced by \(\Phi _{Bl}\) and \(\Phi _{Bh}\) in each iteration. The same implementation occurs in the other steps, so it will not take too much description here. The specific experimental evaluation is provided in the next section.

4 Experiments

Several experiments were performed to evaluate the proposed method. These experiments could be divided into two classes based on whether the adaptive sampling was integrated into the reconstruction or not. In addition, all the random measurement matrices selected were orthonormal in this paper, the stopping parameter was set as \(\varepsilon =0.001\), and the dimension of all the experiment images was \(512\times 512\). Figure 2 shows all the images used in the experiments.

4.1 The first experiment

In order to evaluate the impact of different sparse bases for reconstruction, DCT, DWT, DDWT, CT, DDDTCWT were deployed, along with the combination of DCT and DDDTCWT (DCT-DDDTCWT) in the reconstruction. Further, this experiment was divided into two groups according to the type of images. In the first group, some gray images were reconstructed, and the color images were reconstructed in the second group. Specifically, for the reconstruction of color image, the image was decomposed into three channels (R, G, B) firstly, secondly the image was reconstructed in different channels, and lastly the reconstructed results were combined into one image.

Fig. 6
figure 6

Images Deer, Furniture, Plant, and House reconstruction utilizing different methods. a DCT-DDDTCWT, b adaptive-TV, c this paper’s methodology

Full size image

Figure 3 illustrates the visual reconstruction results for the gray images: Lena, Barbara, and Curtain, and the sampling rates of different images are 0.1, 0.2, 0.2, respectively. As can be seen, the blocking artifacts are apparent in the images obtained by the BCS and the iterative projection algorithms along with DCT, DWT, and CT, even though the Wiener filtering has been applied in the process. On the other hand, the results obtained by integrating DDWT or DDDTCWT could eliminate the blocking artifacts efficiently and provide a superior visual effect. However, the reconstruction images based on DDDTCWT become too smooth, and the texture part of these images becomes blurry. The algorithm described in Sect. 3 achieves a better performance compared to the former. Thus, the results demonstrate that the proposed algorithm can reconstruct the texture and edges of image synthetically. In addition, Table 1 shows the PSNR of different reconstruction images at different sampling rates ranging from 0.1 to 0.5. In this table, the maximum value for each set of comparison results is bolded. It is evident that the algorithm combined with DCT and DDDTCWT simultaneously is competitive in the image reconstruction.

Table 4 PSNR performance of color image utilizing different methods
Full size table

Figure 4 illustrates the visual reconstruction results for the color images: Rose, Plant. The sampling rates of different images are 0.1, 0.2, respectively. Obviously, the images reconstructed by the first five kinds of sparse bases contain more noise. Especially when the sparse base is DWT, the reconstruction results are very poor. Table 2 shows the PSNR of different reconstruction images at different sampling rates ranging from 0.1 to 0.5. In this table, the maximum value for each set of comparison results is also bolded as in Table 1. The results are similar to that of the gray images, the algorithm integrated with DCT and DDDTCWT can raise the PSNR further, especially when the sampling rate is relatively low.

Therefore, all the results of the first experiment have proved that the algorithm of this paper is very competitive in the reconstruction of both the gray images and color images, especially for the content-rich image reconstruction.

4.2 The second experiment

In this experiment, this paper’s method based on the adaptive sampling and the joint sparse bases was compared with the method mentioned in the first experiment. Meanwhile, another approach known as “adaptive-TV” was also added to the comparison, which means the iterative projection algorithm was replaced by the minimum TV optimization algorithm in Candes’s work [25]. In addition, this experiment was also divided into two groups: the gray image reconstruction and the color image reconstruction.

When the sampling rate is 0.2, the experimental results are displayed in Fig. 5. It is noted that the blocking artifacts are extremely severe in Fig. 5b, because the optimization is performed on each image block separately and the smoothing is not added to the reconstruction process, even though the adaptive sampling has been utilized. Further, comparing the results obtained from the other two methods, it can be seen that the reconstruction precision is improved after using the adaptive sampling, and the most distinct improvement is that the texture part of each image is clearer. Table 3 provides the objective evaluation of reconstruction for the three methods. Likewise, the maximum value in each set of comparison results is also bolded. Obviously, the results are consistent with the visual results. The PSNR of image reconstructed by this paper’s method could be increased by 2.3 dB, compared with the PSNR of image reconstructed based on “adaptive-TV”. Furthermore, comparing the results of this paper’s method with that of the method integrated with a fixed sampling, the adaptive sampling can improve the PSNR of image about 1 dB effectively. Thus, it illustrates that the adaptive sampling is conducive to the reconstruction of a higher-quality gray image.

Figure 6 illustrates the visual reconstruction results for the color images: Deer, Furniture, Plant, and House. The sampling rates for different images are 0.1, 0.2, 0.2, 0.2. Obviously, Fig. 6c is clearer than Fig. 6a, b in each image group, the blocking artifacts are extremely severe in Fig. 6b, and the reconstruction results are similar to that of the gray images. In addition, Table 4 displays the objective evaluation and the significance of the bold font in this table is same as the previous tables. Clearly, this paper’s method can increase the PSNR of color image by about 1 dB on average, compared with the PSNR of image reconstructed by “adaptive-TV”. Therefore, the paper’s method is effective for the reconstruction of gray images and color images, and it is the most competitive in the three methods.

5 Conclusion

Considering the influences of different sparse bases and the adaptive sampling for image reconstruction in CS, this paper has proposed a new reconstruction method employing the adaptive sampling and an SPL algorithm integrated with DCT and DDDTCWT simultaneously. Experimental results show that, in most cases, the optimization algorithm based on DCT and DDDTCWT performs better than that based on one sparse base alone. Moreover, the reconstruction integrated with the adaptive sampling mentioned above can lead to the higher-quality image reconstruction. However, there remain many issues regarding this paper’s method to be studied in the future. One example would be how to optimize the adaptive sampling further to improve the reconstruction precision.