Investigation of Priority Based Optical Packet Switch Under Self-Similar Variable Length Input Traffic Using Matrix Queueing Theory

Abstract

In this paper, queueing behavior of the optical packet switch (OPS) employing priority based partial buffer sharing (PBS) mechanism under asynchronous self-similar variable length packet input traffic is investigated. Markov modulated Poisson process (MMPP) emulating self-similar traffic is used as input process. In view of wavelength division multiplexing (WDM)OPS output port of switch is modeled as multi-server (MMPP∕M∕c∕K) queueing system. Service times (packet lengths) are assumed to be exponential distributed as traffic under consideration is unslotted asynchronous. Performance measures, namely, high priority packet loss probability and low priority packet loss probability against the system parameters and traffic parameters are computed by means of matrix-geometric solutions and approximate Markovian model. This kind of analysis is useful in dimensioning the switch employing PBS mechanism under self-similar variable length packet input traffic and to provide differentiated services (DiffServ) and quality of service (QoS) guarantee.

1 Introduction

Internet Protocol (IP) traffic of both Ethernet and wide area network (WAN) traffic are shown to be self-similar and long-range dependent (LRD) [6, 10, 13]. Markov modulated Poisson process (MMPP) could be used to model the self-similar traffic over the desired time-scales [2, 8, 19] to investigate the queueing behavior of network switches. These models hold good for queueing based performance analysis and are computationally tractable. Optical packet switch (OPS) with wavelength division multiplexing (WDM) technology is promising a good quality of service (QoS). In OPS, there are N input fiber lines, N output fiber lines, and each fiber line has K wavelength channels and a wavelength converter pool of size c (0 ≤ c ≤ K), dedicated to each output fiber line. In general, OPS networks are classified into two categories: synchronous (slotted) and asynchronous (unslotted) [15]. In the case of first one, all the packets have same size [4, 14]. In asynchronous OPS networks all the packets have variable lengths and are not aligned before they enter the OPS [5, 16, 18]. The specific output port of asynchronous OPS with self-similar variable length packet input traffic is modeled as MMPP∕M∕c∕K queueing system. Therefore, performance analysis of OPS is equivalent to solving a problem of MMPP∕M∕c∕K queueing system.

The another issue is to provide differentiated service (DiffServ) as Internet traffic is moving towards DiffServ rather than integrated services. Broadband integrated services digital network (B-ISDN) has to support different kinds of communication services such as video phone, video conferencing, data traffic, and voice sources in more efficient manner. High demand of network traffic results in congestion problems. Congestion problem in network traffic can be dealt with some priority mechanisms. One of such mechanisms is buffer access control (BAC), also called space priority mechanism. There are several strategies by which one can implement this BAC mechanism; one of such strategies is partial buffer sharing (PBS) mechanism. In this scheme, a threshold is imposed on both high priority and low priority packets. The part of buffer on or below the threshold is shared by all arriving packets. When the buffer occupancy is above the threshold, the arriving low priority packets will be rejected. High priority packets will be lost only when buffer is full. If the threshold is relatively high, then the high priority packets will be lost more than expectedly. Whereas, if the threshold is relatively low, then low priority packets will be lost excessively [14, 16, 17, 21]. This way, there is a trade-off between threshold setting and packet loss. Hence, optimal threshold setting is very important in buffer dimensioning. Priority queue models are briefly discussed below. In the paper [20], the queueing analysis of infinite buffer priority system with MMPP as the input process is investigated with an assumption that the delay sensitive cells and non-delay sensitive cells arrive at two separate queues. This kind of scheme is not realistic as the buffers consist of limited number of fiber delay lines (FDLs) with fixed granularity. The loss behavior of finite buffer space priority queues with discrete batch Markovian arrival process (D −BMAP) has been analyzed in the paper [21] which is not the case, since the router under consideration is handling self-similar traffic with continuous time Markov process. In the papers [14, 16], switch is modeled as single server queueing system which is not appropriate for the reason mentioned in the first paragraph. To the best of our knowledge, WDMOPS with self-similar variable length packet input traffic employing PBS mechanism is not yet investigated. In this paper, we model WDMOPS with self-similar variable length packet input traffic as MMPP∕M∕c∕K queueing system with PBS mechanism.

The rest of the paper is organized as follows: In Sect. 2, queueing model of the switch employing PBS mechanism is briefly introduced. In Sect. 3, numerical results are presented graphically. Finally, conclusion is given in Sect. 4.

Fig. 1

The operation and the equivalent queueing model of a specific output port of OPS employing PBS mechanism with two different priority input traffic

2 Queueing Model of the Switch Employing Partial Buffer Sharing Mechanism

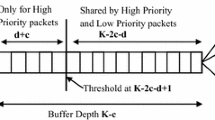
Consider the WDM asynchronous N × N OPS with each output fiber line consisting of K wavelength channels and a wavelength converter pool of size c. Buffer depth then is K − c. Such a switch with self-similar variable length packet input traffic can be modeled as MMPP∕M∕c∕K queueing system. The operation and queueing model of the OPS employing PBS mechanism is shown in Fig. 1. As shown in the figure, the threshold is set at the level K − 2c − d, where d is a positive integer. The low priority packets can only access first K − 2c − d − 1 buffer spaces, whereas the high priority packets can utilize the whole buffer space [14, 20]. For the sake of simplicity, two priorities are considered. Each priority traffic is characterized by MMPP. Assume that high priority (class1) packets and low priority (class2) packets arrive at the system according to MMPPs with number of states m ₁ and m ₂, respectively. These MMPPs are characterized by the matrices $\{Q(1),\Lambda (1)\}$ and $\{Q(2),\Lambda (2)\}$, respectively. The service time is generally and identically distributed with distribution function H(t). Let B _m ^(k)(t), {m ≥ 0, k = 1, 2} denote the matrices whose (i, j)th element is the probability that given departure of class k at time 0, there is at least one packet left in the system and the process is in state i, the next departure of class k occurs no later than time t with the arrival process in state k, and during that service time there are m arrivals. Then B _m ^k(t) satisfies the following equation

$$\displaystyle{ \sum \limits _{m=0}^{\infty }B_{ m}^{(k)}(t)\ z^{m}\ =\ \int \limits _{ 0}^{t}e^{[\ Q(k)-\Lambda (k)+\ \Lambda (k)\ z]\ \tau }\ dH(\tau ),\ \ \ k = 1,2. }$$

(1)

where H(t) is the service time distribution. When the service time is exponential with mean service rate μ, we have

$$\displaystyle{ \sum \limits _{m=0}^{\infty }\ B_{ m}^{(k)}\ z^{m} =\mu ^{2}\sum \limits _{ m=0}^{\infty }\ [\ \frac{Q(k) - \Lambda (k) +\ \Lambda (k)\ z} {\mu } ]\ ^{m},\ \ \ k = 1,2. }$$

(2)

It is obvious that the matrices B _m ^(k) can be evaluated by comparing the coefficient of z ^m on both sides of the Eq. (2) and the procedure is outlined in the paper [16]. We consider the embedded Markov chain {L _n , J _n ∕n ≥ 0} at the departure epochs of the queueing system on the state space U = { (b, i, j)∕0 ≤ b ≤ K − c, 1 ≤ i ≤ m ₁, 1 ≤ j ≤ m ₂}, where L _n denotes the buffer occupancy and J _n denotes the phase of superposed MMPP. For convenience, a queueing system is said to be at level b, if its buffer occupancy is equal to b (excluding the ones in service). The embedded Markov chain has an irreducible transition probability matrix P(with the dimension (K − c + 1)m ₁ m ₂×(K − c + 1)m ₁ m ₂) given as follows:

$$\displaystyle{ P = [P_{1}: P_{2}] }$$

(3)

where,

$$\displaystyle\begin{array}{rcl} P_{1}\ & =& \ \left [\begin{array}{*{10}c} B_{0} & B_{1} & \cdots &B_{K-3c-d-1} & B_{K-3c-d} &\cdots &B_{K-2c-d-1} & C_{K-2c-d}\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \vdots \\ B_{0} & B_{1} & \cdots &B_{K-3c-d-1} & B_{K-3c-d} &\cdots &B_{K-2c-d-1} & C_{K-2c-d} \\ 0 &B_{0} & \cdots &B_{K-3c-d-2} & B_{K-3c-d-1} & \cdots &B_{K-2c-d-2} & C_{K-2c-d-1}\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 &\cdots & B_{0} & B_{1} & \cdots & B_{c} & C_{c+1} \\ 0 & 0 &\cdots & 0 & B_{0} & \cdots & B_{c-1} & C_{c}\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 &\cdots & 0 & 0 &\cdots & B_{0} & C_{1} \\ 0 & 0 &\cdots & 0 & 0 &\cdots & 0 & B_{0}^{(1)}\bigotimes \ B_{-2}\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 &\cdots & 0 & 0 &\cdots & 0 & 0\\ \end{array} \right ]{}\end{array}$$

(4)

$$\displaystyle\begin{array}{rcl} P_{2}& =& \left [\begin{array}{*{10}c} B_{K-2c-d+1}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{K-2c}^{(1)}\bigotimes \ B_{-2} & \cdots &B_{K-c-1}^{(1)}\bigotimes \ B_{-2} & E(K - c)\\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ B_{K-2c-d+1}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{K-2c}^{(1)}\bigotimes \ B_{-2} & \cdots &B_{K-c-1}^{(1)}\bigotimes \ B_{-2} & E(K - c) \\ B_{K-2c-d}^{(1)}\bigotimes \ B_{-2} & \cdots &B_{K-2c-1}^{(1)}\bigotimes \ B_{-2} & \cdots &B_{K-c-2}^{(1)}\bigotimes \ B_{-2} & E(K - c - 1)\\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ B_{c+2}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{c+d+1}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{2c+d}^{(1)}\bigotimes \ B_{-2} & E(2c + d + 1) \\ B_{c+1}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{c+d}^{(1)}\bigotimes \ B_{-2} & \cdots &B_{2c+d-1}^{(1)}\bigotimes \ B_{-2} & E(2c + d)\\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ B_{2}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{d+1}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{c+d}^{(1)}\bigotimes \ B_{-2} & E(2c + d + 1) \\ B_{1}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{d}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{c+d-1}^{(1)}\bigotimes \ B_{-2} & E(2c + d)\\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ 0 &\cdots & B_{0}^{(1)}\bigotimes \ B_{-2} & \cdots & B_{c-1}^{(1)}\bigotimes \ B_{-2} & E(c)\\ \end{array} \right ]\quad {}\end{array}$$

(5)

In (4) and (5),

$B_{i}\ =\ \sum \limits _{i^{{\prime}}=0}^{i}\ (B_{i^{{\prime}}}^{(1)}\ \bigotimes \ B_{i-i^{{\prime}}}^{(2)})$

$B_{-2}\ =\ \sum \limits _{i=0}^{\infty }\ B_{i}^{(2)}$

$C_{l}\ =\ \sum \limits _{i=0}^{l}\ (B_{i}^{(1)}\ \bigotimes \ B_{-2}^{(l-1)})$

$E(p)\ =\ B_{-1}^{(p)}\ \bigotimes \ B_{-2},\ \ \ p = c,c + 1,\ldots,K - c.$

$B_{k}^{(l)}\ =\ \sum \limits _{i=l}^{\infty }\ B_{i}^{(k)},\ \ \ k = 1,2.$

In the above, the elements of the first (c + 1) rows are identical. The fundamental arrival rate of class k packets is $\lambda ^{(k)} =\pi (k)\Lambda (k)e,\ k = 1,2$, where π(k) is the steady state probability vector of Q(k). The traffic intensity ρ = (λ ⁽¹⁾ +λ ⁽²⁾) E[H(t)]. From the PBS mechanism, it is clear that high priority packet loss occurs if buffer is full, whereas low priority packet loss is due to the threshold mechanism. Let $x = (x_{0},x_{1},\ldots,x_{K-c})$, where $x_{q} = (x_{q,11},x_{q,12},\ldots,x_{q,m_{1},m_{2}})$, q = 0, 1, …, K − c, and x _q, l, m is the conditional probability that there are q packets in the system given that embedded Markov chain is in the (l, m) state. Therefore, we have xP = x,  xe = 1 where e is the column vector consisting of all 1. Then, in the steady state, high priority packet loss probability, P ^hp, and low priority packet loss probability,P ^lp, respectively, are [21],

$$\displaystyle\begin{array}{rcl} P^{hp}& =& \frac{1} {\lambda ^{(1)}}\{\ \sum \limits _{r=0}^{c}\ \sum \limits _{ i=1}^{\infty }\ ix_{ r}\ (B_{K-c+i}^{(1)}\bigotimes \ B_{ -2})e \\ & & +\ \sum \limits _{r=1}^{K-2c}\ \sum \limits _{ i=1}^{\infty }\ ix_{ c+r}\ (B_{K-c+i-r}^{(1)}\bigotimes \ B_{ -2})e\}{}\end{array}$$

(6)

$$\displaystyle{P^{lp} = \frac{1} {\lambda ^{(2)}}\{\sum \limits _{r=0}^{c}(\ \sum \limits _{ i=1}^{\infty }\ ix_{ r}[\ \sum \limits _{j=0}^{K-2c-d}\ (B_{ j}^{(1)}\bigotimes \ B_{ K-2c-d+i-j}^{(2)})}$$

$$\displaystyle{+\ (B_{-1}^{(K-2c-d+1)}\bigotimes \ B_{ -2})]e])}$$

$$\displaystyle{+\sum \limits _{r=1}^{K-2c-d-1}\ (\sum \limits _{ i=1}^{\infty }\ i\ x_{ c+r}\ [\sum \limits _{j=0}^{K-2c-d-r}\ (B_{ j}^{(1)}\ \bigotimes \ B_{ K-2c-d+i-j}^{(2)})}$$

$$\displaystyle{+(B_{-1}^{(K-2c-d+1+r)}\ \bigotimes \ B_{ i}^{(2)})]\ e)}$$

$$\displaystyle{ +\sum \limits _{r=K-2c-d}^{K-2c}\ (\ \sum \limits _{ i=1}^{\infty }\ i\ x_{ c+r}\ (B_{-1}\ \bigotimes \ B_{i}^{(2)})\ e)\} }$$

(7)

Further, in view of threshold setting we decompose the state space U into two subsets:

$$\displaystyle{U_{nc}\ =\ \{(b,i,j)/\ 0 \leq \ b \leq \ K - 2c - d - 1,\ 1 \leq \ i \leq \ m_{1},\ 1 \leq \ j \leq \ m_{2}\}}$$

$$\displaystyle{U_{c}\ =\ \{(b,i,j)/\ K - 2c - d \leq \ b \leq \ K - c,\ 1 \leq \ i \leq \ m_{1},\ 1 \leq \ j \leq \ m_{2}\}}$$

This partition of U makes the transition probability matrix Q decomposed as follows:

$$\displaystyle\begin{array}{rcl} Q\ & =& \ \left [\begin{array}{*{10}c} Q_{nc} &Q_{nc,c} \\ Q_{c,nc}& Q_{c}\\ \end{array} \right ]\quad {}\end{array}$$

(8)

The sub-matrices Q _nc , Q _nc, c , Q _c, nc , and Q _c are the left upper part, right upper part, left lower part, and right lower part of the matrix Q with dimensions of (K − 2c − d)m ₁ m ₂× (K − 2c − d)m ₁ m ₂,  (K − 2c − d)m ₁ m ₂× (d + c + 1)m ₁ m ₂, (d + c + 1)m ₁ m ₂× (K − 2c − d)m ₁ m ₂, and (d + c + 1)m ₁ m ₂× (d + c + 1)m ₁ m ₂, respectively. These sub-matrices govern the transitions from U _nc into itself, from U _nc into U _c , from U _c into U _nc , and from U _c into itself, respectively. Following the algorithm in the paper [21], we compute the high priority packet loss probability and low priority packet loss probability.

3 Numerical Results

Following matrix-geometric solutions, [3, 9, 11, 12], we compute the steady state packet loss probabilities. We follow the generalized variance based Markovian fitting method proposed in [19] to emulate the second order self-similar variable length packet input traffic for both high priority and low priority packet traffic. The mean arrival rate and variance of the self-similar traffic is set to be 1 and 0.6, respectively [19], the interested time-scale range to emulate self-similarity is over [10², 10⁷], [2, 19]. It is shown from [2, 19] that in order to emulate self-similar traffic well, the minimum number of states of the resultant MMPPs must be greater than or equal to 16. That is, both m ₁ and m ₂ must be ≥ 16. Therefore, each class is characterized by 16 × 16 matrices. With such a high dimensional MMPP for both high priority and low priority traffic, it is a great challenge for the numerical process. In order to reduce the computation complexity, we use approximate model [14], which is based on the papers [1, 7]. The resultant 16-state MMPP of low priority packets is approximated by a 2-state MAP. By applying this approximated model, the computational complexity is reduced by 8³ = 512 times. We employ two different traffic corresponding to the Hurst parameter values H = 0. 7 and H = 0. 8, and the buffer depth,K, of the router and the number of servers, c, are set to be 24 and 4, respectively, and the results are presented in Figs. 2, 3, 4, 5. From Fig. 2, we observe that the high priority packet loss probability decreases and the low priority packet loss probability increases as the threshold increases. In order to find out the optimal level of the threshold, we illustrate a plot of high priority packet loss probabilities against the low priority ones at various d in Fig. 3. We could find out that the optimal level of the threshold is the one located nearest to the left lower corner of the plot, which is around d = 6. Figures 4, 5 depict the variation of packet loss probability against traffic intensity and buffer capacity, respectively. From Fig. 4, it is clear that packet loss probability increases as traffic intensity increases. From Fig. 5, we observe that of high priority and low priority packet loss probabilities both decrease as the buffer capacity increases.

4 Conclusion

We investigate the loss behavior of asynchronous router employing PBS mechanism to provide differentiated services under Markovian modeled self-similar variable length packet input traffic. The performance measures, namely, the steady state high priority and low priority packet loss probabilities are computed and presented graphically. To reduce the computation complexity, the original high dimensional of the low priority packets is approximated by 2-state. With this analysis, we could locate the optimal threshold position of buffer to obtain the greatest performance.

Fig. 2

Variation of packet loss probability with threshold

Fig. 3

Comparison of high priority PLP with low priority packet loss probability

Fig. 4

Variation of packet loss probability with traffic intensity

Fig. 5

Variation of packet loss probability with buffer capacity