1 Introduction

Both local area network (LAN) and wide area network (WAN) traffic are proved to be self-similar and long-range dependent (LRD) [7, 11, 16]. Markov modulated Poisson process (MMPP) is employed to emulate the self-similar traffic [2, 9, 22]. Queueing system with MMPP input process can be used to investigate the queueing behavior of network nodes such as routers or switches. Internet router with wavelength division multiplexing (WDM) guarantees the quality of service (QoS). The router consists of N input fiber lines, N output fiber lines, and each fiber line has K wavelength channels and a wavelength converter pool of size c, \( \left( {0 \le c \le K} \right) \) dedicated to each output fiber line. In general, networks are divided into two categories: one is synchronous (slotted) and other is asynchronous (unslotted) [18]. In the case of first one, all the packets have same size and arrive at regular intervals [6, 17, 23]. In asynchronous networks, packets are of variable lengths [4, 19, 21]. In this paper, synchronous router with self-similar traffic input is modelled as \( {\text{MMPP/D/c/K}} \) queueing system. Therefore, performance study of Internet router is equivalent to solving a problem of \( {\text{MMPP/D/c/K}} \) queueing system.

On the other hand, Broadband integrated services digital network (B–ISDN) is to provide different kinds of communication services such as video phone, video conferencing, data and voice in more efficient way. This kind of high demand traffic results in congestion problems. We can handle these problems with some priority mechanism. One of such mechanisms is space priority mechanism. There are several strategies by which we can implement this mechanism. One of such strategies is partial buffer sharing (PBS) mechanism [20, 24]. In this scheme, a threshold is set on both high priority and low priority packets. On or below the threshold, all arriving packets are allowed, when the buffer occupancy exceeds the threshold, low priority packets will be rejected. High priority packets will be lost if the buffer is full. It is clear that if the threshold is relatively high, then the high priority packet loss will be high. Whereas, if the threshold is relatively low, then low priority packets will be lost excessively. The threshold setting induces two time periods, namely, critical and non-critical periods [19, 24]. The critical period is the time period during which buffer occupancy of the queueing system is on or above threshold level and the non-critical period is the time period during which buffer occupancy is below the threshold level. This way, there is a trade-off between threshold setting and packet loss. Hence, optimal threshold setting is very important in buffer dimensioning. Priority queue models are briefly discussed below. In paper [23], the queueing analysis of infinite buffer priority system with MMPP input is investigated with an assumption that the delay sensitive cells and non-delay sensitive cells arrive at two separate queues. This scheme is not realistic as the buffers consist of limited number of fiber delay lines (FDLs) with fixed granularity. The loss behavior of finite buffer space priority queues with discrete batch Markovian arrival process (D–BMAP) has been analyzed [24] which is not the case, since the router under consideration is handling self-similar traffic which is modelled by continuous-time Markov process. In papers [17, 19], router is modelled as single-server queueing system which is not appropriate for the reason mentioned in the first paragraph. In this paper, WDM Internet router with self-similar traffic input is modelled as \( {\text{MMPP/D/c/K}} \) queueing system with PBS mechanism to investigate its queueing behavior.

The rest of the paper is organized as follows: In Sect. 2, fundamentals of self-similar process and MMPP arrival process are briefed. Queueing model of the router and \( {\text{MMPP/D/c/K}} \) queueing system employing PBS mechanism is discussed in Sect. 3. In Sect. 4, numerical results are presented graphically. Finally, conclusion is given in Sect. 5.

2 Fundamemtals of self-similar process and Markov modulated Poisson process (MMPP) arrival process

In this section, we present the fundamentals of self-similar process and MMPP arrival process. The definition of exact second-order self-similar processes is given as follows [22]. If we consider X as a second-order stationary process with variance \( \sigma^{2} \), and divide time axis into disjoint intervals of unit length, we could define \( X = \{ X_{t} /t = 1,\,2,\,3, \ldots \} \) to be the number of points (packet arrivals) in the \( t^{th} \) interval. A new sequence \( X^{(m)} = \left\{ {X_{t}^{(m)} } \right\} \), where

$$ X_{t}^{(m)} = \frac{1}{m}\sum\limits_{i = 1}^{m} {X_{(t - 1)m + i} } ,\quad t = 1,\,2,\,3, \ldots, $$
(1)

is the average of the original sequence in m non-overlapping blocks. Then the process X is defined as an exact second-order self-similar process with the Hurst parameter, H, if

$$ Var(X^{(m)} ) = \sigma^{2} m^{{ - \beta_{1} }} ,\quad \forall m \ge 1. $$
(2)

where \( \beta_{1} = 2 - 2H \). For the self-similarity and long range dependent (LRD), Hurst parameter, \( \frac{1}{2} < H < 1 \), i.e., \( 0 < \beta_{1} < 1 \).

Next we present the fundamentals of MMPP arrival process [21]. The MMPP is the doubly stochastic Poisson process whose arrival rate is given by \( \lambda^{*} [J_{t} ] \), where \( J_{t} \), \( t \ge 0 \) is an m-state Markov process. The MMPP has m arrival rates \( \lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} \), of a Poisson process according to an m-state continuous-time Markov chain. The arrivals occur according to a Poisson of rate \( \lambda_{j} \), when the Markov chain is in state \( j,\,\,\,1 \le j \le m \). The MMPP is characterized by the matrices \( Q \) and \( \varLambda \), (inhomogeneous), where \( Q \) is the infinitesimal generator matrix and \( \varLambda \) is the diagonal matrix with Poisson arrival rates, are given as follows:

$$ Q = \left[ {\begin{array}{*{20}c} { - c_{1} } & {c_{12} } & \cdots & {c_{1m} } \\ {c_{21} } & { - c_{2} } & \cdots & {c_{2m} } \\ \vdots & \vdots & \ddots & \vdots \\ {c_{m1} } & {c_{m2} } & \cdots & { - c_{m} } \\ \end{array} } \right], $$
(3)

where \( c_{i} = \sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{m} {c_{ij} } \) for \( i = 1,\,2, \ldots ,\,m \) and

$$ \varLambda = diag(\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} ). $$
(4)

The steady state vector of the Markov chain is \( \pi \) such that \( \pi Q = 0,\,\pi e = 1 \), where e is the column vector of length m consisting of all 1. The mean arrival rate \( \lambda \) of MMPP is given by \( \lambda = \pi \varLambda e \). In the 2-state case, \( Q \), \( \varLambda \), and \( \pi \) are given as follows:

$$ Q = \left[ {\begin{array}{*{20}c} { - c_{1} } & {c_{1} } \\ {c_{2} } & { - c_{2} } \\ \end{array} } \right],\,\quad\varLambda = \left[ {\begin{array}{*{20}c} {\lambda_{1} } & 0 \\ 0 & {\lambda_{2} } \\ \end{array} } \right]\,\quad{\text{and}}\,\quad\pi = \frac{1}{{c_{1} + c_{2} }}(c_{2} ,c_{1} ). $$
(5)

Let \( N_{t} ,\,t \ge 0 \), be the number of arrivals in \( (0,t] \), for the stationary MMPP, the mean of N t is,

$$ E[N_{t} ] = \frac{{c_{2} \lambda_{1} + c_{1} \lambda_{2} }}{{c_{1} + c_{2} }}t. $$
(6)

The variance of N t is,

$$ Var[N_{t} ] = E[N_{t} ] + \frac{{2c_{1} c_{2} (\lambda_{1} - \lambda_{2} )^{2} }}{{(c_{1} + c_{2} )^{3} }}t - \frac{{2c_{1} c_{2} (\lambda_{1} - \lambda_{2} )^{2} }}{{(c_{1} + c_{2} )^{4} }}[1 - e^{{ - (c_{1} + c_{2} )t}} ]. $$
(7)

The interesting feature of MMPP is that a superposition of MMPPs is still MMPP. Special cases of the MMPP are the switched Poisson process (SPP), which is a two-state MMPP, and the interrupted Poisson process (IPP), which is an SPP with one of the arrival rates being zero, we take \( \lambda_{2} = 0 \).

3 Queueing model of the router and MMPP/D/c/K queueing system employing partial buffer sharing (PBS) mechanism

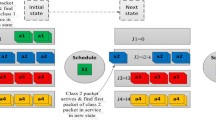
Consider the WDM synchronous \( N \times N \) router with each output fiber line consisting of K wavelength channels and a wavelength converter pool of size c. Buffer depth then is \( K - c \). Such a router with self-similar traffic input can be modelled as \( {\text{MMPP/D/c/K}} \) queueing system. The operation and multi-server queueing model of the router employing PBS mechanism is shown in Fig. 1. For the simplicity, two priority traffics are considered. The threshold is set at the level \( K - 2c - d + 1 \), where d is a positive integer. The low priority packets can only access first \( K - 2c - d \) buffer spaces and the high priority packets are for the whole buffer space. The threshold setting induces two time periods, namely, non-critical period and critical period [19, 24]. Non-critical period is the time period during which buffer occupancy is below the threshold level and critical period is the time period during which buffer occupancy is on or above threshold. Each priority traffic is characterized by MMPP process. Assume that high priority (class 1) packets and low priority (class 2) packets arrive at the system according to MMPPs of the states m 1 and m 2, respectively. These MMPPs are governed by the matrices \( \left\{ {Q(1),\,\varLambda (1)} \right\} \) and \( \left\{ {Q(2),\varLambda (2)} \right\} \), respectively. The service time is generally and identically distributed with distribution function \( H(t) \). Let \( B_{m}^{(k)} (t), \) \( \{ m \ge 0,\,k = 1,2\} \) be the matrices whose \( (i,j)^{th} \) element is the probability that given departure of class k at time 0, there is at least one packet left in the system and the process is in state i, the next departure of class k occurs no later than time t with the process in state j, during the service time there are m packets. We consider the Markov chain \( \{ (L_{n} ,J_{n} )/n \ge 0\} \) at the departure epochs of the queueing system on the state space \( U = \{ (b,(i,j))/0 \le b \le K - c,\,\,1 \le i \le m_{1} ,\,\,1 \le j \le m_{2} \} , \) where \( L_{n} \) denotes the buffer occupancy and \( J_{n} \) denotes the phase of superposed MMPP. For convenience, a queueing system is said to be at level b, if buffer occupancy is equal to b (excluding the ones in service). We ignore the time spent in a state and consider only the number of packets arrived during the sojourn time. Therefore, pertinent system is embedded Markov chain and has the following irreducible transition probability matrix P (with the dimension \( \left( {K - c + 1} \right)m_{1} m_{2} \, \times \,\left( {K - c + 1} \right)m_{1} m_{2} \)):

$$ P = \left[ {P_{1} :P_{2} } \right], $$
(8)

where

(9)
(10)
Fig. 1
figure 1

Operation and queueing model of a specific output port of router employing PBS mechanism with two different priority traffic input

Full size image

In Eqs. (9) and (10), the elements of row and column outside the matrices \( P_{1} \) and \( P_{2} \) are state spaces of the Markov chain and the elements of first (\( c + 1 \)) rows are identical. \( B_{i}^{(1)} ,i \ge 0 \), consists of the conditional probabilities that there are i high priority packet arrivals. \( B_{i}^{(2)} ,i \ge 0 \), consists of the conditional probabilities that there are i low priority packet arrivals.

$$ B_{i} = \sum\limits_{j = 0}^{i} {(B_{j}^{(1)} \otimes B_{i - j}^{(2)} } ),\quad i \ge 0, $$
(11)

i.e., \( B_{i} = B_{0}^{(1)} \otimes B_{i}^{(2)} + B_{1}^{(1)} \otimes B_{i - 1}^{(2)} + B_{2}^{(1)} \otimes B_{i - 2}^{(2)} + \cdots + B_{r}^{(1)} \otimes B_{i - r}^{(2)} + \cdots + B_{i}^{(1)} \otimes B_{0}^{(2)} \).

B i is the matrix consists of the conditional probabilities that there are i high priority and low priority packet arrivals and the general term \( B_{r}^{(1)} \otimes B_{i - r}^{(2)} \) is the matrix consists of the conditional probabilities that there are \( r \) high priority packet arrivals and \( i - r \) low priority packet arrivals.

$$ C_{l} = \sum\limits_{i = 0}^{l} {\left( {B_{i}^{(1)} \otimes \sum\limits_{j = l - i}^{\infty } {B_{j}^{(2)} } } \right)} ,\,\,\,l = 1,2, \ldots ,K - 2c - d + 1, $$
(12)
$$ \begin{aligned} i.e.,\quad C_{l} &= B_{0}^{(1)} \otimes \sum\limits_{j = l}^{\infty } {B_{j}^{(2)} } + B_{1}^{(1)} \otimes \sum\limits_{j = l - 1}^{\infty } {B_{j}^{(2)} } + B_{2}^{(1)} \otimes \sum\limits_{j = l - 2}^{\infty } {B_{j}^{(2)} } \\ &\quad + \cdots + B_{r}^{(1)} \otimes \sum\limits_{j = l - r}^{\infty } {B_{j}^{(2)} } + \cdots + B_{l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } \\ &= B_{0}^{(1)} \otimes \left( {B_{l}^{(2)} + B_{l + 1}^{(2)} + B_{l + 2}^{(2)} + \cdots } \right) & + B_{1}^{(1)} \otimes \left( {B_{l - 1}^{(2)} + B_{l}^{(2)} + B_{l + 1}^{(2)} + \cdots } \right) \\ & \quad +\,B_{2}^{(1)} \otimes \left( {B_{l - 2}^{(2)} + B_{l - 1}^{(2)} + B_{l}^{(2)} + \cdots } \right) \\ & \quad +\, B_{r}^{(1)} \otimes \left( {B_{l - r}^{(2)} + B_{l - r + 1}^{(2)} + B_{l - r + 2}^{(2)} + \cdots } \right) \\ & \quad + \cdots + B_{l}^{(1)} \otimes \left( {B_{0}^{(2)} + B_{1}^{(2)} + B_{2}^{(2)} + \cdots } \right) \\ \end{aligned} $$

\( C_{l} \) is the matrix consists of the conditional probabilities that there are \( l \) packet arrivals. In the above sum, the general term \( B_{r}^{(1)} \otimes \sum\nolimits_{j = l - r}^{\infty } {B_{j}^{(2)} } \, = B_{r}^{(1)} \otimes \left( {B_{l - r}^{(2)} + B_{l - r + 1}^{(2)} + B_{l - r + 2}^{(2)} + \cdots } \right) \) is the matrix consists of the conditional probabilities that there are r high priority packet arrivals and at least there are \( l - r \) low priority packet arrivals.

\( B_{{}}^{(2)} = \sum\nolimits_{i = 0}^{\infty } {B_{i}^{(2)} } \) consists of the conditional probabilities that there are \( \ge 0 \) low priority packet arrivals.

$$ A(p) = \sum\limits_{i = p}^{\infty } {B_{i}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } ,\quad p = c,c + 1, \ldots ,K - c, $$
(13)
$$\begin{aligned} i,e., \quad A(p) &= \left( {B_{p}^{(1)} + B_{p + 1}^{(1)} + B_{p + 2}^{(1)} + \cdots + B_{p + r}^{(1)} + \cdots } \right) \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} }\\ &= \left( {B_{p}^{(1)} + B_{p + 1}^{(1)} + B_{p + 2}^{(1)} + \cdots + B_{p + r}^{(1)} + \cdots } \right) \otimes \left( {B_{0}^{(2)} + B_{1}^{(2)} + B_{2}^{(2)} + \ldots } \right) \\&= B_{p}^{(1)} \otimes \left( {B_{0}^{(2)} + B_{1}^{(2)} + B_{2}^{(2)} + \cdots } \right) + B_{p + 1}^{(1)} \otimes \left( {B_{0}^{(2)} + B_{1}^{(2)} + B_{2}^{(2)} + \cdots } \right) \\&+ B_{p + 2}^{(1)} \otimes \left( {B_{0}^{(2)} + B_{1}^{(2)} + B_{2}^{(2)} + \cdots } \right) + \cdots + B_{p + r}^{(1)} \otimes \left( {B_{0}^{(2)} + B_{1}^{(2)} + B_{2}^{(2)} + \cdots } \right) + \cdots.\end{aligned} $$

\( A(p) \) is the matrix consists of the conditional probabilities that there are \( p \) packet arrivals.

In the above sum, the general term \( B_{p + r}^{(1)} \otimes \sum\nolimits_{j = 0}^{\infty } {B_{j}^{(2)} } \, = B_{p + r}^{(1)} \otimes \left( {B_{0}^{(2)} + B_{1}^{(2)} + B_{2}^{(2)} + \cdots } \right) \) is the matrix consists of the conditional probabilities that there are \( p + r \) high priority packet arrivals and \( \ge 0 \) low priority packet arrivals. All the above elements (matrices) are derived using the addition law and multiplication law of probabilities and the matrices \( B_{m}^{(k)} (t) \) satisfies the following equation [9],

$$ \sum\limits_{m\, = \,0}^{\infty } {\,B\,_{m}^{(k)} } (t)\,\,z^{m} = \int_{0}^{t} {e^{[\,Q\,(k) - \varLambda \,(k) + \varLambda \,(k)\,z]\,\tau } } dH(\tau ),\,\,\,k = 1,\,2. $$
(14)

We assume that service time follows deterministic distribution. The brief description of deterministic distribution is as follows [13]. Let \( Y \) be continuous and non-negative random variable of deterministic (degenerate) distribution. The probability density function (pdf) of \( Y \) is a Derac-delta function at \( h \). The Derac-delta (Impulse) function \( \delta (t) \) is defined as \( \mathop {\lim }\limits_{\varepsilon \to 0} \,F_{\varepsilon } (t) \), where,

$$ F_{\varepsilon } (t) = \left\{ {\begin{array}{*{20}c} {1/\varepsilon ,} & {0 \le t \le \varepsilon } \\ {0,} & {t > \varepsilon }. \\ \end{array} } \right. $$
(15)

Clearly, \( \int\nolimits_{0}^{\infty } {\delta (t)dt = 1} \), and the Laplace–Stieltjes transform (LST) of \( \int\nolimits_{0}^{\infty } {e^{ - st} \delta (t)dt = 1} \) and

$$ \overline{f} (s) = \int\limits_{0}^{\infty } {e^{ - st} \delta (t - h)dt = e^{ - sh} }. $$
(16)

The cumulative distribution function of the deterministic distribution is a unit step function (at \( h \)),

$$ F(t,h) = \left\{ \begin{aligned} 1,\,\,\,\,t \ge h \hfill \\ 0,\,\,\,t < h. \hfill \\ \end{aligned} \right. $$
(17)

The mean is \( E[Y] = ( - 1)\left[ {\frac{{d\overline{f} (s)}}{ds}} \right]_{s = 0} = \left[ {he^{ - sh} } \right]_{s = 0} = h \), and \( E[Y^{2} ] = ( - 1)^{2} \left[ {\frac{{d^{2} \overline{f} (s)}}{{ds^{2} }}} \right]_{s = 0} = \left[ {h^{2} e^{ - sh} } \right]_{s = 0} = h^{2} \).

Then the variance is \( Var[Y] = E[Y^{2} ] - E[Y]^{2} = h^{2} - [ - h]^{2} = 0 \).

When the service time is deterministic and is h units/packet, the Eq. (14) reduces to

$$ \sum\limits_{m\, = \,0}^{\infty } {\,B\,_{m}^{(k)} } (h)\,z\,^{m} = e^{[\,Q\,(k) - \varLambda \,(k) + \varLambda \,(k)\,z]\,h} ,\quad k = 1,\,2. $$
(18)

The matrices of counting function \( B_{m}^{(k)} (h) \) can be computed following the procedure [6, 17]. We drop the superscript ‘\( k \)’ for convenience and the procedure holds good for both high priority and low priority packets. From the Eq. (18), we have

$$ \begin{aligned} \sum\limits_{m\, = \,0}^{\infty } {\,B\,_{m} } (h)\,z\,^{m} & = e^{[\,Q\, - \varLambda + \varLambda \,z]\,h} , \\ & = \sum\limits_{r = 0}^{\infty } {\frac{{\left[ {\left( {Q - \varLambda + \varLambda z} \right)h} \right]\,^{r} }}{r!}} . \\ \end{aligned} $$
(19)

For \( m = 0 \) in Eq. (19), we have

$$ B_{0} = I + \sum\limits_{r = 1}^{\infty } {\frac{{\left[ {(Q - \varLambda )h} \right]\,^{r} }}{r!}} $$
(20)

where \( I \) is the identity matrix of designated dimension.

For \( w,n \ge 1 \), let \( G(n,w) \) be the coefficient of \( z^{w - 1} \) in \( \frac{{\left[ {(Q - \varLambda + \varLambda z)h} \right]\,^{n} }}{n!} \), nth term of the series on right hand side of Eq. (19). Then we have

$$ G(1,1) = \left[ {(Q - \varLambda )h} \right],\,G(1,2) = \left[ {(\varLambda )h} \right], \ldots ,\,G(n,1) = \frac{{\left[ {(Q - \varLambda )h} \right]\,^{n} }}{n!}, \ldots,$$

\( G(n,w) = 0 \), if \( w > n + 1 \), and

$$ G(n,1)\,{\kern 1pt} + \,G(n,2)z\, + \,G{\kern 1pt} (n,3)z^{2} \, + \, \cdots + G(n,w)z^{w - 1} \, + \cdots + G(n,n + 1)z^{n} \, = \sum\limits_{n = 0}^{\infty } {\frac{{\left[ {\left( {Q - \varLambda + \varLambda z} \right)h} \right]\,^{n} }}{n!}} . $$

Now, multiply on both sides of above equation by \( \left[ {\frac{(Q - \varLambda + \varLambda z)h}{n + 1}} \right] \), we obtain

$$ \begin{aligned} & G(n,1)\,{\kern 1pt} + \,G(n,2)z\, + \,G{\kern 1pt} (n,3)z^{2} \, + \, \cdots + G(n,w)z^{w - 1} \, + \cdots + G(n,n + 1)z^{n} \,\left[ {\frac{(Q - \varLambda + \varLambda z)h}{n + 1}} \right] \\ &\quad= \sum\limits_{n = 0}^{\infty } {\frac{{\left[ {\left( {Q - \varLambda + \varLambda z} \right)h} \right]^{n + 1} }}{(n + 1)!}} \\ &= G(n + 1,1)\,{\kern 1pt} + \,G(n + 1,2)z\, & + G{\kern 1pt} (n + 1,3)z^{2} \, + \, \cdots + G(n + 1,w)z^{w - 1} \, \\ & \quad + \cdots + G(n + 1,n + 2)z^{n + 1}. \\ \end{aligned} $$

In above equation, equating the coefficients of like powers of \( z \), we obtain,

$$\begin{aligned}G(n + 1,1) &= G(n,1)\left[ {\frac{(Q - \varLambda )h}{n + 1}} \right],\\ G(n + 1,2) &= G(n,2)\left[ {\frac{(Q - \varLambda )h}{n + 1}} \right] + G(n,1)\left[ {\frac{(\varLambda )h}{n + 1}} \right], \\ & \ldots,\\ G(n + 1,w) &= G(n,w)\left[ {\frac{(Q - \varLambda )h}{n + 1}} \right] + G(n,w - 1)\left[ {\frac{(\varLambda )h}{n + 1}} \right],\quad {\text{for}}\,w = 2,3,4, \ldots.\end{aligned}$$

Equating the coefficients of \( z^{n} \) in the Eq. (19), we get

$$ B_{m} = \sum\limits_{s = m}^{\infty } {G(s,m + 1)} ,\quad {\text{for}}\,s = 1,2,3, \ldots $$
(21)

The fundamental arrival rate of class \( k \) packets is \( \lambda^{(k)} = \pi (k)\varLambda (k)\,e \), where \( \pi (k) \) is the steady state probability vector of \( Q(k) \). The traffic intensity \( \rho = \left( {\lambda^{(1)} + \lambda^{(2)} } \right)\,h/c \). Let \( x = (x_{0} ,x_{1} , \ldots ,x_{K - c} ) \), where \( x_{q} = (x_{q,(1,1)} ,x_{q,(1,2)} , \ldots ,x_{{q,(m_{1} ,m_{2} )}} ) \), for \( q = 0,1, \ldots ,K - c \), when \( x_{q,(l,m)} \) is the conditional probability that there are \( q \) packets in the system given that embedded Markov chain is in the \( (l,m) \) state. Therefore, we have \( xP = x,\,\,\,xe = 1 \), where \( e \) is the column vector consisting of all 1. Then, in the steady state, high priority packet loss probability \( P^{hp} \) and low priority packet loss probability \( P^{lp} \), respectively, are derived as follows [6, 24]. Let \( PL^{hp} \) denote the number of high priority packets lost due to the fact that buffer is full. Then the expected value of \( PL^{hp} \)

$$ E[PL^{hp} ] = \sum\limits_{r = 0}^{c} {\sum\limits_{i = 1}^{\infty } {ix_{r} \left(B_{K - c + i}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } \right)e} } + \sum\limits_{r = c + 1}^{K - c} {\sum\limits_{i = 1}^{\infty } {ix_{r} \left(B_{K - r + i}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } \right)e} } $$
(22)

This is obtained by considering the last column of the \( (K - c + 1)\, \times \,(K - c + 1) \) block transition probability matrix \( P \) as that column consists of matrices containing conditional probabilities that the buffer is full. Then high priority packet loss probability \( P^{hp} \) is given by

$$ P\,^{hp} = \frac{{E[PL^{hp} ]}}{\lambda E[H(t)]} = \frac{1}{{\lambda^{(1)} h}}\left\{ \begin{aligned} &\sum\limits_{r = 0}^{c} {\sum\limits_{i = 1}^{\infty } {ix_{r} \left(B_{K - c + i}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} }\right)e} } \hfill \\ &+ \sum\limits_{r = c + 1}^{K - c} {\sum\limits_{i = 1}^{\infty } {ix_{r} \left(B_{K - r + i}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } \right)e} } \hfill \\ \end{aligned} \right\}, $$
(23)

where \( \lambda E[H(t)] \) is the number of packet arrivals during the mean service time. Let \( PL^{lp} \) denote the number of low priority packets lost due to the fact that buffer occupancy exceeds the threshold. Then expected value of \( PL^{lp} \)

$$ E[PL^{lp} ] = \left\{ \begin{array}{l} \sum\limits_{r = 0}^{c} {\left( {\sum\limits_{i = 1}^{\infty } {ix_{r} \left[ {\left( {\sum\limits_{j = 0}^{K - 2c - d + 1} {B_{j}^{(1)} \otimes B_{K - 2c - d + 1 - j + i}^{(2)} } } \right) + \left( {\sum\limits_{l = K - 2c - d + 2}^{\infty } {B_{l}^{(1)} } \otimes B_{i}^{(2)} } \right)} \right]e} } \right)} \hfill \\ + \sum\limits_{r = c + 1}^{K - c - d} {\left( {\sum\limits_{i = 1}^{\infty } {ix_{r} \left[ {\left( {\sum\limits_{j = 0}^{K - c - d + 1 - r} {B_{j}^{(1)} \otimes B_{K - c - d + 1 - r - j + i}^{(2)} } } \right) + \left( {\sum\limits_{l = K - c - d + 2 - r}^{\infty } {B_{l}^{(1)} } \otimes B_{i}^{(2)} } \right)} \right]e} } \right)} \hfill \\ + \sum\limits_{r = K - c - d + 1}^{K - c} {\sum\limits_{i = 1}^{\infty } {ix_{r} \left( {\sum\limits_{l = 0}^{\infty } {B_{l}^{(1)} \otimes B_{i}^{(2)} } } \right)e} } \hfill \\ \end{array} \right\} $$
(24)

This is obtained by considering the last \( (d + c) \) columns of the \( (K - c + 1)\, \times \,(K - c + 1) \) block transition probability matrix \( P \) as these columns consists of matrices containing conditional probabilities that the buffer occupancy is greater than or equal to threshold. The low priority packet loss probability \( P^{lp} \) is given by

$$ P\,^{lp} = \frac{{E[PL^{hp} ]}}{\lambda E[H(t)]} = \frac{1}{{\lambda^{(2)} h}}\left\{ \begin{array}{l} \sum\limits_{r = 0}^{c} {\left( {\sum\limits_{i = 1}^{\infty } {ix_{r} \left[ {\left( {\sum\limits_{j = 0}^{K - 2c - d + 1} {B_{j}^{(1)} \otimes B_{K - 2c - d + 1 - j + i}^{(2)} } } \right) + \left( {\sum\limits_{l = K - 2c - d + 2}^{\infty } {B_{l}^{(1)} } \otimes B_{i}^{(2)} } \right)} \right]e} } \right)} \hfill \\ + \sum\limits_{r = c + 1}^{K - c - d} {\left( {\sum\limits_{i = 1}^{\infty } {ix_{r} \left[ {\left( {\sum\limits_{j = 0}^{K - c - d + 1 - r} {B_{j}^{(1)} \otimes B_{K - c - d + 1 - r - j + i}^{(2)} } } \right) + \left( {\sum\limits_{l = K - c - d + 2 - r}^{\infty } {B_{l}^{(1)} } \otimes B_{i}^{(2)} } \right)} \right]e} } \right)} \hfill \\ + \sum\limits_{r = K - c - d + 1}^{K - c} {\sum\limits_{i = 1}^{\infty } {ix_{r} \left( {\sum\limits_{l = 0}^{\infty } {B_{l}^{(1)} \otimes B_{i}^{(2)} } } \right)e} } \hfill \\ \end{array} \right\} $$
(25)

In general, problem of computing performance measures such as packet loss probability is reduced to the problem of computing steady state probability vector of pertinent Markov system. The embedded Markov chain of buffer occupancy considered in the Sect. 3 consists of repeated states and boundary states. The steady state probability distribution for the repeating portion of the \( P \) satisfies geometric form. M. F. Neuts [14] has taken the advantage of this particular form and developed to solve for steady state probability distribution. This technique is called matrix-geometric method and this domain popularity known as matrix-geometric solutions. Taking the advantage of this matrix-geometric form, alternate and suitable methods are proposed [3, 12, 24]. In the paper [24], input process is assumed to be discrete batch Markovian arrival process (D–BMAP) and the pertinent queueing system is of single-server. Here we have extended it to multi-server queueing system with continuous input process. In view of threshold setting we decompose the state space \( U \) into two subsets:

$$ U_{nc} = \left\{ {\left( {b,(i,j)} \right)/0 \le b \le K - 2c - d,\,\,1 \le i \le m_{1} ,\,\,1 \le j \le m_{2} } \right\}, $$
(26)

and

$$ U_{c} = \left\{ {\left( {b,(i,j)} \right)/K - 2c - d + 1 \le b \le K - c,\,\,1 \le i \le m_{1} ,\,\,1 \le j \le m_{2} } \right\}. $$
(27)

This partition of \( U \) makes the transition probability matrix \( P \) decomposed as follows:

$$ P = \left[ {\begin{array}{*{20}c} {P_{nc} } & {P_{nc,c} } \\ {P_{c,nc}^{*} } & {P_{c} } \\ \end{array} } \right], $$
(28)

where

$$ P_{nc} = \left[ {\begin{array}{*{20}c} {B_{0} } & {B_{1} } & \cdots & {B_{K - 3c - d} } & {B_{K - 3c - d + 1} } & \cdots & {B_{K - 2c - d} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {B_{0} } & {B_{1} } & \cdots & {B_{K - 3c - d} } & {B_{K - 3c - d + 1} } & \cdots & {B_{K - 2c - d} } \\ 0 & {B_{0} } & \cdots & {B_{K - 3c - d - 1} } & {B_{K - 3c - d} } & \cdots & {B_{K - 2c - d - 1} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {B_{0} } & {B_{1} } & \cdots & {B_{c} } \\ \end{array} } \right], $$
(29)
$$ P_{c,nc}^{*} = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 & {B_{0} } & \cdots & {B_{c - 1} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & 0 & \cdots & {B_{0} } \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \end{array} } \right], $$
(30)
$$ P_{nc,c} = \left[ {\begin{array}{*{20}c} {C_{K - 2c - d + 1} } & {B_{K - 2c - d + 2}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{K - 2c}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{K - c - 1}^{(1)} \otimes B_{{}}^{(2)} } & {A(K - c)} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {C_{K - 2c - d + 1} } & {B_{K - 2c - d + 2}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{K - 2c}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{K - c - 1}^{(1)} \otimes B_{{}}^{(2)} } & {A(K - c)} \\ {C_{K - 2c - d} } & {B_{K - 2c - d + 1}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{K - 2c - 1}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{K - c - 2}^{(1)} \otimes B_{{}}^{(2)} } & {A(K - c - 1)} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {C_{c + 1} } & {B_{c + 2}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{c + d}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{2c + d - 1}^{(1)} \otimes B_{{}}^{(2)} } & {A(2c + d)} \\ \end{array} } \right], $$
(31)
$$ P_{c} = \left[ {\begin{array}{*{20}c} {C_{c} } & {B_{c + 1}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{c + d - 1}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{2c + d - 2}^{(1)} \otimes B_{{}}^{(2)} } & {A(2c + d - 1)} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {C_{1} } & {B_{2}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{d}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{c + d - 1}^{(1)} \otimes B_{{}}^{(2)} } & {A(c + d)} \\ {B_{0}^{(1)} \otimes B_{{}}^{(2)} } & {B_{1}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{d - 1}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{c + d - 2}^{(1)} \otimes B_{{}}^{(2)} } & {A(c + d - 1)} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {B_{0}^{(1)} \otimes B_{{}}^{(2)} } & \cdots & {B_{c - 1}^{(1)} \otimes B_{{}}^{(2)} } & {A(c)} \\ \end{array} } \right], $$
(32)

The sub-matrices \( P_{nc} \), \( P_{nc,c} \), \( P_{c,nc}^{*} \), and \( P_{c} \) are the left upper part, right upper part, left lower part, and right lower part of the matrix \( P \) with dimensions of \( (K - 2c - d + 1)m_{1} m_{2} \, \times \,(K - 2c - d + 1)m_{1} m_{2} \), \( (K - 2c - d + 1)m_{1} m_{2} \, \times \,(d + c)m_{1} m_{2} \), \( (d + c)m_{1} m_{2} \, \times \,(K - 2c - d + 1)m_{1} m_{2} \) and \( (d + c)m_{1} m_{2} \, \times \,(d + c)m_{1} m_{2} \), respectively. These sub-matrices govern the transitions from \( U_{nc} \) into itself, from \( U_{nc} \) into \( U_{c} \), from \( U_{c} \) into \( U_{nc} \) and from \( U_{c} \) into itself, respectively. Next, we derive the mean length of non-critical and critical periods that occur alternately. For non-critical period, the transition probability matrix (TPM) of the absorbing Markov chain that has transient states \( U_{nc} \) and absorbing state \( U_{c} \) is given by

$$ P^{nc} = \left[ {\begin{array}{*{20}c} {P_{nc} } & {P_{nc,c} } \\ 0 & I \\ \end{array} } \right]. $$
(33)

Similarly, in the case of critical period, the TPM of the absorbing Markov chain that has transient states \( U_{c} \) and absorbing states \( U_{nc} \) is given by

$$ P^{c} = \left[ {\begin{array}{*{20}c} I & 0 \\ {P_{c,nc} } & {P_{c} } \\ \end{array} } \right], $$
(34)

where \( P_{c,nc} \) is the last \( (cm_{1} m_{2} ) \) columns of the matrix \( P_{c,nc}^{*} \). This is followed from the fact that for a critical period it suffices to attain the buffer level \( K - 2c - d + 1 \) rather than all other below levels which is the starting point of non-critical period of each cycle except the first one. The absorbing probability vectors \( \alpha_{K - 2c - d} \) and \( \beta \) of the Markovian chain \( P^{nc} \) and \( P^{c} \) described in the paper [24] are given by,

$$ \alpha_{K - 2c - d} = \alpha_{K - 2c - d} \left( {S_{nc} P_{nc,c} [I - P_{c} ]^{ - 1} P_{c,nc} } \right),\quad \alpha_{K - 2c - d} e = 1 $$
(35)

and

$$ \beta = \beta \left( {[I - P_{c} ]^{ - 1} P_{c,nc} S_{nc} P_{nc,c} } \right),\quad\beta e = 1, $$
(36)

where \( S_{nc} \) be the sub-matrix of \( [I - P_{nc} ]^{ - 1} \) which consists of the last \( (cm_{1} m_{2} ) \) rows in \( [I - P_{nc} ]^{ - 1} \). That is, the matrices absorbing probability vectors \( \alpha_{K - 2c - d} \) and \( \beta \) are steady state probability vectors of \( S_{nc} P_{nc,c} [I - P_{c} ]^{ - 1} P_{c,nc} \) and \( [I - P_{c} ]^{ - 1} P_{c,nc} S_{nc} P_{nc,c} \), respectively. The average length of non-critical and critical periods are \( E[L_{nc} ] \) and \( E[L_{c} ] \), respectively, given by

$$ E[L_{nc} ] = \alpha_{K - 2c - d} S_{nc} e $$
(37)

and

$$ E[L_{c} ] = \beta {\kern 1pt} [I - P_{c} ]^{ - 1} e $$
(38)

The average total number of high priority packets lost during a critical period is \( E[PL^{hpc} ] \),

$$ E[PL^{hpc} ] = \alpha_{K - 2c - d} S_{nc} \left( {\sum\limits_{l = 1}^{\infty } {lP_{nc,c}^{hp} } (l)} \right)e + \beta {\kern 1pt} [I - P_{c} ]^{ - 1} \left( {\sum\limits_{l = 1}^{\infty } {lP_{c}^{hp} (l)} } \right)e $$
(39)

The average total number of low priority packets lost during a critical period is \( E[PL^{lpc} ] \),

$$ E[PL^{lpc} ] = \alpha_{K - 2c - d} S_{nc} \left( {\sum\limits_{l = 1}^{\infty } {lP_{nc,c}^{lp} } (l)} \right)e + \beta [I - P_{c} ]^{ - 1} \left( {\sum\limits_{l = 1}^{\infty } {lP_{c}^{lp} (l)} } \right)e $$
(40)

where \( P_{nc,c}^{hp} \) and \( P_{c}^{hp} P_{c}^{hp} \) are the high priority packet loss during a critical period and \( P_{nc,c}^{lp} P_{nc,c}^{lp} \) and \( P_{c}^{lp} \) are the low priority packet loss during a critical period, and are given below, for \( l > 0 \),

$$ P_{nc,c}^{hp} (l) = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{K - c + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{K - c + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{K - c - 1 + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{2c + d + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ \end{array} } \right], $$
(41)
$$ P_{c}^{hp} (l) = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{2c + d - 1 + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{c + d + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{c + d - 1 + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & \cdots & 0 & {B_{c + l}^{(1)} \otimes \sum\limits_{j = 0}^{\infty } {B_{j}^{(2)} } } \\ \end{array} } \right], $$
(42)
$$ P_{nc,c}^{lp} (l) = \left[ {\begin{array}{*{20}c} {\sum\limits_{i = 0}^{K - 2c - d + 1} {\left( {B_{i}^{(1)} \otimes B_{K - 2c - d + 1 - i + l}^{(2)} } \right)} } & {B_{K - 2c - d + 2}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{K - 2c}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{K - c - 1}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = K - c}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {\sum\limits_{i = 0}^{K - 2c - d + 1} {\left( {B_{i}^{(1)} \otimes B_{K - 2c - d + 1 - i + l}^{(2)} } \right)} } & {B_{K - 2c - d + 2}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{K - 2c}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{K - c - 1}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = K - c}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ {\sum\limits_{i = 0}^{K - 2c - d} {\left( {B_{i}^{(1)} \otimes B_{K - 2c - d - i + l}^{(2)} } \right)} } & {B_{K - 2c - d + 1}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{K - 2c - 1}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{K - c - 2}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = K - c - 1}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {\sum\limits_{i = 0}^{c + 1} {\left( {B_{i}^{(1)} \otimes B_{c + 1 - i + l}^{(2)} } \right)} } & {B_{c + 2}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{c + d}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{2c + d - 1}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = 2c + d}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ \end{array} } \right], $$
(43)
$$ P_{c}^{lp} (l) = \left[ {\begin{array}{*{20}c} {\sum\limits_{i = 0}^{c} {\left( {B_{i}^{(1)} \otimes B_{c - i + l}^{(2)} } \right)} } & {B_{c + 1}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{c + d - 1}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{2c + d - 2}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = 2c + d - 1}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {\sum\limits_{i = 0}^{1} {\left( {B_{i}^{(1)} \otimes B_{1 - i + l}^{(2)} } \right)} } & {B_{2}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{d}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{c + d - 1}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = c + d}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ {B_{0}^{(1)} \otimes B_{l}^{(2)} } & {B_{1}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{d - 1}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{c + d - 2}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = c + d - 1}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {B_{0}^{(1)} \otimes B_{l}^{(2)} } & \cdots & {B_{c - 1}^{(1)} \otimes B_{l}^{(2)} } & {\sum\limits_{i = c}^{\infty } {B_{i}^{(1)} \otimes B_{l}^{(2)} } } \\ \end{array} } \right], $$
(44)

The high priority packet loss probability \( P^{hp} \) and low priority packet loss probability \( P^{lp} \) are

$$ P^{hp} = \frac{1}{{\lambda^{(1)} h}}\left[ {\frac{{E[PL^{hpc} ]}}{{E[L_{nc} ] + E[L_{c} ]}}} \right], $$
(45)

and

$$ P^{lp} = \frac{1}{{\lambda^{(2)} h}}\left[ {\frac{{E[PL^{lpc} ]}}{{E[L_{nc} ] + E[L_{c} ]}}} \right] $$
(46)

Algorithm of this model is briefly given in “Appendix 1” section.

4 Numerical results

Using the Eqs. (37, 38, 45, 46), the steady state packet loss probabilities and mean length of non-critical and critical periods are computed [24]. The generalized variance based Markovian fitting method proposed in [22] is employed to emulate the self-similar traffic for both high priority and low priority packet traffic. The mean arrival rate (\( \lambda \)) and variance (\( \sigma^{2} \)) of the self-similar traffic is set to be 1 and 0.6, respectively [22], the interested time-scale range to emulate self-similarity is over \( [10^{2} ,10^{7} ] \), [6, 7]. The fitting parameters of resultant MMPP are given by the matrices placed in “Appendix 2” section. It is shown in the papers [2, 22] that in order to emulate self-similar traffic well, the minimum number of states of the resultant MMPPs must be greater than or equal to 16. That is, both \( m_{1} \) and \( m_{2} \) must be ≥16. So each class is here characterized by \( 16 \times 16 \) matrices. Such a high dimensional MMPP for both high priority and low priority traffic results in computational complexity. In order to reduce the computational complexity, we use approximate model [17], which is based on the papers [1, 8]. The resultant 16-state MMAP of low priority packets is approximated by a 2-state Markovian arrival process (MAP). By applying this approximated model, the computational complexity is reduced by \( 8^{3} = 512 \) times [4]. For the validation of proposed model, we compare analytic results with that of simulation results when the number of servers is 1. In this case, the system capacity (\( K \)) and traffic intensity (\( \rho \)) are set to be 15 and 0.8, respectively, then buffer depth of the router is 14. We also demonstrated three cases of the Hurst parameters; \( H = 0.7 \), \( H = 0.8 \) and \( H = 0.9 \). From Figs. 2, 3 and 4, depict the packet loss probability against threshold (\( d \)). Analytical results are compared with that of simulation results [5]. In [5], for simulation results, Fractional Brownian Traffic (FBT) is used as input process. The FBT is based on Fractional Brownian Motion (FBM) [15] and can be used as standard self-similar traffic. FBT is a Gaussian process with self-similar characteristics. The random midpoint displacement (RMD) algorithm [10] is used to generate FBT. We could observe that the analytical results and fractional Brownian traffic (FBT) simulation results [15] in the case of \( H = 0.7 \) and \( H = 0.8 \) are closer, and in the case of \( H = 0.9 \) there is some discrepancy. Next, we take multi-server queueing model \( {\text{MMPP/D/c/K}} \), the number of servers (\( c \)) is set to be 4, the system capacity (\( K \)) is set to be 20 then buffer depth of the router is 16 and two different traffic corresponding to the Hurst parameter values \( H = 0.7 \) and \( H = 0.8 \), and the results are presented in Figs. 5, 6, 7, 8, 9, 10 and 11. From Fig. 5, we observe that the high priority packet loss probability decrease and the low priority packet loss probability increase as the threshold increases. In order to find out the optimal level of the threshold, we illustrate a plot of high priority packet loss probabilities against the low priority ones at various \( d \) in Fig. 6. We could find out that the optimal level of the threshold is the one located nearest to the left lower corner of the plot, which is around \( b = 5 \). We also include the numerical results of the queueing systems \( M/D/4/20 \) without \( {\text{PBS}} \) and \( M/D/4/20 \) with \( {\text{PBS}} \) in the Figs. 7 and 8. That is, input process here is Poisson. From Figs. 7, 8 depict the variation of packet loss probability against traffic intensity and buffer capacity, respectively. From Fig. 7, it is clear that packet loss probability increase as traffic intensity increases. From Fig. 8, we observe that of high priority and low priority packet loss probabilities both decrease as the buffer capacity increases. From Fig. 9, we observe that the mean length of non-critical periods (ELNC) and critical periods (ELC) are decreases as the threshold increases. From Figs. 10 and 11, depict the variation of mean length at the optimum level of threshold against traffic intensity and buffer capacity, respectively. From Fig. 10, it is clear that the mean length of non-critical periods decrease and critical periods increases as traffic intensity increases. From Fig. 11, we observe that the mean length of non-critical and critical periods both increase as the buffer capacity increases.

Fig. 2
figure 2

Packet loss probabilities against threshold when K = 15, c = 1, rho = 0.8, and H = 0.7

Full size image
Fig. 3
figure 3

Packet loss probabilities against threshold when K = 15, c = 1, rho = 0.8, and H = 0.8

Full size image
Fig. 4
figure 4

Packet loss probabilities against threshold when K = 15, c = 1, rho = 0.8, and H = 0.9

Full size image
Fig. 5
figure 5

Packet loss probabilities against threshold when K = 20, c = 4, rho = 0.85, H = 0.7, and H = 0.8

Full size image
Fig. 6
figure 6

High priority packet loss probability against low priority packet loss probability when K = 20, c = 4, rho = 0.85, H = 0.7, and H = 0.8

Full size image
Fig. 7
figure 7

Packet loss probabilities against traffic intensity when d = 5, K = 20, c = 4, H = 0.7, and H = 0.8

Full size image
Fig. 8
figure 8

Packet loss probabilities against buffer capacity when d = 5, c = 4, rho = 0.85, H = 0.7, and H = 0.8

Full size image
Fig. 9
figure 9

Mean length of non-critical and critical periods against threshold when K = 20, c = 4, rho = 0.85, H = 0.7, and H = 0.8

Full size image
Fig. 10
figure 10

Mean length of non-critical and critical periods against traffic intensity when d = 5, K = 20, c = 4, H = 0.7, and H = 0.8

Full size image
Fig. 11
figure 11

Mean length of non-critical and critical periods against buffer capacity when d = 5, c = 4, rho = 0.85, H = 0.7, and H = 0.8

Full size image

5 Conclusion

Loss behavior of synchronous router employing PBS mechanism to provide differentiated services under Markovian modelled self-similar traffic input is investigated. The performance measures, namely, the steady state high priority and low priority packet loss probabilities, and average length of non-critical and critical periods, are computed and presented graphically. To reduce the computation complexity, the original high dimensional MMPP of the low priority packets is approximated by 2-state MAP. With this analysis, we can locate the optimal threshold position of buffer to obtain the greatest performance.