Keywords

1 Introduction

Cooperative communication is a new paradigm that draws from the ideas of using the broadcast nature of the wireless channels to make communicating nodes help each other. In [1], two cooperative protocols were proposed: amplify-and-forward and decode-and-forward (DF). In this paper, we consider the AF strategy, where the relays only need to transmit a scaled version of the signal received from the source, which significantly simplifies the implementation. The performance of cooperative AF relay networks has been widely studied in the literature, e.g. [2, 3].

Very recently, Bit-interleaved coded modulation [4], which is a bandwidth-efficient technique for fading channels, have been begun to be studied with cooperative techniques. The ref. [5] derived the asymptotic bit error rate (BER) bounds of the cooperative system with the serial concatenated BICM over Additive White Gaussian Noise (AWGN) channels and Rayleigh fading channels. Meanwhile, Babarossa [6] explored the application of space-time code [7] to cooperative diversity. In [8], the GABBA codes were employed to design a practical distributed space-time codes for wireless relay networks using the amplify-and-forward scheme. To obtain both space and time diversity, concatenated BICM and ST codes (BI-STC) is extensively used for the point to point transmission [9]. BI-STC can provide robust performance under wide variety of fading conditions [10]. However, the using of BI-STC in relay networks has not been investigated thoroughly in existing literatures.

In this paper, we consider the analysis and design of AF cooperative relaying BI-STC scheme (BI-STC-AF). Our main contribution can be described as follows. Firstly, we design the AF relay networks based on the BI-STC technique. Secondly, we derive a closed-form expression for of the bit error rate (BER) of the proposed cooperative diversity scheme, which is important to evaluate the system performance and can be used to develop guidelines for modulation constellation selection, space-time code design and relay selection, etc. Simulation results confirm the validity of the derived analytical results and show the effectiveness of the proposed scheme.

2 System Models

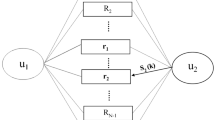
As is shown in Fig. 1, we consider a cooperative relaying scheme with one source, n relays and one destination. The channels between the source and the relay nodes, between the relays nodes and the destination, and the direct path are assumed to be Rayleigh flat fading and independent from each other. The channel coefficients are modeled as independent complex Gaussian random variables with zero mean and variances ρ 2 i,j  ( i ∈ {S,R}, j ∈ {R,D}). The additive noises are zero mean and have variance N 0.

Fig. 1
figure 1

A cooperative relaying network

Full size image

The information bit s is first encoded by a convolutional code of rate R c  = k c /n c . Then, the encoder output is bit-interleaved and each K = mq bits of the interleaved sequence are grouped as a channel symbol. The modulator maps each symbol to a complex-valued signal chosen from a 2m -ary constellation χ according to the labeling map μ with average symbol energy equal to E s . The space-time block encoder take the constellation signals to form an L × n ST codeword matrix X t  = [x i l ], where L is the number of the time slots for transmitting one ST codeword. x i l , 1 ≤ i ≤ n, 1 ≤ l ≤ L is the transmitted signal from the i th antenna at time l.

The source broadcasts the packet to all relays. The received signal at relays are given by

$$ {y}_{s,{r}_j}=\sqrt{P_1}{h_s}_{,{r}_j}{v}^p+{n}_{s,{r}_j}, $$
(1)

where j = 1, 2, ⋯, n, P 1 is the source transmit power and \( {n}_{s,{r}_j} \) is noise at the j th relay.

Upon receiving \( {y}_{s,{r}_j} \), each relay will normalize the received signal by the factor \( \beta \triangleq \sqrt{\left({P}_2/n\right)/\left({P}_1{\rho}_{s,r}^2+{N}_0\right)} \) to satisfy a long-term power constraint before forwarding it to the destination in phase 2 P 2 is the power of relays. The n × 1 received vector data vector from the relay nodes at the destination node can be modeled as

$$ {\mathbf{y}}_d=\beta {\mathbf{X}}_r\mathbf{H}+{\mathbf{n}}_d, $$
(2)

where \( \mathbf{H}={\left[{h}_{s,{r}_1}{h}_{r_1,d},\cdots, {h}_{s,{r}_n}{h}_{r_n,d}\right]}^T \) and X r  = [A 1 s, ⋯, A n s] plays the role of the Space-Time codeword. n d is the noise vector.

At the receiver of the destination, the STB decoders first apply the MAP decoding algorithm to decode the signals received from the different relays. After that, the LLR for the i th bit of the considered label is evaluated and are de-interleaved before being passed to the decoder.

3 BER Performance Analysis

Assuming ideal interleaving, the BICM union bound of the probability of bit error is given by [4]

$$ {p}_b\le \frac{1}{k_c}{\displaystyle \sum_{d={d}_f}^{\infty }{W}_I(d)f\Big(d,\mu },\chi \Big), $$
(3)

where d f is the minimum Hamming distance of the convolution code and W I (d) is the total input weight of error events at Hamming distance d. f(d,μ,χ) depends only on the Hamming distance d, the mapping rule μ, and the signal constellation χ.For BI-STC, the union bound of the f(d,μ,χ) can be upper-bounded using the Cherbnoff technique

$$ {f}_{ub}\left(d,\mu, \chi \right)\le {\left[\frac{1}{K{2}^K}{\displaystyle \sum_{k=1}^K{\displaystyle \sum_{b=0}^1{\displaystyle \sum_{X\in {\chi}_b^k}{\displaystyle \sum_{Z\in {\chi}_{\overline{b}}^k}\underset{s}{ \min }{\varPhi}_{\Delta \left(\mathbf{X},\mathbf{Z}\right)}(s)}}}}\right]}^d, $$
(4)

where X and Z are the transmitted and erroneously decoded signals, respectively. Φ Δ(X,Z)(s) is the Laplace transform of the pdf of the metric difference Δ(X,Z). To evaluate (4), the key is to evaluate \( \underset{s}{ \min }{\Phi}_{\Delta \left(\mathbf{X},\mathbf{Z}\right)}(s) \), which can be replaced by the PEP of space coding in a BI-STC system [11].

For simplicity, symmetry is assumed between all relays, i.e., \( {\rho}_{s,{r}_m}^2={\rho}_{s,r}^2 \), \( {\rho}_{r_m,d}^2={\rho}_{r,d}^2 \) for all m ∈ {1, ⋯,n}.

The conditional PEP for a certain channel realization can be given by

$$ P\left(\mathbf{X}\to \mathbf{Z}\Big|\mathbf{H}\right)=Q\left(\frac{\beta }{\sqrt{2}}\left\Vert \left(\mathbf{X}-\mathbf{Z}\right)\mathbf{H}\right\Vert \right). $$
(5)

Using the Craig expression, (5) can be written as

$$ P\left(\mathbf{X}\to \mathbf{Z}\mathbf{\Big|}\mathbf{H}\right)=\frac{1}{\pi }{\displaystyle {\int}_0^{\pi /2} \exp \left(-\frac{\beta^2{\left\Vert \left(\mathbf{X}-\mathbf{Z}\right)\mathbf{H}\right\Vert}^2}{4{ \sin}^2\theta}\right)} d\theta. $$
(6)

Defining a matrix Γ as Γ ≜ (X − Z)H(X − Z), a constant C as \( C\triangleq \frac{P_1{P}_2{\rho}_{s,r}^2}{4n{N}_0\left({P}_1{\rho}_{s,r}^2+{P}_2{\rho}_{r,d}^2+{N}_0\right)} \), where P 1 and P 2 are the power at source and relays, respectively. Defining another matrix Ω as \( \varOmega \triangleq C\varGamma diag\left({\left|{h}_{r_1,d}\right|}^2,\mathrm{L},{\left|{h}_{r_n,d}\right|}^2\right) \), by taking the expectation in (6) over the source-to-relay channel coefficients, we get

$$ \begin{array}{l}P\left(\mathbf{X}\to \mathbf{Z}\right)=\frac{1}{\pi }{\displaystyle {\int}_0^{\pi /2}{E}_{\left[{h}_{r_1,d},\mathrm{L},{h}_{r_n,d}\right]}\left[1/{\displaystyle \prod_{i=1}^n\left(1+\frac{\beta^2}{4{ \sin}^2\theta }{\lambda}_{\varOmega_i}\right)}\right]} d\theta \\ {}\kern1em \le \frac{1}{2}{E}_{\left[{h}_{r_1,d},\mathrm{L},{h}_{r_n,d}\right]}\left[1/{\displaystyle \prod_{i=1}^n\left(1+\frac{\beta^2}{4}{\lambda}_{\varOmega_i}\right)}\right]\simeq \frac{1}{2}{E}_{\left[{h}_{r_1,d},\mathrm{L},{h}_{r_n,d}\right]}\left[1/{\displaystyle \prod_{i=1}^n\frac{\beta^2}{4}{\lambda}_{\Omega_{\mathrm{i}}}}\right]\\ {}\kern0.9em =\frac{\beta^{2n}}{4^{n+{\scriptscriptstyle \frac{1}{2}}}}{E}_{\left[{h}_{r_1,d},\mathrm{L},{h}_{r_n,d}\right]}\left[1/{\displaystyle \prod_{i=1}^n{\lambda}_{\Omega_{\mathrm{i}}}}\right],\end{array} $$
(7)

where \( {\lambda}_{\varOmega_i} \) is the i th eigenvalue of matrix Ω. Since the determinant of a matrix is equal to the product of the matrix eigenvalues, and the determinant of the product of the multiplication of two matrices is equal to the product of the individual matrices’ determinants, we can write

$$ {\displaystyle \prod_{i=1}^n{\lambda}_{\varOmega_i}}={\displaystyle \prod_{i=1}^nC{\lambda}_i}{\displaystyle \prod_{i=1}^n{\left|{h}_{r_i,d}\right|}^2}, $$
(8)

where λ i is the i th eigenvalue of Γ. Averaging the expression in (8) over the exponential distribution of \( {\left|{h}_{r_i,d}\right|}^2 \) gives

$$ P\left(\mathbf{X}\to \mathbf{Z}\right)=\frac{\beta^{2n}{C}^{-n}}{4^{n+{\scriptscriptstyle \frac{1}{2}}}}\left(1/{\displaystyle \prod_{i=1}^n{\lambda}_i}\right){\displaystyle \sum_{i=0}^n\left(\begin{array}{l}n\\ {}i\end{array}\right){2^i}_2{F}_1\left(2n,2n+2+i;4n-1;{\scriptscriptstyle \frac{1}{2}}\right)}{\lambda}_i, $$
(9)

where 2 F 1(x) is the hyper geometric function. At high SNR, (9) can be written as

$$ P\left(\mathbf{X}\to \mathbf{Z}\right)\simeq \frac{1}{2}{\left(\frac{\alpha^2{\rho}_{s,r}^3}{\alpha {\rho}_{s,r}^2+\left(1-\alpha \right){\rho}_{r,d}^2}\right)}^{-n} SN{R}^{-n}\times \left(1/{\displaystyle \prod_{i=1}^n{\lambda}_i}\right){\displaystyle \sum_{i=0}^n\left(n,i\right){2^i}_2{F}_1\left(2n,2n+2+i;4n-1;{\scriptscriptstyle \frac{1}{2}}\right)}{\lambda}_i\triangleq \frac{1}{2}{\left({\alpha}_{AF}\right)}^{-n}g\left({\lambda}_i\right) SN{R}^{-n} $$
(10)

where we define the following expressions:

SNR ≜ P/N 0, and P ≜ P 1 + P 2 is the transmitted power per source symbol,

P 1 ≜ αP, α ∈ (0,1), \( \kern0.1em {\alpha}_{AF}\triangleq \frac{\alpha^2{\rho}_{s,r}^3}{\alpha {\rho}_{s,r}^2+\left(1-\alpha \right){\rho}_{r,d}^2} \) and

$$ g\left({\lambda}_i\right)\triangleq \left(1/{\displaystyle \prod_{i=1}^n{\lambda}_i}\right){\displaystyle \sum_{i=0}^n\left(\begin{array}{l}n\\ {}i\end{array}\right){2^i}_2{F}_1\left(2n,2n+2+i;4n-1;{\scriptscriptstyle \frac{1}{2}}\right)}{\lambda}_i $$

For computing briefness, (4) can be effectively expurgated to approach the “error-free feedback” performance as [12]

$$ {f}_{ef}\left(d,\mu, \chi \right)\le {\left[\frac{1}{K{2}^K}{\displaystyle \sum_{k=1}^K{\displaystyle \sum_{b=0}^1{\displaystyle \sum_{X\in {\chi}_b^k}\underset{s}{ \min }{\varPhi}_{\Delta \left(X,Z\right)}(s)}}}\right]}^d. $$
(11)

Placing (10) into (11) provides

$$ \begin{array}{l}{f}_{ef}\left(d,\mu, \chi \right)\le {\left[\frac{1}{K{2}^K}{\displaystyle \sum_{k=1}^K{\displaystyle \sum_{b=0}^1{\displaystyle \sum_{X\in {\chi}_b^k}\frac{1}{2}{\left({\alpha}_{AF}\right)}^{-n}g\left({\lambda}_i\right) SN{R}^{-n}}}}\right]}^d\\ {}\kern5.4em ={\left({\alpha}_{AF} SNR\right)}^{- nd}{\left[\frac{1}{K{2}^{K+1}}{\displaystyle \sum_{k=1}^K{\displaystyle \sum_{b=0}^1{\displaystyle \sum_{X\in {\chi}_b^k}g\left({\lambda}_i\right)}}}\right]}^d.\end{array} $$
(12)

By defining \( {d}_b^2\left(\chi, \mu, n\right)\triangleq {\left[\frac{1}{K{2}^{K+1}}{\displaystyle \sum_{k=1}^K{\displaystyle \sum_{b=0}^1{\displaystyle \sum_{X\in {\chi}_b^k}g\left({\lambda}_i\right)}}}\right]}^{-1/n} \), (12) can be rewritten as

$$ {f}_{ef}\left(d,\mu, \chi \right)\le {\left({\alpha}_{AF}{d}_b^2\left(\chi, \mu, n\right) SNR\right)}^{- nd}. $$
(13)

When only including the dominant error event associated with d f in (3), we get

$$ {p}_b\simeq \frac{1}{k_c}{W}_I\left({d}_f\right){f}_{ef}\left(d,\mu, \chi \right)=\frac{W_I\left({d}_f\right)}{k_c} SN{R}^{- nd}{\left[{\alpha}_{AF}{d}_b^2\left(\chi, \mu, n\right)\right]}^{- nd}. $$
(14)

From (10) (12) and (14), the BEP of AF cooperative relaying based on BI-STC systems can be calculated.

4 Simulation Results

In this section, we present simulation results to illustrate the performance of the proposed BI-ST-AF scheme and to support the analytical results in Sect. 3. In our numerical experimentations, we adopt the convolutional codes that are the best known rate 2/3 codes [13], the worst-case error event length is d = 6 and free distance d f  = 5. The bit interleaver is S-random with length of 6,144 and depth of 20. The modulation constellation is 16PSK with Gray labeling. Equation (3) are used to evaluate the LLRs at destinations. The space-time code is proposed by Alamouti [14]. All links are supposed to be independent, identically distributed Ryleigh fading with ρ 2 i,j  = 1.

Figure 2 depicts the BER against SNR with different number of relay nodes in the BI-STC-AF relay networks. The total power is equally allocated between the source and the relays, that is, α = 0.5. From the figure, one can see that the BER performances of BI-STC-AF scheme upgrades in terms of the number of relay nodes. It can also be seen that the improvement speed of BER performance comes down with the increasing number of relays nodes.

Fig. 2
figure 2

BER versus SNR of the proposed cooperative diversity scheme with different number of relay nodes

Full size image

The comparative curves of the BER performance versus mean SNR for BICM, BI-STC and BI-ST-AF are drawn in Fig. 3. As shown in this figure, the proposed BI-ST-AF scheme has better performance than the BICM and the BI-STC schemes in terms of BER. The reason that the proposed scheme outperforms BICM lies in that the concatenated BICM and STC is more robust in fading channel. When compared with BI-STC scheme, the cooperative relying system performs better due to the distributed relays mitigate interference among antennas in multiple-input-multiple-output schemes. It can be also seen from the figure that these two schemes have about the similar performance when SNR is high enough.

Fig. 3
figure 3

BER versus SNR of various schemes

Full size image

5 Conclusion

We have proposed an Amplify-and-Forward cooperative diversity scheme based on the concatenation of bit-interleaved coded modulation and space-time block codes technique. The bit error probability of the scheme depends on the SNR, the channel conditions and the modulation and codes parameters of the BICM system. Simulation results show that the proposed scheme outperforms BICM and BI-ST schemes in terms of BER. Optimal power allocation between the source and the relays remains a future problem.