Hybrid Control of a 3-D Structure by Using Semi-Active Dampers

Abstract

A base isolated three storey 3-D building is semi-actively controlled not to exceed the maximum allowable base displacement. Large displacements are likely to cause failure in the isolation system, and hence, failure in the superstructure is expected. If a base isolated structure is positioned next to a very long fault line, such as the North Anatolian Fault, the structure will mostly undergo far field type excitations. Near field effects will be seen less occasionally, but design considerations should be made to account for both types of excitations. In case of nearby seismic action, the isolated building should be smart enough to modify its isolation impedance to resist against large ground displacement and velocities. For this study, an isolated three storey building model together with four dampers, which are all placed at the base level, is considered. The dampers have controllable orifices (damping coefficients) and the magnitudes of these damping coefficients are assigned by using a linear quadratic regulator (LQR). During an earthquake excitation, the storey displacements and velocities are used as feedback in the calculation of the optimal control force that is producible by viscous dampers, at each time step. This force, however, is applied only at times when critical displacements and/or velocities occur. The performance of the set of controllers is presented via time simulations of the system for three recorded earthquakes. In addition, these records are time shifted five folds to see the effect of near field action. The results indicate that the control effectively reduces the maximum displacements of the isolation system, while maintaining a reasonable isolation to the superstructure.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

18.1 Introduction

Semi-active dampers are foolproof control devices being widely accepted in structural control. Dampers are utilized to absorb energy from the structure. Thus, the larger the damping, the less will be the relative velocity and displacement. The accelerations, however, will increase. For building-type structures, the only case with semi-active control via dampers is the case at which buildings are seismically isolated. The role of the dampers in this type of structures is to limit the displacement of the dampers so that they don’t rupture. The presence of a damper in parallel to a base isolation system obviously decreases the effectiveness of the structure’s earthquake isolation. Nevertheless, it will keep the elastomeric bearings from being driven into large displacements, thus securing the base isolation system.

Extensive research has been conducted to model and implement variable orifice dampers. Kurata et al. (1999) designed a full scale building that is controlled by semi-active dampers. The damper used in his design is capable of producing a 1,000 kN damping force, while only 70 W electric energy is consumed for this purpose. Wongprasert and Symans (2005) used variable-orifice fluid dampers to enhance the response of a base isolated 1:4 scale three storey frame model. They simulated the response of the system both with software and on an earthquake simulator. Aldemir and Bakioğlu (2000) designed a time varying controller for a damper in a single degree of freedom system. They showed that the maximum displacement of the controlled response is about 18 % less than the passive response. Çetin et al. (2009) worked on a six storey building that was to be controlled via a Magneto rheological damper at the floor level. Although the device is different from a variable orifice damper, the principle remains the same. They modeled the structure as a single degree of freedom system and designed a robust Hinf controller.

In this study, a set of linear quadratic regulator based controllers are designed for various damping levels in the isolated structure. These damping levels arise due to the orifice settings of the dampers. These various settings comprise the control which is smartly applied. An upper controller selects the controller that corresponds to the system with the set damping value, and decides if it should apply the optimum damping. This last phenomenon is crucial, because a maximum damping level would normally be the choice of the optimal control. Large damping in the base level, on the other hand, is not beneficial for the superstructure. Here, one needs to design for an acceptable maximum isolator displacement and inter-storey drift values. To overcome this economic balance problem an upper controller is designed and simulation results are presented.

18.2 Three Storey 3-D Building Model

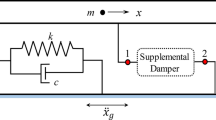
A three storey building model is considered for the control effectiveness evaluation. Elastomeric base isolators are used at the base and four dampers are connected to the two opposite corners of the building. Figure 18.1 shows the three dimensional view of this structure. A total number of four hydraulic dampers are connected in-between the structure base and the ground; two in the x-direction and two in the y-direction. The building is modeled by using 3-D steel beam elements (columns: 17.5 mm × 17.5 mm, beams: 90 mm × 90 mm × 5 mm). The storey heights are 80 cm, the structures cross sectional dimensions are 100 cm (x-dir) by 60 cm (y-dir). Each storey, including the base, has a total mass of 200 kg. The structure is constraint at the ground level and in the vertical direction. The remaining degrees of freedom (dof) except for the lateral dof at and above the damper connections are statically condensed, and finally a damping ratio of 0.006 is assigned to all modes. This number is based on the calculated damping ratios of a similar structure that exists in the IYTE Structural Mechanics Laboratory (Turan and Aydin 2010).

Fig. 18.1

3-D building model

The resulting system is a second order differential equation with 12 dof for the fixed base building, and 16 dof for the isolated building. Table 18.1 displays the major modes of vibration in which the fixed building has periods denoted by T0, and the periods with isolators are denoted by Ti. The first three modes of the building occur mostly in the base, which are the isolation modes. Modes 13 through 16 of the building have high frequencies that correspond to a skew deformation in the denoted storey level only. All modes are preserved in the simulation model, because the added dampers cause non-proportional damping.

Table 18.1 Vibration modes

The fixed building has a fundamental period of 0.67 s, which is indicated as a vertical line in Fig. 18.2. The figure shows the influence of the chosen earthquakes onto the building. In order to isolate the building from the effect of these earthquakes, the elastomeric bearing stiffness is appropriately chosen as 1,200 N/m (for comparison purposes, the columns have a stiffness of 36,600 N/m). Thus, the fundamental period of the isolated building is increased to 3.19 s. This change is beneficial for far field earthquakes as it can be seen on Fig. 18.2a. Here, the expected absolute acceleration of the isolated building is significantly reduced. For near field type earthquakes, on the other hand, Fig. 18.2b shows that the expected absolute acceleration may increase or decrease for various types of earthquakes as the fundamental structural period is increased. This unknown trend in the structural response shows the importance of an appropriate control mechanism.

Fig. 18.2

Earthquake spectra and the influence on the first vibration mode of the fixed and isolated buildings, respectively. (a) Original earthquakes. (b) Modified (generic) earthquakes to simulate near field seismic action

18.3 Semi-Active Damper

A hydraulic piston is modified by a pipe that interconnects the two chambers, and a stepper motor controlled valve is placed in series with this pipe. Figure 18.3 shows the modified piston.

Fig. 18.3

Cross section of the semi-active damper

The force exerted onto the damper is assumed to have a linear relation with the piston head’s velocity as shown in Eq. 18.1.

$$ {F_d}=-{c_d}{{\dot{x}}_d} $$

(18.1)

${F_d}$ is the damper force, ${{\dot{x}}_d}$ the damper velocity and ${c_d}$ the damping coefficient. The damper constant is evaluated to be in the range of 5,000–25,000 Ns/m. The upper limit is selected so that the piston’s capacity of 5,000 N is not exceeded, whereas the lower limit corresponds to the valve being completely open.

18.4 Control Design

A hybrid control method, namely Gain Scheduling, is utilized in this study. The isolated building model is constructed with each damper valve opening possibility. The damping constants of the four dampers are each varied by 5,000 Ns/m increments, resulting in 5 possible damping positions for each damper, and 625 damping positions for the structure with four dampers. Feedback gains are designed for each of these possible configurations by using the linear quadratic regulator (LQR) scheme. During an earthquake simulation, the required force is calculated, and the closest damping constants for all four devices are selected such that the dampers are able to produce the required control forces.

18.4.1 Linear Quadratic Regulator (LQR) Design

Equation 18.2 shows the differential equation of the isolated building with damping control forces and earthquake effect.

$$ M\ddot{x}+C\dot{x}+Kx=-M{\varGamma_{eq }}{{\ddot{x}}_g}+\varGamma {F_d} $$

(18.2)

Here, M, C, and K are the structural mass, damping and stiffness matrices, respectively, and x is the structural displacement with respect to the ground. ${{\ddot{x}}_g}$ is the ground acceleration, ${\varGamma_{eq }}$ is the ground acceleration application matrix, $\varGamma$ is the damper force application matrix, and ${F_d}$ is the damping force vector of the four dampers, which is constructed as follows

$$ {F_d}={{\left\{ {F_d^{(1) },F_d^{(2) },F_d^{(3) },F_d^{(4) }} \right\}}^T} $$

(18.3)

where $F_d^{(i) }$ is the i’th damper force. Since ${F_d}$ is a force vector of passive devices and is linearly related to the structural velocity, as indicated in Eq. 18.1, it can be moved to the left hand side of Eq. 18.2.

$$ M\ddot{x}+\left( {C+\varGamma {C_d}{\varGamma^T}} \right)\dot{x}+Kx=-M{\varGamma_{eq }}{{\ddot{x}}_g} $$

(18.4)

Equation 18.4 is transformed to a first order differential equation by introducing a variable transformation of $q={{\left\{ {x,\dot{x}} \right\}}^T}$, which is the system state.

$$ \dot{q}=Aq+{B_1}{{\ddot{x}}_g}+{B_2}u $$

(18.5)

Matrices A, ${B_1}$, and ${B_2}$ are defined below, and the variable u is the optimal control force vector to be evaluated.

$$ A=\left[ {\begin{array}{lll} 0 & I \\{-{M^{-1 }}K} & {-{M^{-1 }}\left( {C+\varGamma {C_d}{\varGamma^T}} \right)} \\\end{array}} \right],\;{B_1}=\left[ {\begin{array}{lll} 0 \\{{\varGamma_{eq }}} \\\end{array}} \right],\;{B_2}=\left[ {\begin{array}{lll} 0 \\{{M^{-1 }}\varGamma } \\\end{array}} \right] $$

(18.6)

The aim, is to design a controller so that the base displacements in the x and y directions are minimized. This is established by making use of the linear quadratic regulator formulation in which the cost function to be minimized is as follows

$$ {V_q}=\int\nolimits_0^{\infty } {{q^T}Qq+{u^T}Rudt} $$

(18.7)

where Q and R are positive semi definite weighting matrices. Q is arranged to be a diagonal matrix with values of unity corresponding to the base displacements and zero for all other states. The purpose of this setting is to make the base return to the zero state at times when the controller is active. The matrix R is taken as an identity matrix (same weights for all dampers) with a common multiplier of 1e-8. This common multiplier is the relative weight among the matrices Q and R. The optimal control effort that minimizes Eq. 18.7 requires that

$$ {u^o}=-{R^{-1 }}B_2^T\bar{P}{q^o}={K_c}{q^o} $$

(18.8)

where ${K_c}$ is the feedback gain matrix, ${q^o}$ and ${u^o}$ are the optimum results of the state and control force, respectively. $\bar{P}$ is the symmetric matrix that is the solution to the Riccati equation

$$ {A^T}\bar{P}+\bar{P}A+Q-\bar{P}{B_2}{R^{-1 }}B_2^T\bar{P}=0 $$

(18.9)

Equations 18.6, 18.7, 18.8 and 18.9 are evaluated for all 625 damping constant possibilities, resulting in 625 ${K_c}$ matrices. These matrices are stored as a hyper matrix (3 dimensional) and they are recalled during the simulation when needed.

18.4.2 Upper Controller (Gain Scheduling)

An upper controller is designed to switch between the 625 feedback control gains during earthquake simulations. At each time step, the optimal control force is calculated based on the feedback gain for the system with damping constants that are calculated in the previous step. The force that is required for the i’th device is divided by the i’th dampers velocity to obtain the optimum damping constant (see Eq. 18.1). Then the closest damping constant within [5,000–25,000 Ns/m at increments of 5,000] is selected for the next time step.

A passive device, as is the case for dampers, may only absorb energy from the system. That is why the damping force can only act in the opposite direction of its velocity. Hence, if the calculated optimum damping constant has a negative sign, the required force will not be producible. In this case, the damping constant will take its minimum value of 5,000 Ns/m. In addition a numerical precaution is taken to prevent a “divide by zero” error. During the calculation of the optimum damper constant, the smallest absolute damper velocity is limited to 1 mm/s. This does not have a detrimental effect to the structural response, since the worst case causes a force of 25 N only.

The upper controller also decides when the optimum control forces should be applied. The control should only take effect when the isolators are in danger; where “danger” in this study is defined as an isolator displacement of 15 mm or more. Once an isolator exceeds this value, the controller is activated until a minimum or maximum displacement instance is reached that is less than 15 mm. Figure 18.4 shows a schematic representation of the working principle of this upper controller.

Fig. 18.4

Schematic working principle of the upper controller

18.5 Simulations

Six different earthquakes are selected for the simulation of the hybrid controlled isolated 3-D building. The first three are the 19-05-1940 Imperial Valley (El Centro Station), 12-11-1999 Düzce (Bolu Station) and the 17-08-1999 Kocaeli (Sakarya Station) earthquake acceleration records (http://peer.berkeley.edu). The North-South and the East-West components of the earthquake records are applied to the x and y-directions of the structure, respectively. Unfortunately, the North-south component of the Sakarya Station is not available; therefore the East-West components of this earthquake are used in both directions. In order to obtain near fault seismic action, these three earthquake records are modified to obtain earthquakes with high period responses. This is done by simply extending the sampling period to fivefold of the original sampling time (dt = 0.01 s. → dt = 0.05 s). Thereafter, cubic spline interpolation is carried out to obtain data with dt = 0.01 s. The response characteristics of the earthquakes used in this study are presented in Table 18.2.

Table 18.2 Earthquake characteristics

The generated earthquake records in Table 18.2 have much larger velocity and displacement values due to the increased time step. The use of spline interpolation also introduced slightly larger maximum accelerations than the original data. This fact is expected from the numerical procedure and it can be neglected.

The simulations are carried out for the first 20 s of the first three, and the first 100 s of the last three earthquakes. The major response is seen in this time frame, and it also allows for more detail in the illustrations. A direct integration method for the solution of the equation of motion in Eq. 18.2 is used. Superposition of modal responses is not possible for systems with non-proportional damping, as is the case with the current structure with added dampers. The Newmark β method (by using the unconditionally stable average acceleration method) is used as the solver for all simulations in this study. The function that implements this ordinary differential equation (ODE) solver makes sure that the simulation time step is 20 times smaller than the smallest period of the structure. If this is not the case, it interpolates the excitation data for a smaller time step, and later outputs the response at a 0.01 s. In this work, the building type structure has a minimum period of 0.108 s. Thus, the simulation takes place at 0.108/20 = 0.0054 s.

Figures 18.5, 18.6, 18.7, 18.8, 18.9 and 18.10 show simulation responses of the isolated building subjected to the selected earthquake records (see Table 18.2) with the upper controller. Each figure shows three responses on a single plot together with a digital indicator at the bottom. The three plots are the responses of the isolated building with damping at minimum stage, damping at maximum stage, and optimally controlled damping by using the upper controller. The digital indicator at the bottom shows if the upper controller is activated or not. The plotted responses are in the x-direction (North-South) of the building. The y-directional responses have smaller amplitudes, and hence are not shown.

Fig. 18.5

El Centro simulation response. (a) Base displacement (node 3, x-dir.). (b) 1. Floor displacement (node 5, x-dir.)

Fig. 18.6

12KasBOL simulation response. (a) Base displacement (node 3, x-dir.). (b) 1. Floor displacement (node 5, x-dir.)

Fig. 18.7

17AguSKR simulation response. (a) Base displacement (node 3, x-dir.). (b) 1. Floor displacement (node 5, x-dir.)

Fig. 18.8

El Centro-DF simulation response. (a) Base displacement (node 3, x-dir.). (b) 1. Floor displacement (node 5, x-dir.)

Fig. 18.9

12KasBOL-DF simulation response. (a) Base displacement (node 3, x-dir.). (b) 1. Floor displacement (node 5, x-dir.)

Fig. 18.10

17AguSKR-DF simulation response. (a) Base displacement (node 3, x-dir.). (b) 1. Floor displacement (node 5, x-dir.)

It is expected that the controlled response of the semi-active seismically isolated building stays in between the responses of the isolated building with passive minimum and maximum damping levels. Figures 18.5a, 18.6, 18.7, 18.8, 18.9 and 18.10a show the base displacement response for the earthquakes under consideration in which the expected response behavior cannot be seen directly in these figures. The reason seems to arise from the over-damping effect, which hinders the base from returning to the origin at some instances. If these specific instances are neglected, the controlled response obeys the above mentioned rule. Figures 18.5b, 18.6, 18.7, 18.8, 18.9 and 18.10b show the first floor response of the controlled simulation and these are always in-between the lower and upper bounds of the pure minimum and pure maximum damping levels, as expected.

The major benefit of the control mechanism can be seen in the comparison of the far field with the near field earthquake responses. The maximum base displacement of the structure with minimum damping is below 0.05 m for the far field earthquakes according to Figs. 18.5a, 18.6 and 18.7a. These maximum values rise to about 0.25 m for the near field earthquakes (Figs. 18.8a, 18.9 and 18.10a). The controlled base displacement is affected much less. It is below 0.05 m for both near field and far field earthquakes.

In Figs. 18.5b, 18.6 and 18.7b the controlled first floor response approaches the minimum damping behavior, while in Figs. 18.8b, 18.9 and 18.10b, the controlled first floor response approaches the maximum damping behavior. In other words, the structure reaction is soft for far field type of ground excitations, and stiff for near field type of ground excitations. This behavior can also be verified by the fact that the upper controller is active for a much longer time period during the near field type earthquakes (see the red digital line at the bottom of these figures).

18.6 Conclusions

The aim of seismic isolation is to decrease the drift in the superstructure, and the aim of the present control design is to avoid damage in the isolators and hence the superstructure. From the superstructure’s point of view the case with minimum damping, or even further, no damping at the base level appears to be the most feasible control solution for far-field earthquake excitations. From the isolation system’s point of view, the highest damping case would be the preferred one since the base displacements will be small. On the contrary, in the case of near field earthquakes, the most feasible solution for both the isolators and the superstructure is to have large damping. A balance is established by using the upper controller. It can smoothly switch between minimum and maximum damping values and thereby reduce the structural response based on any given excitation type.

A damper with a fixed damping coefficient will not be able to achieve a similar performance as the presented control method. The best response in far field type earthquakes is established by minimum damping with an extra control force at some time instances; near field type earthquakes, on the other hand, appear to be best handled with a fixed base. Therefore, in either case a fixed valued damper will not suffice to produce a desirable structural response. At last, a smartly controlled semi-active damper is able to protect a seismically isolated building from both near and far field type earthquakes.